Subnetting is the practice of logically dividing a single large IPV4 subnet address network into multiple networks for better performance.
A Subnet Mask is used to denote the network size in the subnetting process. In networking, there are two types of broadly used addresses available in this world. They are the IPV4 address and the IPV6 address.
There are five classes available in the IPV4 address space. They are
- Class A
- Class B
- Class C
- Class D
- Class E
| No | Class Type | Range | Public or Private | Use and application |
|---|---|---|---|---|
| 1 | Class A | Public range is 1.0.0.0 to 127.0.0.0 and Private range is 10.0.0.0 to 10.255.255.255 | Public and Private | ISP Network |
| 2 | Class B | Public Range is 128.0.0.0 to 191.255.0.0, Private Range is 172.16.0.0 to 172.31.255.255 | Public and Private | Enterprise and Organization |
| 3 | Class C | Public Range is 192.0.0.0 to 223.255.255.0, Private Range is 192.168.0.0 to 192.168.255.255 | Public and Private | Local Area Network |
| 4 | Class D | Private Range is 224.0.0.0 to 239.255.255.255 | Private | Multicasting such as video streaming |
| 5 | Class E | Private Range is 240.0.0.0 to 255.255.255.255 | Private | Research and Development |
Why Use Subnetting?
Subnetting helps utilize network bandwidth more intelligently. Subnetting provides four benefits over the IPV4 subnet address.
- Network Security:
By subnetting the network, only the device that relies on the network will be able to communicate with another device within the network, achieving the goal of sending a message or data within the same network. - Network Congestion:
Without subnetting, the network would generate a lot of unnecessary traffic, resulting in network congestion. Subnetting is used to avoid this. - Multiple Broadcast Domain
All of the hosts on the network use the broadcast domain. We limit the broadcast domain used by the host by subnetting the network. As a result, security has been enhanced while latency has been reduced. - Organizational Structure
Subnetting is mostly used for segregating and structuring the organization’s purposes. For instance, one network is for production use and another for testing use, and so on.
How to Subnet?
IPV4 address comprises two Identifiers. They are Network identifiers and Host identifier.
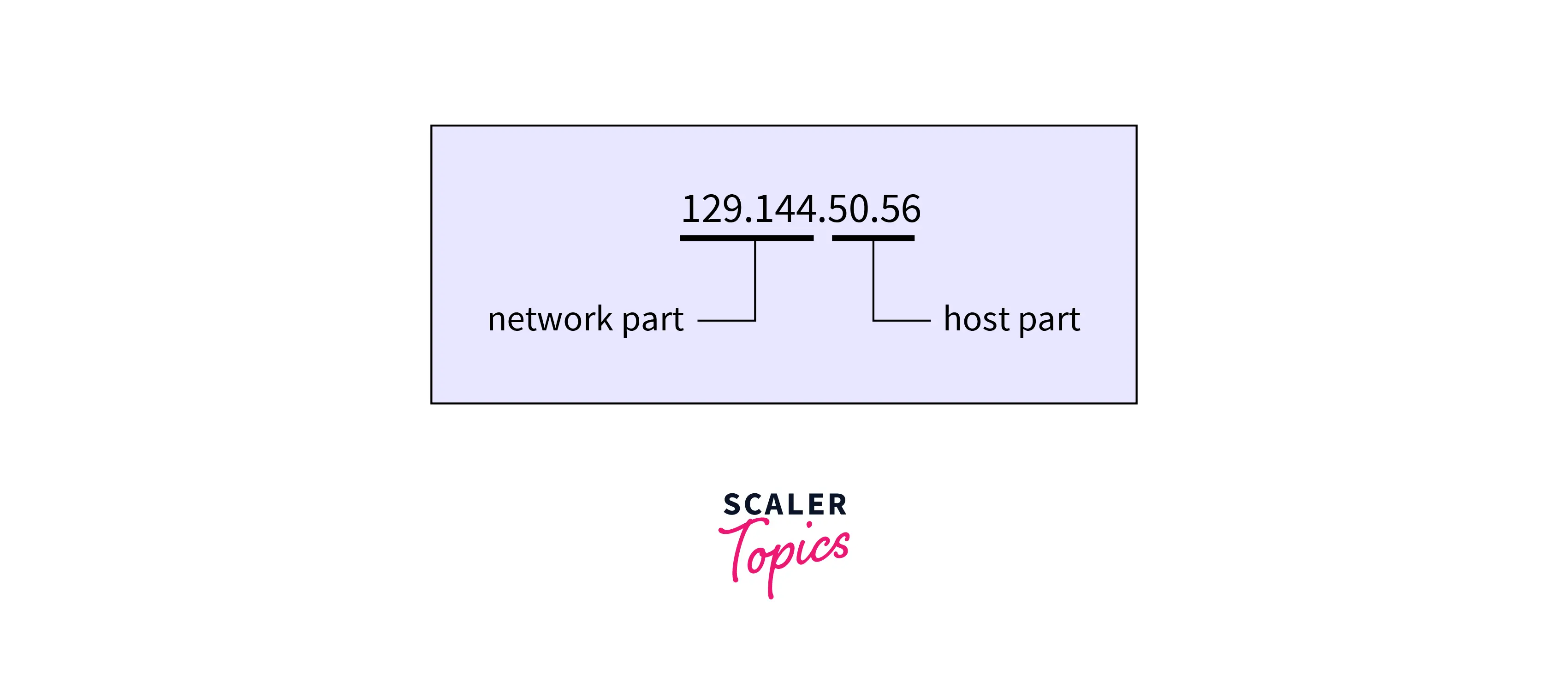
Instead of using the IPV4 subnet address range, we can use the concept of a subnet mask in the IPV4 subnet address.
For example
| Class Type | Subnet Mask | Network ID | Host ID | Example Network | Network ID | Host ID |
|---|---|---|---|---|---|---|
| Class A | 8 | First Octet | Second ,Third and Fourth Octet | 10.0.0.0/8 | 10 | 0.0.0 |
| Class B | 16 | First Octet and Second Octet | Third and Fourth Octet | 172.16.0.0/16 | 172.16 | 0.0 |
| Class C | 24 | First Octet, Second Octet, and Third Octet | Fourth Octet | 192.168.0.0/24 | 192.168.0 | 0 |
If the IPV4 address belongs to class A, we can mention it as an IPV4 subnet address divided by the subnet mask.
Class A Example
Class A range – 10.0.0.0 to 10.255.255.255
There are four octets in the class A address.
Here 10 is the Network ID, remaining octet represents the host identifier
It can be represented as 10.0.0.0/8.
Formula:- $2^{(32-n)}$
Where n is the subnet mask
Here for the network 10.0.0.0/8, n is 8
Available IP = $2^{32-8}$
= $2^{24}$
Available IP = 16777216
Class A Network 10.0.0.0/8 consists of a 16777216 IPV4 address.
Class B Example
Class B Network Range – 172.16.0.0 to 172.31.255.255
There are four octets in the class B address.
Out of 4 octets, the first and second octet comprises the network ID (172.16)
The third and fourth comprises the host ID.
First octet + second octet = 8+ 8 => 16
It can be represented as 172.16.0.0/16
Formula:- $2^{(32-n)}$
Where n is the subnet mask
Here for the network 172.16.0.0/16, n is 16
Available IP = $2^{(32-16)}$
= $2^{16}$
Available IP = 65536
Class B Network 172.16.0.0/16 consists of 65536 IPV4 addresses.
Class C Example
Class C Network Range – 192.168.0.0 to 192.168.255.255
There are four octets in the class C address. Out of 4, the first octet, second octet, and third octet comprise the network ID (192.168.0)
The fourth octet comprises the host ID
First octet + second octet + third octet = 8 + 8 + 8 => 24
It can be represented as 192.168.0.0/24
Formula:- $2^(32-n)$
Where n is the subnet mask
Here for the network 192.168.0.0/24, n is 24
Available IP = $2^{(32-24)}$
= $2^8$
Available IP = 256
Class C Network 192.168.0.0/24 consists of 256 IPV4 address.
How to Subset a Class C Address using the Binary Method?
Layer 4 Devices such as Routers see the IPV4 subnet address in binary format only. So they will convert the decimal representation of the IPV4 address into a binary version of the IPV4 address.
Ex- 110000.10101000.00000001.00101101
The binary method consists of one binary chart like this.
| 8th bit | 7th bit | 6th bit | 5th bit | 4th bit | 3th bit | 2th bit | 1th bit |
|---|---|---|---|---|---|---|---|
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
Class C address – 192.168.2.10
Now we are going to convert the below-mentioned Class C IPV4 address to bits using the binary method
192.168.2.10
We should work our way from left to right.
For number 192
We need to add the bit value as 1 for the allocated bit and o for the nonallocated bit.
For example, 192.168.2.10
In the below table, we can see that by adding the 8th bit 128 and the 7th bit 64, we can get 192.
| 8th bit | 7th bit | 6th bit | 5th bit | 4th bit | 3th bit | 2th bit | 1th bit |
|---|---|---|---|---|---|---|---|
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
8th bit is 128
7th bit is 64
128+64 = 192
The sum of the 8th and 7th bits is 192.
So put 1’s in the 8th bit and 7th bit. Put 0’s in the remaining bit.
And write it as 11000000.
The binary representation for the number 192 is 11000000.
Similarly, we need to do it for the remaining octets. 192.168.2.10
Take the second octet, 168
Here, by adding the 8th bit, 6th bit, and 4th bit, we can get 168
| 8th bit | 7th bit | 6th bit | 5th bit | 4th bit | 3th bit | 2th bit | 1th bit |
|---|---|---|---|---|---|---|---|
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
The 8th bit is 128.
6th bit is 32
4th bit is 8
128+32+8 = 168
The sum of the 8th, 6th, and 4th bits is 168
The binary representation of 168 is 10101000.
Take the third octet 2
Here, by putting 1 in the 2nd bit, we get 2.
| 8th bit | 7th bit | 6th bit | 5th bit | 4th bit | 3th bit | 2th bit | 1th bit |
|---|---|---|---|---|---|---|---|
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
2nd bit is 2
So the binary representation of 2 is 00000010.
Take the fourth and last octet 10
By adding the 4th bit and 2-bit value, we get 10
| 8th bit | 7th bit | 6th bit | 5th bit | 4th bit | 3th bit | 2th bit | 1th bit |
|---|---|---|---|---|---|---|---|
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
4th bit is 8
2nd bit is 2
The sum of the 4th and 2nd bits is 10.
The binary representation of the number 10 is 00001010.
192 is 11000000
168 is 10101000
2 is 00000010
10 is 00001010
Represented in binary format
192.168.2.10 = 11000000.10101000.00000010.00001010
How to Subset a Class C Address using the Fast Way?
The fast way is also known as the Decimal way
Example 1-
Class C address in binary format
11000000.10101000.00000101.00011001
The first octet is 11000000.
The second octet is 10101000.
The third octet is 00000101.
The fourth octet is 00011001.
**Formula **
The summation of the product of individual binary values and bit positional value.
First Octet
11000000
Put all the 1 and 0s as per the order in the below table format
| 8th bit | 7th bit | 6th bit | 5th bit | 4th bit | 3th bit | 2th bit | 1th bit |
|---|---|---|---|---|---|---|---|
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
The 8th-bit positional value is 1
The 8th-bit value is 128
The 7th-bit positional value is 1
The 7th-bit value is 64
From the 6th to the 1st bit, the positional value is 0. So we can ignore them
Summation of value = 1 * 128 + 1* 64 + 0*32+0*16+0*8+0*4 +0*2 +0*1 =128 + 64 = 192
The decimal value of 11000000 is 192.
Second octet
10101000
Put all the 1 and 0s as per the order in the below table format
| 8th bit | 7th bit | 6th bit | 5th bit | 4th bit | 3th bit | 2th bit | 1th bit |
|---|---|---|---|---|---|---|---|
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
The 8th-bit positional value is 1
The 8th-bit value is 128.
The 6th-bit positional value is 1
The 6th-bit value is 32.
The 4th-bit positional value is 1
The 4th-bit value is 8.
The 7th, 5th, 3rd, 2nd, and 1st-bit positional value is 0. So we can ignore them.
Summation of value = 1 * 128 + 0* 64 + 1*32+0*16+1*8+0*4 +0*2 +0*1
=128 + 32+ 8 = 168
The decimal value of 10101000 is 168.
Third octet
00000101
Put all the 1 and 0s as per the order in the below table format.
| 8th bit | 7th bit | 6th bit | 5th bit | 4th bit | 3th bit | 2th bit | 1th bit |
|---|---|---|---|---|---|---|---|
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
The 3rd-bit positional value is 1
The 3rd-bit value is 4.
The 1st-bit positional value is 1
The 1st-bit value is 1.
The 8th, 7th, 6th, 5th, 4th, and 2nd-bit positional value is 0. So we can ignore them.
Summation of value = 0 * 128 + 0 * 64 + 0*32+0*16+0*8+1*4 +0*2 +1*1 =4 + 1 = 5
The decimal value of 00000101 is 5.
Fourth octet
00011001
Put all the 1 and 0s as per the order in the below table format
| 8th bit | 7th bit | 6th bit | 5th bit | 4th bit | 3th bit | 2th bit | 1th bit |
|---|---|---|---|---|---|---|---|
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
The 5th-bit positional value is 1
The 5th-bit value is 16.
The 4th-bit positional value is 1
The 4th-bit value is 8.
The 1st-bit positional value is 1
The 5th-bit value is 1.
The 8th, 7th, 6th, 3rd, and 2nd-bit positional values are 0. So we can ignore them.
Value sum = 0 * 128 + 0 * 64 + 0 * 32+1*16+1*8+0*4 +0*2 +1*1 =16 + 8 + 1 = 25
The decimal value of 00011001 is 25.
11000000 is 192
10101000 is 168
00000101 is 5
00011001 is 25
The decimal representation of 11000000.10101000.00000101.00011001 is 192.168.5.25
Conclusion
- IPV4 subnet addresses are widely used in the world for all kinds of communication over a network.
- Subnetting provides flexibility toward traffic flow control and congestion control and security control over a network.
- The subnet mask is used to represent the subnetting process in a network.
- The router and switches use the decimal to binary conversion to understand the program.
- Layer 4 and above devices in OSI or TCP/IP architecture use binary-to-decimal conversion to represent the payload.