The Two Generals problem in TCP

The Two Generals’ Problem, also known as the Two Generals’ Paradox or the Two Generals’ Dilemma, is a thought experiment and a famous problem in computer science and distributed systems. While it is not particular to TCP (Transfer Control Protocol), it is a notion that pertains to the issues of reliable communication in distributed systems, including those that use TCP for data transmission.

In The Two Generals’ Problem , two generals, each leading their individual armies, are separated by an unfathomable distance and must coordinate a simultaneous attack on a shared target—an invincible stronghold. The essence of the problem is their inability to communicate directly because their signals must travel through an unreliable channel susceptible to delays and losses. This inherent unpredictability casts a pall on their coordinated assault plans.

The Story of the Two Generals’ Problem

In the Two Generals’ Problem, the scenario involves two generals, each leading their army, who are situated in separate locations and must coordinate an attack on a common enemy fortress. The only way to defeat the enemy is if first general soldiers and other general soldiers make a coordinated attack from opposite sides of the valley, and they must agree on the attack’s timing and strategy. However, there are several challenges:

1. Lack of Direct Communication: The generals are located at a distance from each other, making direct communication difficult. They can only exchange messages through messengers or some form of communication channel, which is not entirely reliable.
2. Uncertainty: There needs to be more certainty in message delivery times. Messages between the generals may be delayed or lost in transit, leading to a lack of synchronization in their attack plans.
3. Double Confirmation: The generals need a way to confirm that they have both agreed on the plan before initiating the attack. They must ensure that neither of them prematurely attacks the fortress while the other is not ready.

How is this Related to Computer Science and TCP?

Consider a scenario where two computer systems engage in communication. The central challenge in this context remains the presence of an unreliable communication channel and the potential for inconsistent states between the two machines. The TCP protocol is a frequently used example when discussing the Two Generals’ Problem.

As you may be aware, TCP employs a procedure known as the 4-way handshake (or 3-way handshake) to gracefully terminate a connection. In this process, one system wishing to end the connection sends a FIN (Finish) message, to which the opposing system responds with an ACK (Acknowledgment) and initiates its own FIN transmission. Finally, the initiating system acknowledges the termination by sending another ACK. This mechanism appears sound, but it reintroduces the familiar issue of shared knowledge between the two systems.

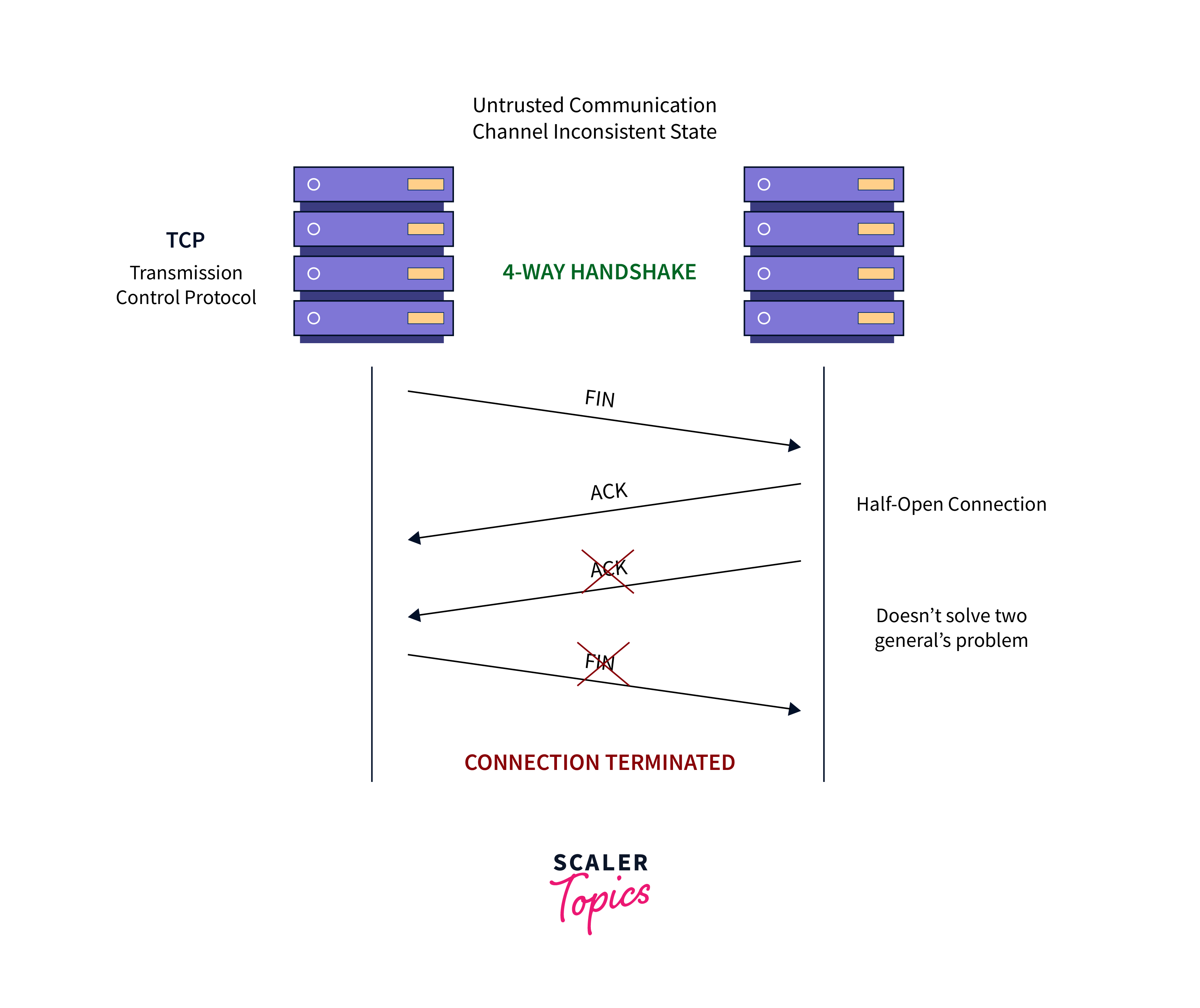
For example, when the second FIN message is lost in transit, it results in a situation called a half-open connection, where one side remains unaware of the closure. This highlights that, despite TCP’s overall reliability as a protocol, it does not resolve the Two Generals’ Problem due to the inherent uncertainty in communication channels.

Solution to Two Generals’ Problem

As one might anticipate, several attempts have been made to solve the intrinsically unsolvable Two Generals Problem, resulting in several practical alternatives. The key idea driving these approaches is to recognize the inherent uncertainty in the communication channel and identify effective strategies to handle it.

Let’s return to our generals and name them General A and General B, respectively.

• What if General A sends a group of 100 messengers instead of sending a single messenger, assuming that General B will receive at least one of them?
• Each message could be uniquely identified by a serial number ranging from 1 to 100. General B, by noting which numbers are missing in the sequence, could assess the reliability of the communication channel and respond with an appropriate number of confirmations.
• Although this approach may be resource-intensive due to the large number of messengers involved, it bolsters the generals’ confidence and facilitates consensus-building.

If the expense of sending numerous messengers is a concern, an alternative approach could be considered, where the absence of messengers enhances the generals’ confidence.

• In this scenario, let’s assume it takes 20 minutes for a messenger to traverse the valley, deliver a message, and return. General A initiates the process by dispatching messengers every 20 minutes until he receives a confirmation from General B.
• Upon receiving the confirmation, General A discontinues sending messengers. Meanwhile, after sending a messenger with confirmation, General B awaits the arrival of any additional messengers from General A.
• Interestingly, in this case, the absence of messengers from General A reinforces General B's confidence, aligning with their prior agreement.

Conclusion

• The Two Generals’ Problem, also known as the Two Generals’ Paradox or the Two Generals’ Dilemma, is a famous problem in computer science and distributed systems.
• In the Two Generals’ Problem, the scenario involves two generals, each leading their army, who are situated in separate locations and must coordinate an attack on a common enemy fortress.
• In the context of computer networks, the central challenge remains the presence of an unreliable communication channel and the potential for inconsistent states between the two machines.
• Despite TCP’s overall reliability as a protocol, it does not resolve the Two Generals’ Problem due to the inherent uncertainty in communication channels.
• One solution to The Two Generals’ Problem is instead of one messenger, General A sends 100 messengers, each with a unique serial number, to General B. General B gauges communication reliability by noting missing serial numbers and responds accordingly, enhancing confidence and consensus-building.
• Another solution to conserve resources is: General A sends messengers every 20 minutes until receiving confirmation from General B. General B, after confirming, waits for more messengers, enhancing confidence as agreed.