Level Order Traversal of Binary Tree

Level Order Traversal is a technique used to traverse a Tree where all nodes at the same level are visited entirely before moving to the next level.

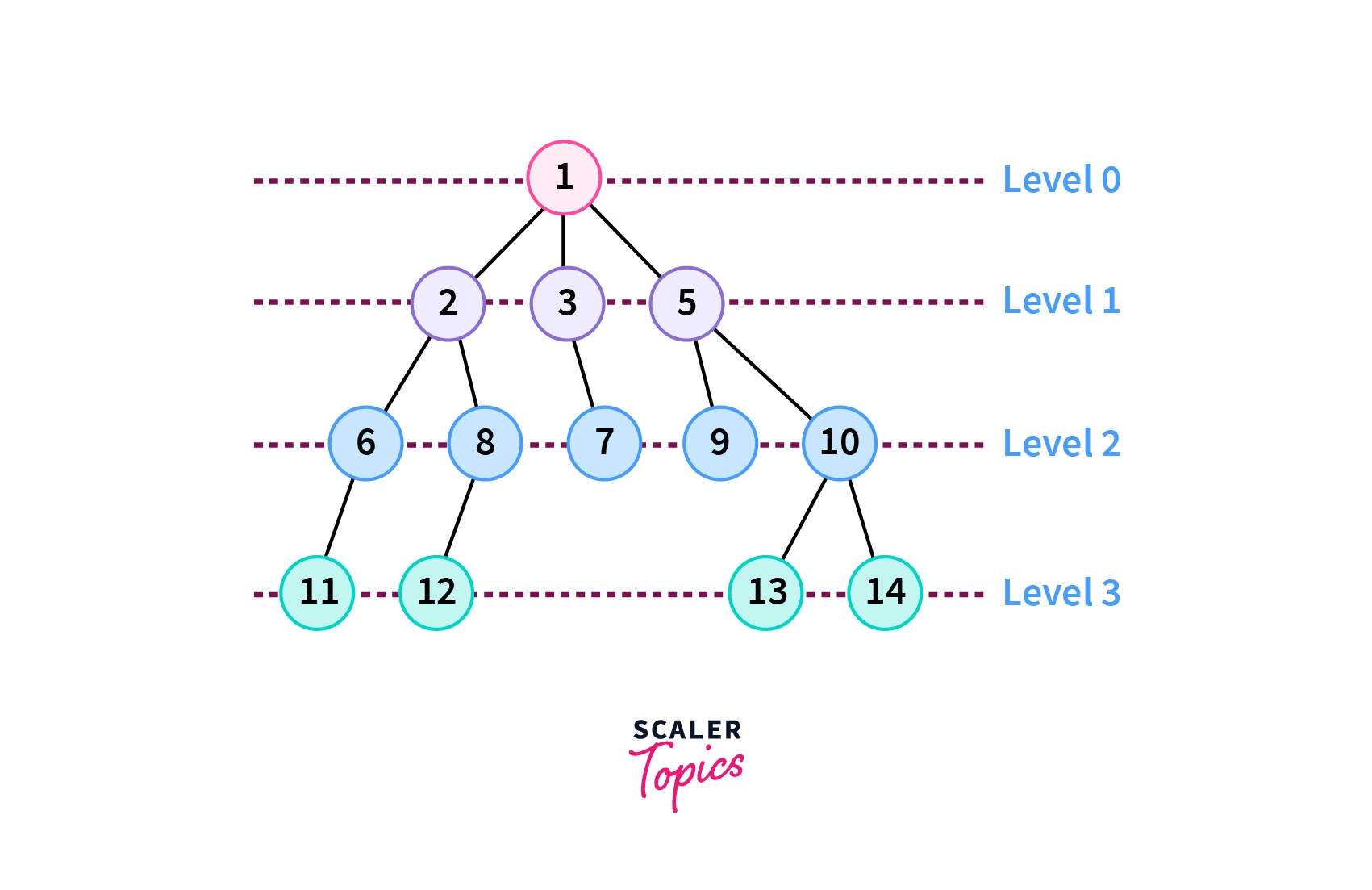
The level order traversal of this tree will be as follows:

1
2 3 5
6 8 7 9 10
11 12 13 14

Working of Level Order Traversal

Level order traversal involves visiting all nodes at a lower level before proceeding to any nodes at a higher level. This can be achieved through two main approaches:

1. Naive method: Determining the height of the tree and traversing each level sequentially, printing the nodes of each level.
2. Efficient method: Utilizing a queue data structure to traverse the tree level by level, ensuring nodes at the same level are visited before moving to the next level.

Level Order Traversal Using Recursion

1. Finding Tree Height: Initially, find the height of the tree using a recursive function or any suitable method. This provides the total number of levels in the tree.
2. Recursive Traversal with Level Tracking: Implement a recursive function that traverses the tree, maintaining the current height or level as a parameter.
3. Printing Nodes at Target Level: Within the recursive function, whenever the current level matches the target level for which nodes need to be printed, print the value of the node.
4. Recursion Termination: Ensure that the recursive function terminates appropriately when it reaches the end of the tree or the desired level.

Code Implementation in C++

#include <iostream>
using namespace std;

// A binary tree node has data,
// pointer to left child
// and a pointer to right child
class TreeNode {
public:
    int data;
    TreeNode* left, * right;
};

// Function prototypes
void printCurrentLevelNodes(TreeNode* root, int level);
int calculateTreeHeight(TreeNode* node);
TreeNode* createNewNode(int data);

// Function to print level order traversal of a tree
void performLevelOrderTraversal(TreeNode* root)
{
    // Base case: If the tree is empty
    if (root == NULL)
        return;

    // Get the height of the tree
    int height = calculateTreeHeight(root);

    // Iterate over each level
    for (int i = 1; i <= height; i++) {
        // Print nodes at the current level
        printCurrentLevelNodes(root, i);
    }
}

// Print nodes at a current level
void printCurrentLevelNodes(TreeNode* root, int level)
{
    if (root == NULL)
        return;
    if (level == 1)
        cout << root->data << " ";
    else if (level > 1) {
        printCurrentLevelNodes(root->left, level - 1);
        printCurrentLevelNodes(root->right, level - 1);
    }
}

// Determine the "height" of a tree, which represents the count of nodes  // on the path which is longest from the root node to the deepest leaf node.
int calculateTreeHeight(TreeNode* node)
{
    if (node == NULL)
        return 0;
    else {
        // Compute the height of each subtree
        int leftHeight = calculateTreeHeight(node->left);
        int rightHeight = calculateTreeHeight(node->right);

        // Use the larger one
        if (leftHeight > rightHeight) {
            return (leftHeight + 1);
        }
        else {
            return (rightHeight + 1);
        }
    }
}

// This function creates a new node with the specified data and initializes // its left and right pointers to NULL.
TreeNode* createNewNode(int data)
{
    TreeNode* newNode = new TreeNode();
    newNode->data = data;
    newNode->left = NULL;
    newNode->right = NULL;

    return newNode;
}

// Driver code
int main()
{
    // Create a binary tree
    TreeNode* root = createNewNode(1);
    root->left = createNewNode(2);
    root->right = createNewNode(3);
    root->left->left = createNewNode(4);
    root->left->right = createNewNode(5);

    // Get the level order traversal of the given tree
    cout << "Level Order traversal: ";
    performLevelOrderTraversal(root);

    return 0;
}

Code Implementation in Java

class TreeNode {
    int data;
    TreeNode left, right;

    public TreeNode(int data) {
        this.data = data;
        this.left = null;
        this.right = null;
    }
}

public class LevelOrderTraversal {

    // Function to print nodes at the current level
    static void printCurrentLevelNodes(TreeNode root, int level) {
        if (root == null)
            return;
        if (level == 1)
            System.out.print(root.data + " ");
        else if (level > 1) {
            printCurrentLevelNodes(root.left, level - 1);
            printCurrentLevelNodes(root.right, level - 1);
        }
    }

    // Function to find the height of the givtree
    static int calculateTreeHeight(TreeNode node) {
        if (node == null)
            return 0;
        else {
            // Find the height of the left and right subtrees
            int leftHeight = calculateTreeHeight(node.left);
            int rightHeight = calculateTreeHeight(node.right);

            // Return the maximum height
            return Math.max(leftHeight, rightHeight) + 1;
        }
    }

    // Function to have a level order traversal of the binary tree
    static void performLevelOrderTraversal(TreeNode root) {
        // Get the height of the tree
        int height = calculateTreeHeight(root);

        // Iterate over each level and print the nodes
        for (int i = 1; i <= height; i++) {
            printCurrentLevelNodes(root, i);
        }
    }

    // Driver code
    public static void main(String[] args) {
        // Create a binary tree
        TreeNode root = new TreeNode(1);
        root.left = new TreeNode(2);
        root.right = new TreeNode(3);
        root.left.left = new TreeNode(4);
        root.left.right = new TreeNode(5);

        // Get the  level order traversal of the given tree
        System.out.println("Level Order traversal: ");
        performLevelOrderTraversal(root);
    }
}

Code Implementation in Python

class TreeNode:
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None

# Function to print nodes at the current level
def printCurrentLevelNodes(root, level):
    if root is None:
        return
    if level == 1:
        print(root.data, end=" ")
    elif level > 1:
        printCurrentLevelNodes(root.left, level - 1)
        printCurrentLevelNodes(root.right, level - 1)

def calculateTreeHeight(node):
    if node is None:
        return 0
    else:
        # Calculate the height of the left and right subtrees
        leftHeight = calculateTreeHeight(node.left)
        rightHeight = calculateTreeHeight(node.right)

        # Return the maximum height
        return max(leftHeight, rightHeight) + 1

# Function to find level order traversal of the binary tree
def performLevelOrderTraversal(root):
    # Get the height of the tree
    height = calculateTreeHeight(root)

    # Iterate over each level and print the nodes
    for i in range(1, height + 1):
        printCurrentLevelNodes(root, i)

# Driver code
if __name__ == "__main__":
    # Create a binary tree
    root = TreeNode(1)
    root.left = TreeNode(2)
    root.right = TreeNode(3)
    root.left.left = TreeNode(4)
    root.left.right = TreeNode(5)

    # Get the level order traversal of the given tree
    print("Level Order traversal: ")
    performLevelOrderTraversal(root)

Output:

Level Order traversal: 1 2 3 4 5 

Complexity Analysis

Time Complexity:

The level order traversal algorithm has a time complexity of O(N), where N denotes the count of total number of nodes in the skewed tree.

Space Complexity:

As for space complexity, it’s O(1) if we only consider the variables used within the function. However, if we consider the recursion stack, then it can be O(N) in the worst case, particularly for skewed trees.

Level Order Traversal Using Queue

Level order traversal follows the principle of visiting nodes in lower levels before higher ones, similar to a queue. Nodes of lower levels are enqueued first, and when visiting a node, it’s dequeued and its children are enqueued. This guarantees traversal from lower to higher levels orderly.

Code Implementation in C++

#include <iostream>
#include <queue>

using namespace std;

struct Node {
    int data;
    Node* left;
    Node* right;
};

Node* createNode(int data) {
    Node* newNode = new Node();
    if (!newNode) {
        cout << "Memory error\n";
        return nullptr;
    }
    newNode->data = data;
    newNode->left = newNode->right = nullptr;
    return newNode;
}

void levelOrderTraversal(Node* root) {
    if (root == nullptr)
        return;

    queue<Node*> q;
    q.push(root);

    while (!q.empty()) {
        Node* current = q.front();
        q.pop();

        cout << current->data << " ";

        if (current->left)
            q.push(current->left);
        if (current->right)
            q.push(current->right);
    }
}

int main() {
    // Create a binary tree
    Node* root = createNode(1);
    root->left = createNode(2);
    root->right = createNode(3);
    root->left->left = createNode(4);
    root->left->right = createNode(5);
    root->right->left = createNode(6);
    root->right->right = createNode(7);

    // Perform level order traversal
    cout << "Level Order Traversal: ";
    levelOrderTraversal(root);

    return 0;
}

Code Implementation in Java

import java.util.LinkedList;
import java.util.Queue;

class Node {
    int data;
    Node left, right;

    public Node(int item) {
        data = item;
        left = right = null;
    }
}

public class LevelOrderTraversal {
    Node root;

    void levelOrderTraversal() {
        if (root == null)
            return;

        Queue<Node> queue = new LinkedList<>();
        queue.add(root);

        while (!queue.isEmpty()) {
            Node current = queue.poll();
            System.out.print(current.data + " ");

            if (current.left != null)
                queue.add(current.left);
            if (current.right != null)
                queue.add(current.right);
        }
    }

    public static void main(String args[]) {
        LevelOrderTraversal tree = new LevelOrderTraversal();
        tree.root = new Node(1);
        tree.root.left = new Node(2);
        tree.root.right = new Node(3);
        tree.root.left.left = new Node(4);
        tree.root.left.right = new Node(5);
        tree.root.right.left = new Node(6);
        tree.root.right.right = new Node(7);

        System.out.print("Level Order Traversal: ");
        tree.levelOrderTraversal();
    }
}

Code Implementation in Python

class Node:
    def __init__(self, key):
        self.data = key
        self.left = None
        self.right = None

def levelOrderTraversal(root):
    if root is None:
        return

    queue = []
    queue.append(root)

    while queue:
        current = queue.pop(0)
        print(current.data, end=" ")

        if current.left:
            queue.append(current.left)
        if current.right:
            queue.append(current.right)

# Create a binary tree
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(6)
root.right.right = Node(7)

# Perform level order traversal
print("Level Order Traversal:", end=" ")
levelOrderTraversal(root)

Output:

Level Order Traversal: 1 2 3 4 5 6 7

Complexity Analysis

Time Complexity:

The algorithm’s time complexity is O(N), where N denotes the number of nodes present in the binary tree.

Space Complexity:

The space complexity is O(N) due to the queue used for level order traversal, which can hold up to N nodes at its maximum capacity.

Conclusion

1. Level Order Traversal: It’s a technique to traverse a tree where all nodes at the same level are visited before moving to the next level.
2. Working Principle: Nodes at lower levels are visited entirely before proceeding to any nodes at higher levels.
3. Two Approaches: It can be implemented using either a naive method or an efficient method utilizing a queue.
4. Naive Method: Involves determining the height of the tree and sequentially traversing each level, printing the nodes of each level.
5. Efficient Method: Utilizes a queue data structure to traverse the tree level by level, ensuring nodes at the same level are visited before moving to the next level.