Red-Black Trees are balanced binary search trees where nodes are colored red or black. This color scheme ensures O(log n) time complexity for search, insert, and delete operations. They self-balance, adapting to changes, making them efficient for managing large datasets. Simple rules govern their structure, ensuring fast searching, sorting, and data management.
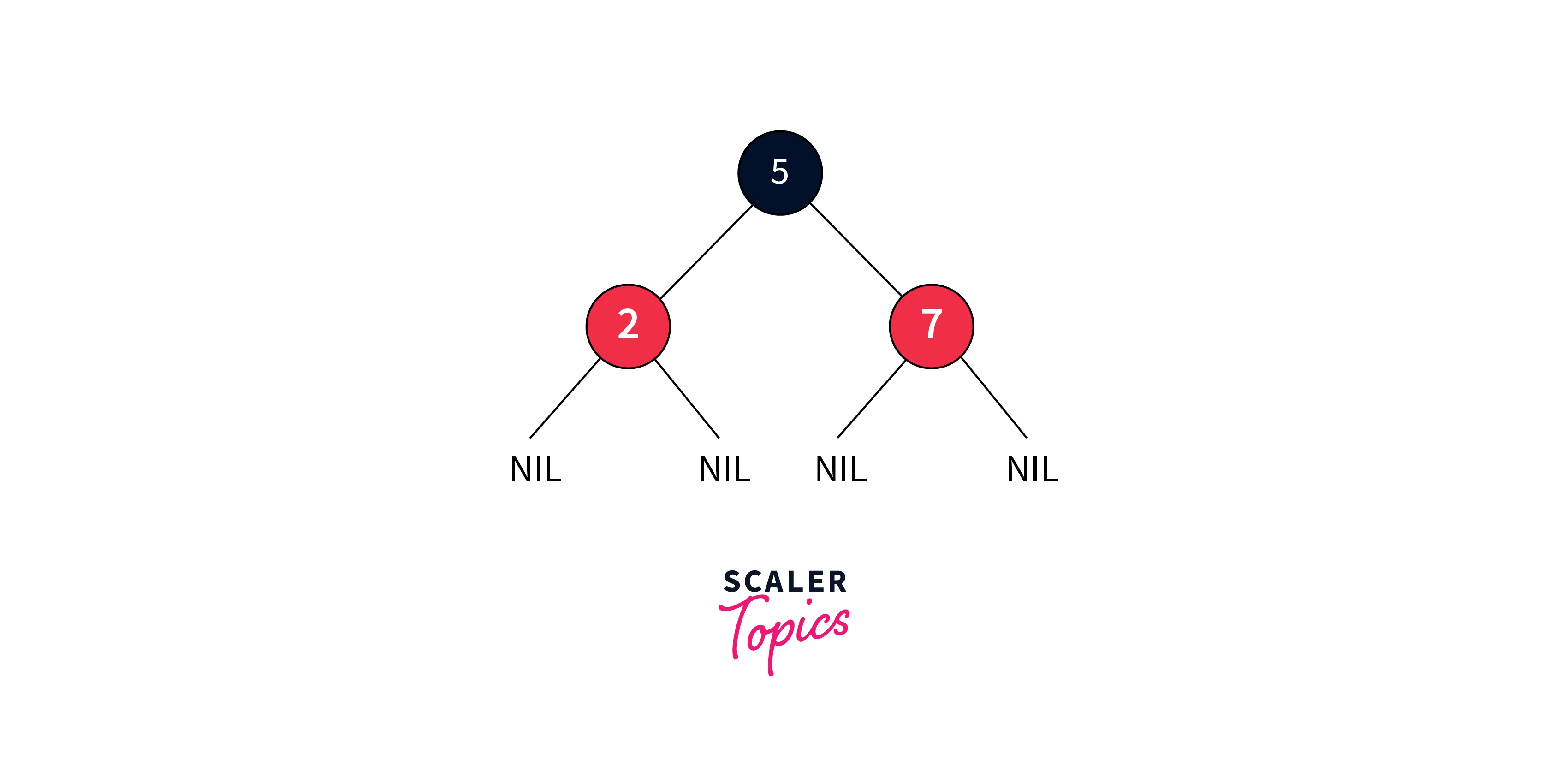
Properties of Red Black Tree
In addition to the standard properties of a binary search tree, Red-Black Trees have specific rules:
- Internal Property: If a node is red, its parent must be black.
- Depth Property: All leaves have the same depth of black nodes.
- Path Property: Equal black node count along root-to-leaf paths.
- Root Property: The top node is always black.
- External Property: All leaf nodes are black.
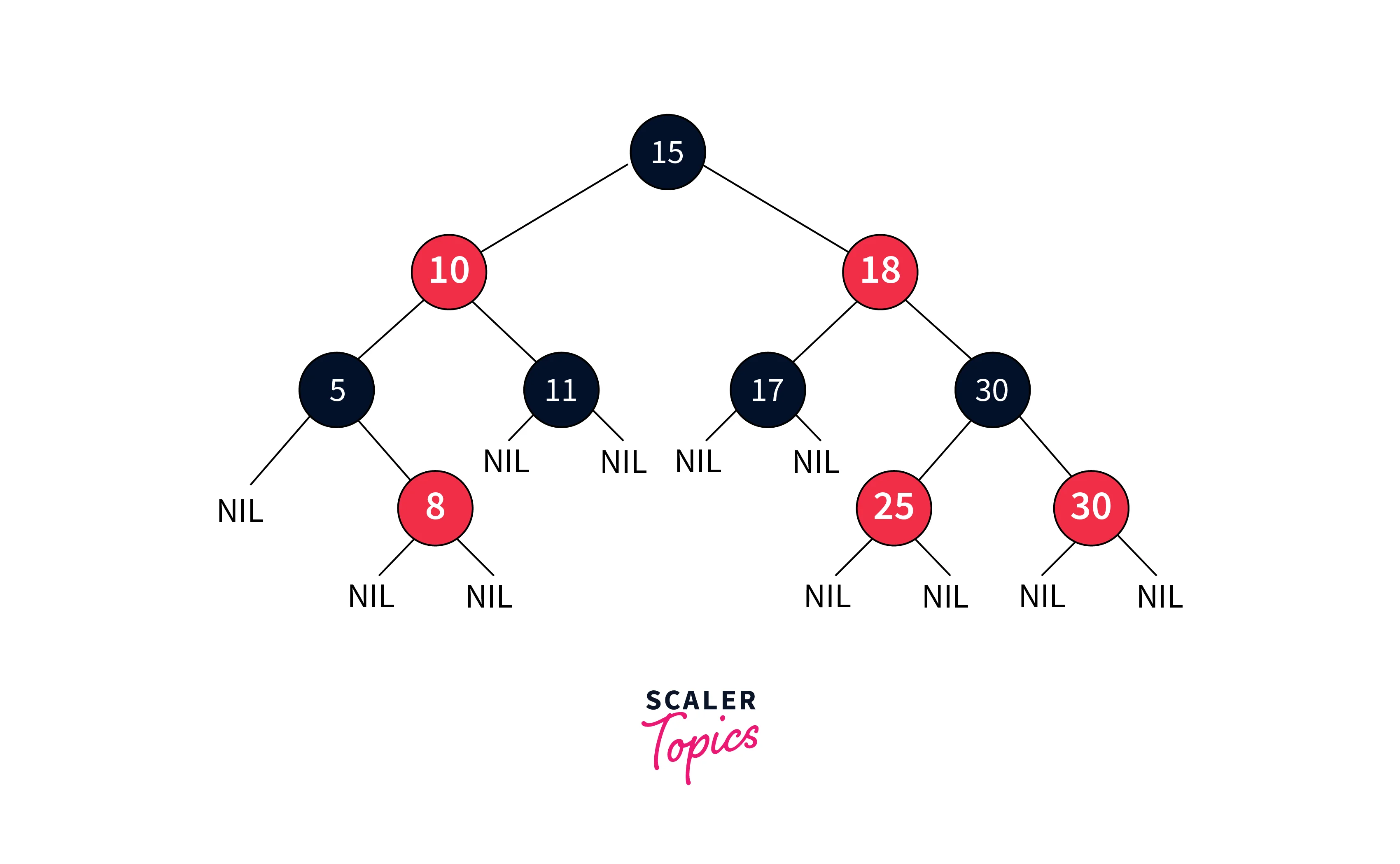
Rules That Every Red-Black Tree Follows
- Coloring Rule: Each node is either red or black.
- Root Rule: The root node is black.
- Red Constraint: No parent-child pair can have both nodes red.
- Uniform Black Depth: Every path from a node to its descendant leaves has the same count of black nodes.
- Leaf Color: All leaf nodes are black.
Why Red-Black Trees?
In binary search trees (BSTs), operations like search, insertion, and deletion usually have a time complexity of O(h), height-dependent. Red-Black Trees ensure O(log n) time complexity for all operations, maintaining efficiency regardless of initial shape. Their self-adjusting mechanism prevents skewing, providing stable performance suitable for tasks needing fast search, insertions, and deletions, making them versatile for diverse applications.
The time complexity for Search, Insert and Delete operations in Red-Black Tree is O(logn).
Comparison With AVL Tree
AVL trees prioritize balance but can undergo more rotations during changes, impacting performance. Red-Black Trees are preferred for frequent data changes due to efficient self-balancing, reducing rotation overhead. AVL suits less dynamic data with frequent searches, while Red-Black Trees prioritize efficiency over strict balance, ideal for frequent insertions and deletions.
Operations of Red-Black Trees
Red-Black Trees support below fundamental operations:
- Insertion: Adding new elements while maintaining balance.
- Deletion: Removing elements while preserving tree properties.
- Search: Finding elements efficiently within the tree.
Insertion in Red-Black Tree
Following are the steps to insert a node in the red-black tree:
- Check if the tree is empty: If it is, make the new element the root and color it black.
- If the tree isn’t empty:
- Create a new node and color it red.
- Check if the new node’s parent is black; if so, we’re done.
- If the parent is red:
- Check the color of the parent’s sibling.
- If the sibling is black or doesn’t exist, perform a rotation and adjust colors.
- If the sibling is red, recolor the parent, sibling, and grandparent nodes (unless the grandparent is the root, then just recolor parent and sibling).
This process ensures the Red-Black Tree remains balanced and maintains its properties.
Example:
Constructing an R-B tree for the first 8 integers to understand the whole process:
Insert 2:
When you add the very first piece of data to an empty Red-Black Tree, that data becomes the root, and it’s automatically marked as black.

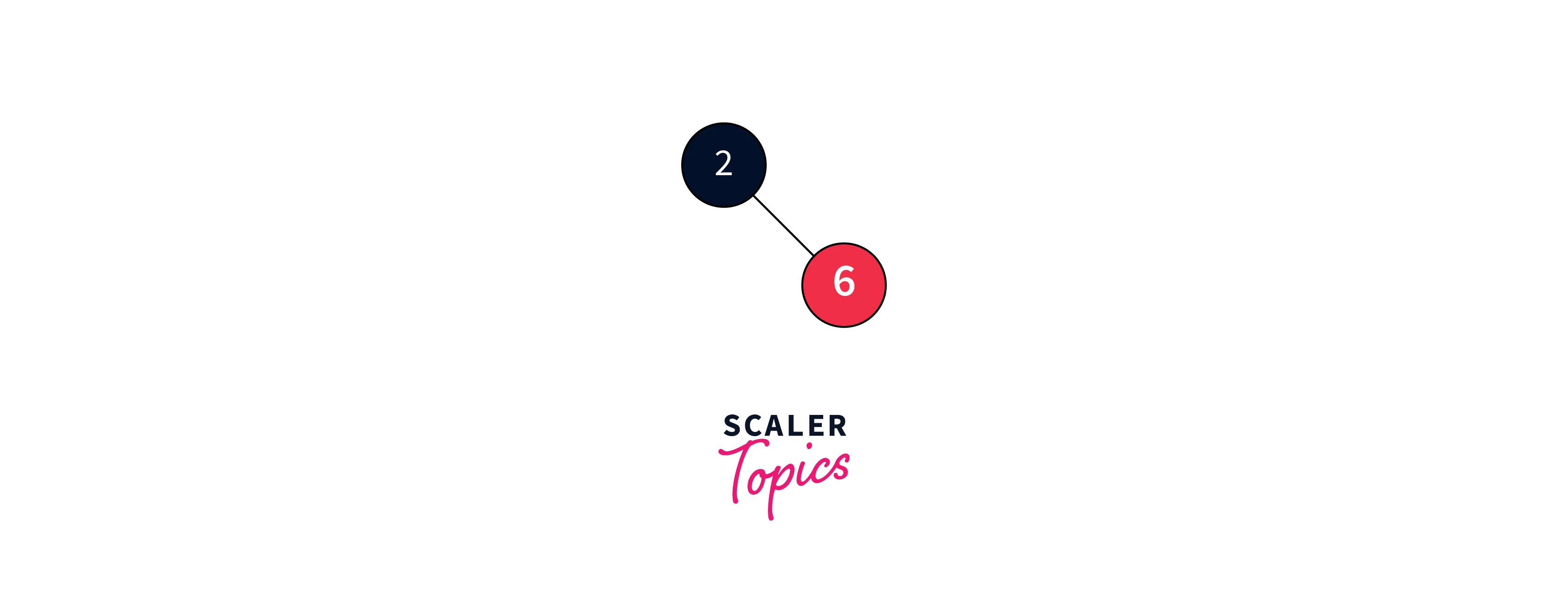
Insert 6:
As the tree already contains nodes, we add a new node with the next integer, coloring it red. This addition ensures that both the binary search tree and Red-Black Tree properties are maintained. We proceed with adding more nodes without violating these rules.
Insert 11:
Since the tree isn’t empty, we add a new node with the next integer, coloring it red. However, the parent of the new node isn’t black, which violates the rules of both the binary search tree and Red-Black Tree.
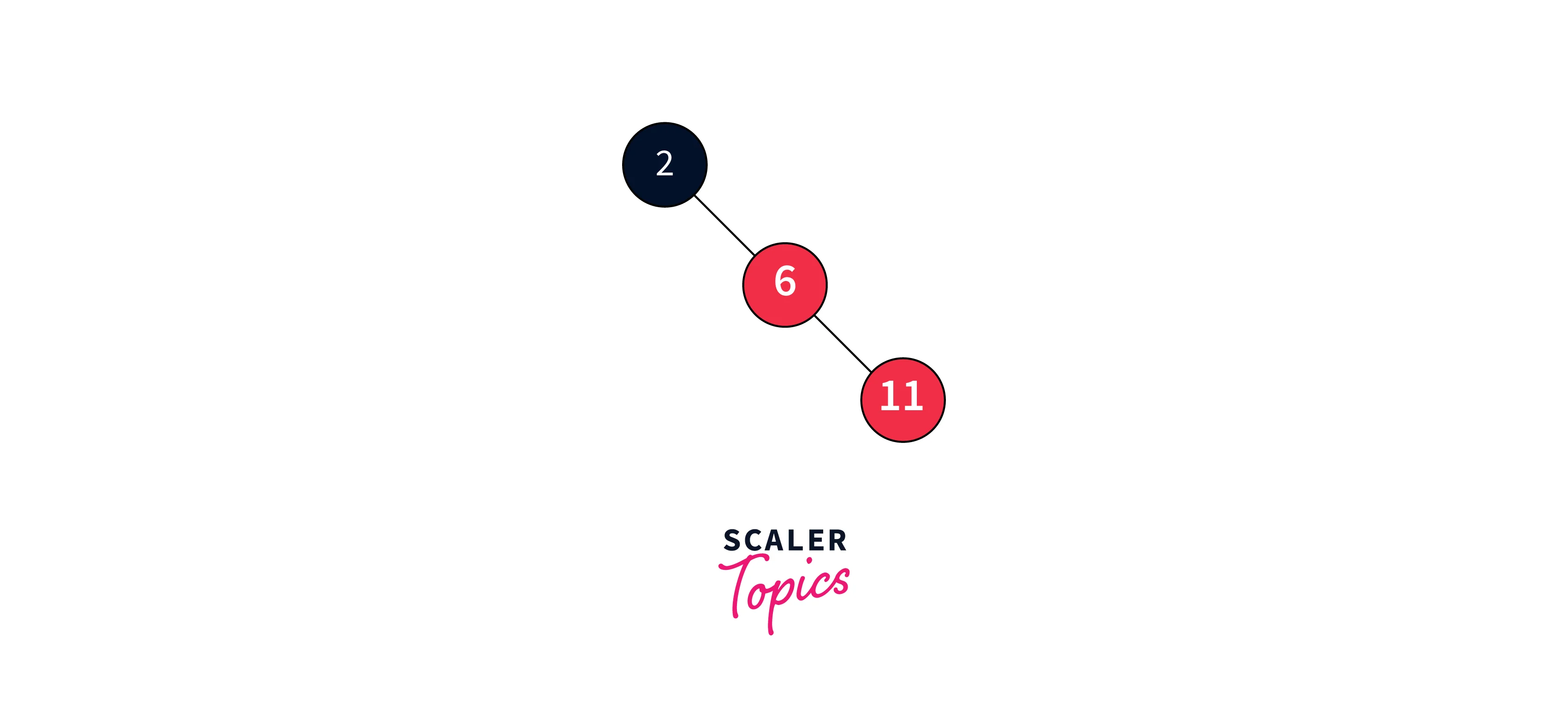
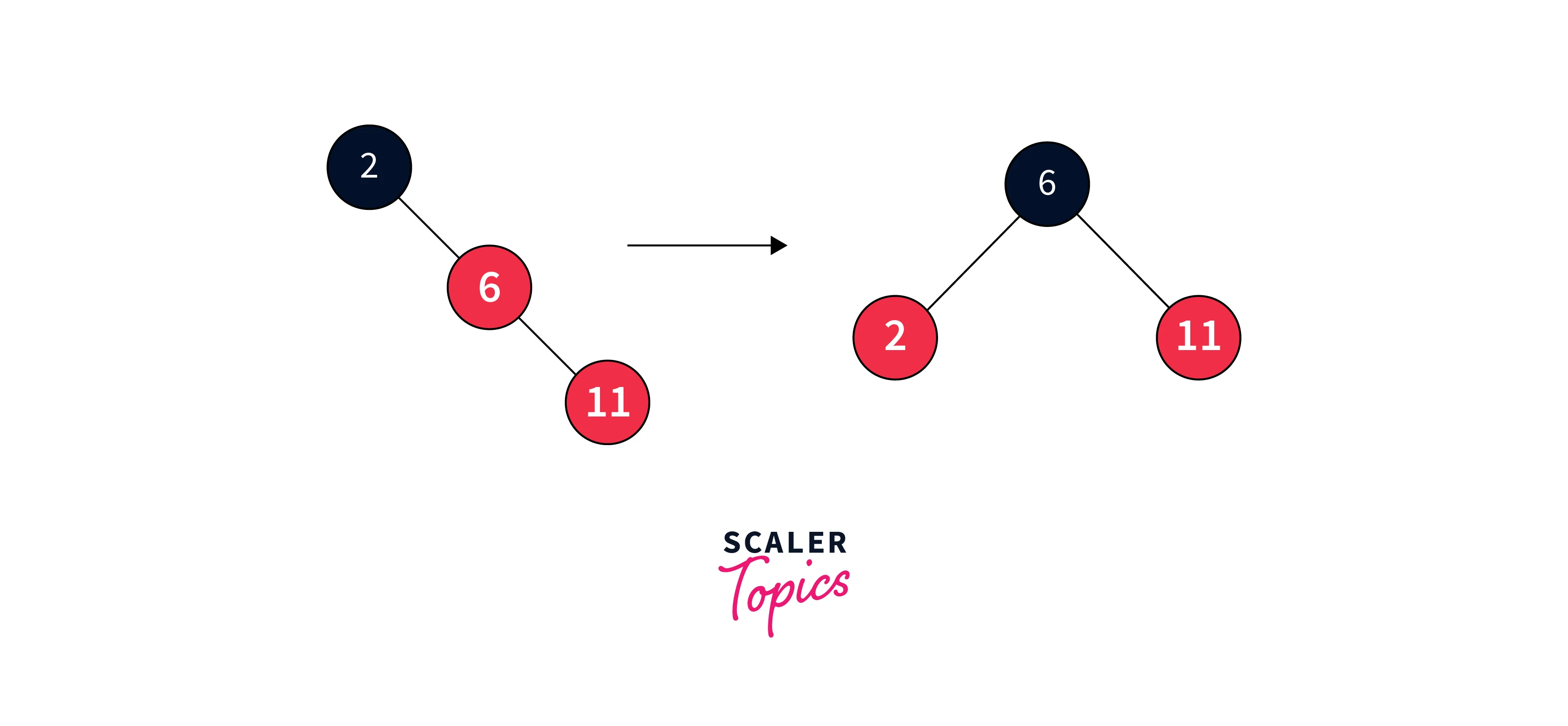
As the sibling of the parent is null, we perform a rotation and recolor the initial parent and grandparent of the nodes to restore balance. Recoloring means interchanging the color i.e. if it is red then turn it to black and vice versa.
Insert 17:
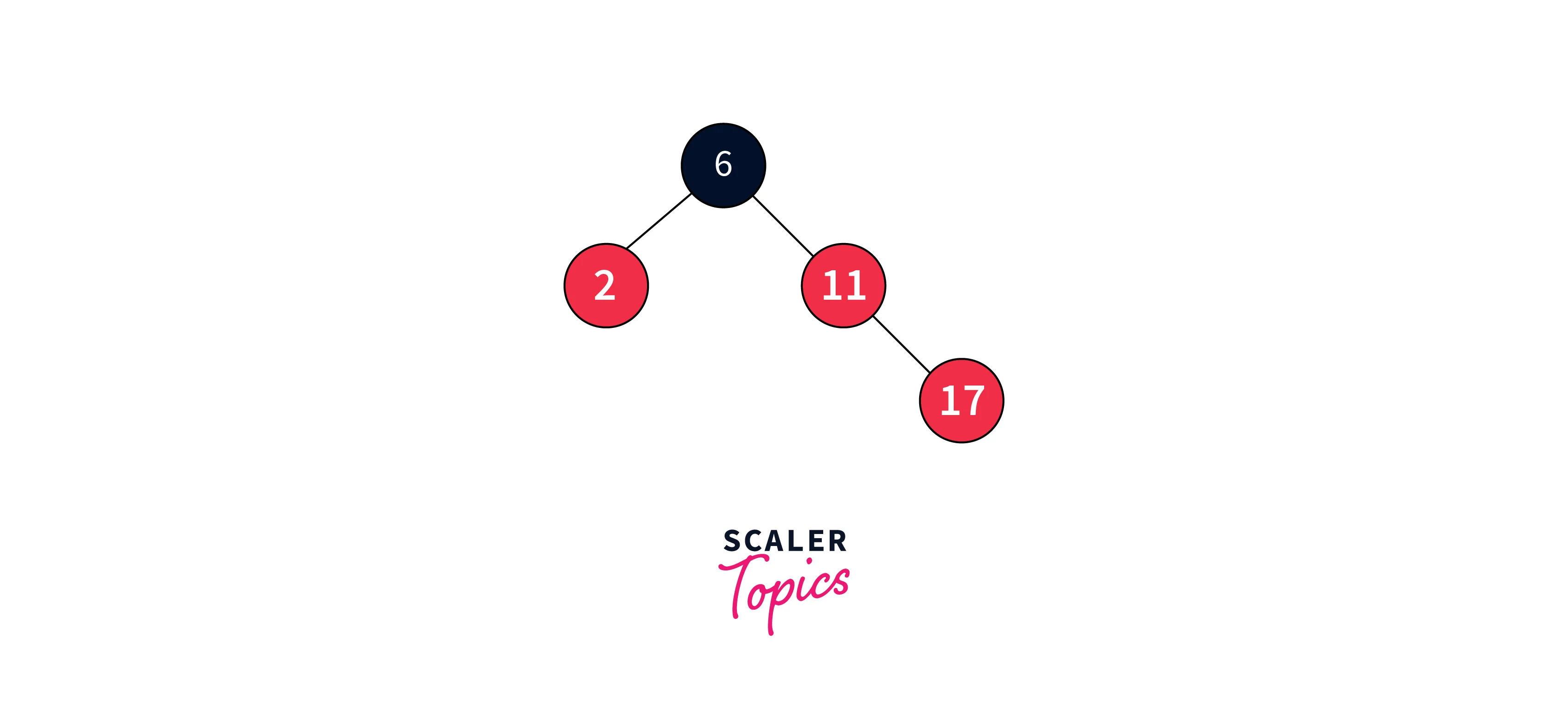
Once again, the Red-Black Tree balance property is violated. We examine the color of the parent’s sibling node, which is red. To restore balance, we simply recolor the parent and the sibling nodes.
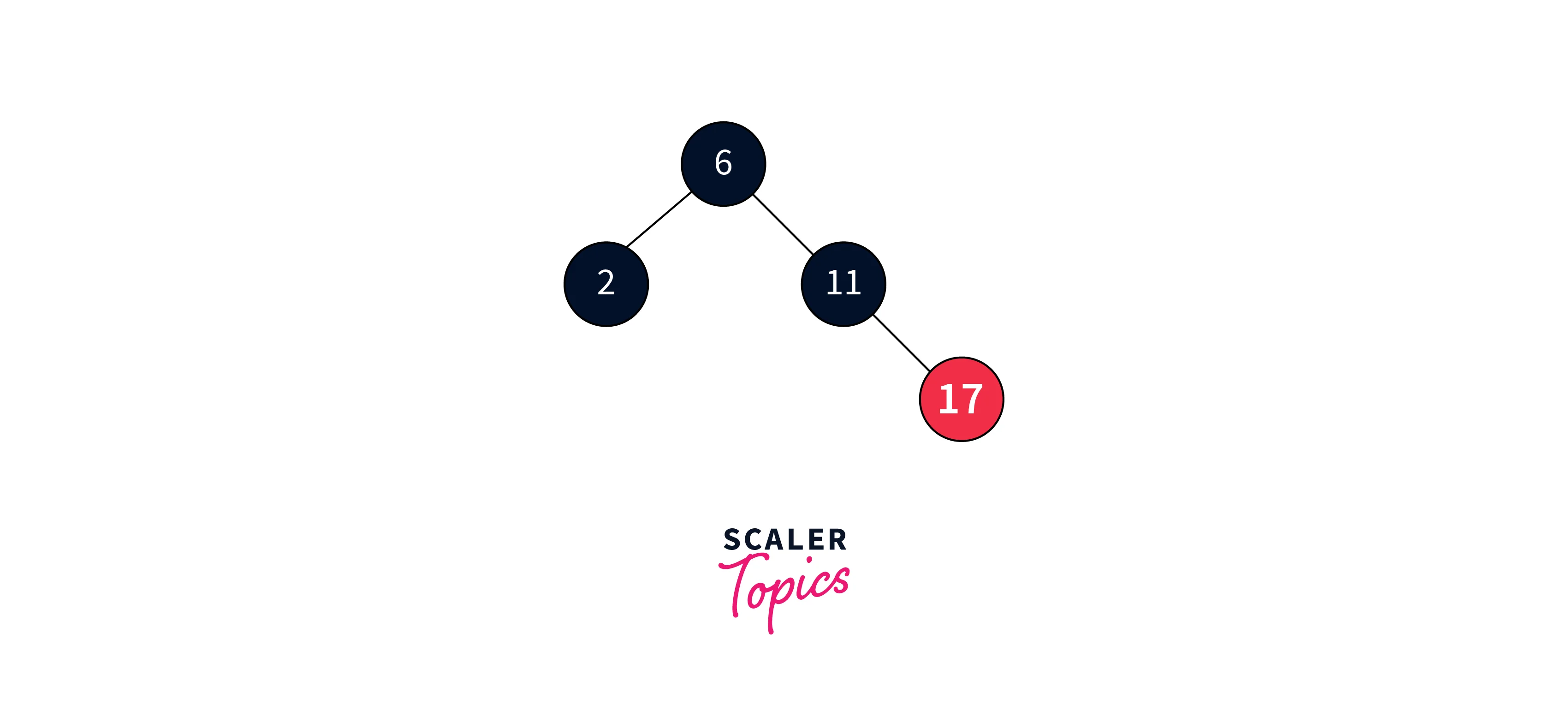
Insert 22:
Inserting the element 5 causes another violation of the Red-Black Tree balance property.
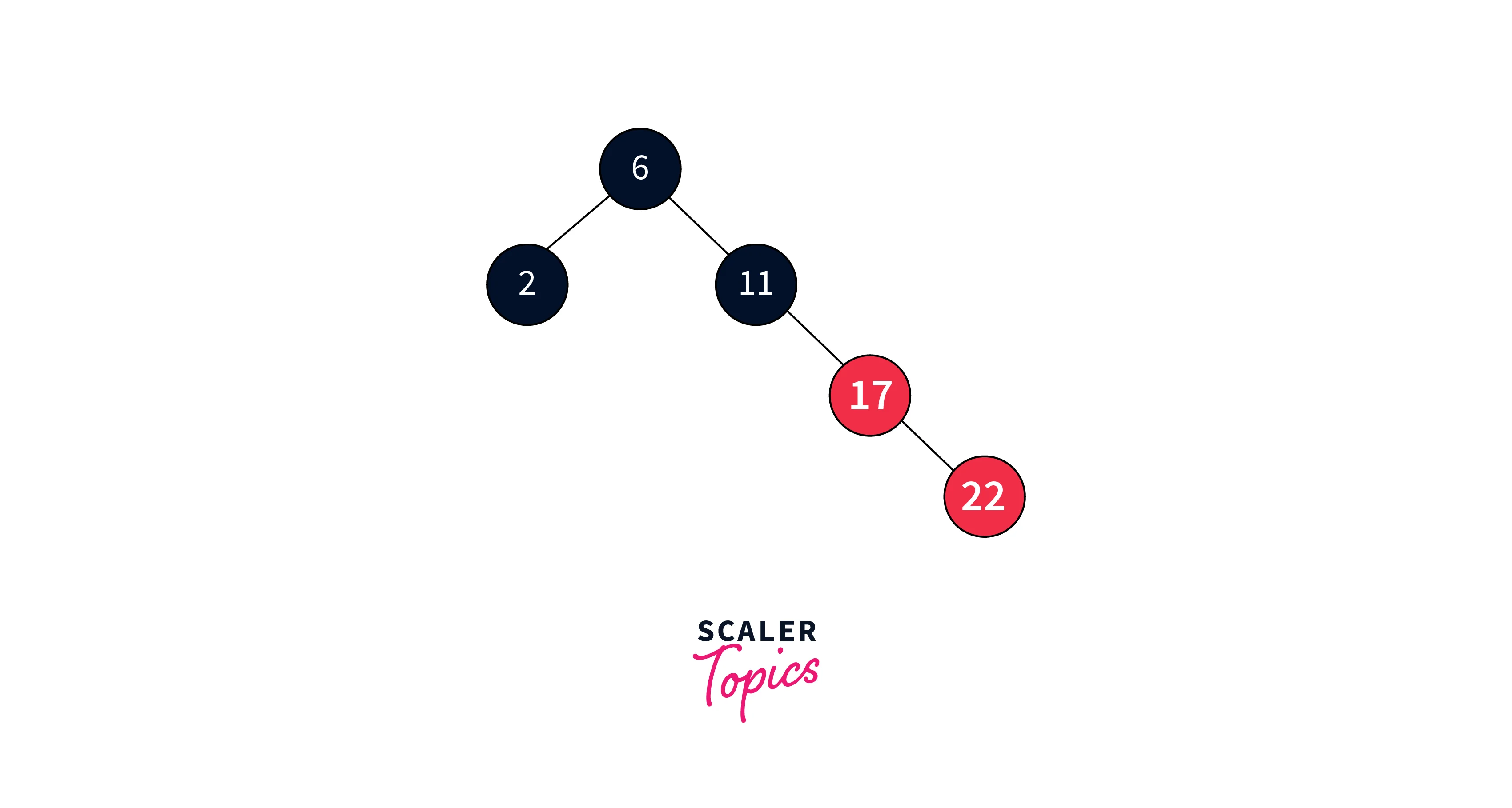
As the sibling node is null, we perform a rotation and adjust colors to restore balance.
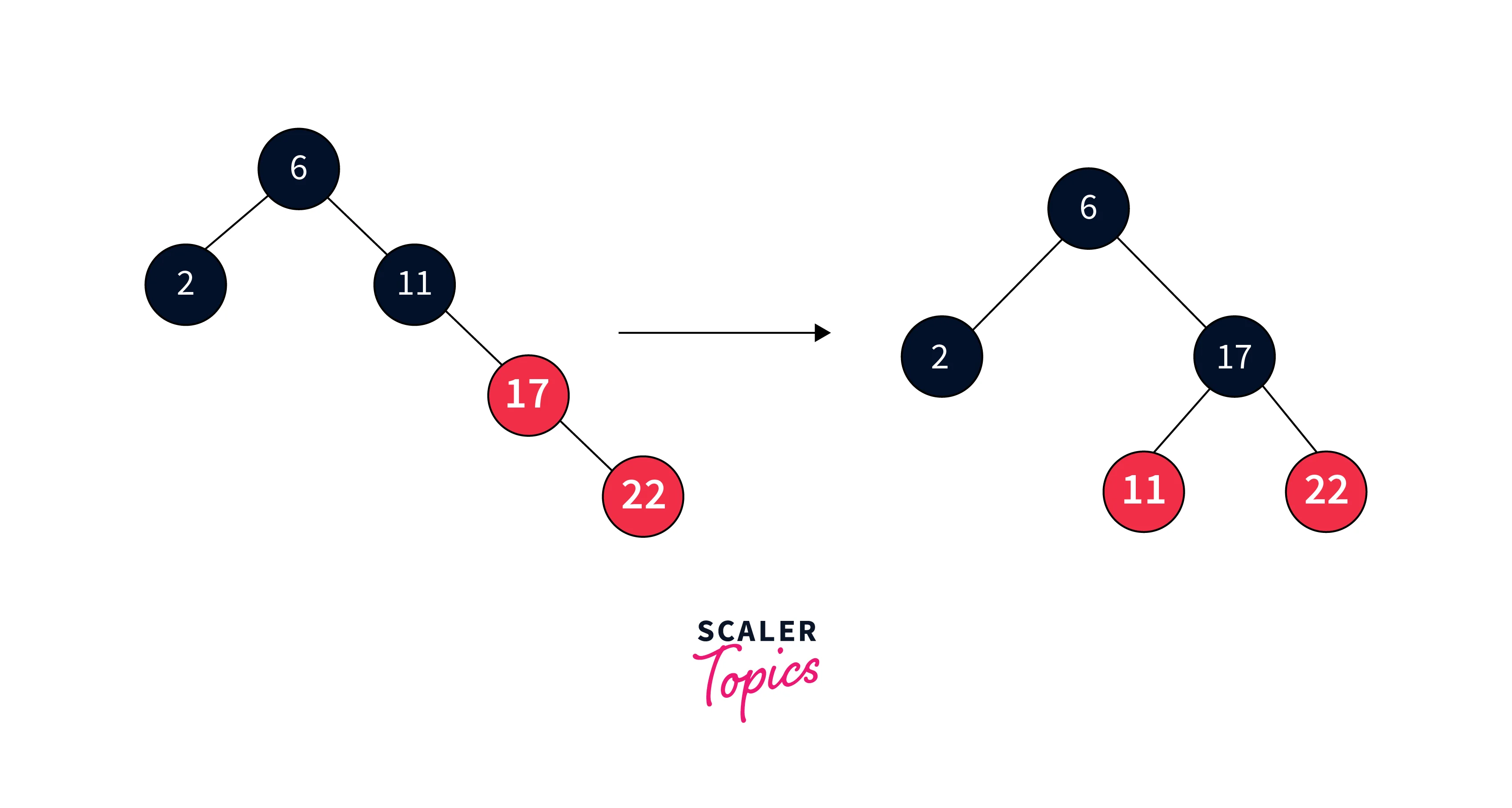
Insert 30:
Inserting element 6 leads to a violation of the Red-Black Tree property, requiring the application of one of the insertion cases.
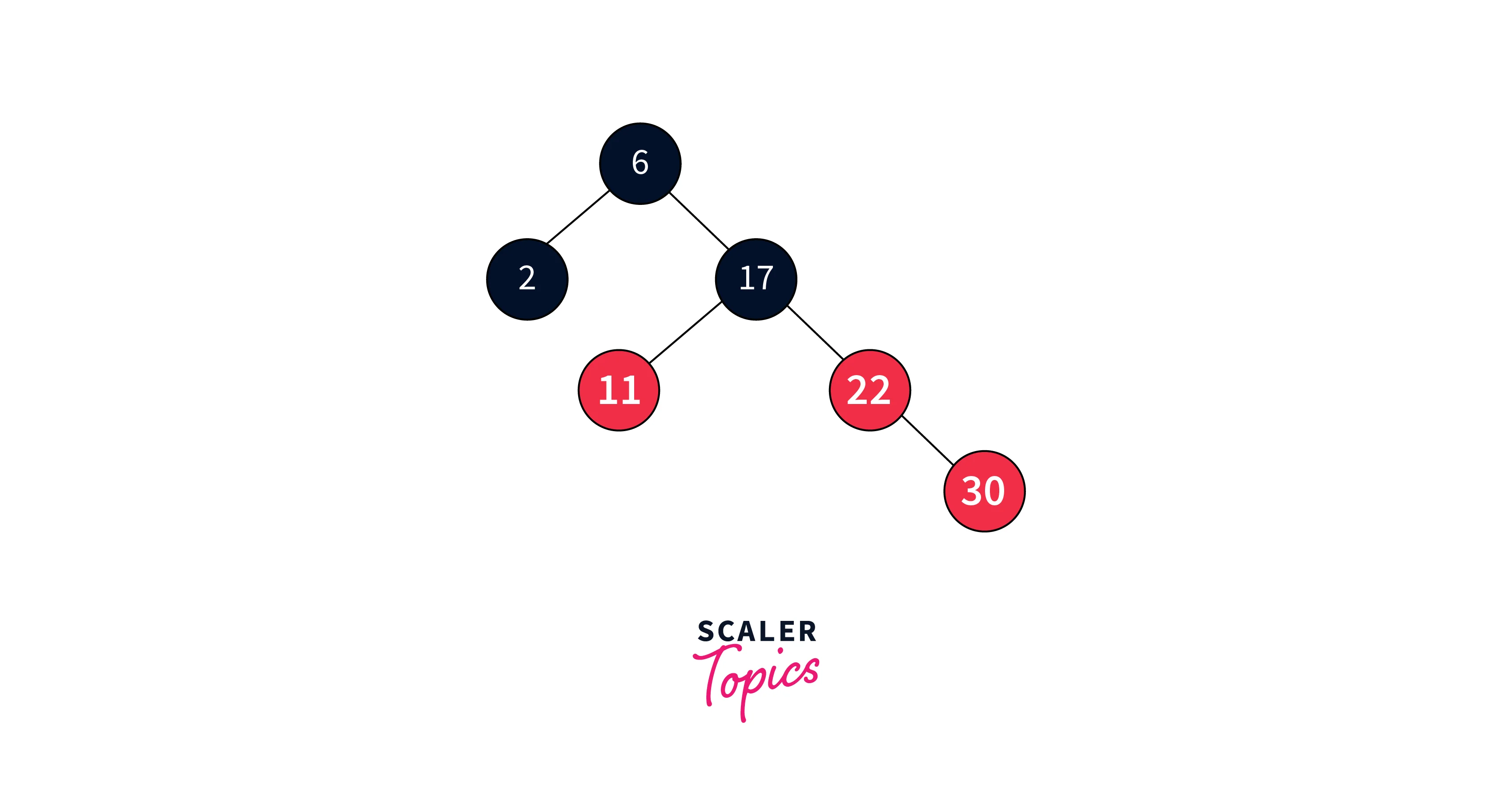
As the parent’s sibling is red, we recolor the parent, its sibling, and the grandparent nodes, unless the grandparent is the root.
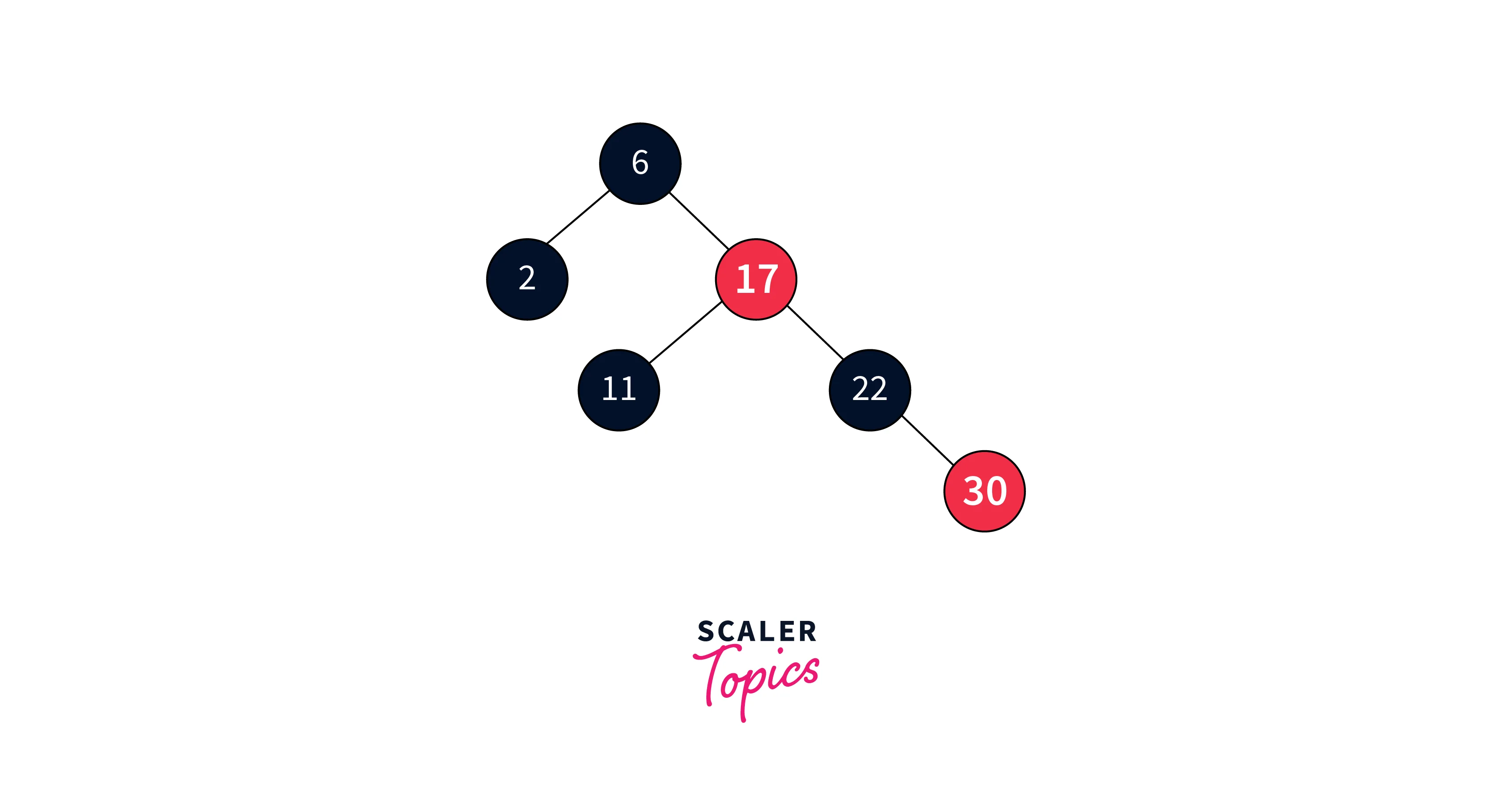
Insert 49:
This again violates the rule.
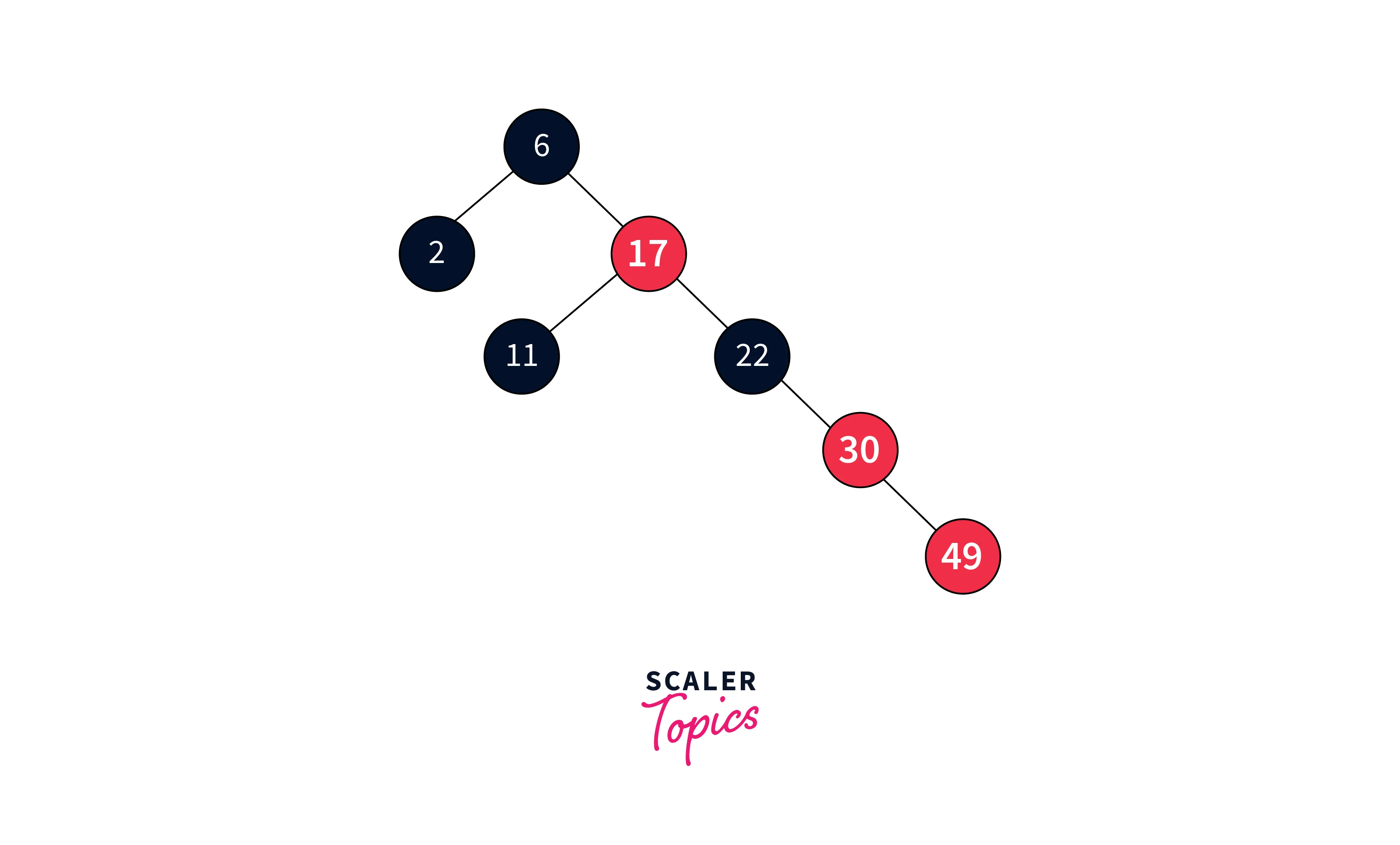
Since the parent’s sibling is null, we perform the appropriate rotation, which in this case is a right-right (RR) rotation and recolor the parent and grandparent node.
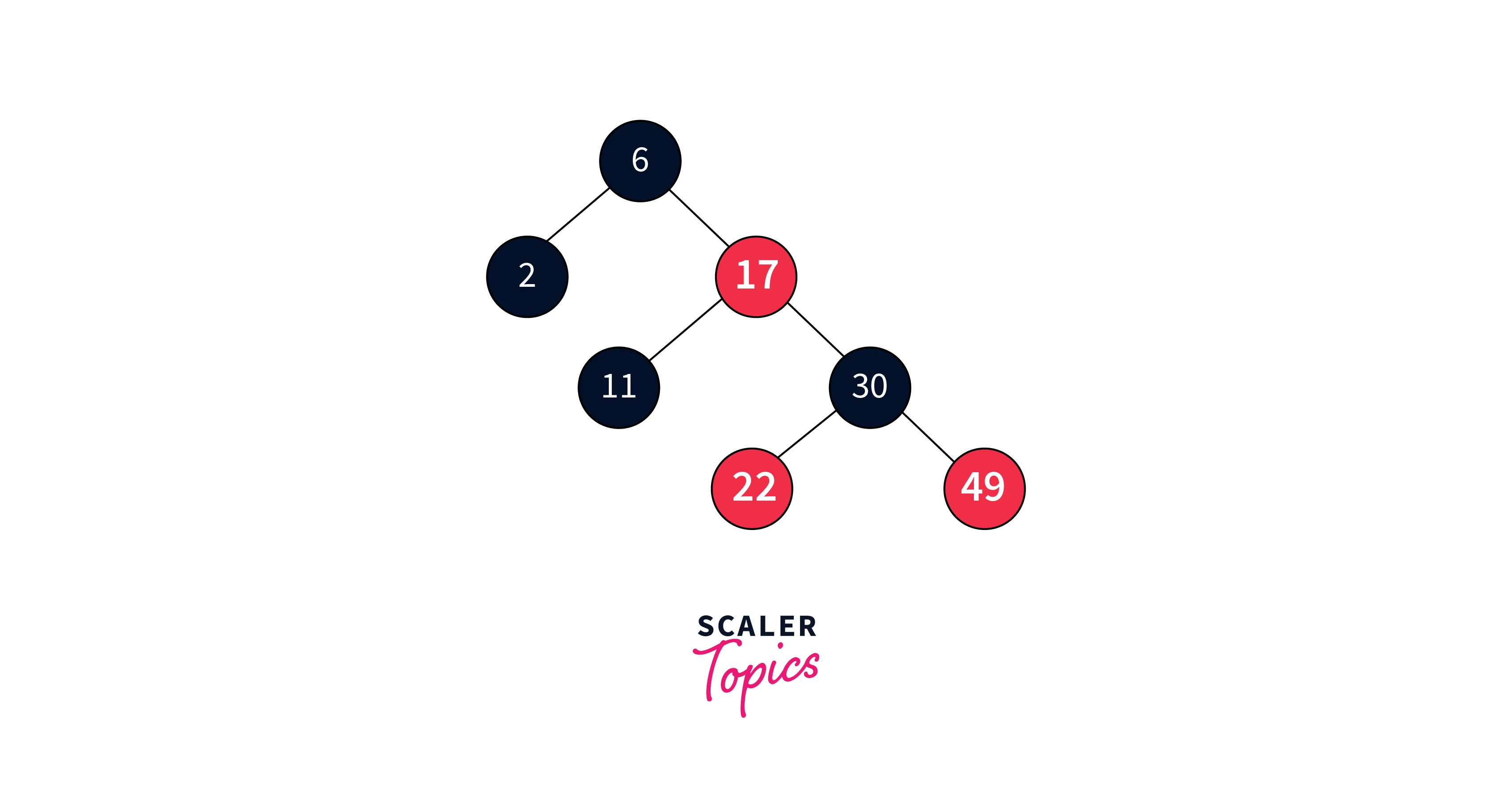
Insert 58:
Inserting 58 results in violation of the rule.
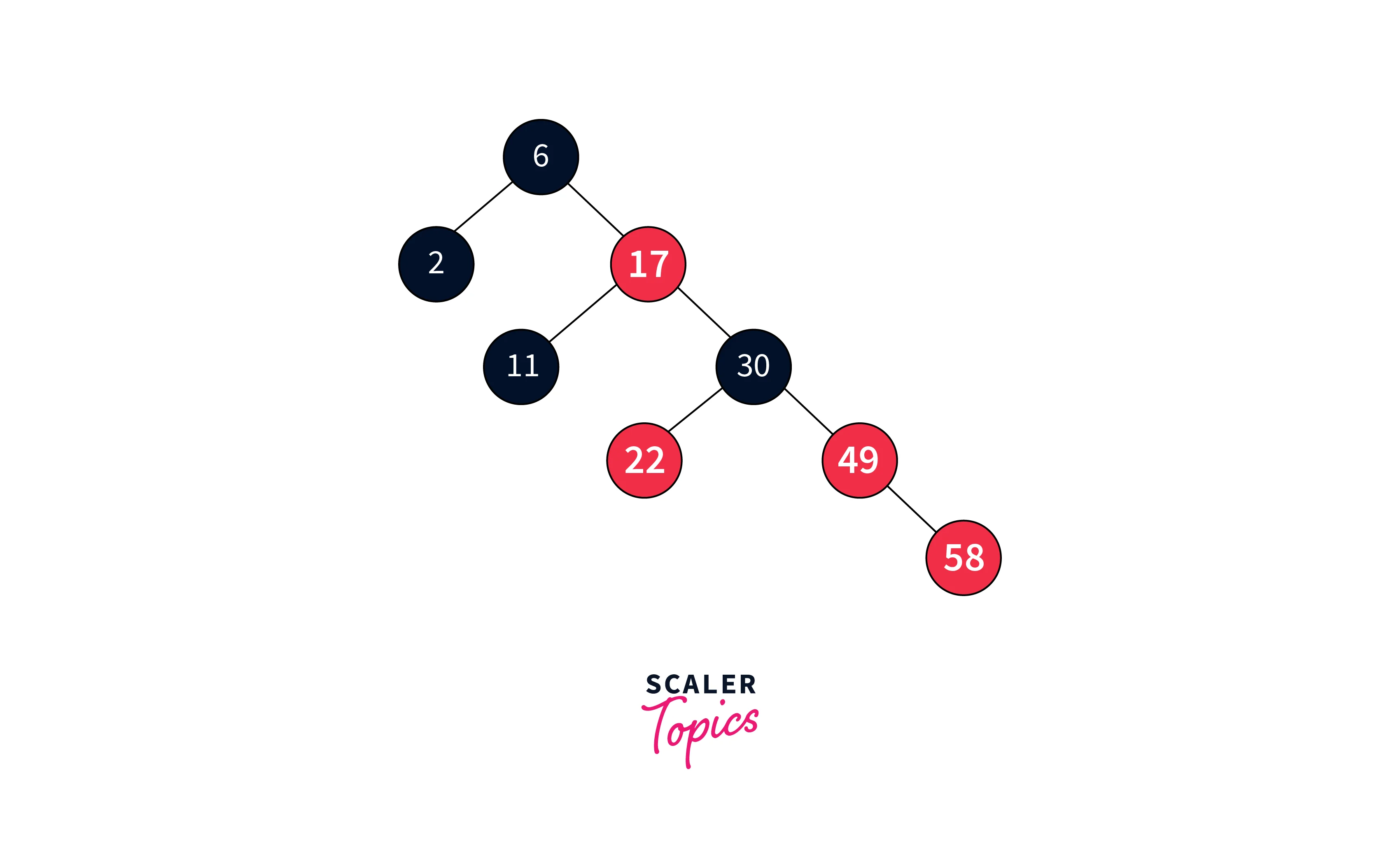
The parent node’s sibling is red so we recolor sibling, parent and grandparent node.
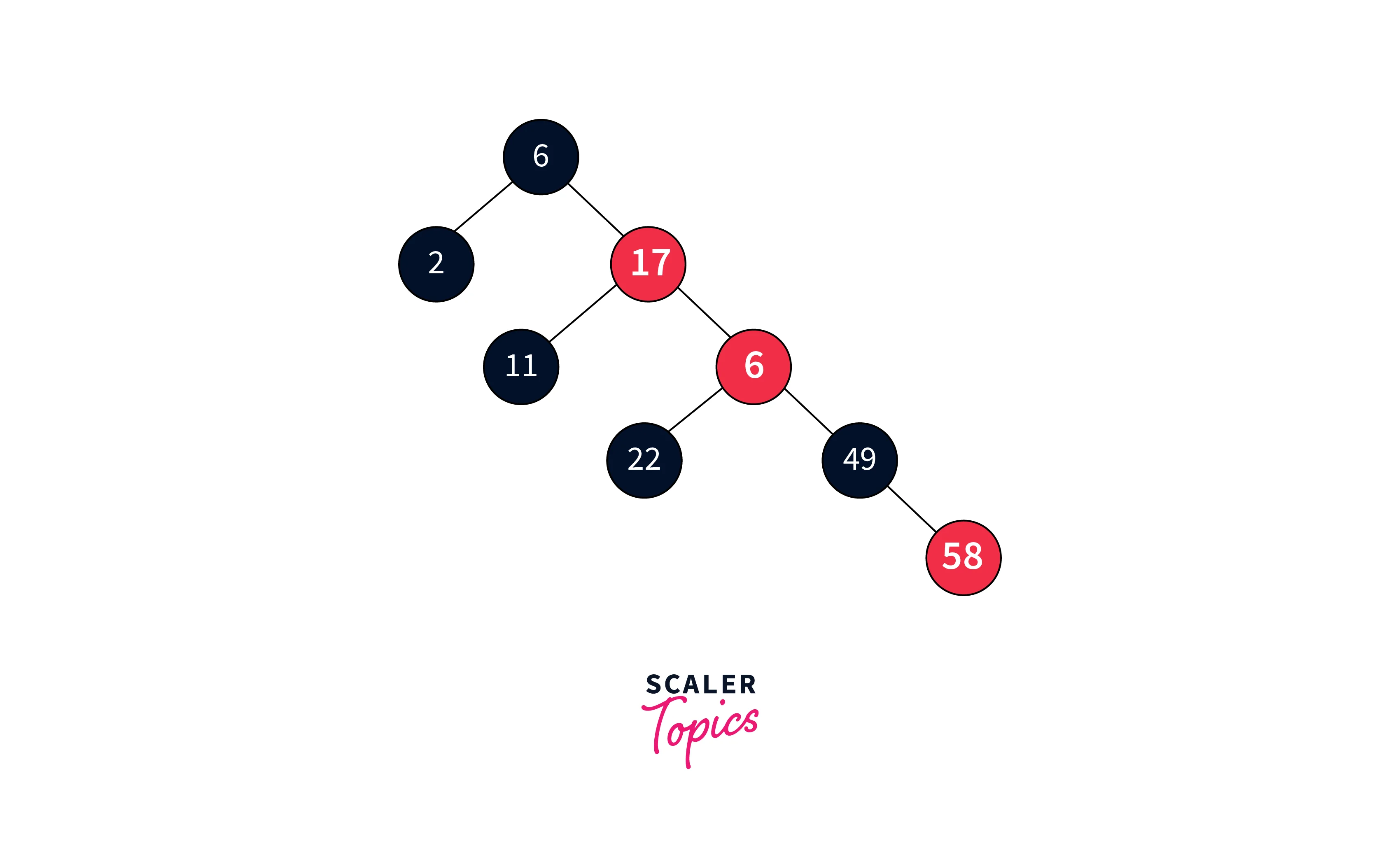
But the problem in above orientation is that two adjacent nodes have red color which violates the property (node 17 and node 30).
Since, the node 30 is in trouble, so we check the color of sibling parent’s node (i.e. node 2). Node 2 is black, so we apply the RR rotation on (6-17-30) and recolor the node 6 and node 17 as per the rule.
Hence, the final tree will become like below:
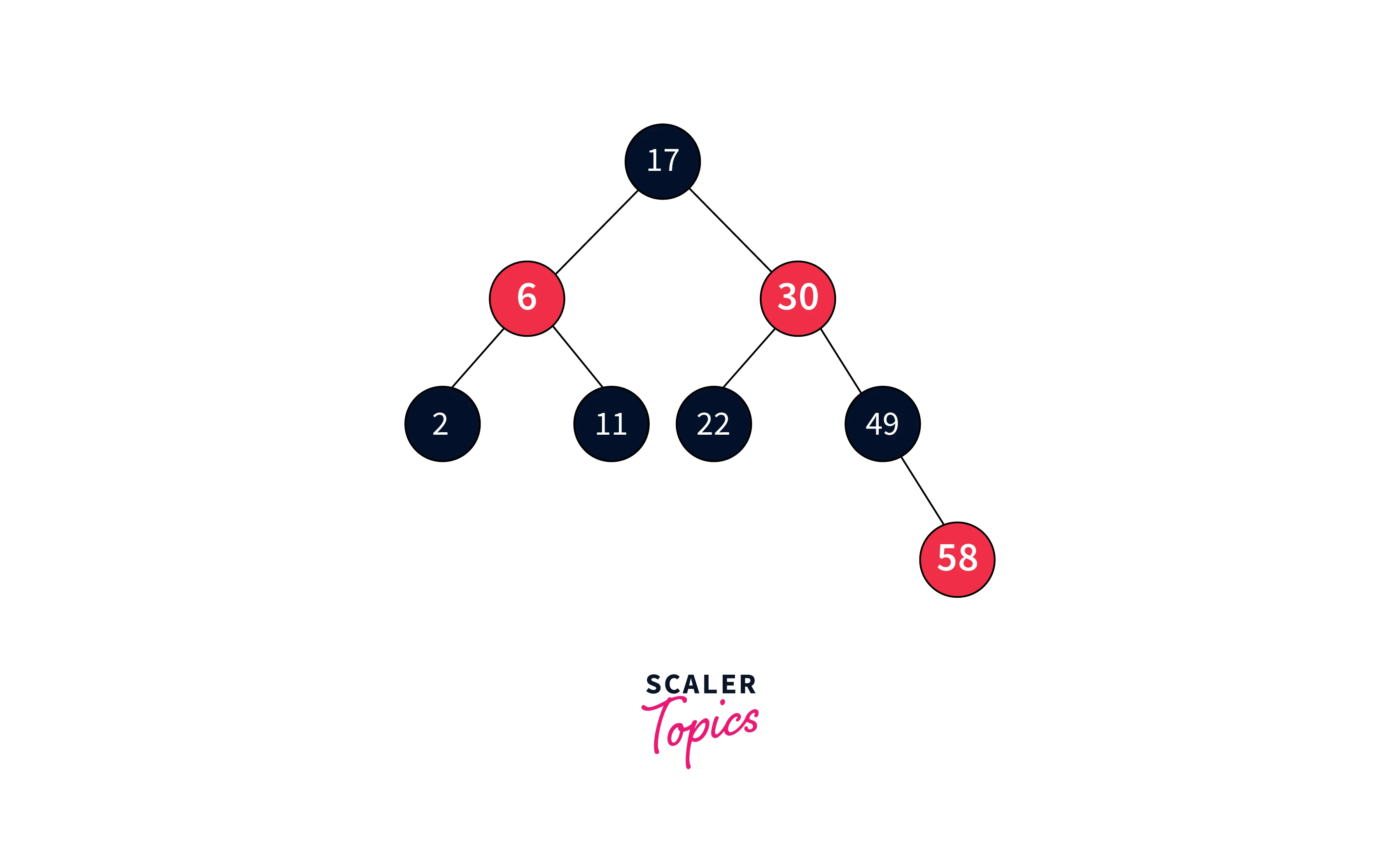
Deletion in Red Black Tree
To ensure the Red-Black Tree properties are preserved during deletion, follow these steps:
- Initial Deletion:
- Delete the node based on binary search tree rules.
- If the deleted node or its parent is red, simply remove it.
- If the deleted node is a black leaf, creating a double black situation, proceed to handle it.
- Double Black Handling:
- If the double black’s sibling and its children are black, recolor parent to black, sibling to red, and handle potential double black at parent.
- If the sibling is red, swap colors of parent and sibling, rotate parent towards double black, and continue with other cases if needed.
- If the sibling’s closer child is red, swap colors of sibling and that child, rotate sibling away from double black, and proceed to below case.
- If the farther child is red, swap colors of parent and sibling, rotate parent towards double black, remove double black, and adjust colors.
These steps ensure that after deletion, both the binary search tree and Red-Black Tree properties are maintained, preserving the integrity and balance of the tree.
Example:
Consider the below tree:
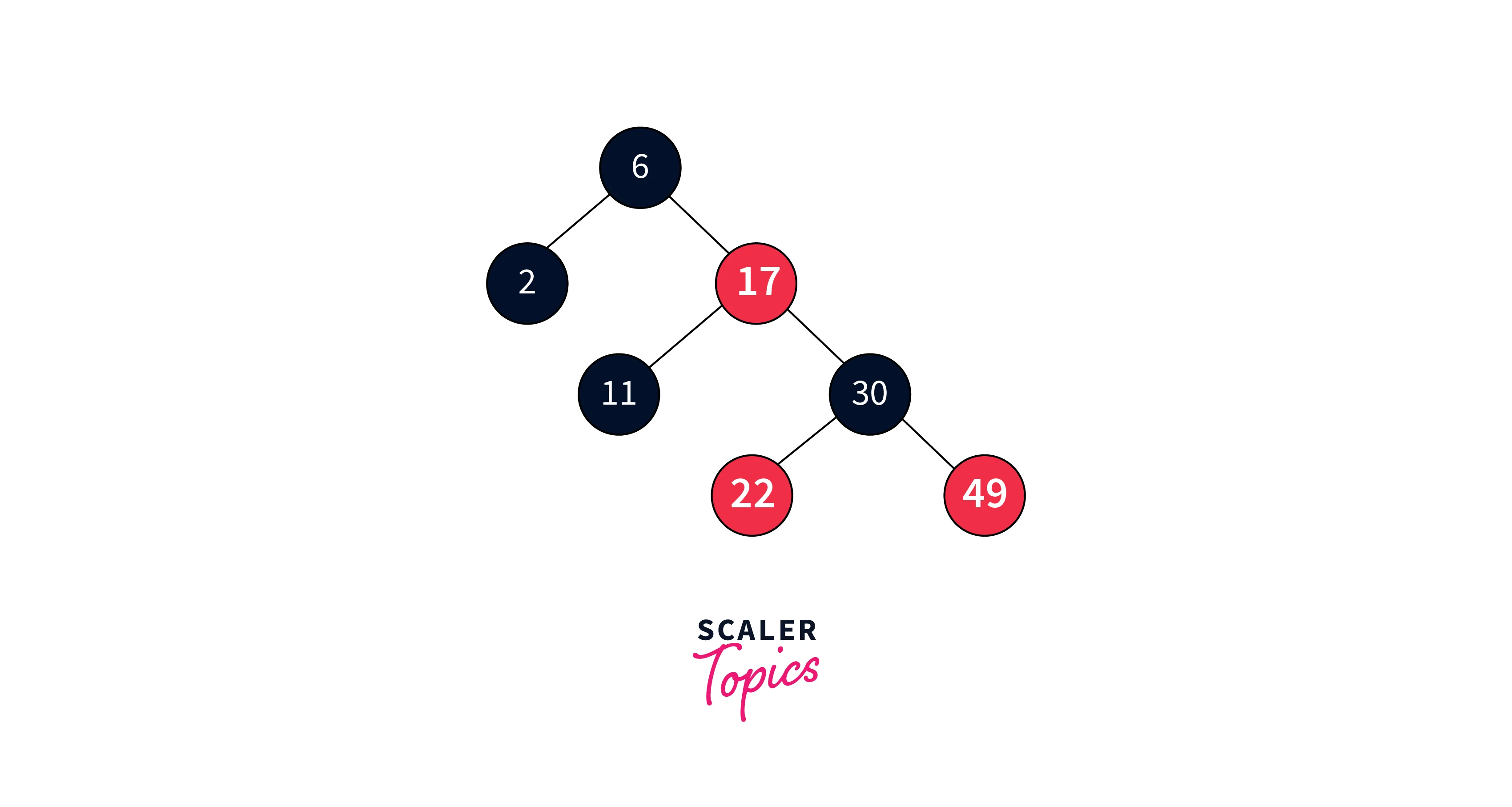
- Delete 17:
Perform binary search deletion first.
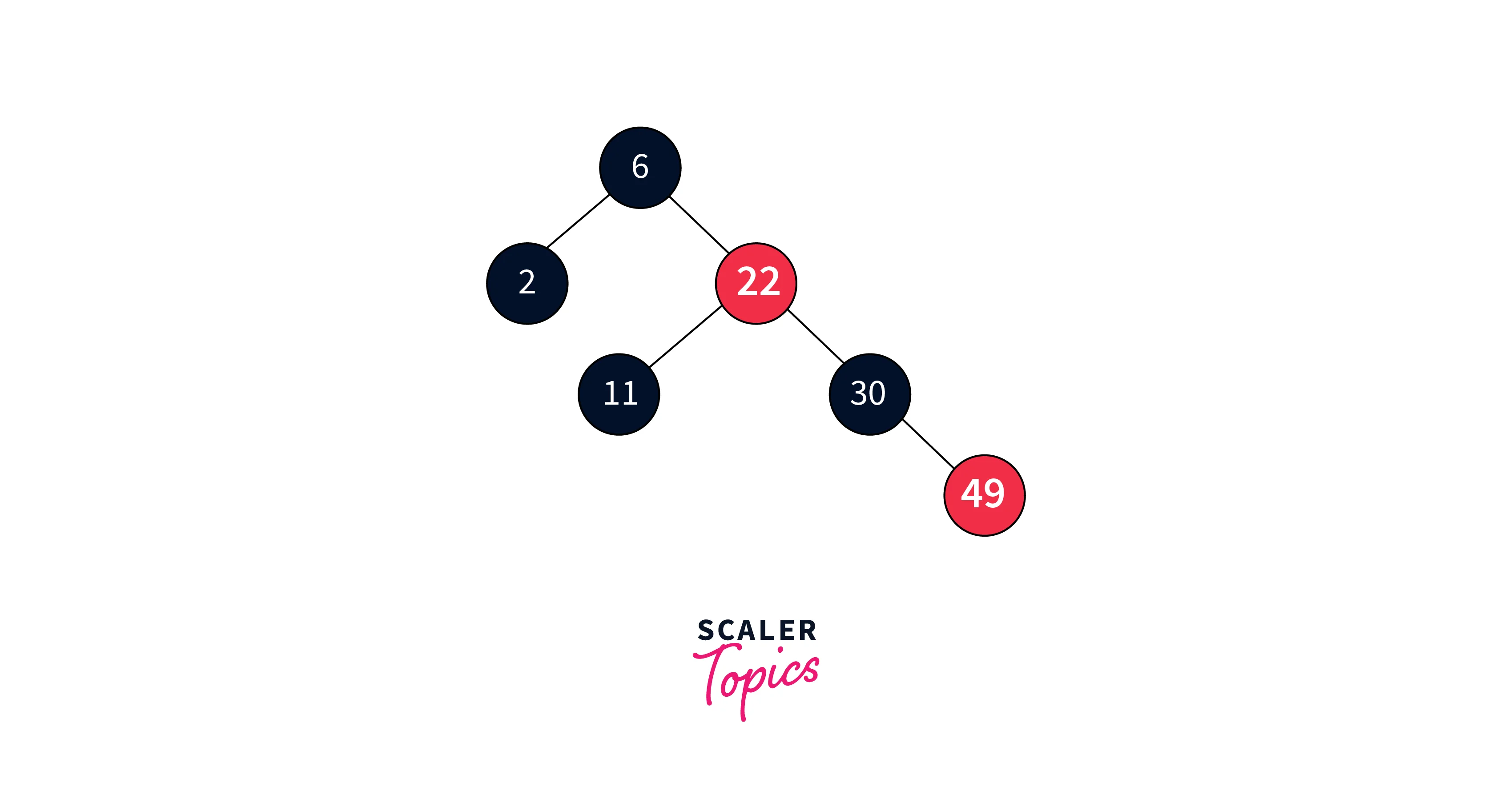
After completing the binary search tree deletion, the Red-Black Tree properties remain intact, so the tree remains unchanged.
- Delete 22:
Following the binary search tree deletion, the Red-Black Tree properties are violated as the paths no longer contain the same number of black nodes. To restore balance, we adjust the colors of nodes accordingly.
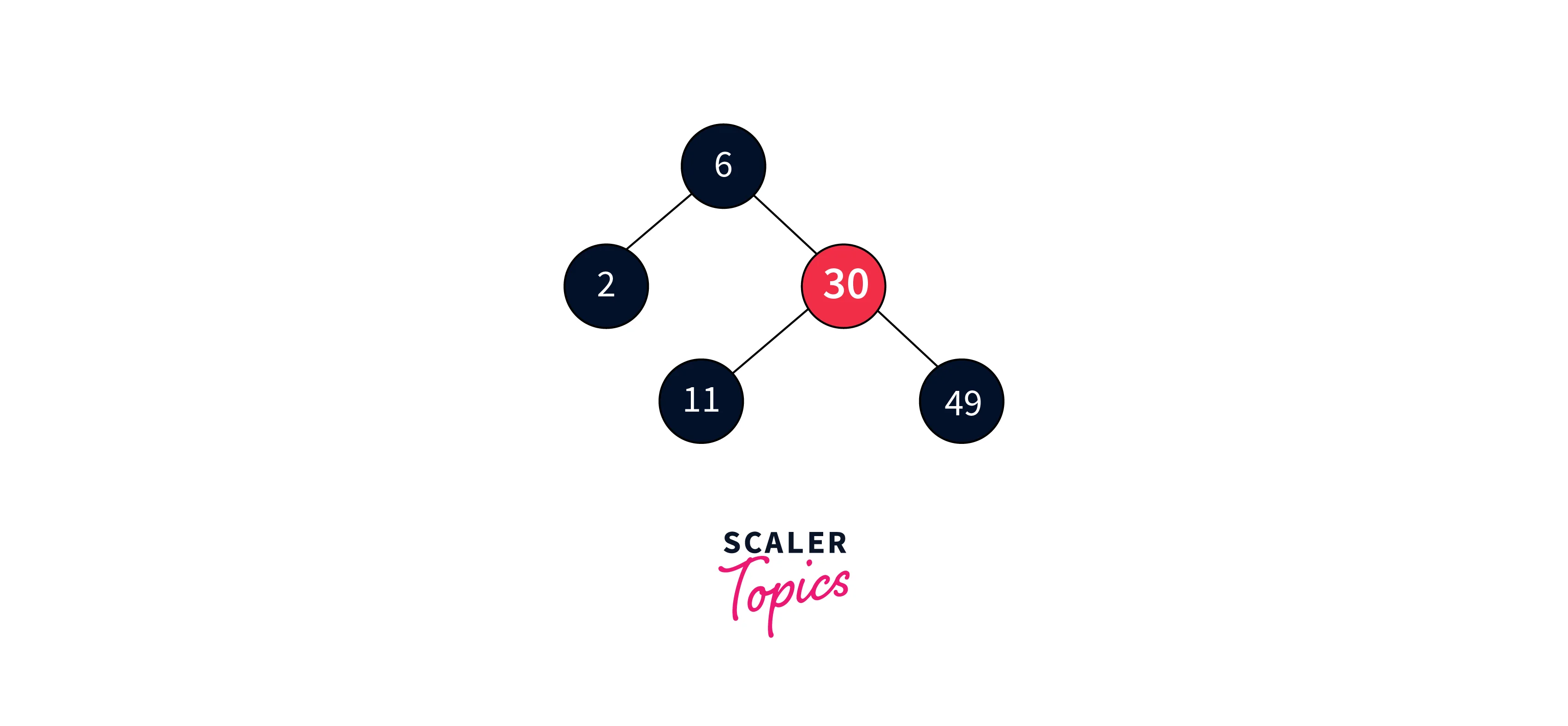
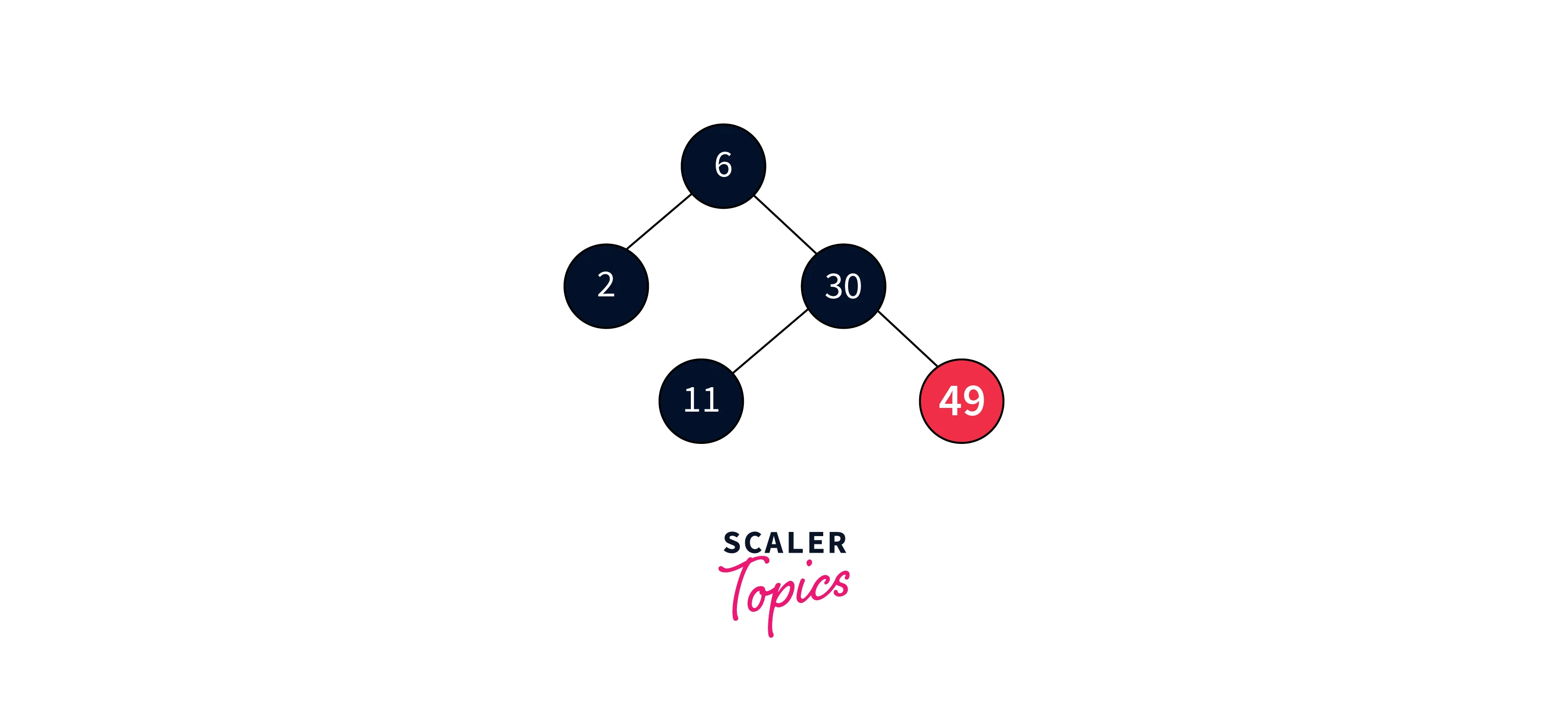
- Delete 11:
After executing the binary search deletion, we remove node 3 as it’s a leaf node. This deletion results in a situation where the node 3 being black, leaves a double black node in its place.
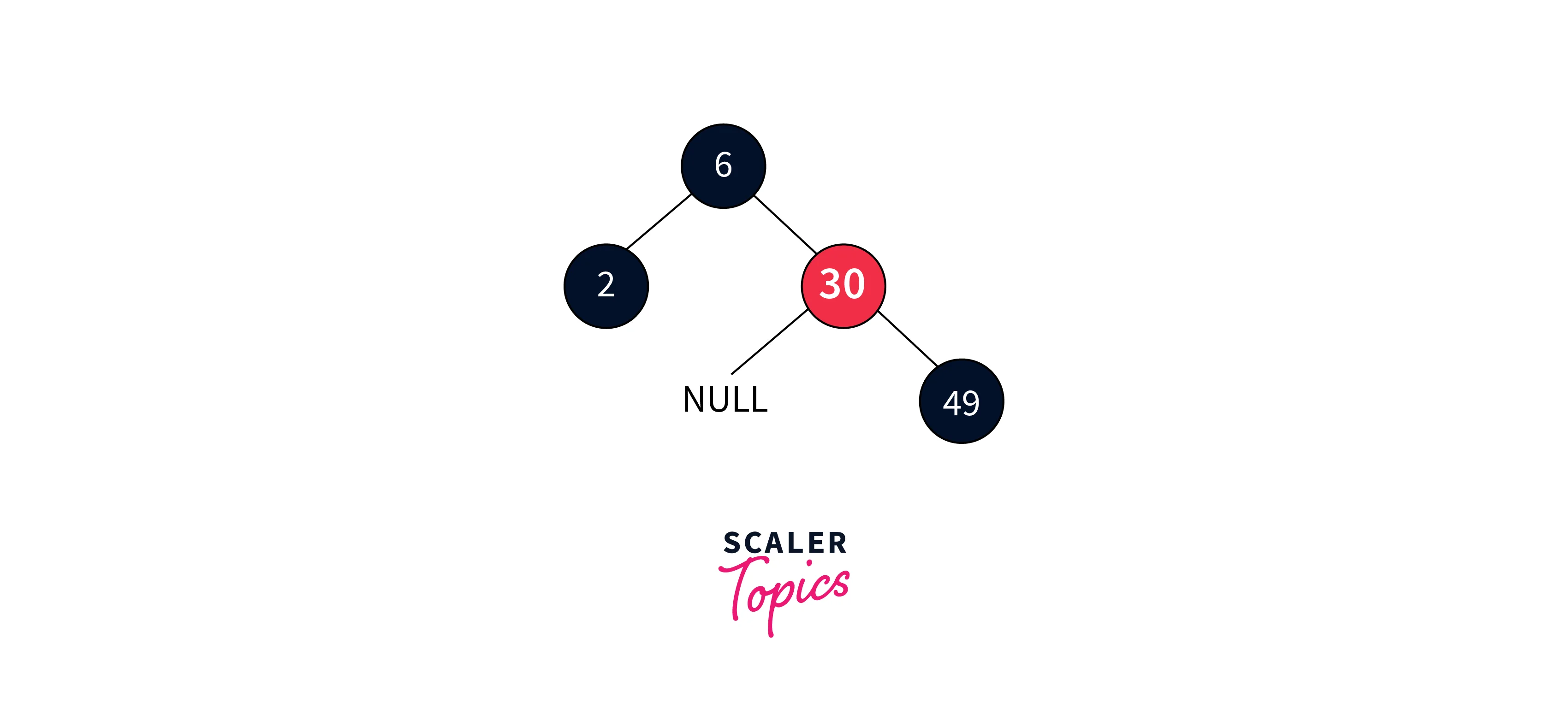
We address case 3 deletion since the double black’s sibling node is black, and its children are also black. In this scenario, we remove the double black node and adjust the colors of its parent and sibling accordingly.
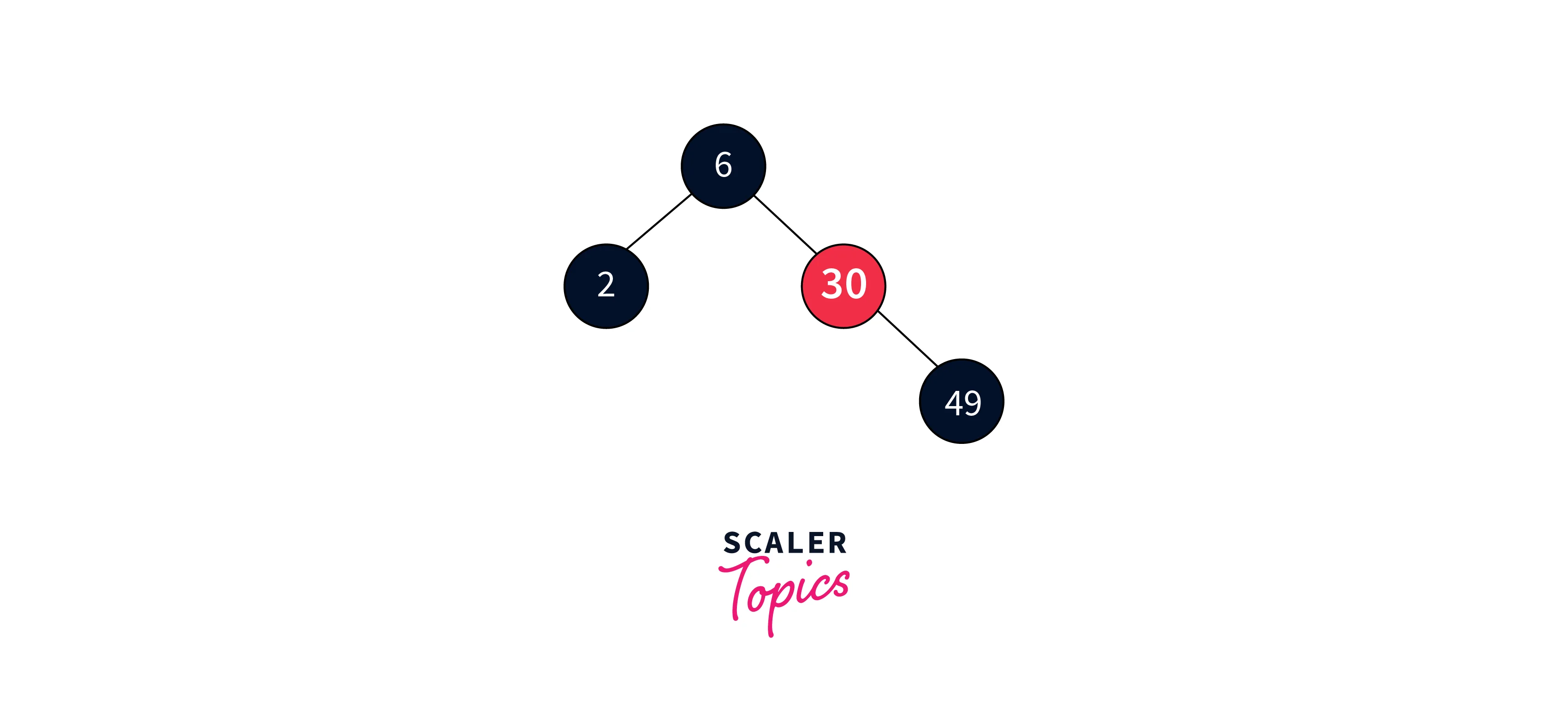
All target nodes have been successfully deleted while ensuring that the Red-Black Tree properties are maintained throughout the process.
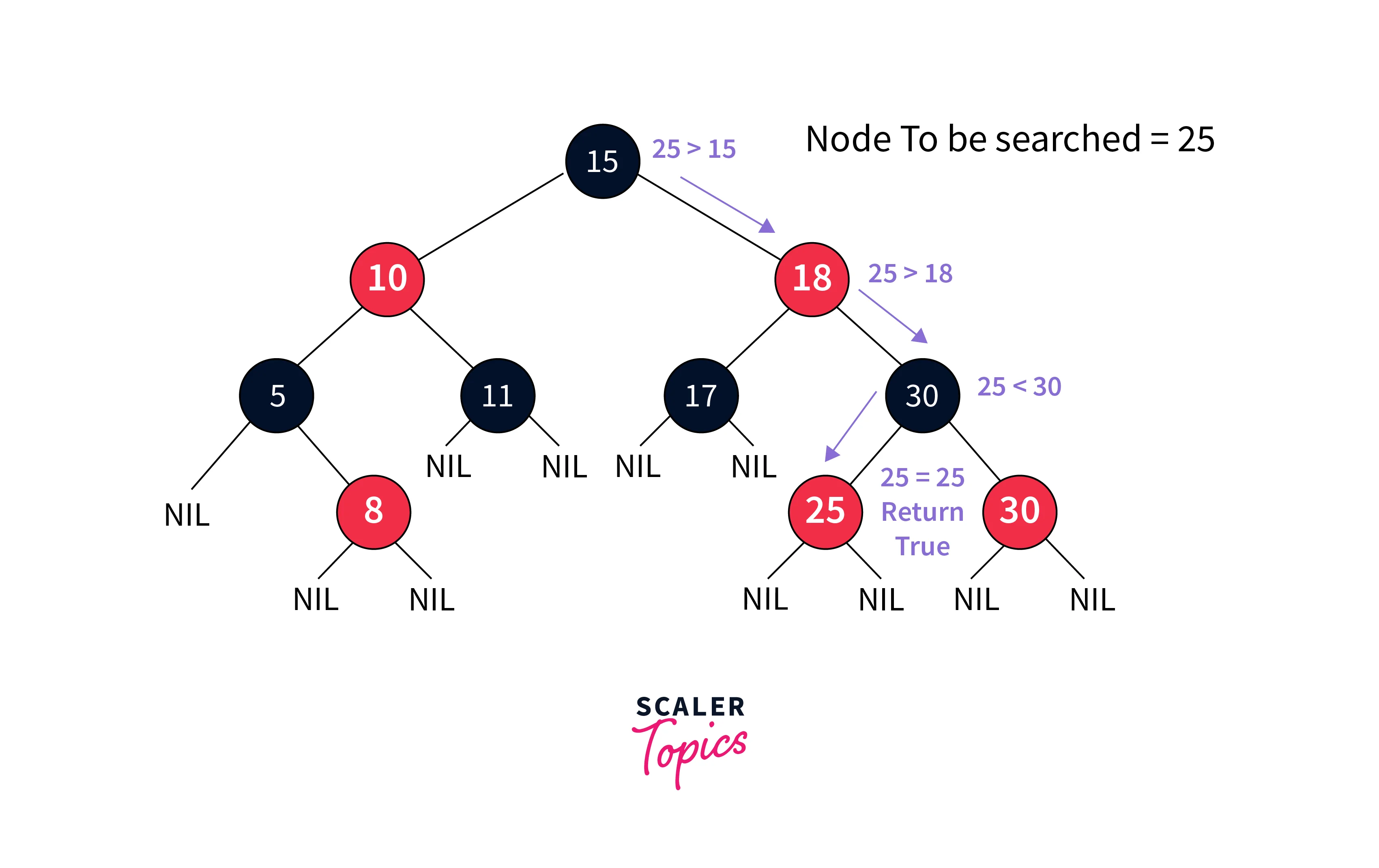
Searching in a Red Black Tree
Searching in a Red-Black Tree uses a similar algorithm to that of a binary search tree. It involves traversing the tree and comparing each node’s value with the key element being searched. If the element is found, a successful search is returned. Otherwise, an unsuccessful search is returned.
Code Implementation
C++:
#include <iostream>
using namespace std;
// Node structure for Red-Black Tree
struct Node {
int data;
bool isRed;
Node *left, *right, *parent;
};
// Function to create a new node
Node* createNode(int key) {
Node* newNode = new Node;
newNode->data = key;
newNode->isRed = true; // Newly inserted node is always red
newNode->left = newNode->right = newNode->parent = nullptr;
return newNode;
}
// Function to perform left rotation
void leftRotate(Node *&root, Node *&x) {
Node *y = x->right;
x->right = y->left;
if (y->left != nullptr)
y->left->parent = x;
y->parent = x->parent;
if (x->parent == nullptr)
root = y;
else if (x == x->parent->left)
x->parent->left = y;
else
x->parent->right = y;
y->left = x;
x->parent = y;
}
// Function to perform right rotation
void rightRotate(Node *&root, Node *&y) {
Node *x = y->left;
y->left = x->right;
if (x->right != nullptr)
x->right->parent = y;
x->parent = y->parent;
if (y->parent == nullptr)
root = x;
else if (y == y->parent->left)
y->parent->left = x;
else
y->parent->right = x;
x->right = y;
y->parent = x;
}
// Function to fix violations after insertion
void fixInsertion(Node *&root, Node *&z) {
while (z != root && z->parent->isRed) {
if (z->parent == z->parent->parent->left) {
Node *y = z->parent->parent->right;
if (y != nullptr && y->isRed) {
z->parent->isRed = false;
y->isRed = false;
z->parent->parent->isRed = true;
z = z->parent->parent;
} else {
if (z == z->parent->right) {
z = z->parent;
leftRotate(root, z);
}
z->parent->isRed = false;
z->parent->parent->isRed = true;
rightRotate(root, z->parent->parent);
}
} else {
Node *y = z->parent->parent->left;
if (y != nullptr && y->isRed) {
z->parent->isRed = false;
y->isRed = false;
z->parent->parent->isRed = true;
z = z->parent->parent;
} else {
if (z == z->parent->left) {
z = z->parent;
rightRotate(root, z);
}
z->parent->isRed = false;
z->parent->parent->isRed = true;
leftRotate(root, z->parent->parent);
}
}
}
root->isRed = false;
}
// Function to insert a node in Red-Black Tree
void insertNode(Node *&root, int key) {
Node *z = createNode(key);
Node *y = nullptr;
Node *x = root;
while (x != nullptr) {
y = x;
if (z->data < x->data)
x = x->left;
else
x = x->right;
}
z->parent = y;
if (y == nullptr)
root = z;
else if (z->data < y->data)
y->left = z;
else
y->right = z;
fixInsertion(root, z);
}
// Function to find the minimum node in a subtree
Node* minValueNode(Node* node) {
Node* current = node;
while (current->left != nullptr)
current = current->left;
return current;
}
// Function to fix violations after deletion
void fixDeletion(Node *&root, Node *&x) {
Node *s;
while (x != root && !x->isRed) {
if (x == x->parent->left) {
s = x->parent->right;
if (s->isRed) {
s->isRed = false;
x->parent->isRed = true;
leftRotate(root, x->parent);
s = x->parent->right;
}
if (!s->left->isRed && !s->right->isRed) {
s->isRed = true;
x = x->parent;
} else {
if (!s->right->isRed) {
s->left->isRed = false;
s->isRed = true;
rightRotate(root, s);
s = x->parent->right;
}
s->isRed = x->parent->isRed;
x->parent->isRed = false;
s->right->isRed = false;
leftRotate(root, x->parent);
x = root;
}
} else {
s = x->parent->left;
if (s->isRed) {
s->isRed = false;
x->parent->isRed = true;
rightRotate(root, x->parent);
s = x->parent->left;
}
if (!s->right->isRed && !s->left->isRed) {
s->isRed = true;
x = x->parent;
} else {
if (!s->left->isRed) {
s->right->isRed = false;
s->isRed = true;
leftRotate(root, s);
s = x->parent->left;
}
s->isRed = x->parent->isRed;
x->parent->isRed = false;
s->left->isRed = false;
rightRotate(root, x->parent);
x = root;
}
}
}
x->isRed = false;
}
// Function to delete a node from Red-Black Tree
void deleteNode(Node *&root, int key) {
Node *z = root;
while (z != nullptr) {
if (key == z->data)
break;
else if (key < z->data)
z = z->left;
else
z = z->right;
}
if (z == nullptr) {
cout << "Node not found." << endl;
return;
}
Node *x, *y = z;
bool y_original_color = y->isRed;
if (z->left == nullptr) {
x = z->right;
transplant(root, z, z->right);
} else if (z->right == nullptr) {
x = z->left;
transplant(root, z, z->left);
} else {
y = minValueNode(z->right);
y_original_color = y->isRed;
x = y->right;
if (y->parent == z)
x->parent = y;
else {
transplant(root, y, y->right);
y->right = z->right;
y->right->parent = y;
}
transplant(root, z, y);
y->left = z->left;
y->left->parent = y;
y->isRed = z->isRed;
}
delete z;
if (!y_original_color)
fixDeletion(root, x);
}
// Function to search for a node in Red-Black Tree
Node* search(Node* root, int key) {
while (root != nullptr && root->data != key) {
if (key < root->data)
root = root->left;
else
root = root->right;
}
return root;
}
// Function to perform inorder traversal of Red-Black Tree
void inorderTraversal(Node *root) {
if (root != nullptr) {
inorderTraversal(root->left);
cout << root->data << " ";
inorderTraversal(root->right);
}
}
// Driver code
int main() {
Node* root = nullptr;
// Insert nodes
insertNode(root, 10);
insertNode(root, 20);
insertNode(root, 30);
insertNode(root, 40);
insertNode(root, 50);
insertNode(root, 60);
cout << "Inorder traversal after insertion: ";
inorderTraversal(root);
cout << endl;
// Search for a node
Node* foundNode = search(root, 40);
if (foundNode != nullptr)
cout << "Node 40 found." << endl;
else
cout << "Node 40 not found." << endl;
// Delete a node
deleteNode(root, 30);
cout << "Inorder traversal after deletion: ";
inorderTraversal(root);
cout << endl;
return 0;
}Java:
class RedBlackTree {
class Node {
int data;
boolean isRed;
Node left, right, parent;
public Node(int data) {
this.data = data;
this.isRed = true;
left = right = parent = null;
}
}
private Node root;
public RedBlackTree() {
root = null;
}
private Node createNode(int key) {
return new Node(key);
}
private void leftRotate(Node x) {
Node y = x.right;
x.right = y.left;
if (y.left != null)
y.left.parent = x;
y.parent = x.parent;
if (x.parent == null)
root = y;
else if (x == x.parent.left)
x.parent.left = y;
else
x.parent.right = y;
y.left = x;
x.parent = y;
}
private void rightRotate(Node y) {
Node x = y.left;
y.left = x.right;
if (x.right != null)
x.right.parent = y;
x.parent = y.parent;
if (y.parent == null)
root = x;
else if (y == y.parent.left)
y.parent.left = x;
else
y.parent.right = x;
x.right = y;
y.parent = x;
}
private void fixInsertion(Node z) {
while (z != root && z.parent.isRed) {
if (z.parent == z.parent.parent.left) {
Node y = z.parent.parent.right;
if (y != null && y.isRed) {
z.parent.isRed = false;
y.isRed = false;
z.parent.parent.isRed = true;
z = z.parent.parent;
} else {
if (z == z.parent.right) {
z = z.parent;
leftRotate(z);
}
z.parent.isRed = false;
z.parent.parent.isRed = true;
rightRotate(z.parent.parent);
}
} else {
Node y = z.parent.parent.left;
if (y != null && y.isRed) {
z.parent.isRed = false;
y.isRed = false;
z.parent.parent.isRed = true;
z = z.parent.parent;
} else {
if (z == z.parent.left) {
z = z.parent;
rightRotate(z);
}
z.parent.isRed = false;
z.parent.parent.isRed = true;
leftRotate(z.parent.parent);
}
}
}
root.isRed = false;
}
public void insert(int key) {
Node z = createNode(key);
Node y = null;
Node x = root;
while (x != null) {
y = x;
if (z.data < x.data)
x = x.left;
else
x = x.right;
}
z.parent = y;
if (y == null)
root = z;
else if (z.data < y.data)
y.left = z;
else
y.right = z;
fixInsertion(z);
}
private Node minValueNode(Node node) {
Node current = node;
while (current.left != null)
current = current.left;
return current;
}
private void fixDeletion(Node x) {
Node s;
while (x != root && !x.isRed) {
if (x == x.parent.left) {
s = x.parent.right;
if (s.isRed) {
s.isRed = false;
x.parent.isRed = true;
leftRotate(x.parent);
s = x.parent.right;
}
if (!s.left.isRed && !s.right.isRed) {
s.isRed = true;
x = x.parent;
} else {
if (!s.right.isRed) {
s.left.isRed = false;
s.isRed = true;
rightRotate(s);
s = x.parent.right;
}
s.isRed = x.parent.isRed;
x.parent.isRed = false;
s.right.isRed = false;
leftRotate(x.parent);
x = root;
}
} else {
s = x.parent.left;
if (s.isRed) {
s.isRed = false;
x.parent.isRed = true;
rightRotate(x.parent);
s = x.parent.left;
}
if (!s.right.isRed && !s.left.isRed) {
s.isRed = true;
x = x.parent;
} else {
if (!s.left.isRed) {
s.right.isRed = false;
s.isRed = true;
leftRotate(s);
s = x.parent.left;
}
s.isRed = x.parent.isRed;
x.parent.isRed = false;
s.left.isRed = false;
rightRotate(x.parent);
x = root;
}
}
}
x.isRed = false;
}
public void delete(int key) {
Node z = root;
while (z != null) {
if (key == z.data)
break;
else if (key < z.data)
z = z.left;
else
z = z.right;
}
if (z == null) {
System.out.println("Node not found.");
return;
}
Node x, y = z;
boolean y_original_color = y.isRed;
if (z.left == null) {
x = z.right;
transplant(z, z.right);
} else if (z.right == null) {
x = z.left;
transplant(z, z.left);
} else {
y = minValueNode(z.right);
y_original_color = y.isRed;
x = y.right;
if (y.parent == z)
x.parent = y;
else {
transplant(y, y.right);
y.right = z.right;
y.right.parent = y;
}
transplant(z, y);
y.left = z.left;
y.left.parent = y;
y.isRed = z.isRed;
}
if (!y_original_color)
fixDeletion(x);
}
private void transplant(Node u, Node v) {
if (u.parent == null)
root = v;
else if (u == u.parent.left)
u.parent.left = v;
else
u.parent.right = v;
if (v != null)
v.parent = u.parent;
}
public Node search(int key) {
Node current = root;
while (current != null && current.data != key) {
if (key < current.data)
current = current.left;
else
current = current.right;
}
return current;
}
private void inorderTraversal(Node root) {
if (root != null) {
inorderTraversal(root.left);
System.out.print(root.data + " ");
inorderTraversal(root.right);
}
}
public static void main(String[] args) {
RedBlackTree tree = new RedBlackTree();
// Insert nodes
tree.insert(10);
tree.insert(20);
tree.insert(30);
tree.insert(40);
tree.insert(50);
tree.insert(60);
System.out.print("Inorder traversal after insertion: ");
tree.inorderTraversal(tree.root);
System.out.println();
// Search for a node
Node foundNode = tree.search(40);
if (foundNode != null)
System.out.println("Node 40 found.");
else
System.out.println("Node 40 not found.");
// Delete a node
tree.delete(30);
System.out.print("Inorder traversal after deletion: ");
tree.inorderTraversal(tree.root);
System.out.println();
}
}Python:
class Node:
def __init__(self, data):
self.data = data
self.isRed = True
self.left = None
self.right = None
self.parent = None
class RedBlackTree:
def __init__(self):
self.root = None
def createNode(self, key):
return Node(key)
def leftRotate(self, x):
y = x.right
x.right = y.left
if y.left:
y.left.parent = x
y.parent = x.parent
if not x.parent:
self.root = y
elif x == x.parent.left:
x.parent.left = y
else:
x.parent.right = y
y.left = x
x.parent = y
def rightRotate(self, y):
x = y.left
y.left = x.right
if x.right:
x.right.parent = y
x.parent = y.parent
if not y.parent:
self.root = x
elif y == y.parent.left:
y.parent.left = x
else:
y.parent.right = x
x.right = y
y.parent = x
def fixInsertion(self, z):
while z != self.root and z.parent.isRed:
if z.parent == z.parent.parent.left:
y = z.parent.parent.right
if y and y.isRed:
z.parent.isRed = False
y.isRed = False
z.parent.parent.isRed = True
z = z.parent.parent
else:
if z == z.parent.right:
z = z.parent
self.leftRotate(z)
z.parent.isRed = False
z.parent.parent.isRed = True
self.rightRotate(z.parent.parent)
else:
y = z.parent.parent.left
if y and y.isRed:
z.parent.isRed = False
y.isRed = False
z.parent.parent.isRed = True
z = z.parent.parent
else:
if z == z.parent.left:
z = z.parent
self.rightRotate(z)
z.parent.isRed = False
z.parent.parent.isRed = True
self.leftRotate(z.parent.parent)
self.root.isRed = False
def insert(self, key):
z = self.createNode(key)
y = None
x = self.root
while x:
y = x
if z.data < x.data:
x = x.left
else:
x = x.right
z.parent = y
if not y:
self.root = z
elif z.data < y.data:
y.left = z
else:
y.right = z
self.fixInsertion(z)
def minValueNode(self, node):
current = node
while current.left:
current = current.left
return current
def fixDeletion(self, x):
while x != self.root and not x.isRed:
if x == x.parent.left:
s = x.parent.right
if s.isRed:
s.isRed = False
x.parent.isRed = True
self.leftRotate(x.parent)
s = x.parent.right
if not s.left.isRed and not s.right.isRed:
s.isRed = True
x = x.parent
else:
if not s.right.isRed:
s.left.isRed = False
s.isRed = True
self.rightRotate(s)
s = x.parent.right
s.isRed = x.parent.isRed
x.parent.isRed = False
s.right.isRed = False
self.leftRotate(x.parent)
x = self.root
else:
s = x.parent.left
if s.isRed:
s.isRed = False
x.parent.isRed = True
self.rightRotate(x.parent)
s = x.parent.left
if not s.right.isRed and not s.left.isRed:
s.isRed = True
x = x.parent
else:
if not s.left.isRed:
s.right.isRed = False
s.isRed = True
self.leftRotate(s)
s = x.parent.left
s.isRed = x.parent.isRed
x.parent.isRed = False
s.left.isRed = False
self.rightRotate(x.parent)
x = self.root
x.isRed = False
def delete(self, key):
z = self.root
while z:
if key == z.data:
break
elif key < z.data:
z = z.left
else:
z = z.right
if not z:
print("Node not found.")
return
x, y = z, z
y_original_color = y.isRed
if not z.left:
x = z.right
self.transplant(z, z.right)
elif not z.right:
x = z.left
self.transplant(z, z.left)
else:
y = self.minValueNode(z.right)
y_original_color = y.isRed
x = y.right
if y.parent == z:
x.parent = y
else:
self.transplant(y, y.right)
y.right = z.right
y.right.parent = y
self.transplant(z, y)
y.left = z.left
y.left.parent = y
y.isRed = z.isRed
if not y_original_color:
self.fixDeletion(x)
del z
def transplant(self, u, v):
if not u.parent:
self.root = v
elif u == u.parent.left:
u.parent.left = v
else:
u.parent.right = v
if v:
v.parent = u.parent
def search(self, key):
current = self.root
while current and current.data != key:
if key < current.data:
current = current.left
else:
current = current.right
return current
def inorderTraversal(self, root):
if root:
self.inorderTraversal(root.left)
print(root.data, end=" ")
self.inorderTraversal(root.right)
# Driver code
if __name__ == "__main__":
tree = RedBlackTree()
# Insert nodes
tree.insert(10)
tree.insert(20)
tree.insert(30)
tree.insert(40)
tree.insert(50)
tree.insert(60)
print("Inorder traversal after insertion: ", end="")
tree.inorderTraversal(tree.root)
print()
# Search for a node
foundNode = tree.search(40)
if foundNode:
print("Node 40 found.")
else:
print("Node 40 not found.")
# Delete a node
tree.delete(30)
print("Inorder traversal after deletion: ", end="")
tree.inorderTraversal(tree.root)
print()Output:
Inorder traversal after insertion: 10 20 30 40 50 60
Node 40 found.
Inorder traversal after deletion: 10 20 40 50 60 Complexity Analysis of Red Black Tree
Time Complexity
The time complexity for search, insert, and delete operations in a Red-Black Tree are all O(log n), where n specifies the number of nodes in the tree.
Space Complexity
It has the space complexity of O(n), where n denotes the number of nodes in the tree.
Applications of Red Black Tree
- Common libraries and data structures like maps and sets in C++, as well as Java’s TreeMap and TreeSet, use Red-Black Trees for efficient searching and sorting.
- Operating systems like Linux employ Red-Black Trees in the CPU scheduling algorithm, such as the Completely Fair Scheduler.
- In machine learning, Red-Black Trees are utilized in algorithms like K-means clustering to reduce time complexity.
- MySQL utilizes Red-Black Trees for indexing tables, enhancing search and insertion efficiency.
- Widely used programming languages such as Java, C++, and Python integrate Red-Black Trees as a built-in data structure for effective data searching and sorting.
- Graph algorithms like Dijkstra’s shortest path and Prim’s minimum spanning tree rely on Red-Black Trees for efficient implementation.
Advantages of Red Black Tree
- Red Black Trees ensure fast operations like insertion, deletion, and searching with a guaranteed time complexity of O(log n).
- They automatically balance themselves, ensuring efficient performance without manual intervention.
- Red Black Trees find use in various applications due to their reliable performance and adaptability.
- The method for balancing Red Black Trees is straightforward and easy to grasp, enhancing their practicality.
Disadvantages of Red Black Tree
- Each node in a Red Black Tree requires an additional bit of storage to store its color (red or black).
- Implementing Red Black Trees may involve some complexity due to the need for managing node colors and ensuring balanced tree structure.
- While Red Black Trees offer efficient performance for common operations, they might not always be the optimal choice for every type of data or specific scenarios.
Conclusion
- Efficiency: Red-Black Trees ensure fast operations with O(log n) time complexity for search, insert, and delete operations.
- Automatic Balancing: Their self-balancing mechanism eliminates the need for manual adjustments, maintaining efficient performance.
- Versatility: Red-Black Trees find applications in various domains like programming, databases, and machine learning due to their reliable performance.
- Simplicity: The rules for balancing Red-Black Trees are straightforward, enhancing their practicality.
- Space Efficiency: While requiring additional storage for color information, Red-Black Trees offer space-efficient storage compared to some other balanced tree structures.