Complete Binary Tree

A binary tree is called complete binary tree when all the level of binary tree is completely filled except possibly the last level, which is filled from left side.

In other words all the nodes are as far left as possible in complete binary tree.

Takeaways

Benefits :

• Make insertion and deletion faster than linked lists and arrays.
• A flexible way of holding and moving data.
• Are used to store as many nodes as possible.

Introduction to Complete Binary Tree

A binary tree is called complete binary tree when all the level of binary tree is completely filled except possibly the last level, which is filled from left side.

Difference between a complete binary tree and a full binary tree is that, in a complete binary tree all leaf nodes should lean towards left and the last nodes need not to have a right sibling.

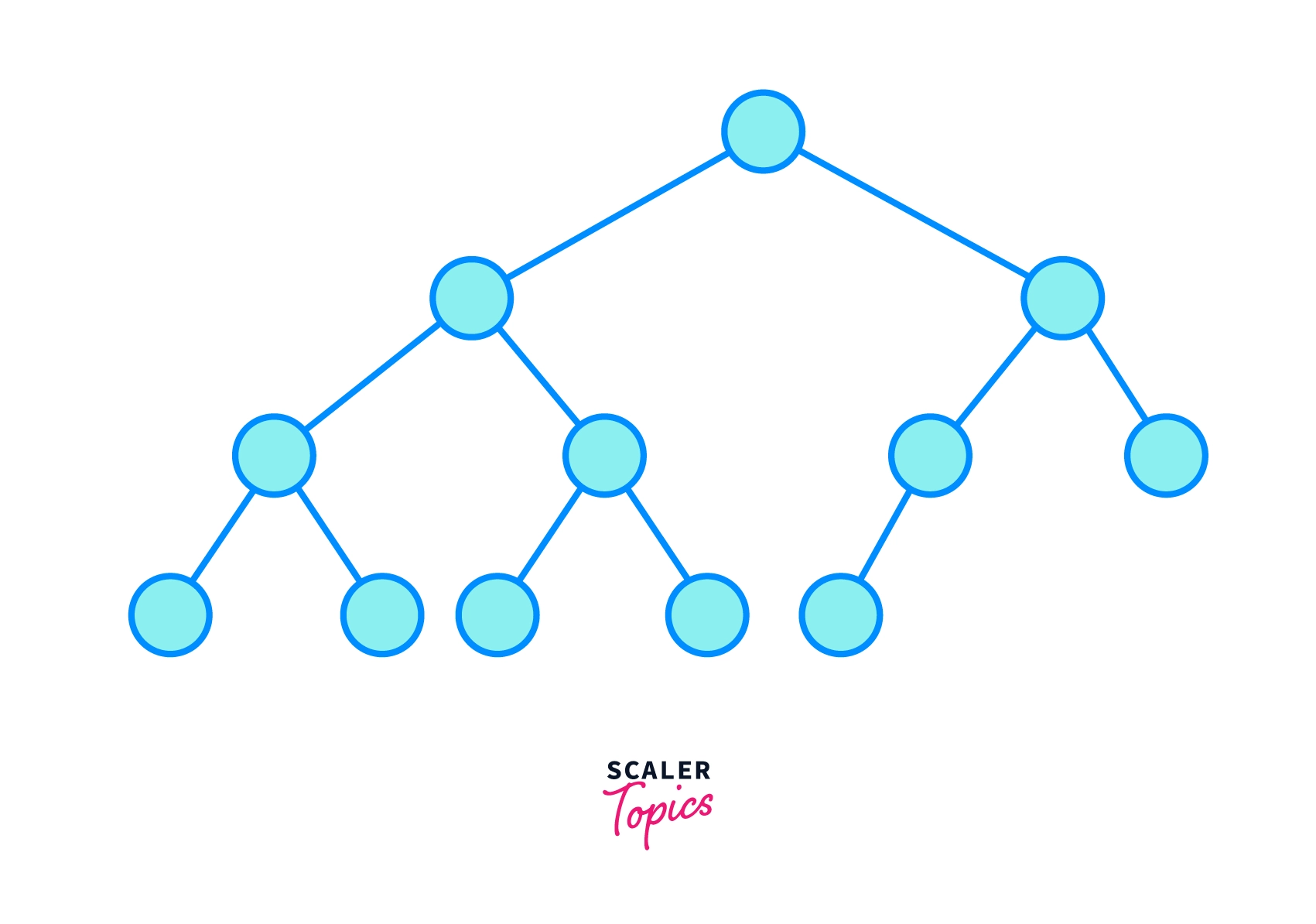
In the above image we can see that in complete binary tree all the level except the last one is completely filled and in the last level all the nodes filled from the left side.

It is used in Heap Data Structure and Heap sorting. In Dijkstra’s algorithm that finds the shortest path where Heap Sort is implemented.

Min heap maintain the shape property , so it is a complete binary tree. The shape property of the tree ensures that all levels are fully filled, except the last one, and, if the last level is not filled completely, then fill the elements from left to right.

What is a Complete Binary Tree?

Tree is a non linear data structure. A general tree has no limitation on his children it can be more than two but this is not true in case of binary tree .

A binary tree is a tree data structure in which each node has atmost two child which are referred to as the left child and right child.

Complete Binary Tree

A complete binary tree is a type of binary tree in which all the levels are completely filled(i.e, have two children), except the possibly the deepest level. The deepest level can have nodes that can have either one left child or can be completely full.

A complete binary tree can be a full binary tree (when the deepest levels are completely full).

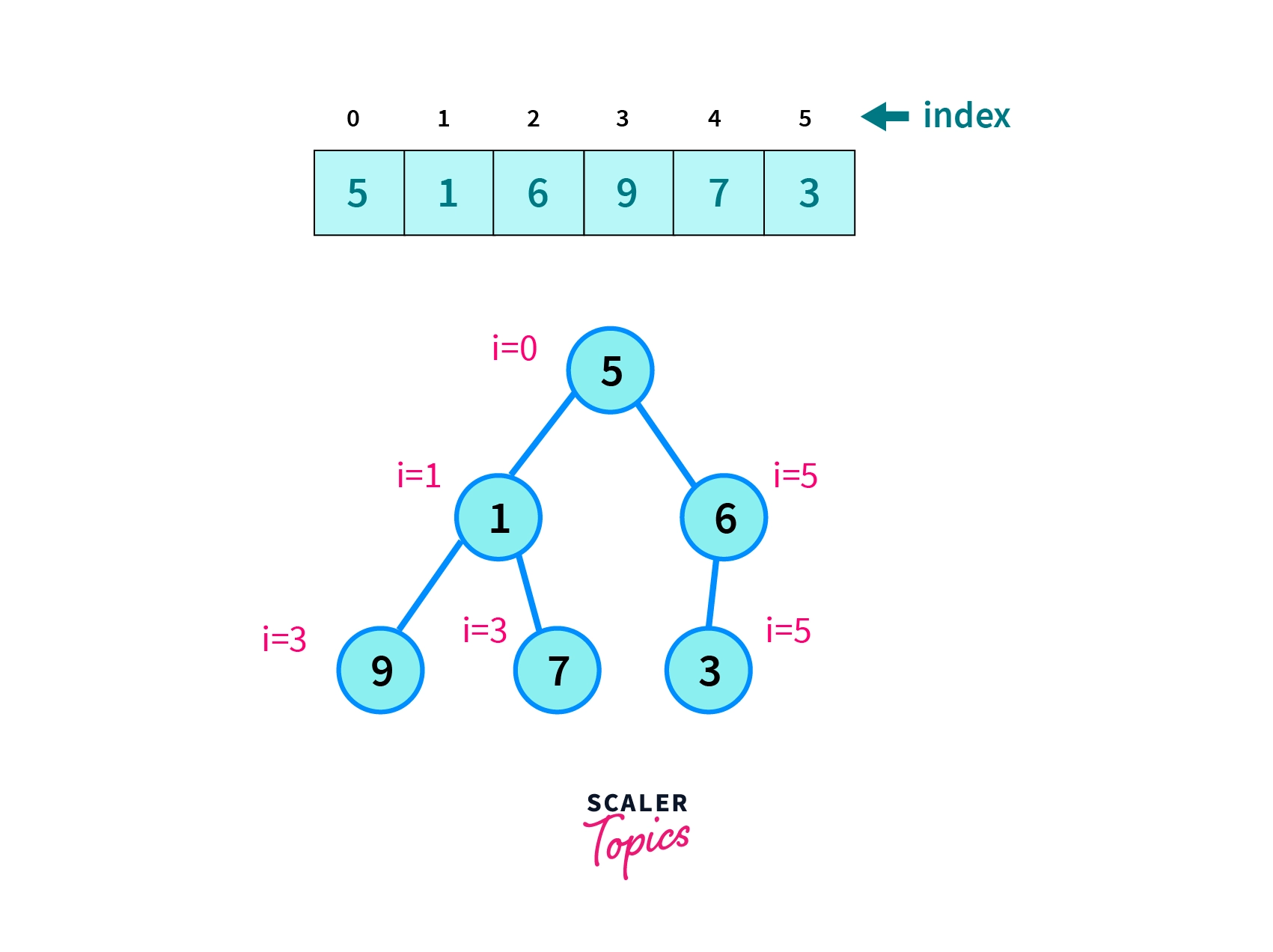
How a Complete Binary Tree is Created?

Complete Binary Tree is a binary Tree in which at every level l except the last level has 2l nodes and the nodes at last nodes are line up from left side.

It can be represented using array. Given parent is at index i so its left child is at 2i+1 and its right child is given by 2i+2

Algorithm

For creation of Complete Binary Tree when nodes is inserted in a tree in level order manner and it should be inserted from leftmost position.

Queue data structure is used to keep track of inserted nodes.

Steps to insert a node in a Complete Binary Tree:-

1. Initialize the root with new node if the tree is empty.
2. If the tree is not empty then get the front element of the queue
   • If the front element doesn’t have left child , then set the left child as a new node
   • else if right child is not present then set the right child as the new node
3. And if the front node has both the children then dequeue it from the queue
4. Enqueue the new data

Intuition behind the Algorithm

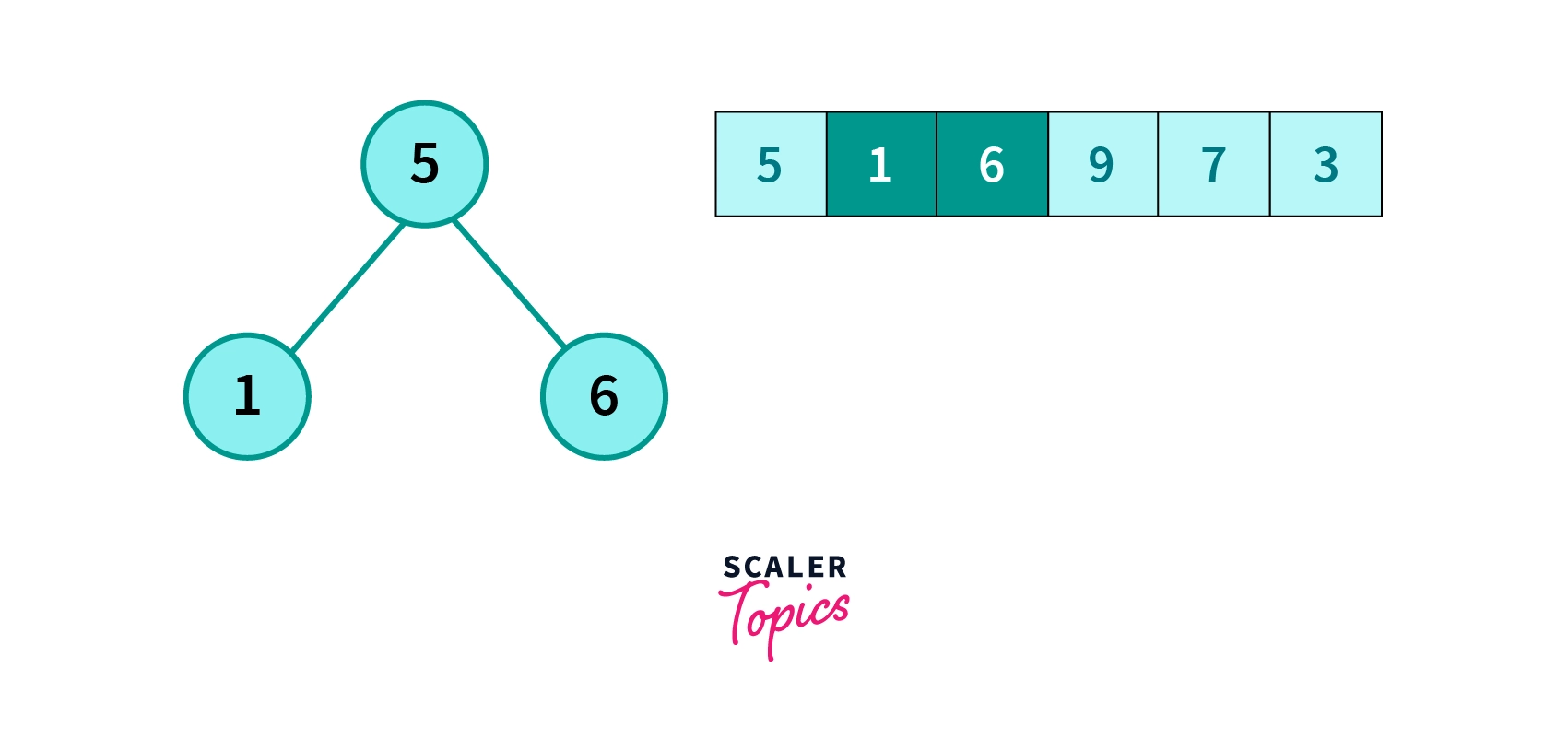
1. The first element from left of the list is selected as root node.

2. The next element will be left child and third element will be right child of the root node.

3. The fourth and fifth element will be left and right child of the left child of root node.

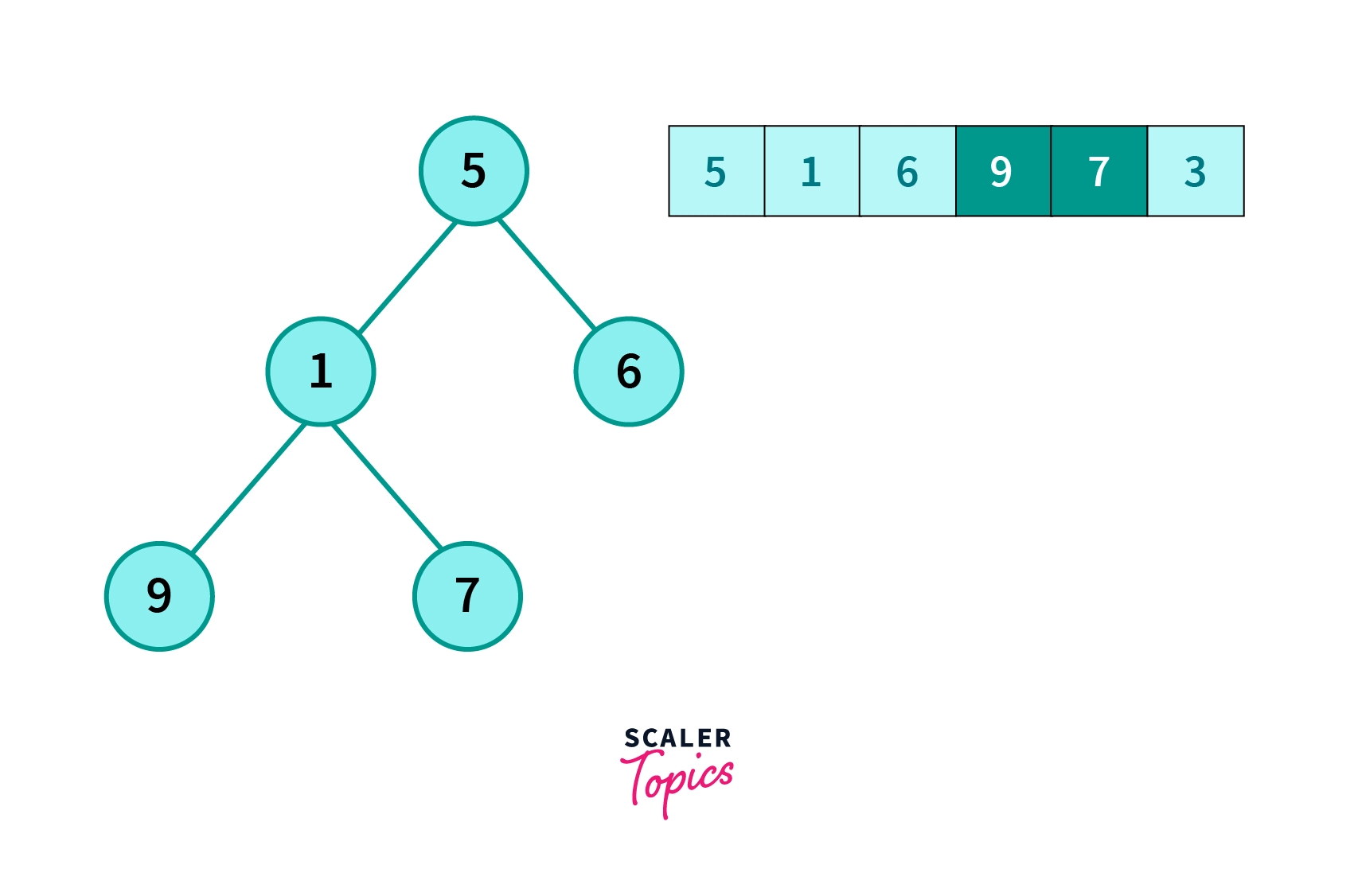
4. The next element will be left child of the right child of root node.

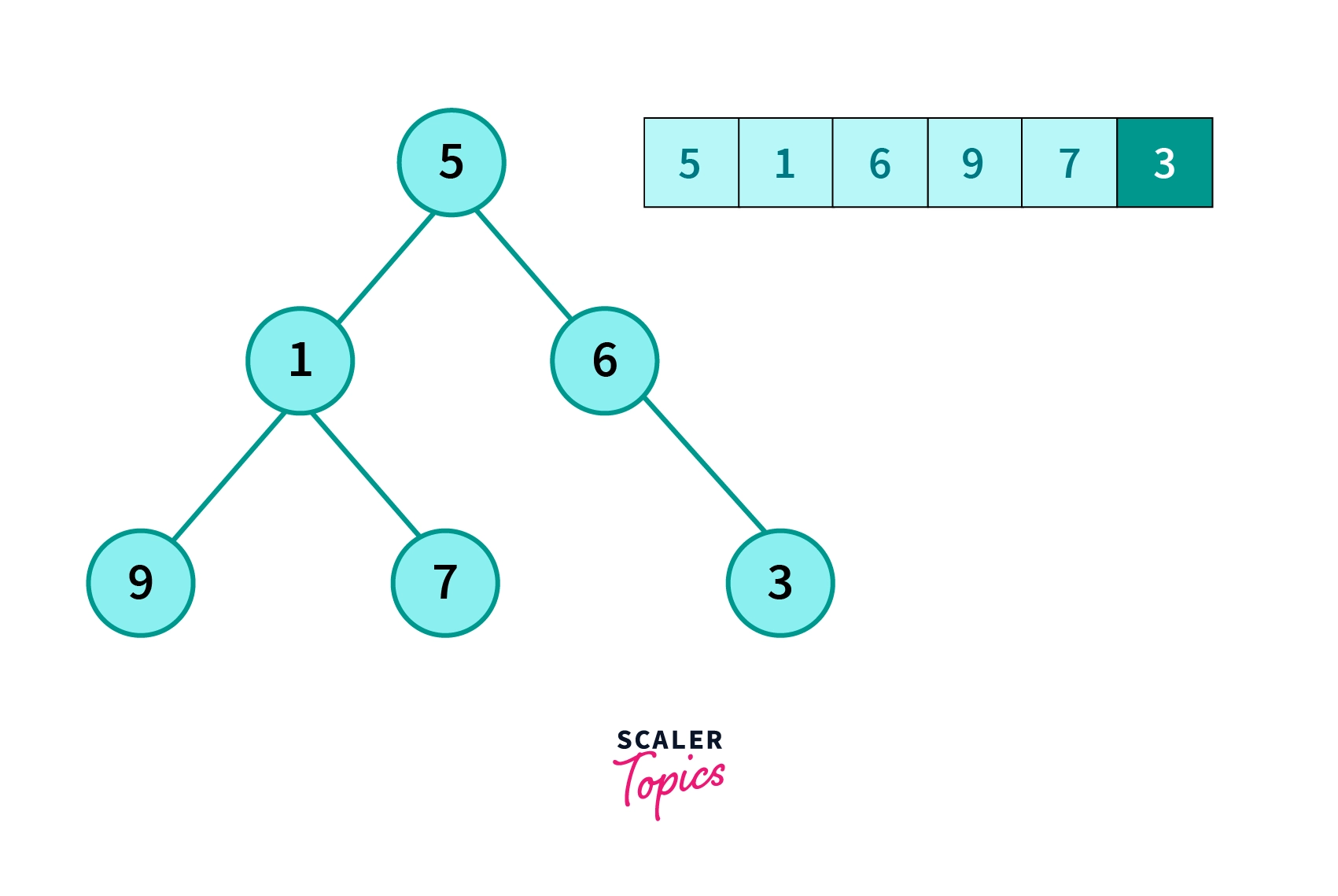
Example of Complete Binary Tree

If a binary tree is a complete binary tree then its left and the right child’s index of any node is less than the total number of nodes for every node.

1. Check if a binary tree is a complete binary tree in Java

class Node {
  int data;
  Node left_child, right_child;

  Node(int info) {
    data = info;
    left_child = null;
    right_child = null;
  }
}

class Tree {
  Node root;

// Funtion to Check if the Tree is complete binary Tree or not
  boolean check(Node root, int index, int numberNodes) 
 {

    // Checking if tree is empty or not 
    if (root == null)
      return true;

    // if index of node is greater than number of nodes then return false
    if (index >= numberNodes)
      return false;

    return (check(root.left_child, 2 * index + 1, numberNodes) && check(root.right_child, 2 * index + 2, numberNodes));
  }

  // Funtion to calculate numbers of node
  int count(Node root) {
    if (root == null)
      return (0);
    return (1 + count(root.left_child) + count(root.right_child));
  }

  public static void main(String args[]) 
 {


    Tree tree = new Tree();

    tree.root = new Node(5);
    tree.root.left_child = new Node(8);
    tree.root.right_child = new Node(11);
    tree.root.left_child.right_child = new Node(13);
    tree.root.left_child.left_child = new Node(16);
    tree.root.right_child.left_child = new Node(19);

    int node_count = tree.count(tree.root);
    int index = 0;

    if (tree.check(tree.root, index, node_count))
      System.out.println("This tree is a Complete Binary Tree \n");
    else
      System.out.println("This tree is not a Complete Binary Tree \n");

  }
}

2. Check if a binary tree is a complete binary tree in C++

#include <bits/stdc++.h>

using namespace std;

class Node{
    public:
    int key;
    Node *left_child;
    Node *right_child;
    Node(int data)
    {
        key=data;
        left_child=right_child=NULL;
    }
};


// Funtion to Check if the Tree is complete binary Tree or not
bool check(struct Node *Root, int index, int Node_number) 
{
  // Checking if tree is empty or not 
  if (Root == NULL)
    return true;

  // if index of node is greater than number of nodes then return false
  if (index >= Node_number)
    return false;

  return (check(Root->left_child, 2 * index + 1, Node_number) && check(Root->right_child, 2 * index + 2, Node_number));
}

// Funtion to calculate numbers of node
int count(struct Node *Root) 
{
  if (Root == NULL)
    return 0;
  int a=1 + count(Root->left_child) + count(Root->right_child);
  return a;
}

int main() 
{

  Node *Root = NULL;

  Root = new Node(5);
  Root->left_child = new Node(8);
  Root->right_child = new Node(11);
  Root->left_child->left_child = new Node(13);
  Root->left_child->right_child = new Node(16);
  Root->right_child->left_child = new Node(19);


  int index = 0;
  int Node_count = count(Root);

  if (check(Root, index, Node_count))
    cout<<"This tree is a Complete Binary Tree"<<endl;
  else
    cout<<"This tree is not a Complete Binary Tree"<<endl;

  return 0;
}

Other Methods to Check if a Binary Tree is a Complete Binary Tree or Not

Given a binary tree, check if it is a complete binary tree or not.

A binary tree is called complete binary tree when all the level of binary tree is completely filled except possibly the last level, which is filled from left side.

In other words all the nodes are as far left as possible in complete binary tree.

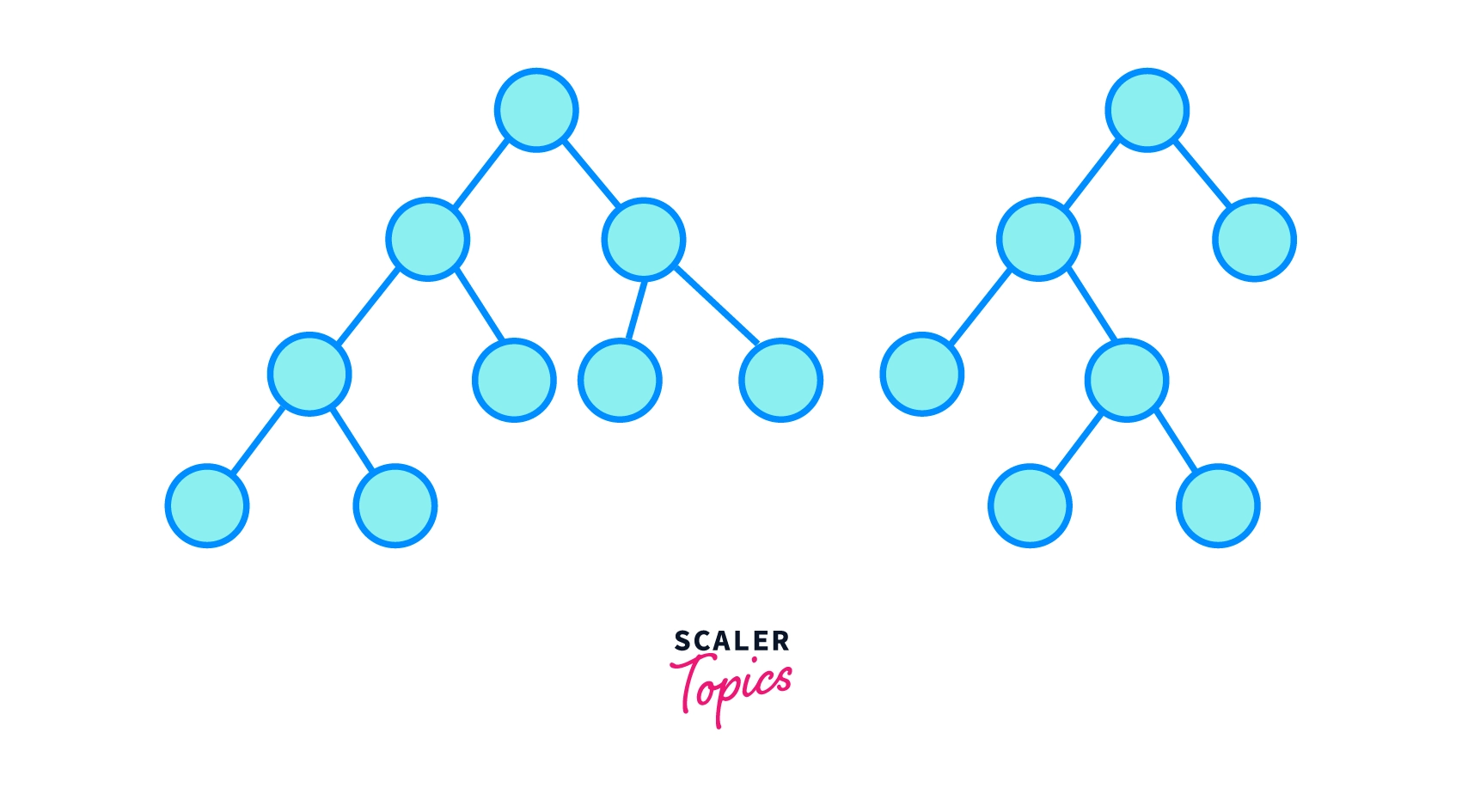
1. Level Order Traversal (BFS)

By modifying the level order traversal one can check if a given binary tree is complete or not. This is achieved by checking that each node is full node(having both right and left child) .

If any node is not a full node i.e having zero or only one child , then one should check the remaining nodes. The remaining nodes must not have any children .

If the remaining nodes have children then it is not a complete binary tree.

In this implementation we will use deque data structure. First we will insert the root node in deque and then we iterate over the deque until its size become 0.

In each iteration pop the front element and check if we have encountered a non-full node before and the current node is not a leaf node then tree is not a complete binary tree or if the left child is empty and right child is exist of the current node , then tree is not complete so return false.

If this two conditions are not true then check if the left child exist then enqueue it and do the same thing for the right child also.

a. Implementation of algorithm in C++

#include <bits/stdc++.h>

using namespace std;

class Node{
    public:
    int key;
    Node *left_child;
    Node *right_child;
    Node(int data)
    {
        key=data;
        left_child=right_child=NULL;
    }
};


// Funtion to Check if the Tree is complete binary Tree or not
bool check(Node *Root) 
{
    // if the tree is empty return true
    if (Root == NULL) {
        return true;
    }

    // cur denotiong the currnt node
    Node* cur = NULL;

    // create an deque
    deque<Node*> pq;
    pq.push_back(Root);

    // flag to mark the end of full nodes
    bool flag = false;

    while (pq.size())
    {
        // remove front node
        cur = pq.front();
        pq.pop_front();

        //if we have encountered a non-full node before and the current node is not a leaf node 
        // then tree is not a complete binary tree
        if (flag && (cur->left_child || cur->right_child)) {
            return false;
        }

        // if the left child is empty and right child is exist of the current
        // node , then tree is not complete so return false
        if (cur->left_child == NULL && cur->right_child) {
            return false;
        }

        // if the left child exists of the current node, enqueue it
        if (cur->left_child) {
            pq.push_back(cur->left_child);
        }
        // if the current node doestn't have both children, 
        // set the flag to true
        else {
            flag = true;
        }


        // if the right child exists of the current node, enqueue it
        if (cur->right_child) {
            pq.push_back(cur->right_child);
        }
        // if the current node doestn't have both children, 
        // set the flag to true
        else {
            flag = true;
        }
    }

    return true;
}

int main() 
{

  Node *Root = NULL;

  Root = new Node(5);
  Root->left_child = new Node(8);
  Root->right_child = new Node(11);
  Root->left_child->left_child = new Node(13);
  Root->left_child->right_child = new Node(16);
  Root->right_child->left_child = new Node(19);


  int index = 0;
//   int Node_count = count(Root);

  if (check(Root))
    cout<<"This tree is a Complete Binary Tree"<<endl;
  else
    cout<<"This tree is not a Complete Binary Tree"<<endl;

  return 0;
}

Time Complexity :- O(n) Space Complexity :- O(n)

where n is the size of binary tree.

b. Implementation of algorithm in JAVA

import java.util.ArrayDeque;
import java.util.Queue;
class Node {
  int data;
  Node left_child, right_child;

  Node(int info) {
    data = info;
    left_child = null;
    right_child = null;
  }
}

class Tree {
  Node root;

// Funtion to Check if the Tree is complete binary Tree or not
  boolean check(Node Root) 
 {

    // if the tree is empty return true
    if (Root == null) {
        return true;
    }

    // cur denotiong the currnt node
    Node cur = null;

    // create an empty queue 
    Queue<Node> pq = new ArrayDeque<>();
    pq.add(root);

    // flag to mark the end of full nodes
    boolean flag = false;


        while (!pq.isEmpty())
        {
            // dequeue front node
            cur = pq.poll();

        //if the current node is not a leaf node and if it doesn't have both
        //left and right children the return false
        if (flag && ( cur.left_child!=null || cur.right_child!=null )) {
            return false;
        }

        // if the left child is empty and right child is exist of the current
        // node , then tree is not complete so return false
        if (cur.right_child!=null && cur.left_child == null) {
            return false;
        }

        // if the left child exists of he current node, enqueue it
        if (cur.left_child!=null) {
            pq.add(cur.left_child);
        }
        // if the current node doestn't have both children, 
        // set the flag to true
        else {
            flag = true;
        }


        // if the right child exists of he current node, enqueue it
        if (cur.right_child!=null) {
            pq.add(cur.right_child);
        }
        // if the current node doestn't have both children, 
        // set the flag to true
        else {
            flag = true;
        }
  }
  return true;
}


  public static void main(String args[]) 
 {


    Tree tree = new Tree();

    tree.root = new Node(5);
    tree.root.left_child = new Node(8);
    tree.root.right_child = new Node(11);
    tree.root.left_child.right_child = new Node(13);
    tree.root.left_child.left_child = new Node(16);
    tree.root.right_child.left_child = new Node(19);



    if (tree.check(tree.root))
      System.out.println("This tree is a Complete Binary Tree \n");
    else
      System.out.println("This tree is not a Complete Binary Tree \n");

  }
}

Time Complexity :- O(n) Space Complexity :- O(n)

where n is the size of binary tree.

2. Array representation of a complete binary tree

This problem can be solved by using a property of complete binary tree. In array representation, the left child and right child for any given node at index 'i' is present at '2i+1' and '2i+2' respectively.

Now, when constructing an array from the tree, the elements will be at their respective positions with respect to complete binary tree.

Thus presence of any vacant position means the tree is not complete.

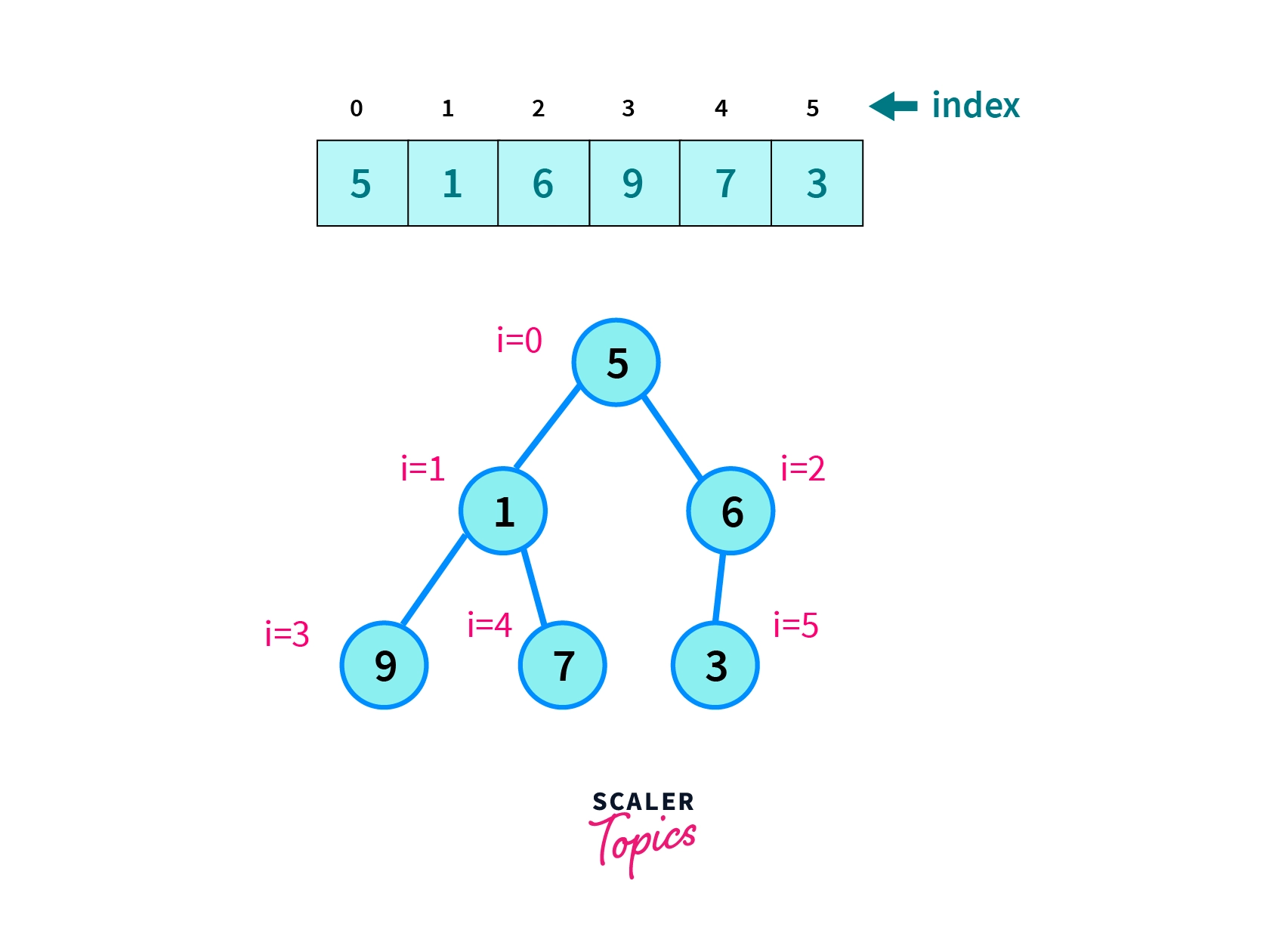
Array representation of a complete binary tree

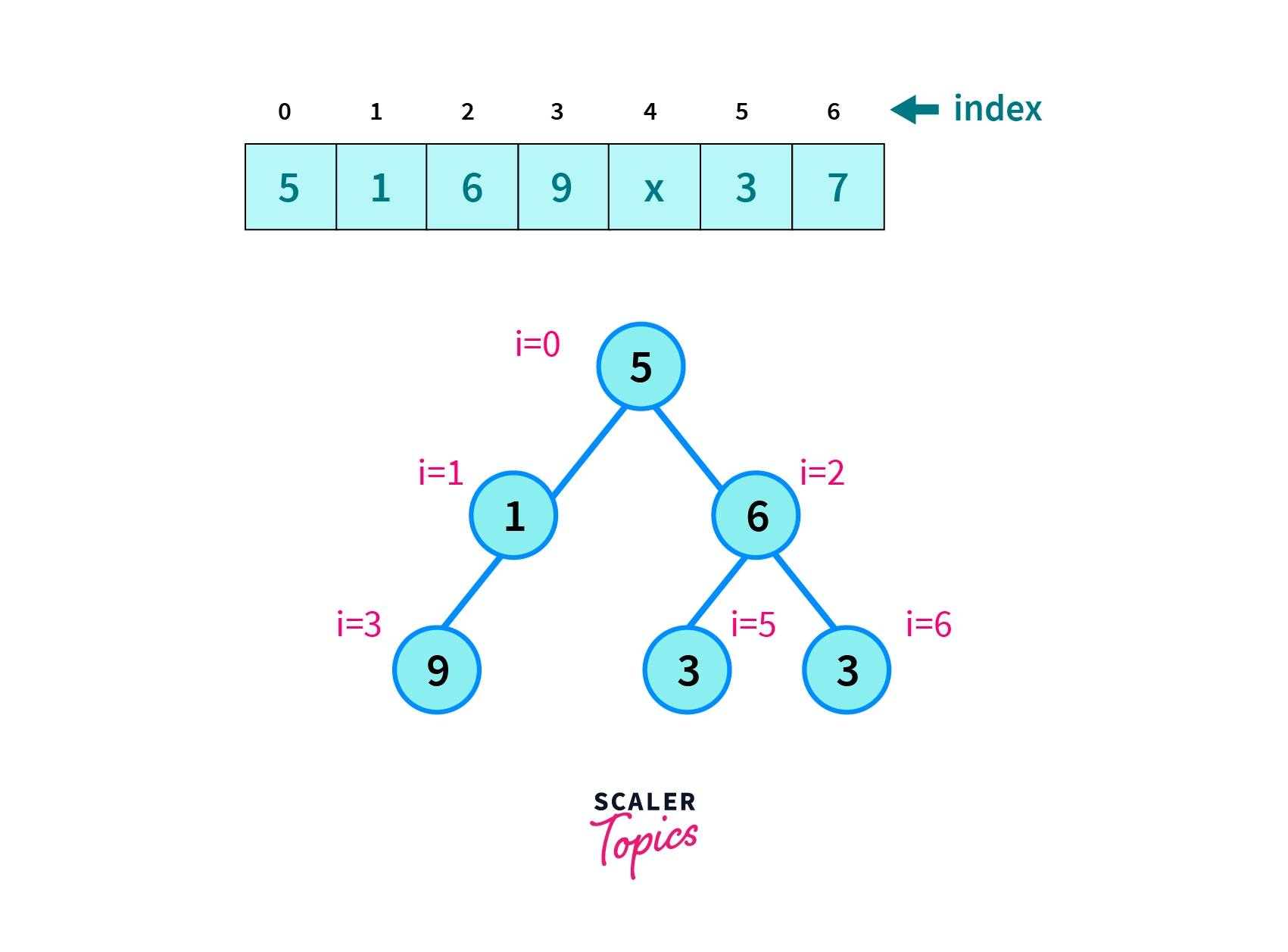
Array representation of a non-complete binary tree

a. Implementation of algorithm in C++

#include <bits/stdc++.h>

using namespace std;

class Node{
    public:
    int key;
    Node *left_child;
    Node *right_child;
    Node(int data)
    {
        key=data;
        left_child=right_child=NULL;
    }
};

void Inorder_traversal(vector<int> &v, int i ,Node* Root)
{
    if (Root == NULL) {
        return;
    }

    Inorder_traversal(v, 2*i + 1,Root->left_child);

    v[i] = 1;

    Inorder_traversal(v, 2*i + 2,Root->right_child);
}
// Funtion to Check if the Tree is complete binary Tree or not
bool check(struct Node *Root, int Node_number) 
{
  // Checking if tree is empty or not 
  if (Root == NULL)
    return true;

  //create a vector of lenght of Node_number
  vector<int> v(Node_number);

  // store the inorder traversal in vector v
  Inorder_traversal(v,0,Root);

  //check if all the position is filled or not
  for(int i=0;i<Node_number;i++)
  {
      if(v[i]==0)
      return false;
  }
  return true;
}

// Funtion to calculate numbers of node
int count(struct Node *Root) 
{
  if (Root == NULL)
    return 0;
  int a=1 + count(Root->left_child) + count(Root->right_child);
  return a;
}

int main() 
{

  Node *Root = NULL;

  Root = new Node(5);
  Root->left_child = new Node(8);
  Root->right_child = new Node(11);
  Root->left_child->left_child = new Node(13);
  Root->left_child->right_child = new Node(16);
  Root->right_child->left_child = new Node(19);

  int Node_count = count(Root);

  if (check(Root, Node_count))
    cout<<"This tree is a Complete Binary Tree"<<endl;
  else
    cout<<"This tree is not a Complete Binary Tree"<<endl;

  return 0;
}
}

Time Complexity :- O(n) Space Complexity :- O(n)

where n is the size of binary tree.

b. Implementation of algorithm in JAVA

class Node {
  int data;
  Node left_child, right_child;

  Node(int info) {
    data = info;
    left_child = null;
    right_child = null;
  }
}

class Tree {
  Node root;

  void Inorder_traversal(int[] v, int i ,Node Root)
{
    if (Root == null) {
        return;
    }

    Inorder_traversal(v, 2*i + 1,Root.left_child);

    v[i] = 1;

    Inorder_traversal(v, 2*i + 2,Root.right_child);
}
  // Funtion to Check if the Tree is complete binary Tree or not
  boolean check(Node Root, int numberNodes) 
 {

    // Checking if tree is empty or not 
  if (Root == null)
    return true;

  //create a array of lenght of Node_number
  int[] v=new int[numberNodes];

  // store the inorder traversal in vector v
  Inorder_traversal(v,0,Root);

  //check if all the position is filled or not
  for(int i=0;i<numberNodes;i++)
  {
      if(v[i]==0)
      return false;
  }
  return true;
  }

  // Funtion to calculate numbers of node
  int count(Node root) {
    if (root == null)
      return 0;
    return (1 + count(root.left_child) + count(root.right_child));
  }

  public static void main(String args[]) 
 {


    Tree tree = new Tree();

    tree.root = new Node(5);
    tree.root.left_child = new Node(8);
    tree.root.right_child = new Node(11);
    tree.root.left_child.right_child = new Node(13);
    tree.root.left_child.left_child = new Node(16);
    tree.root.right_child.left_child = new Node(19);

    int node_count = tree.count(tree.root);
    int index = 0;

    if (tree.check(tree.root, node_count))
      System.out.println("This tree is a Complete Binary Tree \n");
    else
      System.out.println("This tree is not a Complete Binary Tree \n");

  }
}

Time Complexity :- O(n) Space Complexity :- O(n)

where n is the size of binary tree.

3. Space-optimized Way to Represent Complete Binary Tree as an Array

The above method uses extra space for the storage of boolean array. And know that in a complete binary tree, index of the child of left and right node is less than the total number of nodes for every node. The extra space can be avoided by passing the index as recursion parameter and checking for each and every node that their left and right child’s index are in the correct range.

a. Implementation of algorithm in C++

#include <bits/stdc++.h>

using namespace std;

class Node{
    public:
    int key;
    Node *left_child;
    Node *right_child;
    Node(int data)
    {
        key=data;
        left_child=right_child=NULL;
    }
};


// Funtion to Check if the Tree is complete binary Tree or not
bool check(struct Node *Root, int index, int Node_number) 
{
  // Checking if tree is empty or not 
  if (Root == NULL)
    return true;

  if (index >= Node_number)
    return false;

  return (check(Root->left_child, 2 * index + 1, Node_number) && check(Root->right_child, 2 * index + 2, Node_number));
}

// Funtion to calculate numbers of node
int count(struct Node *Root) 
{
  if (Root == NULL)
    return 0;
  int a=1 + count(Root->left_child) + count(Root->right_child);
  return a;
}

int main() 
{

  Node *Root = NULL;

  Root = new Node(5);
  Root->left_child = new Node(8);
  Root->right_child = new Node(11);
  Root->left_child->left_child = new Node(13);
  Root->left_child->right_child = new Node(16);
  Root->right_child->left_child = new Node(19);


  int index = 0;
  int Node_count = count(Root);

  if (check(Root, index, Node_count))
    cout<<"This tree is a Complete Binary Tree"<<endl;
  else
    cout<<"This tree is not a Complete Binary Tree"<<endl;

  return 0;
}

Time Complexity :- O(n) Space Complexity :- O(h) space requires for call stack .

where n is the size of binary tree and h is the height of tree.

b. Implementation of algorithm in JAVA

class Node {
  int data;
  Node left_child, right_child;

  Node(int info) {
    data = info;
    left_child = null;
    right_child = null;
  }
}

class Tree {
  Node root;

// Funtion to Check if the Tree is complete binary Tree or not
  boolean check(Node root, int index, int numberNodes) 
 {

    // Checking if tree is empty or not 
    if (root == null)
      return true;

    if (index >= numberNodes)
      return false;

    return (check(root.left_child, 2 * index + 1, numberNodes) && check(root.right_child, 2 * index + 2, numberNodes));
  }

  // Funtion to calculate numbers of node
  int count(Node root) {
    if (root == null)
      return (0);
    return (1 + count(root.left_child) + count(root.right_child));
  }

  public static void main(String args[]) 
 {


    Tree tree = new Tree();

    tree.root = new Node(5);
    tree.root.left_child = new Node(8);
    tree.root.right_child = new Node(11);
    tree.root.left_child.right_child = new Node(13);
    tree.root.left_child.left_child = new Node(16);
    tree.root.right_child.left_child = new Node(19);

    int node_count = tree.count(tree.root);
    int index = 0;

    if (tree.check(tree.root, index, node_count))
      System.out.println("This tree is a Complete Binary Tree \n");
    else
      System.out.println("This tree is not a Complete Binary Tree \n");

  }
}

Time Complexity :- O(n) Space Complexity :- O(h) space requires for call stack .

where n is the size of binary tree and h is the height of tree.

Full Binary Tree vs Complete Binary Tree

Full Binary Tree

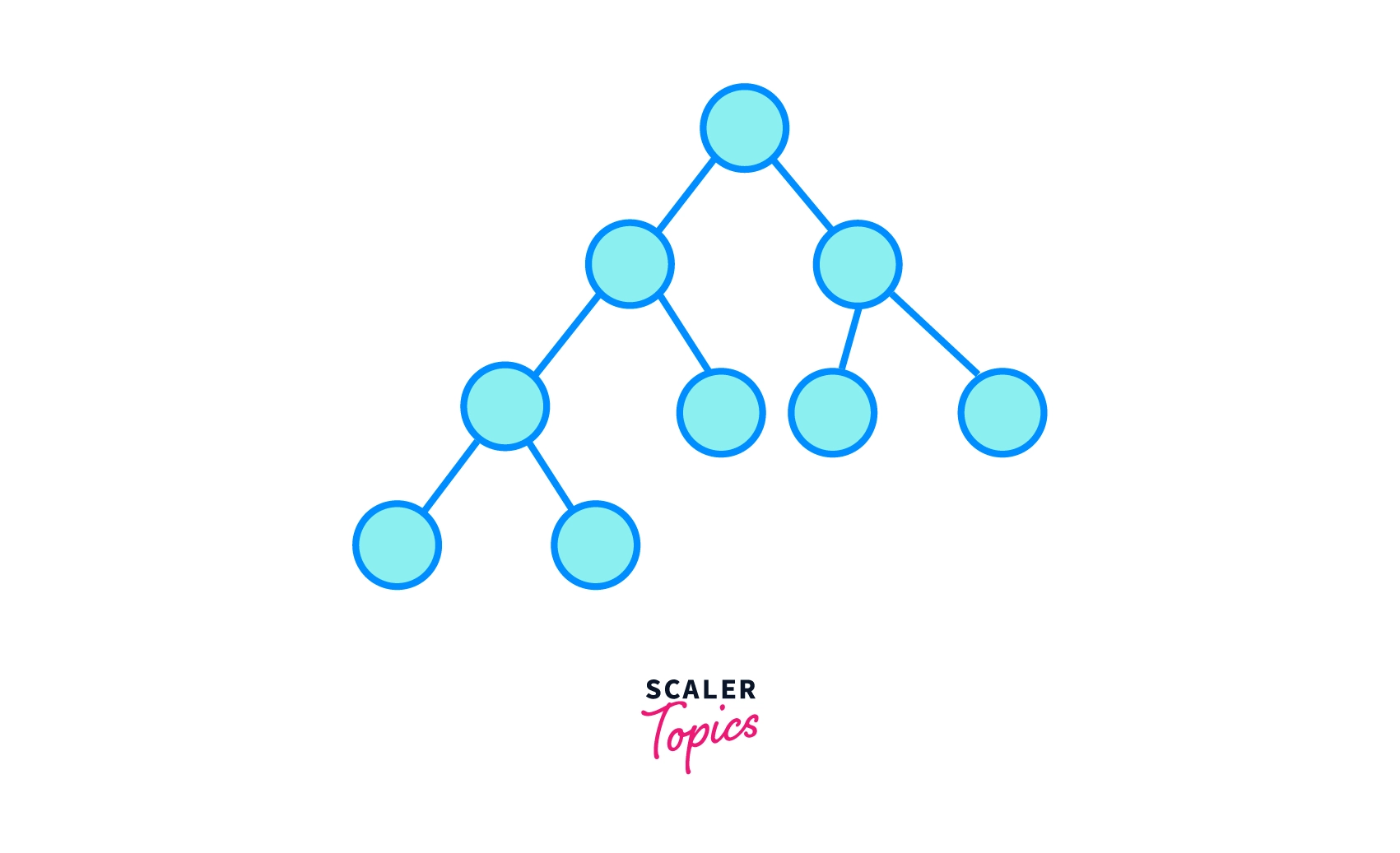
Given binary tree can be called a full binary tree if all the nodes have two children except for the leaf nodes which shouldn’t have any child.

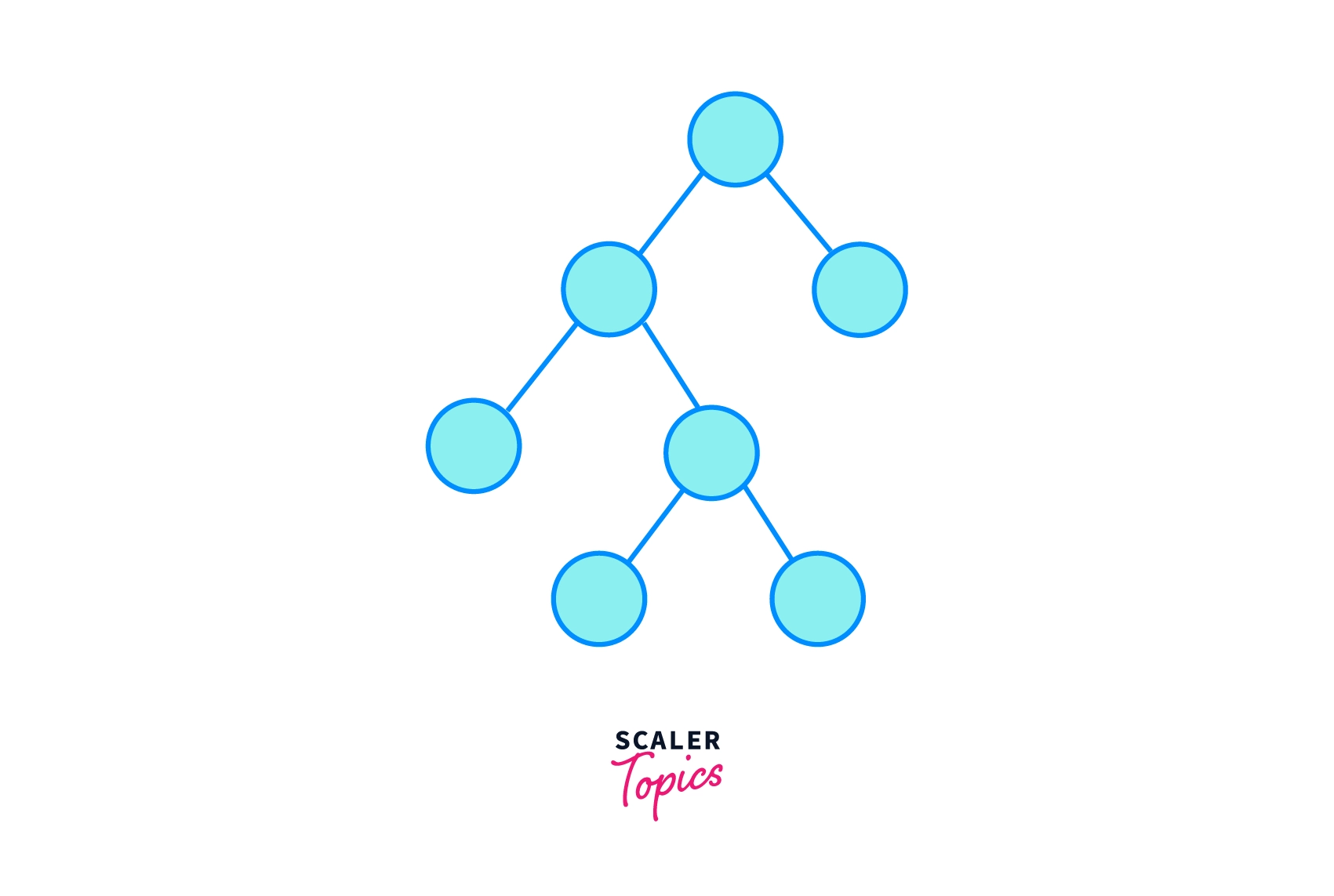
The above tree is Full Binary Tree

Complete Binary Tree

Given binary tree can be called a complete binary tree if all the levels have both child except for the deepest nodes (which is filled from left) which can be partially or completely filled.

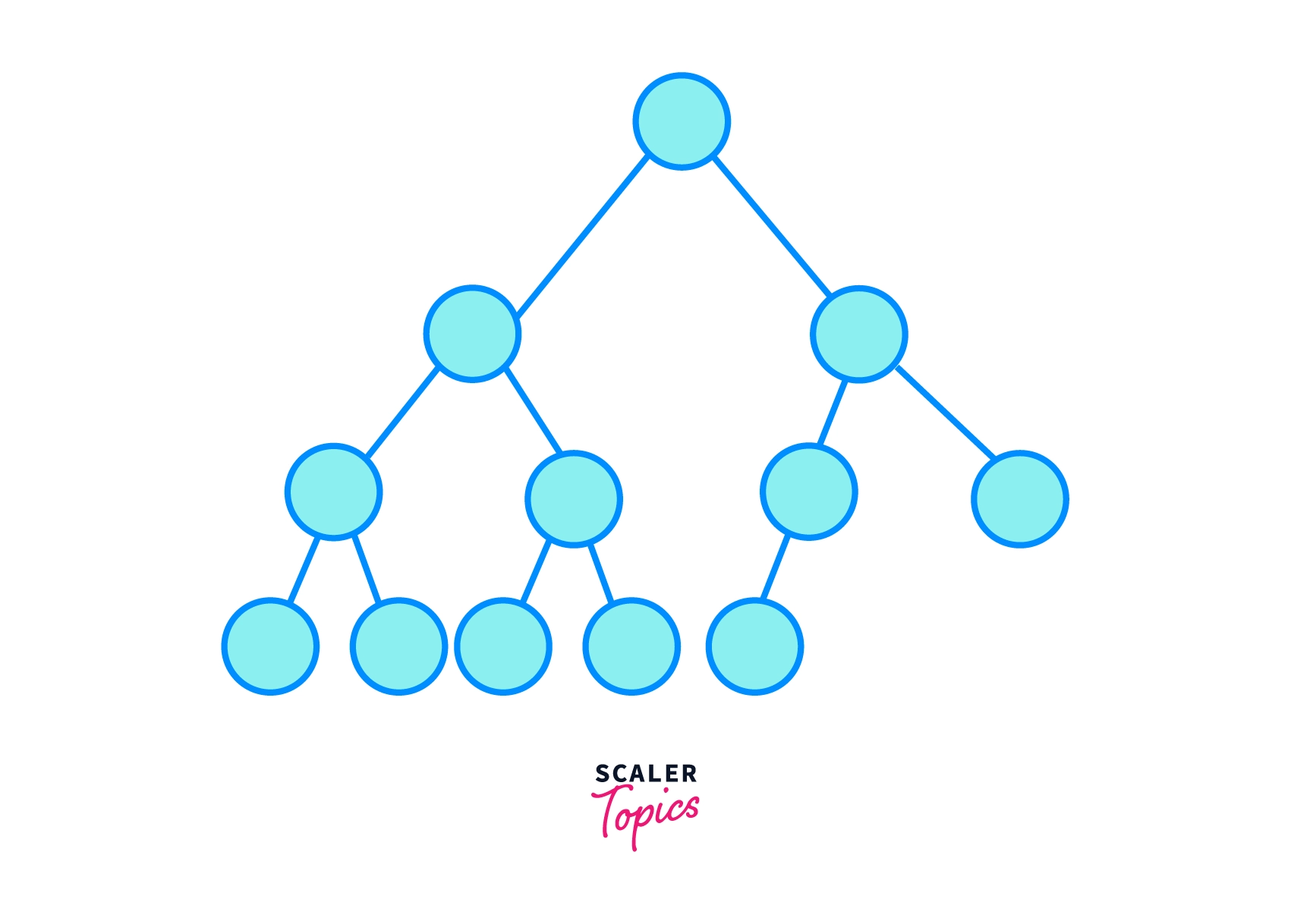
The above tree is Full Binary Tree

Complete binary tree and full binary tree are similar besides the following two difference:

1. The left node must be filled from left side.
2. The deepest node may not have the right sibling

Complete Binary Tree Applications

• Heap-based data structures
• Heap Sort

Conclusion

• In this article we learned about complete binary tree in which all the level are completely filled expect the last level which is filled from left side.
• We learned algorithm for creation of complete binary tree.
• In this article we learned different methods to check whether a tree is complete binary tree or not.
• We learned how complete binary tree is different from full binary tree.
• We learned Application of complete binary tree.