Problem Statement
Given an array aa, and an integer kk, find the maximum element for every contiguous subarray of size kk.
Examples
Example 1
Input :
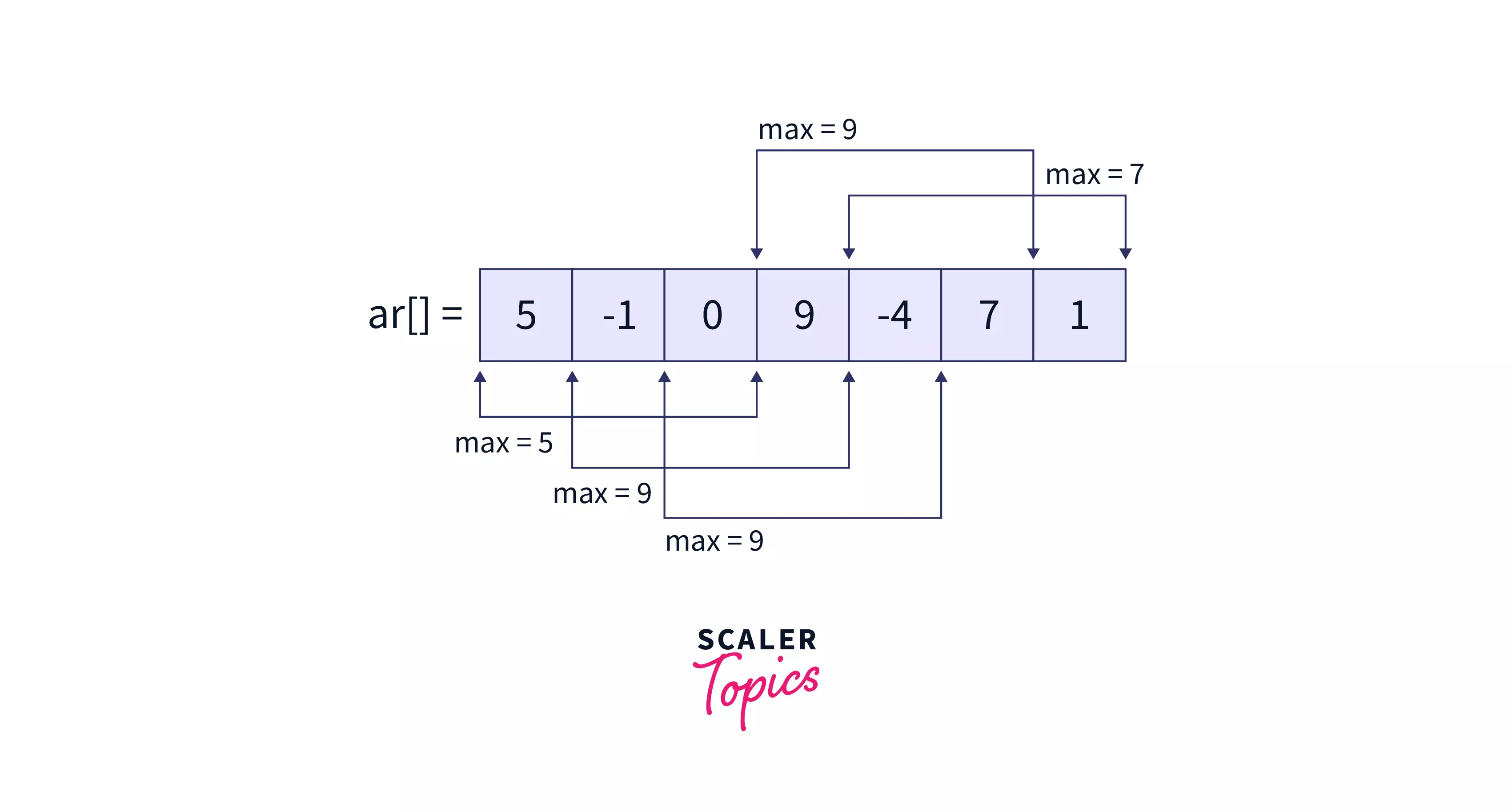
a[ ] = [5, -1, 0, 9, -4, 7, 1], k=3
Output :
5 9 9 9 7
Explanation :
- Maximum of first window $i.e. [5, -1, 0]$ is
5. - Maximum of second window $i.e. [-1, 0, 9]$ is
9. - Maximum of third window $i.e. [0, 9, -4]$ is
9. - Maximum of fourth window $i.e. [9, -4, 7]$ is
9. - Maximum of fifth window $i.e. [-4, 7, 1]$ is
7.
Example 2
Input :
a[ ] = [2, -3, 6, 6, -1, 7, -6, 8], k=5
Output :
6 7 7 8
Explanation :
- Maximum of first window $i.e. [2, -3, 6, 6, -1]$ is
6. - Maximum of second window $i.e. [-3, 6, 6, -1, 7]$ is
7. - Maximum of third window $i.e. [6, 6, -1, 7, 1]$ is
7. - Maximum of fourth window $i.e. [6, -1, 7, 1, 8]$ is
7.
Constraints
- $0\leq a.length \leq 10^5$
- $-10^9 \leq a[i] \leq 10^9$
- $1\leq k\leq n$
Approach 1: Brute Force
The first approach that comes to our mind while reading the problem, is to run two nested loops to find the maximum element of each window of size $k$.
The idea is quite basic, we will use two nested for loops, where the first loop will mark the starting point (say $i$) of the subarray of length $k$, and the inner loop will run from $i$ to $i+k$ and find the maximum element in the range.
The algorithm is as follows –
- Let’s say we have an array $a$ of size $n$, we need to print the maximum of every window of size $k$.
- Iterate from $i=0$ to $i=n-k$ and do the following –
- Declare a variable (say $max$) and initialize it very small value (say $-\infty$).
- Iterate from $j=i$ to $j=i+k-1$ and do the following –
- If $a[j]>max$, update the value of $max$ to $a[j]$.
- Print $min$, which now denotes the maximum element of the window of size $k$ starting from $i$.
Note that in the outer loop we are iterating till $i=n-k$ because the starting point of the last window will be $n-k$.
Pseudocode
// Function to pr maximum element of
// each window of size k.
function slidingWindowMaximum(a, n, k)
// Iterate from i=0 to i = n-k
For (i = 0 To i = n - k)
// Intialize a variable 'max',
// with a very samll value.
max = -Infinity
// Iterate for the window of size 'k', starting from 'i'.
For (j = i To j = i + k - 1)
// If a[j] is greater than max,
// update it.
If (a[j] > max):
max = a[j]
// Print the maximum element found
// in this window.
print (max)
end function
Java Implementation
public class Main{
// Function to print maximum element of
// each window of size k.
static void slidingWindowMaximum(int a[], int n, int k){
// Iterate from i=0 to i = n-k
for (int i = 0; i <= n-k; i++){
// Intialize a variable 'max',
// with a very samll value/
int max = Integer.MIN_VALUE;
// Iterate for the window of size 'k', starting from 'i'.
for(int j = i; j < i + k; j++){
// If a[j] is greater than max,
// update it.
if (a[j] > max)
max = a[j];
}
// Print the maximum element found
// in this window.
System.out.print(max + " ");
}
System.out.println();
}
// Main function
public static void main(String args[]){
// Defining array.
int a[] = {5, -1, 0, 9, -4, 7, 1};
// Printing maximum of every window of size 3.
slidingWindowMaximum(a, a.length, 3);
// Defining array.
a = new int[]{2, -3, 6, 6, -1, 7, -6, 8};
// Printing maximum of every window of size 5.
slidingWindowMaximum(a, a.length, 5);
}
}
C++ Implementation
#include<bits/stdc++.h>
using namespace std;
// Function to print maximum element of
// each window of size k.
void slidingWindowMaximum(int a[], int n, int k){
// Iterate from i=0 to i = n-k
for (int i = 0; i <= n-k; i++){
// Intialize a variable 'max',
// with a very samll value/
int max = INT_MIN;
// Iterate for the window of size 'k', starting from 'i'.
for(int j = i; j < i + k; j++){
// If a[j] is greater than max,
// update it.
if (a[j] > max)
max = a[j];
}
// Print the maximum element found
// in this window.
cout << max << " ";
}
cout << endl;
}
// Main function
int main(){
// Defining array.
int a[] = {5, -1, 0, 9, -4, 7, 1};
int n = sizeof (a) / sizeof (a[0]);
// Printing maximum of every window of size 3.
slidingWindowMaximum(a, n, 3);
// Defining array.
int b[] = {2, -3, 6, 6, -1, 7, -6, 8};
n = sizeof (b) / sizeof (b[0]);
// Printing maximum of every window of size 5.
slidingWindowMaximum(b, n, 5);
}
Python Implementation
# Function to pr maximum element of
# each window of size k.
def slidingWindowMaximum(a, n, k):
# Iterate from i=0 to i = n-k
for i in range (n - k + 1):
# Intialize a variable 'max',
# with a very samll value/
max = -999999999
# Iterate for the window of size 'k', starting from 'i'.
for j in range (i, i + k):
# If a[j] is greater than max,
# update it.
if (a[j] > max):
max = a[j]
# Print the maximum element found
# in this window.
print (max, end = " ")
print()
# Driver code
# Defining array.
a = [5, -1, 0, 9, -4, 7, 1]
# Pring maximum of every window of size 3.
slidingWindowMaximum(a, len(a), 3)
# Defining array.
a = [2, -3, 6, 6, -1, 7, -6, 8]
# Pring maximum of every window of size 5.
slidingWindowMaximum(a, len(a), 5)
Output
5 9 9 9 7
6 7 7 8
Complexity Analysis
- Time Complexity – The outer loops run for $n-k+1$ times while the inner loops run for $k$ times in each iteration. Hence the overall time complexity is $O((n-k+1)\times k)$ which is equivalent to $O(n\times k)$.
- Space Complexity – Since we are not using any extra space. The overall space complexity is $O(1)$.
Approach 2: Using Self-Balancing BST
In the last section, we used a loop to iterate for each window and find its maximum element which had cost us $O(n\times k)$ time on an average. Using Self-Balancing BST (AVL Tree) we can reduce this to $O(n\log k)$.
As we have seen in AVL Tress, all the operations like searching, deleting, and inserting a node are $O(\log{n})$ time taking operations in both the average case and the worst case. If you are interested in knowing, why it is so, please go through the detailed article on AVL Trees.
The main idea is to, insert the first $k$ elements in the AVL tree and then for each $i=k$ to $i=n-1$ find the largest element present in the tree (which denotes the maximum element of the current window), remove elements that are no longer part of the window, and insert the element which is added to the window during $i^{th}$ iteration.
Since at most $k$ nodes can be present in the tree at any instant of time, therefore all these operations will cost $O(k)$ time on an average. And we are iterating for $n$ times, which makes the overall time complexity $O(n\log{k})$ which is pretty efficient.
The algorithm is as follows –
- Define an AVL tree (say
tree). - Iterate through the first $k$ elements of the array, and insert them in the tree.
- Iterate from $i=k$ to $i=n-1$ and do the following –
- Print the maximum element of the tree.
- Delete the element at index $(i-k)$ from the tree, as it is no longer part of the window.
- Insert the $i^{th}$ element of the array in the AVL tree.
- Print the maximum element of the tree, this denotes the maximum element of the last window of size k.
Pseudocode
// Function to print maximum element of
// each window of size k.
function slidingWindowMaximum(a, n, k):
// Define the AVL Tree.
AVL tree= New AVL Tree Object
// Insert first k elements in the AVL tree.
for i = 0 To i = k - 1:
tree.insert(a[i])
// Iterate from i = k to i = n - 1
for i = k To i = k - 1
// Find maximum element present in the
// tree/window and print it.
maxElement = tree.findMaxElement()
print (maxElement)
// Delete the i-k th element as it is no
// longer part of the window.
tree.delete(a[i-k])
// Insert the new element.
tree.insert(a[i])
// Printing the maximum element, that is the
// maximum element of the last window.
print (tree.findMaxElement())
end function
Note that the Code of AVL tree is very large and complicated, hence it’s not worth it to discuss it here therefore we are just importing the code already written to implement it. If you are interested to learn more about AVL trees, kindly go through this.
Java Implementation
// Importing AVL class from package avl.
import avl.AVL;
public class Main{
// Function to print maximum element of
// each window of size k.
static void slidingWindowMaximum(int a[], int n, int k){
// Define the AVL Tree.
AVL tree=new AVL();
// Insert first k elements in the AVL tree.
for (int i = 0; i < k; i++)
tree.root = tree.insert(tree.root, a[i]);
// Iterate from i = k to i = n - 1
for (int i = k; i < n; i++){
// Find maximum element present in the
// tree/window and print it.
int maxElement = tree.findMaxElement();
System.out.print(maxElement+" ");
// Delete the i-k th element as it is no
// longer part of the window.
tree.root = tree.delete(tree.root, a[i-k]);
// Insert the new element.
tree.root = tree.insert(tree.root, a[i]);
}
// Printing the maximum element, that is the
// maximum element of the last window.
System.out.println(tree.findMaxElement());
}
// Main function
public static void main(String args[]){
// Defining array.
int a[] = {5, -1, 0, 9, -4, 7, 1};
// Printing maximum of every window of size 3.
slidingWindowMaximum(a, a.length, 3);
// Defining array.
a = new int[]{2, -3, 6, 6, -1, 7, -6, 8};
// Printing maximum of every window of size 5.
slidingWindowMaximum(a, a.length, 5);
}
}
C++ Implementation
#include<bits/stdc++.h>
#include "avl_tree.h"
using namespace std;
// Function to print maximum element of
// each window of size k.
static void slidingWindowMaximum(int a[], int n, int k){
// Define the AVL Tree.
AVL tree=new AVL();
// Insert first k elements in the AVL tree.
for (int i = 0; i < k; i++)
tree->root = tree.insert(tree->root, a[i]);
// Iterate from i = k to i = n - 1
for (int i = k; i < n; i++){
// Find maximum element present in the
// tree/window and print it.
int maxElement = tree.findMaxElement();
cout << maxElement << " ";
// Delete the i-k th element as it is no
// longer part of the window.
tree->root = tree.delete(tree->root, a[i-k]);
// Insert the new element.
tree->root = tree.insert(tree->root, a[i]);
}
// Printing the maximum element, that is the
// maximum element of the last window.
cout << tree.findMaxElement() << endl;
}
// Main function
int main(){
// Defining array.
int a[] = {5, -1, 0, 9, -4, 7, 1};
int n = sizeof (a) / sizeof (a[0]);
// Printing maximum of every window of size 3.
slidingWindowMaximum(a, n, 3);
// Defining array.
int b[] = {2, -3, 6, 6, -1, 7, -6, 8};
n = sizeof (b) / sizeof (b[0]);
// Printing maximum of every window of size 5.
slidingWindowMaximum(b, n, 5);
}
Complexity Analysis
- Time Complexity – For each $i$ ranging from 0 to $n-1$, we are doing at most $O(\log{n})$ operations $i.e.$ removing from AVL tree and inserting in it. Hence the time complexity is $O(n\log{n})$.
- Space Complexity – The maximum number of nodes present in the AVL tree can reach up to $k$ at any instant of time. Hence the space complexity is $O(k)$.
Approach 3: Max-Heap
In the previous approach, we have seen how we can find the sliding window maximum efficiently using AVL trees. This approach is also very similar to the previous one, here we will be using the Max-Heaps instead of AVL trees, and the rest of the logic will be the same only.
The idea is to insert all the elements which are part of the first window of size $k$, then find the maximum among them and print it. Now before moving to the next window, remove the element that is no longer the part of any subsequent window, and add the element that will the part of the further window(s).
The algorithm is as follows –
- Define a Heap (PriorityQueue), let it be
pq. Make sure that it is a max-heap and not a min-heap. - Iterate through the first $k$ elements of the array, and insert them into the heap.
- Iterate from $i=k$ to $i=n-1$ and do the following –
- Print the maximum element of the heap $i.e.$ root node.
- Remove the element at index $(i-k)$ from the heap, as it is no longer part of the window.
- Insert $i^{th}$ element of the array in the Max-Heap.
- Print the maximum element of
pq, this denotes the maximum element of the last window of size k.
Pseudocode
// Function to print maximum element of
// each window of size k.
function slidingWindowMaximum(int a[], int n, int k)
// Define the Max-Heap i.e. PriorityQueue in Java
pq = PriorityQueue
// Add first 'k' elements in pq.
for i = 0 to i = k - 1:
pq.insert(a[i])
// Iterate for i = k To i = n - 1
for i = k to i = n - 1:
// Find the maximum element of pq
// and print it.
maxElement = pq.top
print (maxElement)
// Remove the (i-k)th element, as
// it is no longer in next windows.
pq.delete(a[i-k])
// Add a[i] in pq, as it will be part
// of the next windows.
pq.insert(a[i])
// Print maximum element of pq, that will
// denote the maximum element of last window.
print (pq.top)
end function
Java Implementation
import java.util.*;
public class Main{
// Function to print maximum element of
// each window of size k.
static void slidingWindowMaximum(int a[], int n, int k){
// Define the Max-Heap i.e. PriorityQueue in Java
PriorityQueue<Integer> pq = new PriorityQueue<>(
Collections.reverseOrder()
);
// Add first 'k' elements in pq.
for(int i = 0; i < k; i++)
pq.add(a[i]);
// Iterate for i = k To i = n - 1
for(int i = k; i < n; i++){
// Find the maximum element of pq
// and print it.
int maxElement = pq.peek();
System.out.print(maxElement+" ");
// Remove the (i-k)th element, as
// it is no longer in next windows.
pq.remove(a[i-k]);
// Add a[i] in pq, as it will be part
// of the next windows.
pq.add(a[i]);
}
// Print maximum element of pq, that will
// denote the maximum element of last window.
System.out.println(pq.peek());
}
// Main function
public static void main(String args[]){
// Defining array.
int a[] = {5, -1, 0, 9, -4, 7, 1};
// Printing maximum of every window of size 3.
slidingWindowMaximum(a, a.length, 3);
// Defining array.
a = new int[]{2, -3, 6, 6, -1, 7, -6, 8};
// Printing maximum of every window of size 5.
slidingWindowMaximum(a, a.length, 5);
}
}
C++ Implementation
#include<bits/stdc++.h>
using namespace std;
// Function to print maximum element of
// each window of size k.
void slidingWindowMaximum(int a[], int n, int k){
// Define the Max-Heap i.e. PriorityQueue in Java
multiset<int> pq;
// Add first 'k' elements in pq.
for(int i = 0; i < k; i++)
pq.insert(a[i]);
// Iterate for i = k To i = n - 1
for(int i = k; i < n; i++){
// Find the maximum element of pq
// and print it.
int maxElement = *pq.rbegin();
cout << maxElement << " ";
// Remove the (i-k)th element, as
// it is no longer in next windows.
pq.erase(pq.find(a[i-k]));
// Add a[i] in pq, as it will be part
// of the next windows.
pq.insert(a[i]);
}
// Print maximum element of pq, that will
// denote the maximum element of last window.
cout << *pq.rbegin() << endl;
}
// Main function
int main(){
// Defining array.
int a[] = {5, -1, 0, 9, -4, 7, 1};
int n = sizeof (a) / sizeof (a[0]);
// Printing maximum of every window of size 3.
slidingWindowMaximum(a, n, 3);
// Defining array.
int b[] = {2, -3, 6, 6, -1, 7, -6, 8};
n = sizeof (b) / sizeof (b[0]);
// Printing maximum of every window of size 5.
slidingWindowMaximum(b, n, 5);
}
Output
5 9 9 9 7
6 7 7 8
Complexity Analysis
- Time Complexity – For each element we are performing
logarithmictime operations (Inserting, removing from the heap). Due to this, the time complexity is $O(n\log{k})$. - Space Complexity – The size of the heap can reach up to $k$, therefore the space complexity is $O(k)$.
Approach 4: Deque
An important observation that we can easily make here is that, we can only consider the promising candidates of the current window. An element is considered to be promising for being a sliding window maximum if it lies in the current window and it is greatest among all the elements that lies in the window range (towards the right side).
To implement this functionality, we will introduce an interesting data structure $i.e.$ monotonic doubly-ended queue. Don’t get afraid of the name, it is just a doubly ended queue in which elements from head to tail is in decreasing order (hence it is named monotonic).
To transform a simple doubly-ended queue into a monotonic doubly ended queue, we will modify the push operation so that – “Before we push x in the queue, we pop out all elements less than x“.
The algorithm is as follows –
- Create a doubly ended queue (say $dq$) of size $k$.
- Iterate from $i=0$ to $i=k-1$ and do the following –
- Pop out all elements from tail of $dq$ until the inequality $dq.tail\leq a[i]$ holds true.
- Push $a[i]$ in $dq$.
- Now iterate from $i=k$ to $i=n$ and do the following –
- Print the element at the head of $dq$, this denotes the maximum element of the current window.
- Pop all the elements from the head of $dq$ which no longer lie in the current window.
- Pop all the elements from the tail of $dq$ which are smaller than or equal to $a[i]$.
- Push $a[i]$ into the queue.
- Print the element at the head of the queue, this marks the maximum element of the last window.
Psuedocode
// Function to print maximum element of
// each window of size k.
function slidingWindowMaximum(a, n, k):
// Define the doubly ended queue, that will
// behave like a monotonic doubly ended queue.
dq = deque
// Iterate from i = 0 to i = k - 1.
For i = 0 To i = k - 1
// Pop out all elements from tail
// which are smaller than a[i].
While dq is not empty
and
a[dq[-1]] <= a[i]:
// Removing from rear (tail side).
dq.pop()
// Add the current element.
dq.add(i)
// Iterate from i = k to i = n - 1.
For i = k To i = k - 1
// Print the element at the head of the queue.
print(a[dq.first()])
// Remove the elements which no longer
// lies in the window.
while dq is not empty
and
q[0] <= i - k:
// Removing from front (head side).
dq.popleft()
// Pop out all elements from tail
// which are smaller than a[i].
while dq is not empty
and
a[dq[-1]] <= a[i]:
// Removing from rear (tail side).
dq.pop()
// Add the current element.
dq.add(i)
// Print the element at head of the queue
// that is maximum element of last window.
print(a.first())
end function
Java Implementation
import java.util.*;
public class Main{
// Function to print maximum element of
// each window of size k.
static void slidingWindowMaximum(int a[], int n, int k){
// Define the doubly ended queue, that will
// behave like a monotonic doubly ended queue.
Deque<Integer> dq = new LinkedList<>();
// Iterate from i = 0 to i = k - 1.
for (int i = 0; i < k; i++){
// Pop out all elements from tail
// which are smaller than a[i].
while(!dq.isEmpty() &&
a[dq.peekLast()] <= a[i])
// Removing from rear (tail side).
dq.removeLast();
// Add the current element.
dq.addLast(i);
}
// Iterate from i = k to i = n - 1.
for(int i = k; i < n; i++){
// Print the element at the head of the queue.
System.out.print(a[dq.peek()] + " ");
// Remove the elements which no longer
// lies in the window.
while(!dq.isEmpty() &&
dq.peek() <= i - k)
// Removing from front (head side).
dq.removeFirst();
// Pop out all elements from tail
// which are smaller than a[i].
while(!dq.isEmpty() &&
a[dq.peekLast()] <= a[i])
// Removing from rear (tail side).
dq.removeLast();
// Add the current element.
dq.addLast(i);
}
// Print the element at head of the queue
// that is maximum element of last window.
System.out.println(a[dq.peek()]);
}
// Main function
public static void main(String args[]){
// Defining array.
int a[] = {5, -1, 0, 9, -4, 7, 1};
// Printing maximum of every window of size 3.
slidingWindowMaximum(a, a.length, 3);
// Defining array.
a = new int[]{2, -3, 6, 6, -1, 7, -6, 8};
// Printing maximum of every window of size 5.
slidingWindowMaximum(a, a.length, 5);
}
}
C++ Implementation
#include<bits/stdc++.h>
using namespace std;
// Function to print maximum element of
// each window of size k.
void slidingWindowMaximum(int a[], int n, int k){
// Define the doubly ended queue, that will
// behave like a monotonic doubly ended queue.
deque<int> dq(k);
// Iterate from i = 0 to i = k - 1.
for (int i = 0; i < k; i++){
// Pop out all elements from tail
// which are smaller than a[i].
while(!dq.empty() &&
a[dq.back()] <= a[i])
// Removing from rear (tail side).
dq.pop_back();
// Add the current element.
dq.push_back(i);
}
// Iterate from i = k to i = n - 1.
for(int i = k; i < n; i++){
// Print the element at the head of the queue.
cout << a[dq.front()] << " ";
// Remove the elements which no longer
// lies in the window.
while(!dq.empty() &&
dq.front() <= i - k)
// Removing from front (head side).
dq.pop_front();
// Pop out all elements from tail
// which are smaller than a[i].
while(!dq.empty() &&
a[dq.back()] <= a[i])
// Removing from rear (tail side).
dq.pop_back();
// Add the current element.
dq.push_back(i);
}
// Print the element at head of the queue
// that is maximum element of last window.
cout << a[dq.front()] << endl;
}
// Main function
int main(){
// Defining array.
int a[] = {5, -1, 0, 9, -4, 7, 1};
int n = sizeof (a) / sizeof (a[0]);
// Printing maximum of every window of size 3.
slidingWindowMaximum(a, n, 3);
// Defining array.
int b[] = {2, -3, 6, 6, -1, 7, -6, 8};
n = sizeof (b) / sizeof (b[0]);
// Printing maximum of every window of size 5.
slidingWindowMaximum(b, n, 5);
}
Python Implementation
from collections import deque
# Function to print maximum element of
# each window of size k.
def slidingWindowMaximum(a, n, k):
# Define the doubly ended queue, that will
# behave like a monotonic doubly ended queue.
dq = deque()
# Iterate from i = 0 to i = k - 1.
for i in range (k):
# Pop out all elements from tail
# which are smaller than a[i].
while(dq and
a[dq[-1]] <= a[i]):
# Removing from rear (tail side).
dq.pop()
# Add the current element.
dq.append(i)
# Iterate from i = k to i = n - 1.
for i in range (k, n):
# Print the element at the head of the queue.
print(a[dq[0]], end =" ")
# Remove the elements which no longer
# lies in the window.
while(dq and
dq[0] <= i - k):
# Removing from front (head side).
dq.popleft()
# Pop out all elements from tail
# which are smaller than a[i].
while(dq and
a[dq[-1]] <= a[i]):
# Removing from rear (tail side).
dq.pop()
# Add the current element.
dq.append(i)
# Print the element at head of the queue
# that is maximum element of last window.
print(a[dq[0]])
# Driver code
# Defining array.
a = [5, -1, 0, 9, -4, 7, 1]
# Pring maximum of every window of size 3.
slidingWindowMaximum(a, len(a), 3)
# Defining array.
a = [2, -3, 6, 6, -1, 7, -6, 8]
# Pring maximum of every window of size 5.
slidingWindowMaximum(a, len(a), 5)
Output
5 9 9 9 7
6 7 7 8Complexity Analysis
- Time Complexity – It can be noticed that every element of the array is pushed and popper at most once. Hence there are at max $2\times n$ operations, and hence the time complexity is $O(n)$.
- Space Complexity – Since the maximum size of the queue can reach up to $k$, the space complexity is $O(k)$. Also, the max value $k$ can attain is $n$, hence we can say the upper bound is $O(n)$ in the worst case.
Approach 5: Using Dynamic Programming
In all the approaches we have seen in the previous sections, we were processing the elements as we are sliding our window (towards the right). But if we can store some sort of information that can be used in the future to find the maximum element of the window, that will be more than good.
One good idea is – for each 0 <= i < n, store the index of next greater element to the right. Now let’s see how this can help us to find the maximum element of each window of size $k$.
We will iterate from $i=0$ to $i=n-k-1$, and for each window starting at the $i^{th}$ index, we will find the greatest element that lies in the current window, and in case there is no greater element than the $i^{th}$ element in the range of window we will consider it to be the greatest element of the window.
The algorithm is as follows –
We will split this program into two parts, In part 1 for each element, we will find the index of the next greater element toward the right, and in part 2 we will find the sliding window maximum.
Part 1 –
- Define an array (say
right) of size $n$, whereright[i]will store index of the next greater element towards the right. - Assign $n$ to
right[n-1], because for the last element we consider there is an imaginary number at the $n^{th}$ position which is very large. - Iterate from $i=n-2$ to $i=0$ and do the following –
- Assume the element at index $i+1$ is the next greater element, so store $i+1$ in a variable (say
p). - Now till $p<n$ (
p lies in array bounds) and $a[p] \leq a[i]$ (element at indexpis smaller than or equal to element at indexi), update the value ofptoright[p](Index of next greater element fora[p]). - Store the final value of
pinright[i].
- Assume the element at index $i+1$ is the next greater element, so store $i+1$ in a variable (say
Part 2 –
- Initialize two variables (say
iandj), whereiwill be used to iterate over the array andjwill be used to mark the maximum element of the window. - Iterate from $i=0$ to $i = n – k – 1$ and do the following –
- If
jis less thani$i.e.$ the current maximum element is no longer in the window then assign the value ofitoj. - Iterate till
right[j]lies in the current window and update value ofjasj = right[j]. - If now the value of
jisn, it meansa[i]is the greatest element of the current window, hence print it. - Otherwise, print
a[j]that denotes the greatest element that lies in the window.
- If
Pseudocode
// Function to print maximum element of
// each window of size k.
function slidingWindowMaximum(a, n, k):
// Define right array to store indices
// of next greater element toward right.
right = Array of size n
// Assign n to rightmost element.
right[n-1] = n
// Iterate from i = n - 2 to i = 0.
For i = n - 2 To i = 0:
// Assume i + 1 to be next
// greater element.
p = i + 1
// Iterate while p lies in the array bounds
// and smaller than the current element.
While p < n AND a[p] <= a[i]
p = right[p]
// Assing p's value to right[i]
right[i] = p
i = 0
j = 0
// Now iterate from i = 0 to i = n - k
While i <= n - k:
// If j is no longer in the window.
If i > j:
j = i
// Finding greatest element of the window.
While right[j] < i + k:
j = right[j]
// If j is out of array bound, which means
// a[i] is greatest element
if j == n:
print(a[i])
// Otherwise a[j] is the greatest element
// of the window.
else:
print(a[j])
i++
end function
Java Implementation
import java.util.*;
public class Main{
// Function to print maximum element of
// each window of size k.
static void slidingWindowMaximum(int a[], int n, int k){
// Define right array to store indices
// of next greater element toward right.
int right[] = new int[n];
// Assign n to rightmost element.
right[n-1] = n;
// Iterate from i = n - 2 to i = 0.
for (int i = n - 2; i > -1; i--){
// Assume i + 1 to be next
// greater element.
int p = i + 1;
// Iterate while p lies in the array bounds
// and smaller than the current element.
while (p < n && a[p] <= a[i])
p = right[p];
// Assing p's value to right[i]
right[i] = p;
}
int i = 0, j = 0;
// Now iterate from i = 0 to i = n - k
while (i <= n - k){
// If j is no longer in the window.
if (i > j)
j = i;
// Finding greatest element of the window.
while (right[j] < i + k)
j = right[j];
// If j is out of array bound, which means
// a[i] is greatest element
if(j == n)
System.out.print(a[i]+" ");
// Otherwise a[j] is the greatest element
// of the window.
else
System.out.print(a[j]+" ");
i++;
}
System.out.println();
}
// Main function
public static void main(String args[]){
// Defining array.
int a[] = {5, -1, 0, 9, -4, 7, 1};
// Printing maximum of every window of size 3.
slidingWindowMaximum(a, a.length, 3);
// Defining array.
a = new int[]{2, -3, 6, 6, -1, 7, -6, 8};
// Printing maximum of every window of size 5.
slidingWindowMaximum(a, a.length, 5);
}
}
C++ Implementation
#include<bits/stdc++.h>
using namespace std;
// Function to print maximum element of
// each window of size k.
void slidingWindowMaximum(int a[], int n, int k){
// Define right array to store indices
// of next greater element toward right.
int right[n];
// Assign n to rightmost element.
right[n-1] = n;
// Iterate from i = n - 2 to i = 0.
for (int i = n - 2; i > -1; i--){
// Assume i + 1 to be next
// greater element.
int p = i + 1;
// Iterate while p lies in the array bounds
// and smaller than the current element.
while (p < n && a[p] <= a[i])
p = right[p];
// Assing p's value to right[i]
right[i] = p;
}
int i = 0, j = 0;
// Now iterate from i = 0 to i = n - k
while (i <= n - k){
// If j is no longer in the window.
if (i > j)
j = i;
// Finding greatest element of the window.
while (right[j] < i + k)
j = right[j];
// If j is out of array bound, which means
// a[i] is greatest element
if(j == n)
cout << a[i] << " ";
// Otherwise a[j] is the greatest element
// of the window.
else
cout << a[j] << " ";
i++;
}
cout << endl;
}
// Main function
int main(){
// Defining array.
int a[] = {5, -1, 0, 9, -4, 7, 1};
int n = sizeof (a) / sizeof (a[0]);
// Printing maximum of every window of size 3.
slidingWindowMaximum(a, n, 3);
// Defining array.
int b[] = {2, -3, 6, 6, -1, 7, -6, 8};
n = sizeof (b) / sizeof (b[0]);
// Printing maximum of every window of size 5.
slidingWindowMaximum(b, n, 5);
}
Python Implementation
# Function to print maximum element of
# each window of size k.
def slidingWindowMaximum(a, n, k):
# Define right array to store indices
# of next greater element toward right.
right = [0 for i in range(n)]
# Assign n to rightmost element.
right[n-1] = n
# Iterate from i = n - 2 to i = 0.
for i in range(n-2, -1, -1):
# Assume i + 1 to be next
# greater element.
p = i + 1
# Iterate while p lies in the array bounds
# and smaller than the current element.
while (p < n and a[p] <= a[i]):
p = right[p]
# Assing p's value to right[i]
right[i] = p
i = 0
j = 0
# Now iterate from i = 0 to i = n - k
while (i <= n - k):
# If j is no longer in the window.
if (i > j):
j = i
# Finding greatest element of the window.
while (right[j] < i + k):
j = right[j]
# If j is out of array bound, which means
# a[i] is greatest element
if(j == n):
print(a[i], end = " ")
# Otherwise a[j] is the greatest element
# of the window.
else:
print(a[j], end = " ")
i+=1
print()
# Driver code
# Defining array.
a = [5, -1, 0, 9, -4, 7, 1]
# Pring maximum of every window of size 3.
slidingWindowMaximum(a, len(a), 3)
# Defining array.
a = [2, -3, 6, 6, -1, 7, -6, 8]
# Pring maximum of every window of size 5.
slidingWindowMaximum(a, len(a), 5)
Output
5 9 9 9 7
6 7 7 8
Complexity Analysis
- Time Complexity – Both part 1 and part 2 of the algorithm requires $O(n)$ time to get executed, hence the overall time complexity is $O(n+n) \simeq O(n)$.
- Space Complexity – Since we have used the
rightarray to store indices of the next greater element which is of size $n$. The overall space complexity is $O(n)$.
Conclusion
- Sliding Window Maximum is nothing but the maximum element present in each contiguous subarray of size $k$ (given).
- They can be found in $O(n^2)$ time when using the naive brute-force approach.
- However, with certain optimizations it can be brought down to $O(n\log{k})$ by using Heaps or AVL Trees.
- Optimally it can be solved in linear time complexity either using dynamic programming or Monotonic Deque.