Segmented Sieve

Given a number N, print all the prime numbers less than N. Prime numbers are the numbers which are divisible by 1and itself only.

Example:

Input:

12

Output:

2, 3, 5, 7, 11

Example Explanation:

The given input number is 12, and prime numbers which are smaller than 12 are only 2, 3, 5, 7, 11. So, they are printed.

Constraints:

$2<=N<=10^{6}$

Approach 1: Brute Force

• Just run the loop from 1 to N
• For every number check whether it is a prime or not.
• If the number is prime, then print the number.

Time Complexity: $O(N^2)$

• For the first loop, it takes O(N)
• The nested loop to check whether it is a prime number takes O(N)
• So, the overall time complexity sums up to be O(N^2)

Space Complexity: O(1)

• No extra space is needed for this approach.

This approach fails for the large test case(from constraints) as we get a TLE verdict, So to optimize it we use the famous algorithm Sieve of Eratosthenes. This approach helps in optimizing the time complexity for finding the primes smaller than N.

Approach 2: Using Sieve of Eratosthenes

Explanation with an example:
Let’s take an example N=25, find all the numbers which are less than 25 and are primes.

1. Firstly initialize a boolean array, sieve of size 26 with all values as true.
   

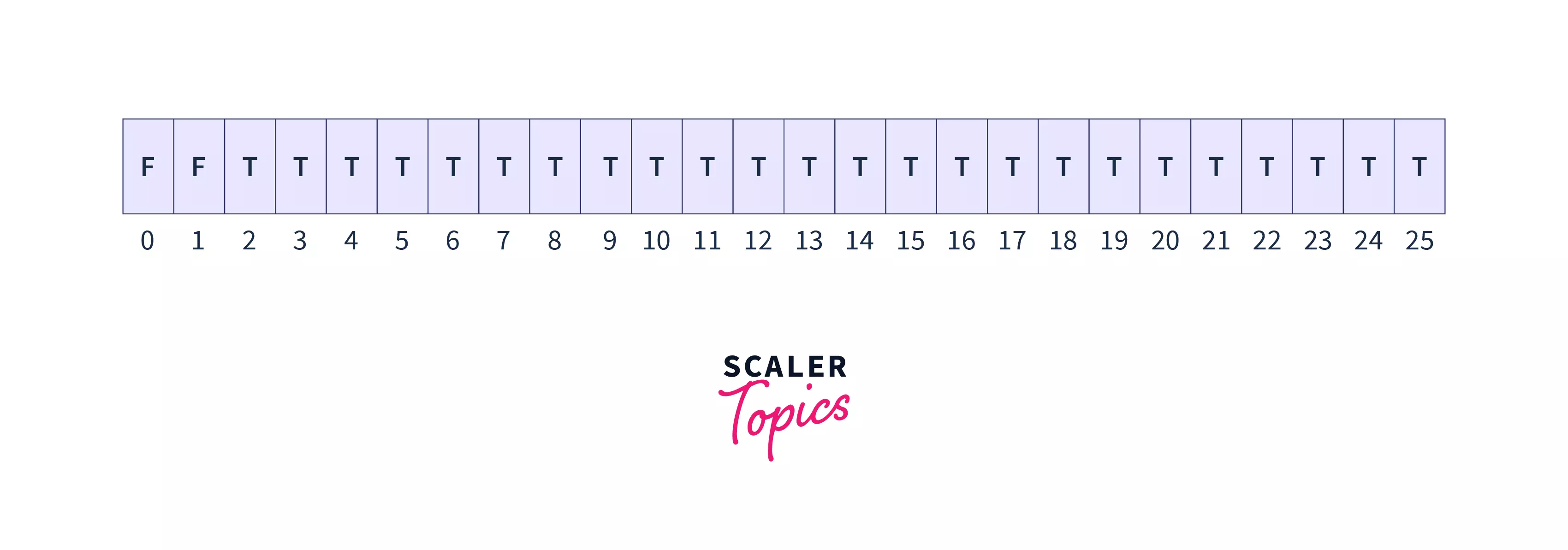
Then start traversing the iterator i from 2.
If sieve[i] is found to be true, then mark all the multiples ofi as false in the sieve array, it means that the numbers that are marked as false can’t be prime since they’ve i as their factor.

• In our example all the numbers which are multiples of 2 are marked as false in the sieves array, the array looks like this:

• Now as we increment i to i, so i=3, since the sieve[3] is true, we mark all its multiples as false i.e,
  
  

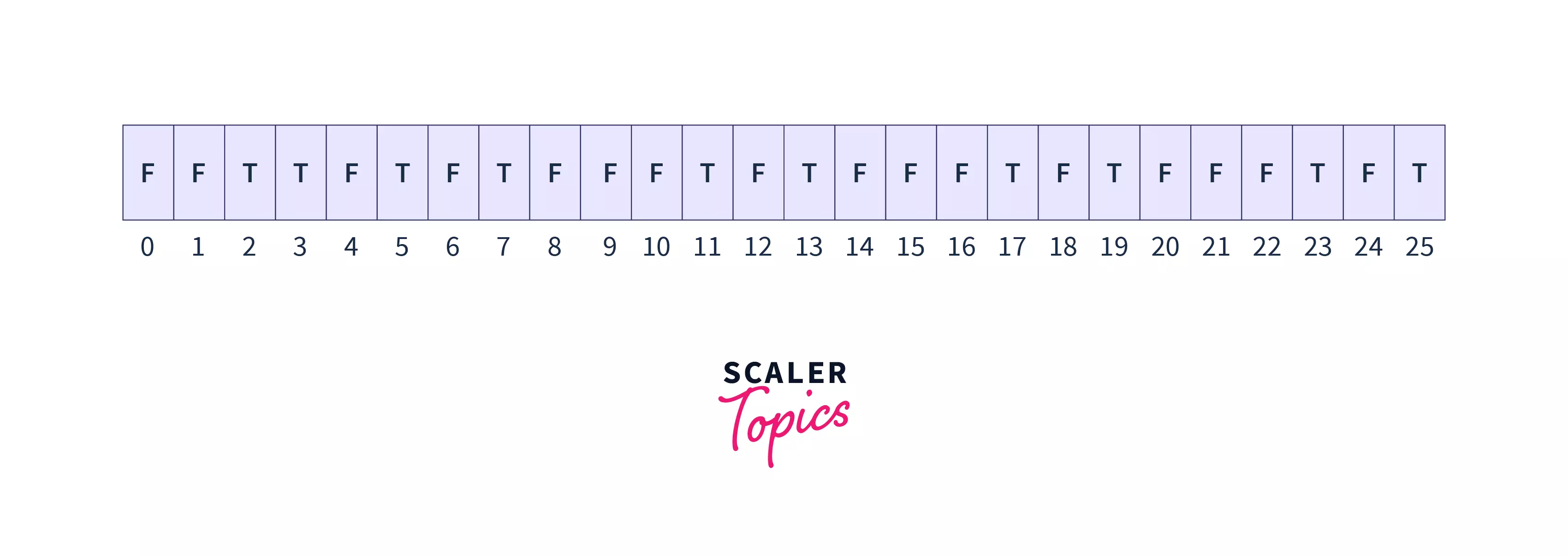
• After incrementing i it is 4 now, but sieve[4] is already false, which means that all the factors of 4 are already marked false. So, increment i.
  11. Now i=5, since sieve[5] is not false, mark all its multiples as false, the array looks like this:

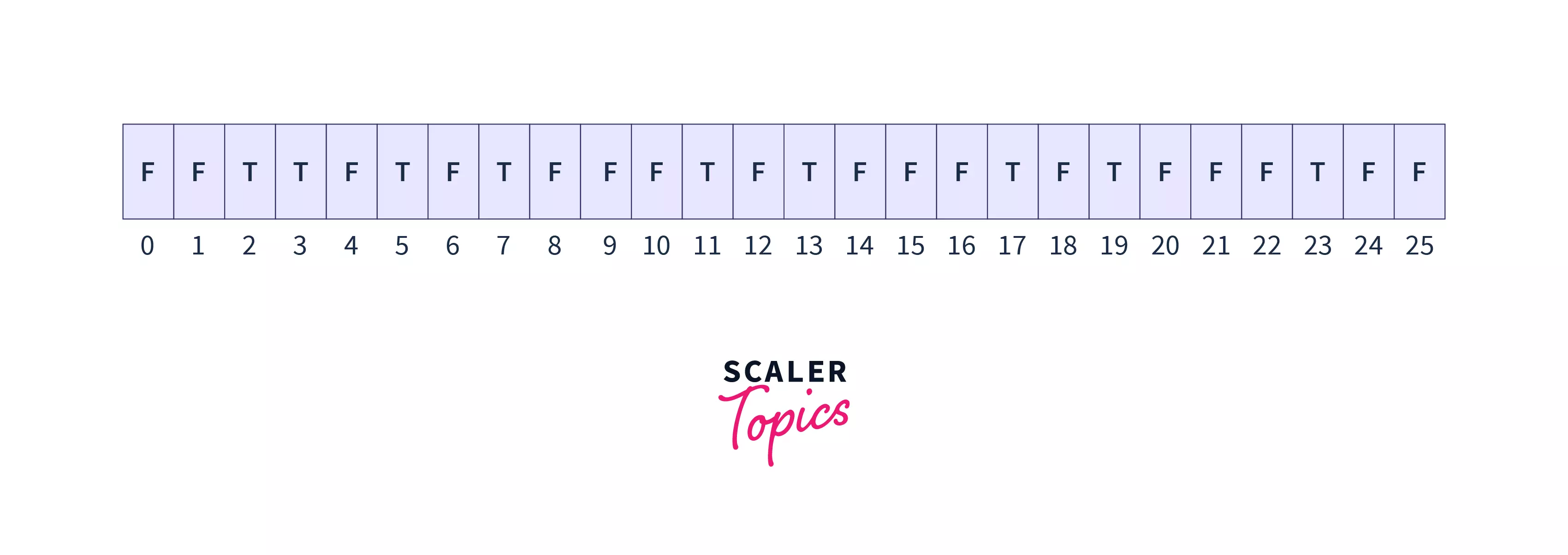
• We can observe that non-prime(composite) numbers below 25 are already marked as false, so we can say that loop can run till $\sqrt{25}$ which is till 5, so the loop traverses till $\sqrt{N}$ (first optimization).
• So, Now let’s talk about how we mark i’s multiples as false.

• Observe that for i=3, we need to mark [6, 9, 12, 15, 18, 21, 24] we can notice that 6 is already been marked as false by 2’s multiples, so we can start this loop from i^2^(second optimization in the sieve of primes) instead of starting the second loop from2*i.
• So the final array sieve has all the prime numbers less than 25 as true.

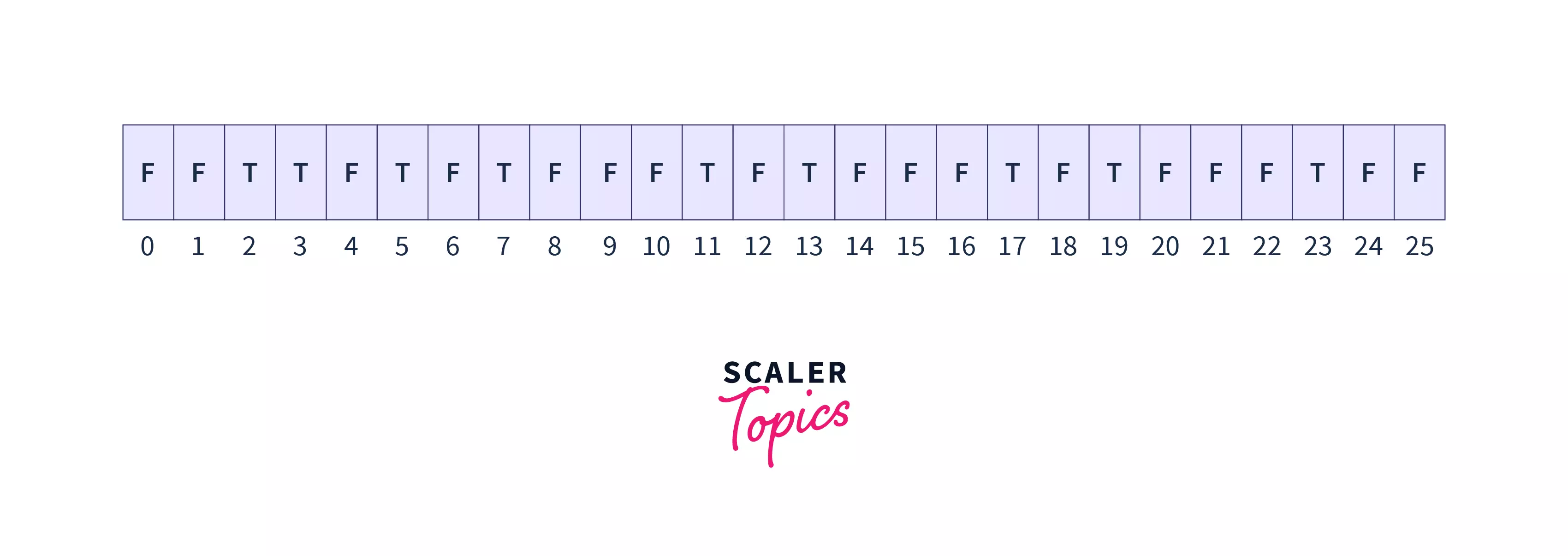
Output:
cpp 2, 3, 5, 7, 9, 11, 13, 17, 19, 23

Algorithm:

Below is the algorithm to be followed for Sieve of Eratosthenes:

• Initialise a boolean array of size N+1 with all values as true.
• Run a for loop from 2 to $\sqrt{N}$
• if sieve[i]==True
• Mark all the multiples of iin the sieve as false.
• This can be done by running a nested loop from i^2^ to n, where we increment the iterator by i, since we are marking its multiples as false.
• Else increment i.
• Finally, return all the indices where sieve[i] is True, they are the prime numbers smaller than n.

Implementation:

The above-discussed algorithm has been implemented in this section:

Python implementation of simple sieve:

# Python program to print all
# primes present less than or equal to
# n using Sieve method
import math
def Sieve(n):
    # Create a boolean array
    # "prime[0..n]" and initialize
    #  all entries it as true.
    sieve = [True for i in range(n+1)]
    pn = 2
    k=int(math.sqrt(n))
    for i in range(2,k):
        # If sieve[i] is true make 
        # the multiples of p as false
        if (sieve[i] == True):
 
            # mark all its multiples as false
            for j in range(i*i, n+1, i):
                sieve[j] = False
    # Print all prime numbers in the given range
    for prime in range(2, n+1):
        if sieve[prime]:
            print(prime, end=" ")
# Driver code
if __name__ == '__main__':
    # input number
    n = 25
    # calling the function Sieve to get the prime numbers smaller than n
    Sieve(n)

Java implementation of simple sieve:

// Java program to print all primes smaller than or equal to
// n using Sieve of Eratosthenes
 
class Main{
    static void sieve(int n){
        // Create a boolean array "sievearr[0..n]" and
        // initialize all entries it as true. 
        boolean sievearr[] = new boolean[n + 1];
        for (int i = 0; i <= n; i++)
            sievearr[i] = true;
 
        for (int i = 2; i * i <= n; i++){
            // If sievearr[i] is not changed, then it is a
            // prime
            if (sievearr[i] == true){
                // If sievearr[i] is true make 
                // the multiples of i as false which are less than or equal to n
                for (int j = i * i; j <= n; j += i)
                    sievearr[j] = false;
            }
        }
 
        // Print all prime numbers
        for (int prime = 2; prime <= n; prime++){
        //A value in
        // prime[i] will finally be false if i is Not a
        // prime, else true.
            if (sievearr[prime] == true)
                System.out.print(prime + " ");
        }
    }
 
    // Driver Code
    public static void main(String args[]){
        // input number
        int n = 25;
        // calling the method sieve to get the prime numbers less than n
        sieve(n);
    }
}

C++ implementation of simple sieve:

// C++ program to print all primes smaller than or equal to
// n using Sieve of Eratosthenes
#include <bits/stdc++.h>
using namespace std;
 
void Sieve(int n){
    // Create a boolean array sieve of size n
    // Intialise all entries as true. 
    bool sieve[n + 1];
    memset(sieve, true, sizeof(sieve));
 
    for (int i = 2; i * i <= n; i++){
        // If sieve[i] is not changed, then it is a prime
        if (sieve[i] == true) {
           // If sieve[i] is true make 
          // the multiples of i as false in the sieve array less than or equal to n
            for (int j = i * i; j <= n; j += i)
                sieve[j] = false;
        }
    }
 
    // Print all prime numbers
    for (int prime = 2; prime <= n; prime++){
        //A value in
        // sieve[i] will finally be false if i is not a
        // prime, else true.
        if (sieve[prime])
            cout << prime << " ";
    }
}
 
// Driver Code
int main(){
    // input number
    int n = 25;
    //calling the Sieve function to print all prime numbers
    Sieve(n);
    return 0;
}

Output:

2 3 5 7 11 13 17 19 23

Explanation: All the prime numbers which are less than 25 are printed as the result, this is achieved by using the Sieve of Eratosthenes algorithm.

Complexity Analysis:

Time Complexity: O(N log(logN))

• It is assumed that time taken to mark as false takes constant time, then the number of times the loop runs is:
  

• (N/2+N/3+N/5+N/7+….p)
• By solving this we get:
• N(1/2+1/3+1/5+1/7….)N(1/2+1/3+1/5+1/7….)
• The Harmonic progression of the sum of primes is log(log(N)).
• Therefore the overall time complexity is O(N log(log(N)))

Space Complexity: O(N)

• A boolean array of size N for keeping track of elements that are prime and smaller than N. Steps to be followed during Competitive Programming:

• In this approach, generally if the queries are given for each test case and if the constraints are huge, we get a TLE verdict. So to overcome that we can pre-compute the sieve array only once. That can be done in a function/ globally before starting the main program.
• And we can call this function and check for prime numbers in the given range.
• For checking the prime numbers in the given range takes about O(1) from the sieve array which is already formed, however for computing the sieve it takes O(10^6^) if the size of the sieve is 10^6^.
• This method helps in cases where queries are given for each test case, we need to print the prime numbers.
• There are many questions based on this sieve, a few of them are :
  • Print K^th^ prime number
  • Print the K^th^ prime factor for the given number
  • Count the number of primes in the given range All these can be solved using a Sieve of Eratosthenes in the optimized and efficient way.

Segmented Sieves

Find the primes in the given range.

Given the range, Left ( L ) and Right ( R ), print all the numbers which are prime in the given range. Prime numbers are numbers which are divisible by 1 and itself.

Example:

Input:

    L = 10 
    R = 30

Output:

    11 13 17 19 23 29 

Explanation: The prime numbers present in the given range i.e, from 10 to 30 are printed.

This problem uses the Segmented Sieve concept. To understand this in a better manner, the basic prerequisite is the simple sieve concept, also called as Sieve of Eratosthenes which we discussed earlier.

Constraints:

$1 <= L, R <= 10^{12}$

$1 <= R-L <= 10^{6}$

For the given constraints simple sieve, can’t be used (we get memory error in many languages) as we exceed the maximum limit for the boolean array. So, we use the concept of the segmented sieve to overcome the issue. The main difference between segmented sieve and sieve is that in segmented sieve we limit the range from L to R instead of 1 to R.
This algorithm uses Sieve, which is discussed above to find primes smaller than or equal to RR​ Our next question is why only up to RR​, because non-prime numbers till range R, will be marked as false by numbers smaller than RR​ already.

Approach: (Using Segmented Sieve)

Generate all the primes in the range $\sqrt{R}$.

• Now instead of keeping track of all primes just keep track of primes only between the given range by creating a boolean (dummy) array of size (R-L+1) and initialising every element as true.
• Each index in the dummy array represents L+i, so now the question is divided into segment.
• Now from each element p, in the generated primes, mark its multiples as false in the dummy array.
• This can be done by running a loop on dummy array. The starting index i.e. first multiple in the range [L-R] can be calculated as:
• low_idx= ((L//p)p) (integer division)
• if the low_idx is less than L, then add p.
• Now the low_idx can be max(low_idx, p*p).
• For example if we take the range as [110, 130], here for the prime number 11, multiples start from 110. We can simply start from 121, because start index is max(low_idx, p*p)
• The below image explains more clearly:
  
  

• After computing this we get the primes in the given range from the dummy array(which are marked as True).

Algorithm:

1. Firstly generate all the primes smaller than the $\sqrt{R}$ which is done using a sieve of primes and store the result in an array. This is the prerequisite for the next steps.
2. Initialise the boolean array/dummy array of size (R-L+1) and initialize all the values to true.
3. The idea is to partition the interval [L, R] into smaller segments and calculate the primes only upto $\sqrt{R}$.
4. This is where we optimize the space complexity. This ensures that the algorithm runs for a large value of R (up to 10^12^) because it takes space of the order of 10^6^.
5. For all primes p in the generated primes array which is calculated from step-1, we cancel out its multiples in the range [L, R**] in the dummy array, by marking them as false.
6. Get the first multiple in the range, and start cancelling it’s multiples smaller than or equal to R.
7. The element at index0 represents L, and the element at the last index represents R.
8. Iterate over the dummy array, if the dummy array value is true print (i+L), which is the prime number in the given range.

So unlike the simple sieve we discussed earlier, we check for all multiples of every number less than or equal to RR​, this reduces the space complexity as well considered to be more time-efficient.

Implementation of the above approach:

Python implementation of segmented sieves:

import math
# GetPrime function gets all the primes in the range L to sqrt of R
def GetPrimes(prime, R):
    # A boolean array indicates the sieve
    c = [True]*(R +1)
 
    M = int(math.sqrt(R))
    for i in range(2, M+1):
    # removing the multiples if c[i] is true
        if c [i]:
            for j in range(i*i, M+1, i):
                c[j] = False
    # traversing over the c array and getting all the primes in given range            
    for l in range(2, M+1):
        if c[l]:
            prime.append(l)
 
# A segment of  sieve used to get primes in given range[L, R]
# in segmented sieve we calculate primes in range [low,high]
# here we initially we find primes in range [2,sqrt(high)] to mark all their multiples as not prime
# then we mark all their(primes) multiples in range [low,high] as false
# this is a modified sieve of eratosthenes , in standard sieve of  eratosthenes we find prime from 1 to n(given number)
# in segmented sieve we only find primes in a given interval
def Segmented_Sieve(L, R):
    prime = list()
    GetPrimes(prime, R)
# primes has primes in range [L,sqrt(R)]
# dummy array to keep track of only between the given range
# first element means L, second element means L+1 and so on. 
# dummy has elements between L and R so size is {R-L+1}
    dummy = [True] * (R-L + 1)
# here dummy[0] indicates whether L is prime or not similarly dummy[1] indicates whether low+1 is prime or not
    for i in prime:
        # getting the first index for prime multiples in the given range
        low = (L//i)
# here low means the first multiple of prime which is in range [L,R]  
        if low <= 1:
            low = i+i
        elif (L % i) != 0:
            low = (low * i) + i
        else:
            low = low*i
        for j in range(low, R+1, i):
            dummy[j-L] = False
             
             
    for k in range(L, R + 1):
            if dummy[k-L]:
                print(k, end=" ")
 
 
#DRIVER CODE
#   low must greater than or equal to 2
# L is the lower limit
# R is the upper limit
L = 110
R = 130
# Calling for segment of sieves to get the answer
Segmented_Sieve(L, R)

Java implementation of segmented sieves:

// a java program for segmented sieves when the input n is given
import java.util.*;
import java.lang.Math;
 
public class Main{
//  GetPrime function gets all the primes in the range L to sqrt of R in prime ArrayList   
    public static void GetPrime(ArrayList<Integer> prime,int R){
        boolean[] c=new boolean[R+1];
        // initialising all elements as true in boolean array except 0,1 position
        Arrays.fill(c,true);
        c[1]=false;
        c[0]=false;
    // iterate the loop from 2 till sqrt of R
    for(int i=2;(i*i)<=R;i++){
        if(c[i]==true){
            // if it is true mark all its multiples as false
            for(int j=i*i;j<=Math.sqrt(R);j=j+i){
                c[j]=false;
            }
        }
    }
        // storing all the primes in given range in prime array.
    for(int i=2;i*i<=R;i++){
        if(c[i]==true){
           prime.add(i);
        }
    }
}
// A segment of  sieve used to get primes in given range[L, R]
// in segmented sieve we calculate primes in range [low,high]
// here we initially we find primes in range [2,sqrt(high)] to mark all their multiples as not prime
// then we mark all their(primes) multiples in range [low,high] as false
// this is a modified sieve of eratosthenes , in standard sieve of  eratosthenes we find prime from 1 to n(given number)
// in segmented sieve we only find primes in a given interval
    public static void Segmented_Sieve(int L,int R){
        ArrayList<Integer> chprime= new ArrayList<Integer>();
        GetPrime(chprime,R);
// primes has primes in range [L,sqrt(R)]
// dummy array to keep track of only between the given range
// first element means L, second element means L+1 and so on. 
// dummy has elements between L and R so size is {R-L+1}       
         
        boolean[] dummy=new boolean [R-L+1];
        //initialise all its elements as true
        Arrays.fill(dummy,true);
// here dummy[0] indicates whether L is prime or not similarly dummy[1] indicates whether low+1 is prime or not       
        for(int i:chprime){
            // getting the first index for prime multiples in the given range
            int low=(L/i);
//  here low means the first multiple of prime which is in range [L,R] 
            if(low<=1){
            low=i+i;
            }
            else if(L%i!=0){
            low=(low*i)+i;
            }
            else{
                low=(low*i);
            }
            for(int j=low;j<=R;j=j+i){
            dummy[j-L]=false;
            }
        }
        for(int i=L;i<=R;i++){
            if(dummy[i-L]==true){
            // if it is true it is a prime number and we print as result
            
            System.out.printf("%d ",i);
            }
        }    
    }
public static void main(String[] args){
// DRIVER CODE
// low must greater than or equal to 2
// L is the lower limit
// R is the upper limit
        int L=110;    
        int R=130;
// Calling for segment of sieves to get the answer
        Segmented_Sieve(L,R);
    }
}

C++ implementaion of segmented sieves:

// C++ program for segmented sieve when the input number is given
#include <bits/stdc++.h>
using namespace std;
//  GetPrime function gets all the primes in the range L to sqrt of R in prime(vector) array
void GetPrimes(vector<int>& prime, int R){
    bool c[R + 1];
    memset(c, true, sizeof(c));
    // initialising all elements as true in boolean array except 0,1 position
    c[1] = false;
    c[0] = false;
    // iterate the loop from 2 till sqrt of R
    for (int i = 2; (i * i) <= R; i++){
        if (c[i] == true){
            // if it is true mark all its multiples as false
            for (int j = i * i; j <= sqrt(R); j = j + i) {
                c[j] = false;
            }
        }
    }
    // storing all the primes in given range in prime array.
    for (int i = 2; i * i <= R; i++){
        if (c[i] == true) {
            prime.push_back(i);
        }
    }
}
// A segment of  sieve used to get primes in given range[L, R]
// in segmented sieve we calculate primes in range [low,high]
// here we initially we find primes in range [2,sqrt(high)] to mark all their multiples as not prime
// then we mark all their(primes) multiples in range [low,high] as false
// this is a modified sieve of eratosthenes , in standard sieve of  eratosthenes we find prime from 1 to n(given number)
// in segmented sieve we only find primes in a given interval
void Segmented_Sieve(int L, int R){
    // a dummy array of size R-L+1 is used for tracking the prime numbers in the given range
    bool dummy[R - L + 1];
    //initialise all its elements as true
    memset(dummy, true, sizeof(dummy));
    //here dummy[0] indicates whether low is prime or not similarly dummy[1] indicates whether low+1 is prime or not
    vector<int> prime;
    GetPrimes(prime, R);
    // primes has primes in range [L,sqrt(R)]
    // dummy array to keep track of only between the given range
    // first element means L, second element means L+1 and so on. 
    // dummy has elements between L and R so size is {R-L+1}    
    for (int i : prime){
        // getting the first index for prime multiples in the given range
        int low = (L/ i);
        // here dummy[0] indicates whether L is prime or not similarly dummy[1] indicates whether low+1 is prime or not   
        if (low <= 1){
            low = i + i;
        }
        else if (L % i){
            low = (low * i) + i;
        }
        else{
            low = (low * i);
        }
        for (int j = low; j <= R; j = j + i){
            dummy[j - L] = false;
        }
    }
   
    for (int i = L; i <= R; i++){
        if (dummy[i - L] == true){
            // if it is true it is a prime number and we print as result
            cout << (i) << " ";
        }
    }
}
int main(){
    // DRIVER CODE
    // low must greater than or equal to 2
    // L is the lower limit
    // R is the upper limit
    int L = 110;
    int R = 130;
// Calling for segment of sieves to get the answer
    Segmented_Sieve(L, R);
}

Output:

     113 127 

Explanation: The prime numbers(divisible by only 1 and itself) in the given range i.e, from 110 to 130 are printed using the segmented sieves algorithm.

Complexity Analysis:

Time Complexity: $O((R-L+1) log log( R ) + $\sqrt{R}$ log log( $\sqrt{R}$ ))
$Log (log $\sqrt{R}$) can be negligible and the final time complexity will be

 O((R-L+1) log log( R ) +  $\sqrt{R}$)

• For iterating over the dummy array takes $O(R-L+1)$ times and generating the primes using the sieve takes around $\sqrt{R}$
• However this runs faster than it looks, and is considered to be the most efficient algorithm for finding the primes in the given range.
• So, let’s assume the worst-case i.e, if the R is $10^{12}+1200$ and L is some $10^{12}+410$, then also this segmented sieve doesn’t show TLE because for segmented sieve we take $\sqrt{R}$ which is $10^{6}$^, and for boolean array, we take $10^{6}$, so the code is efficient for large test cases also.

Space Complexity: O(R-L+1)

• A dummy array of size R-L+1 is used for keeping track of the prime numbers in the given range.

Conclusion

• We observed that both the segmented sieve and the simple sieve algorithms have the same time complexity, but what affects most is the space optimization which is done in the segmented sieve as we use a dummy array to store the values only in the given range and return prime numbers.
• If the constraints are very large, the segmented sieve algorithm consumes less space and therefore it is considered to be more efficient than simple sieve.
• We have used a boolean array in the sieve algorithm or the segmented sieve algorithm to keep track of the prime numbers according to the given input, instead of that we can also use an integer array by keeping 0 and 1 as values for indication of prime or non-prime number.
• Why is the boolean array more preferable?
• It is because a boolean array when declared globally can take up to 10^8^ values, if it is in the function it can take up to 10^7^ which is advantageous when the input is very huge.
• This can be done in C++ and also in java.

HAPPY CODING!!