Detect Cycle in Directed Graph

Problem Statement

Given a Directed graph $G=(V, E)$ with $V$ vertices numbered from $0$ to $V-1$ and $E$ edges. The task is to detect cycle in the directed graph $i.e.$ to check if there exists a cycle in the given graph.

Examples

Example 1

Input:

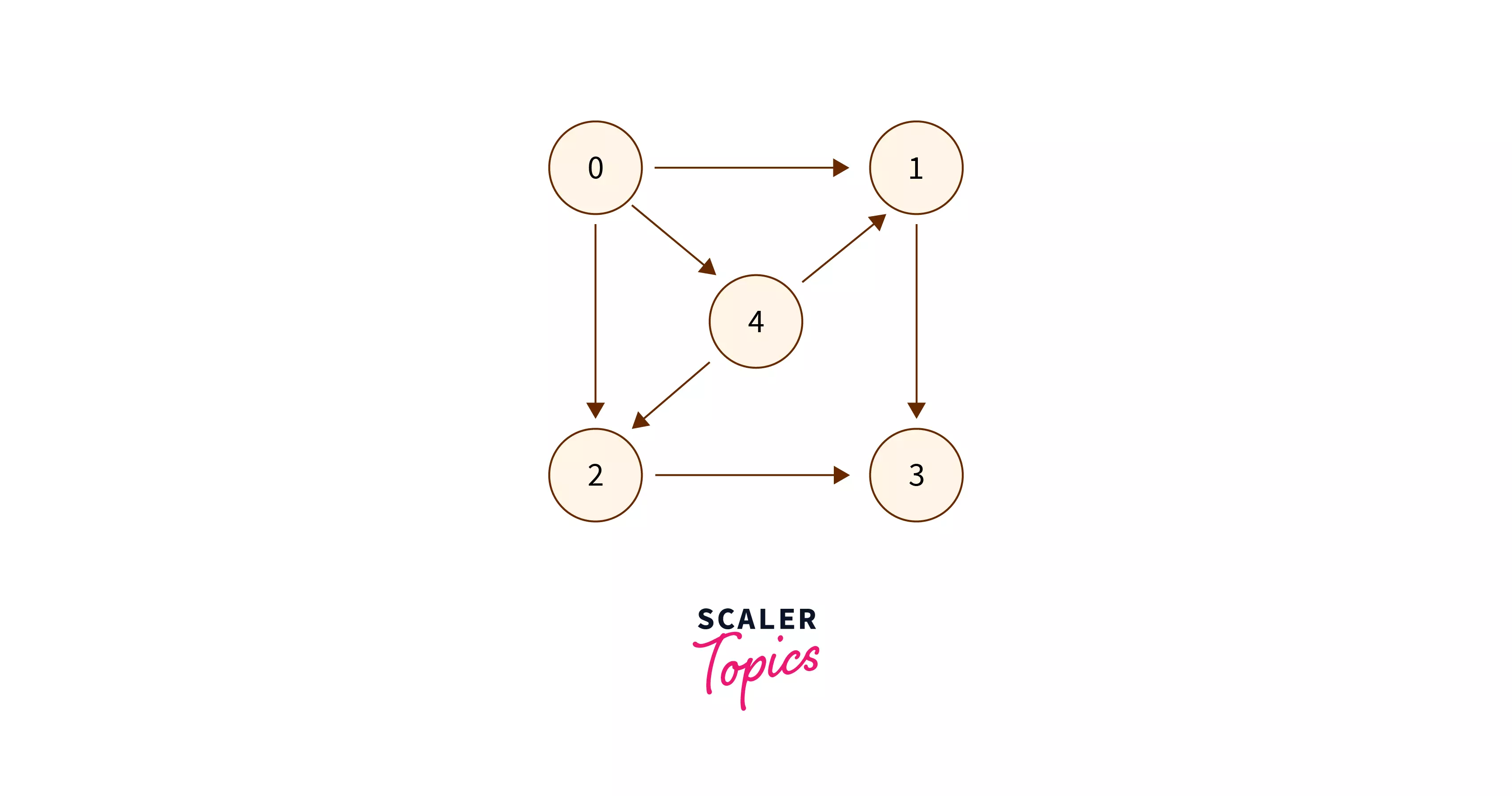
Output:
NO

Explanation:

No cycle exists in the above give Directed graph, hence we printed “NO” as the output.

Example 2

Input:

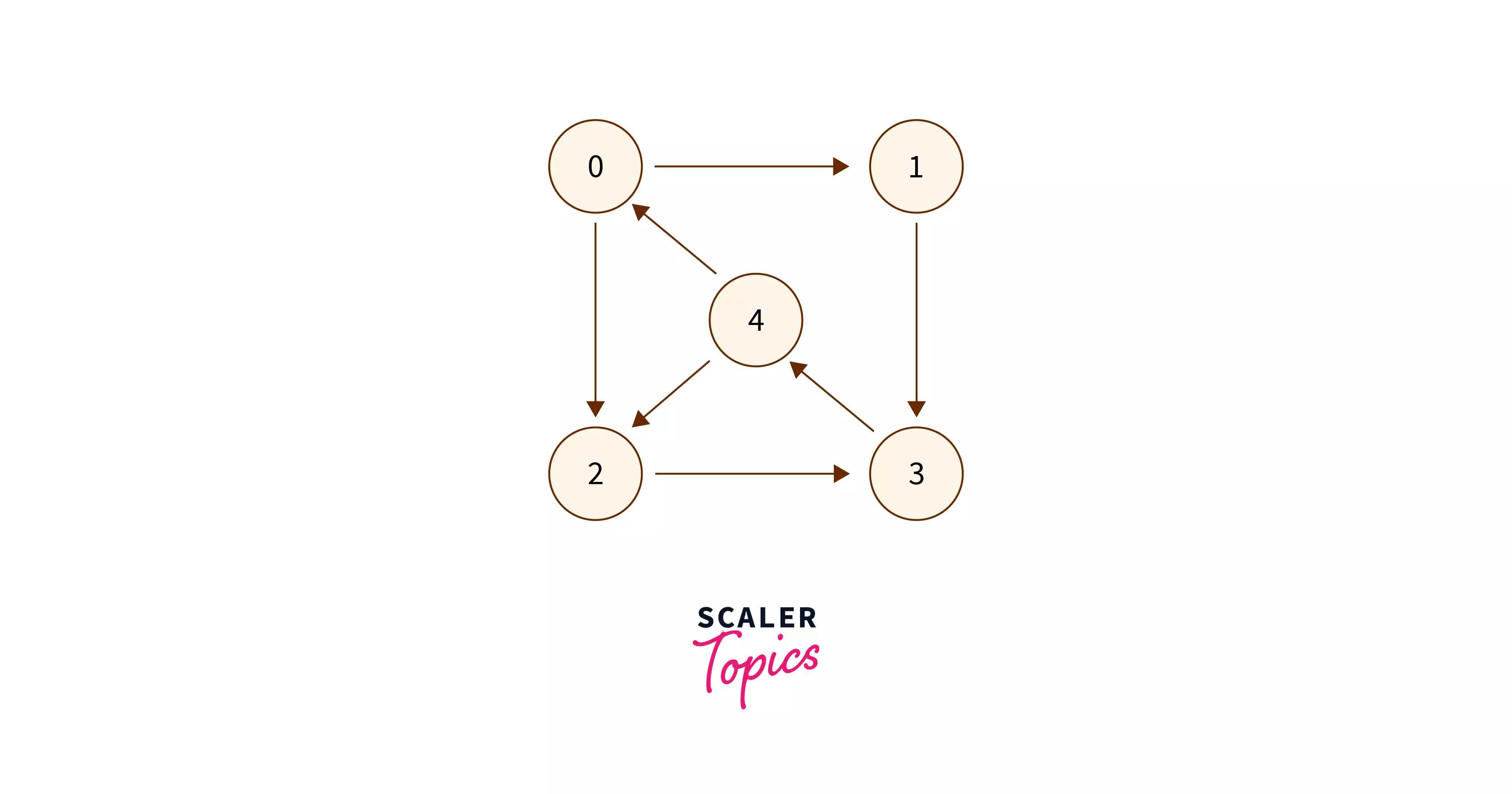
Output:
YES

Explanation:
There exists a cycle $0\rightarrow 1\rightarrow3 \rightarrow 4 \rightarrow 1$, hence we had printed “YES” in the output.

Constraints

$1\leq V, E\leq 10^5$

Approach 1: Using Depth First Search (DFS)

To detect the cycle in a directed graph, we will be using the DFS technique. We know that the DFS of the directed graph generates a DFS tree(s), which is nothing but the representation of vertices and edges of the provided graph.

When we perform DFS on a disconnected graph, multiple such trees hence we use the term DFS Forest to denote all of them. Each of these trees has a certain different type of edges that are –

1. Tree Edge
2. Forward Edge
3. Cross Edge
4. Back Edge

Here to detect the cycle in a directed graph, we are only concerned about the Back Edge. Back Edge is an edge that connects a vertex (say $u$) to one of its descendants. Let us understand the concept of back edge through an example –
Consider the following graph and its DFS tree obtained by performing DFS starting from vertex $A$

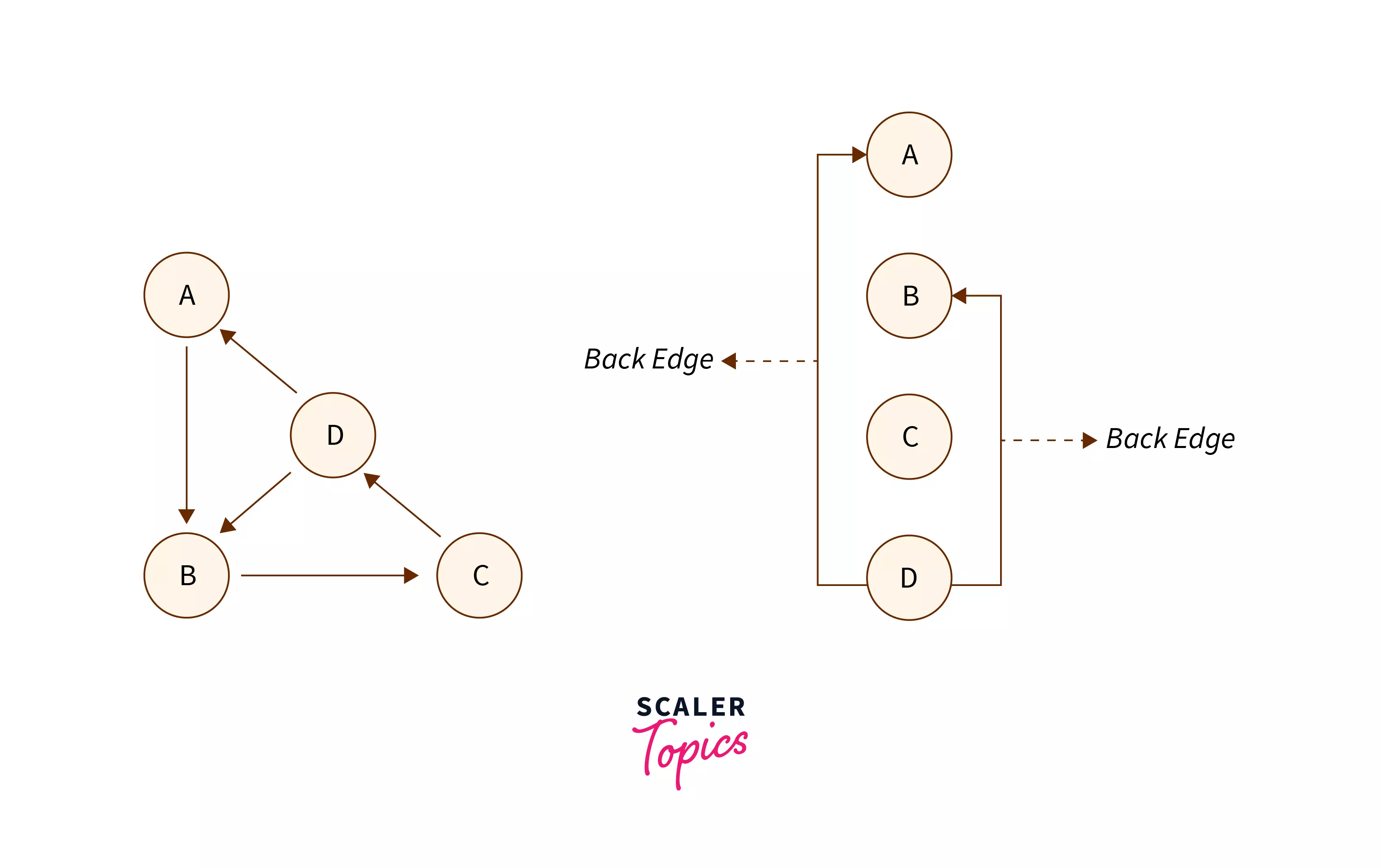
It is easily noticeable that due to the presence of the back edge we can form a cycle $B\rightarrow C\rightarrow D \rightarrow B$. So it is understood that the presence of a back edge indicates there is a cycle in the graph.

Now we will how we can use the DFS to find whether there exists a back edge. To detect the back edge we will keep track of vertices currently present in the recursion stack of the DFS function. If we encounter a vertex that is present in the recursion stack, we can say a back edge is present and there exists a cycle in the graph.

The algorithm is as follows –

• Let $DFS$ be boolean type recursive function, accepting three arguments $i.e.$ the vertex number (say node), visited array, and inStack array.
• In the function, firstly we will check if node is already present in the recursion stack. If found true, a cycle exists in the graph.
• After that, we will proceed if node has not been visited in the previous DFS call(s).
• We will mark node and then recurse for all the neighbors of node.

Dry Run

Let’s use the graph used in Example 2 to do a dry run of this approach.
Graph –

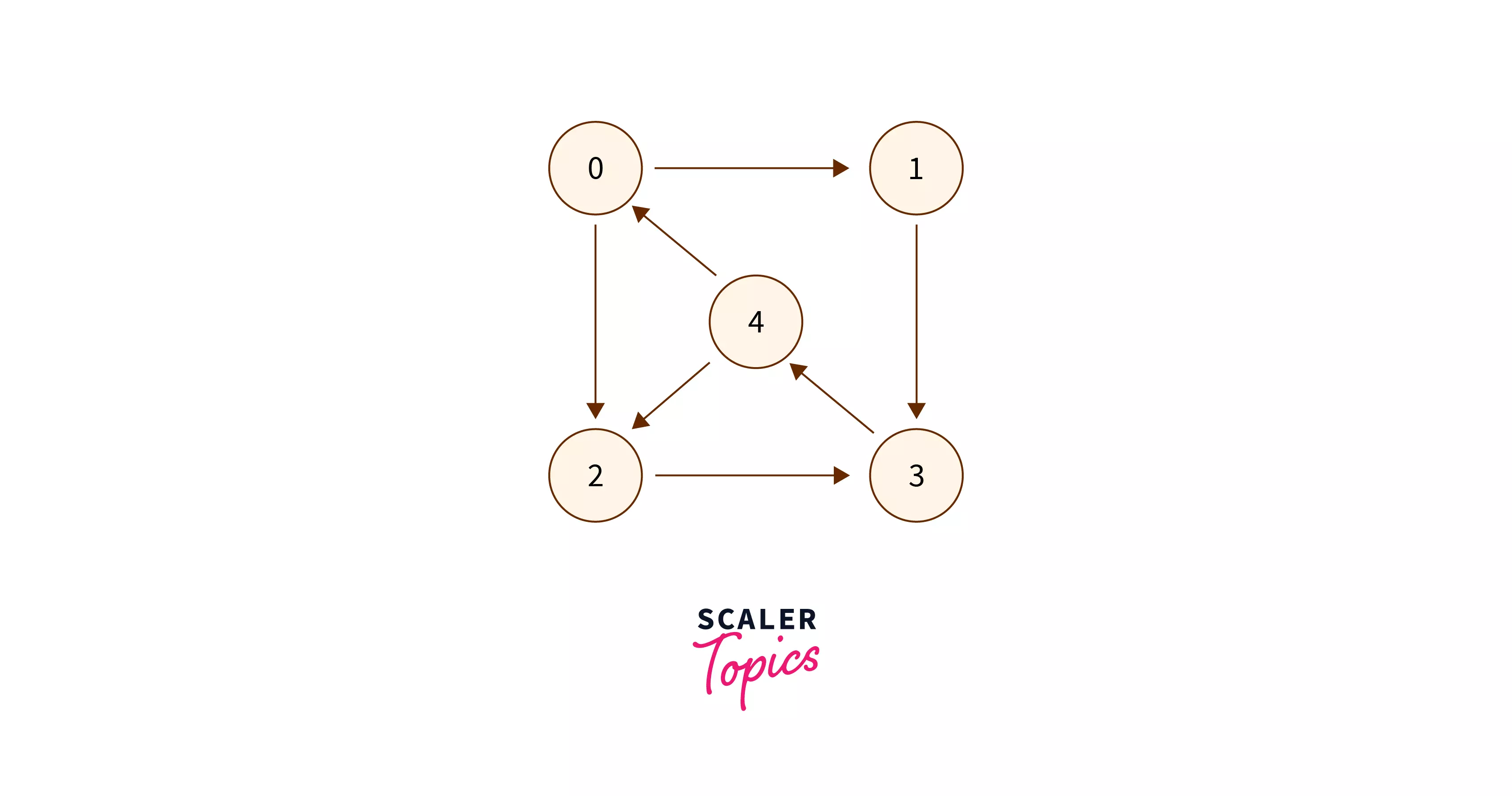
Proceeding as per the algorithm –

• Define visited and inStack array to keep track of visited vertices and vertices present in the recursive stack respectively. So we have
  • visited[] = [F, F, F, F, F]
  • inStack[] = [F, F, F, F, F]
    Note that F means False and T means True.
• Start DFS from vertex $0$. Mark $0$ as visited and to be present in the recursive stack. Now we will recurse for one of the adjacents of $0$ i.e. $1$ and $2$. Let’s say we recurse for $2$ first with our arrays as
  • visited[] = [T, F, F, F, F]
  • inStack[] = [T, F, F, F, F]
• Mark $2$ as visited and to be present in recursive stack. After that, we will recurse for only adjacent of $2$ i.e. $3$ with our arrays as –
  • visited[] = [T, F, T, F, F]
  • inStack[] = [T, F, T, F, F]
• Mark $3$ as visited and to be present in the recursive stack. After that we will recurse for only adjacent of $3$ i.e. $4$ with our arrays as –
  • visited[] = [T, F, T, T, F]
  • inStack[] = [T, F, T, T, F]
• Mark $4$ as visited and to be present in the recursive stack. After that, we will recurse for one of the adjacents of $4$ Viz. $0$ and $2$. No matter for which one we recurse, we will find the cycle let’s see how.
  • Choice 1 – Recurse for vertex $0$
    We find that inStack[0] is true, which means it is present in the recursive stack, hence we can conclude cycle exists.
  • Choice 2 – Recurse for vertex $2$
    We find that inStack[2] is also True, which means it is present in the recursive stack, hence we can conclude cycle exists.

It is clear from the dry run that a cycle exists in the graph. We would strongly recommend you to pick a pen and paper and dry run this approach for the graph of example 1.

Pseudocode

// Helper function to check for cycle.
function checkCycleUtil (node, visited, inStack):
    // Check if node exists in the
    // recursive stack.
    if (inStack[node]):
        return true
    
    // Check if node is already visited.
    if (visited[node]):
        return false
    
    // Marking node as visited.
    visited[node] = true

    // Marking node to be present in
    // recursive stack.
    inStack[node] = true

    // Iterate for all adjacent of 
    // 'node'.
    for (int v : adj[node]):
        // Recurse for 'v'.
        if (checkCycleUtil(v, visited, inStack)):
            return true
    

    // Mark 'node' to be removed
    // from the recursive stack.
    inStack[node] = false

    // Return false if no cycle exists.
    return false

end function
// Function to check for the cycle.
function checkCycle(V, E):
    // Defining visited and inStack array
    // to keep track of visited vertices 
    // and vertices in Recursive stack. 
    visited[V] 
    inStack[V] 

    // Iterating for i = 0 To i = V - 1
    // to detect cycle in different 
    // DFS trees. 
    for i = 0 To i = V - 1:
        // Check if cycle exists.
        if (checkCycleUtil(i, visited, inStack)):
            return true

    // Returning false, if no cycle is found.
    return false
end function

Java Implementation

import java.util.*;
public class Main{
    // Adjacency List
    static List<List<Integer>> adj;
    // Function to add edge u --> v
    static void addEdge(int u, int v){
        adj.get(u).add(v);
    }
	// Helper function to check for cycle.
    static boolean checkCycleUtil (int node, 
                boolean visited[], boolean inStack[]){
        // Check if node exists in the
        // recursive stack.
        if (inStack[node])
            return true;
        
        // Check if node is already visited.
        if (visited[node])
            return false;
        
        // Marking node as visited.
        visited[node] = true;

        // Marking node to be present in
        // recursive stack.
        inStack[node] = true;

        // Iterate for all adjacent of 
        // 'node'.
        for (int v : adj.get(node)){
            // Recurse for 'v'.
            if (checkCycleUtil(v, visited, inStack))
                return true;
        }

        // Mark 'node' to be removed
        // from the recursive stack.
        inStack[node] = false;

        // Return false if no cycle exists.
        return false;
    }
    // Function to check for the cycle.
    static boolean checkCycle(int V, int E){
        // Defining visited and inStack array
        // to keep track of visited vertices 
        // and vertices in Recursive stack. 
        boolean visited[] = new boolean[V];
        boolean inStack[] = new boolean[V];

        // Iterating for i = 0 To i = V - 1
        // to detect cycle in different 
        // DFS trees. 
        for (int i = 0; i < V; i++){
            // Check if cycle exists.
            if (checkCycleUtil(i, visited, inStack)){
                return true;
            }
        }
        // Returning false, if no cycle is found.
        return false;

    }
    public static void main(String args[]){
        // Defining the number of Vertices
        // and the number of edges. 
        int V = 5, E = 7;

        // Defining Adjacency List
        adj = new ArrayList<>();
        for (int i = 0; i < V; i++) 
            adj.add(new ArrayList<>());

        // Building the Graph same as example 1.
        addEdge(0, 1);
        addEdge(0, 4);
        addEdge(0, 2);
        addEdge(1, 3);
        addEdge(2, 3);
        addEdge(4, 1);
        addEdge(4, 2);

        // If the graph contains cycle 
        // Print YES
        if(checkCycle(V, E))
            System.out.println("YES");
        // Otherwise Print NO
        else
            System.out.println("NO");
    }
    
}

C++ Implementation

#include<bits/stdc++.h>
using namespace std;

// Adjacency List
vector<vector<int>> adj;

// Function to add edge u --> v
void addEdge(int u, int v){
    adj[u].push_back(v);
}
// Helper function to check for cycle.
bool checkCycleUtil (int node, 
            bool *visited, bool *inStack){
    // Check if node exists in the
    // recursive stack.
    if (inStack[node])
        return true;
    
    // Check if node is already visited.
    if (visited[node])
        return false;
    
    // Marking node as visited.
    visited[node] = true;

    // Marking node to be present in
    // recursive stack.
    inStack[node] = true;

    // Iterate for all adjacent of 
    // 'node'.
    for (int v : adj[node]){
        // Recurse for 'v'.
        if (checkCycleUtil(v, visited, inStack))
            return true;
    }

    // Mark 'node' to be removed
    // from the recursive stack.
    inStack[node] = false;

    // Return false if no cycle exists.
    return false;
}
// Function to check for the cycle.
bool checkCycle(int V, int E){
    // Defining visited and inStack array
    // to keep track of visited vertices 
    // and vertices in Recursive stack. 
    bool visited[V]; 
    bool inStack[V]; 
    for(int i = 0; i < V; i++){
        visited[i] = false;
        inStack[i] = false;
    }
    
    // Iterating for i = 0 To i = V - 1
    // to detect cycle in different 
    // DFS trees. 
    for (int i = 0; i < V; i++){
        // Check if cycle exists.
        if (checkCycleUtil(i, visited, inStack)){
            return true;
        }
    }
    // Returning false, if no cycle is found.
    return false;

}
int main(){
    // Defining the number of Vertices
    // and the number of edges. 
    int V = 5, E = 7;

    // Defining Adjacency List
    adj.resize(V);
    // Building the Graph same as example 1.
    addEdge(0, 1);
    addEdge(0, 4);
    addEdge(0, 2);
    addEdge(1, 3);
    addEdge(2, 3);
    addEdge(4, 1);
    addEdge(4, 2);

    // If the graph contains cycle 
    // Print YES
    if(checkCycle(V, E))
        cout << "YES\n";
    // Otherwise Print NO
    else
        cout << "NO\n";
}

Python Implementation

# Adjacency List
adj=[]

# Function to add edge u --> v
def addEdge (u, v):
    adj[u].append(v)

# Helper function to check for cycle.
def checkCycleUtil (node, visited, inStack):
    # Check if node exists in the
    # recursive stack.
    if (inStack[node] == True):
        return True
    
    # Check if node is already visited.
    if (visited[node] == True):
        return False
    
    # Marking node as visited.
    visited[node] = True

    # Marking node to be present in
    # recursive stack.
    inStack[node] = True

    # Iterate for all adjacent of 
    # 'node'.
    for v in adj[node]:
        # Recurse for 'v'.
        if (checkCycleUtil(v, visited, inStack) == True):
            return True
    

    # Mark 'node' to be removed
    # from the recursive stack.
    inStack[node] = False

    # Return false if no cycle exists.
    return False

# Function to check for the cycle.
def checkCycle(V, E):
    # Defining visited and inStack array
    # to keep track of visited vertices 
    # and vertices in Recursive stack. 
    visited = [False] * V
    inStack = [False] * V
    
    # Iterating for i = 0 To i = V - 1
    # to detect cycle in different 
    # DFS trees. 
    for i in range(V):
        # Check if cycle exists.
        if (checkCycleUtil(i, visited, inStack) == True):
            return True
        
    
    # Returning false, if no cycle is found.
    return False

# Defining the number of Vertices
# and the number of edges. 
V, E = 5, 7

# Defining Adjacency List
adj = [[] for i in range(V)]
# Building the Graph same as example 1.
addEdge(0, 1)
addEdge(0, 4)
addEdge(0, 2)
addEdge(1, 3)
addEdge(2, 3)
addEdge(4, 1)
addEdge(4, 2)

# If the graph contains cycle 
# Print YES
if(checkCycle(V, E)):
    print("YES")
# Otherwise Print NO
else:
    print("NO")

Complexity Analysis

• Time Complexity – Since we are doing a DFS traversal with some minor modifications, the time complexity in the worst case (when the cycle does not exists) is O(V+E).
• Space Complexity – We are using boolean arrays of size V, and maximum recursive stack height can reach up to V. Therefore, the space complexity is O(V).

Approach 2: Using Breadth First Search (BFS)

In the previous section, we have seen how we can detect a cycle in a directed graph using Depth First Search. In this section, we will be seeing how we can detect a cycle in directed graph using the Breadth First Search technique.

The idea is very simple, we learned in Topological Sorting that, topological sort is possible only if the graph is DAG (Directed Acyclic Graph) i.e.i.e. Graph should be directed and it should not contain any cycle. Therefore we will just check if the topological ordering is possible for the given graph or not.

To check if topological ordering is possible or not, we will use Kahn’s Algorithm which uses the idea of indegrees of the vertices where the in-degree of a vertex (say $v$) is nothing but the number of incoming edges toward the vertex $v$.

The algorithm is as follows –

• Define an array (sat deg) of size $V$, which will be used to store indegrees of the vertices.
• Compute indegrees of all the vertices by iterating over the adjacency list provided as the input.
• Define a Queue (say q), and insert all the vertices with indegree 0.
• Define a variable (say counter) and initialize it with 0, this will be used to count the number of processed vertices.
• Iterate using a while loop, until $q$ is not empty and do the following –
  • Dequeue element from the queue and store it in a variable (say u).
  • Now increase the counter by 1, because u is considered to be processed.
  • Now iterate over all the adjacents of u and do the following –
    • Let adjacent be v.
    • Decrease the indegree of v.
    • If indegree of v reaches 0, add v to the q.
• If the condition counter = V holds true, it means the graph does not contain any cycle otherwise cycle is present.

To understand the above algorithm more clearly, we will dry run this algorithm on the below sample graph (same as given in the examples section)

Dry Run

Graph –

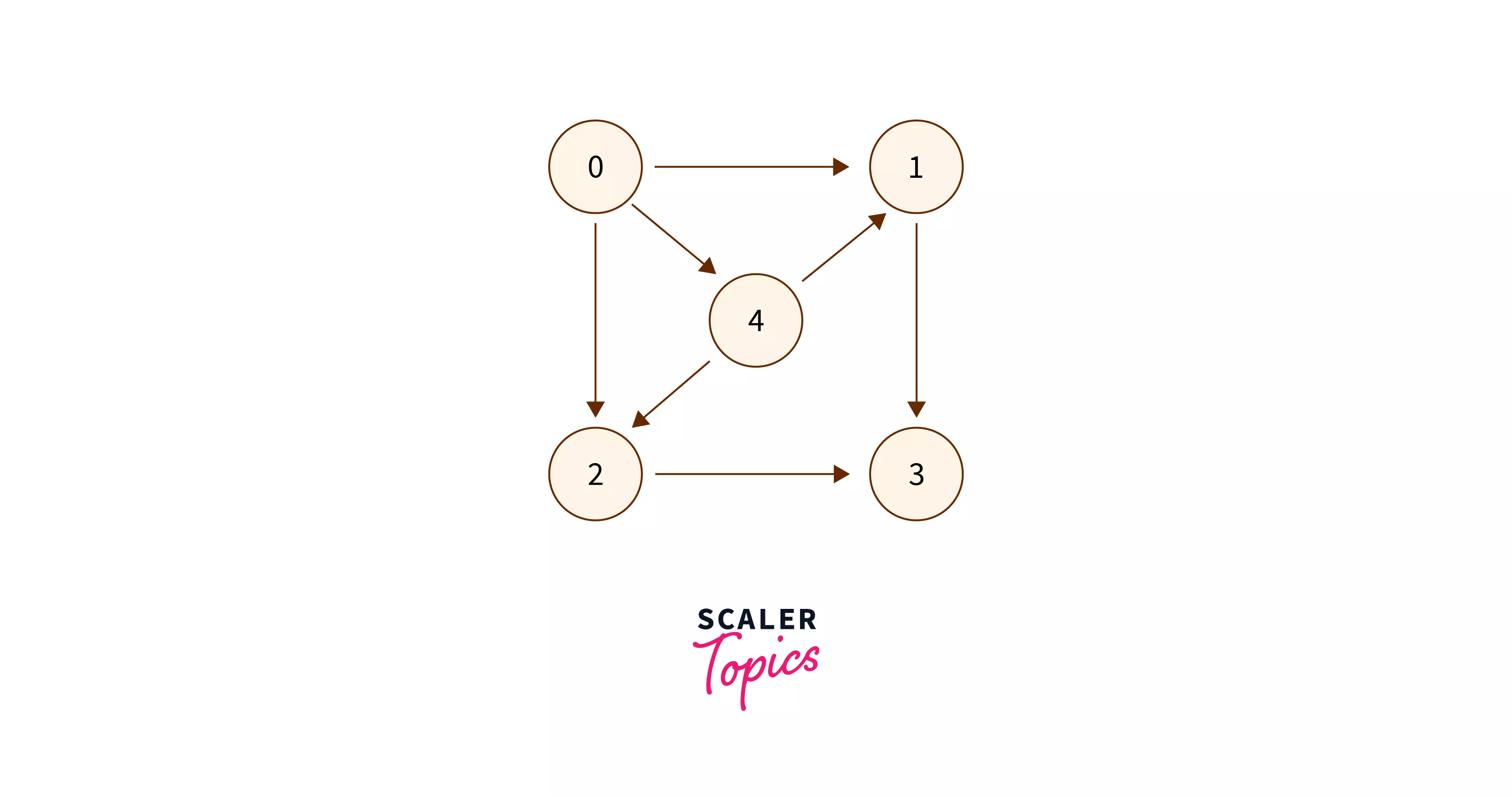
• Step 1 – Calculate Indegrees
  After calculating the indegrees, we have deg = [0, 2, 2, 2, 1]
• Step 2 – Insert vertices with 0 indegrees in q.
  We have only one vertex with indegree as 0, so we will insert that in q. After which we have q = [0]. Note that q contains the number of the vertices.
• Step 3 – Iterating until q is not empty
  • Iteration 1 –
    • Dequeue the vertex $\implies$ v = 0
    • Increase counter by 1.
    • Iterate over all adjacent of 0 and reduce indegree by 1.
      After which we have deg = [0, 1, 1, 2, 0]
    • Insert 4 in q because deg[4] = 0.
      After which we have q = [4]
  • Iteration 2 –
    • Dequeue the vertex $\implies$ v = 4
    • Increase counter by 1.
    • Iterate over all adjacent of 4 and reduce indegree by 1.
      After which we have deg = [0, 0, 0, 2, 0]
    • Insert 1 and 2 in q because deg[1]=0 and deg[2]=0.
      After which we have q = [1, 2]
  • Iteration 3 –
    • Dequeue the vertex $\implies$ v = 1
    • Increase counter by 1.
    • Iterate over all adjacent of 1 and reduce indegree by 1.
      After which we have deg = [0, 0, 0, 1, 0]
    • Now we have q = [2]
  • Iteration 4 –
    • Dequeue the vertex $\implies$ v = 2
    • Increase counter by 1.
    • Iterate over all adjacent of 3 and reduce indegree by 1.
      After which we have deg = [0, 0, 0, 0, 0]
    • Insert 3 in q because deg[3]=0.
      After which we have q = [3]
  • Iteration 5 –
    • Dequeue the vertex $\implies$ v = 3
    • Increase counter by 1.
    • Vertex 3 does not have any adjacent vertices.
    • Now we have q = [].
• Step 4 – Check if counter = V
  This condition holds true because after Step 3 we have counter = 5 and as per the input V = 5. So we will print “NO”.

We would strongly recommend you to Pick a pen and paper and dry run the algorithm on the graph provided in Example 2.

Pseudocode

// Function to check for the cycle.
function checkCycle (adj, V, E):
    // Defining the array to
    // store indegrees.
    deg = Array of length V

    // Computing indegree of 
    // each vertex using.
    For i = 0 To i = V - 1:
        For x in adj[i]:
            deg[x]++

    // Queue to store vertices 
    // with  having 0 indegree.
    q = Queue

    // Iterate from i = 0 To i 
    // = V - 1 and find vertices 
    // having indegree as 0.
    For i = 0 To i = V - 1:
        If (deg[i] == 0):
            q.enqueue(i)

    // Defining the counter.
    counter = 0

    // Iterating while the queue is 
    // not empty.
    While (q is not empty):
        // Dequeue from 'q'.
        u = q.dequeue()

        // Increase the counter.
        counter++

        // Iterate for all neighours 
        // of vertex 'u'.
        For v in adj[u]:
            // Decrease the indegree.
            deg[v]--

            // If deg[v] is 0, insert
            // it the q.
            If (deg[v] == 0):
                q.enqueue(v)
                
    // Returning true if counter != V.
    return counter != V
    
end function

Java Implementation

import java.util.*;
public class Main{
    // Adjacency List
    static List<List<Integer>> adj;
    // Function to add edge u --> v
    static void addEdge(int u, int v){
        adj.get(u).add(v);
    }
    // Function to check for the cycle.
    static boolean checkCycle(int V, int E){
        int deg[] = new int[V];

        // Computing indegree of 
        // each vertex using.
        for (int i = 0; i < V; i++)
            for (int x : adj.get(i))
                deg[x]++;

        // Queue to store vertices 
        // with  having 0 indegree.
        Queue<Integer> q = new LinkedList<>();

        // Iterate from i = 0 To i 
        // = V - 1 and find vertices 
        // having indegree as 0.
        for (int i = 0; i < V; i++)
            if (deg[i] == 0)
                q.add(i);

        // Defining the counter.
        int counter = 0;

        // Iterating while the queue is 
        // not empty.
        while (!q.isEmpty()){
            // Dequeue from 'q'.
            int u = q.poll();

            // Increase the counter.
            counter++;

            // Iterate for all neighours 
            // of vertex 'u'.
            for (int v : adj.get(u)){
                // Decrease the indegree.
                deg[v]--;

                // If deg[v] is 0, insert
                // it the q.
                if (deg[v] == 0)
                    q.add(v);
            }
        }
        
        // Returning true if counter != V.
        return counter != V;
    }
    public static void main(String args[]){
        // Defining the number of Vertices
        // and the number of edges. 
        int V = 5, E = 7;

        // Defining Adjacency List
        adj = new ArrayList<>();
        for (int i = 0; i < V; i++) 
            adj.add(new ArrayList<>());

        // Building the Graph same as example 1.
        addEdge(0, 1);
        addEdge(0, 4);
        addEdge(0, 2);
        addEdge(1, 3);
        addEdge(2, 3);
        addEdge(4, 1);
        addEdge(4, 2);

        // If the graph contains cycle 
        // Print YES
        if(checkCycle(V, E))
            System.out.println("YES");
        // Otherwise Print NO
        else
            System.out.println("NO");
    }
    
}

C++ Implementation

#include<bits/stdc++.h>
using namespace std;

// Adjacency List
vector<vector<int>> adj;

// Function to add edge u --> v
void addEdge(int u, int v){
    adj[u].push_back(v);
}

// Function to check for the cycle.
bool checkCycle(int V, int E){
    // Defining the array to
    // store indegrees.
    int deg[V];
    for (int i = 0; i < V; i++)
        deg[i] = 0;

    // Computing indegree of 
    // each vertex using.
    for (int i = 0; i < V; i++)
        for (int x : adj[i])
            deg[x]++;

    // Queue to store vertices 
    // with  having 0 indegree.
    queue<int> q;

    // Iterate from i = 0 To i 
    // = V - 1 and find vertices 
    // having indegree as 0.
    for (int i = 0; i < V; i++)
        if (deg[i] == 0)
            q.push(i);

    // Defining the counter.
    int counter = 0;

    // Iterating while the queue is 
    // not empty.
    while (!q.empty()){
        // Dequeue from 'q'.
        int u = q.front();
        q.pop();
        // Increase the counter.
        counter++;

        // Iterate for all neighours 
        // of vertex 'u'.
        for (int v : adj[u]){
            // Decrease the indegree.
            deg[v]--;

            // If deg[v] is 0, insert
            // it the q.
            if (deg[v] == 0)
                q.push(v);
        }
    }
    
    // Returning true if counter != V.
    return counter != V;
}
int main(){
    // Defining the number of Vertices
    // and the number of edges. 
    int V = 5, E = 7;

    // Defining Adjacency List
    adj.resize(V);
    // Building the Graph same as example 1.
    addEdge(0, 1);
    addEdge(0, 4);
    addEdge(0, 2);
    addEdge(1, 3);
    addEdge(2, 3);
    addEdge(4, 1);
    addEdge(4, 2);

    // If the graph contains cycle 
    // Print YES
    if(checkCycle(V, E))
        cout << "YES\n";
    // Otherwise Print NO
    else
        cout << "NO\n";
}

Python Implementation

# Adjacency List
adj=[]

# Function to add edge u --> v
def addEdge (u, v):
    adj[u].append(v)

# Function to check for the cycle.
def checkCycle (V, E):
    # Defining the array to
    # store indegrees.
    deg = [0]*V

    # Computing indegree of 
    # each vertex using.
    for i in range(V):
        for x in adj[i]:
            deg[x] += 1

    # Queue to store vertices 
    # with  having 0 indegree.
    q = []

    # Iterate from i = 0 To i 
    # = V - 1 and find vertices 
    # having indegree as 0.
    for i in range(V):
        if (deg[i] == 0):
            q.append(i)

    # Defining the counter.
    counter = 0

    # Iterating while the queue is 
    # not empty.
    while (q):
        # Dequeue from 'q'.
        u = q.pop(0)

        # Increase the counter.
        counter += 1

        # Iterate for all neighours 
        # of vertex 'u'.
        for v in adj[u]:
            # Decrease the indegree.
            deg[v] -= 1

            # If deg[v] is 0, insert
            # it the q.
            if (deg[v] == 0):
                q.append(v)
                
    # Returning true if counter != V.
    return counter != V


# Defining the number of Vertices
# and the number of edges. 
V, E = 5, 7

# Defining Adjacency List
adj = [[] for i in range(V)]
# Building the Graph same as example 1.
addEdge(0, 1)
addEdge(0, 4)
addEdge(0, 2)
addEdge(1, 3)
addEdge(2, 3)
addEdge(4, 1)
addEdge(4, 2)

# If the graph contains cycle 
# Print YES
if(checkCycle(V, E)):
    print("YES")
# Otherwise Print NO
else:
    print("NO")

Complexity Analysis

• Time Complexity – The Time required to find indegrees of vertices is O(E) and finding vertices with 0 indegrees is O(V), also O(V) time is required in the while loop. Therefore overall time complexity is O(E + V + V) which is nothing but O(V + E).
• Space Complexity – Since, we are using a deg array of size V and a Queue that can reach a size up to V. Hence, the overall space complexity is O(V).

Conclusion

• To detect a cycle in a directed graph, we can either use the Depth First Search or the Breadth First Search approach.
• In the DFS technique, we check if there exists a back edge in the DFS tree of the graph because the existence of the back edge indicates the presence of a cycle.
• In the BFS technique, we check if topological ordering is possible for the given graph because topological ordering is only possible for the acyclic graph.