The worst time complexity of bucket sort is O(N^2). This is because, as the name suggests, in this algorithm, the buckets are created, and the elements which are in the buckets are sorted separately and independently and then combined to form the solution, so the time complexity increases. The complete details and the internal working of the algorithm are given below.
What is Bucket Sort?
Bucket sort is a sorting algorithm that divides the elements of an unsorted array into several groups which are known as buckets. After that, each bucket is sorted individually and independently by using suitable sorting algorithms like insertion sort, selection sort, etc.. or by recursively applying the bucket sort algorithm itself. The bucket sort algorithm follows a scatter-gather approach for sorting the elements. In this approach, the elements are first scattered into the buckets, then the elements in each bucket are sorted, and finally, all the elements are gathered, and now they are in the sorted form.
Example
Let us take an example of an unsorted array of size 10.
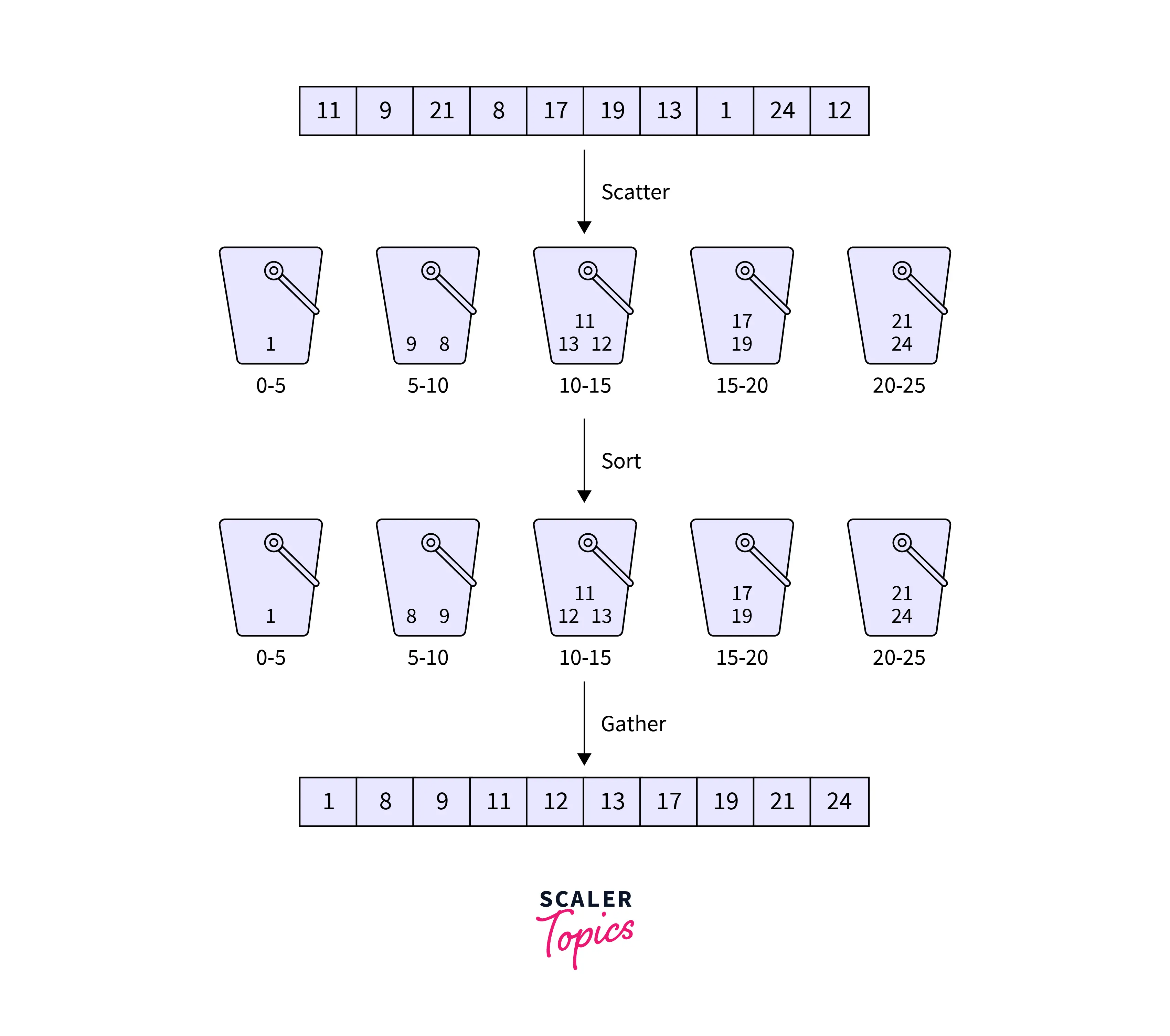
Input: [11,9,21,8,17,19,13,1,24,12]
Output: [1,8,9,11,12,13,17,19,21,24]
The following steps will lead to the algorithm of the bucket sort.
- First, we will make the buckets of size 5 each
- Then we will start scattering the elements into the buckets according to their values
- Then we will sort each bucket independently by using suitable sorting algorithms
- Finally, we will merge all the buckets starting from the smallest value bucket to the last bucket.
Complexity Analysis of Bucket Sort Algorithm
Time Complexity of Bucket Sort Algorithm
The time complexity of the bucket sort algorithm is highly dependent on the number of elements in the array, the number of elements in each bucket, and the total number of buckets. Let us have a look at the best case, average case, and worst case time complexity of the bucket sort.
- Best Case Complexity
- The algorithm shows the best-case complexity when all the elements are distributed uniformly in the buckets, i.e. when there is almost the same number of elements in each bucket.
- If the buckets are already sorted, then the time complexity may increase
- Let there be k buckets in total, if we use insertion sort to sort the elements in the buckets, the time complexity will become O(N+k), this is because every time we will push the element into the bucket, it has to travel to the very extreme point to reach its original position.
- The time complexity of creating the buckets will be O(N) and the complexity for sorting the buckets will be O(k), so the overall time complexity of bucket sorting in the best case will be O(N+k).
- Average Case Complexity
- The algorithm shows the average case complexity when all the elements are distributed randomly in the buckets.
- It will run in linear time complexity i.e. O(N), even if the elements are not distributed uniformly in the array.
- Worst Case Complexity
- The algorithm shows the worst-case complexity when all the elements are placed in the same bucket.
- As a result, only one bucket will be formed, containing all the elements
- So now if we sort this bucket using insertion or selection sort, it will take O(N) worst case time complexity for each element, so the total time complexity comes out to be O(N^2).
Space Complexity of Bucket Sort Algorithm
The space complexity of the bucket sort algorithm is highly dependent on the number of elements in the array, and the total number of buckets. Assuming there is a total of k buckets, the total space complexity for this algorithm will be O(N+k). This is because every element will go inside exactly one bucket, and there are total k buckets and N elements, so
O(N)+O(k) = O(N+k)
Learn more about Bucket Sort Bucket Sort
Conclusion
In this quick tutorial, we have discussed the following
- We saw the intuition behind the bucket sort algorithm
- We studied the internal working of the bucket sort algorithm
- We visualized the bucket sort algorithm through an example and the diagram
- Finally, we discussed the time complexity and the space complexity of the bucket sort algorithm.