Skip List in Data structure

Skip list data structure is an extension to a sorted linked list; it provides indexing and querying data with reduced time complexity because there is a concept of skipping nodes while exploring data, somewhat similar to binary search. Each node contains a few forward pointers (not just one or two as in a linked list), therefore we are not constrained to move only one step during traversal, but we can also skip some nodes; technical phrases which are used in this concept are “express line” and “layers” of data structure.

What Are Skip Lists in Data Structure?

Why Skip List?

Before going to the actual concept let’s start from the very beginning. We implement some data structures to store our data in a well-organized format so that we can further access that data and use it according to our needs. Let us now reduce our thinking scope and focus solely on linear data structures. In the linked list we store linear data which provides us with better insertion and deletion as compared to the array but linked lists are very bad at searching because we need to traverse via each node to search for a particular one. Consider the case of a binary search on a sorted array. When doing a search, we always reduce the search scope in half, which makes the searching process considerably faster. However, we are unable to do this with linked lists since they don’t have random access. Just take a moment to stop reading and consider this: Insertion and deletion in linked lists already need constant time complexity, so it would be excellent if we could improve search performance for sorted linked lists. Can we create a more advanced data structure with the capability to search over the sorted linked list in a binary search manner? The answer is Yes, Skip Lists.

Concept of Skip List

The problem of inefficient searching on a sorted linked list is solved by skip lists, which can skip over nodes while traversal. We will see the exact procedure in the upcoming paragraphs.

The core concept of a skip list is, here our nodes not only contain a single forward pointer as a traditional linked list but contain several pointers that point to different nodes(the only one which is in a forward direction from the current node) of the skip list. In addition, we use several methods to determine which forward pointer to choose while proceeding in the linked list.

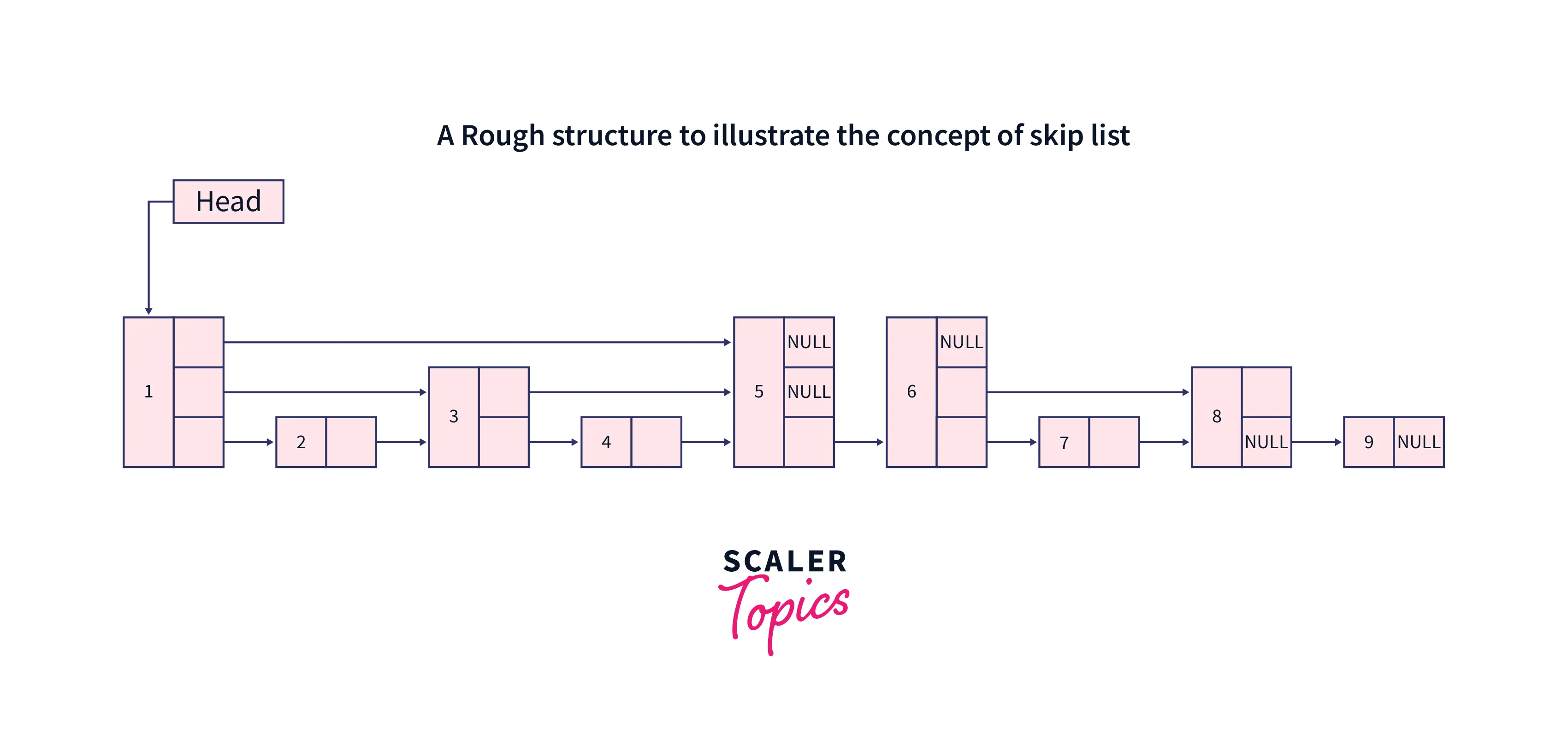
For Example:

If 1st node is pointing to the 2nd, 3rd, and 5th node of the linked list, then while traversing we have the option to choose from the 2nd, 3rd, and 5th node. In this way, if we are searching for 6 then we can skip 3 nodes, if we are searching for 4 we can skip the 1 node. This was a general explanation of a skip list; in the paragraph that follows, we’ll examine its precise structure and technical terminologies.

Skip List Definition and Structure

A skip list is a probabilistic data structure that contains a set of sorted linked lists. It is considered to be a good alternative to balanced search trees.

A skip list is a multi-layer linked list. The bottom-most layer is a plain linked list that has elements in sorted order. Then there are several layers or levels above that, as additional linked lists, however, these additional layers have only a few important nodes which are chosen from the linked list of the last layer, in the same sorted order just like the bottom-most linked list. These additional layers form sort of an “express line” with the elements of the main list. The bottom-most linked list is called as “normal line“.

A 2-level skip list,

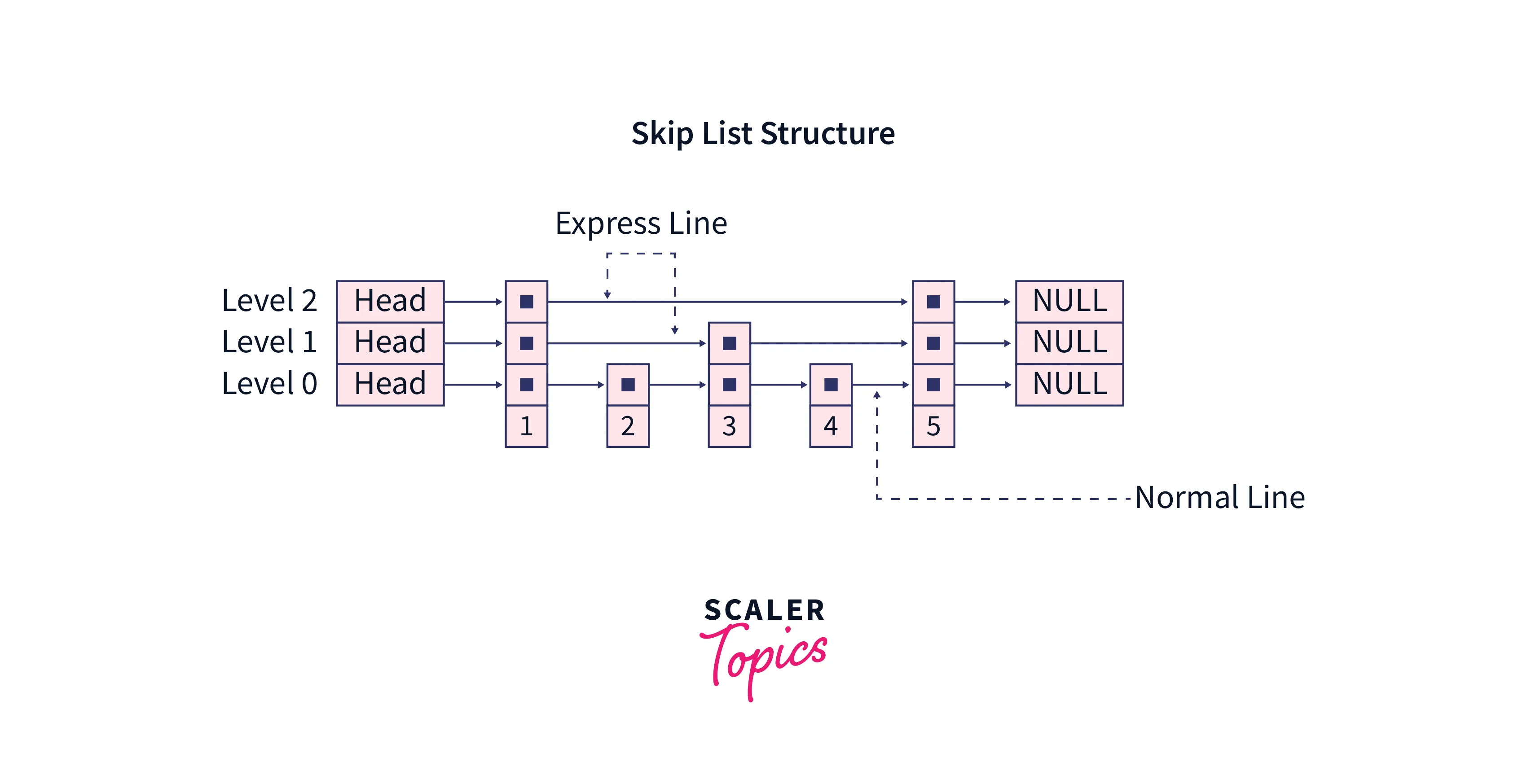
Working Demonstration of the Skip list with Example

Working: The working of a skip list is as follows, The searching process starts from the topmost layer, and the element is searched in the express line, The traversal proceeds until the element of the node is less than the one which is being searched, Now there exist two scenarios during traversal,

1. The next node of the express line is equal to the searched element.
2. The next node of the express line is greater than the element to be searched.

In the first case, searching stops immediately because the element is found, in the second case the searching proceeds in the next express line of the lower layer but it doesn’t start from the beginning but instead from the node from where the searching was stopped in the last express line. Then again the all steps are repeated.

Example: Assume we have the following linked list with 6 sorted elements, a layer above it with 3 elements from the main linked list, and again a layer above that with 1 element from the main list. Suppose we want to find node 18 in the main linked list.

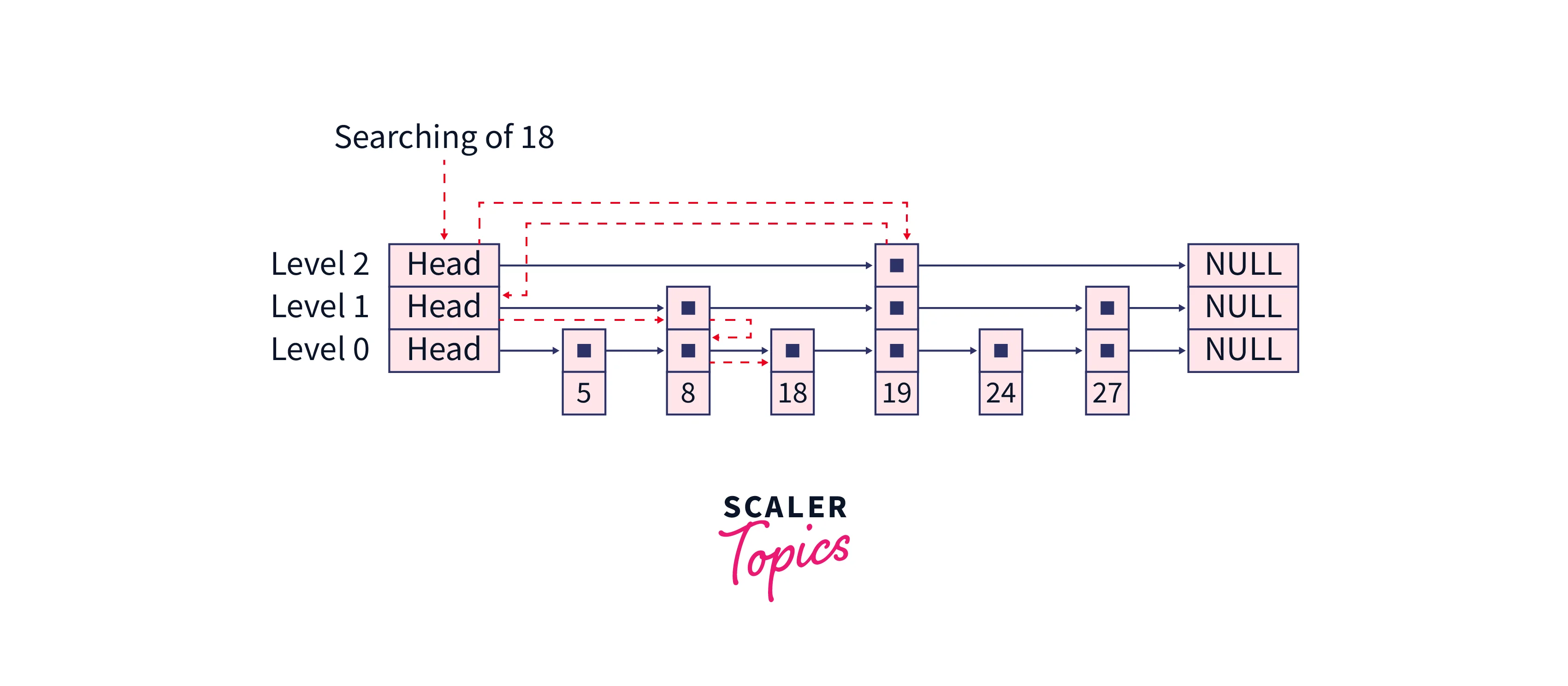
We will start iterating through the “express line” of the top layer. The first node contains 19 which is greater than 18 hence our element will be found on the left of that node, Now start searching from the next lower layer, so we will first encounter 8 but 8 is less than 18 hence we will continue iterating and the next element is 19 but 19 is greater than 18 so instead of moving forward we will go down to the lower layer, and again start searching so while searching we will see that immediate next node contains a value 18 means we have found our element.

Types of Operations in the skip list

A skip list, like a standard linked list, can perform the following operations, but skip lists allow faster insertion, deletion, and searching of elements than a linked list. Insertion Operation: To add a new node to the skip list. Deletion Operation: To delete a node from the skip list. Search Operation: To search for a node in the skip list.

All operations in the skip list start from the topmost layer, as the topmost layer is the entry point to the skip list. Each iteration through a layer leads us to the bottom layers and we eventually reach the bottom linked list to actually perform any of the insertion, deletion, or searching operations.

What is the Meaning of the Term Probabilistic Data Structure in the Context of Skip List?

Before we move to the algorithms of operations on skip lists, let us understand why skip lists are called probabilistic data structures.

Let us first see what an ideal skip list looks like: An ideal skip list will have half the number of nodes in every successive layer. If the main bottommost linked list has n nodes, the upper one will have n/2, then n/4, and so on till we reach the top layer that has one node only.

When new nodes are to be inserted, what would happen if only do so in the bottom-most layer? Over a period of time, the skip list shall become skewed; only the bottom-most layer would keep on increasing, and our skip list would no longer be an ideal skip list that has double the nodes in the successive layers. We would start losing out on the benefits of a skip list, as for the majority of search operations we would need to iterate to the bottom layer of the skip list. Even if we try to maintain the skip list at each step so that we can have a perfect structure after each iteration but it would require lots of changes hence this solution is impractical.

Hence, to ensure that this skewness does not happen, we have a random algorithm for selecting the layer in which a new node should be inserted. Initially, we insert the node in the bottom linked list then we try to change the layer of that node, let’s say we choose this algorithm to find out the layer where the new node should be,

1. Every time a new node is to be inserted, we toss a coin
2. If the result is HEADS, we shift the node one layer up.
3. If the result is TAILS, we stop and insert the new node at that layer.

Thus, every new node will be assigned a random layer for insertion. This will ensure our skip list remains balanced most of the time. The term probabilistic means based on some probability, so we are doing the probability-based insertion here. Hence, a skip list is a probabilistic data structure because of the way elements are inserted.

Search Operation

It’s quite simple to understand the search operation in a skip list. We have already discussed searching in the second last paragraph but here we will see a detailed description of the algorithm in pseudocode.

1. We will iterate through the layers, till we find an element that is just greater or equal to the node we are trying to find.
2. If any node is found that is equal to the given searched value, it would end the search. This is because the searched node has been found in one of the express lines itself.
3. Otherwise, we will use the current node’s pointer to go down to the next layer.
4. We will repeat steps 1-3 till we reach the bottom-most layer in the worst case, print the node once encountered during the iteration on the bottom-most layer.
5. If the element doesn’t exist in the bottom-most layer also then it implies that the element doesn’t exist in the skip list.

Pseudo Code

// Parameters: 
// skipList: The original skipList
//           1. skipList->header is a header Node, header node doesn't have key it only have some forward pointers.
//           2. skipList->maxLevel contains the current maximum level of the skip list.
// searchKey: The element which is going to be searched.

// Node Structure: 
//               1. value, the actual value of the node
//               2. forward, an array of size "skipList->maxLevel", which contains the address of the forward pointers 
//                  for each level denoted by index, from "0" to "skipList->maxLevel"

Search(skipList, searchKey):
    // This line means we are accessing the header node of the skip list and storing it in the variable named current
    current = skipList -> header
    
    // This line is to loop from maxLevel of skip list 
    // to the "0th" or bottom-most level in a reverse manner
    loop i from skipList->maxLevel downto 0:
        // Update the current pointer until the value of the node is less than the element
        // "current->forward[i]!=NULL" is to make sure that the current node is 
        // at enough level to have a forward pointer 
        while current->forward[i]!=NULL AND current->forward[i]->value < searchKey
            current = current->forward[i];
    
    // After that loop we will be at the bottom-most level
    // Once the value of the current pointer is no less than the searchKey 
    // then either the immediate next node will be the searchKey so return the value.
    if current->forward[0]->value == searchKey:
        return current->forward[0]->value
    
    // Or, there would be some greater value so return failure means the searchKey doesn't exist
    else return failure 

Dry Run with Example

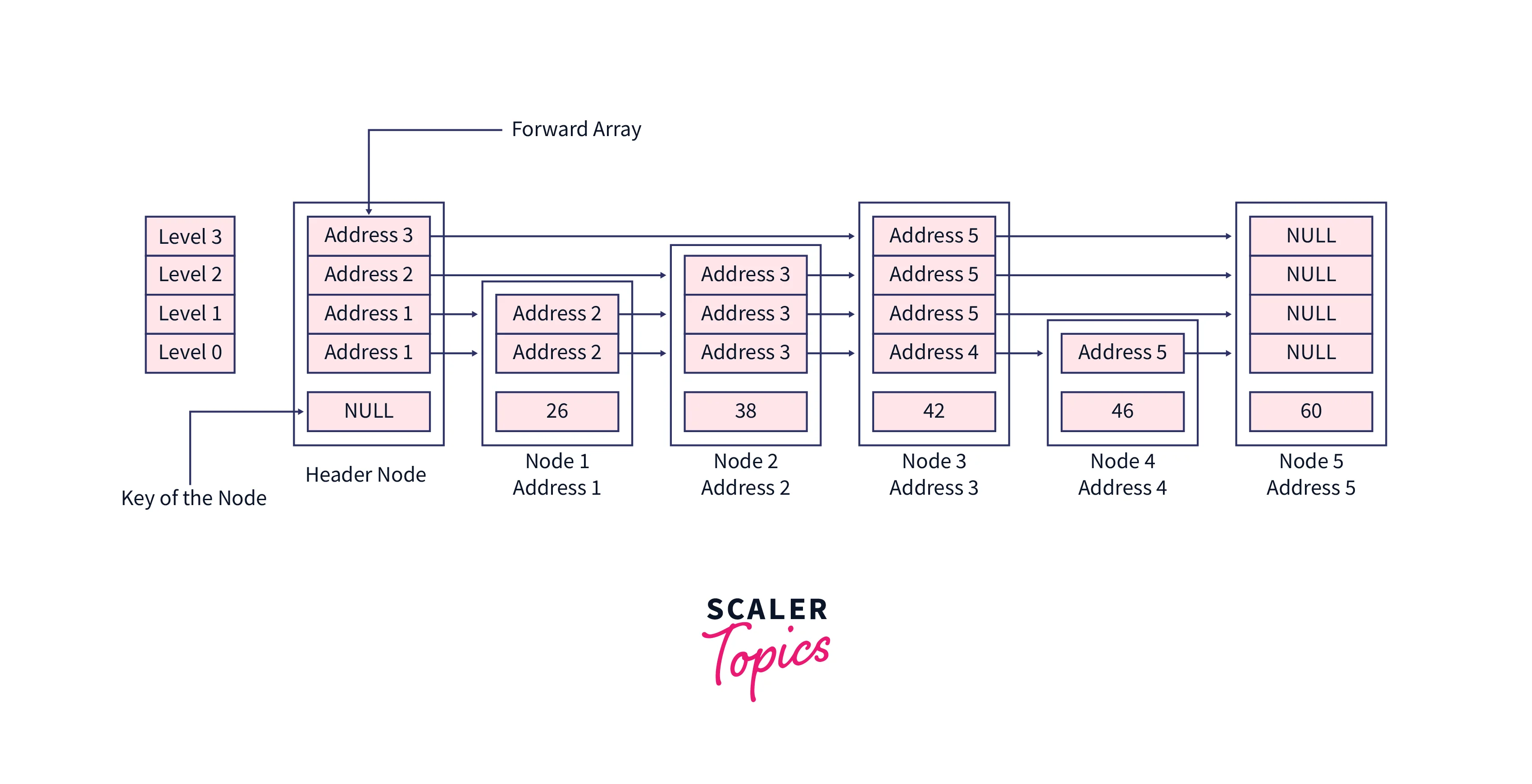
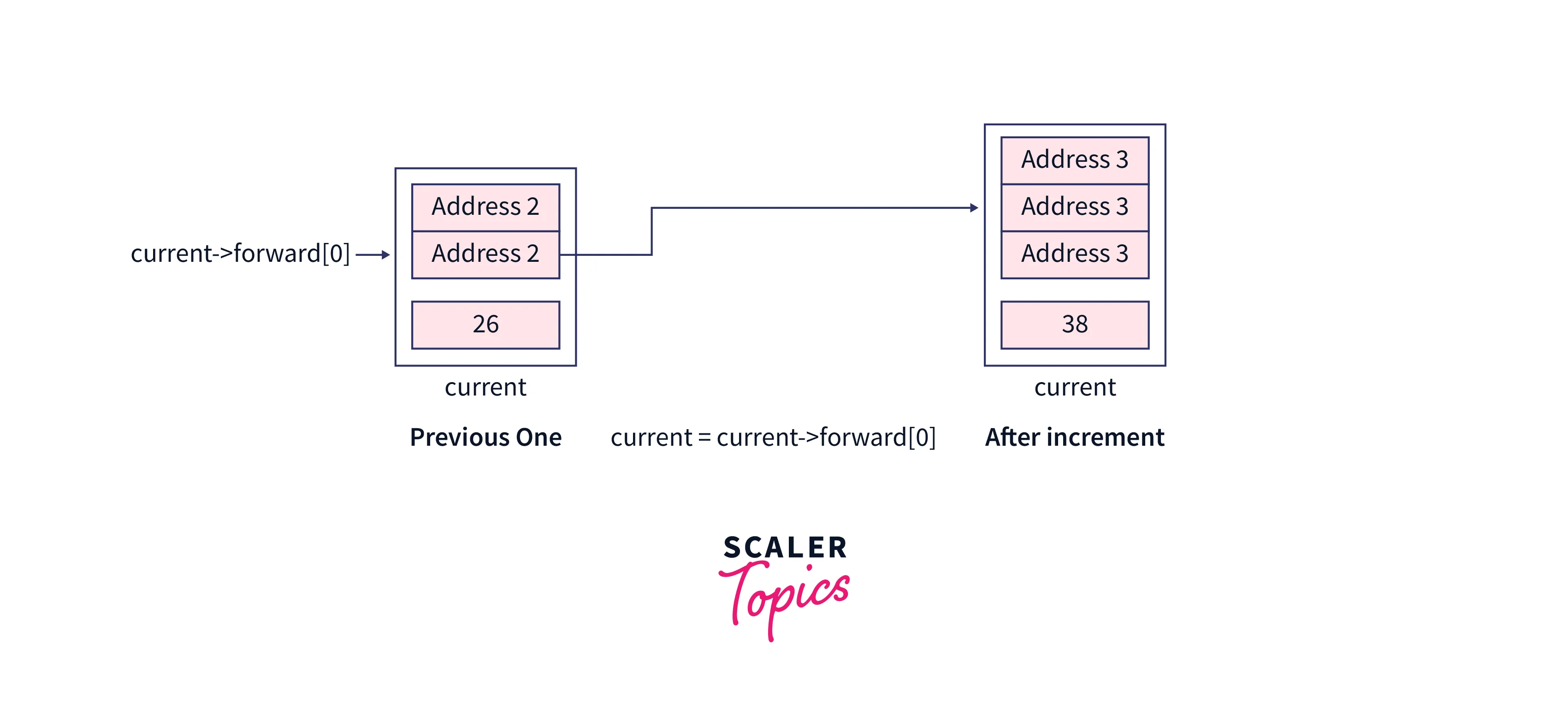
Let’s search element 38 in this skip list, the value at the header node will be NULL, also we are using dummy addresses here, but in the program, these addresses are determined by CPU.

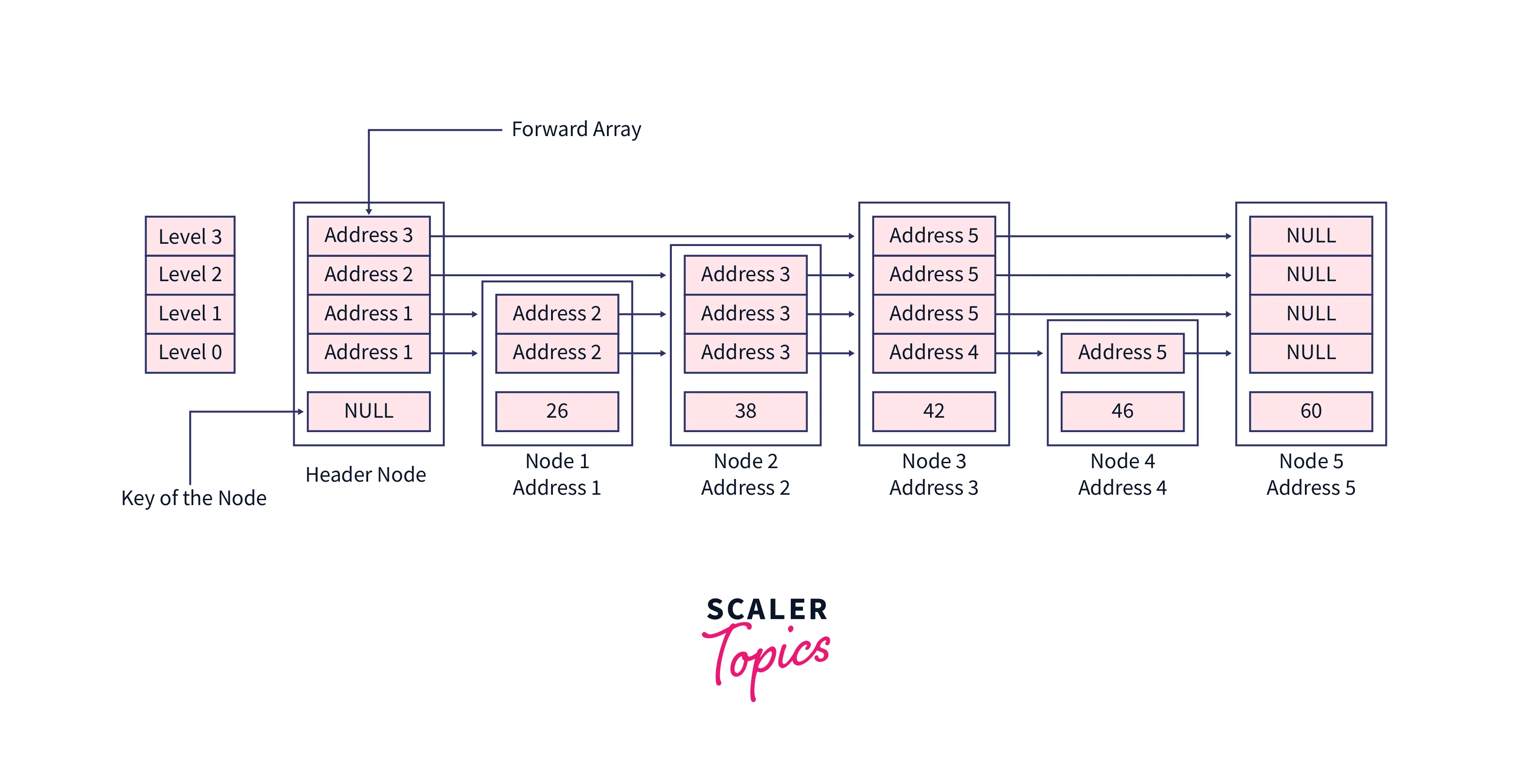
Initially, our current pointer will contain header node, 

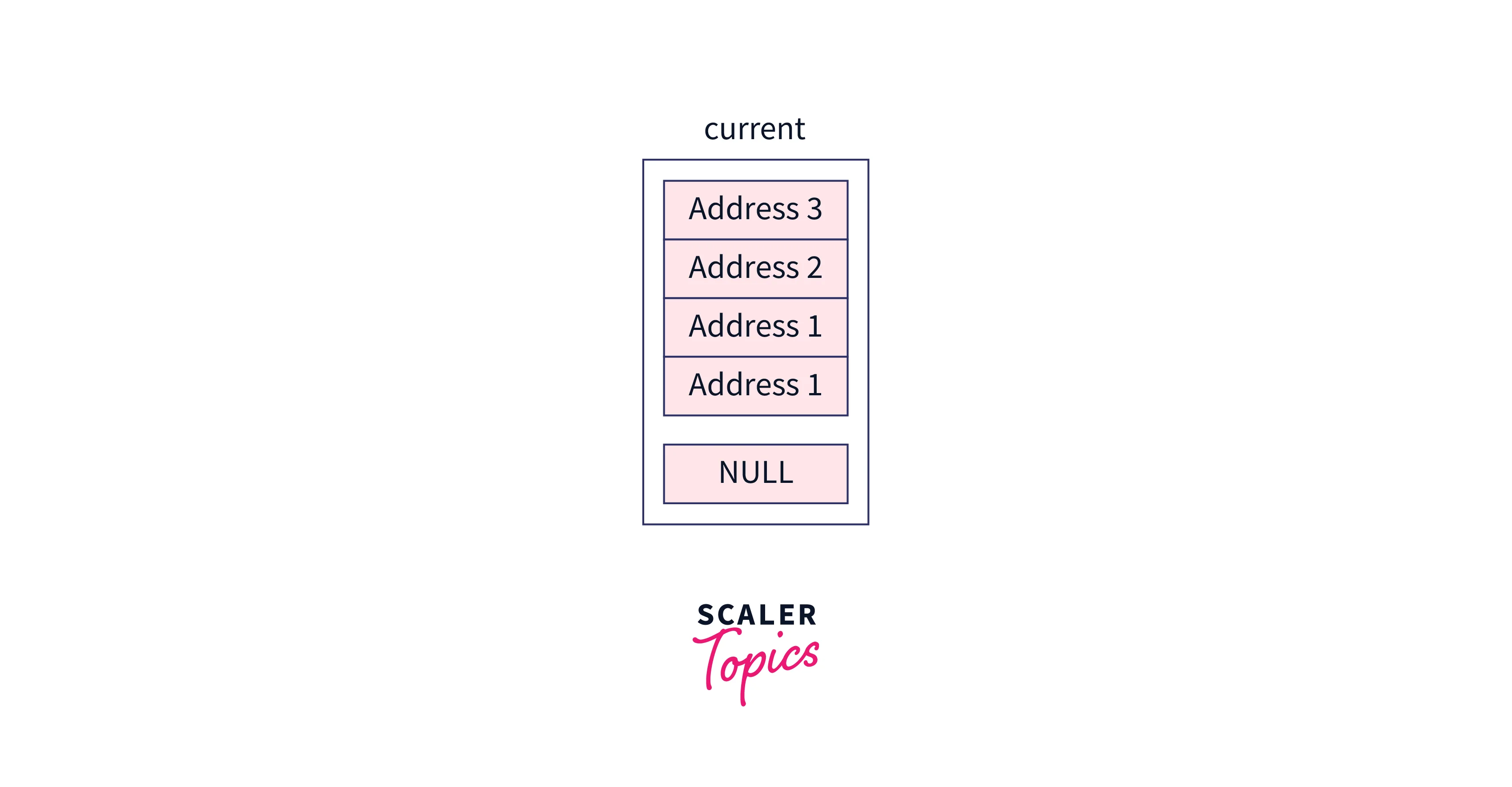
While looping on the levels, these nodes will be assigned to the current pointer, 

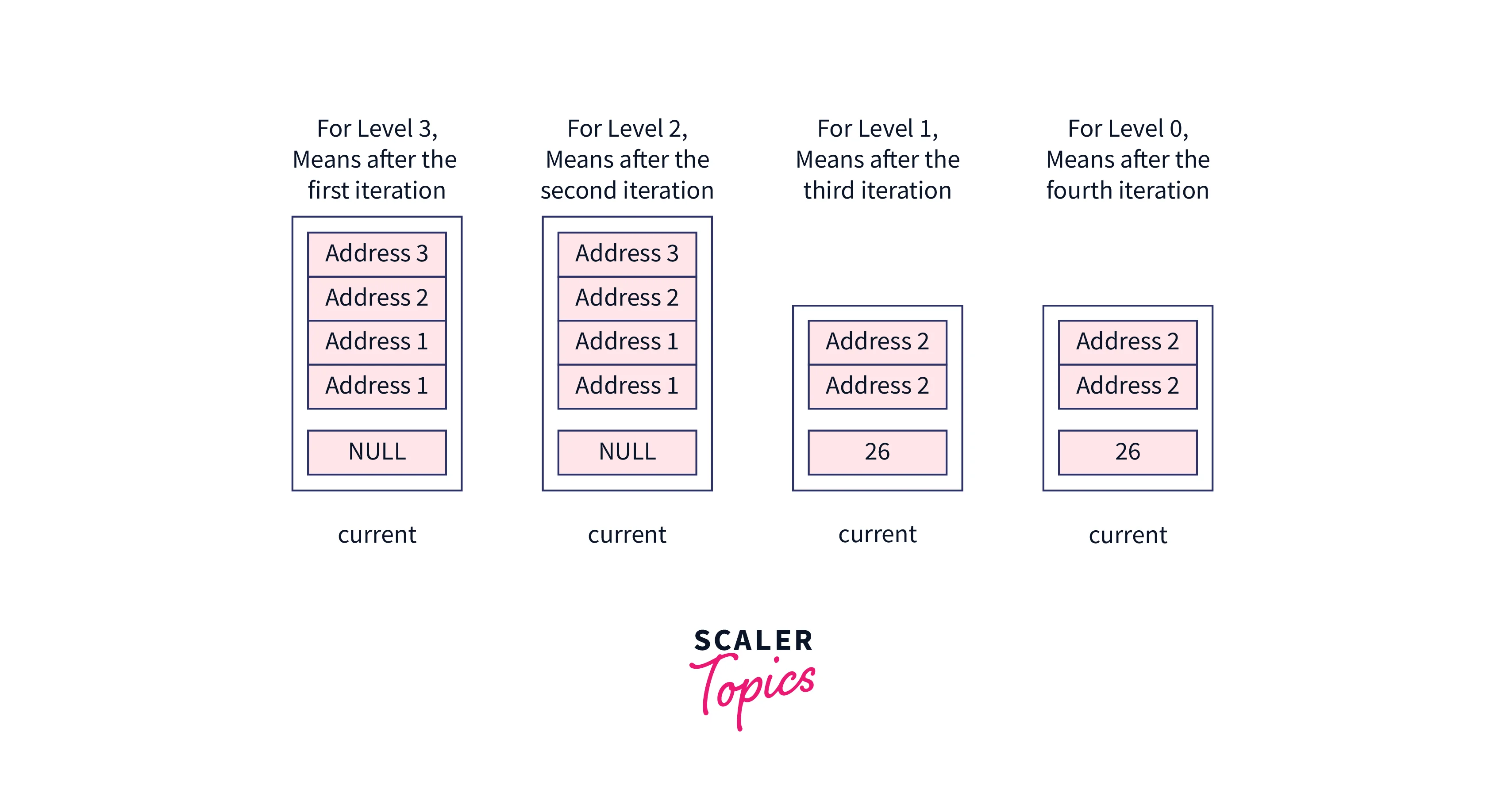
After the loop, we will be at the bottom-most level of the skip list and the current will contain the node whose value is just less than the one having the value assearchKey.

So now the next element to the current node for level 0 will be our required node. See the sub-section of our skip list for a better understanding,

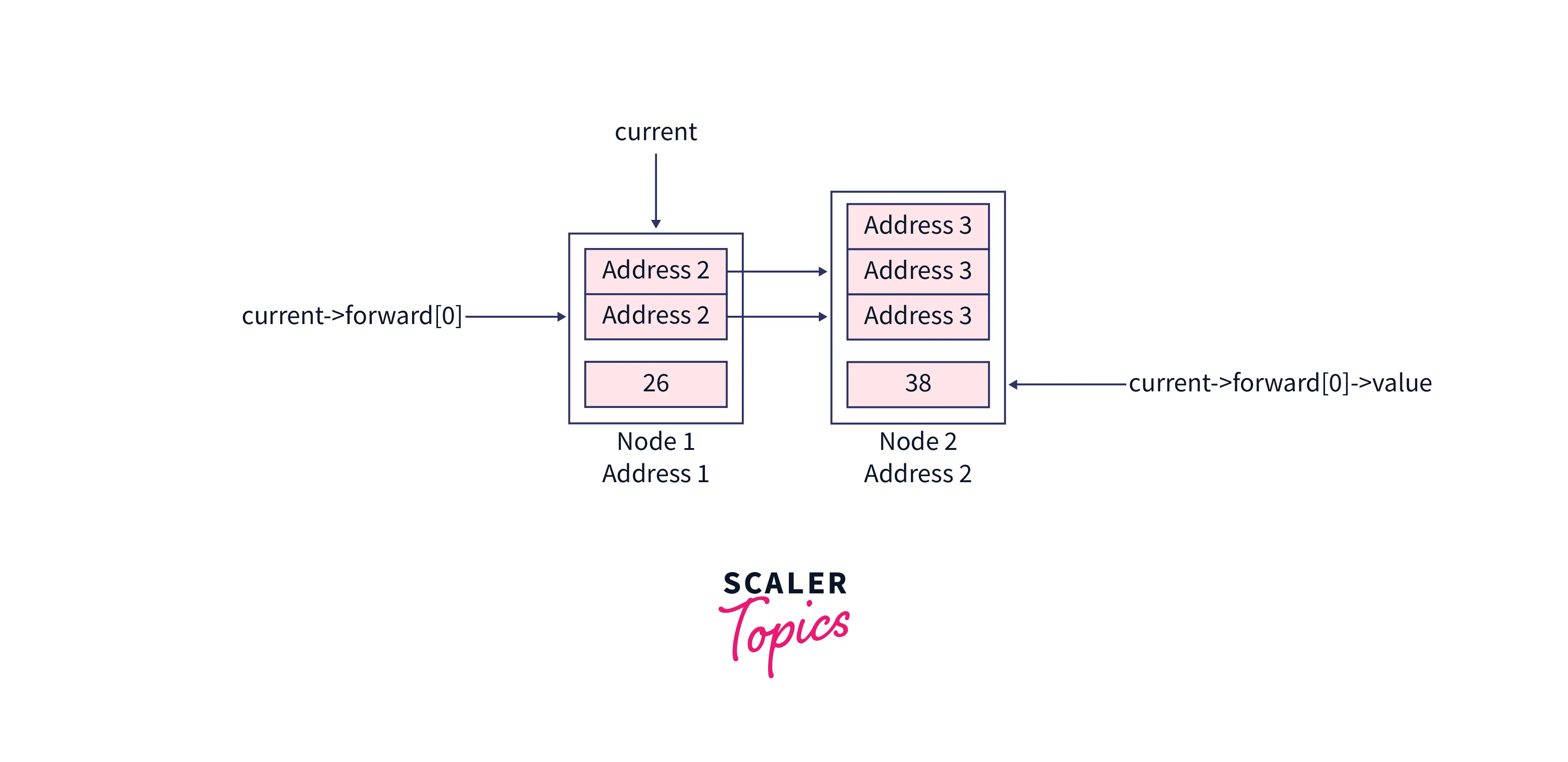
If the next node to the current pointer doesn’t have a value equal to the searchKey , then the searchKey is not present in the skip list.

Insertion Operation

Insertion of a node in a skip list needs to be in such a manner that after insertion of the new node the list should still be in sorted order and there is a randomization method based on the probability to ensure that skewness will never happen and we will never lose the efficiency of operations on skip list. We first need to find a particular node in the bottom linked list, only then we will insert the new node at the appropriate location.

As discussed in the above section, we will start the process of searching from the top layer of our skip list. Let us break down the insertion algorithm in steps:

1. We will iterate through the layer till we find an element that is just greater than the new node we are trying to insert.
2. Once we find such a node we will use its pointer to go down to the lower layer.
3. We will repeat steps 1 and 2 till we reach the bottom-most layer, once we reached the required node while performing step 1, do the insertion of the new node.
4. A random level will be chosen for the inserted node and finally we have to rearrange a few pointers to reflect the insertion in the skip list.

Pseudo Code

// Parameters: 
// skipList: The original skipList
//           1. skipList->header is a header Node, header node doesn't have key it only have some forward pointers.
//           2. skipList->maxLevel contains the current maximum level of the skip list.
// searchKey: The element which is going to be inserted, we are calling it searchKey 
//            because we will search for the position of this key.

// Node Structure: 
//               1. value, the actual value of the node
//               2. forward, an array of size "skipList->maxLevel", which contains the address of the forward pointers
//                  for each level denoted by index, from "0" to "skipList->maxLevel"

Insert(skipList, searchKey)

    // This line means we are accessing the header node of the skip list 
    // and storing it in the variable named current
    current = skipList -> header
    
    // Create a local array to contain a collection of pointers for each level
    // This local array will contain the pointers which are currently pointing to 
    // the element greater than the one which is going to be inserted. 
    // And we are maintaining this because further, we will change those pointers 
    // to not point to the last existing element of the skip list 
    // but to point to the newly inserted element of the skip list and then 
    // the pointer of the newly inserted element will point to the one to which
    // the pointers which are stored in the updateArray were pointing.
    // This is the scenario before insertion updateArray -> oldElement
    // After insertion updateArray -> newElement and newElement -> oldElement
    local updateArray[skiplist->maxLevel] <-- Initialize with NULL 
    
       
    // This line means to loop from maxLevel of skip list to 
    // "0th" bottom-most level in a reverse manner
    loop i from skipList->maxLevel downto 0:
        // Update the pointer until the value of the node is less than 
        // the element "searchKey"  
        // check "current->forward[i]!=NULL" to make sure that the current node 
        // is at enough level to have a forward pointer 
        while current->forward[i]!=NULL AND current->forward[i]->value < searchKey
            current = current->forward[i]

        // After possible iterations, store the pointer for each level in the updateArray indexes
        updateArray[i] = current

    // We have reached till last "0th" bottom-most level
    // Now increment our pointer by one more node
    current = current->forward[0]
            
    // Just check whether the value of the next node is equal to the searchKey,
    // Now it's our decision whether we want duplicate elements,
    // or not but as of now, we will not insert duplicates
    if(current->value==searchKey):
        print "The element already exists"
        return failure
    else:
        // Add an element between updateArray pointers and the current pointer
        // Generate a random Level for the new node according to probability.
        // The random level will be in the range of [0, fixedLevel]
        // This "fixedLevel" could be any number but generally, we use 
        // current level + 1 as the upper range of random level to avoid unnecessary time and space complexity
        randomLevel <-- A randomly generated level
        
        if randomLevel > skipList->maxLevel:
            // Add the header for the new generated level
            // So that next time we can iterate on this newly added level
            loop i from skipList->maxLevel+1 to randomLevel+1
                updateArray[i] = header
 
            // Update the maximum level of the List
            skipList->maxLevel = randomLevel

        // create a new level with calculated randomLevel and searchKey as value
        node <-- createNode(searchKey, randomLevel)
            
        // Rearrange pointers for insertion
        loop i from 0 to random level-1:
            // Assign the forward pointer of the updateArray to the node
            node->forward[i] = updateArray[i]->forward[i]

            //Assign the node to the last forward pointer 
            updateArray[i]->forward[i] = node
                
        return success

Dry Run with Example

Let’s insert a node with the value 30 in this skip list, the value at the header node will be NULL, also we are using dummy addresses here, but in the program, these addresses are determined by CPU. 

Initially, our current pointer will contain the header node, 

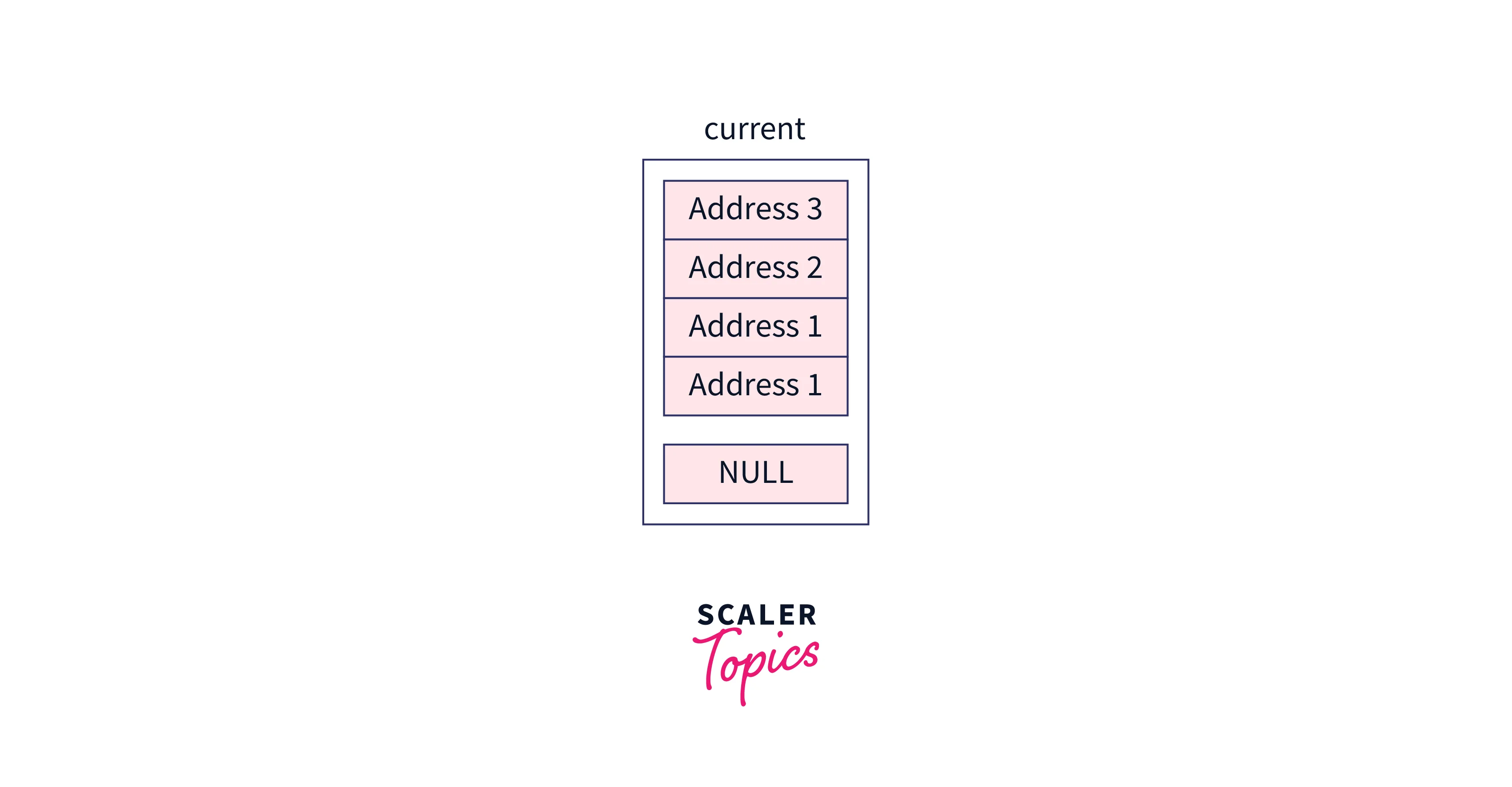
After initialization of the local array named updateArray, this will be the structure, 

While looping on the levels, these nodes will be assigned the current pointer,

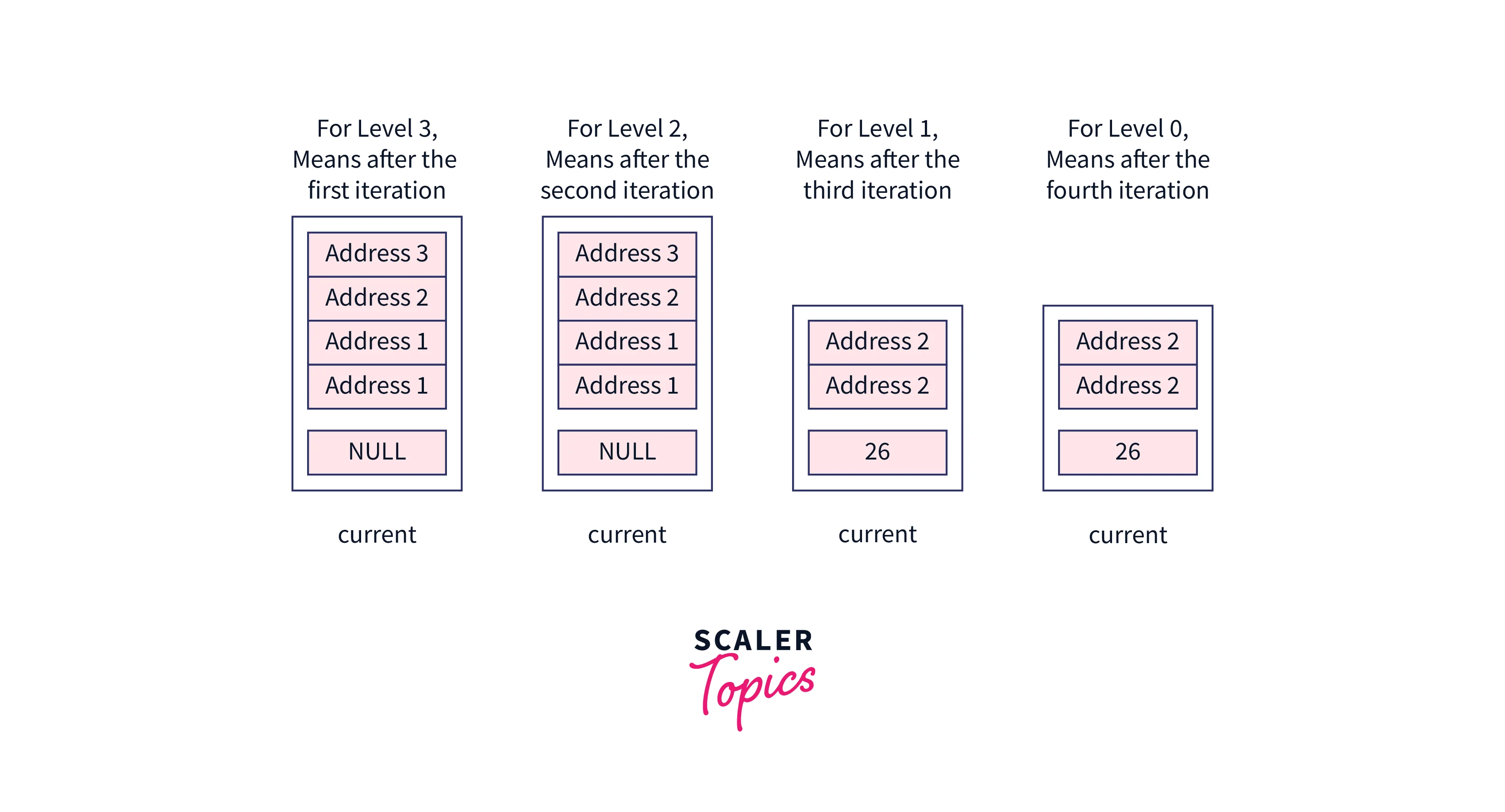
After looping on the levels, these nodes will be stored at each index of the updateArray, 

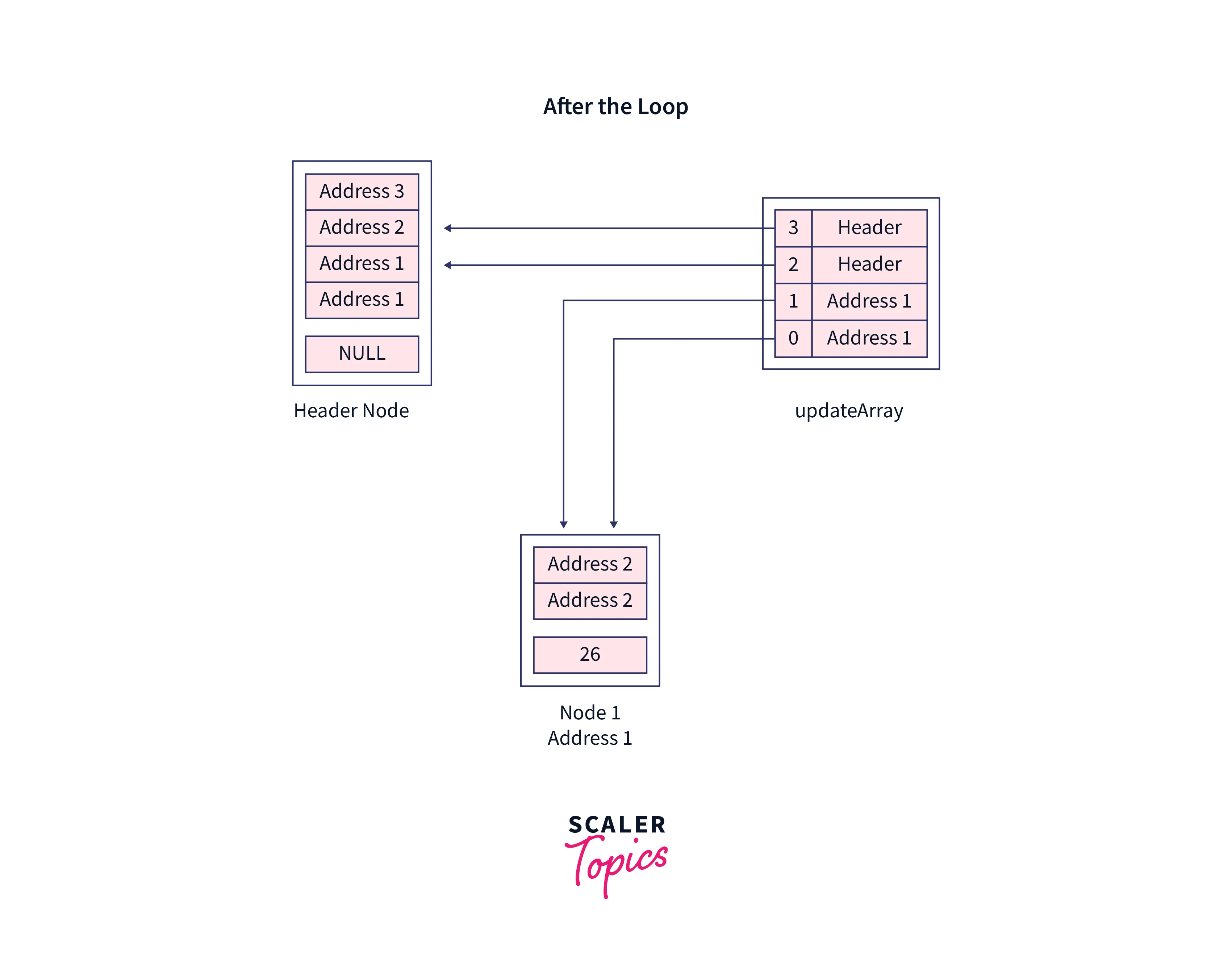
Increment the current pointer, after reaching the bottom-most level, from here we can see that the value which is going to be inserted doesn’t exist

already.

Now our new node will be inserted between the current pointer and updateArray pointers, Let’s say the random level of our node is 1. So when we create a new node, its structure would be, let’s give an Address 6 to it.

Inside the last loop, rearrange the pointers to insert the new node,

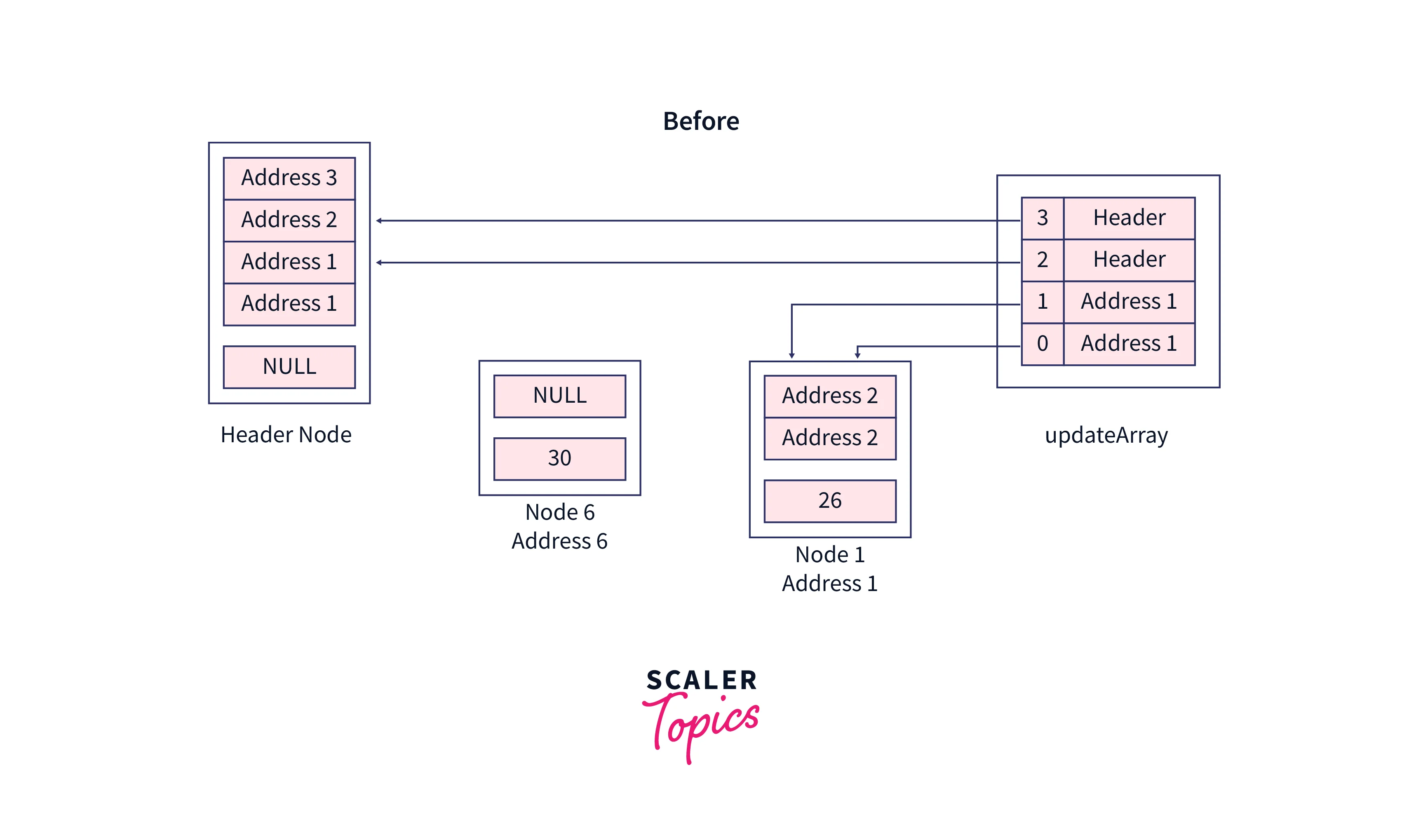
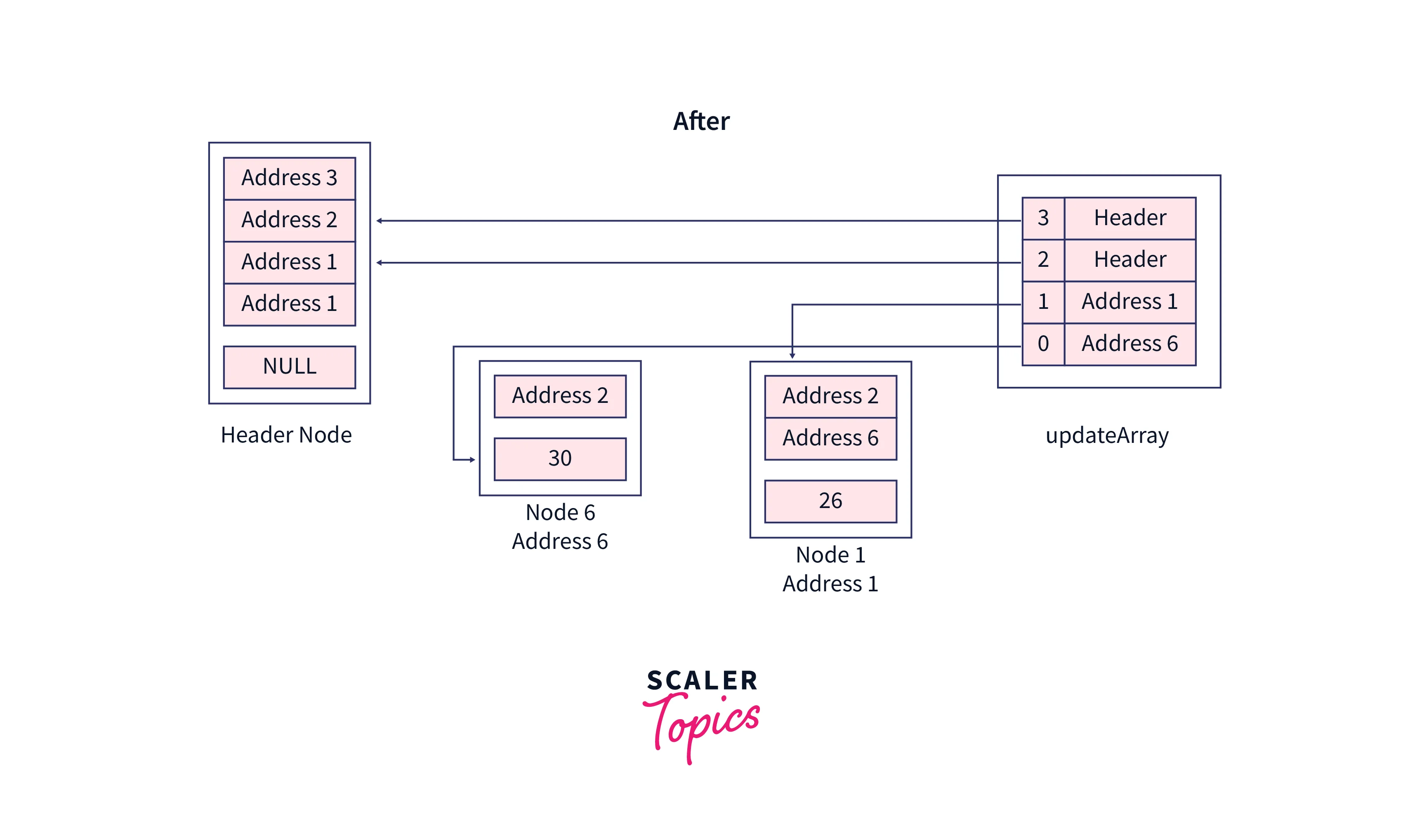
Now, see the pointer rearrangement in the original skip list, 

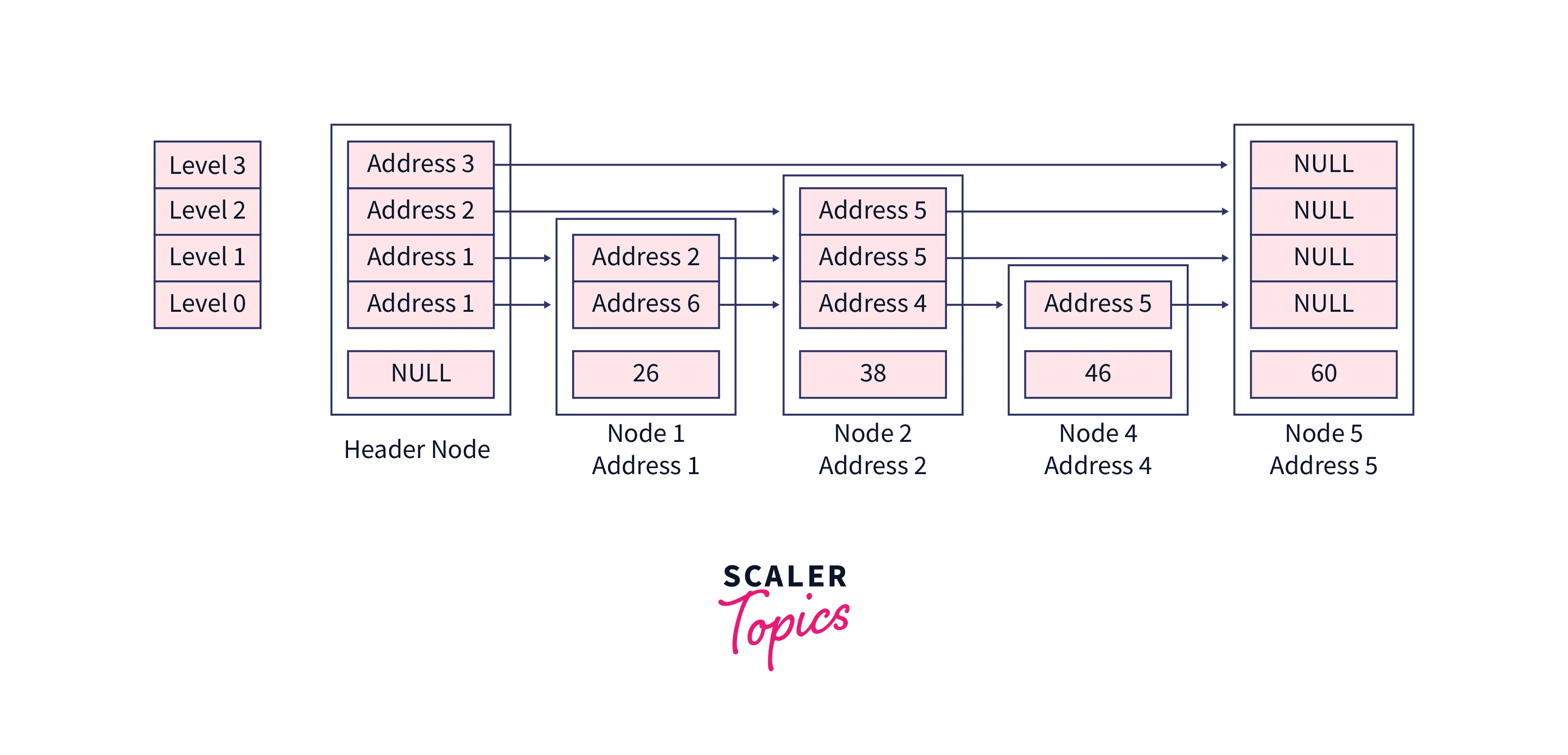
Deletion Operation

For deletion operation, similar to insertion, we will first try to find the node to be deleted, and then we will do some pointers rearrangement to remove the node from the skip list, and finally, we can release the memory of that node but that is not the point of discussion.

1. We will iterate through the layer till we find an element that is just greater than the node we are trying to delete.
2. Once we find such a node we will use its pointer to go down to the lower layer.
3. We will repeat steps 1 and 2 till we reach the bottom-most layer, once we reached the required node while performing step 1, do remove that node.

Pseudo Code

// Parameters: 
// skipList: The original skipList
//           1. skipList->header is a header Node, header node doesn't have a key it only have some forward pointers.
//           2. skipList->maxLevel contains the current maximum level of the skip list.
// searchKey: The element which is going to be deleted, we are calling it searchKey 
//            because we will search for the position of this key.

// Node Structure: 
//               1. value, the actual value of the node
//               2. forward, an array of size "skipList->maxLevel", which contains the address of the forward pointers 
//                  for each level denoted by index, from "0" to "skipList->maxLevel"

Delete(skipList, deleteKey):
    // This line means we are accessing the header node of the skip list 
    // and storing it in the variable named current
    current = skipList -> header
    
    // Create a local array to contain a collection of pointers for each level
    // This local array will contain the pointers which are currently pointing to 
    // the element greater than the one which is going to be deleted. 
    // And we are maintaining this because further, we will change those pointers 
    // to not point to the element going to be deleted instead point to the next element of the skip list
    // This is the scenario before deletion updateArray -> toBeDeletedElement -> nextOfToBeDeletedElement
    // After deletion updateArray -> nextOfToBeDeletedElement
    local updateArray[skiplist->maxLevel] <-- Initialize with NULL 
    
       
    // This line means to loop from maxLevel of skip list to 
    // "0th" bottom-most level in a reverse manner
    loop i from skipList->maxLevel downto 0:
        // Update the pointer until the value of the node is less than 
        // the element "searchKey"
        // check "current->forward[i]!=NULL" to make sure that the current node 
        // is at enough level to have a forward pointer 
        while current->forward[i]!=NULL AND current->forward[i]->value < searchKey
            current = current->forward[i]

        // After possible iterations, store the pointer in the updateArray
        updateArray[i] = current

    // We have reached till last "0th" bottom-most level
    // Now increment our pointer by one more node
    current = current->forward[0]
            
    // After that increment either we will be at our desired node
    // with value as "searchKey" or not
    if current == NULL OR current->key > searchKey:
        print "The Key which needs to be deleted Doesn't Exist"
        return failure

    else:
        // Rearrange pointers from the lowest level
        loop i from 0 to skipList->maxLevel:
            // If the next node has the value different from "deleteKey"
            // As we do not have to delete that, hence no change
            if updateArray[i]->forward[i] != current:
                break

            // Otherwise point the current node by the node which contains the value
            // less than the element to be deleted 
            updateArray[i]->forward[i] = current->forward[i]
        
        // After deletion it is a possibility that we might have deleted the node which 
        // was a single node at the highest level
        // So we have to remove levels that do not have any nodes 
        // We are not concerned with memory release, we are just decreasing the "maxLevel" of "skipList"
         loop i from skipList->maxLevel downto 0:
            if header->forward[i] == 0:
                skipList->maxLevel = skipList->maxLevel - 1 
            else
                break
                
        return success

Dry Run with Example

Let’s delete the node with value 42 in this skip list, the value at the header node will be NULL, also we are using dummy addresses here, but in the program, these addresses are determined by CPU.

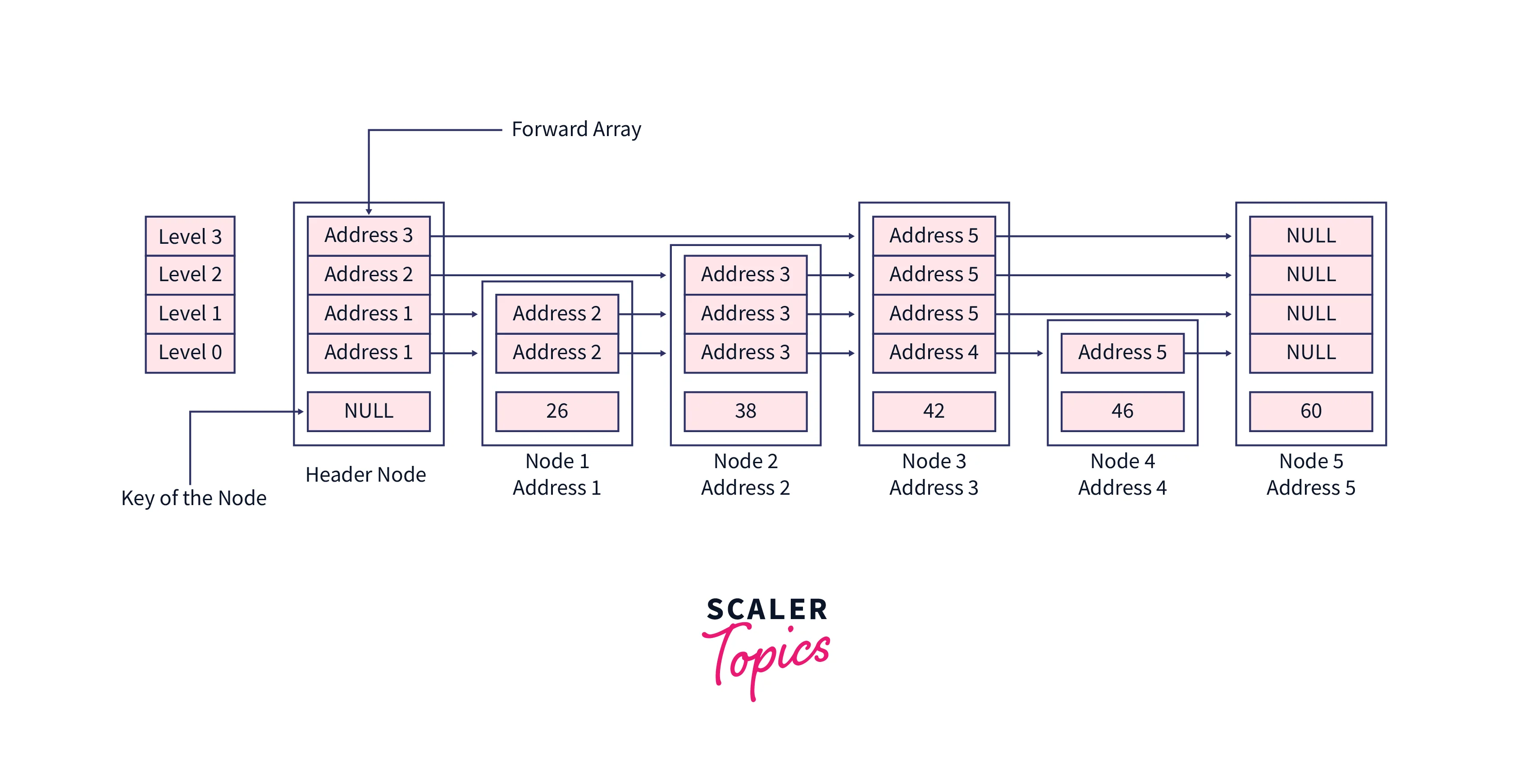
Initially, our current pointer will contain the header node,

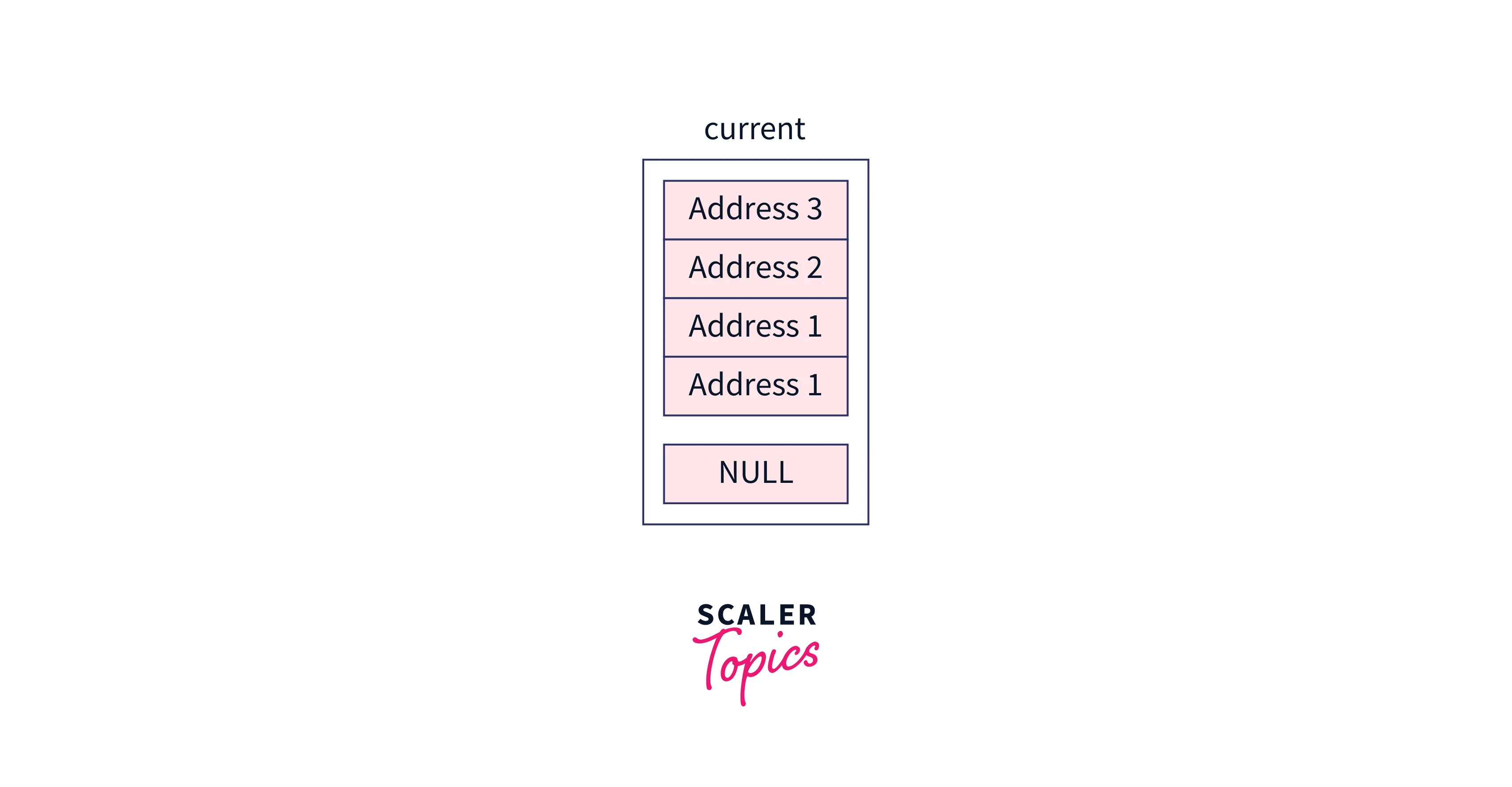
After initialization of the local array named updateArray, this will be the structure, 

When we loop on the levels, the updateArray will get these addresses at each index, 

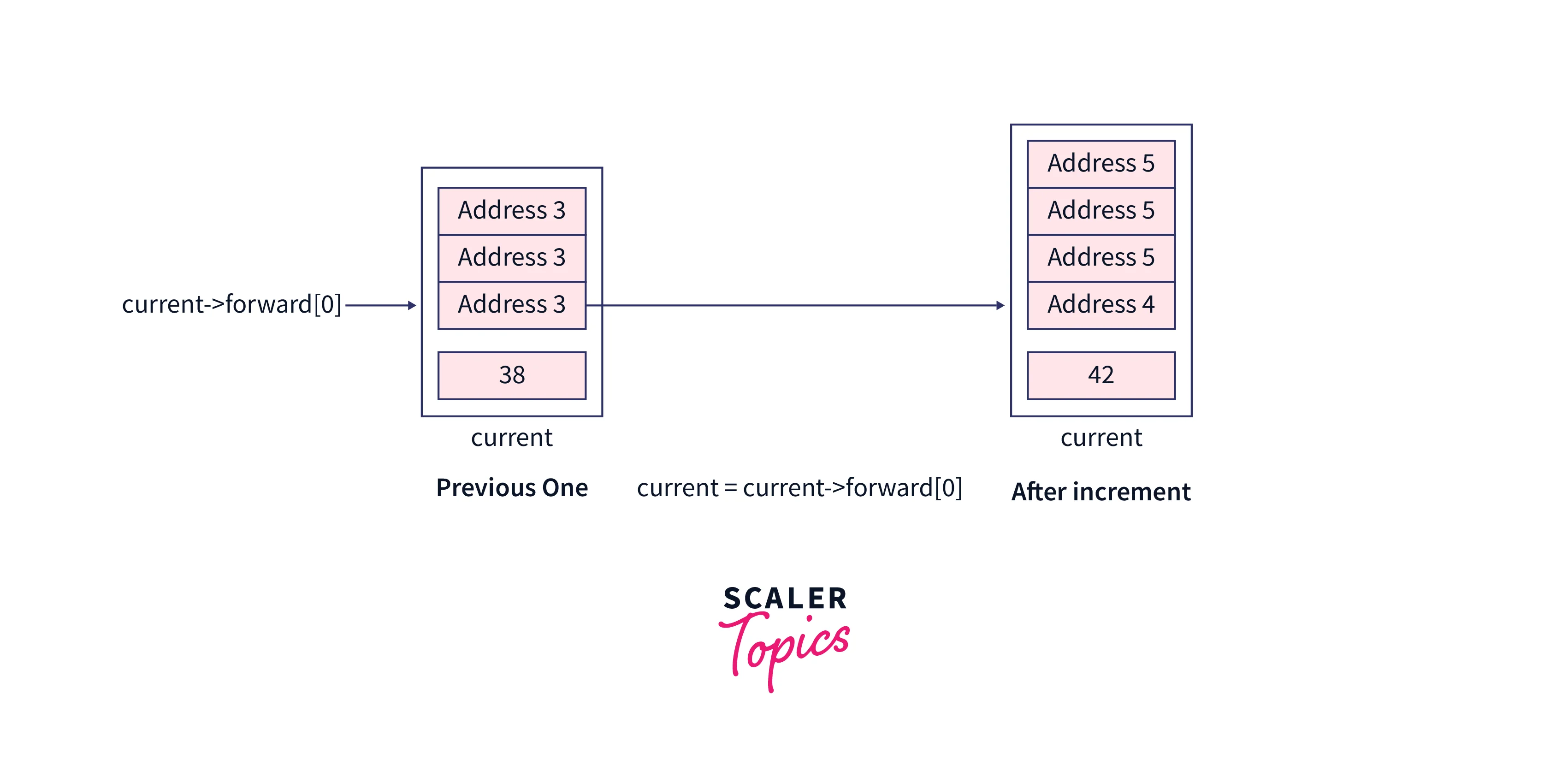
After the loop, our current pointer will point to the node having a value as 38, and if we increment the current pointer to point next node of the list, we will be at the node which is going to be deleted, And if the next node is not the one which is going to be deleted then the desired element doesn’t exist in the skip list. In our case the next node has the value 42 means the node which we want to delete exists in the skip list.

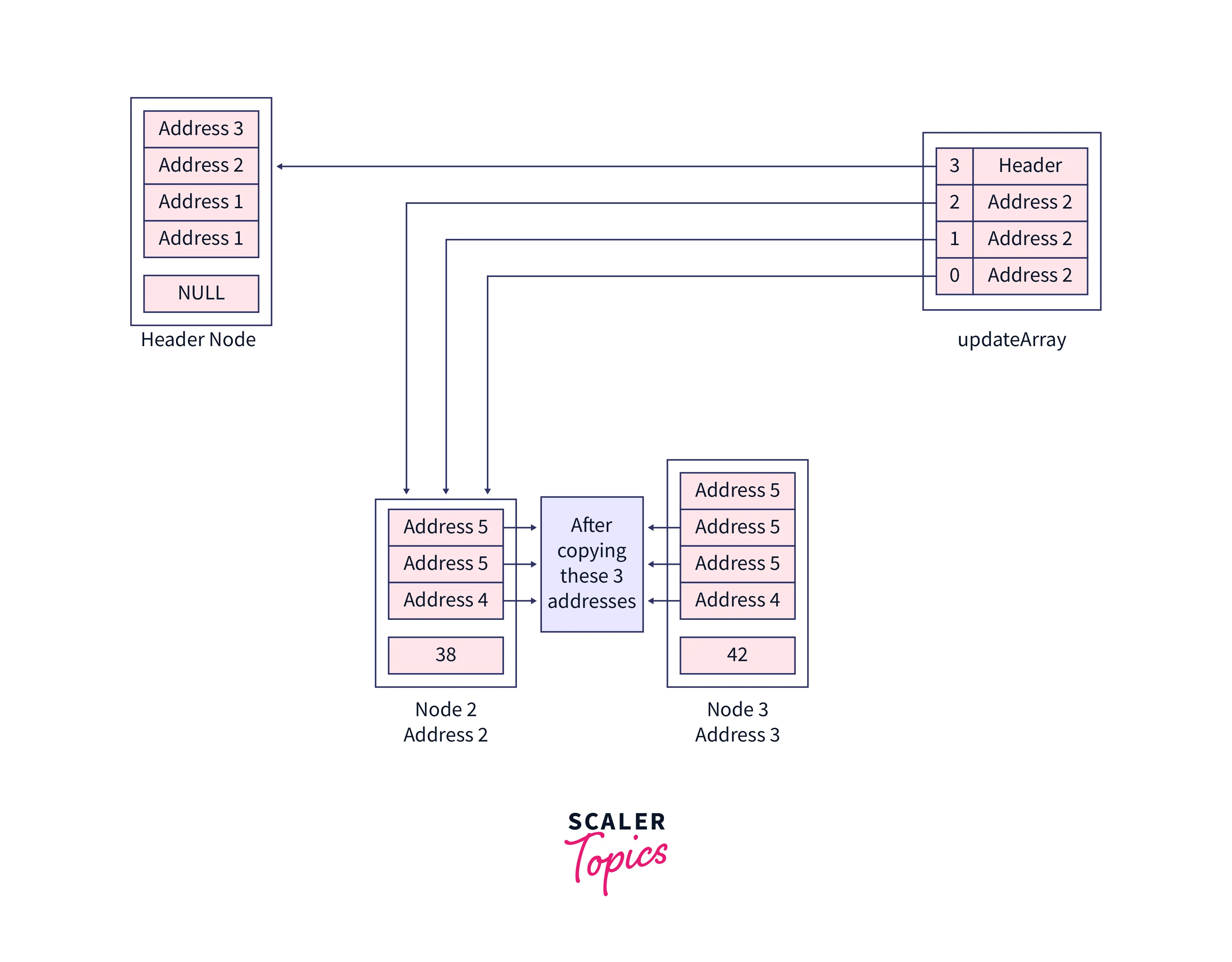
Inside the last loop, rearrange the pointers to remove the node, for the first three iterations the expression updateArray[i]->forward[i] != current will be false, hence three changes will happen here, now our Node 2 will not point to Node 3 but instead it will point to the addresses to which earlier Node 3 was pointing means Node 4. So, technically we have to copy three addresses from Node 3 to Node 2.

In the last 4th iteration we will update the address in the header node, updateArray[i]->forward[i] != current is again false here because our updateArray[3]->forward[3] contains a header and the header points to the element which is going to be deleted. Let’s copy that address as well,

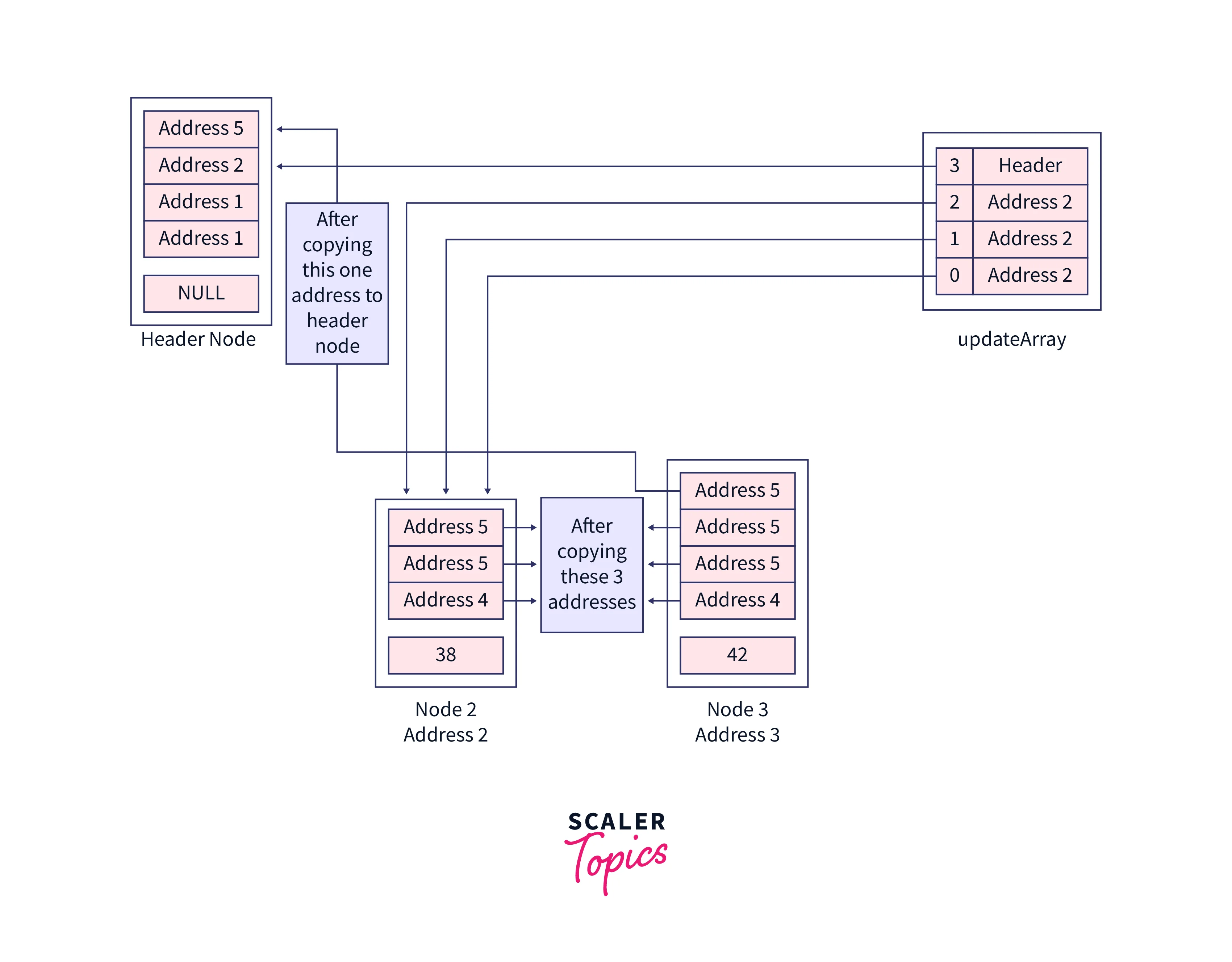
After this iteration, we will be out of the loop and as of now, no node is pointing to Node 3. Let’s rearrange the structure of our skip list, this structure rearrangement is the basis of the pointer value contained by each node.

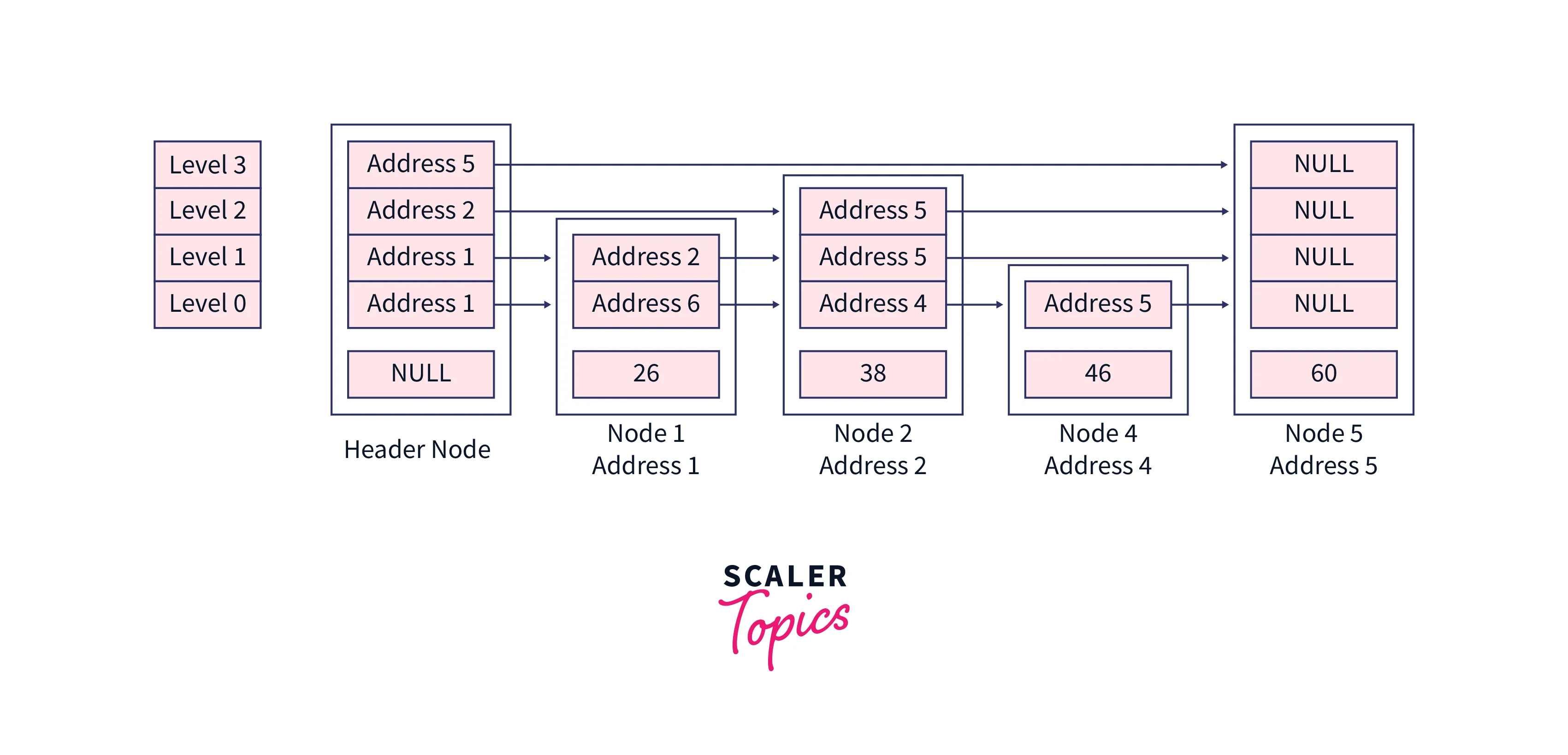
Now, it’s time to remove the extra levels, you can see we don’t have any element at the last level. so the last loop will run for one iteration to remove the last level currently we are not concerned about the memory release we will just decrease the maximum level of the skip list so that further we could not able to access that level skipList->maxLevel = skipList->maxLevel – 1,

Logical structure after level decrement, 

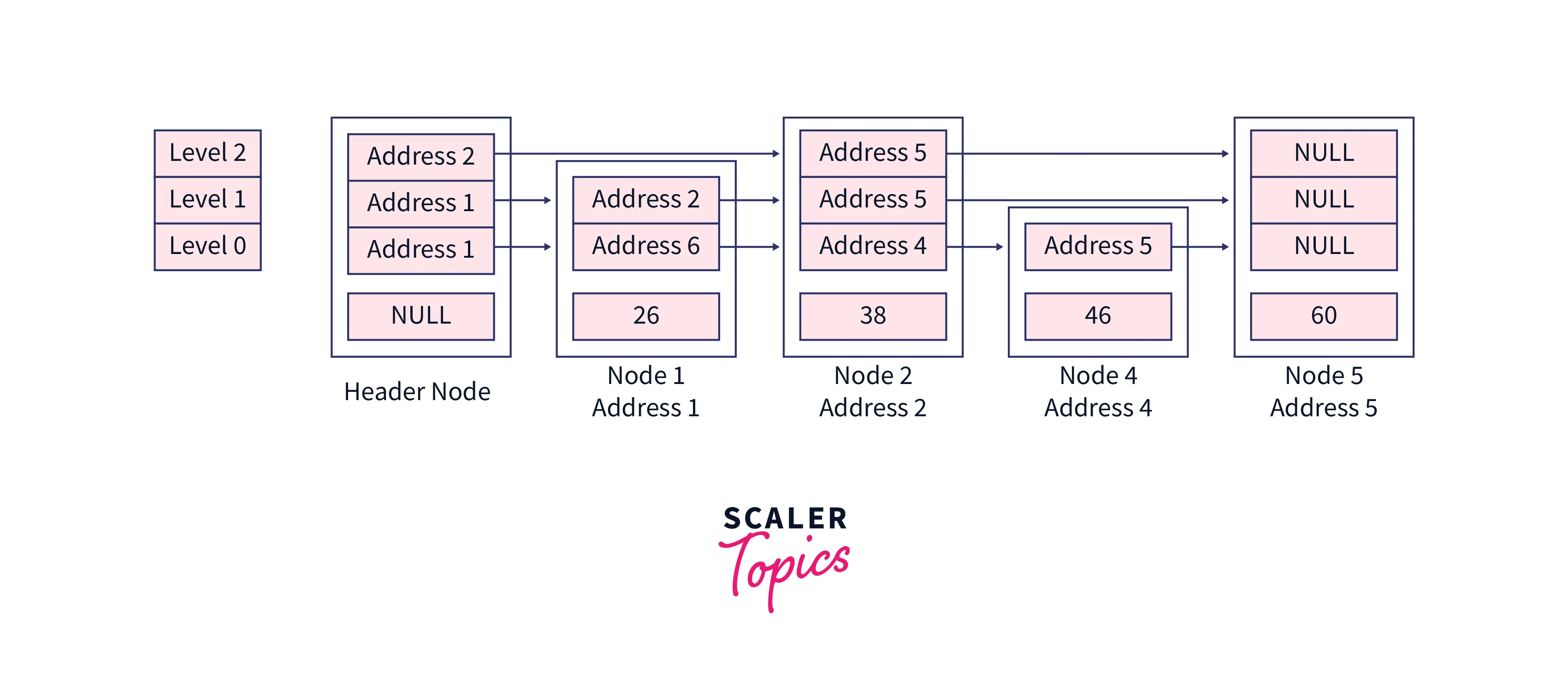
Hence we have deleted the element successfully.

Time Complexity Analysis

Here we will discuss the time complexity of the operation shown above. As of now, you might have got an idea about the operations, so one thing is clear, the time complexity of all operations is dominated by the search operation. Now the complexity analysis of search operation further depends on the randomization of the skip list, because things are very simple in the case of a perfect skip list, there is no matter of discussion, and it is pretty simple to understand that there will be of O(logN) complexity for search operation but it is very impractical to balance the skip list after insertion and deletion operations. If we talk practically then we have two things to discuss before we analyze any time complexity.

1. How Many Levels Will Be There in Skip List?

According to a lemma, the skip list of n elements can have a maximum of clogn levels with high probability.

Proof:

The levels in the skip list may or may not increase each time we insert an element. Therefore, our goal is to demonstrate that levels will only extend up to a specific fixed constant.

We only promote the element to a higher level when we get a head with $1/2$ probability. If we can get continuous $i$ heads then only our element can be at $i^{th}$ level. Hence, probability of at least one element at $i^{th}$ level will be,

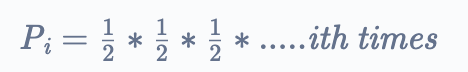
$P_{i} = {1 \over2^i }$

From the above discussion, we can conclude the probability of n elements at $i^{th}$ level will always be,

$P_{ni} \le {n \over2^i }$

Substitute $i$ by $clogn$, where $c$ is just a constant. So the probablity of $n$ elements at $clogn$ level will be,

$P_{clogn} \le {n \over2^{clogn} } \le {1 \over n^{c-1} }$

If we increase c then, our probability of getting any element at the clogn level will be very less or near about 0. But there could be some elements at lower levels which is fine to us.

2. How Many Expected Steps Will Be There While Searching in Skip List?

Till now as you might know in the search operation we start from the topmost layer and then go right and then go down then right and so on, to finally reach the required node. Here we will do reverse or can say backward search analysis.

Let’s say we are already at the searched node and we have x levels in the skip list.

Let’s say the cost of searching in the $x^{th}$ level skip list is $C_x$. This cost is nothing but the expected number of nodes that appeared while searching or can say expected steps.

$C_x = [Searched Node] + Pr[Getting Head]C_{x-1} + Pr[Getting Tail]C_{x}$

$C_x = 1 + {1\over2}C_{x-1} + {1\over2}C_{x}$

$1$ cost is for the node which is being searched, and ${1\over2}C_{x}$ is the cost if we have come from left in the skip list, ${1\over2}C_{x-1}$ is the cost if we have come from the upper level.

Finally, we will get our cost as,
$C_x = 2 + 2C_{x-1}$

$C_x = 2 + 2 + 2C_{x-2}$

$C_x = 2 + 2 + 2 + 2C_{x-3}$

$C_x = 2 + 2 + 2 + 2 + 2C_{x-4}$

$.$

$.$

We know the maximum possible number of levels in the skip list is $clogn$, hence the cost will be,

$C_x = 2 + 2 + 2+2+2+2+2+2….{logn} \ times$

$C_x = 2logn$

Search Operation

According to the above discussion we have 2logn expected number of steps in a search operation. Hence, our search operation will be of order logn.

Time Complexity: O(logn)

Insert Operation

In the insertion operation, we are doing a search operation and then some pointers manipulation.
We are looping through the levels of the skip list after searching for the location where the element will be inserted. So total time complexity will be, Searching + Updating the pointers by running loop on levels.

As we know total levels are of logn order so the loop will be also of logn order and the searching operation is also of logn order,
Hence time complexity of the insertion operation will be also of logn order.

Time Complexity: O(logn)

Delete Operation

Similarly, in the deletion operation, we first search for the element and then rearrange the pointers at each level.
So total time complexity will be, Searching + Rearranging the pointers by running loop on levels.

As we know total levels are of logn order so loop will be also of logn and searching operation is also of logn order,
Hence time complexity of deletion operation will be also of logn order.

Time Complexity: O(logn)

Note: In the worst case when the skip list degenerates to a linked list because of the very less difference between the number of elements for two consecutive levels, the time complexity of operations becomes O(n) but on average the time complexity of operations always remains as Θ(logn).

Advantages of Skip List

• Iteration in a skip list is relatively easier than in balanced search trees.
• Almost all operations require log(n) time complexity, where n is the number of elements in the main linked list.
• We have complete control over the number of layers we want to include in a skip list based on the space versus time tradeoff. More layers increase the space but reduce the time complexity of operations.

Disadvantages of Skip List

• Skip lists require more memory to store the data. This overhead is due to the additional memory required to store the additional nodes in all layers.
• Since a linked list is unidirectional, we cannot do a reverse search in a skip list because traversal in a skip list is also uni-directional.
• Skip lists cannot leverage the locality of reference, adjacent nodes in a skip list might not be present in the same logical region in memory, making the skip list less optimized for caching.

Applications of Skip List

• Skip lists are used in distributed applications, to devise an execution plan in processing frameworks that process distributed data.
• Skip lists can be used to implement priority queues, that work very well in multi-threaded environments. This is because skip lists do not require the whole data structure to be locked while performing concurrent writes. Only the adjacent nodes to a node on which we are operating need to be locked.

Conclusion

• Skip lists are probabilistic data structures that are essentially multi-layered linked lists.
• When a node is inserted in the skip list, the layer of that node is selected using a random probability-based algorithm.
• The bottom-most layer in a skip list is the main linked list whereas each subsequent layer is an express line that has fewer nodes.
• We can perform search, insertion, and deletion in a skip list in logarithmic time.
• Skip lists require more memory for storage but give faster lookup times.