Zero Sum Subarrays

Problem Statement

Given an integer array where the array has both negative and positive values, print all the subarrays from the given array whose sum is zero.

Example

Let’s consider the below-given integer array:

Input : arr = [0, -1, 8, -5, -3, -7, 4, 2, 1]

Output for the given array is:

Zero-sum Subarray is from 0 to 0
Zero-sum Subarray is from 2 to 4
Zero-sum Subarray is from 2 to 8
Zero-sum Subarray is from 5 to 8

Explanation

Subarrays formed are clearly shown in the figure:

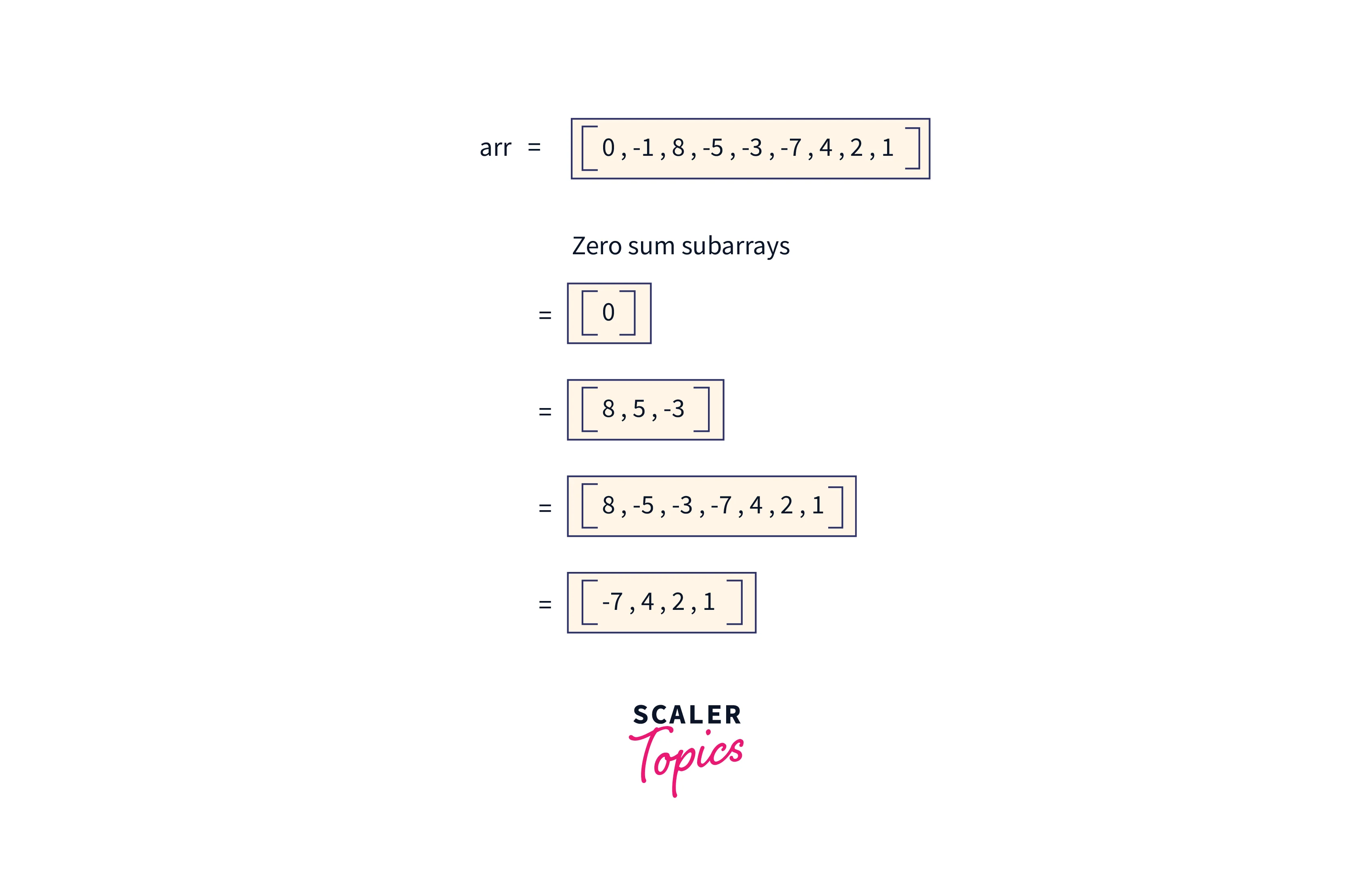
• Subarrays from the following start and end indices give zero sum subarray:
• $0^{th}$ index to $0^{th}$ index:
  • Elements present: $[0]$
  • Subarray sum obtained is: $0$.
• $2^{nd}$ index to $4^{th}$ index:
  • Elements present: $[8, -5, -3]$
  • Subarray sum obtained is: $8 + (-5) + (-3) = 0$.
• $2^{nd}$ index to $8^{th}$ index:
  • elements present: $[8, -5, -3, -7, 4, 2, 1]$
  • Subarray sum obtained is: $8 + (-5) +(-3) + (-7) + 4 + 2 + 1 = 0$.
• $5^{th}$ index to $8^{th}$ index:
  • elements present: $[-7, 4, 2, 1]$
  • Subarray sum obtained is: $(-7) + 4 + 2 + 1 = 0$.

Therefore, from these starting indices to the ending indices it indicates that the sum of subarrays is zero.

Constraints

• $1 ~<=~ N~ (Length~ of~ the~ input~ array)~ <=10^5$
• $-10^6~ <=~ arr[i]~ <=~ 10^6$
• All the elements in the array are integers

Approach 1

We can say that for N number of elements in the given array, the number of subarrays possible is:
$$
\dfrac{N*(N+1)}{2}
$$
But we only need to find the subarrays whose sum is zero. Our brute force approach can be generating all the subarrays and to check whether the subarray generated has a sum that is equal to zero. If the subarray’s sum is zero then we will print the starting and ending index of the subarray which is formed.
Below is the algorithm which clearly explains the approach.

Algorithm

• Firstly we need to generate all the subarrays. For generating subarrays we use two nested loops.
  • The first loop with the iterator, i which starts from $0^{th}$ index to the last index of the array.
  • Initialise the sum variable which keeps track of the subarray sum until that time.
  • The second loop starts with iterator j, starts from $i^{th}$ index to the last index of the array.
• After computing the subarrays, we need to calculate their respective sum and check whether the subarray sum is zero.
  • For computing the sum of each subarray we need to run a loop for all the elements present in the subarray.
• Instead of creating all the subarrays stored in one data structure and later checking for the zero-sum of the subarray, we can just keep track of the sum of the subarray using a variable in the second loop, this is considered to be a more efficient approach for both in space and in time complexities wise.
• Every time increment the subarray sum with the value of the element present at $j^{th}$ index and check whether it is zero or not.
• If the subarray sum is obtained to be zero, we need to print the i and $j^{th}$ indices in the output.

Implementation

Below is the implementation of this approach in C++, Python, and Java:

C++ implementation of Zero subarray sum using brute force:

// C++ program for subarray sum
#include <iostream>
#include <unordered_map>
using namespace std;
 
// Main function which prints all the subarrays whose sum is zero
void ZeroSubarraySum(int arr[], int N){
    // We need two nested loops
    // First loop starts from 0th index to the end of the array
    for (int i = 0; i < N; i++){
        // initialize the sum to zero 
        int subarraysum = 0;
        // Here i is the start index of the subarray, j is the end index of the subarray
        for (int j = i; j < N; j++){
            //  Compute the sum from ith index to jth index
            subarraysum += arr[j];
            //  After computing the sum, check whether it is zero.If zero print the output
            if (subarraysum == 0) {
                cout << "Zero-sum subarray sum is from  " << i << " to " << j << "  \n";
            }
        }
    }
}
// Driver Code
int main(){
    // given set of input integer array
    int arr[] = { 0, -1, 8, -5, -3, -7, 4, 2, 1 };
    int N = sizeof(arr)/sizeof(arr[0]);
    // main function for printing all subarrays with zero sum
    ZeroSubarraySum(arr, N);
    return 0;
}

Output for the given array is:

Zero-sum subarray sum is from  0 to 0  
Zero-sum subarray sum is from  2 to 4  
Zero-sum subarray sum is from  2 to 8  
Zero-sum subarray sum is from  5 to 8

Python implementation of Zero subarray sum using brute force:

# Python program of zero subarray sum
# Main function which prints all the subarrays whose sum is zero
def ZeroSubarraySum(arr):
    # We need two nested loops
    # First loop starts from 0th index to the end of the array
    for i in range(len(arr)):
        #intialise the sum to zero 
        subarraysum = 0
        # Here i is the start index of the subarray, j is the end index of the subarray
        for j in range(i, len(arr)):
            # Compute the sum from ith index to jth index
            subarraysum += arr[j]
            # After computing the sum, check whether it is zero.If zero print the output
            if subarraysum == 0:
                print('Zero-sum Subarray is from '+ str(i)+ " to " +str(j))
 
# Driver Code
if __name__ == '__main__':
    # Input the integer array
    arr = [0, -1, 8, -5, -3, -7, 4, 2, 1]
    # Call the function which prints the zero subarray sum
    ZeroSubarraySum(arr)
 

Output for the given array is:

Zero-sum Subarray is from 0 to 0
Zero-sum Subarray is from 2 to 4
Zero-sum Subarray is from 2 to 8
Zero-sum Subarray is from 5 to 8

Java implementation of Zero subarray sum using brute force:

// Java program for subarray sum equal to zero
class Solution{
    import java.io.*;
import java.util.*;
public class Solution {

    public static void ZeroSubarraySum(int[] arr){
        // We need two nested loops
        // First loop starts from 0th index to the end of the array
        for (int i = 0; i < arr.length; i++){
            // initialize the sum to zero 
            int subarraysum = 0;
            // Here i is the start index of the subarray, j is the end index of the subarray
            for (int j = i; j < arr.length; j++){
                //  Compute the sum from ith index to jth index
                subarraysum += arr[j];
                //  After computing the sum, check whether it is zero.If zero print the output
                if (subarraysum == 0) {
                    System.out.println("Zero-sum subarray sum is from " + i + " to " + j);
                }
            }
        }
    }
    // Driver code
    public static void main (String[] args){
        // given set of input integer array
        int[] arr = { 0, -1, 8, -5, -3, -7, 4, 2, 1 };
        // main function for printing all subarrays with zero sum
        ZeroSubarraySum(arr);
    }

}

Output for the given array is:

Zero-sum Subarray is from 0 to 0
Zero-sum Subarray is from 2 to 4
Zero-sum Subarray is from 2 to 8
Zero-sum Subarray is from 5 to 8

Explanation:

We can observe that the subarrays from the start index and end index from the output have the subarray sum which is zero. All the subarrays whose sum is zero are being printed by indicating the starting and ending index of the subarray which is formed.

Complexity Analysis

Time Complexity: $O(N^2)$ where N is the length of the input integer array.

• For generating the $(N*\frac{(N+1)}{2})$ number of subarrays, it takes time complexity of $O(N^2)$ because we consider the starting index of the subarrays can be from the 0th index and the ending index can go upto last index of the array.
• The ending index of any subarray can be from the $i^{th}$ index to any index in the array which is larger or equal to i.
• For computing the sum of each subarray and checking whether it is equal to zero, it takes a time complexity of $O(1)$.
• Therefore the overall time complexity of a zero-sum subarray using brute force is $O(N^2)$.

Space Complexity: O(1)

• It doesn’t need any of extra space as we are updating the value of the subarray and also keeping track of the sum of the subarray using a variable.

Approach 2: (Using Hashing)

In the above approach, we generate all the possible subarrays of the given integer array and check whether its sum is zero. Instead of this, we can use hashing for solving the zero subarray sum. In this approach, we store the sum of all the subarrays starting from the $0^{th}$ index to the current index using a hash map. If we encounter the sum of the subarray calculated as zero we print the output giving the starting index as 0 and the ending index as the current index.
If the sum computed is already present in the hashmap, it indicates that there is already a subarray from nums[0] to the current index i.e, nums[i], and now the same sum is obtained for the current subarray which means the sum of the subarray is zero.

Algorithm:
For all the elements in the given integer input array follow the below-mentioned steps:

• Compute the sum of elements till the current index and store it in subarray_sum.
• If the subarray_sum computed is zero, then it means that we have found a subarray with zero-sum starting from $0^{th}$ index to the current index i.e, $i^{th}$ index.
• And also if the subarray_sum is already present in the hashmap then it indicates that the subarray_sum was the sum of some subarray i.e, which starts from nums[0] to nums[i] as in the above example.
• Now the same sum is obtained for the current subarray which is computed and it means that it is the same as the sum of the subarray from nums[0] to nums[j], (where j is the previous index where the current sum is already found) which means that the sum of the subarray nums[i+1] to nums[j] must also be 0.
• We store all the starting index and ending index of the zero-sum subarray in the data structure like array or vector, etc.
• And at last we need to add the current sum to the hashmap.

Example

Let’s consider the below example as the input integer array:

Input :

arr = [0, -1, 8, -5, -3, -7, 4, 2, 1]

Firstly, declare the hashmap and answer array where we store the starting and ending index. All the steps to be followed to find the zero-sum subarray using hashing is clearly shown in the below image:

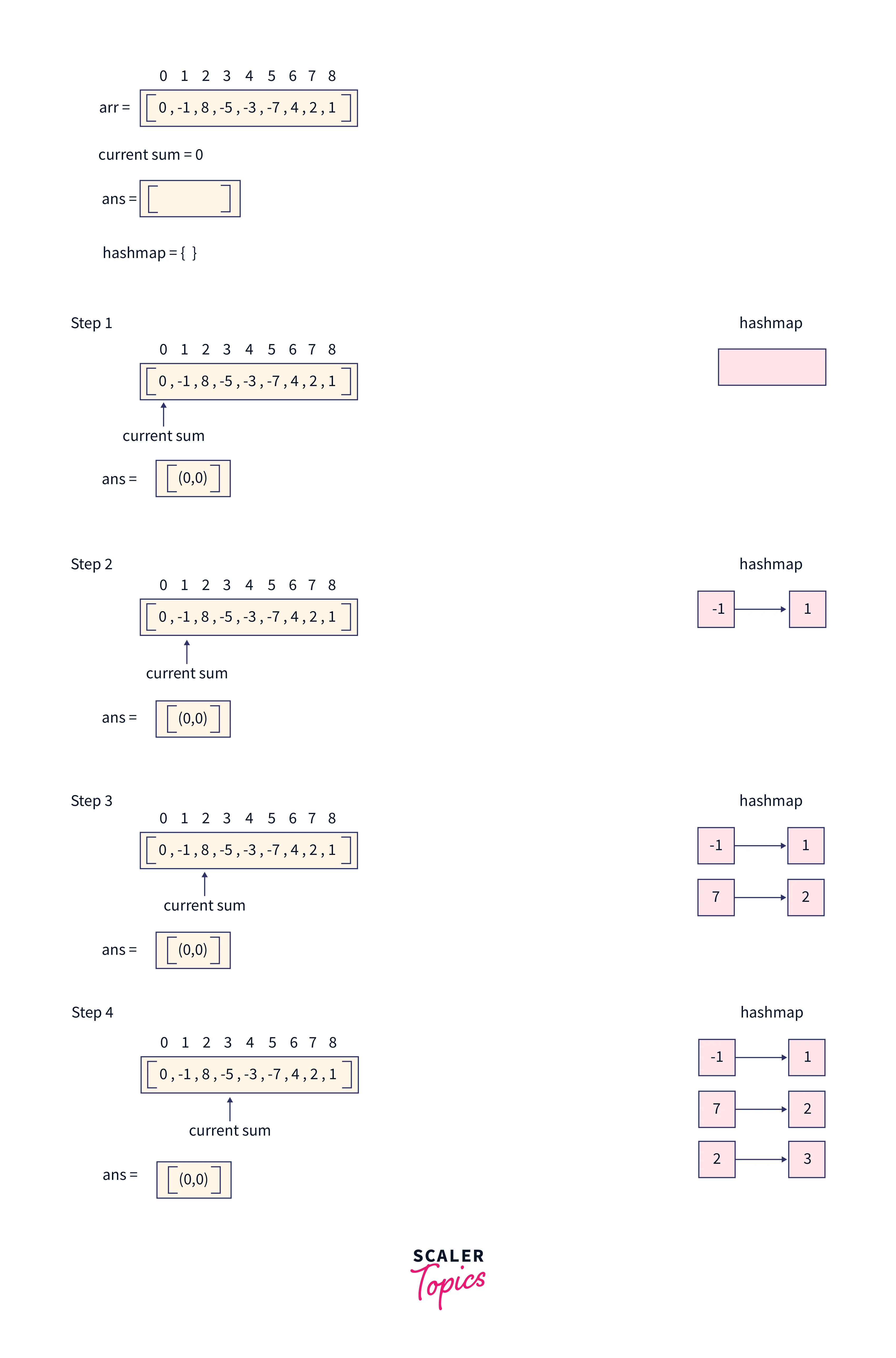
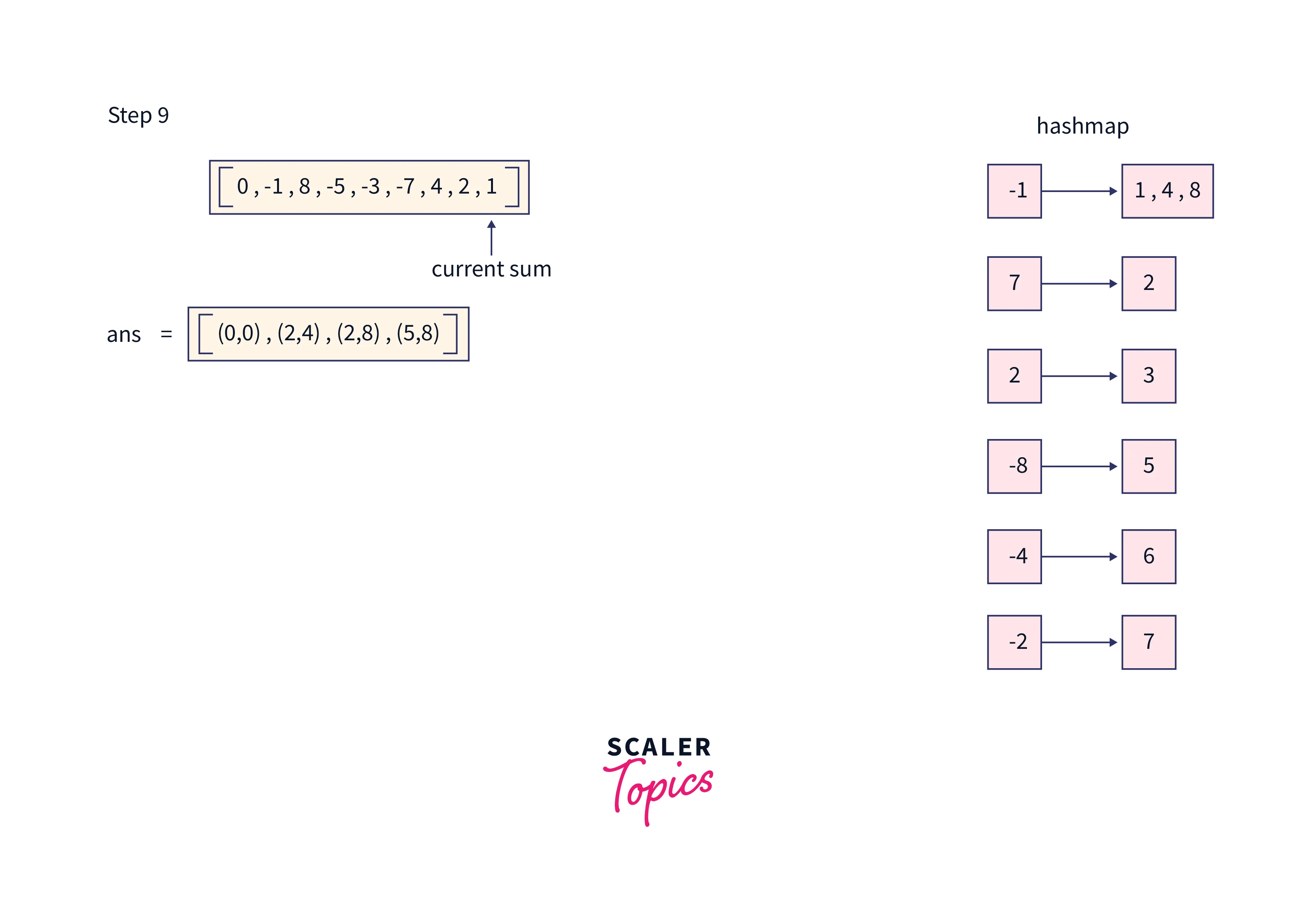
Output for the given array is:

Zero-sum Subarray is from 0 to 0
Zero-sum Subarray is from 2 to 4
Zero-sum Subarray is from 2 to 8
Zero-sum Subarray is from 5 to 8

Explanation: We can observe that the subarrays from the start index and end index from the output have the subarray sum which is zero. All the subarrays whose sum is zero are being printed by indicating the starting and ending index of the subarray which is formed.

Implementation

Below is the implementation of this approach using hashing in C++, python, and java.

C++ implementation of zero subarray sum using hashing:

// C++ program for finding the subarrays whose sum is zero
#include <bits/stdc++.h>
using namespace std;
  
// Main function required for printing all the zero subarray sum
vector< pair<int, int> > ZeroSubarraySum(int nums[], int N){
    // A hashtable is created which is used to store current subarray sum
    unordered_map<int, vector<int> > hashtable;
  
    // to store the starting and ending indices store the indices in the ans array
    vector <pair<int, int>> ans;
  
    // helps in computing the sum of elements 
    int currentsum = 0;
  
    for (int i = 0; i < N; i++){
        // add the value of nums[i] to the current sum
        currentsum += nums[i];
  
        // if the current sum is zero then it means that there is a zero subarray sum with starting index as 0 and ending index as the current index.
        if (currentsum == 0)
            // append the values of indices into the ans array
            ans.push_back(make_pair(0, i));
  
        // If sum already exists in the hashtable then there exists at-least one subarray which is ending at index i with zero subarray sum
        if (hashtable.find(currentsum) != hashtable.end()){
            // map[sum] stores starting index of all subarrays
            vector<int> ans1 = hashtable[currentsum];
            for (auto k = ans1.begin(); k != ans1.end(); k++)
                ans.push_back(make_pair(*k + 1, i));
        }
  
        // Important - no else
        hashtable[currentsum].push_back(i);
    }
  
    // return output vector
    return ans;
}

// Driver code
int main()
{
    int nums[] = { 0, -1, 8, -5, -3, -7, 4, 2, 1 };
    int N = sizeof(nums)/sizeof(nums[0]);
  
    vector<pair<int, int> > ans = ZeroSubarraySum(nums, N);
  
    // if we didn’t find any subarray with 0 sum,
    // then subarray doesn’t exists
    if (ans.size() == 0)
        cout << "No subarray exists";
    else
        for (auto k = ans.begin(); k != ans.end(); k++)
        cout << "Subarray found from Index " <<
        k->first << " to " << k->second << endl;
  
    return 0;
}

Output for the given array is:

Zero-sum Subarray is from 0 to 0
Zero-sum Subarray is from 2 to 4
Zero-sum Subarray is from 2 to 8
Zero-sum Subarray is from 5 to 8

Python implementation of zero subarray sum using hashing:

# Python program for printing the subarrays whose sum is zero using hashing
def ZeroSubarraySum(nums,N):
    # A hashtable is created which is used to store current subarray sum
    hashtable = {}
    # to store the starting and ending indices store the indices in the ans array 
    ans = []
    # helps in computing the sum of elements 
    currentsum = 0
    for i in range(N):
        # add the value of nums[i] to the current sum
        currentsum += nums[i]
        # if the current sum is zero then it means that there is a zero subarray sum with starting index as 0 and ending index as the current index.
        if currentsum  == 0:
            # append the values of indices into the ans array
            ans.append((0, i))
        
        ans1 = []
         
        # If sum already exists in the hashtable then there exists at-least one subarray which is ending at index i with zero subarray sum
        if currentsum in hashtable:
            # this helps in storing the indices
            ans1 = hashtable.get(currentsum)
            for k in range(len(ans1)):
                ans.append((ans1[k] + 1, i))
        ans1.append(i)
        hashtable[currentsum] = ans1
    return ans
 
# Driver Code
if __name__ == '__main__':
    # Input the integer array
    nums = [0, -1, 8, -5, -3, -7, 4, 2, 1]
    # Call the function which prints the zero subarray sum
    ans = ZeroSubarraySum(nums, len(nums))
    # if there is no subarray whose sum is zero return not present
    if (len(ans) == 0):
        print ("No subarray with zero-sum is present")
    # else print the subarrays whose sum is zero
    else:
        for i in ans:
            print ("Zero sum subarray is from " + str(i[0]) + " to " + str(i[1]))

Output for the given array is:

    Zero-sum Subarray is from 0 to 0
    Zero-sum Subarray is from 2 to 4
    Zero-sum Subarray is from 2 to 8
    Zero-sum Subarray is from 5 to 8

Java implementation of zero subarray sum using hashing:

// java program for printing the subarray start and end indices whose sum is zero
import java.io.*;
import java.util.*;
 
// Pair class defined for storing and extracting indices
class Pair
{
    int first, second;
    Pair(int a, int b)
    {
        first = a;
        second = b;
    }
}
// Main class
public class Solution{
    // Main function required for printing all the zero subarray sum
    static ArrayList<Pair> ZeroSubarraySum(int[] nums, int N){
        
            // A hashtable is created which is used to store current subarray sum
            HashMap<Integer,ArrayList<Integer>> hashtable = new HashMap<>();
        
            //to store the starting and ending indices store the indices in the ans array
            ArrayList<Pair> ans = new ArrayList<>();
 
            // helps in computing the sum of elements 
            int currentsum  = 0;
 
            for (int i = 0; i < N; i++){
                // add the value of nums[i] to the current sum
                currentsum  += nums[i];
                // if the current sum is zero then it means that there is a zero subarray sum with starting index as 0 and ending index as the current index.
                if (currentsum  == 0)
                    // append the values of indices into the ans array
                    ans.add(new Pair(0, i));
                ArrayList<Integer> ans1 = new ArrayList<>();
                 
                // If sum already exists in the hashtable then there exists at-least one subarray which is ending at index i with zero subarray sum
                if (hashtable.containsKey(currentsum)){
                    // this helps in storing the indices
                    ans1 = hashtable.get(currentsum );
                    for (int k = 0; k < ans1.size(); k++){
                            ans.add(new Pair(ans1.get(k) + 1, i));
                    }
                }
                ans1.add(i);
                hashtable.put(currentsum , ans1);
            }
            return ans;
    }
    // Utility function needed to print all the subarrays starting and ending indices whose sum is zero
    static void Print_Ans(ArrayList<Pair> ans){
            for (int it = 0; it < ans.size(); it++){
                Pair k = ans.get(it);
                System.out.println("Zero sum subarray is from " + k.first + " to " + k.second);
            }
    }
    // Driver code
    public static void main (String[] args){
        // given set of input integer array
        int[] nums = { 0, -1, 8, -5, -3, -7, 4, 2, 1 };
        int N= nums.length;
        // main function for printing all subarrays with zero sum
             
            ArrayList<Pair> ans = ZeroSubarraySum(nums, N);
             
            // if there is no subarray whose sum is zero return not present
            if (ans.size() == 0)
                System.out.println("No subarray exists");
            else
                // else print the subarrays whose sum is zero
                Print_Ans(ans);
    }
}

Output for the given array is:

    Zero-sum Subarray is from 0 to 0
    Zero-sum Subarray is from 2 to 4
    Zero-sum Subarray is from 2 to 8
    Zero-sum Subarray is from 5 to 8

Explanation:

We can observe that the subarrays from the start index and end index from the output have the subarray sum which is zero. All the subarrays whose sum is zero are being printed by indicating the starting and ending index of the subarray which is formed.

Complexity Analysis

Time Complexity: O(N) where N is the length of the input integer array.

• We can find all the subarrays with sum equal to zero in one single traversal using a hashtable.
• For each lookup in hashmap i.e, for checking whether the current sum is present already in the hashmap or not takes the time complexity of O(log N) and for computing the current sum it takes constant time i.e, O(1).
• Therefore the overall time complexity obtained for zero subarray sum is O(N) if hashmap is used for storing the subarray sums.

Space Complexity: O(N) where N is the length of the input integer array.

• This extra space is needed for the hashmap to store the current sum values during the computation of the zero-sum subarray.

Conclusion

• In this article we have discussed two approaches for finding the zero subarray sum from the given set of elements.
• In the first approach, it is a brute force approach where we use two nested loops to compute the subarrays and find the sum and check whether it is zero or not.
• This method has a time complexity of $O(N^2)$, where N is the length of the integer input array and a space complexity of O(1).
• In the second method we use hashing, where we store the current computed subarray sum in it.
• This method has a time complexity of O(N), where N is the length of the integer input array, and has a space complexity of O(N) which is used for a hashmap.