This article explains the concept of isomorphism in graph data structures. A pair of given graphs are said to be isomorphic graphs if they are structurally equivalent. It means there exists a mapping(bijection) between the vertices of the two graphs. Using this mapping, one graph can be converted into the other by replacing its vertices with the corresponding mapped vertices in the other graph.
In other words, these graphs have similar kind of structure with same number of vertices and edges.
What is an Isomorphic Graph?
Two graphs are said to be isomorphic if there exists a mapping between the vertices of these graphs. Mapping between the vertices of both the graphs simply means that the one graph can be derived/obtained by just replacing its corresponding mapped vertex from other graph. Let us assume the given graphs are A and B, these graphs are said to be isomorphic if:
- there is a structure that satisfies a one-to-one mapping between the vertices and edges of graphs A and B.
- Simply, it means that the two graphs differ only by the names of the edges and vertices but are structurally equivalent.
For a better understanding of the definition of isomorphic graphs, let’s look at the below graphs which are said to be isomorphic.
Example 1
Consider the first set of graphs A and B which are isomorphic and their respective structures are as follows:
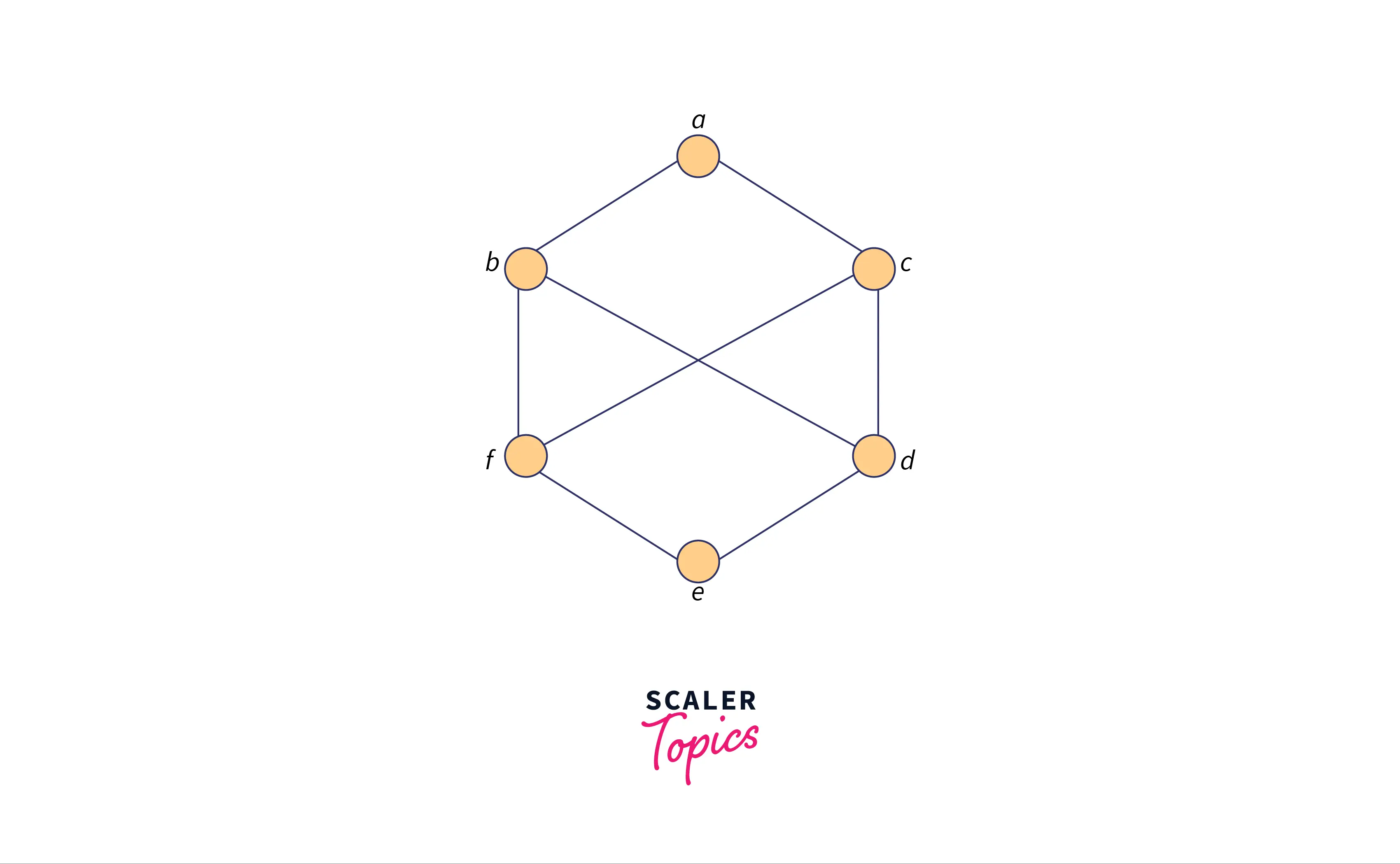
Graph A:
Graph B:
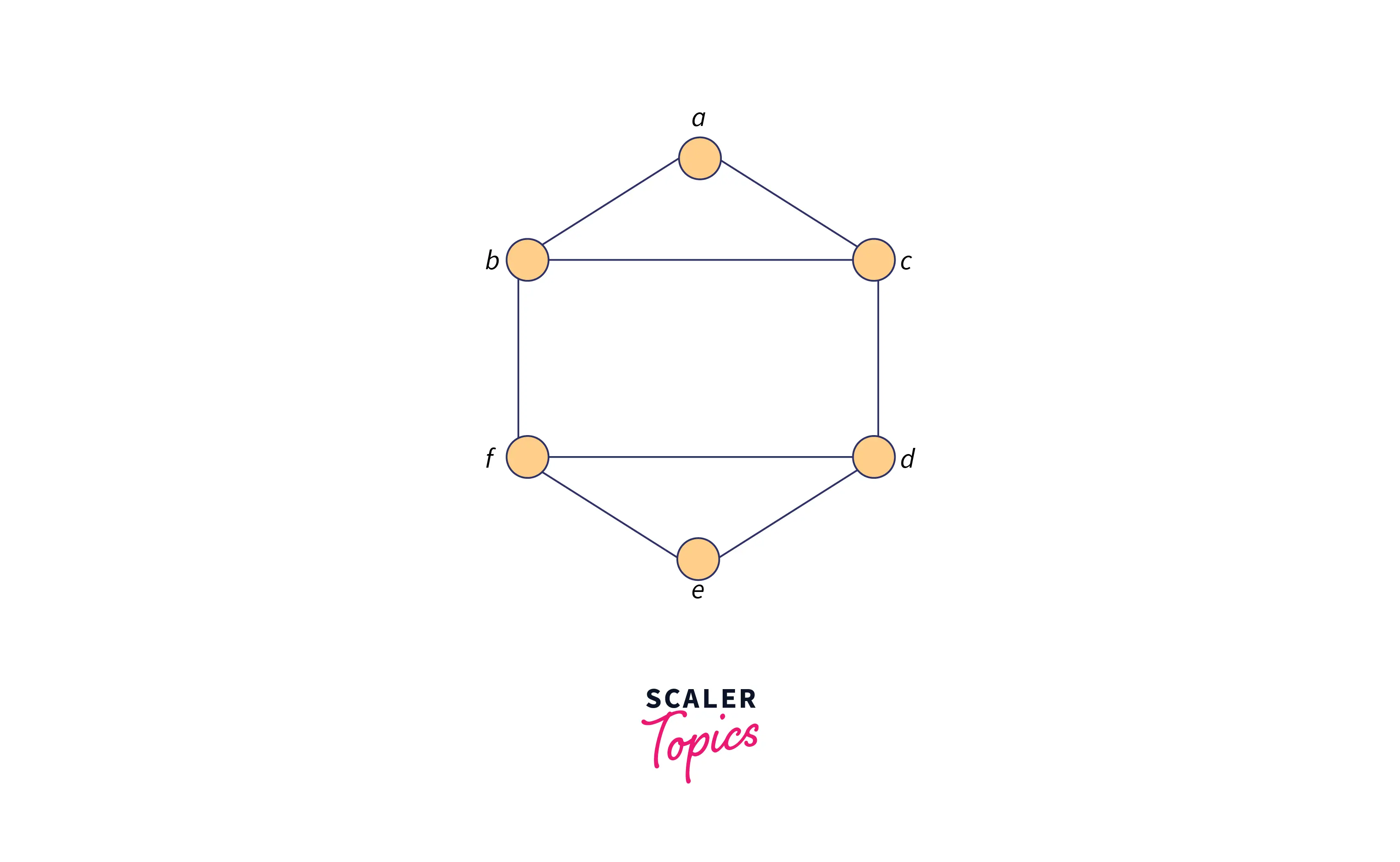
The above-mentioned graphs have same number of vertices, edges and most importantly are similar in structure so they are said to be isomorphic graphs. If we rename b to f and f to b in the first graph keeping other vertices intact, the second graph will be generated.
Example 2
For a better understanding of the isomorphism concept, let’s look at another set of graphs that exhibit the property of isomorphism:
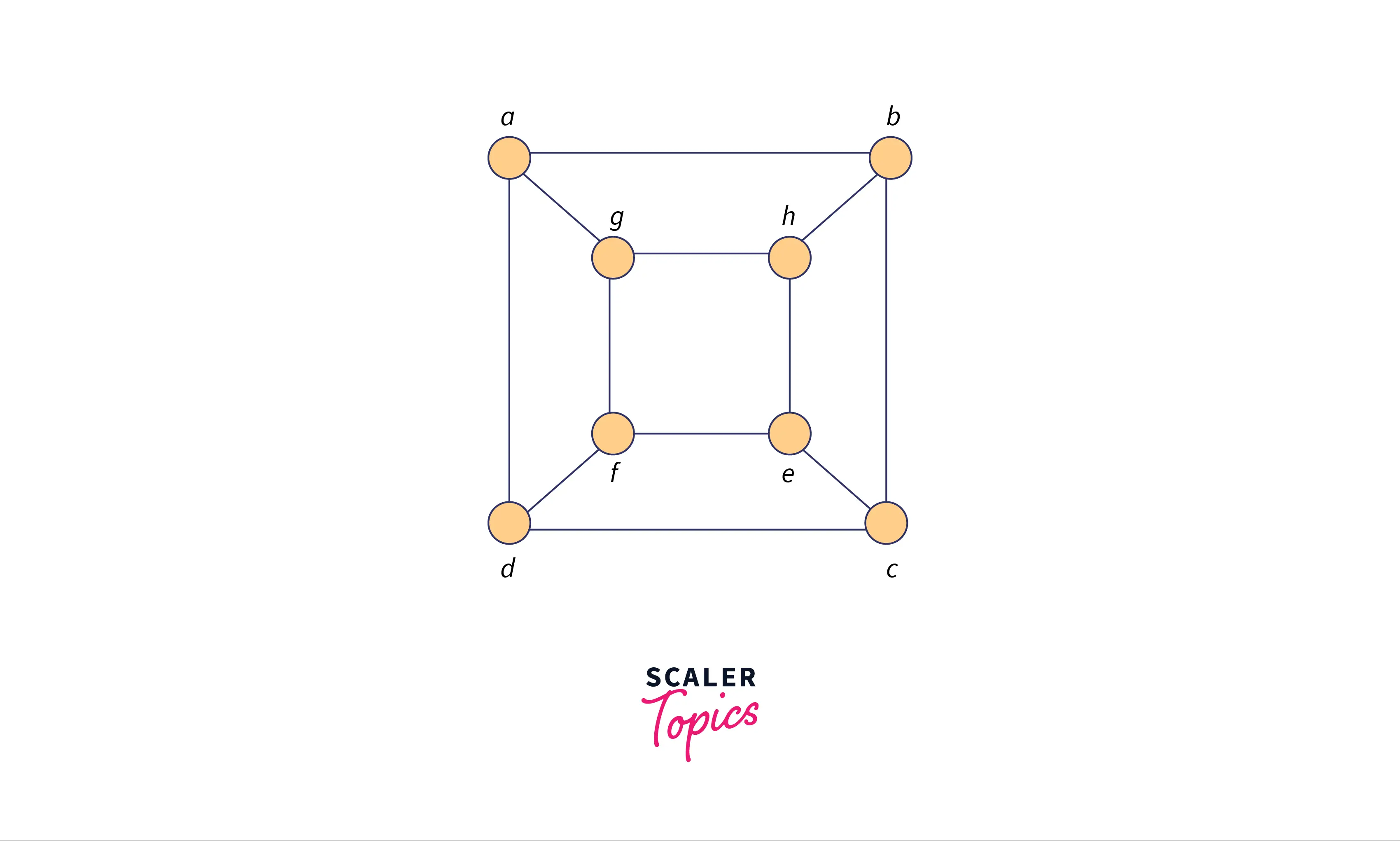
Graph A:
Graph B:
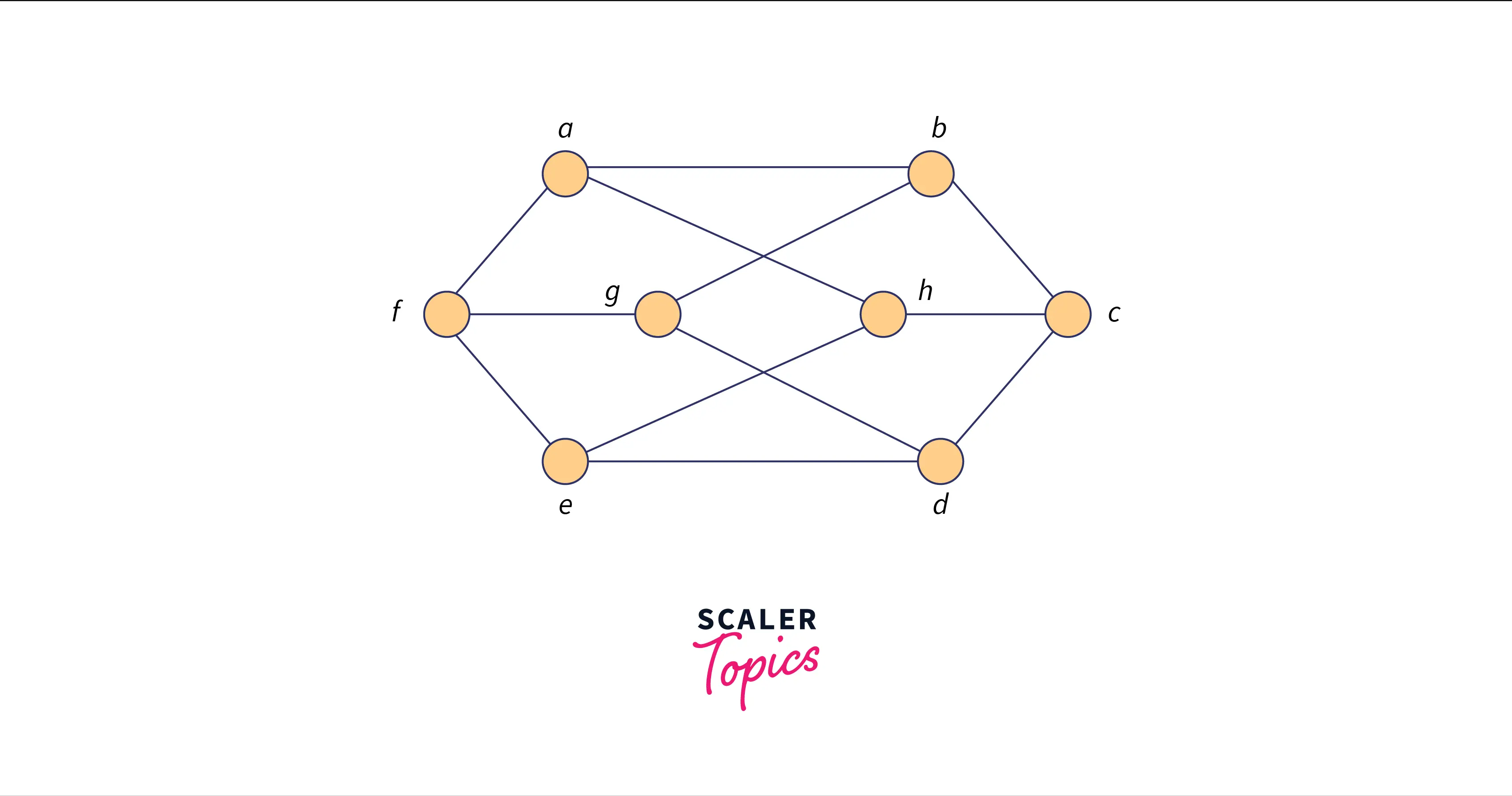
We can observe that the given two graphs are said to be isomorphic graphs. They have same number of vertices and edges for these graphs are said to be isomorphic graphs.
Graph Isomorphism Conditions
Now as we know what are isomorphic graphs, let’s look at the necessary conditions to be satisfied to say that the given two graphs are said to be isomorphic graphs. Below are a few necessary conditions to be followed to say that the given graphs are isomorphic:
- Number of nodes/ vertices in both the graphs must be the same say number N.
- Number of edges between these vertices in both the graphs must be equal in number.
- Degree sequence of both the given graphs must be the same.
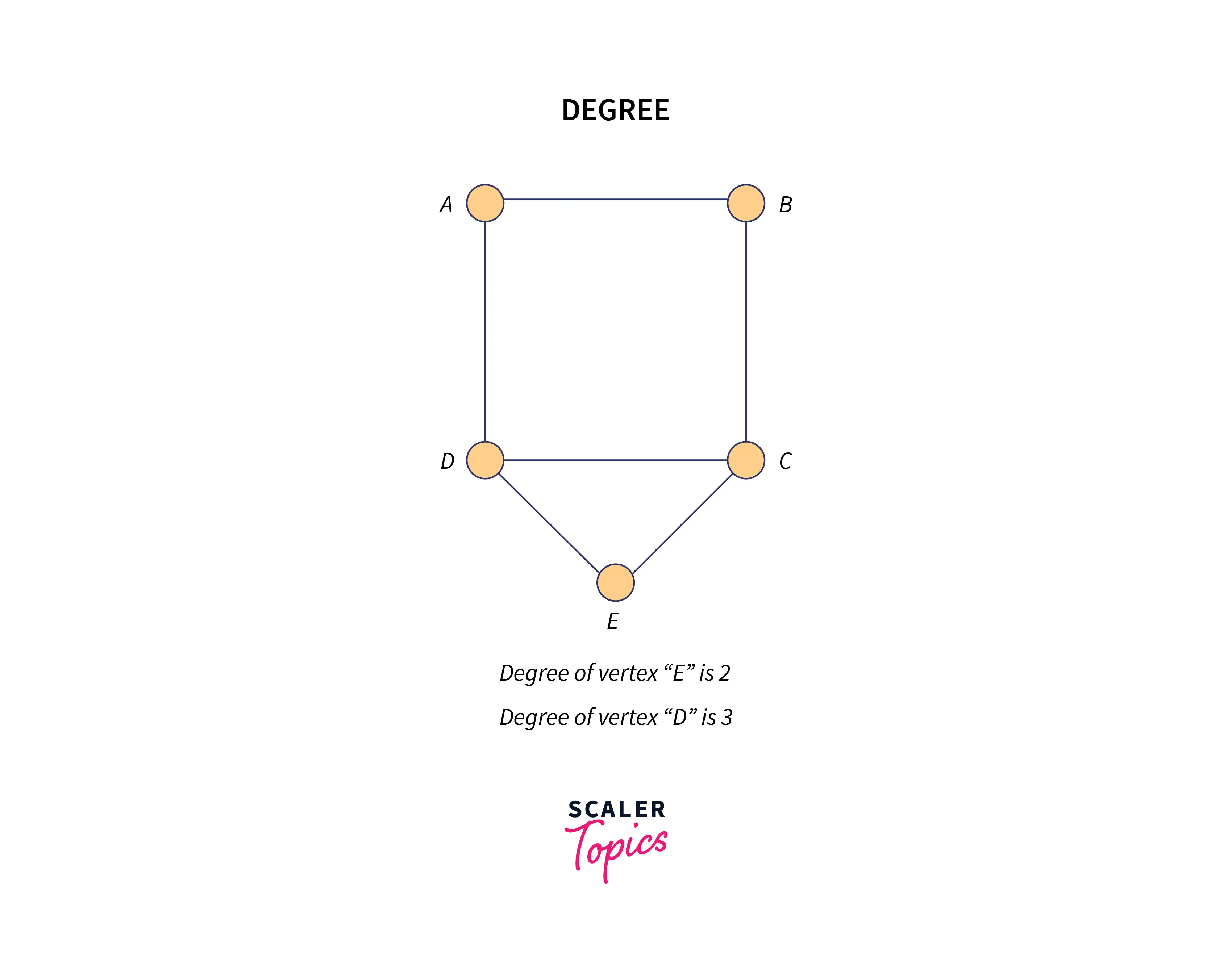
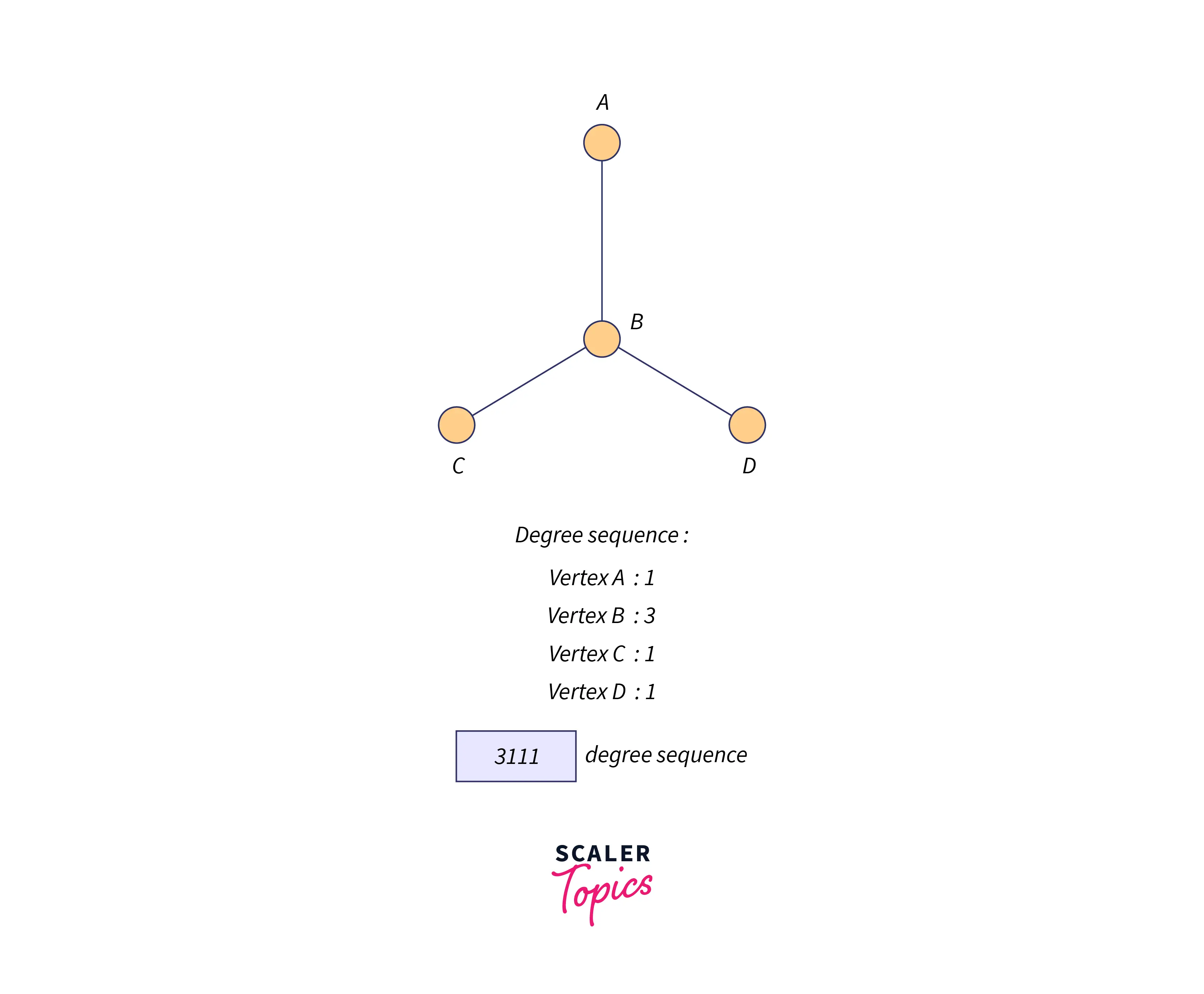
Mapping between the vertices of both the graphs A and B means, one-to-one correspondence or invertible function which is present between the two vertices of the graphs.
Isomorphism of graphs A and B is a one-to-one correspondence or invertible function between the vertex sets of A and B.
function f: vertex(A) -> vertex(B)
such that any two vertices u and v of A are adjacent in A if and only if f(u) and f(v) are adjacent in B. This kind of mapping is known as edge-preserving mapping.
- Both graphs A and B must preserve the one-to-one mapping between all the vertices and edges of graphs A and B.
Examples – Which of the Following Graphs are Isomorphic?
Below given are a few examples of the graphs, indicate which pair of the graphs are said to be isomorphic by following all the necessary conditions mentioned above.
Example 1
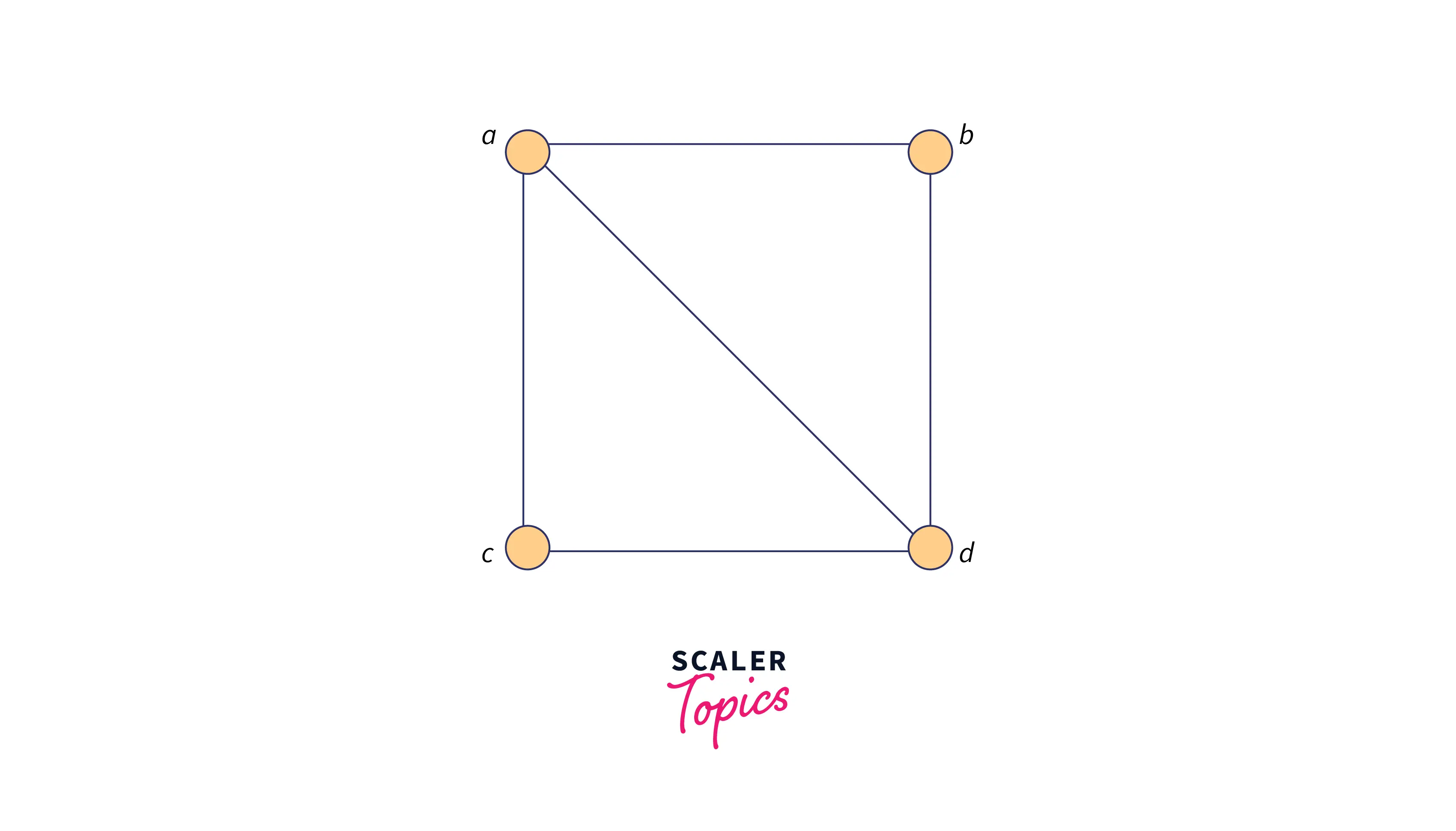
Consider the first pair of graphs A and B and their respective structures are as follows:
Graph A:
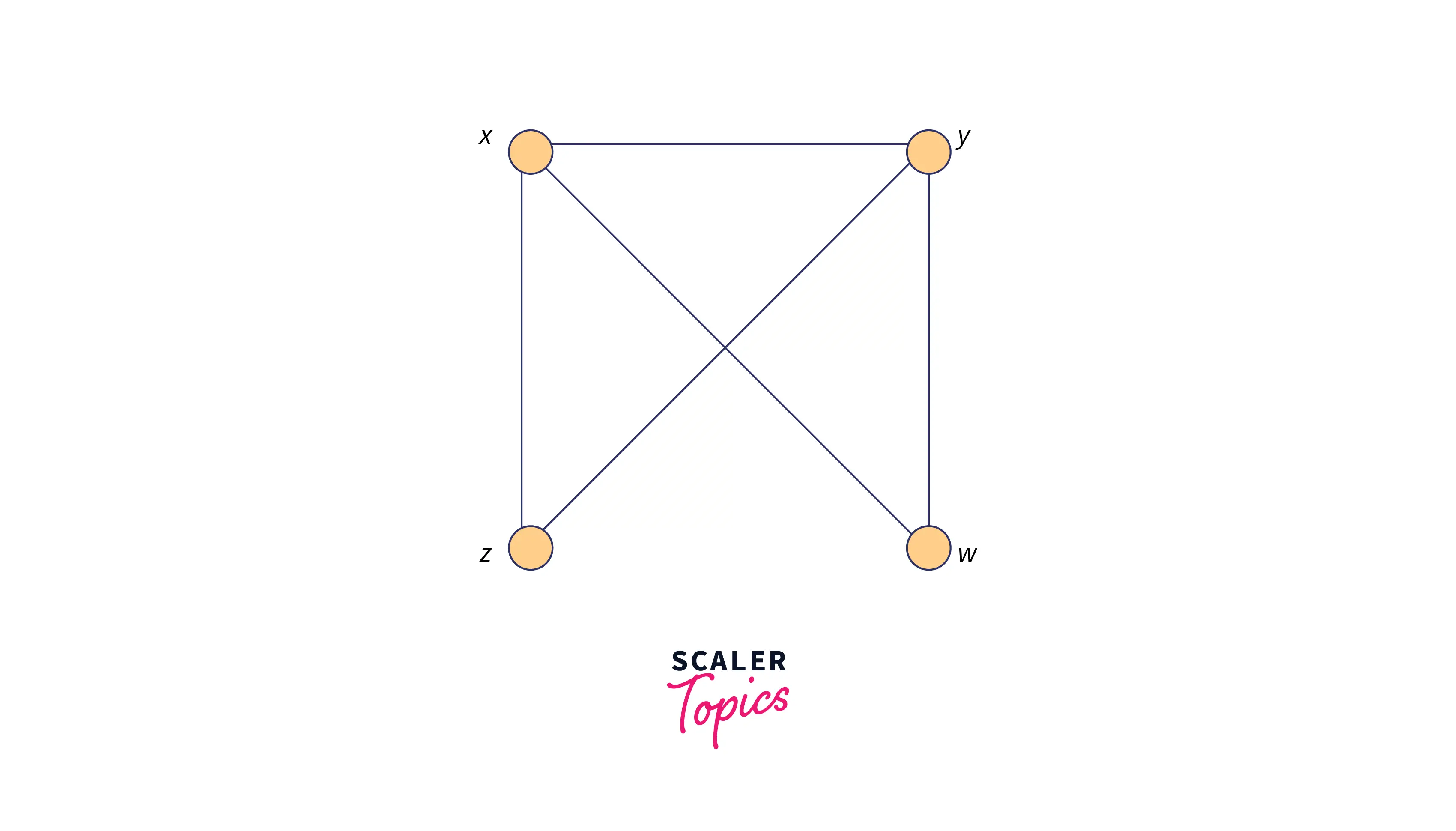
Graph B:
- For checking the number of vertices are same or not in the given graphs:
- number of vertices in graph A is: 4
- number of vertices in graph B is: 4
- For checking the number of edges are same or not in the given graphs:
- number of edges present in Graph A is: 5
- number of edges present in Graph B is: 5
- To check for the degree sequence of all the vertices present in the given pair of graphs:
- Degree sequence of Graph A is: [3, 3, 2, 2]
- Degree sequence of Graph B is: [3, 3, 2, 2]
- The mapping of vertices and their respective edges of the given graphs: For the above pair of graphs Graph A and Graph B, which has the vertices are [a, b, c, d] and [x, y, z, v] respectively. Here, one vertex from Graph A is mapped to another vertex of map B only when the degree of the vertices of one graph is same as in other graph.
- Therefore the mapping of the vertices and edges obtained is as follows:
- Consider vertex “a ” from graph A and vertex ” x “ from graph B, both vertices have the degree as 3, so they can be mapped, Our first mapping is:
- For vertex ” b “ in graph A and vertex ” z “ in graph B, have a degree of 2, even the degree of ” w “ in graph B is 2, so we can either map with any of these and at the end of mapping of vertices, we need to cross-cross by following the below-mentioned way. So let’s assume we map ” b “ with ” z “: b -> z.
- In the same way, we get the mapping of ” c “ with ” w “ which is as follows:
- And the last mapping is between ” d “ and ” y “, which is as follows:
The mapping obtained is as follows:

Mapping between these vertices simply means that the one graph can be obtained by other by just replacing its corresponding mapped vertex from other graph. Once the mapping is performed, we have to cross-check all the vertices by considering two mappings at a time. In the above example we can see that vertex ” a “ is mapped with vertex ” x “ and vertex ” b “ is mapped with vertex ” y “. This mapping is only satisfied if the number of edges between vertex ” a “ and vertex ” b “ in graph A is equal to the number of edges present between the vertex ” x “ and ” y “ in Graph B. In the same way, we need to check for all the pairs of vertices in the mapping within Graph A and Graph B. Since all these conditions are satisfied we can say that the given Graph A and Graph B can be isomorphic.
Example 2:
Let’s consider the next pair of graphs and check whether all the conditions are satisfied and say whether the graphs are isomorphic or not:
Graph A:
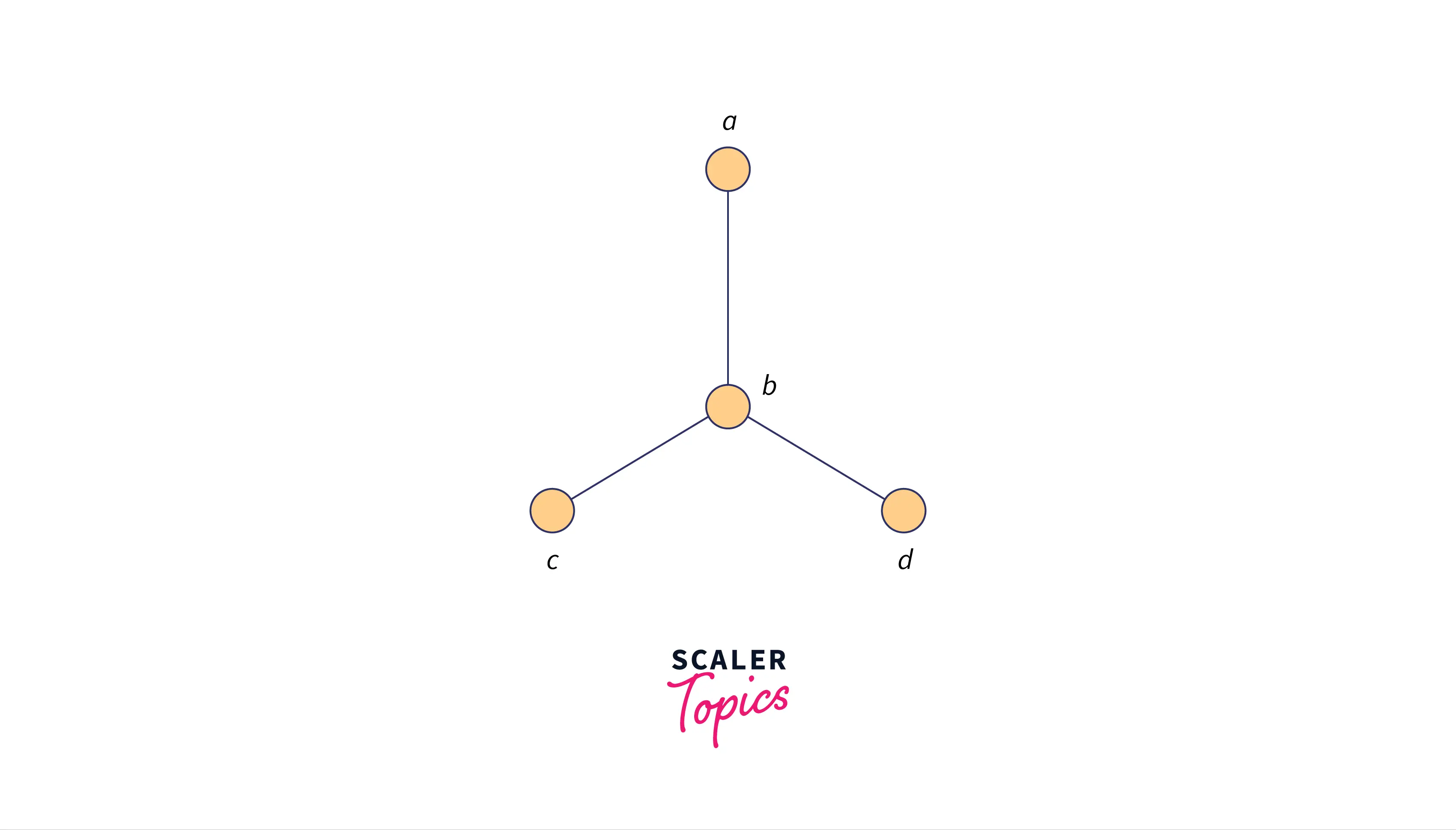
Graph B:
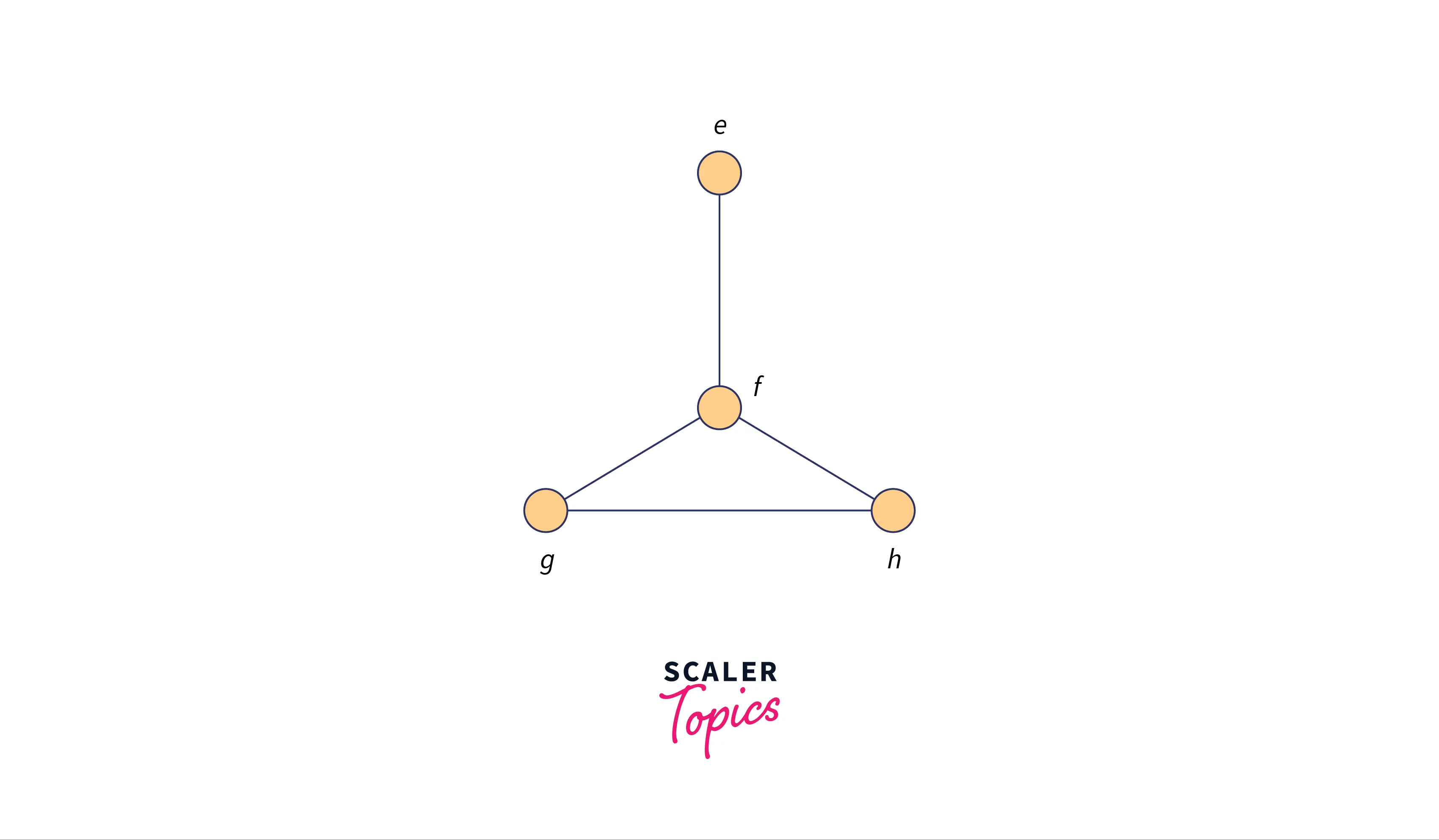
- The first condition to be satisfied is the number of vertices in the graphs:
- Number of vertices in Graph A is: 4
- Number of vertices in Graph B is: 4
- The second condition to be satisfied to say that the graphs are isomorphic is the same number of edges between the vertices of the graphs:
- Number of edges in Graph A is: 3
- Number of edges in Graph B is: 4
We can see that the second condition failed so we can say that the given graphs are not isomorphic.
Important points
These are a few important points to be followed to say that given pair of graphs is isomorphic completely. The above-mentioned conditions are not completely sufficient to prove that the given two graphs are isomorphic, they are just necessary conditions to be satisfied.
- If the above-mentioned conditions are satisfied we may or may not say the given graphs are isomorphic.
- If any of the above-mentioned conditions is failed or not satisfied, we can surely say that the given pair of graphs are not isomorphic graphs.
Then what are the sufficient conditions to say that the given graphs are isomorphic are as follows:
If any of these conditions are satisfied, we can automatically say that the given pair of graphs is isomorphic.
- If the adjacency matrices of the given graphs are matching, then the given pair of graphs is said to be isomorphic. Adjacency matrices are the same for isomorphic graphs. not necessary, it would depend on how you label the vertices.
- The given pair of graphs are isomorphic if and only if their complement graphs are isomorphic.
- Suppose G and H are isomorphic graphs. Then there is a bijection f from the vertex set of G to that of H that preserves adjacencies, that is, if u and v are adjacent in G, then f(u) and f(v) are adjacent in H. Since f is a bijection, it is also true that if u and v are not adjacent in G, then f(u) and f(v) are not adjacent in H. Thus, the complements of G and H are isomorphic.
- The given pair of graphs can also be said isomorphic if their corresponding sub-graphs of the graphs are obtained by deleting some of the vertices of one graph and their corresponding structures in the other graph are isomorphic.
Conclusion
- This article mainly explained the concept of isomorphism and isomorphism in graphs.
- We have seen the basic definitions of isomorphism and isomorphic graphs.
- There were many examples of isomorphic graphs which are clearly explained in the examples discussed above.
- All the basic necessary conditions to be satisfied to say that the given pair of graphs are isomorphic are mentioned in the article.
- However we also explained the sufficient conditions apart from the necessary conditions to be followed to say that the given graphs are isomorphic.
- We have seen examples of pairs of graphs and evaluated whether the graphs are isomorphic or not.
- Graph isomorphism is the area of pattern matching and, is widely used in various applications such as image processing, protein structure, computer and information systems, and in many social Networks.