An infix expression is one that we use regularly. A single letter or operator followed by one infix string and another infix string makes up an infix expression such as A, A + B, and (A + B) + (C – D). Therefore, there are operators between operands in this.
If the operator appears in an expression before the operands, the expression is referred to as the prefix expression, One of the simplest forms possible (operator operand1 operand2) as in _+AB-CD.
In infix notation, the expression _+AB-CD is written as: (A + B) * (C – D)
In prefix notation (also known as Polish notation), the expression _+AB-CD is written as: _ + A B – C D
In this article, we will learn infix-to-prefix conversion in depth.
Infix and Prefix Notations
What is Infix Notation?
An expression is written in a conventional or typical manner in an infix notation. The operators are placed between the operands in this notation. A+B, A*B, and A/B, is an example of infix notation.
These examples are infix notations because, as we can see, all operators are present between the operands. As a result, the syntax of infix notation is as follows:
<operand> <operator> <operand>
Operators are symbols or keywords in programming and mathematics that perform specific operations on one or more operands.
Operands are the values or variables that operators act upon to produce a result.
Operators can be unary (acting on one operand) or binary (acting on two operands), and they define the type of operation to be performed, such as addition (+), subtraction (-), multiplication (*), or division (/).
Operands can be numeric values, variables, or expressions that evaluate values.
In an expression like “5 + 3,” the “+” operator acts on the operands 5 and 3 to produce the result 8, where 5 and 3 are the operands.
What is Prefix Notation?
A prefix notation does not require knowledge about precedence or associativity, whereas an infix notation requires information about precedence and associativity. Polish notation is another name for it. An operator comes before the operands in prefix notation. The following is the prefix notation’s syntax:
<operator> <operand> <operand>
Example for Infix to Prefix Conversion
Example – 1:
For instance, if the infix expression is 5+1, the comparable prefix expression would be +51.
The infix expression be:
a * b + c
↓
*ab+c
↓
(Prefix expression) +*abc
Example – 2:
A + B \* C
- First scan:
The prefix notation for B*C would be (*BC) because the multiplication operator has priority over the addition operator in the previously mentioned expression.A + \*BC - Second scan:
The prefix for the second scan would be:+A \*BC
To transform the infix to the prefix expression in the previous expression, we utilize two scans. A greater number of scans are needed if the expression is complicated. We must employ the technique that only needs one scan and yields the desired outcome. The algorithm will be efficient if we can complete the task in a single scan. Only a stack can accomplish this.
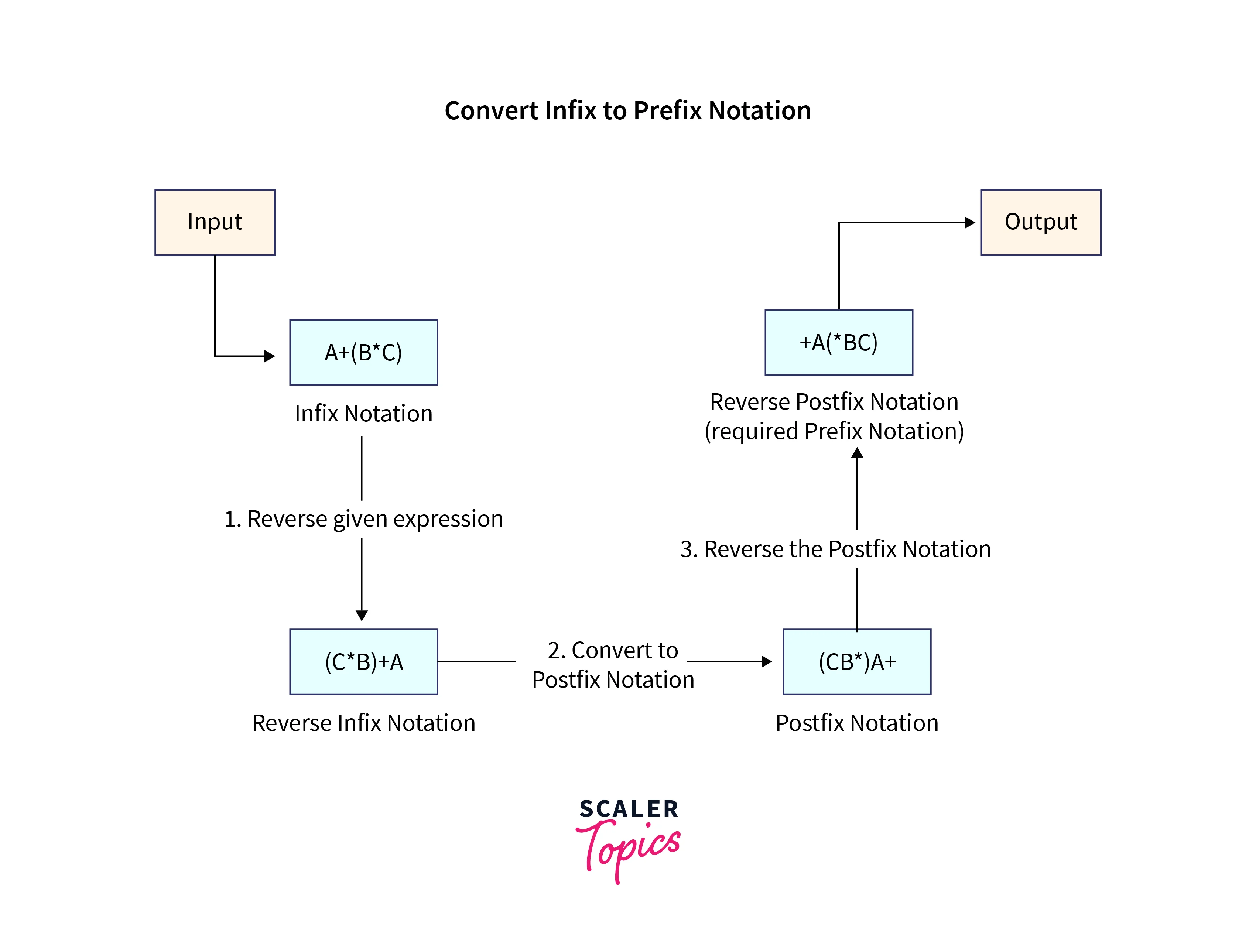
Converting Infix Expression to Prefix Expression
We can use the stack data structure for an Infix to prefix conversion. Here’s the concept:
- First, flip the infix expression. Keep in mind that when reversed, each “(” will become a “)” and each “)” a “(“.
- The second step is to “nearly” postfix the reversed infix expression.
- Instead of performing the pop operation to remove operators with greater than or equal precedence during the conversion to postfix expression, we will only remove the operators from the stack that have a higher precedence in this case.
- Reverse the postfix expression in step three.
- Infix expressions are converted to postfix forms using the stack.
C++ Program to Convert Infix to Prefix
#include <iostream>
#include <stack>
#include <algorithm>
using namespace std;
bool isOp(char c) {
return (!isalpha(c) && !isdigit(c));
}
int getPrecedence(char op) {
if (op == '-' || op == '+')
return 1;
else if (op == '*' || op == '/')
return 2;
else if (op == '^')
return 3;
return 0;
}
// method to convert infix to postfix
string infixToPostfixConversion(string infixExpr) {
infixExpr = '(' + infixExpr + ')';
int length = infixExpr.size();
stack<char> charStack;
string postfixOutput;
for (int i = 0; i < length; i++) {
if (isalpha(infixExpr[i]) || isdigit(infixExpr[i]))
postfixOutput += infixExpr[i];
else if (infixExpr[i] == '(')
charStack.push('(');
else if (infixExpr[i] == ')') {
while (charStack.top() != '(') {
postfixOutput += charStack.top();
charStack.pop();
}
charStack.pop();
} else {
if (isOp(charStack.top())) {
if (infixExpr[i] == '^') {
while (getPrecedence(infixExpr[i]) <= getPrecedence(charStack.top())) {
postfixOutput += charStack.top();
charStack.pop();
}
} else {
while (getPrecedence(infixExpr[i]) < getPrecedence(charStack.top())) {
postfixOutput += charStack.top();
charStack.pop();
}
}
charStack.push(infixExpr[i]);
}
}
}
while (!charStack.empty()) {
postfixOutput += charStack.top();
charStack.pop();
}
return postfixOutput;
}
// method to convert infix to prefix
string infixToPrefixConversion(string infixExpr) {
reverse(infixExpr.begin(), infixExpr.end());
int length = infixExpr.size();
for (int i = 0; i < length; i++) {
if (infixExpr[i] == '(')
infixExpr[i] = ')';
else if (infixExpr[i] == ')')
infixExpr[i] = '(';
}
string prefixExpr = infixToPostfixConversion(infixExpr);
reverse(prefixExpr.begin(), prefixExpr.end());
return prefixExpr;
}
// main method
int main() {
string expression = "a+b*c/d+e";
cout << "Infix Expression: " << expression << endl;
string prefixResult = infixToPrefixConversion(expression);
cout << "Prefix Expression: " << prefixResult << endl;
return 0;
}
Output:
Infix Expression: a+b*c/d+e
Prefix Expression: ++a/*bcde
Java Program to Convert Infix to Prefix
import java.util.Stack;
class ExpressionConverter {
// Function to check if the character is a letter
static boolean isLetter(char c) {
if ((c >= 'a' && c <= 'z') || (c >= 'A' && c <= 'Z')) {
return true;
}
return false;
}
// Function to check if the character is a digit
static boolean isDigit(char c) {
if (c >= '0' && c <= '9') {
return true;
}
return false;
}
// Function to check if the character is an operator
static boolean isOperator(char c) {
return (!isLetter(c) && !isDigit(c));
}
// Function to get priority of operators
static int getOperatorPriority(char operator) {
if (operator == '-' || operator == '+')
return 1;
else if (operator == '*' || operator == '/')
return 2;
else if (operator == '^')
return 3;
return 0;
}
// Reverse the characters in a string
static String reverseString(char str[], int start, int end) {
char temp;
while (start < end) {
temp = str[start];
str[start] = str[end];
str[end] = temp;
start++;
end--;
}
return String.valueOf(str);
}
// Function to convert infix to postfix expression
static String infixToPostfix(char[] infixExpression) {
String infix = '(' + String.valueOf(infixExpression) + ')';
int length = infix.length();
Stack<Character> operatorStack = new Stack<>();
String postfixOutput = "";
for (int i = 0; i < length; i++) {
if (isLetter(infix.charAt(i)) || isDigit(infix.charAt(i))) {
postfixOutput += infix.charAt(i);
} else if (infix.charAt(i) == '(') {
operatorStack.add('(');
} else if (infix.charAt(i) == ')') {
while (operatorStack.peek() != '(') {
postfixOutput += operatorStack.peek();
operatorStack.pop();
}
operatorStack.pop();
} else {
if (isOperator(operatorStack.peek())) {
while ((getOperatorPriority(infix.charAt(i)) < getOperatorPriority(operatorStack.peek()))
|| (getOperatorPriority(infix.charAt(i)) <= getOperatorPriority(operatorStack.peek())
&& infix.charAt(i) == '^')) {
postfixOutput += operatorStack.peek();
operatorStack.pop();
}
operatorStack.add(infix.charAt(i));
}
}
}
while (!operatorStack.empty()) {
postfixOutput += operatorStack.pop();
}
return postfixOutput;
}
static String infixToPrefix(char[] infixExpression) {
int length = infixExpression.length;
String reversedInfix = reverseString(infixExpression, 0, length - 1);
infixExpression = reversedInfix.toCharArray();
for (int i = 0; i < length; i++) {
if (infixExpression[i] == '(') {
infixExpression[i] = ')';
i++;
} else if (infixExpression[i] == ')') {
infixExpression[i] = '(';
i++;
}
}
String prefixOutput = infixToPostfix(infixExpression);
prefixOutput = reverseString(prefixOutput.toCharArray(), 0, length - 1);
return prefixOutput;
}
public static void main(String[] args) {
String expression = ("x+y*z/w+u");
System.out.print(infixToPrefix(expression.toCharArray()));
}
}
Output:
++x/*yzwu
Python Code to Convert Infix to Prefix Expression
# Function to determine if a character is an operator
def isOperator(character):
return (not character.isalpha()) and (not character.isdigit())
# Function to retrieve the precedence of operators
def getPriority(operator):
if operator == '-' or operator == '+':
return 1
elif operator == '*' or operator == '/':
return 2
elif operator == '^':
return 3
return 0
# Function to convert infix expression to postfix
def infixToPostfix(expression):
expression = '(' + expression + ')'
length = len(expression)
operator_stack = []
output = ""
for i in range(length):
if expression[i].isalpha() or expression[i].isdigit():
output += expression[i]
elif expression[i] == '(':
operator_stack.append(expression[i])
elif expression[i] == ')':
while operator_stack[-1] != '(':
output += operator_stack.pop()
operator_stack.pop()
else:
if isOperator(operator_stack[-1]):
if expression[i] == '^':
while getPriority(expression[i]) <= getPriority(operator_stack[-1]):
output += operator_stack.pop()
else:
while getPriority(expression[i]) < getPriority(operator_stack[-1]):
output += operator_stack.pop()
operator_stack.append(expression[i])
while len(operator_stack) != 0:
output += operator_stack.pop()
return output
# Function to convert infix expression to prefix
def infixToPrefix(expression):
length = len(expression)
reversed_expression = expression[::-1]
for i in range(length):
if reversed_expression[i] == '(':
reversed_expression[i] = ')'
elif reversed_expression[i] == ')':
reversed_expression[i] = '('
prefix = infixToPostfix(reversed_expression)
prefix = prefix[::-1]
return prefix
# Driver code
if __name__ == '__main__':
expression = "x+y*z/w+u"
print(infixToPrefix(expression))
Output:
++x/*yzwu
C# Program to Convert Infix to Prefix
using System;
using System.Collections.Generic;
public class ExpressionConverter {
static bool IsAlphabet(char c) {
if ((c >= 'a' && c <= 'z') || (c >= 'A' && c <= 'Z')) {
return true;
}
return false;
}
static bool IsDigit(char c) {
if (c >= '0' && c <= '9') {
return true;
}
return false;
}
static bool IsOperator(char c) {
return (!IsAlphabet(c) && !IsDigit(c));
}
static int GetPriority(char op) {
if (op == '-' || op == '+')
return 1;
else if (op == '*' || op == '/')
return 2;
else if (op == '^')
return 3;
return 0;
}
static string ReverseString(char[] str, int start, int end) {
char temp;
while (start < end) {
temp = str[start];
str[start] = str[end];
str[end] = temp;
start++;
end--;
}
return string.Join("", str);
}
static string InfixToPostfix(char[] infixExpression) {
string infix = '(' + string.Join("", infixExpression) + ')';
int length = infix.Length;
Stack<char> operatorStack = new Stack<char>();
string postfixOutput = "";
for (int i = 0; i < length; i++) {
if (IsAlphabet(infix[i]) || IsDigit(infix[i]))
postfixOutput += infix[i];
else if (infix[i] == '(')
operatorStack.Push('(');
else if (infix[i] == ')') {
while (operatorStack.Peek() != '(') {
postfixOutput += operatorStack.Peek();
operatorStack.Pop();
}
operatorStack.Pop();
} else {
if (IsOperator(operatorStack.Peek())) {
while ((GetPriority(infix[i]) < GetPriority(operatorStack.Peek()))
|| (GetPriority(infix[i]) <= GetPriority(operatorStack.Peek()) && infix[i] == '^')) {
postfixOutput += operatorStack.Peek();
operatorStack.Pop();
}
operatorStack.Push(infix[i]);
}
}
}
while (operatorStack.Count != 0) {
postfixOutput += operatorStack.Pop();
}
return postfixOutput;
}
static string InfixToPrefix(char[] infixExpression) {
int length = infixExpression.Length;
string reversedInfix = ReverseString(infixExpression, 0, length - 1);
char[] reversedParenthesesSwapped = new char[length];
for (int i = 0; i < length; i++) {
if (reversedInfix[i] == '(')
reversedParenthesesSwapped[i] = ')';
else if (reversedInfix[i] == ')')
reversedParenthesesSwapped[i] = '(';
else
reversedParenthesesSwapped[i] = reversedInfix[i];
}
string postfixExpression = InfixToPostfix(reversedParenthesesSwapped);
string prefixOutput = ReverseString(postfixExpression.ToCharArray(), 0, length - 1);
return prefixOutput;
}
public static void Main(string[] args) {
string inputExpression = "x+y*z/w+u";
Console.Write(InfixToPrefix(inputExpression.ToCharArray()));
}
}
Output:
++x/*yzwu
Illustration
Complexity
Complexity Analysis
Time Complexity: O(n)
Push() and pop() on the stack are constant-time operations. The complexity is linear in time since we only ever scan one set of characters in the expression.
Because we are maintaining a stack, the auxiliary space is O(n).
FAQs
Q. What rules should be applied when changing infix to prefix?
A. To switch from infix to prefix notation, the expression’s order must be reversed, each operator must be replaced with its matching prefix operator, and the locations of each operand must be switched. Prefix expressions are the result, with the operator occurring before the operands.
Q. What differentiates infix from postfix data structures?
A. Infix expressions, such as operand operator operand, place the operator in the center of the operands. A postfix expression is one in which the operator, like the operand operator, comes after the operands. Postfix expressions are not understandable by humans but are easily computed by the system.
Q. We convert infix to prefixes for what reason?
A. We are aware that the compiler may find it challenging to interpret an infix expression since it can only begin operations or assignments once it has read the entire expression and is aware of the priority of each operation.
Q. How are brackets handled when converting to postfix notation?
A. When converting parentheses to postfix notation, we can manage them by pushing any opening parenthesis into the stack. When a closing parenthesis is encountered, we pop operators from the stack and add them to the postfix notation up until the opening parenthesis is encountered, which we then discard.
Conclusion
- This article explained how to use stack to convert infix to postfix in several languages.
- We discussed the stack-based infix-to-postfix conversion mechanism.
I hope that this article explains the Infix to prefix conversion and provides a better code solution.