Merge K Sorted Arrays

Problem Statement

k number of arrays are given, the task is to merge all the given integer arrays in such a manner that the resultant array is sorted in the runtime only.

Note: arrays are of equal size.

Example:

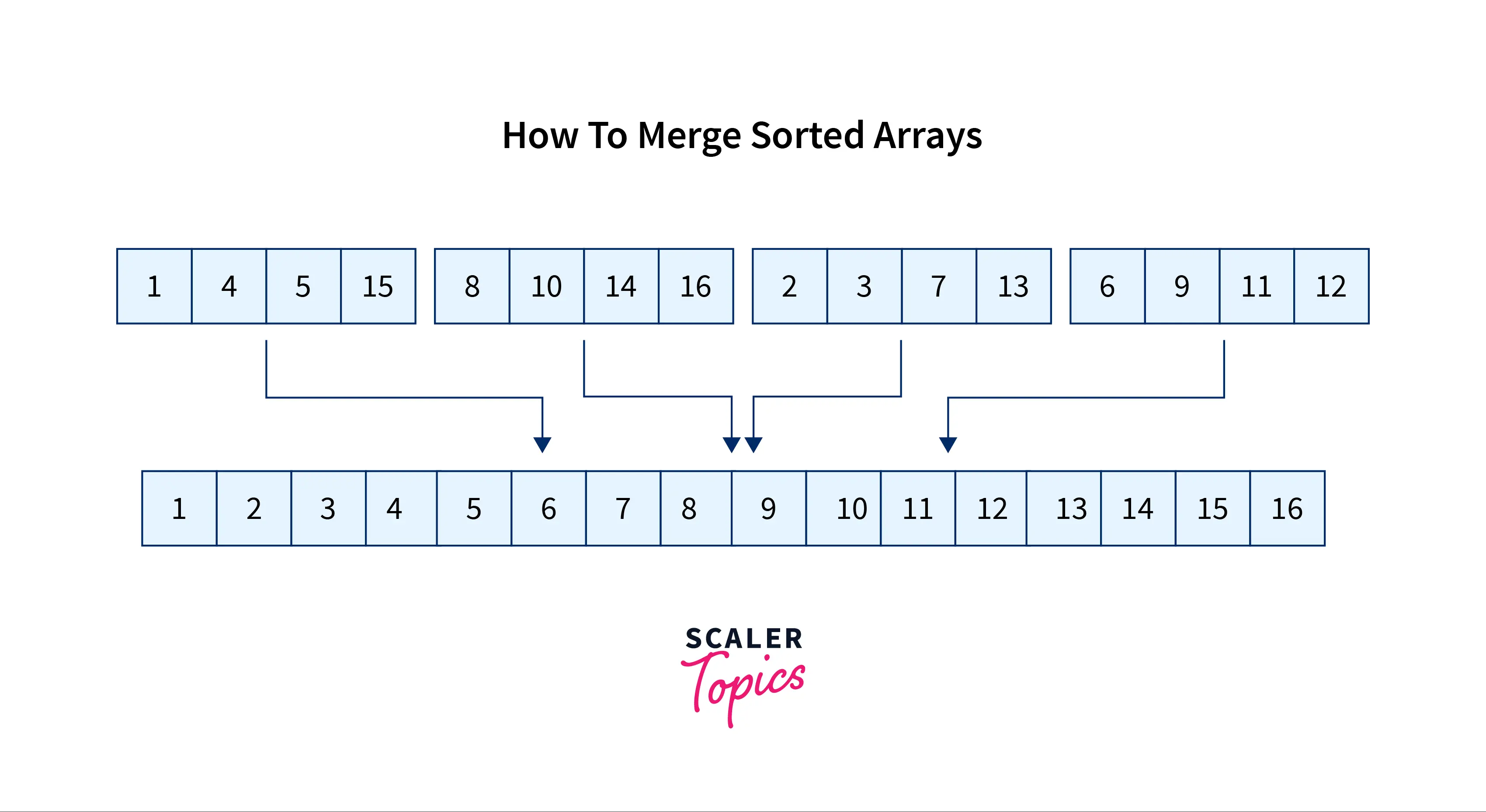
k = 4, n = 4 
arr[][] = { {1, 4, 5, 15}, 
{8, 10, 14, 16}, 
{2, 3, 7, 13}} ,
{6,9,11,12};

Output:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

Explanation

The array at the output is sorted by combining elements of all the three arrays of input.

Constraints

$1 <=n<=10^5$

The Sum of the size of all the arrays will be less than $10^5$

$1<=s[i]<=10^9$

Approach 1 (Naive Approach)

In the naive approach, create an array of size $(k*n)$ and copy elements of the array in another array which is an output array and sort the final output array.

The algorithm of the naive approach is:

1. Create an array for output of size $(k*n)$
2. Traverse the matrix given from start to end and copy or insert all the elements in an output array.
3. Sort the output array and print it.

Code Implementation(in C++, java , python)

C++ program to merge k sorted arrays

#include<bits/stdc++.h>
using namespace std;

// method for printing the array
void ArrayPrint(vector<int>arr){
    for (auto x: arr)
        cout << x << " ";
    cout << endl;
}

// method which is used for merging the elements of k array
void ArrayMerge(vector<vector<int>>arr, vector<int>&outputArr){

    for(auto v: arr)
        for(auto x: v)
            outputArr.push_back(x);

    sort(outputArr.begin(),outputArr.end());
}


int main(){
    // Changing the number of elements in an array
    vector<vector<int>>arr = {vector<int>{2, 6, 12, 34},
                              vector<int>{1, 9, 20, 1000},
                              vector<int>{23, 34, 90, 2000}};
    int n = arr.size();
    int m = arr[0].size();

    vector<int>outputArr;

    ArrayMerge(arr, outputArr);

    cout << "Merged array is " << endl;
    ArrayPrint(outputArr);

    return 0;
}

Java program to merge k sorted arrays

import java.io.*;
import java.util.*;

// class to merge arrays
class Main {
    public static void ArrayMerge(int[][] arr, int a, int[] outputArrr){
        int c = 0;

        // traverse the matrix
        for (int i = 0; i < a; i++) {
            for (int j = 0; j < 4; j++)
                outputArrr[c++] = arr[i][j];
        }

        Arrays.sort(outputArrr);
    }

    // method for printing the array
    public static void printArray(int[] arr, int size){
        for (int i = 0; i < size; i++)
            System.out.print(arr[i] + " ");
    }

    // main method
    public static void main(String[] args){
        int[][] arr = { { 2, 6, 12, 34 },
                        { 1, 9, 20, 1000 },
                        { 23, 34, 90, 2000 } };
        int k = 4;
        int n = 3;
        int[] outputArrr = new int[n * k];
        // calling the function for merging the array
        ArrayMerge(arr, n, outputArrr);

        System.out.println("Merged array: ");
        printArray(outputArrr, n * k);
    }
}

python program for merging the array

#function to merge arrays
def ArrayMerge(arr, a, outputArr):
    c = 0;
# iterating through the array and merging the elements
    for i in range(a):
        for j in range(4):
            outputArr[c] = arr[i][j];
            c += 1;

    outputArr.sort();

def ArrayPrint(arr, size):
    for i in range(size):
        print(arr[i], end = " ");

if __name__ == '__main__':
    arr = [[ 2, 6, 12, 34],[ 1, 9, 20, 1000 ],[ 23, 34, 90, 2000 ]] ;
    k = 4;
    n = 3;
    outputArr = [0 for i in range(n * k)]
    # calling the function for merging the array
    ArrayMerge(arr, n, outputArr);

    print("Merged array is ");
    ArrayPrint(outputArr, n * k);

Output

Merged array is 
1 2 6 9 12 20 23 34 34 90 1000 2000

Time Complexity
O(k*n*log(k*n))
Because the resulting array is of N*k size.

Space Complexity
O(k*n), The output array is of size nk.

Approach 2 (Efficient Approach )

Algorithm

1. Create a function that is recursive, takes the k array, and returns the output array.
2. If the value of k in the recursive function is 1 then return the array else if the value of k is 2 then, merge the array in linear time.
3. If the value of k > 2, then divide the group of k elements in an array in two equal parts and call the function recursively. This means 0 to k/2 in the first recursive function and k/2 to k in the other recursive function.
4. Print the output array

Example:

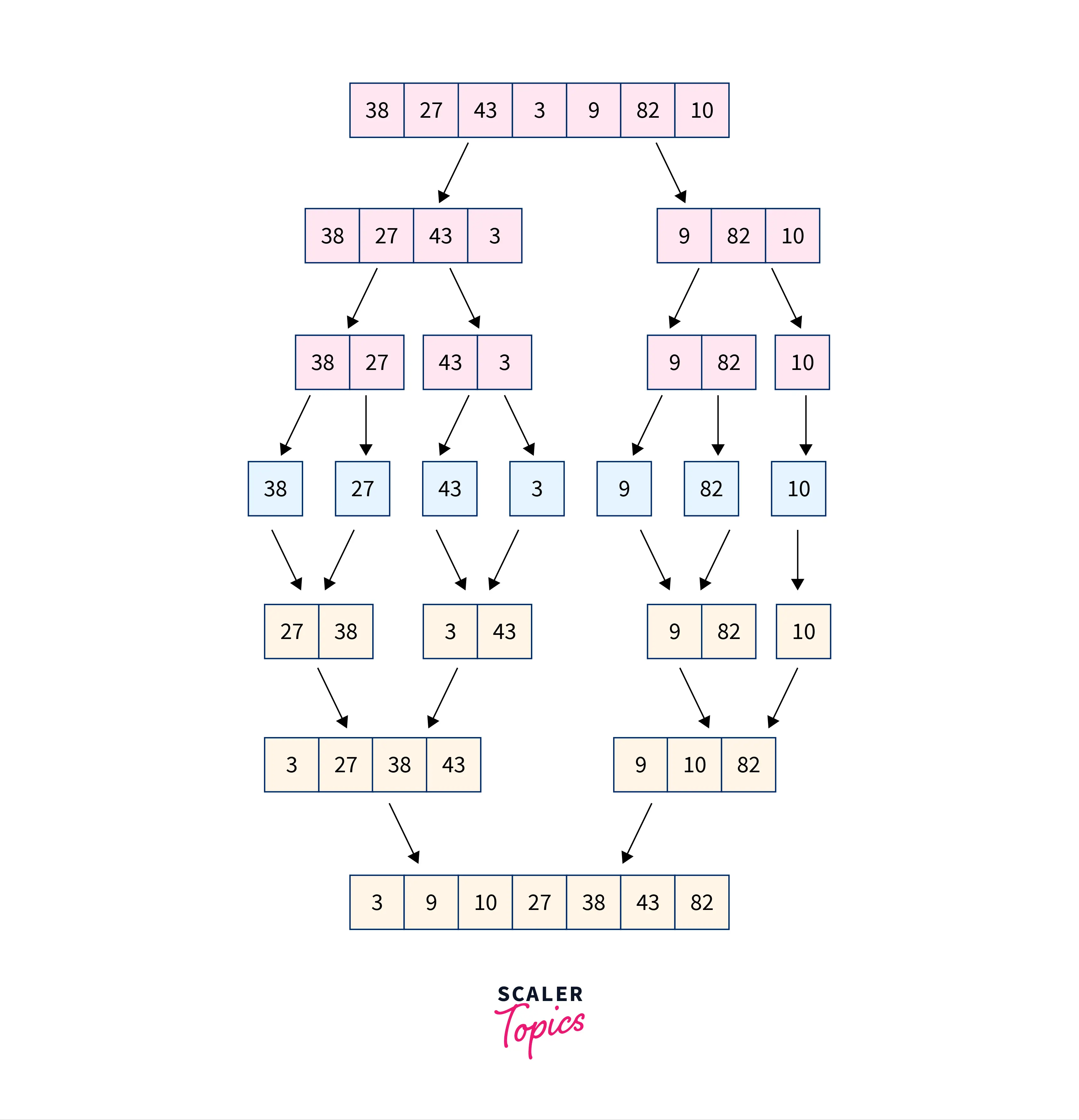
Code Implementation(in C++, java , python)

C++ program to merge k sorted arrays of size n each

#include<bits/stdc++.h>
using namespace std;
#define n 4

// method for merging the array
void ArrayMerge(int arr1[], int arr2[], int n1,
                            int n2, int arr3[])
{
    int i = 0, j = 0, k = 0;

    while (i<n1 && j <n2)
    {
        // Check if current element of first
        // array is smaller than current element
        // of second array. If yes, store first
        // array element and increment first array
        // index. Otherwise do same with second array
        if (arr1[i] < arr2[j])
            arr3[k++] = arr1[i++];
        else
            arr3[k++] = arr2[j++];
    }
    // if i < n1 then putting the element of first array
    while (i < n1)
        arr3[k++] = arr1[i++];

// if j < n2 then putting the element of second array
    while (j < n2)
        arr3[k++] = arr2[j++];
}

// method for printing the array
void ArrayPrint(int arr[], int size)
{
for (int i=0; i < size; i++)
    cout << arr[i] << " ";
}

// method for merging the array
void mergeKArrays(int arr[][n],int i,int j, int outputArr[])
{
// if i and j, both are equal then put the element in output array
    if(i==j)
    {
        for(int p=0; p < n; p++)
        outputArr[p]=arr[i][p];
        return;
    }

    //merge the array
    if(j-i==1)
    {
        ArrayMerge(arr[i],arr[j],n,n,outputArr);
        return;
    }

    int out1[n*(((i+j)/2)-i+1)],out2[n*(j-((i+j)/2))];

    //divide the array into halves
    mergeKArrays(arr,i,(i+j)/2,out1);
    mergeKArrays(arr,(i+j)/2+1,j,out2);

    //merge the outputArr array
    ArrayMerge(out1,out2,n*(((i+j)/2)-i+1),n*(j-((i+j)/2)),outputArr);

}


int main()
{

    int arr[][n] = {{2, 6, 12, 34},
                    {1, 9, 20, 1000},
                    {23, 34, 90, 2000}};
    int k = sizeof(arr)/sizeof(arr[0]);
    int outputArr[n*k];
    mergeKArrays(arr,0,2, outputArr);

    cout << "Merged array is " << endl;
    ArrayPrint(outputArr, n*k);

    return 0;
}

Java program to merge k sorted arrays of size n each.

import java.util.*;

class Main{
    static final int n = 4;

    static void mergeArrays(int arr1[], int arr2[], int n1,
                            int n2, int arr3[])
    {
        int i = 0, j = 0, k = 0;

        while (i<n1 && j <n2)
        {
        // Check if current element of first
        // array is smaller than current element
        // of second array. If yes, store first
        // array element and increment first array
        // index. Otherwise do same with second array
        if (arr1[i] < arr2[j])
            arr3[k++] = arr1[i++];
        else
            arr3[k++] = arr2[j++];
        }

        while (i < n1)
        arr3[k++] = arr1[i++];

        while (j < n2)
        arr3[k++] = arr2[j++];
    }

    static void printArray(int arr[], int size)
    {
        for (int i = 0; i < size; i++)
        System.out.print(arr[i]+ " ");
    }


    static void ArrayMerge(int arr[][], int i, int j, int outputArr[])
    {
        if(i == j)
        {
        for(int p = 0; p < n; p++)
            outputArr[p] = arr[i][p];
        return;
        }


        if(j - i == 1)
        {
        mergeArrays(arr[i], arr[j], n, n, outputArr);
        return;
        }


        int []outputn1 = new int[n*(((i + j) / 2) - i + 1)];
        int []outputn2 = new int[n*(j - ((i + j) / 2))];

        //dividing the array into two halves
        ArrayMerge(arr, i, (i + j) / 2, outputn1);
        ArrayMerge(arr, (i + j) / 2 + 1, j, outputn2);

        // merging the outputArr array
        mergeArrays(outputn1, outputn2, n * (((i + j) / 2) - i + 1), n * (j - ((i + j) / 2)), outputArr);
    }



    public static void main(String[] args)
    {

        // Change n at the top to change number of elements
        // in an array
        int arr[][] = {{2, 6, 12, 34},
                        {1, 9, 20, 1000},
                        {23, 34, 90, 2000}};
        int k = arr.length;
        int []outputArr = new int[n*k];
        ArrayMerge(arr,0,2, outputArr);

        System.out.print("Merged array is " +"\n");
        printArray(outputArr, n*k);
    }
}

Python program to merge k sorted arraysof size n each.

n = 4
# function to merge both the arrays
def ArrayMerge(arrayay1, arrayay2, n1, n2, arrayay3):

    i, j, k = 0, 0, 0

    # Traversing  both the arrayay
    while (i < n1 and j < n2):

        # Check if current element of first
        # arrayay is smaller than current element
        # of second arrayay. If yes, store first
        # arrayay element and increment first arrayay
        # index. Otherwise do same with second arrayay
        if (arrayay1[i] < arrayay2[j]):
            arrayay3[k] = arrayay1[i]
            k += 1
            i += 1
        else:
            arrayay3[k] = arrayay2[j]
            k += 1
            j += 1

    # Store remaining elements of first arrayay
    while (i < n1):
        arrayay3[k] = arrayay1[i]
        k += 1
        i += 1

    # Store remaining elements of second arrayay
    while (j < n2):
        arrayay3[k] = arrayay2[j]
        k += 1
        j += 1

# function to print arrayay elements
def ArrayPrint(array, size):

    for i in range(size):
        print(array[i],end = " ")

# This function takes an arrayay of arrayays
# as an argument and all arrays are assumed
# to be sorted. It merges them together
# and prints the final sorted output.
def mergeKArrays(array, i, j, output):

    global n

    if (i == j):
        for p in range(n):
            output[p] = array[i][p]

        return

    if (j - i == 1):
        ArrayMerge(array[i], array[j],
                    n, n, output)
        return


    out1 = [0 for i in range(n * (((i + j) // 2) - i + 1))]
    out2 = [0 for i in range(n * (j - ((i + j) // 2)))]

    # Divide the arrayay into halves
    mergeKArrays(array, i, (i + j) // 2, out1)
    mergeKArrays(array, (i + j) // 2 + 1, j, out2)

    # Merge the output arrayay
    ArrayMerge(out1, out2,
                n * (((i + j) / 2) - i + 1),
                n * (j - ((i + j) / 2)), output)

array = [ [ 2, 6, 12, 34 ],
            [ 1, 9, 20, 1000 ],
            [ 23, 34, 90, 2000 ] ]
k = len(array)
output = [0 for i in range(n * k)]

mergeKArrays(array, 0, 2, output)

print("Merged arrayay is ")
ArrayPrint(output, n * k)

Output

Merged array is 
1 2 6 9 12 20 23 34 34 90 1000 2000

Time Complexity

$O( n * k * log k)$
Because there are log(k) levels at each recursive level which are divided into two halves at each k level.

Space Complexity

$O( n * k * log k)$
Each level requires O(n * k) space for storing elements in an array.

Approach 3 (Using min-heap)

Algorithm

• Create a min-heap and insert into it all the first elements of all the k number of arrays.
• Iterate through the loop until the length becomes 0
• Remove the element from the top of the min-heap and add it to output array
• Insert the next element in the same array until there are no more elements left.

Example:

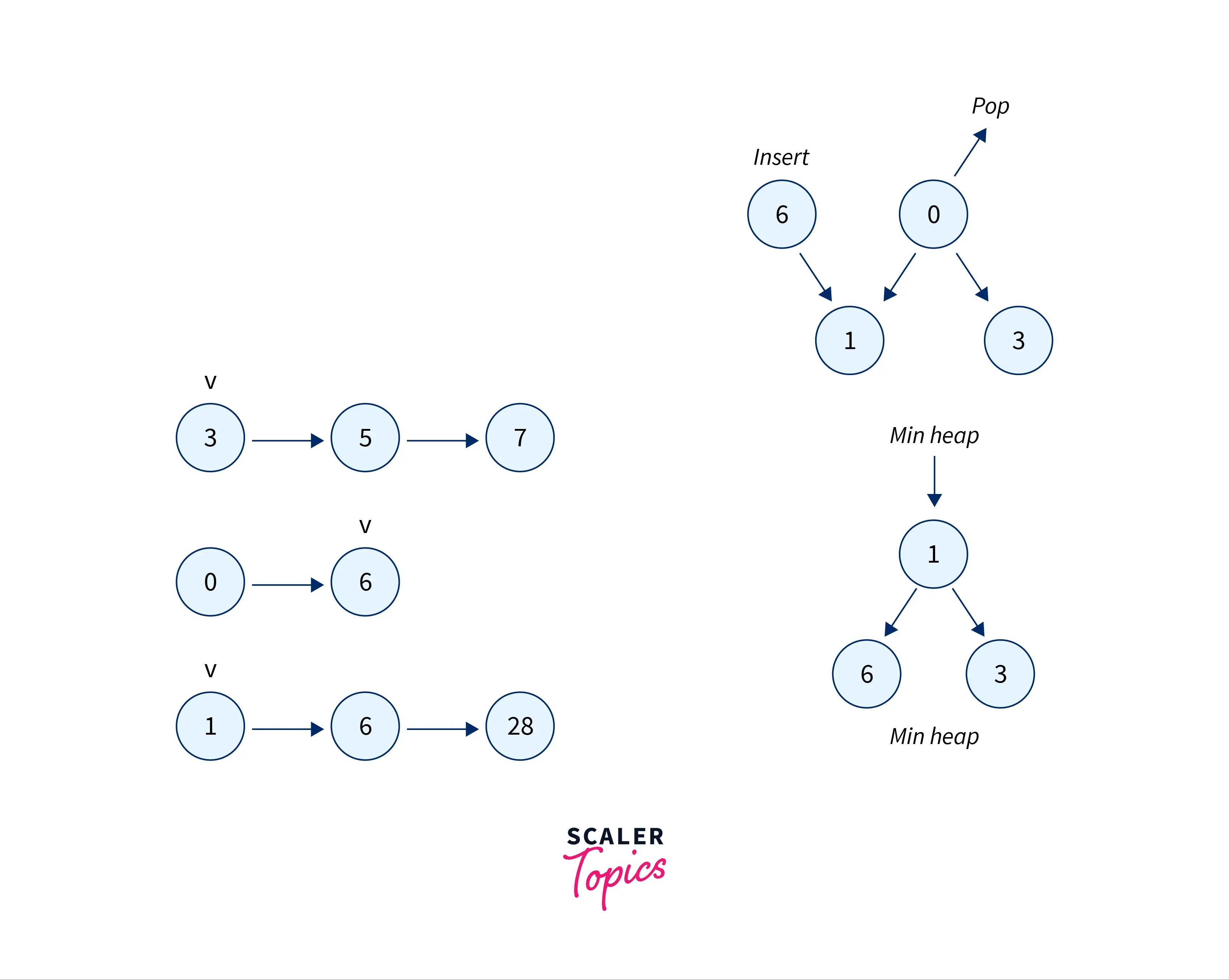
Code Implementation(in C++, java , python)

// C++ program to merge k sorted array

#include<bits/stdc++.h>
using namespace std;

#define n 4

// A min-heap node
struct MinHeapNode
{
// The element to be stored
    int element;

// index of the array from which the element is taken
    int i;

// index of the next element to be picked from the array
    int j;
};

// Prototype of a utility function to swap two min-heap nodes
void swap(MinHeapNode *x, MinHeapNode *y);

// A class for Min Heap
class MinHeap
{

// pointer to array of elements in heap
    MinHeapNode *harr;

// size of min heap
    int heap_size;
public:
    // Constructor: creates a min heap of given size
    MinHeap(MinHeapNode a[], int size);

    // to heapify a subtree with root at given index
    void MinHeapify(int );

    // to get index of left child of node at index i
    int left(int i) { return (2*i + 1); }

    // to get index of right child of node at index i
    int right(int i) { return (2*i + 2); }

    // to get the root
    MinHeapNode getMin() { return harr[0]; }

    // to replace root with new node x and heapify() new root
    void replaceMin(MinHeapNode x) { harr[0] = x; MinHeapify(0); }
};

// This function takes an array of arrays as an argument and
// All arrays are assumed to be sorted. It merges them together
// and prints the final sorted output.
int *mergeKArrays(int arr[][n], int k)
{

// To store output array
    int *output = new int[n*k];

    // Create a min heap with k heap nodes.
    // Every heap node has first element of an array
    MinHeapNode *harr = new MinHeapNode[k];
    for (int i = 0; i < k; i++)
    {

// Store the first element
        harr[i].element = arr[i][0];

// index of array
        harr[i].i = i;

// Index of next element to be stored from the array
        harr[i].j = 1;
    }

// Create the heap
    MinHeap hp(harr, k);

    // iterate through heap and get min element
    for (int count = 0; count < n*k; count++)
    {
        // Get the minimum element and store it in output
        MinHeapNode root = hp.getMin();
        output[count] = root.element;

        // Find the next element that will replace current
        // root of heap. 
        if (root.j < n)
        {
            root.element = arr[root.i][root.j];
            root.j += 1;
        }
        // If root was the last element of its array, INT_MAX is for infinite       
else root.element = INT_MAX;

        // Replace root with next element of array
        hp.replaceMin(root);
    }

    return output;
}

MinHeap::MinHeap(MinHeapNode a[], int size)
{
    heap_size = size;
    harr = a; // store address of array
    int i = (heap_size - 1)/2;
    while (i >= 0)
    {
        MinHeapify(i);
        i--;
    }
}

// A recursive method to heapify a
// subtree with a root at the given index.
// This method assumes that the subtrees
// are already heapified
void MinHeap::MinHeapify(int i)
{
    int l = left(i);
    int r = right(i);
    int smallest = i;
    if (l < heap_size && harr[l].element < harr[i].element)
        smallest = l;
    if (r < heap_size && harr[r].element < harr[smallest].element)
        smallest = r;
    if (smallest != i)
    {
        swap(&harr[i], &harr[smallest]);
        MinHeapify(smallest);
    }
}

// function to swap two elements
void swap(MinHeapNode *x, MinHeapNode *y)
{
    MinHeapNode temp = *x; *x = *y; *y = temp;
}


void printArray(int arr[], int size)
{
for (int i=0; i < size; i++)
    cout << arr[i] << " ";
}

int main()
{
        int arr[][n] = {{2, 6, 12, 34},
                    {1, 9, 20, 1000},
                    {23, 34, 90, 2000}};
    int k = sizeof(arr)/sizeof(arr[0]);

    int *output = mergeKArrays(arr, k);

    cout << "Merged array is " << endl;
    printArray(output, n*k);

    return 0;
}

Java program to merge k sorted array

// min heap node class
class MinHeapNode
{
    int element; // element to be stored    
    int i;  // index

    // index of the next element

    int j;
// min heap node method
    public MinHeapNode(int element, int i, int j)
    {
        this.element = element;
        this.i = i;
        this.j = j;
    }
};


class MinHeap{
    MinHeapNode[] harr; // Array of elements in heap
    int heap_size; 

    // this method builds heap from given array
    public MinHeap(MinHeapNode a[], int size){
        heap_size = size;
        harr = a;
        int i = (heap_size - 1)/2;
        while (i >= 0)
        {
            MinHeapify(i);
            i--;
        }
    }

    // A recursive method to heapify a subtree
    // with the root at the given index This method
    // assumes that the subtrees are already heapified
    void MinHeapify(int i){
        int l = left(i);
        int r = right(i);
        int smallest = i;
        if (l < heap_size && harr[l].element < harr[i].element)
            smallest = l;
        if (r < heap_size && harr[r].element < harr[smallest].element)
            smallest = r;
        if (smallest != i)
        {
            swap(harr, i, smallest);
            MinHeapify(smallest);
        }
    }

    // to get index of left child of node at index i
    int left(int i) { return (2*i + 1); }

    // to get index of right child of node at index i
    int right(int i) { return (2*i + 2); }

    // to get the root
    MinHeapNode getMin(){
        if(heap_size <= 0){
            System.out.println("Heap underflow");
            return null;
        }
        return harr[0];
    }

    // to replace root with new node
    // "root" and heapify() new root
    void replaceMin(MinHeapNode root) {
        harr[0] = root;
        MinHeapify(0);
    }

    // A utility function to swap two min heap nodes
    void swap(MinHeapNode[] arr, int i, int j) {
        MinHeapNode temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
};

class Main{
    // A utility function to print array elements
    static void printArray(int[] arr) {
        for(int i : arr)
            System.out.print(i + " ");
        System.out.println();
    }

    // This function takes an array of
    // arrays as an argument and All
    // arrays are assumed to be sorted.
    // It merges them together and
    // prints the final sorted output.
    static void mergeKSortedArrays(int[][] arr, int k)
    {
        MinHeapNode[] hArr = new MinHeapNode[k];
        int resultSize = 0;
        for(int i = 0; i < arr.length; i++)
        {
            MinHeapNode node = new MinHeapNode(arr[i][0],i,1);
            hArr[i] = node;
            resultSize += arr[i].length;
        }

        // Create a min heap with k heap nodes. Every heap node
        // has first element of an array
        MinHeap mh = new MinHeap(hArr, k);

        int[] result = new int[resultSize];  // To store output array

        // Now one by one get the minimum element from min
        // heap and replace it with next element of its array
        for(int i = 0; i < resultSize; i++)
        {

            // Get the minimum element and store it in result
            MinHeapNode root = mh.getMin();
            result[i] = root.element;

            // Find the next element that will replace current
            // root of heap. The next element belongs to same
            // array as the current root.
            if(root.j < arr[root.i].length)
                root.element = arr[root.i][root.j++];
            // If root was the last element of its array
            else
                root.element = Integer.MAX_VALUE;

            // Replace root with next element of array
            mh.replaceMin(root);
        }

        printArray(result);
    }
    public static void main(String args[]){
        int[][] arr= {{2, 6, 12, 34},
                {1, 9, 20, 1000},
                {23, 34, 90, 2000}};

        System.out.println("Merged array :");

        mergeKSortedArrays(arr,arr.length);
    }
};

Python program to merge k sorted array

#function to merge k sorted arrays
def merge(lists):

   final_list = []    #output array


   heap = [(mylst[0], i, 0) for i, mylst in enumerate(lists) if mylst]

   heapq.heapify(heap)
# iterating through the heap and merging the elements
   while heap:
       val, list_ind, element_ind = heapq.heappop(heap)
       final_list.append(val)
       if element_ind + 1 < len(lists[list_ind]):
           next_tuple = (lists[list_ind][element_ind + 1],
                         list_ind, element_ind + 1)
           heapq.heappush(heap, next_tuple)

   return final_list

Output

Merged array is 
1 2 6 9 12 20 23 34 34 90 1000 2000

Time Complexity

$O( n * k * log k)$ because insertion and deletion of element in min heap requires log k time.

Space Complexity

$O(k)$ space required by min-heap.

Merge k Sorted Arrays | Set 2 (Different Sized Arrays)

Approach

We would use a min-heap that would return the smallest element in constant time O(1) instead of searching through all k elements.

Example:

Input:

k = 3 
arr[][] = { {1, 3},
            {2, 4, 6},
            {0, 9, 10, 11}};

Output:

0 1 2 3 4 6 9 10 11 

Algorithm

1. Create an array for storing the output
2. Create a min heap of k size and insert the first element of heap in all the array
3. Till the priority queue is not empty,, repeat the below steps:
   • Remove min element from the heap and store it in the output array
   • Insert the next element of array and do it until the array is empty

Code Implementation(in C++, java , python)

C++ program to merge k sorted arrays of n size

#include <bits/stdc++.h>
using namespace std;


typedef pair<int, pair<int, int> > ppi;


vector<int> mergeKArrays(vector<vector<int> > arr)
{
    vector<int> output;

    // priority queue to store the vector pair 
    priority_queue<ppi, vector<ppi>, greater<ppi> > pq;

    for (int i = 0; i < arr.size(); i++)
        pq.push({ arr[i][0], { i, 0 } });

    while (pq.empty() == false) {
        ppi curr = pq.top();
        pq.pop();

        // i ==> Array Number
        // j ==> Index of array number
        int i = curr.second.first;
        int j = curr.second.second;

        output.push_back(curr.first);

        // checking if the next element belongs to same array as the current array.
        if (j + 1 < arr[i].size())
            pq.push({ arr[i][j + 1], { i, j + 1 } });
    }

    return output;
}

int main()
{

    vector<vector<int> > arr{ { 2, 6, 12 },
                            { 1, 9 },
                            { 23, 34, 90, 2000 } };

    vector<int> output = mergeKArrays(arr);

    cout << "Merged array is " << endl;
    for (auto x : output)
        cout << x << " ";

    return 0;
}

Java program to merge k sorted arrays of n size

import java.util.ArrayList;
import java.util.PriorityQueue;

public class Main {
    private static class HeapNode
        implements Comparable<HeapNode> {
        int x;
        int y;
        int value;
        // method of heap node
        HeapNode(int x, int y, int value)
        {
            this.x = x;
            this.y = y;
            this.value = value;
        }

        @Override public int compareTo(HeapNode hn)
        {
            if (this.value <= hn.value) {
                return -1;
            }
            else {
                return 1;
            }
        }
    }
    // merging of array function
    public static ArrayList<Integer>
    mergeKArrays(int[][] arr, int K)
    {
        ArrayList<Integer> result
            = new ArrayList<Integer>();
        PriorityQueue<HeapNode> heap
            = new PriorityQueue<HeapNode>();

        // iterating through the array and adding it to the heap

        for (int i = 0; i < arr.length; i++) {
            heap.add(new HeapNode(i, 0, arr[i][0]));
        }

        HeapNode curr = null;
        while (!heap.isEmpty()) {
            curr = heap.poll();
            result.add(curr.value);

            // Check if next element of curr min exists, if yes the add it to the heap
            if (curr.y < (arr[curr.x].length - 1)) {
                heap.add(
                    new HeapNode(curr.x, curr.y + 1,
                                arr[curr.x][curr.y + 1]));
            }
        }

        return result;
    }

    public static void main(String[] args){

        int[][] arr = { { 2, 6, 12 },
                            { 1, 9 },
                            { 23, 34, 90, 2000 } };
        System.out.println(Main.mergeKArrays(arr, arr.length).toString());
    }
}

Python program to merge k sorted arrays of n size

from heapq import merge

# function for meging k arrays
def mergeK(arr, k):

    l = arr[0]
    for i in range(k-1):

        # when k = 0 it merge arr[1] with arr[0] 

        l = list(merge(l, arr[i + 1]))
    return l


def printArray(arr):
    print(*arr)


# main
arr =[[2, 6, 12 ],
    [ 1, 9 ],
    [23, 34, 90, 2000 ]]
k = 3

l = mergeK(arr, k)

printArray(l)

Output

Merged array is 
1 2 6 9 12 23 34 90 2000

Time Complexity

O(N Log k) because it is heap-based.

Space Complexity

O(N) because of output array.

Conclusion

• Approach 1 (Naive Approach)- create an array of size k*n and copy elements of the array in another array which is an output array and sort the output array.
  • Time Complexity :O(k*n*log(k*n))
  • Space Complexity: O(k*n)
• Approach 2 (Efficient Approach)- Create a function that is recursive, takes the k array, and returns the output array.
  • Time Complexity- O( n * k * log k)
  • Space Complexity- O( n * k * log k)
• Approach 3 (Using min-heap)- Create a min-heap and insert into it all the first elements of all the k number of arrays. Iterate and remove the element from the top of the min-heap.
  • Time Complexity- O( n * k * log k)
  • Space Complexity- O(k)
• Merge k sorted arrays | Set 2 (Different Sized Arrays)- The approach for this is to use heap data structure along with the priority queue.
  • Time Complexity- O(N Log k)
  • Space Complexity- O(N)