Strassen’s Matrix Multiplication

Problem Statment

Consider two matrices X and Y each of the size N*N. We want to calculate the resultant matrix Z which is formed by multiplying the given two matrices i.e, X and Y.

Example

Let’s consider the below matrices for multiplication. Matrix A has a size N*M and matrix B has a size A*B. Given two matrices are multiplied only when the number of columns in the first matrix is equal to the number of rows in the second matrix. Therefore, we can say that matrix multiplication is possible only when M==A.
The given two matrices are:
Matrix A of the size: 3 × 3

Below image clearly how matrices are multiplied:

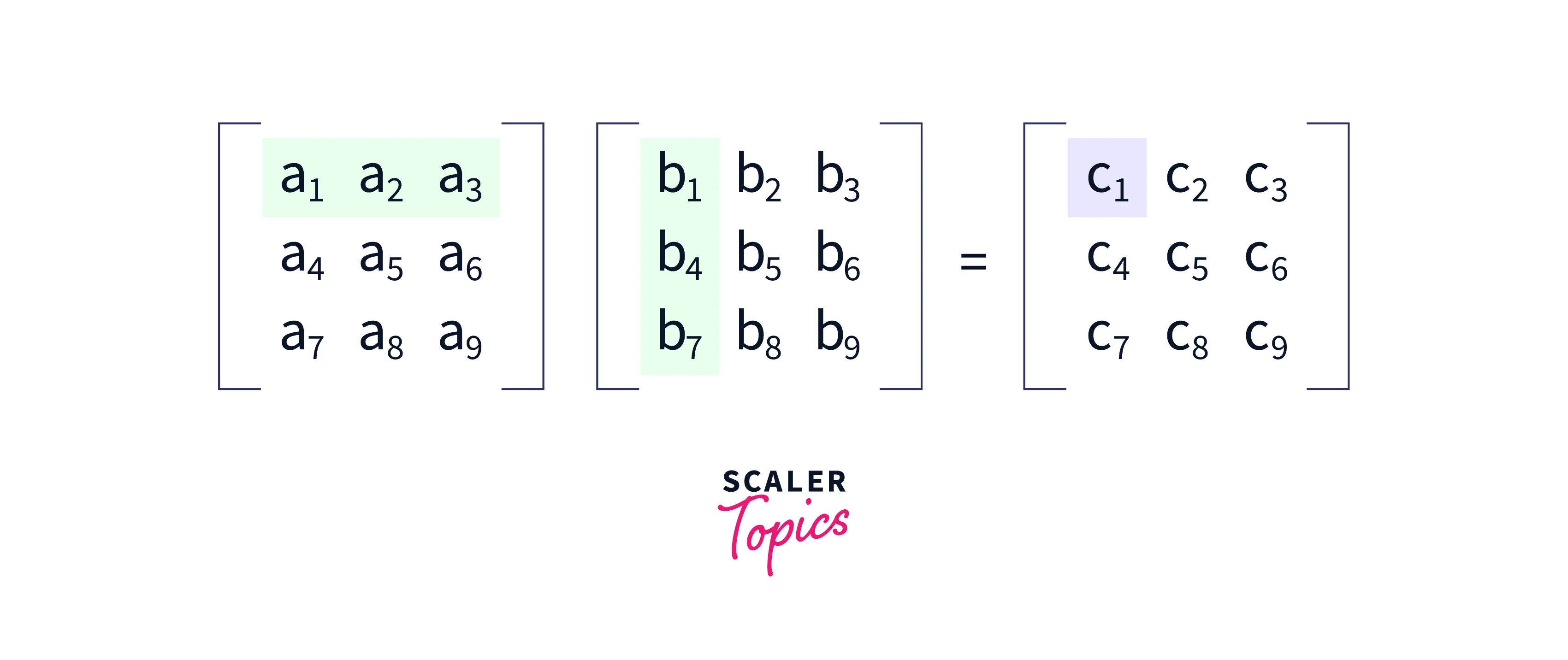
Therefore, the matrix multiplication of given matrices A and B is:

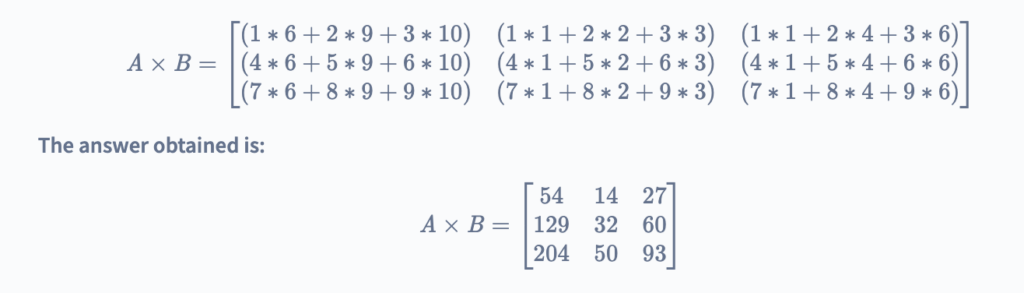
Approach 1: Naive Method

As we have observed in the previous example discussed that the row values are multiplied with each column value and are added to the present value at that cell. By following the below algorithm, a naive method we can obtain the matrix multiplication of given two matrices.

Algorithm: Below is the algorithm for Matrix Multiplication using a naive method:

• Firstly, the number of rows in the second matrix should be the same as the number of columns in the first matrix.
• The size of matrix 1 is N × M and the size of the second matrix is M × P .
• Now, initialize the resultant matrix of size as the number of rows of the first matrix and the number of columns as the second matrix. Therefore the size of the resultant matrix is considered to be as N × P.
• For obtaining the values in the resultant matrix three nested loops are used:
  • First nested loop represents the row number in the matrix. This loop starts at 0 and ends at N.
  • Second nested loop represents the column number in the matrix. This loop starts at 0 and ends at M.
  • And the last nested loop is used for adding the values when each row element is multiplied with all elements in the column respectively.
• Finally, matrix multiplication is done and the values are stored in the resultant matrix.

Implementation

Below is the implementation of this naive approach for matrix multiplication in C++, Python, and Java.

C++ Implementation of Multiplication of Matrices Using the Naive Method:

#include <iostream>
using namespace std;

// sizes of the matrix 1 and matrix 2
#define Row_1 3            
#define Col_1 3        
#define Row_2 3            
#define Col_2 2            

// This function is used for matrix multiplication of given two matrices
void MatMultiplication(int Mat_A[][Col_1], int Mat_B[][Col_2]) {
    // Result matrix should be of size Row_1 and Col_2
    int result[Row_1][Col_2];
    // first loop represents the row in resultant matrix
    for (int i = 0; i < Row_1; i++) {
         // second loop represents the col in resultant matrix
        for (int j = 0; j < Col_2; j++) {
            //initialize the values in result matrix as zero first
            result[i][j] = 0;
            // for adding the values obtained by multipliyng one row and one col particularly
            for (int k = 0; k < Row_2; k++) {
                result[i][j] += Mat_A[i][k] * Mat_B[k][j];
            }
            cout <<result[i][j]<< "  ";
        }
        cout << endl;
    }
}
// Driver program
int main(void) {

    // First matrix Mat_A 
    int Mat_A[Row_1][Col_1] ={ { 1, 2, 3 }, { 4, 5, 6}, { 7, 8, 9 }};
    
    // Second matrix MAt_B given for matrix multiplication
    int Mat_B[Row_2][Col_2] = { { 6, 1, 1}, { 9, 2, 4 }, {10, 3, 6}};
    
    // first condition to be satisfied is col_1==row_2
    if (Col_1 != Row_2) {
        cout << "Matrix Multiplication not possible" << endl;
    }
    // if the first condition is satisfied 
    // Call matrix multiplication function
    MatMultiplication(Mat_A, Mat_B);
    return 0;
}
    

Output:

    54   14   27
    129  32   60
    204  50   93

Python Implementation of Multiplication of Matrices Using the Naive Method:

# Python program for matrix multiplication of given two matrices.
def MatMultiplication(Mat_A, Mat_B, Row_1, Row_2, Col_1, Col_2):
    # matrix result to be stored in mat of size 3 rows and 2 col.
    result = [[0, 0] for i in range(Col_2+1)]
    
    # first loop represents the row
    for i in range(0, Row_1):
        # second loop represents the col
        for j in range(0, Col_2):
            # third loop is used for adding the each value and store it in result matrix
            for k in range(0, Row_2):
                result[i][j] += Mat_A[i][k] * Mat_B[k][j]
    # For printing the result of the matrix obtained
    for row in range(0, Row_1):
        for col in range(0, Col_2):
            print(result[row][col], end=" ")
        print("\n", end="")

# Driver Code
# size of matrix 1 and matrix 2
Row_1 = 3
Col_1 = 3
Row_2 = 3
Col_2 = 2
 
# First matrix Mat_A 
Mat_A = [[1, 2, 3], [4, 5, 6 ], [7, 8, 9]]
 
# Second matrix Mat_b for matrix multiplication
Mat_B = [[6, 1 ], [9, 2 ], [10, 3 ]]

# first condition to be satisfied is col_1==row_2
if Col_1 != Row_2:
    print("Matrix Multiplication not possible", end='')
# first condition is satisfied col_1==row_2
else:
    # Call matrix multiplication function
    MatMultiplication(Mat_A, Mat_B, Row_1, Row_2, Col_1, Col_2)
 

Output:

    54   14   27
    129  32   60
    204  50   93

Java Implementation of Multiplication of Matrices Using the Naive Method:

import java.io.*;
import java.util.*;
 
class Solution{
    // This function is used for matrix multiplication of given two matrices
    static void MatMultiplication(int[][] Mat_A, int[][] Mat_B, int Row_1, int Row_2, int Col_1, int Col_2){
        // Result matrix should be of size Row_1 and Col_2
        int[][] result = new int[Row_1][Col_2];
        int i, j, k;
        // first loop represents the row in resultant matrix
        for (i = 0; i < Row_1; i++) {
            // second loop represents the col in resultant matrix
            for (j = 0; j < Col_2; j++) {
                //initialize the values in the result matrix as zero first
                result[i][j] = 0;
                // for adding the values obtained by multipliyng one row and one col particularly
                for (k = 0; k < Row_2; k++)
                    result[i][j] += Mat_A[i][k] * Mat_B[k][j];
                System.out.print(result[i][j] + " ");
            }
            System.out.println("");
        }
    }
     
    // Driver program
    public static void main (String[] args) {
        // sizes of the matrix 1 and matrix 2
        int Row_1 = 3; 
        int Col_1 = 3; 
        int Row_2 = 3; 
        int Col_2 = 2; 
        
         // First matrix Mat_A 
        int[][] Mat_A = { { 1, 2, 3 }, { 4, 5, 6}, { 7, 8, 9 }};
  
        // Second matrix MAt_B given for matrix multiplication
        int[][] Mat_B = { { 6, 1}, { 9, 2 }, {10, 3}};
        // first condition to be satisfied is col_1==row_2
        if (Row_2 != Col_1){
            System.out.println("Matrix Multiplication not possible");
        }
        // if the first condition is satisfied col_1==row_2
        else {
            // Call matrix multiplication function
            MatMultiplication(Mat_A, Mat_B, Row_1, Row_2, Col_1, Col_2);
        }
    }
}

Output:

    54   14   27
    129  32   60
    204  50   93

Explanation:

The given two matrices are multiplied and the result has been printed as the output.

Complexity Analysis

Time Complexity: O(N^3), where the given matrices are square matrices of size N*N each.

• For multiplying every column with every element in the row from the given matrices uses two loops, and adding up the values takes another loop. Therefore the overall time complexity turns out to be O(N^3^).

Space Complexity: O(N^2), where the given matrices are square matrices of size N*N each.

• The matrix of size N*N has been used to store the result when the two matrices are multiplied.

Approach 2: Using Strassen’s Matrix Multiplication

• To optimize the matrix multiplication Strassen’s matrix multiplication algorithm can be used. It reduces the time complexity for matrix multiplication. Strassen’s Matrix multiplication can be performed only on square matrices where N is a power of 2. And also the order of both of the matrices is N × N.
• The main idea is to use the divide and conquer technique in this algorithm. We need to divide matrix A and matrix B into 8 submatrices and then recursively compute the submatrices of the result.
• In the above approach we are doing $N^3$ multiplications and $N^2$ additions are performed. Therefore the overall time complexity is $O(N^3)$. We need to divide the given A and B matrices each of order $N_2 × N_2$.
• This can be clearly explained in the below image:
  

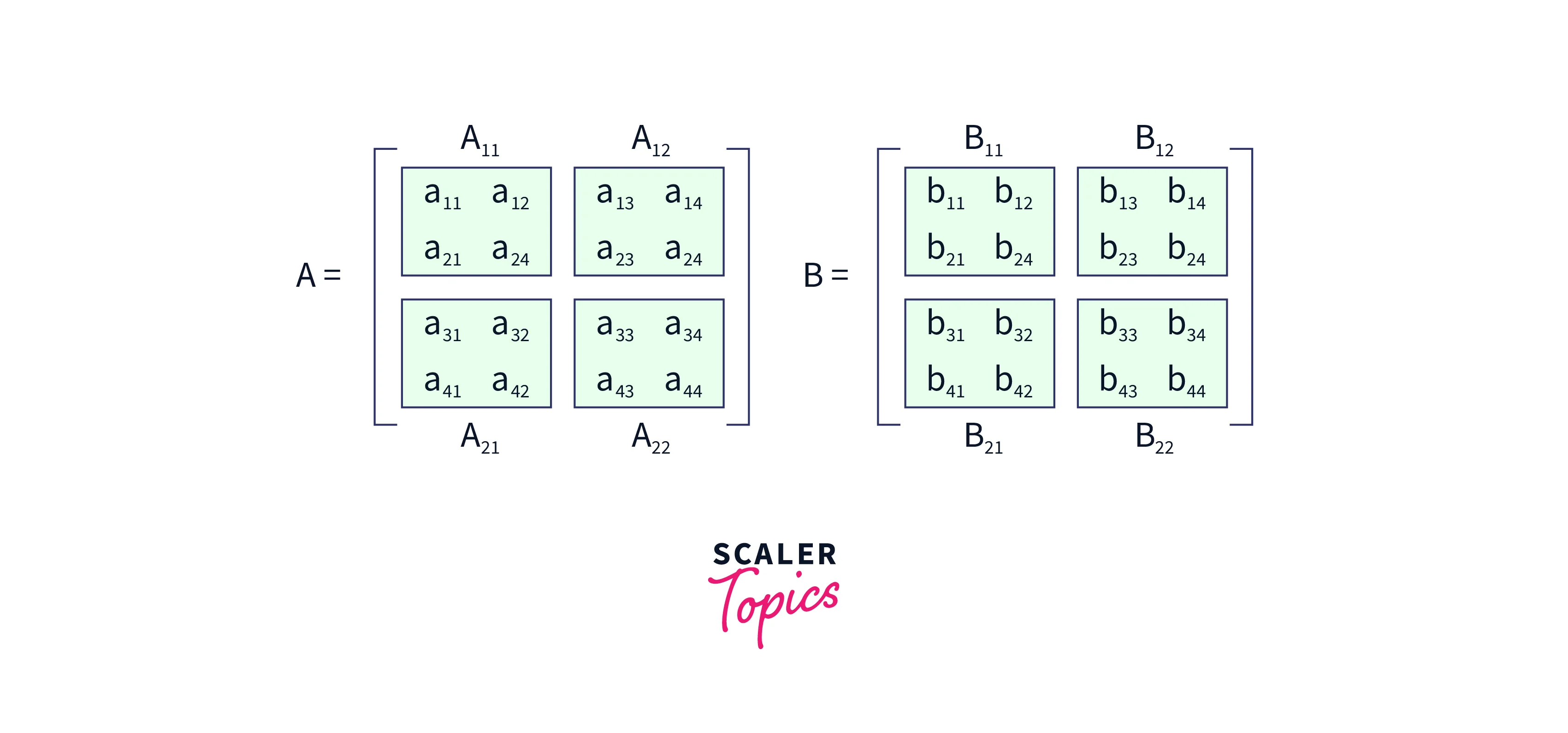
• For each multiplication of size $N_2 × N_2$, follow the below recursive function as shown in the figure:
  

• Where the resultant matrix is C and can be obtained in the following way.
  Now we need to store the result as follows:
• $C_{11}= A_{11} *B_{11} + A_{12} *B_{21}$
• $C_{12}= A_{11} *B_{12} + A_{12} *B_{22}$
• $C_{21}= A_{21} *B_{11} + A_{22} *B_{21}$
• $C_{22}= A_{21} *B_{12} + A_{22} *B_{22}$
• The recurrence relation obtained is:
  $T(N) = 8 T(N_2) + 4 O(N^2)$
• Here O(N^2) term is for matrix addition. Since, addition is performed 4 times during the recursion, Therefore, it is 4 times $O(N^2)$.
• The recurrence relationship can be simplified using the Master’s Theorem.
• And the overall time complexity turns out to be $O(N^3)$ which is not better than the naive method which is discussed earlier.
• To optimize it further, we use Strassen’s Matrix Multiplication where we don’t need 8 recursive calls, as we can solve them using 7 recursive calls and this requires some manipulation which is achieved using addition and subtraction.
• Strassen’s 7 calls are as follows:
  • $p_{1}= ( A_{11} ) * ( B_{11} – B_{22} )$
  • $p_{2}= ( A_{11} + A_{12} )* ( B_{22} )$
  • $p_{3}= ( A_{21} + A_{22} ) * ( B_{11} )$
• $p_{4}= ( A_{22} ) * (B_{21} + B_{22})$
• $p_{5}= ( A_{11} + A_{22} ) * ( B_{11} + B_{22} )$
• $p_{6}= ( A_{12} – A_{21} ) * ( B_{21} + B_{22} )$
• $p_{7}= ( A_{11} – A_{21} ) * ( B_{11} + B_{12} )$ Now the resultant matrix can be obtained in the following way:

$$
Mat_A × Mat_B =
\begin{bmatrix}
p_5 + p_4 – p_2 + p_6 & p_1 + p_2 \
p_3 + p_4 & (p_1 *p_5) -(p_3 * p_7) \
\end{bmatrix}
$$

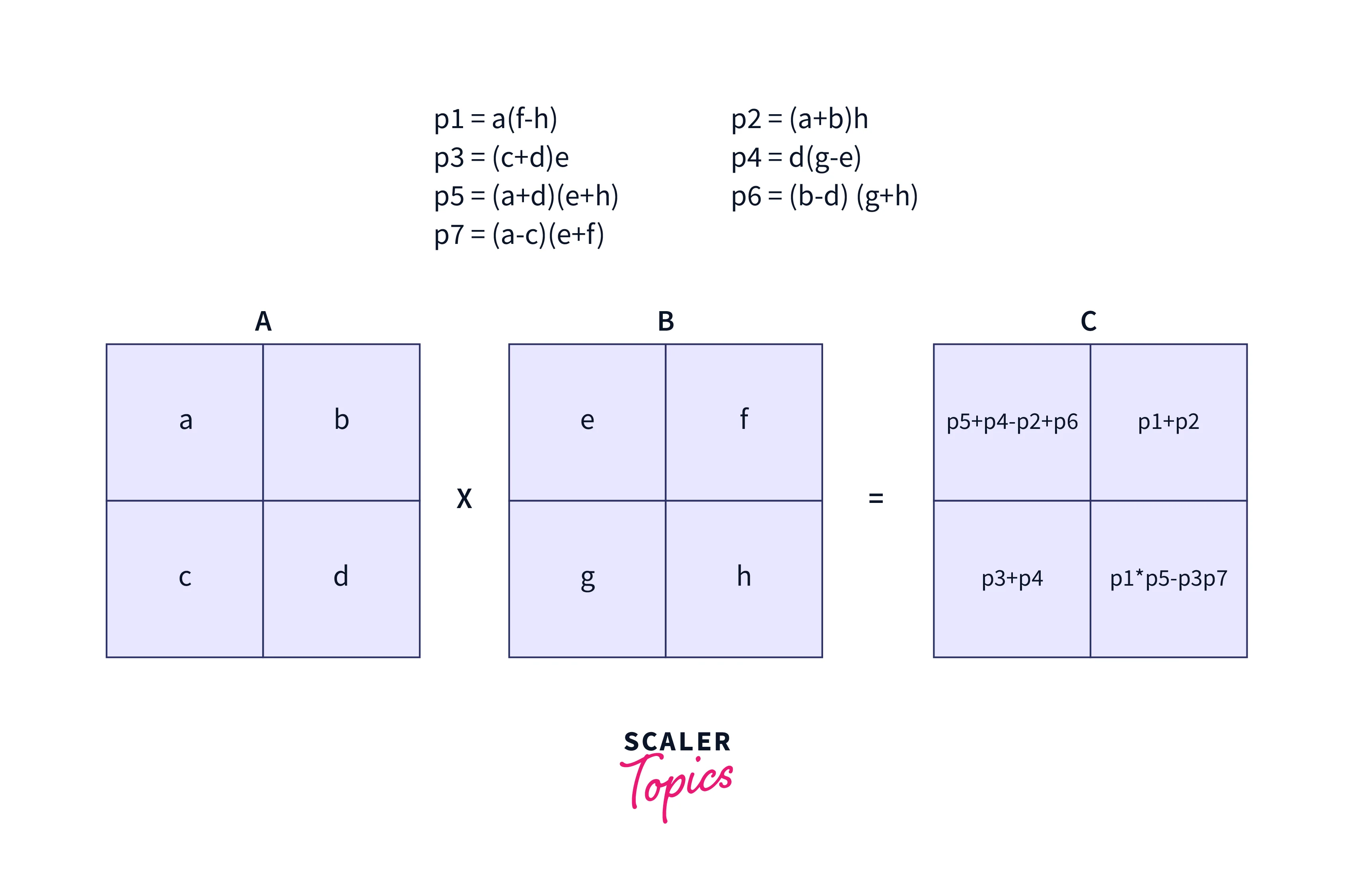
Therefore Strassen’s Matrix Multiplication algorithm has better time complexity and is considered to be more efficient than the other methods for matrix multiplication.

Algorithm:

1. Divide the given matrix A and matrix B into 4 sub-matrices of size each $N_2 x N_2$ as shown in the above diagram.
2. Now, compute Strassen’s 7 calls recursively.
3. Calculate the submatrices of C.
4. Now, we combine these submatrices into our new resultant matrix C.

Implementation

Below is the implementation of Strassen’s Matrix Multiplication algorithm.

C++ Implementation of Strassen’s Matrix Multiplication Algorithm:

#include <bits/stdc++.h>
using namespace std;

// Fixing the sizes of Mat_A and Mat_B
#define Row_1 4
#define Col_1 4
// Mat_A and Mat_B are square matrices of size 4 * 4
#define Row_2 4
#define Col_2 4

vector<vector<int> >Additionofmatrix(vector<vector<int> > Mat_A,
           vector<vector<int> > Mat_B, int divide_idx, int mul = 1)
{
    for (auto i = 0; i < divide_idx; i++)
        for (auto j = 0; j < divide_idx; j++)
            Mat_A[i][j]= Mat_A[i][j] + (mul * Mat_B[i][j]);
    return Mat_A;
}

vector<vector<int> > StrassensMultiplication(vector<vector<int> > Mat_A, vector<vector<int> > Mat_B){
    // Computing the sizes of row and col of the first matrix
    int col_1 = Mat_A[0].size();
    int row_1 = Mat_A.size();
    // Computing the sizes of row and col of the second matrix
    int row_2 = Mat_B.size();
    int col_2 = Mat_B[0].size();

    // If this condition is not satisfied matrix multiplication is not possible 
    if (col_1 != row_2) {
        cout << "Matrix Multiplication not possible";
        return {};
    }

    //initializing the result matrix
    vector<int> Res_Row(col_2, 0);
    vector<vector<int> > Res(row_1, Res_Row);

    if (col_1 == 1)
        Res[0][0] = Mat_A[0][0] * Mat_B[0][0];
    else {
        int divide_idx = col_1 / 2;
        vector<int> Row_vec(divide_idx, 0);

        vector<vector<int> > A_11(divide_idx, Row_vec);
        vector<vector<int> > A_12(divide_idx, Row_vec);
        vector<vector<int> > A_21(divide_idx, Row_vec);
        vector<vector<int> > A_22(divide_idx, Row_vec);
        // dividing the matrices into its components
        vector<vector<int> > B_11(divide_idx, Row_vec);
        vector<vector<int> > B_12(divide_idx, Row_vec);
        vector<vector<int> > B_21(divide_idx, Row_vec);
        vector<vector<int> > B_22(divide_idx, Row_vec);

        for (auto i = 0; i < divide_idx; i++)
            for (auto j = 0; j < divide_idx; j++) {
                A_11[i][j] = Mat_A[i][j];
                A_12[i][j] = Mat_A[i][j + divide_idx];
                A_21[i][j] = Mat_A[divide_idx + i][j];
                A_22[i][j] = Mat_A[i + divide_idx][j + divide_idx];
                B_11[i][j] = Mat_B[i][j];
                B_12[i][j] = Mat_B[i][j + divide_idx];
                B_21[i][j] = Mat_B[divide_idx + i][j];
                B_22[i][j] = Mat_B[i + divide_idx][j + divide_idx];
            }
        // Callin all  7 Strassens calls for finding the p1,p2....
        vector<vector<int> > P_1(StrassensMultiplication(A_11, Additionofmatrix(B_11, B_22, divide_idx, -1)));
        vector<vector<int> > P_2(StrassensMultiplication(Additionofmatrix(A_11, A_12, divide_idx), B_22));
        vector<vector<int> > P_3(StrassensMultiplication(Additionofmatrix(A_21, A_22, divide_idx), B_11));
        vector<vector<int> > P_4(StrassensMultiplication(A_22, Additionofmatrix(B_21, B_11, divide_idx, -1)));
        vector<vector<int> > P_5(StrassensMultiplication(Additionofmatrix(A_11, A_22, divide_idx),Additionofmatrix(B_11, B_22, divide_idx)));
        vector<vector<int> > P_6(StrassensMultiplication(Additionofmatrix(A_12, A_22, divide_idx, -1), Additionofmatrix(B_21, B_22, divide_idx)));
        vector<vector<int> > P_7(StrassensMultiplication(Additionofmatrix(A_11, A_21, divide_idx, -1),
            Additionofmatrix(B_11, B_12, divide_idx)));
        // All the p_1,...are obtained now they are solved to get values in the result matrix
        vector<vector<int> > Res_00(Additionofmatrix(
            Additionofmatrix(Additionofmatrix(P_5, P_4, divide_idx), P_7,divide_idx),
            P_2, divide_idx, -1));
        vector<vector<int> > Res_01(Additionofmatrix(P_1, P_2, divide_idx));
        vector<vector<int> > Res_10(Additionofmatrix(P_3, P_4, divide_idx));
        vector<vector<int> > Res_11(Additionofmatrix(Additionofmatrix(Additionofmatrix(P_5, P_1, divide_idx), P_3, divide_idx, -1), P_7, divide_idx, -1));

        for (auto i = 0; i < divide_idx; i++)
            for (auto j = 0; j < divide_idx; j++) {
                Res[i][j] = Res_00[i][j];
                Res[i][j + divide_idx] = Res_01[i][j];
                Res[divide_idx + i][j] = Res_10[i][j];
                Res[i + divide_idx][j + divide_idx] = Res_11[i][j];
            }

        A_11.clear();
        A_12.clear();
        A_21.clear();
        A_22.clear();
        B_11.clear();
        B_12.clear();
        B_21.clear();
        B_22.clear();
        P_1.clear();
        P_2.clear();
        P_3.clear();
        P_4.clear();
        P_5.clear();
        P_6.clear();
        P_7.clear();
        Res_00.clear();
        Res_01.clear();
        Res_10.clear();
        Res_11.clear();
    }
    return Res;
}

int main(){
    // First matrix for multiplication is :
    vector<vector<int> > Mat_A = { { 1, 2, 1, 4 }, { 5, 2, 9, 6 }, { 4, 3, 2, 0 }, { 3, 5, 7, 6 } };
    // Second matrix for multiplication is:
    vector<vector<int> > Mat_B = { { 8, 1, 14, 13 }, { 2, 9, 5, 3 }, { 1, 2, 6, 7 }, { 2, 4, 9, 6 } };

    // Calculating the matrix multiplication by divide and conquer and using Strassen’s Matrix Multiplication algorithm
    vector<vector<int> > Result (StrassensMultiplication(Mat_A, Mat_B));
    // Print the resultant obtained
    int Row=Row_1-1;
    int Col=Col_2-1;
    for (int i = 0 ; i <= Row_1-1; i++) {
        for (int j = 0 ; j <= Col_2-1; j++) {
            // Printing the value in the matrix at position [i][j]
            cout << setw(10);
            cout << Result[i][j] ;
        }
        cout << endl;
    }
    cout << endl;

}

Output:

    21    37    66    50 
    65    65    188   170 
    40    35     83    75 
    53    86     163   139 

Python Implementation of Strassen’s Matrix Multiplication Algorithm:

# Install the NumPy module which is required during combining the matrices in a horizontal and vertical manner
import numpy as nump

def divide(Mat):
    # This function divides the matrix into n//2, whenever called in the recursive fashion
    Row, Col = Mat.shape
    # Now divide the row and col by 2
    Row_2, Rol_2 = Row//2, Col//2
    # Now you need to divide the matrix into 4 parts:
    # Namely: A_11, A_12, A_21, A_22 which we have discussed earlier.

    return Mat[:Row_2, :Col_2], Mat[:Row_2, Col_2:], Mat[Row_2:, :Col_2], Mat[Row_2:, Col_2:]

# This function computes the product of given two matrices in divide and conquer method recursively/
def StrassenMultiplication( Mat_A, Mat_B):

    # Base case: when the size of matrices is 1x1 simply return the multiplication
    if len(MAt_A) == 1:
        return Mat_A * Mat_B

    # Now we need to divide the matrices into 4 groups each as we discussed in the approach
    A_11, A_12, A_21, A_22 = divide(Mat_A)
    B_11, B_12, B_21, B_22 = divide(Mat_B)

    # Now calling the Strassen’s 7 calls recursively
    P_1 = StrassenMultiplication(A_11, B_12 - B_22) 
    P_2 = StrassenMultiplication(A_11 + A_12, B_22)       
    P_3 = StrassenMultiplication(A_21 + A_22, B_11)       
    P_4 = StrassenMultiplication(A_22, B_21 + B_22)       
    P_5 = StrassenMultiplication(A_11 + A_22, B_11 + B_22)       
    P_6 = StrassenMultiplication(A_12 - A_22, B_21 + B_22) 
    P_7 = StrassenMultiplication(A_11 - A_21, B_11 + B_12) 

    # Calculating the values of the resultant matrix using the Strassen Multiplication recursive calls.
    C_11 = P_5 + P_4 - P_2 + P_6 
    C_12 = P_1 + P_2          
    C_21 = P_3 + P_4           
    C_22 = P_1 + P_5 - P_3 - P_7 

    # Combining(Conquering) these 4 quadrants into a single matrix by arranging them in the horizontal and vertical way using the numpy functions.
    Result = nump.vstack((nump.hstack((C_11, C_12)), nump.hstack((C_21, C_22))))

    return Result

Java Implementation of Strassen’s Matrix Multiplication Algorithm:

// Java Program to Implement Strassen Algorithm

// Class which implements the Strassen matrix multiplication algorithm
class Solution{
    // Function to multiply given two matrices using Strassen matrix multiplication
    public int[][]  StrassenMultiplication(int[][] Mat_A, int[][] Mat_B){
        // size of square matrices
        int N = Mat_A.length;
        // Storing the result 
        int[][] Res = new int[N][N];

       // Base case where only one row and one col is present
        if (N == 1)
            // simply return the multiplication of these numbers
            Res[0][0] = Mat_A[0][0] * Mat_B[0][0];
        // else compute the matrix multiplication using strassen matrix multiplication algorithm
        else {
            // Divide step: where we divide given matrices into 4 quadrants each
            int[][] A_11 = new int[N / 2][N / 2];
            int[][] A_12 = new int[N / 2][N / 2];
            int[][] A_21 = new int[N / 2][N / 2];
            int[][] A_22 = new int[N / 2][N / 2];
            // dividing the second matrix into 4 quadrants
            int[][] B_11 = new int[N / 2][N / 2];
            int[][] B_12 = new int[N / 2][N / 2];
            int[][] B_21 = new int[N / 2][N / 2];
            int[][] B_22 = new int[N / 2][N / 2];

           // dividing the first matrix by calling divide function 
            divide(Mat_A, A_11, 0, 0);
            divide(Mat_A, A_12, 0, N / 2);
            divide(Mat_A, A_21, N / 2, 0);
            divide(Mat_A, A_22, N / 2, N / 2);

            // dividing the second matrix by calling divide function 
            divide(Mat_B, B_11, 0, 0);
            divide(Mat_B, B_12, 0, N / 2);
            divide(Mat_B, B_21, N / 2, 0);
            divide(Mat_B, B_22, N / 2, N / 2);

            // Compute the p1, p2,.. using 7 strassen multiplication 
            int[][] P_1 = StrassenMultiplication(Add_Matrices(A_11, A_22), Add_Matrices(B_11, B_22));
            int[][] P_2 = StrassenMultiplication(Add_Matrices(A_21, A_22), B_11);
            int[][] P_3 = StrassenMultiplication(A_11, Sub_Matrices(B_12, B_22));
            int[][] P_4 = StrassenMultiplication(A_22, Sub_Matrices(B_21, B_11));
            int[][] P_5 = StrassenMultiplication(Add_Matrices(A_11, A_12), B_22);
            int[][] P_6 = StrassenMultiplication(Sub_Matrices(A_21, A_11), Add_Matrices(B_11, B_12));
            int[][] P_7 = StrassenMultiplication(Sub_Matrices(A_12, A_22), Add_Matrices(B_21, B_22));

            // using the values computed above we can find the values of the resultant matrix
            int[][] C_11 = Add_Matrices(Sub_Matrices(Add_Matrices(P_1, P_4), P_5), P_7);
            int[][] C_12 = Add_Matrices(P_3, P_5);
            int[][] C_21 = Add_Matrices(P_2, P_4);
            int[][] C_22 = Add_Matrices(Sub_Matrices(Add_Matrices(P_1, P_3), P_2), P_6);

            // Now after finding the values of the result matrix, we need to combine them 
            JoinMat(C_11, Res, 0, 0);
            JoinMat(C_12, Res, 0, N / 2);
            JoinMat(C_21, Res, N / 2, 0);
            JoinMat(C_22, Res, N / 2, N / 2);
        }
        // return the resultant matrix
        return Res;
    }
    // Function to subtract the given two matrices
    public int[][] Sub_Matrices(int[][] Mat_A, int[][] Mat_B){
        int N = Mat_A.length;
        int[][] Res = new int[N][N];
        for (int i = 0; i < N; i++)
            for (int j = 0; j < N; j++)
                 // subtracting the elements from the given matrices
                Res[i][j] = Mat_A[i][j] - Mat_B[i][j];
        // return the resultant matrix
        return Res;
    }
    // Function to add the given two matrices
    public int[][] Add_Matrices(int[][] Mat_A, int[][] Mat_B){
        int N = Mat_A.length;
        // Intialising the resultant array
        int[][] Res = new int[N][N];
        for (int i = 0; i < N; i++)
            for (int j = 0; j < N; j++)
                // adding the elements from the given matrices
                Res[i][j] = Mat_A[i][j] + Mat_B[i][j];
        // return the resultant matrix
        return Res;
    }
    // This function helps in dividing the matrices into four quadrants
    public void divide(int[][] Mat_A, int[][] Mat_B, int K, int M){
        for (int i_1 = 0, i_2 = K; i_1 < Mat_B.length; i_1++, i_2++)
            for (int j_1 = 0, j_2 = M; j_1 < Mat_B.length; j_1++, j_2++)
                Mat_B[i_1][j_1] = Mat_A[i_2][j_2];
    }

    // This function helps in combining the result obtained 
    public void JoinMat(int[][] A, int[][] B, int K, int M){
        for (int i_1 = 0, i_2 = K; i_1 < A.length; i_1++, i_2++)
            for (int j_1 = 0, j_2 = M; j_1 < A.length; j_1++, j_2++)
                B[i_2][j_2] = A[i_1][j_1];
    }
    // Driver Code
    public static void main(String[] args){
        // creating an object
        Solution obj = new Solution();
        // size of the square matrix taken
        int N = 4;
        // first matrix for matrix multiplication
        int[][] Mat_A =  { { 1, 2, 1, 4 }, { 5, 2, 9, 6 }, { 4, 3, 2, 0 }, { 3, 5, 7, 6 } };
        // second matrix for matrix multiplication
        int[][] Mat_B = { { 8, 1, 14, 13 }, { 2, 9, 5, 3 }, { 1, 2, 6, 7 }, { 2, 4, 9, 6 } };

        // Computing the result array
        int[][] Result = obj.StrassenMultiplication(Mat_A, Mat_B);
       // printing the resultant array formed
        for (int i = 0; i < N; i++) {
            for (int j = 0; j < N; j++)
                // printing values at each position
                System.out.print(Result[i][j] + " ");
            System.out.println();
        }
    }
}

Output:

    21 37 66 50 
    65 65 188 170 
    40 35 83 75 
    53 86 163 139 

Explanation:

The given two matrices are multiplied and the result has been printed as the output. The condition for Strassen’s Matrix Multiplication algorithm is that the given matrices should be square matrices and of order $N * N$, where N is the power of 2.

Complexity Analysis

Time Complexity: O(N^log(7)), where N * N is the order of square matrices given.

• We just need 7 recurrences Strassen’s Matrix Multiplication algorithm and some addition subtraction has to be performed to manipulate the answer. The recurrence relation obtained is:
  $T(N) = 7T(N_2) + O(N^2)$
• By solving the above relation, we get the overall time complexity of Strassen’s Matrix Multiplication is $O(N^{log(7)})$.
• By simplifying that we get the overall time complexity of approximately is $O(N^{2.8074})$ which is better than $O(N^3)$.
• Comparision of the methods used for matrix multiplication is clearly explained in the below image.
  

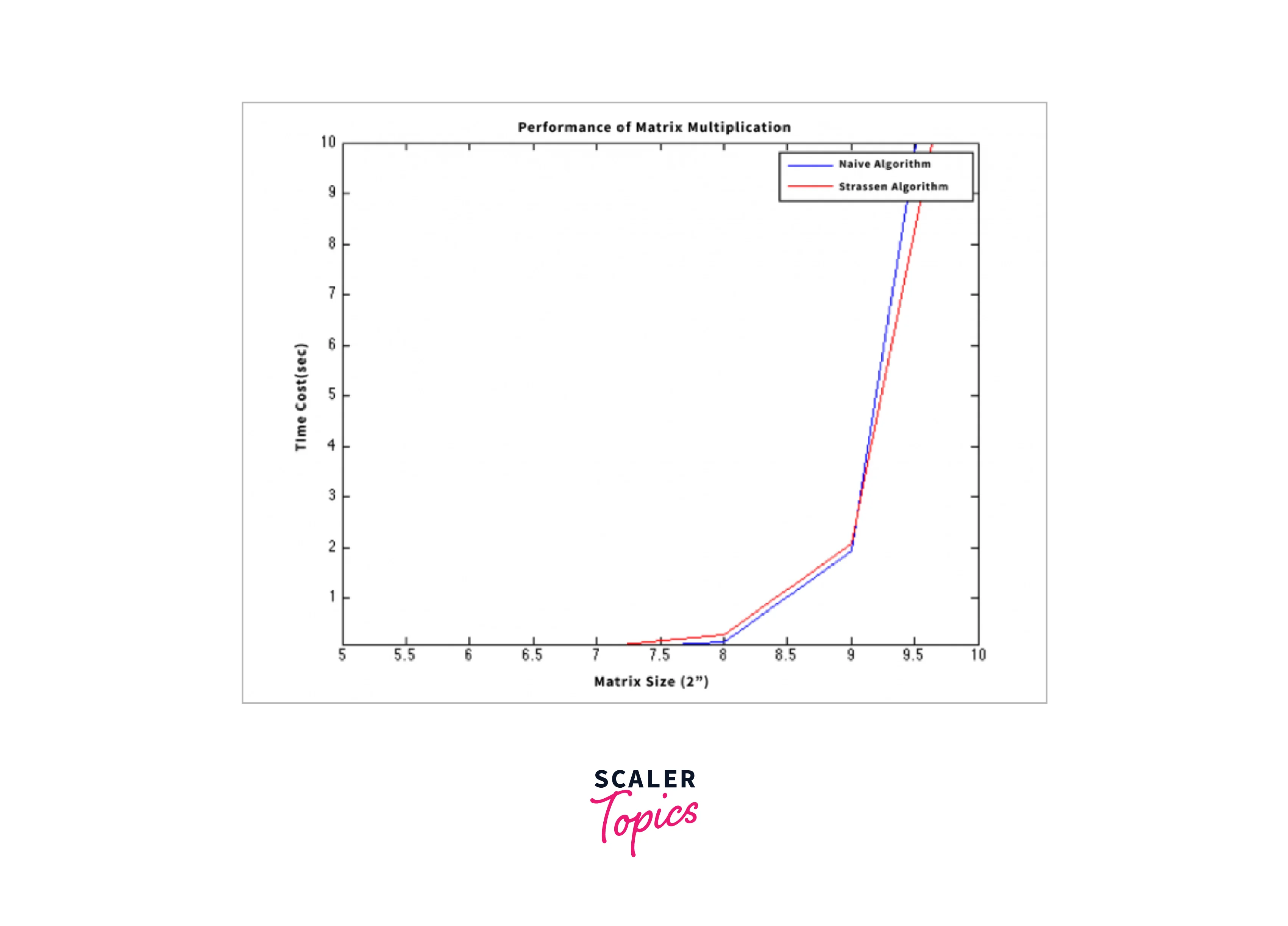
• Therefore we can observe that Strassen’s Matrix Multiplication algorithm is considered to be efficient for matrix multiplication.

Space Complexity: O(log N), where the given matrices are square matrices of size N*N each. The submatrices in recursion take extra space.

Easy Method to Remember Strassen’s Matrix Equations

Strassen’s Matrix Multiplication has 7 recursive calls and computing the values in the resultant matrix. Below are a few ways used for remembering how to compute the values required to fill the resultant matrix.

• Consider the below image:
  

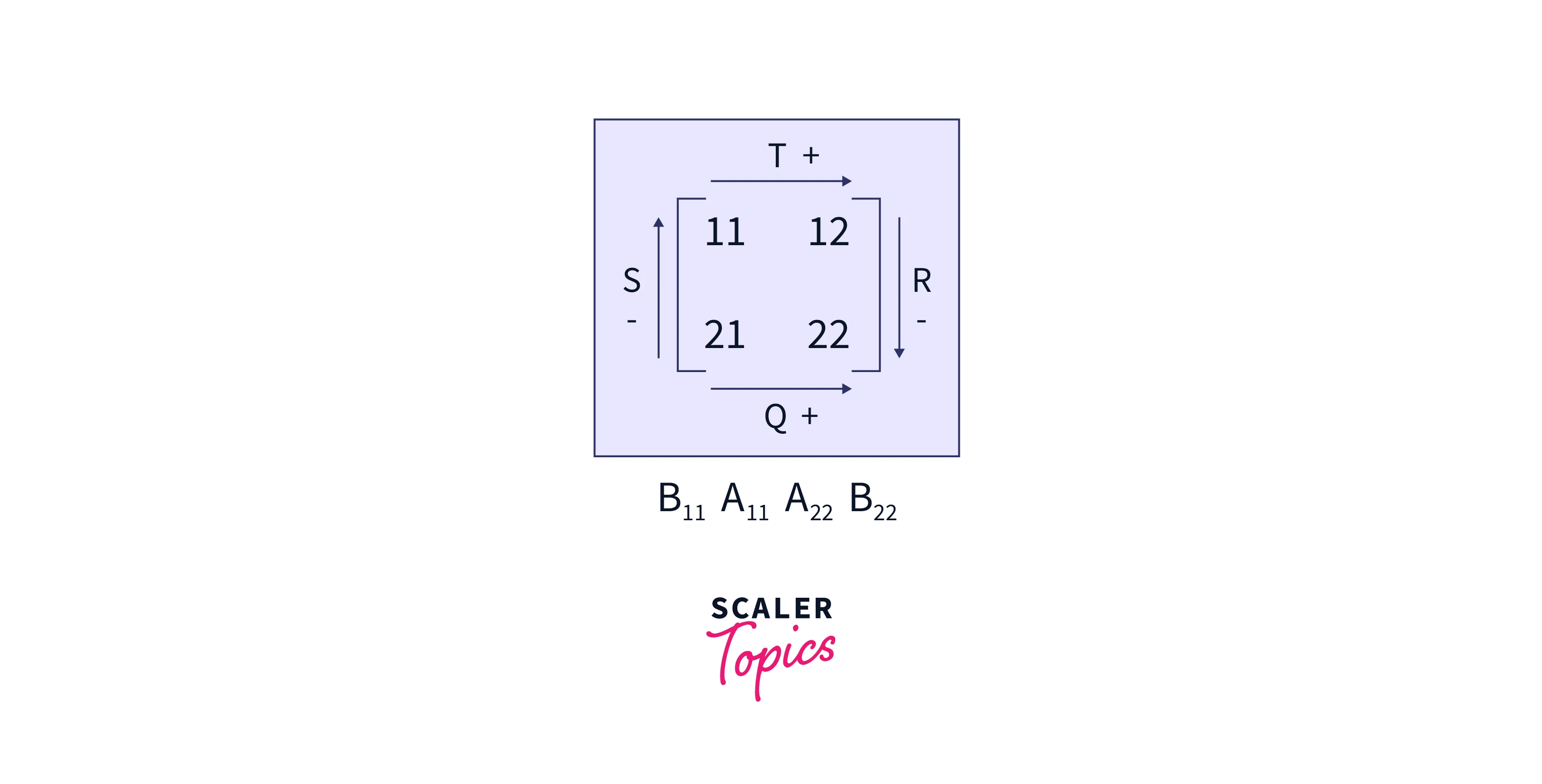
• For calculating the values of P, we just need to multiply the product of the sum of the diagonal elements.
• For writing the values of Q, R, S and T follow the below steps:
• Place the initial values as shown in the figure:
  

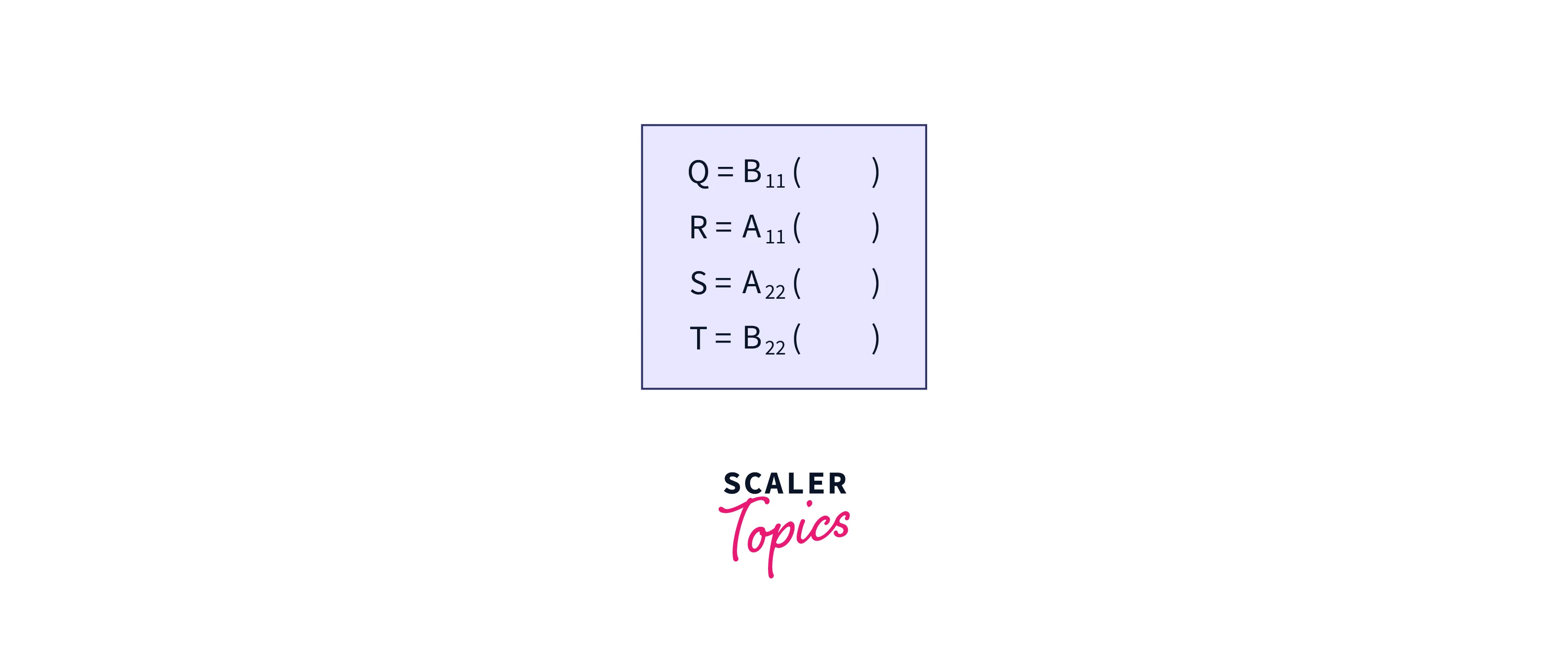
• Now for computing the values of Q, R, S, and T we just need to check whether the initial value’s coefficient we have taken as in the above image is either A or B. If B is taken, then in the brackets we need to have A as the coefficient, whereas if the initial coefficient taken is A as shown in the figure, then the values in the bracket should be of coefficient B.
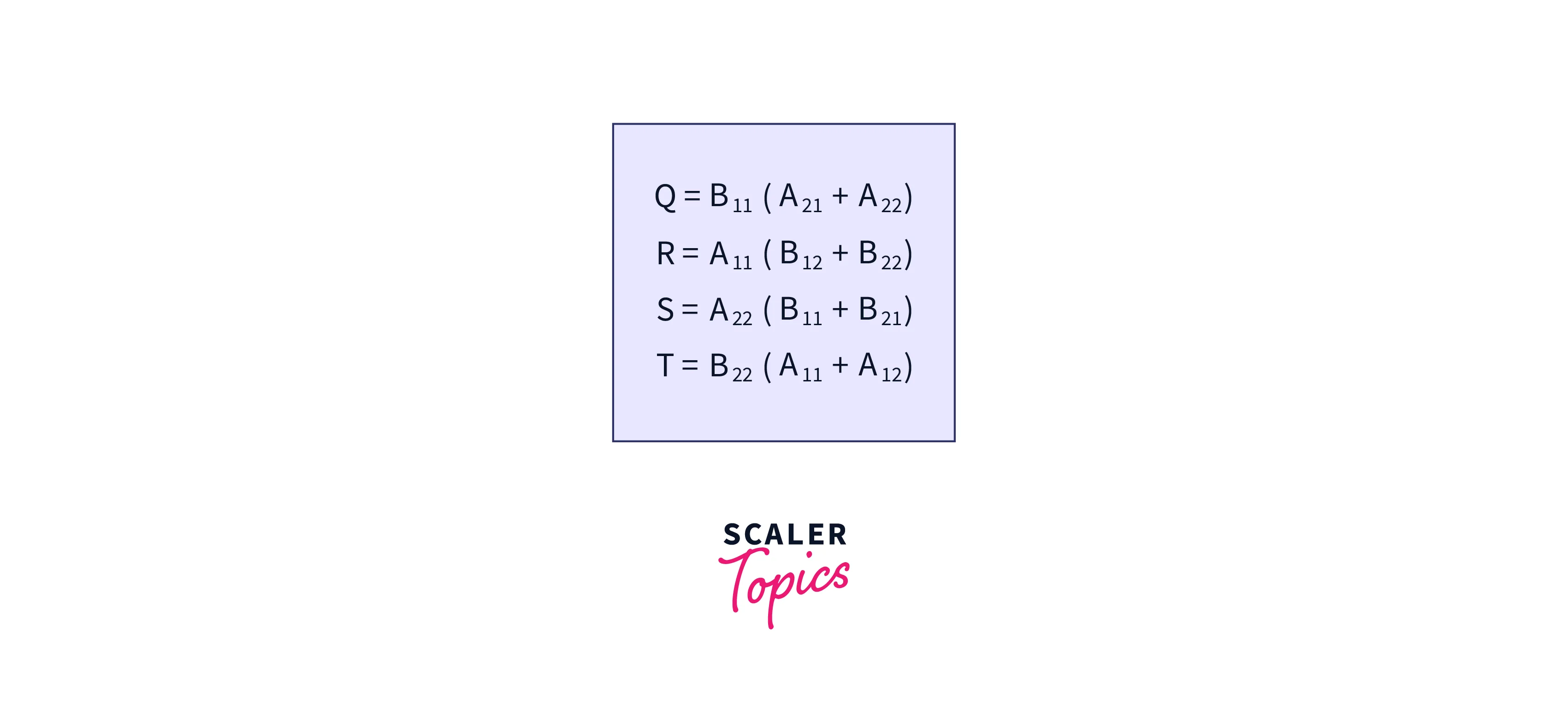
• Now to fill the values taking the reference from image 6, we can say that for T and Q, we need to add the values shown by the arrow direction.
• Whereas for computing the values of S and R, we need to subtract the values indicated by the arrow in the image6.
• The equation of Q, R, S and T can be shown in the below image:
  

• Last step includes calculating the values of U, here we use the values of S and T. We need to toggle the coefficients i.e, A becomes B and B becomes A. So U obtained is as follows: $U=~(A_{21})~~(A_{11})~~(B_{11}~+~B_{12})$
• Similarly, value of V is obtained by using the values of Q and R. Here we just need to toggle A and B present in the brackets. Therefore the value of V is: $V~=~(B_{21}~+~B_{22})~*~(A_{12}~-~A_{22})$.
• After computing the values of P, Q, R, S, T, U, V. We need to calculate the values of $C_{11},~ C_{12},~ C_{21},~ C_{22}$ which are the values of resultant matrix.
• We need to calculate them in the following way:
  • $C_{11} =~ P~ +~ S~ -~T~ +~ V$
  • $C_{12} ~= ~R ~+ ~T$
  • $C_{21} ~= ~Q ~+ ~S$
  • $C_{22} = P + R – Q + U$

Invest in your programming future with our in-depth Dynamic Programming Certification Course. Enroll now and supercharge your coding skills!

Conclusion

• In this article we have discussed methods for matrix multiplication of the given two matrices.
• The first method is the naive method which has a time complexity of $O(N^3)$ and space complexity is $O(N^2)$ required for storing the result matrix.
• The second method is the divide and conquers technique. In this approach 8, recursive calls are made. Therefore the overall time complexity is $O(N^3)$ which is the same as the naive method.
• In Strassen’s Matrix Multiplication algorithm we use the divide and conquer technique but have only 7 recursive calls. Therefore the overall time complexity of Strassen’s Matrix Multiplication algorithm is $O(N^{2.8074})$.
• Therefore it is considered to be the optimal algorithm for matrix multiplication of given matrices.
• Strassen’s Matrix Equations can be applied for the matrices where the given matrices are square matrices and the order of matrices is N*N, where N is the power of 2.
• We also discussed easy ways to remember Strassen’s Matrix Equation recursive calls.

HAPPY CODING!!