Problem Statement
Given an array arr[] of length N, print the reverse of it.
Example
Consider the following example:
arr[] = {1,2,3,4,5}After reversing this array,we have the new array as
arr[] = {5,4,3,2,1}Example Explanation
The initial array [1,2,3,4,5] when reversed gives [5,4,3,2,1].
Constraints
$1 <= N <= 10^5$
There N is the length of the array.
Approach 1- Recursive Approach
In this approach, we recursively divide the array into smaller subarrays while reversing the remaining part.
Let’s define a recursive function reverse(start, end, arr) which reverses the array arr from index start to index end.
Initially start is 0 and end is N-1.
In each recursive step we swap the arr[end] and arr[start] and call the function for the subarray start+1 and end-1.
The above process is simulated as follows:
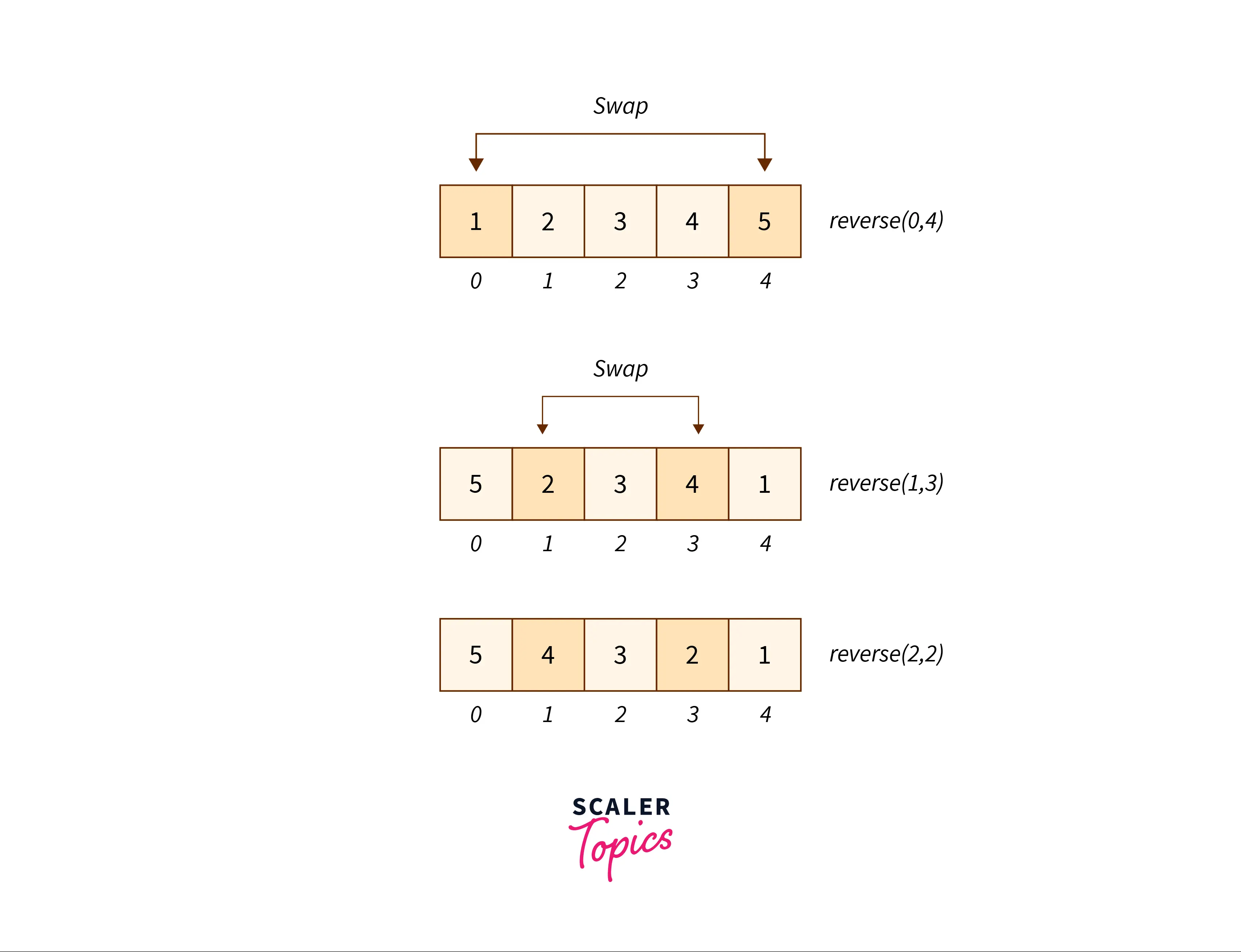
Algorithm
1) Call the function reverse(start, end , arr) where start=0 and end = N-1.
2) Swap the numbers arr[start] and arr[end].
3) Recursively call the same function for the subarray start+1 and end-1.
reverse(start,end,arr):
swap(arr[start],start[end])
reverse(start+1,end-1,arr)Let’t see the implementation part:
Code Implementation in C++
#include<bits/stdc++.h>
using namespace std;
//Reverse array function
void reverse(int start, int end, int arr[]){
// Base case
if(start >= end)
return;
//Swap the arr[start] and arr[end]
swap(arr[start],arr[end]);
//Recursive step.
reverse(start+1,end-1,arr);
}
//Auxuliary function to print the array
void printArray(int n, int arr[]){
for(int i=0;i<n;i++)
cout << arr[i] << " ";
}
//Driver program
int main(){
//Input array
int arr[] = {1,2,3,4,5};
//Size of the input array
int n = sizeof arr/sizeof arr[0];
//call the function for the reverse
reverse(0,n-1,arr);
//Print the array
printArray(n,arr);
}Code Implementation in Java
import java.io.*;
class Main{
//function to reverse the array
static void reverse(int arr[], int start, int end){
//Base case
if(start >= end)
return;
//Swap the numbers
int temp = arr[start];
arr[start] = arr[end];
arr[end] = temp;
//Reverse the remaining array
reverse(arr,start+1,end-1);
}
//Function to print the given array
static void printArray(int arr[], int n){
for(int i=0;i<n;i++)
System.out.print(arr[i] + " ");
}
//Driver program!
public static void main (String[] args) {
int arr[] = {1, 2, 3, 4, 5};
reverse(arr, 0, 4);
printArray(arr, 5);
}
}Code Implementation in python
# Function to reverse arr[] from start to end
def reverse(arr, start, end):
if start >= end:
return
arr[start], arr[end] = arr[end], arr[start]
reverse(arr, start+1, end-1)
# Driver function to test above function
arr = [1, 2, 3, 4, 5]
reverse(arr, 0, 4)
print(arr)Output:
5 4 3 2 1Time Complexity
Since we are calling the reverse function at most n/2 times, where n, is the length of the array, the time complexity is O(n).
Space Complexity
The implementation does not use any auxiliary space, therefore the space complexity is O(1).
Approach 2 – Iterative Approach
In this approach, we iterate the array up to n/2 and for each index i we swap it with $(n-i-1)^{th}$ element of the array.
The approach is a type of two pointer approach where the first pointer is i and the second is (n-i-1).
The process is simulated below:
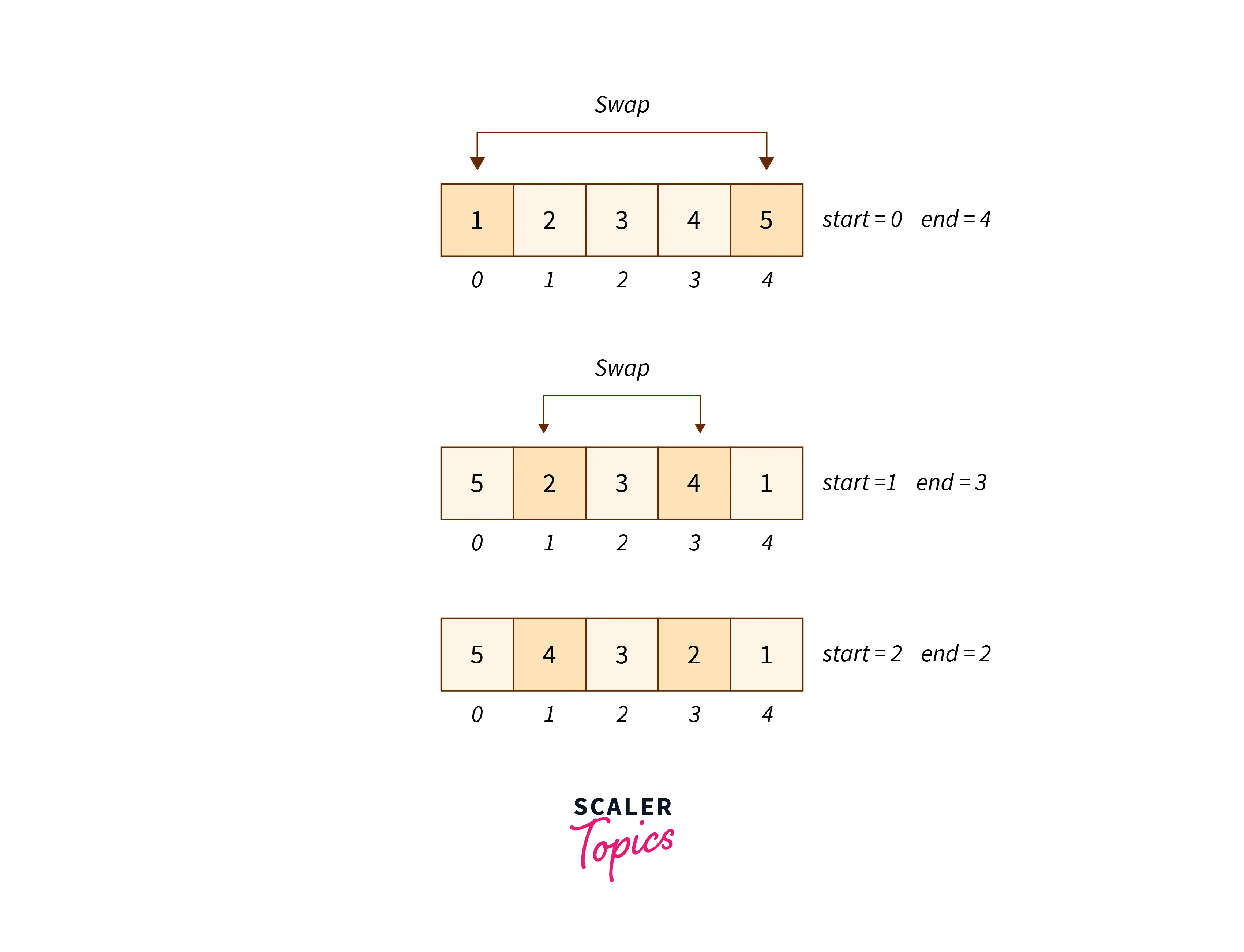
Algorithm
1) Initialize two variable start = 0 and end = n-1.
2) In a loop, iterate over the array and swap the elements at start and end and change the pointers as
start = start + 1 , end = end-1
Code Implementation in C++:
#include<bits/stdc++.h>
using namespace std;
// Function to reverse the array
void reverse(int n, int arr[]){
//start and end pointers
for(int i=0;i<n/2;i++)
swap(arr[i],arr[n-i-1]);
}
//Function to print the array
void printArray(int n, int arr[]){
for(int i=0;i<n;i++)
cout << arr[i] << " ";
}
//Driver function
int main(){
//Input array
int arr[] = {1,2,3,4,5};
//size of the array
int n = sizeof arr / sizeof arr[0];
//reverse the array
reverse(n,arr);
//Print the array
printArray(n,arr);
}Code Implementation in Java:
import java.io.*;
class Main{
//function to reverse the array
static void reverse(int n, int arr[]){
for(int i=0;i<n/2;i++){
int temp = arr[i];
arr[i] = arr[n-i-1];
arr[n-i-1] = temp;
}
}
//Function to print the array
static void printArray(int n, int arr[]){
for(int i=0;i<n;i++)
System.out.print(arr[i] + " ");
}
//main driver function
public static void main(String args[]){
//Input array
int arr[] = {1,2,3,4,5};
reverse(5,arr);
printArray(5,arr);
}
}Code Implementation in python:
# function to reverse the array
def reverse(arr, n):
start = 0
end = n-1
while start < end:
arr[start], arr[end] = arr[end], arr[start]
start = start + 1
end = end - 1
# input array
arr = [1,2,3,4,5]
reverse(arr,5)
print(arr)Output:
5 4 3 2 1Time Complexity
Since we are iterating over the array once, therefore the time complexity is O(n).
Space Complexity
Since we are not using any auxiliary space for the implementation the space complexity is O(1).
Approach 3 – Using Python List Slicing
Array or list in Python can be reversed using the Python List slicing.
Syntax:
list_name[start: end] where list_name represents the name of the list to be reversed while start and end are the starting and ending indices.
To read more about python slicing read python slicing.
Algorithm
1) Printing the list_name[::-1] will simply reverse the input list and print the reversed list.
Code Implementation in Python:
# function to reverse the array
def reverse(arr):
print(arr[::-1])
arr = [1,2,3,4,5]
print("Reversed list is:")
reverse(arr)Output:
5 4 3 2 1Time Complexity
Since we are using the python in-built slice method, where the complexity of the slice method is O(n) for a list to be sliced of length n, therefore the time complexity is O(n).
Space Complexity
Since the implementation does not use any auxiliary space, space complexity is O(1).
Approach 4 – Reverse an Array in C++ Using the reverse() Function
In c++, there is an in-built reverse function that is used to reverse arrays.
Algorithm
Use reverse function and pass the address of first element and ending address of the array.
Syntax:
reverse(arr,arr+n) will reverse the array arr of length n.
Code Implementation in C++:
#include<bits/stdc++.h>
using namespace std;
//reverse the array using in-built function
void reverse(int arr[], int n){
reverse(arr,arr+n);
}
//function to print the array
void printArray(int arr[], int n){
for(int i=0;i<n;i++)
cout << arr[i] << " ";
}
//Driver program
int main(){
//Input array
int arr[] = {1,2,3,4,5};
//Size of the array
int n = sizeof arr/sizeof arr[0];
// reverse the array
reverse(arr,n);
//Print the given array
printArray(arr,n);
}Output:
5 4 3 2 1Time Complexity
The time complexity of the reverse function is O(n), therefore the time complexity of the above implementation is O(n).
Space Complexity
Since the implementation is not using any auxiliary space, the space complexity is O(1).
Approach 5- Using Concept of Swapping
In this approach, we use the concept of swapping i.e. interchanging the values to reverse the array using a third variable.
We iterate over the array from i=0 to i=n/2 and swap the values at arr[i] and arr[n-i-1] using a temporary variable temp.
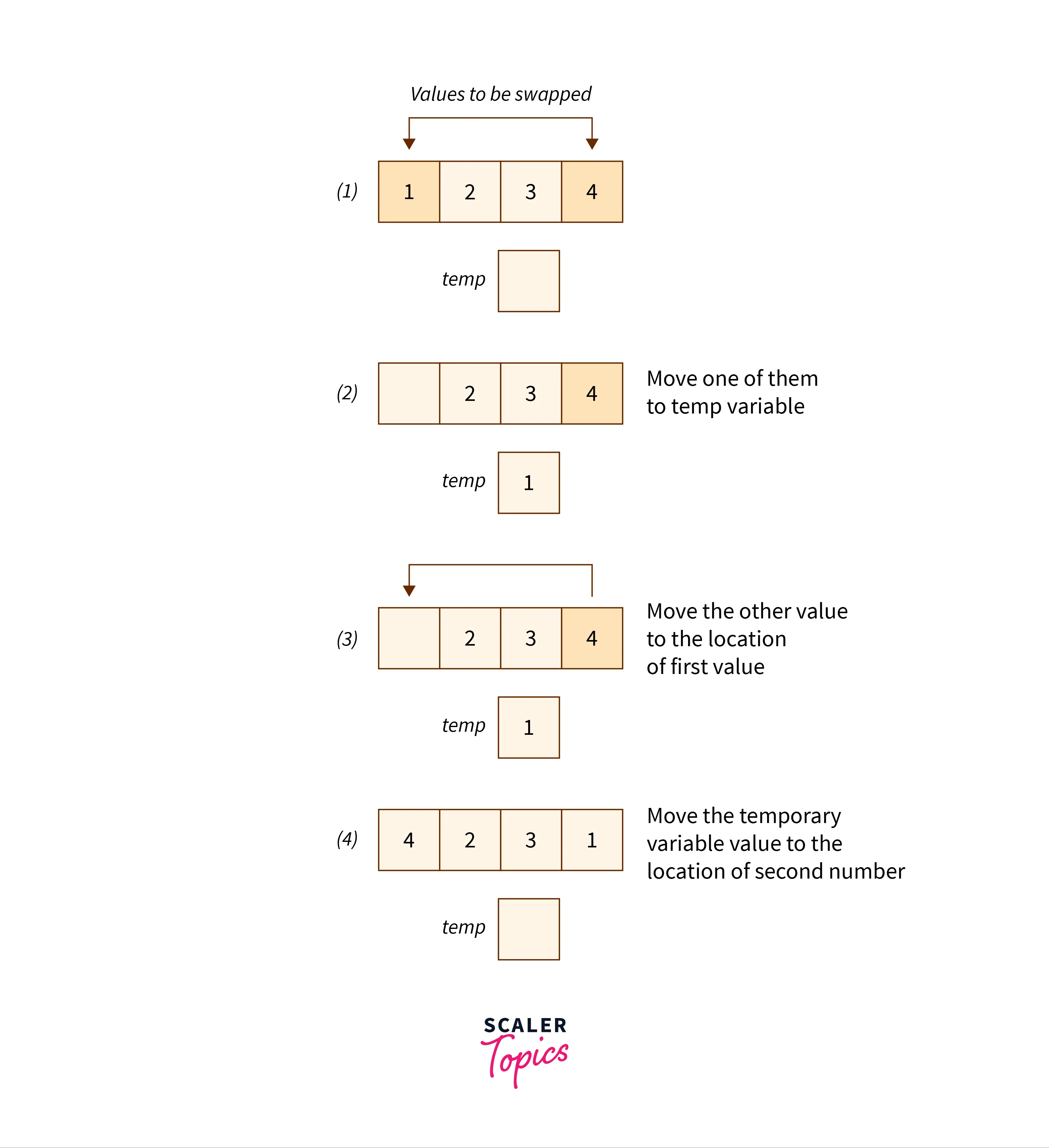
Algorithm
1) Initialize two pointers start = 0 and end = n-1;
2) Swap the values arr[start] and arr[end].
3) Increment start by 1 and decrement end by 1.
4) If start reached the value upto n/2 or start >= end then terminate, else repeat the step 2 and 3.
Code Implementation in C++
#include<bits/stdc++.h>
using namespace std;
//Function to reverse the array
void reverse(int n, int arr[]){
int start = 0 , end = n-1;
while(start < end){
int temp = arr[start];
arr[start] = arr[end];
arr[end] = temp;
start += 1;
end -= 1;
}
}
//Print array
void printArray(int n, int arr[]){
for(int i=0;i<n;i++)
cout << arr[i] << " ";
}
//Driver program
int main(){
//Input array
int arr[] = {1,2,3,4,5};
//Size of the array
int n = sizeof arr / sizeof arr[0];
//call the reverse function
reverse(n,arr);
//Print the array
printArray(n,arr);
}Code Implementation in Java
import java.io.*;
class Main{
//Function to reverse the array
static void reverse(int arr[], int n){
int start = 0, end = n-1;
while(start < end){
int temp = arr[start];
arr[start] = arr[end];
arr[end]=temp;
start += 1;
end -= 1;
}
}
//Print array function
static void printArray(int arr[], int n){
for(int i=0;i<n;i++)
System.out.print(arr[i] + " ");
}
//Driver Function
public static void main(String args[]){
//INput arrat
int arr[] = {1,2,3,4,5};
//Size of the array
int n = arr.length;
//Call the reverse array function
reverse(arr,n);
//Print the reversed array
printArray(arr,n);
}
}Code Implementation in Python
# function to reverse the array
def reverse(n, arr):
start = 0
end = n-1
while start < end:
arr[start],arr[end] = arr[end],arr[start]
start += 1
end -= 1
# input array
arr = [1,2,3,4,5]
reverse(len(arr),arr)
print(arr)Output:
[5 ,4, 3, 2, 1]Time Complexity
Since, we are iterating over the array up to n/2 i.e. the operations are proportional to n hence the time complexity is O(n).
Space Complexity
Since the implementation does not use any extra space, therefore the space complexity is O(1).
Approach 6 – User-defined Function
In this approach, the logic is same as we did in iterative approach,but we do not use any inbuild library function, rather we reverse the array using user-defined functions for reversing as well as swapping.
Algorithm
1) Define a function reverseArray which is used to reverse the array.
2) In the function initialize two pointers start=0 and end=n-1.
3) Swap the elements at start and end and move the pointers start as start+1 and end as end-1.
Code Implementation in C++:
#include<bits/stdc++.h>
using namespace std;
//Function to reverse the array
void reverseArray(int arr[], int n);
void printArray(int arr[], int n){
for(int i=0; i<n; i++) cout << arr[i] << " ";
cout << endl;
}
//Driver program
int main(){
//Input array
int arr[] = {1,2,3,4,5};
//Length of the array
int n = sizeof arr/sizeof arr[0];
//Function to reverse the array
reverseArray(arr,n);
//Function to print the array
printArray(arr,n);
}
//Function to reverse the array
void reverseArray(int ar[], int n){
int i, j, temp;
j = n - 1;
for ( i = 0; i < j; i++, j--)
{
temp = ar[i];
ar[i] = ar[j];
ar[j] = temp;
}
}Output:
5 4 3 2 1Time Complexity
Since we are iterating over the array once, the time complexity becomes O(n).
Space Complexity
Since the implementation does not use any auxiliary space, the space complexity becomes O(1).
Approach 7 – Reverse an Array in C++ Using the Pointers
In this approach, we use the concept of the c++ pointer to reverse the array where we basically use two pointers pointer1 which points to the beginning address of the array, and pointer2 which points to the ending address of the array.
The elements at these two locations are swapped and the pointer1 pointer is moved to the address of the next array element and the pointer2 pointer is moved to the address of the previous array element.
Algorithm
1) Initialize two pointers pointer1 and pointer2 with the beginning and ending address of the array.
2) Swap the values present at the start and end addresses, increment the start pointer by one and decrement the end pointer by 1.
3) Repeat the second step until the start address crosses the end address or they become the same.
We shall use three functions
reverse: Used to reverse the array
swap: Used to swap the values at addresses pointed by pointer1 and pointer2.
print: Used to print the array elements
Code Implementation in C++:
#include<bits/stdc++.h>
using namespace std;
//swap function
void swap(int *a, int *b){
int temp = *a;
*a = *b;
*b = temp;
}
//reverse array function
void reverse(int arr[], int n){
//Pointer pointing at the beginning
int *pointer1 = arr;
//Pointer pointing at the end of the array
int *pointer2 = arr + n -1;
while(pointer1 < pointer2){
swap(pointer1,pointer2);
pointer1++;
pointer2--;
}
}
///Print the array
void print(int *arr, int n){
//size at the end of the array
int *size = arr + n;
//Position pointing to the beginning of the
// array
int *pos = arr;
for(pos = arr;pos < size; pos++)
cout << *pos << " ";
}
//Driver program
int main(){
//Input array
int arr[] = {1,2,3,4,5};
//Length of the array
int n = sizeof arr / sizeof arr[0];
//reverse the array
reverse(arr,n);
//print the array
print(arr,n);
}Output:
5 4 3 2 1Time Complexity
Since, we are iterating over the array exactly once while swapping elements,hence the time complexity is O(n).
Space Complexity
Since we are not using any extra space, therefore the space complexity is O(1).
Conclusion
- We conclude that there are many methods to reverse an array.
- Technically, they are divided into two approaches, either it can be recursive approach or an iterative approach.
- Some languages provide in-built functions to reverse an array like slicing in python and reverse in c++.
- Arrays can be reversed in-place i.e. there is no need to use any extra space.