Implement Queue Using stack

Problem Statement

The problem statement here is to implement queue using stack.
Queue is a linear data structure which follows First In First Out (FIFO) principle. This means that the element which is inserted first will be the one that will be removed first.

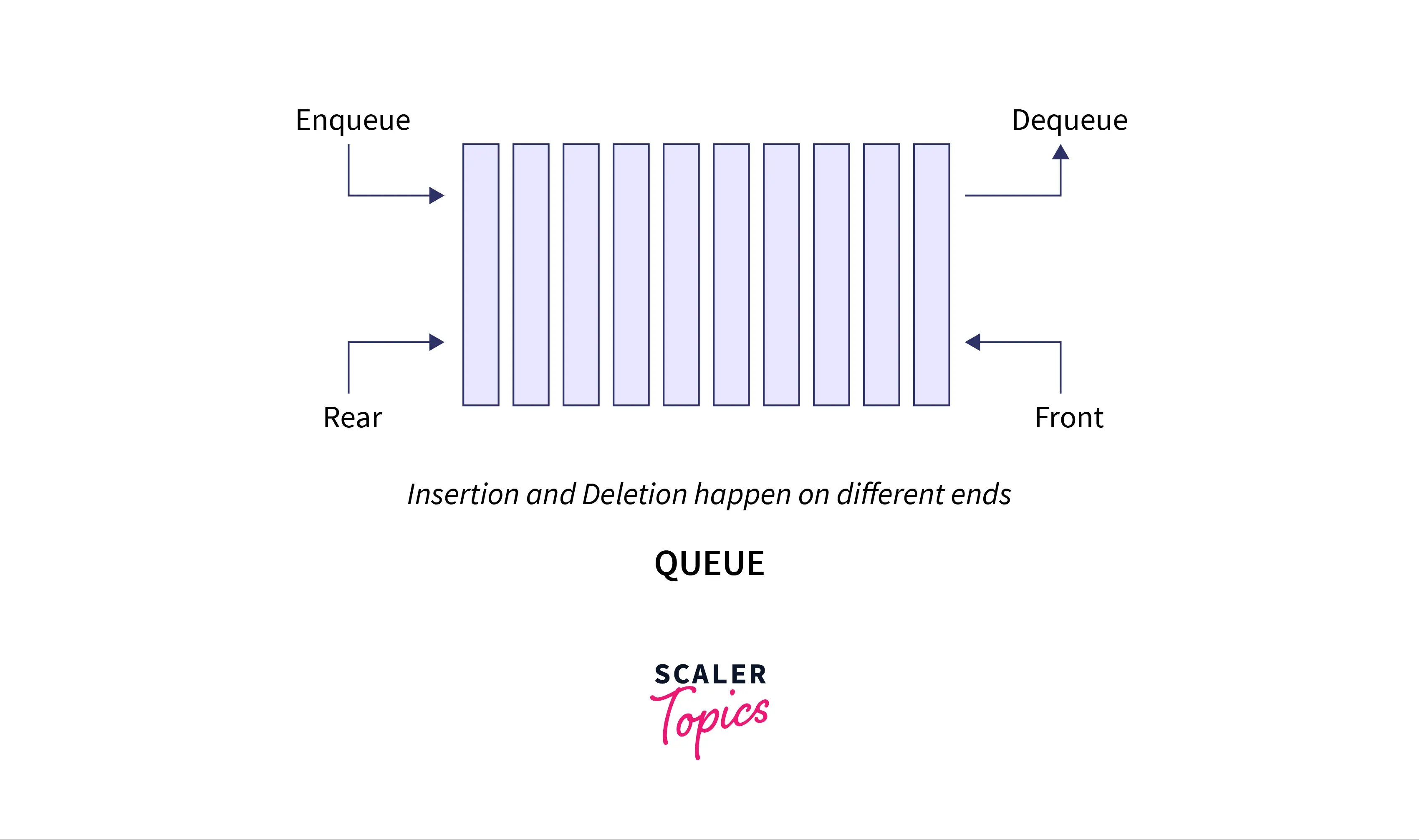
Stack is also a linear data structure which follows Last In First Out (LIFO) principle, means that the element inserted last in the stack will be the one to be removed first from the stack and vice versa.

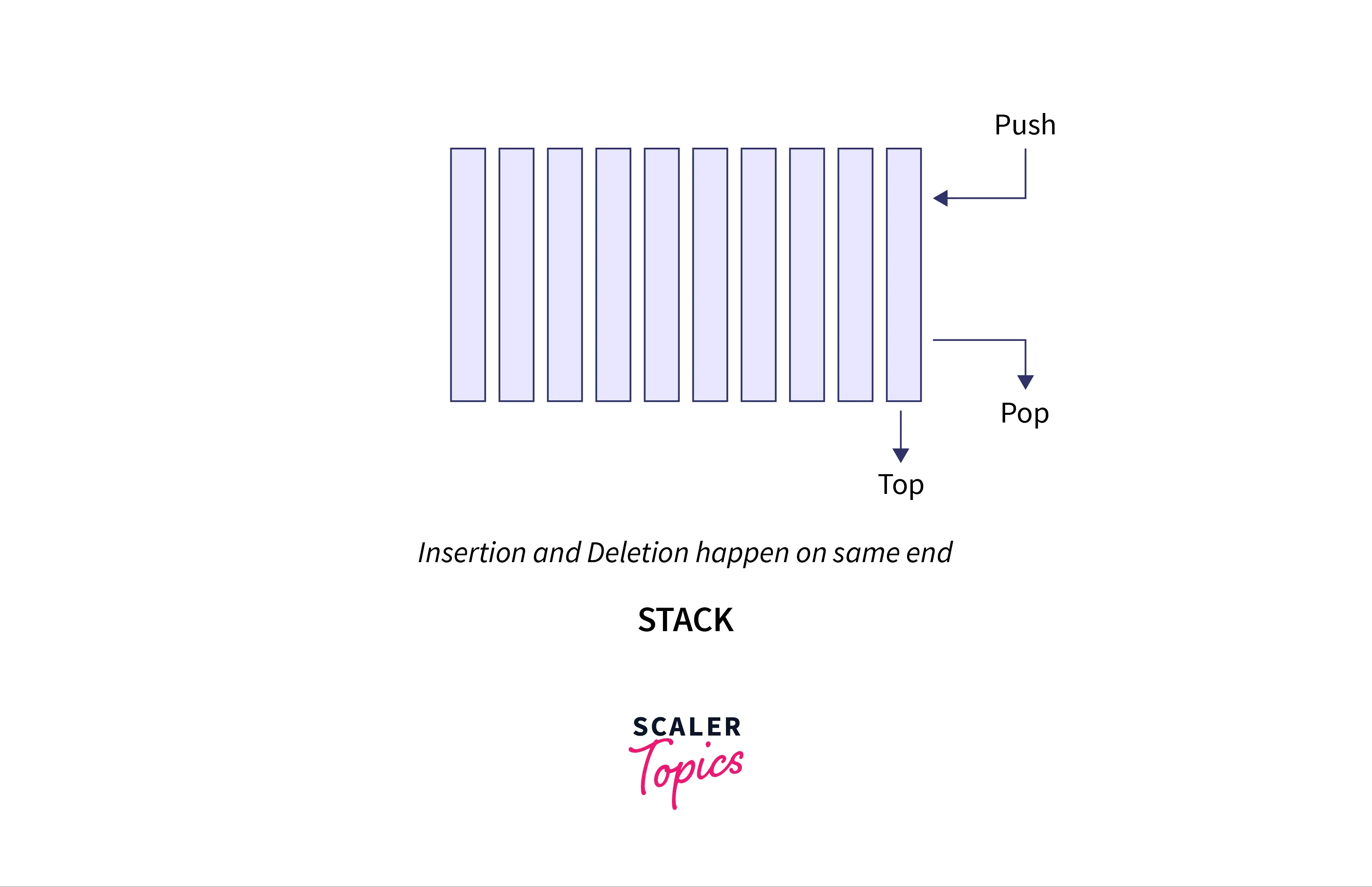
By implementing queue using stack, we should be able to use the First In First Out functionality of the implmented queue with the help of push() and pop() functions. The implemented queue should be able to perform enqueue(insertion) and dequeue(removal) operations.

Example

Input:

queue = []

Operations = [ Push(1), Push(2), Push(3), Pop(), Pop() ]

Output:

For every operations queue will be upldated like: [ [1], [1, 2], [1, 2, 3], [2, 3], [3] ]

Explanation: The queue is using stack operations to implement FIFO functionality, so till the data is pushed to the queue, it will be [1, 2, 3] and for the first Pop() function the firstly entered element will be removed from the queue, so the queue will be [2, 3].
Now for the next Pop() operation, the element 2 will be removed from the queue as it is the most oldest element in the queue, now the queue is [3].

Constraints

$1 <= queue.length <= 1000$

$0 <= queue[i] <= 1000$

Approach 1: Making a dequeue operation costly

As we know that a queue follows FIFO functionality, so to implement queue using stack, we will have to make it in a way that the element entering first in the queue will be the first to be removed.
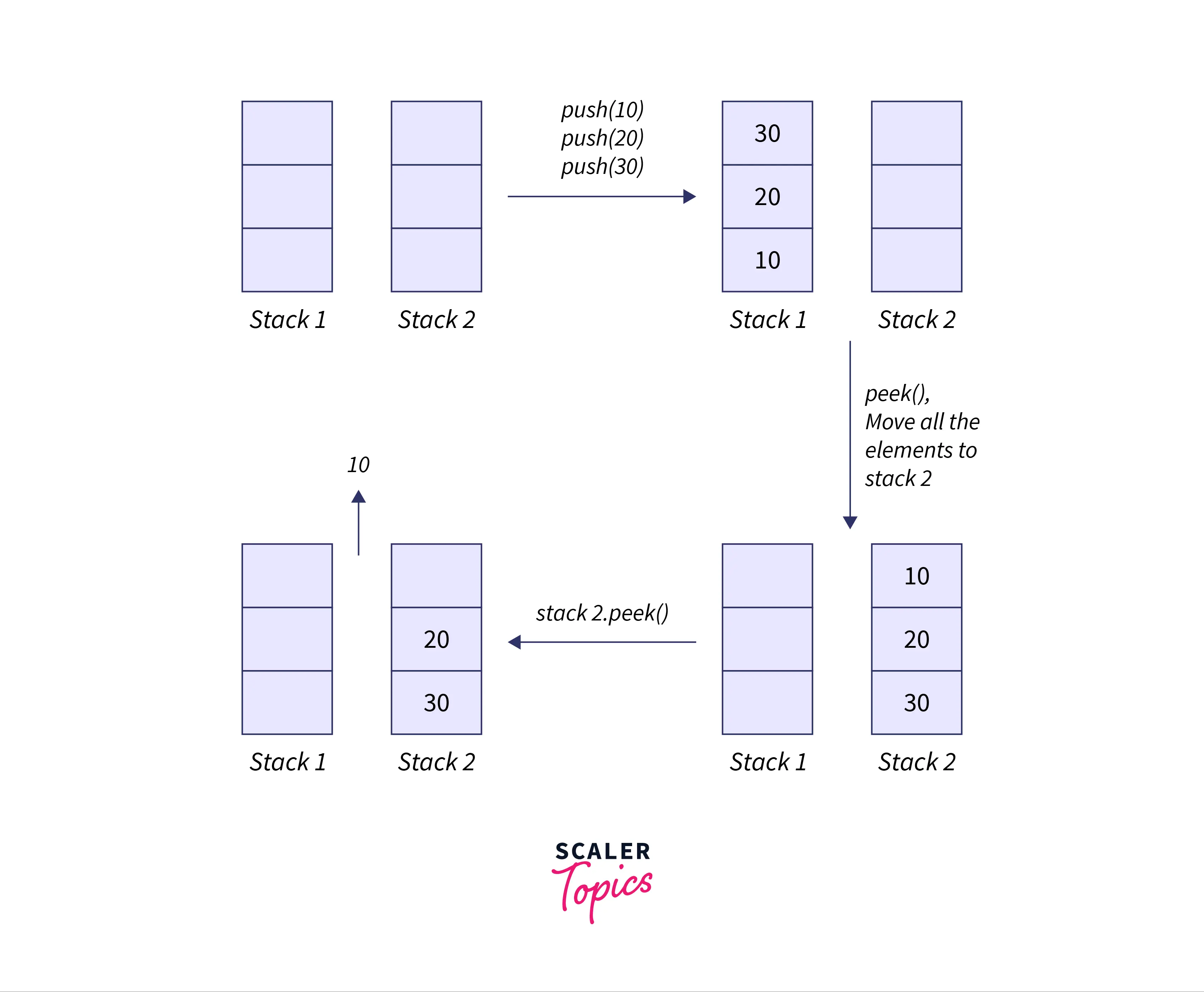
This can be done by using two stacks. By using 2 stacks at a time, we can simply push the element in stack 1 and will pop the first occuring element by pushing all the elements of stack 1 to stack 2 and popping out the top element of stack 2.

In this approach to implement queue using stack, we are making the dequeue operation of one stack costly for reaching the functionality of a queue.

Algorithm: We can implement queue using stack using the below algorithm

Initialize 2 empty stacks s1 and s2

• For enqueue operation
  • push the element to the top of the stack s1.
• For deque operation
  • if s1 and s2 is empty, return -1 as the is no element to remove.
  • If s2 is empty, push all the elements of stack from s1 to s2.
  • remove the top element of the stack s2.

Complexity Analysis

Time Complexity:

• push operation: O(1)
  It is same as the push operation in the stack.
• pop operation: O(N).
  In the worst case we have empty whole of stack 1 into stack 2.

Space Complexity: O(N) => N space for storing N elements in the stacks.

C++ Implementation

struct Queue {
    
    // Initializing the stacks
    stack<int> stack1, stack2;
  
    // Function to implement enqueue
    void enqueue(int element)
    {
        // Pushing element in the stack
        stack1.push(element);
    }
  
    // Function to implement dequeue operation 
    int dequeue()
    {
        // Condition where the queue is empty
        if (stack1.empty() && stack2.empty()) {
            cout << "the queue is empty";
            exit(0);
        }
      
        // Pushing all the elements of stack1 to stack2
        if (stack2.empty()) {
            while (!stack1.empty()) {
                stack2.push(stack1.top());
                stack1.pop();
            }
        }
  
        // Popping the top element from the stack
        int element = stack2.top();
        stack2.pop();
        return element;
    }
};

Java Implementation

static class Queue {
    // Initializing the stacks
    Stack<Integer> stack1;
    Stack<Integer> stack2;
}

// Function to implement enqueue
static void enqueue(Queue q, int element)
{
    // Pushing element in the stack
    push(q.stack1, element);
}

// Function to implement dequeue operation 
static int dequeue(Queue q)
{
    int element;
    
    // Condition where the queue is empty
    if (q.stack1.isEmpty() && q.stack2.isEmpty()) {
        System.out.println("the queue is empty");
        System.exit(0);
    }
    
    // Pushing all the elements of stack1 to stack2
    if (q.stack2.isEmpty()) {
        while (!q.stack1.isEmpty()) {
            element = q.stack1.pop();
            q.stack2.push(element);
        }
    }
    
    // Popping the top element from the stack
    element = q.stack2.pop();
    return element;
}

Python Implementation

class Queue:
    def __init__(self):
        # Initializing the stacks
        self.s1 = []
        self.s2 = []
 
    # Function to implement enqueue
    def enqueue(self, element):
        # Pushing element in the stack
        self.s1.append(element)
 
    # Function to implement dequeue operation 
    def dequeue(self):
        # Condition where the queue is empty
        if (len(self.s1) == 0 and len(self.s2) == 0):
            print("the queue is Empty")
            return
 
        elif (len(self.s2) == 0 and len(self.s1) > 0):
            while len(self.s1):
                element = self.s1.pop()
                self.s2.append(element)
            return self.s2.pop()
 
        else:
            # Popping the top element from the stack
            return self.s2.pop()

Approach 2: Making a enqueue operation costly

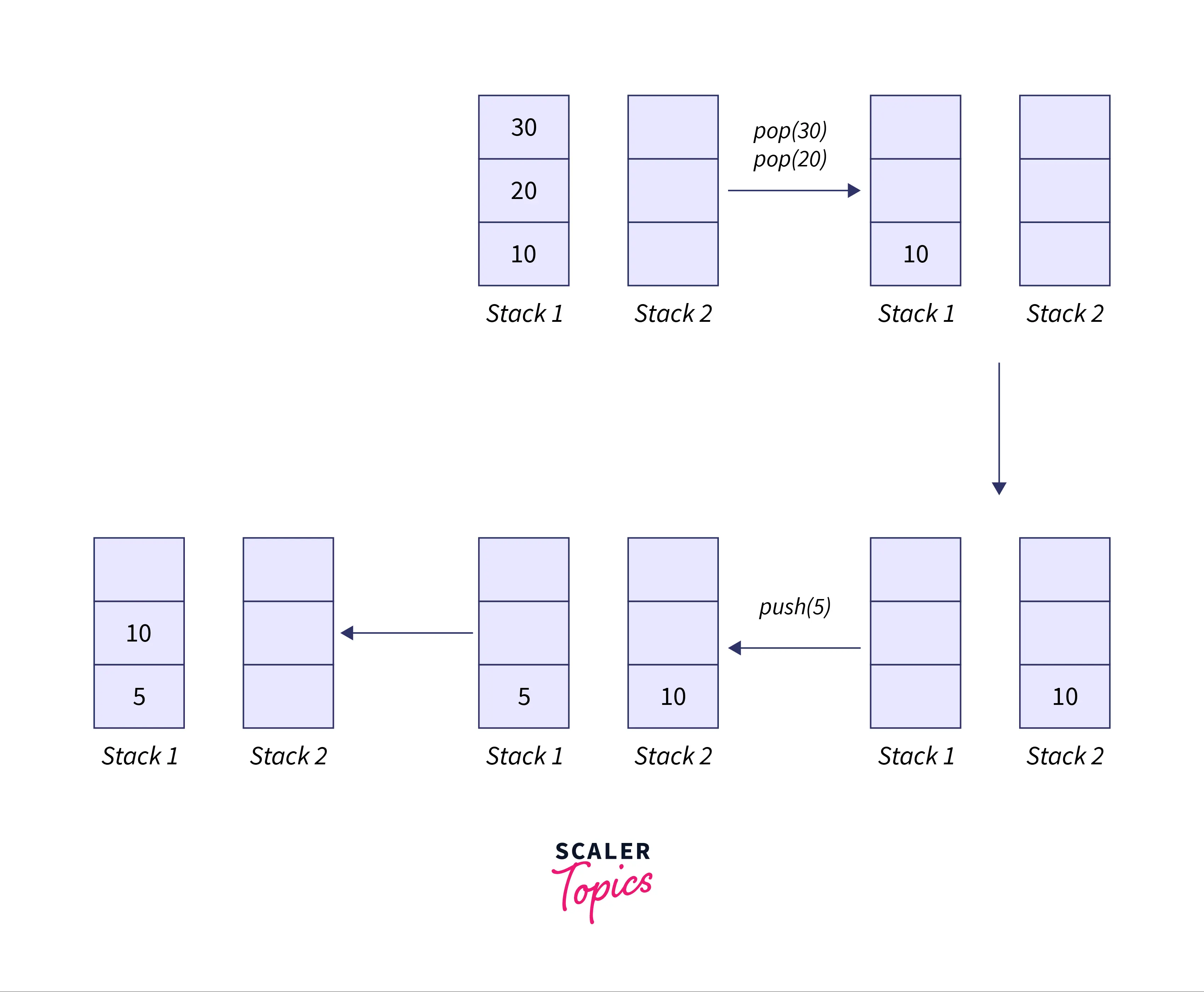
In this approach to implement queue using stack, we are making use of 2 stacks for the opertions by making the enqueue operation of one stack costly for reaching the functionality of a queue.

Algorithm: We can implement queue using stack using the below algorithm

Initialize 2 empty stacks s1 and s2

• For enqueue operation
  • while the stack s1 is empty, push the element to stack s2.
  • else, push all the elements from stack s1 to stack s2, and push the element to the top of the stack s1.
  • Now, Push all the elements from stack s2 to stack s1.
• For deque operation
  • if the stack is empty, return -1.
  • Otherwise, pop and return the top element of the stack s1.

Complexity Analysis

Time Complexity:

• push operation: O(N) In the worst case we have empty whole of stack 1 into stack 2 and vice versa.
• pop operation: O(1). It is same as the pop operation in the stack.

Space Complexity: O(N) => N space for storing N elements in the stacks.

C++ Implementation

struct Queue {
    // Initializing both the stacks
    stack<int> stack1, stack2;
  
    // Function to implement enqeue operation
    void enqueue(int element)
    {
        // Push all the elements of stack1 to stack2
        while (!stack1.empty()) {
            stack2.push(stack1.top());
            stack1.pop();
        }
  
        stack1.push(element);
  
        // Push all the elements back to s1
        while (!stack2.empty()) {
            stack1.push(stack2.top());
            stack2.pop();
        }
    }
  
    // Function to implement deqeue operation
    int dequeue()
    {
        // If stack1 is empty, return -1 or a message
        if (stack1.empty()) {
            cout << "the queue is Empty";
            exit(0);
        }
  
        // Top of the stack is returned
        int element = stack1.top();
        stack1.pop();
        return element;
    }
};

Java Implementation

static class Queue
{
    // Initializing both the stacks
	static Stack<Integer> stack1 = new Stack<Integer>();
	static Stack<Integer> stack2 = new Stack<Integer>();

    // Function to implement enqeue operation
	static void enqueue(int element)
	{
        // Push all the elements of stack1 to stack2
        while (!stack1.isEmpty())
		{
			stack2.push(stack1.pop());
		}

		stack1.push(element);

        // Push all the elements back to s1
		while (!stack2.isEmpty())
		{
			stack1.push(stack2.pop());
			//s2.pop();
		}
	}

    // Push all the elements back to s1
	static int dequeue()
	{
        // If stack1 is empty, return -1 or a message
		if (stack1.isEmpty())
		{
			System.out.println("the queue is Empty");
			System.exit(0);
		}

        // Top of the stack is returned
		int element = stack1.peek();
		stack1.pop();
		return element;
	}

Python Implementation

class Queue: 
    def __init__(self):
        # Initializing both the stacks
        self.stack1 = []
        self.stack2 = []
  
    # Function to implement enqeue operation
    def enqueue(self, element):
          
        # Push all the elements of stack1 to stack2
        while len(self.stack1) != 0: 
            self.stack2.append(self.stack1[-1]) 
            self.stack1.pop()
  
        self.stack1.append(element) 
  
        # Push everything back from stack2 to stack1 
        while len(self.stack2) != 0: 
            self.stack1.append(self.stack2[-1]) 
            self.stack2.pop()
  
    # Function to implement deqeue operation
    def dequeue(self):
          
        # If stack1 is empty, return -1 or a message
        if len(self.stack1) == 0: 
            print("the queue is Empty")
      
        # Top of the stack is returned
        element = self.stack1[-1] 
        self.stack1.pop() 
        return element

Conclusion

• The problem statement here is to implement queue using stack.
• implement queue using stack means we should be able to use the First In First Out functionality of the implmented queue.
• There are two techniques to implement queue using stack:
  • Making a dequeue operation costly: the dequeue operation will take O(N) time and enqueue will be time effective with the time complexity of O(1).
  • Making an enqueue operation costly: The enqueue operation will take O(N) time and dequeue will be time effective with the time complexity of O(1).