As developers, we should be aware of the basic computer science concept of search algorithms such as linear search and binary search. Finding a given element’s occurrence in a list is the process of searching. In this article, we will discuss the difference between linear search and Binary search.
There are two types of searching algorithms
- Sequential / Linear Search
- Binary Search
What is Linear Search?
A linear search, also called as sequential search, simply scans each element one at a time. In this search, an array is sequentially traversed from the first element until the element is found or the end of the array is reached. This method can only be suitable for searching over a small array or an unsorted array.
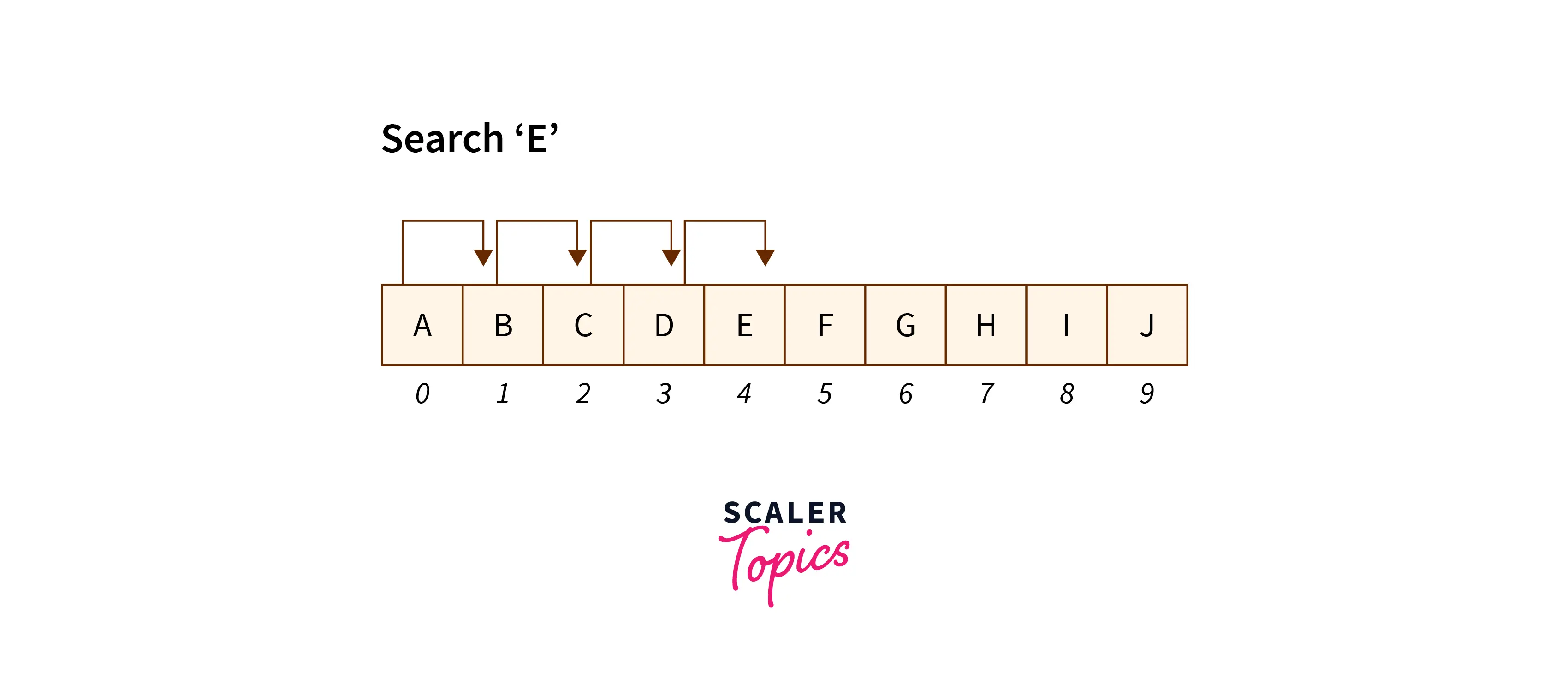
Algorithm
- Assume we need to find an element that is in an array in random order.
- Start with the first position and compare it to the target in order to search for a target element.
- If the current element matches the target element, return the position of the current element.
- If not, move on to the next one until we reach the very end of an array.
- If still unable to find the target, return -1.
Syntax in C++
// Linear Search in C++
#include <iostream>
using namespace std;
int linearSearch(int array[], int n, int target)
{
// traversing through the array sequentially
for (int i = 0; i < n; i++)
if (array[i] == target)
return i;
return -1;
}
Syntax in Java
// Linear Search in Java
import java.io.*;
class Main {
public static int linearSearch(int arr[], int target)
{
for (int a = 0; a< arr.length; a++) {
if (arr[a] == target)
return a;
}
return -1;
}
}
Syntax in Python
# Linear Search in Python
def linearSearch(array, n, target):
for i in range(0, n):
if (array[i] == target):
return i
return -1
Complexity Analysis
Time Complexity
- The Best Case: O(1), when the array’s first element is the target element.
- The Worst Case: O(N) When the array’s last element is the target element.
Space Complexity
- It has a space complexity of O(1).
What is Binary Search?
The Binary search method is only suitable for searching in a sorted array. In this method, the element that has to be searched is compared to the array’s middle element. Search is considered successful only if it matches the target. The binary search algorithm uses the divide-and-conquer approach; it does not scan every element in the list; it only searches half of the list instead of going through each element. It is said to be the best searching algorithm because it is faster to execute than linear search.
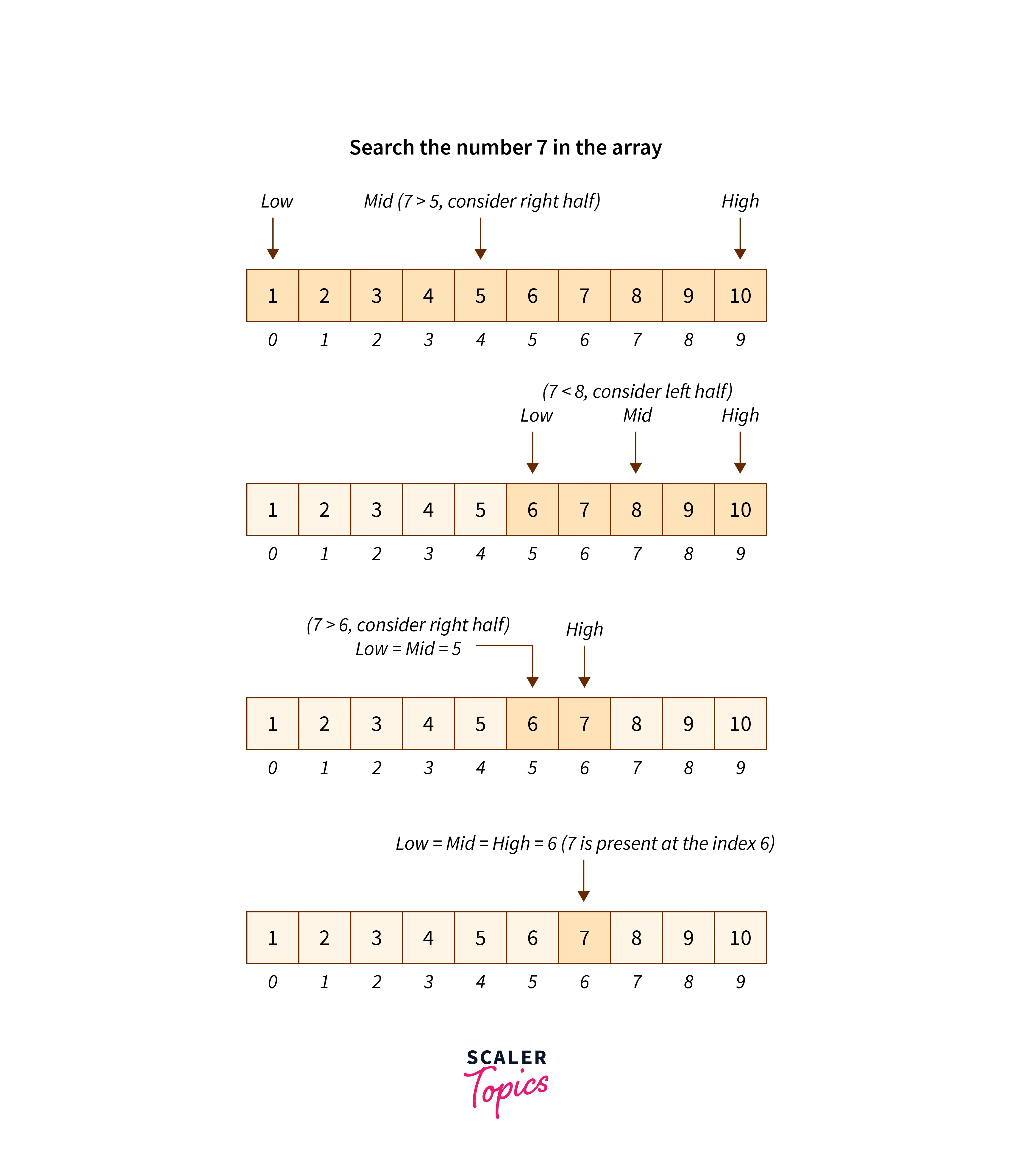
Algorithm
- Start with the middle element of the array as a current key.
- If the middle element value matches the target element then return the index of the middle element.
- Otherwise, check if the target element is less than the middle element, and then continue the search in the left half.
- If the target element is greater than the middle element, then continue the search in the right half.
- Check from the second point repeatedly until the value is found or the array is empty.
- If still unable to find the target, return -1.
The Three Cases That are Used in the Binary Search:
Case 1: arr[mid] == target // then return the index
Case 2: arr[mid] < target // then right=mid-1
Case 3: arr[mid] > target // then left = mid+1.
Syntax in C++
// Linear Search in C++
#include <iostream>
using namespace std;
int binarySearch(int arr[], int target, int low, int high)
{
// Repeat until the pointers low and high meet each other
while (low <= high) {
int mid = low + (high - low) / 2;
// Check if target is present at mid
if (arr[mid] == target)
return mid;
// If target greater, ignore left half
if (arr[mid] < target)
low = mid + 1;
// If target is smaller, ignore right half
else
high = mid - 1;
}
return -1;
}
Syntax in Java
// Linear Search in Java
class Main {
public static int binarySearch(int[] arr, int target)
{
int start = 0;
int end = arr.length - 1;
// Repeat until the pointers low and high meet each other
while (start <= end) {
int mid = (start + end) / 2;
// Check if target is present at mid
if (target == arr[mid]) {
return mid;
}
// If target greater, ignore left half
else if (target > arr[mid]) {
start = mid + 1;
}
// If target is smaller, ignore right half
else {
end = mid - 1;
}
}
return -1;
}
}
Syntax in Python
# Linear Search in Python
def binarySearch(arr, target, low, high):
# Repeat until the pointers low and high meet each other
while low <= high:
mid = low + (high - low) // 2
# Check if target is present at mid
if arr[mid] == target:
return mid
# If target greater, ignore left half
elif arr[mid] < target:
low = mid + 1
# If target is smaller, ignore right half
else:
high = mid - 1
return -1
Complexity Analysis
Time Complexity
- The Best Case: O(1), when the array’s middle element is the target element.
- The Worst Case: O(logN) when the array does not have the target element or is far away from the middle element.
Space Complexity
- It has a space complexity of O(1) for the iterative version.
- It has space complexity of O(log n) for the recursive version.
Difference Between Linear Search and Binary Search
| Linear Search | Binary Search |
|---|---|
| Commonly known as sequential search. | Commonly known as half-interval search. |
| Elements are searched in a sequential manner (one by one). | Elements are searched using the divide-and-conquer approach. |
| The elements in the array can be in random order. | Elements in the array need to be in sorted order. |
| Less Complex to implement. | More Complex to implement. |
| Linear search is a slow process. | Binary search is comparatively faster. |
| Single and Multidimensional arrays can be used. | Only single dimensional array can be used. |
| Does not Efficient for larger arrays. | Efficient for larger arrays. |
| The worst-case time complexity is O(n). | The worst case time complexity is O(log n). |
Explore Scaler Topics Data Structures Tutorial and enhance your DSA skills with Reading Tracks and Challenges.
Conclusion
- As a developer, you should be aware of the basic computer science concepts of search algorithms, such as linear and binary search.
- In a linear search, each element in the list is sequentially searched one after the other until it is found in the list.
- A binary search finds the list’s middle element recursively until the middle element matches a searched element.
- Linear search can be suitable for searching over an unsorted array.
- The binary search algorithm uses the divide-and-conquer approach.