Problem Statement
In this article we are going to discuss a variant of the Permutation of String. The problem statement goes like this, you will be given two strings, say s1 and s2. And, we need to find a substring in s2 that is a permutation of string s1.
What is the Permutation of a String?
The permutation of string is the set of all the strings, that contains the same characters as the original string, but the order of the arrangement of the characters can be different.
Input Format: For the input, you will be given two strings string s1 and string s2.
Input:
s1 = "ab"
s2 = "dqbac"
TASK: Find a substring in s2 that is a permutation of s1.
Output:
True
Let us now look at an example to understand better.
Examples
Example 1: Let us look at the first set of our examples.
Input:
s1 = "ab"
s2 = "mnbac"
Output:
True
Explanation: In the above example, we are given two strings – ab and mnbac. Now, ba is a permutation of string of the string ab. And, ba is a substring of the string s2 = mnbac. Hence we return a True.
Input:
s1 = "xt"
s2 = "axv"
Output:
False
Explanation: In the above example, we are given two strings – s1 = “xt” and s2 = “axv”. Now, since no permutation of our string s1 = “xt” is present in our string s2, we simply return a False.
Constraints
Below given are the constraints for the above code:
In the input, you will be give two strings s1 and s2. Following will be the constraints attached with them:
- $1 <= s1.length, s2.length <= 10^4$
- $s1$ and $s2$ consists of lowercase English letters.
Approach #1 of Permutation of String: Brute Force Approach
Let us begin with the Brute Force approach for getting to our solution for the Permutation of String problem.
The most straightforward approach is to create all possible combinations of the shorter string given and then determine whether each combination produced is a substring of the longer string or not.
Algorithm:
- To create all possible combinations of the shorter string, we utilise the function
permute(string 1, string 2, current index)to create every feasible pairing. - Above method generates every combination of the shorter string
s1that is possible. - Permute accepts as one of the inputs the index of the current element current indexcurrent index, as one of its parameters.
- After that, to create a new ordering of the array items, it then swaps the current element with every other member in the array that is located to its right.
- Following the swapping, it calls
permute(string 1, string 2, current index)once again, but this time using the index of the subsequent element in the array. - As a result, a new ordering of the array’s items is created when reaches the end of the array.
- The procedure for creating the permutations is shown in the following image.
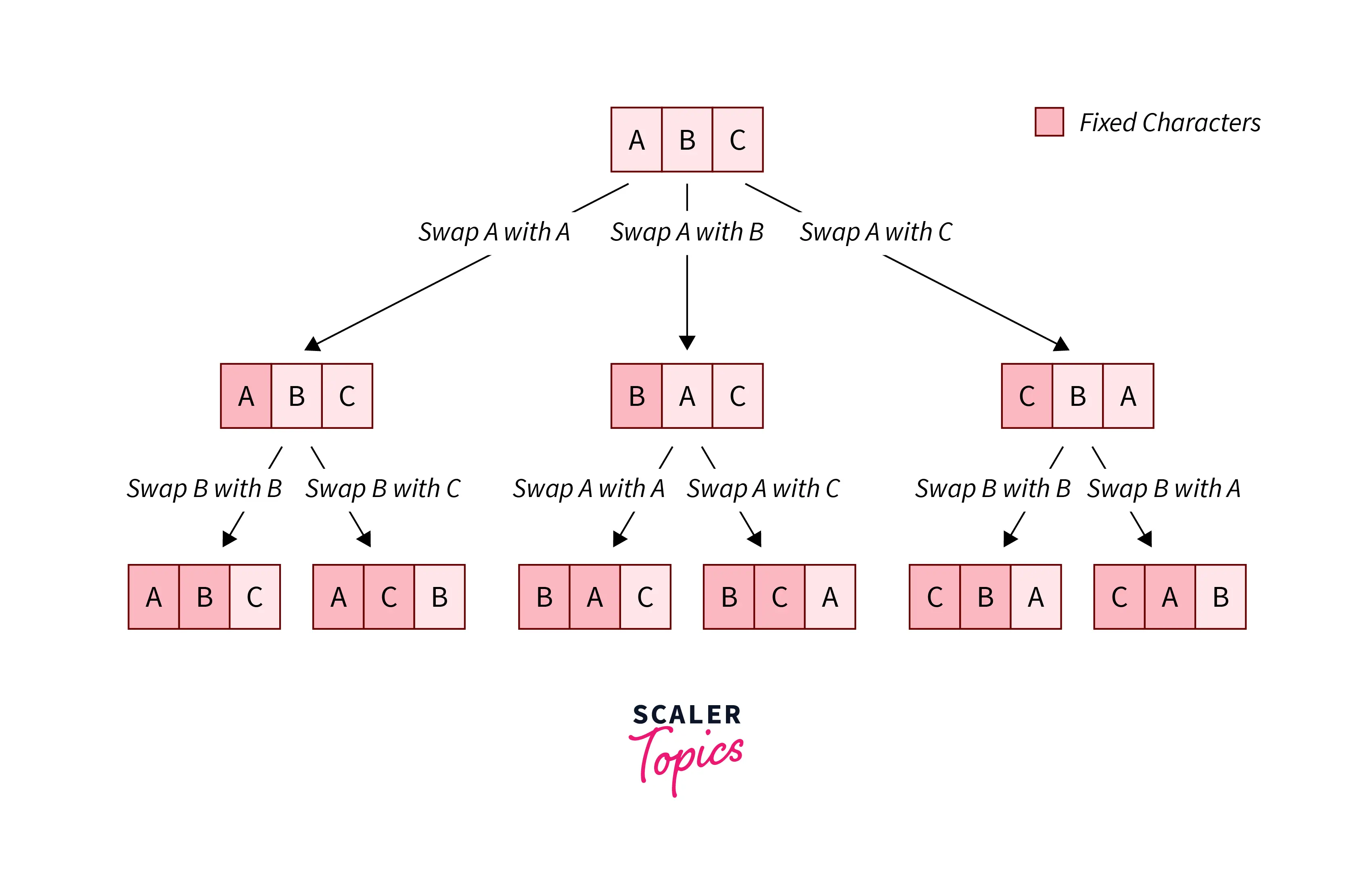
But doing so will result in the TLE (Time Limit Exceed) in most of the coding platforms. Let us look into the code of it, and then we will learn more approaches to solving this of string permutation.
Implementation in C++, Java and Python
Java Code:
public class Solution {
boolean flag = false;
// to check if s2 contains a permutation of s1
// returns a true or false on the basis
// of the flag variable, updated by the
// permute function
public boolean checkInclusion(String s1, String s2) {
// function which will
// check whether the permutation
// of string s1 is present in s2
permute(s1, s2, 0);
return flag;
}
// swap function to swap the substring
// of the given string
public String swap(String s, int i0, int i1) {
if (i0 == i1)
return s;
String s1 = s.substring(0, i0);
String s2 = s.substring(i0 + 1, i1);
String s3 = s.substring(i1 + 1);
return s1 + s.charAt(i1) + s2 + s.charAt(i0) + s3;
}
// code to check whether s2
// contains a permutation of s1
// updates flag on the basis of that
void permute(String s1, String s2, int l) {
if (l == s1.length()) {
if (s2.indexOf(s1) >= 0)
flag = true;
} else {
for (int i = l; i < s1.length(); i++) {
s1 = swap(s1, l, i);
permute(s1, s2, l + 1);
s1 = swap(s1, l, i);
}
}
}
}Python Code:
class Solution:
# flag is a class variable that
# stores True if s2 is permutation of s1
# else false
def __init__(self):
self.flag = False
# to check if s2 contains a permutation of s1
# returns a true or false on the basis
# of the flag variable, updated by the
# permute function
def checkInclusion(self, s1, s2):
# function which will
# check whether the permutation
# of string s1 is present in s2
self.permute(s1, s2, 0)
return self.flag
# swap function to swap the substring
# of the given string
def swap(self, s, i0, i1):
if i0 == i1:
return s
s1 = s[0:i0]
s2 = s[i0 + 1:i1]
s3 = s[i1 + 1:]
return s1 + s[i1] + s2 + s[i0] + s3
# code to check whether s2
# contains a permutation of s1
# updates flag on the basis of that
def permute(self, s1, s2, l):
if l == len(s1):
if s2.find(s1) >= 0:
self.flag = True
else:
i = l
while i < len(s1):
s1 = self.swap(s1, l, i)
self.permute(s1, s2, l + 1)
s1 = self.swap(s1, l, i)
i += 1
# driver code
#creating object of solution class
ob = Solution()
# calling the function
ans = ob.checkInclusion("ab","mnbac")
# displaying results
print(ans)Output:
TrueC++ Code:
// Include header file
#include <iostream>
#include <string>
#include <vector>
class Solution
{
public:
bool flag = false;
// to check if s2 contains a permutation of s1
// returns a true or false on the basis
// of the flag variable, updated by the
// permute function
bool checkInclusion(std::string s1, std::string s2)
{
// function which will
// check whether the permutation
// of string s1 is present in s2
permute(s1, s2, 0);
return flag;
}
// swap function to swap the substring
// of the given string
std::string swap(std::string s, int i0, int i1)
{
if (i0 == i1)
{
return s;
}
std::string s1 = s.substr(0,i0);
std::string s2 = s.substr(i0 + 1,i1);
std::string s3 = s.substr(i1 + 1);
return s1 + std::to_string(s[i1]) + s2 + std::to_string(s[i0]) + s3;
}
// code to check whether s2
// contains a permutation of s1
// updates flag on the basis of that
void permute(std::string s1, std::string s2, int l)
{
if (l == s1.length())
{
if (s2.indexOf(s1) >= 0)
{
flag = true;
}
}
else
{
for (int i = l; i < s1.length(); i++)
{
s1 = swap(s1, l, i);
permute(s1, s2, l + 1);
s1 = swap(s1, l, i);
}
}
}
};Time Complexity Analysis
The worst-case time complexity of the above brute force approach is $O(N!*M)$. The $N$ in the time complexity depicts the length of the shorter string. And, $M$ denotes the length of the larger string. The major reason for this exponential time complexity is that, first of all, we try to match all the permutations of our shorter string S1, which is having a length of $N$, with our larger string S2. And, to generate the permutations of a string of length $N$, we take a time of $O(N!)$. Also, at every step we compare the permutation of the substring S1 with the string S2.
Space Complexity Analysis
The Space complexity for the above approach will be $O(n^2)$ in the worst case. The reason for this is that the depth of the recursion tree will be $n$. Please note that $n$ refers to the length of the shorter string. Also, in our recursion tree, every node will contain a string having a maximum length of $n$.
Approach #2 of Permutation of String: Using Sorting
Let us now look at our second approach to solving the Permutation of String problem. In this approach, we will be using the sorting technique to find out our results. Now let us look at some conditions before implying the method:
- This method is majorly based on the principle that two strings can only be permuted if they both contain the same characters the same number of times.
- Only if $sorted(x) = sorted(y)$, then we can say that the
string xis a permutation of thestring y.
Algorithm:
- We may compare the two strings after sorting them to verify whether they contain the same number of characters or not after sorting.
- So, we sort out the shorter string
S1. - After that, we find all the substrings of the string
s2, of lengths1, sort them and compare them with the strings1. - If both of them completely match, then we can say that the string
s1‘s permutation is a substring ofs2, and we can returnTrue, - Else, we return a
False.
Implementation in C++, Java and Python
Java Code:
public class Solution {
// to check if s2 contains a permutation of s1
// returns a true or false on the basis
// of that
public boolean checkInclusion(String s1, String s2) {
// sort the string s1
s1 = sort(s1);
//run a loop to check if
// any substring of "sorted" string s2 is
// equal to that of s1 or not
for (int i = 0; i <= s2.length() - s1.length(); i++) {
if (s1.equals(sort(s2.substring(i, i + s1.length()))))
// return true if substring of
// s1 is present in s2
return true;
}
//else return false
return false;
}
// our custom sort function
public String sort(String s) {
char[] t = s.toCharArray();
Arrays.sort(t);
return new String(t);
}
}
Python Code:
class Solution:
# to sort given string s
def sort_string(self, s):
# sorted returns a list of
# alphabetically sorted string
# "join" joins the list of string
return str(''.join(sorted(s)))
# to check if s2 contains a permutation of s1
# returns a true or false on the basis of it
def checkInclusion(self, s1, s2):
l = len(s1)
# sort string s1
s1 = self.sort_string(s1)
i = 0
while i <= len(s2) - len(s1):
# checks if sorted substring s2
# is equal to s1 or not
if s1 == self.sort_string(s2[i:i+l]):
return True
i += 1
# returns false if none of the substrings
# of s2 matches with s1
return False
# driver code
#creating object of solution class
ob = Solution()
# calling the function
ans = ob.checkInclusion("ab","mnbac")
# displaying results
print(ans)
Output:
True
C++ Code:
// to check if s2 contains a permutation of s1
// returns a true or false on its basis
bool checkInclusion(string s1, string s2) {
// empty string is always a substring
// so return True
if(s1 == "")
return true;
// if s1 is non-empty and s2 is empty
// then definitely s2 won't contain
// permutation of s1, so return false
if(s2 == "")
return false;
int n = s1.length(), m = s2.length();
// sort string s1
sort(s1.begin(),s1.end());
//run a loop to check if
// any substring of "sorted" string s2 is
// equal to that of s1 or not
for(int i=0; i<m; i++){
if(m-i < n)
break;
else if(find(s1.begin(),s1.end(),s2[i]) != s1.end()){
string str = s2.substr(i,n);
// sort substring of s2
sort(str.begin(),str.end());
// return true if substring of
// s1 is present in s2
if(str == s1)
return true;
}
}
// return false otherwise
return false;
}
Time Complexity Analysis
As we must be already familiar, that the sorting function takes a worst-case time complexity of O(NlogN), our code also has somewhat similar time complexity. Let us analyze the time complexity for this code:
Suppose, the length of our string s1 is $n_1$ and the string s2 is $n_2$. Now, to sort the first string the time taken will be $O(n_1logn_1)$. And to sort the substrings of string s2, for $(n_2-n_1)$ times, the total time taken for will be $(n_2-n_1)*n_2logn_2$ .
So, the total time complexity taken for the sorting approach will be: $O(n_1logn_1)+(n_2-n_1)*n_2logn_2$ .
Space Complexity Analysis
For some of the code, a space of $O(n1)*t$ can be used for storing the sorted array. Here n1 is the length of the shorter string s1.
Approach #3 of Permutation of String: Using Hashmap
As was previously said, two strings may only be called permutations of each other if they share the same characters and occur at the same frequency. We may take into account every feasible substring in the longer string s2, which is the same length as string s1, and compare the character frequencies in the two. Only the permutation of the letters s1 can be a substring of s2 if the letter frequencies are identical.
Instead of sorting and comparing the parts for equality to execute this strategy, we use a hashmap called s1map that holds the frequency of occurrence of each letter in the short string s1.
We look at every s2 substring that is the same length as string s1 and calculate the s2map hashmap that corresponds to it. The substring which we will take into consideration can be thought of as a window having the same length as that of s1 iterating over s2.
We may conclude that s1‘s permutation is a substring of s2 if the two hashmaps we get are identical for any such window, but not if they are unidentical.
Implementation in C++, Java and Python
Java Code:
public class Solution {
// to check if s2 contains a permutation of s1
// returns a true or false on its basis
public boolean checkInclusion(String s1, String s2) {
// if s1's length is greater than
// s2, then definitely no permutation
// of s1 will be contained in s2
// so return false
if (s1.length() > s2.length())
return false;
HashMap < Character, Integer > s1map = new HashMap<> ();
// store the frequency of the characters
// of string s1
for (int i = 0; i < s1.length(); i++)
s1map.put(s1.charAt(i), s1map.getOrDefault(s1.charAt(i), 0) + 1);
// store the frequency of the characters
// of every substring of string s2
for (int i = 0; i <= s2.length() - s1.length(); i++) {
HashMap <Character, Integer> s2map = new HashMap<> ();
for (int j = 0; j < s1.length(); j++) {
s2map.put(s2.charAt(i + j), s2map.getOrDefault(s2.charAt(i + j), 0) + 1);
}
// compare the two hashmaps
// if they are equal then return a true
if (matches(s1map, s2map))
return true;
}
return false;
}
// custom match function to
// match the two hashmaps
public boolean matches(HashMap <Character, Integer> s1map, HashMap <Character, Integer> s2map) {
for (char key: s1map.keySet()) {
if (s1map.get(key) - s2map.getOrDefault(key, -1) != 0)
return false;
}
return true;
}
}
Python Code:
class Solution:
def checkInclusion(self, s1, s2):
if len(s1) > len(s2):
return False
#hashmap to store the first string
s1map = [0 for _ in range(26)]
#hashmap to store the second string
s2map = [0 for _ in range(26)]
i = 0
# s1map and s2map are stores the frequency
# of both the strings s1 and s2
while i < len(s1):
s1map[ord(s1[i]) - ord('a')] += 1
s2map[ord(s2[i]) - ord('a')] += 1
i += 1
i = 0
while i < len(s2) - len(s1):
# compare the two hashmaps
# if they match then return True
if self.matches(s1map, s2map):
return True
# to store the frequency of the
# next window of the substring of
# s2 in the s2map
s2map[ord(s2[i + len(s1)]) - ord('a')] += 1
s2map[ord(s2[i]) - ord('a')] -= 1
i += 1
# compares and matches 2 hashmaps
# whether they are same or not
return self.matches(s1map, s2map)
# custom function to implement matching
# of two dictionaries
def matches(self, s1map, s2map):
for i in range(0, 26):
if s1map[i] != s2map[i]:
return False
return True
# driver code
#creating object of solution class
ob = Solution()
# calling the function
ans = ob.checkInclusion("ab","mnbac")
# displaying results
print(ans)
Output:
True
C++ Code:
// to check if s2 contains a permutation of s1
// returns a true or false on its basis
bool checkInclusion(string s1, string s2) {
// empty string is always a substring
// so return True
if(s1 == "")
return true;
// if s1 is non-empty and s2 is empty
// then definitely s2 won't contain
// permutation of s1, so return false
if(s2 == "")
return false;
int n = s1.length(), m = s2.length();
// store the frequency of the characters
// of string s1
unordered_map<char,int> m1;
for(int i=0; i<n; i++)
m1[s1[i]]++;
for(int i=0; i<m; i++){
if(m1.find(s2[i]) != m1.end() && (m-i) >= n){
// store the frequency of the characters
// of every substring of string s2
unordered_map<char,int> m2;
for(int j=i; j<n+i; j++)
m2[s2[j]]++;
//loop through the map m2
// and compare the frequency of
// the two unordered_maps m1 and m2
int f = 0;
for(auto k : m2) {
if(m1.find(k.first) == m1.end() || m1[k.first] != k.second)
{
f = 1;
break;
}
}
//if no permutation of s1
// present in s2 return true
if(f == 0)
return true;
}
}
// else return false
return false;
}
Time Complexity Analysis
Suppose, the length of our string s1 is n1 and the string s2 is n2. Now, we are storing the frequencies of the characters in the strings in the hashmaps. Hence the worst case time taken for inserting them into hashmap and performing the above operations will be $O(n_1 + 26n_1(n_2-n_1))$. Please note, that the hashmap will store at most 26 keys.
Space Complexity Analysis
As we already know, there is a constant number of alphabets, since there are 26 alphabets in total. Hence, in the worst case, our hashmap will be of size 26. So, we can conclude that the worst-case space taken will remain constant, or $O(1)$ because the number of alphabets is constant.
Approach #4 of Permutation of String: Using Array
In the last approach, we were using a special hashmap data structure to store the frequency of the occurrence of characters in the strings. This was creating an overhead by adding extra space complexity to the hash map data structure. But, in this approach, we will do something better, that is, we will be using an array of length 26(number of characters) to solve the above problem. Let us see how.
Algorithm
Otherwise we can simply return a False, stating the permutation of the string s1 is not present in string s2.
In this approach, we will use an array to store the frequency of each element.
We can assume that each index of the array represents the lowercase English alphabets and for each index, we will store the corresponding character count (frequency of the character).
After storing the frequency of the elements, we can just compare each window(of length equal to s1) of string s2 with that of string s1.
If the frequency matches completely, then we can conclude that the permutation of string s1 is present in string s2, and will return a True.
Implementation in C++, Java and Python
Java Code:
public class Solution {
// to check if s2 contains a permutation of s1
// returns a true or false on its basis
public boolean checkInclusion(String s1, String s2) {
// if s1's length is greater than
// s2, then definitely no permutation
// of s1 will be contained in s2
// so return false
if (s1.length() > s2.length())
return false;
// hashmap to contain frequencies of
// the 26 alphabets
int[] s1map = new int[26];
// store the frequency of the characters
// of string s1
for (int i = 0; i < s1.length(); i++)
s1map[s1.charAt(i) - 'a']++;
for (int i = 0; i <= s2.length() - s1.length(); i++) {
// store the frequency of the characters
// of every substring of string s2
int[] s2map = new int[26];
for (int j = 0; j < s1.length(); j++) {
s2map[s2.charAt(i + j) - 'a']++;
}
// compare the two hashmaps
// if they are equal then return a true
if (matches(s1map, s2map))
return true;
}
return false;
}
// custom match function to
// match the two hashmaps
public boolean matches(int[] s1map, int[] s2map) {
for (int i = 0; i < 26; i++) {
if (s1map[i] != s2map[i])
return false;
}
return true;
}
}
Python Code:
class Solution:
# to check if s2 contains a permutation of s1
# returns a true or false on its basis
def checkInclusion(self, s1, s2):
# if s1's length is greater than
# s2, then definitely no permutation
# of s1 will be contained in s2
# so return false
if len(s1) > len(s2):
return False
# hashmap to contain 26 alphabets
s1map = [0 for _ in range(26)]
i = 0
# store the frequency of the characters
# of string s1
while i < len(s1):
s1map[ord(s1[i]) - ord('a')] += 1
i += 1
i = 0
# iterate till len(s2)-len(s1)
while i <= len(s2) - len(s1):
# store the frequency of the characters
# of every substring of string s2
s2map = [0 for _ in range(26)]
j = 0
while j < len(s1):
s2map[ord(s2[i + j]) - ord('a')] += 1
j += 1
# compare the two hashmaps
# if they are equal then return a true
if self.matches(s1map, s2map):
return True
i += 1
return False
# custom match function to
# match the two hashmaps
def matches(self, s1map, s2map):
for i in range(0, 26):
if s1map[i] != s2map[i]:
return False
return True
# driver code
#creating object of solution class
ob = Solution()
# calling the function
ans = ob.checkInclusion("ab","mnbac")
# displaying results
print(ans)
Output:
True
C++ Code:
// to check if s2 contains a permutation of s1
// returns a true or false on its basis
bool checkInclusion(string s1, string s2) {
// empty string is always a substring
// so return True
if(s1 == "")
return true;
// if s1 is non-empty and s2 is empty
// then definitely s2 won't contain
// permutation of s1, so return false
if(s2 == "")
return false;
int n = s1.length(), m = s2.length();
// vector of length 26 to store
// the frequency of the characters
// of string s1
vector<int> v1(26,0);
for(int i=0; i<n; i++)
v1[s1[i]-'a']++;
for(int i=0; i<m; i++){
if(v1[s2[i]-'a'] != 0 && (m-i) >= n){
// vector of length 26 to store
// the frequency of the substrings of characters
// of string s2
vector<int> v2(26,0);
for(int j=i; j<n+i; j++)
v2[s2[j]-'a']++;
// if the two vectors are equal
// then return a true
if(v1 == v2)
return true;
}
}
return false;
}
Time Complexity Analysis
This time, we are using an array to store the alphabets, instead of a hashmap. Hence, we can say that the length of our array will be 26 (Which is equal to the number of characters).
Now, suppose, the length of our string s1 is n1 and the string s2 is n2. Now, we are storing the frequencies of the characters in the strings in the arrays. Hence the worst-case time taken for calculating the frequency and inserting them into the array and performing the above operations will be O(n1+26∗n1∗(n2−n1)). Please note, that the array will store at most 26 keys.
Space Complexity Analysis
As we already know, there is a constant number of alphabets, since there are 26 alphabets in total. Hence, in the worst case, our arrays will be of size 26. So, we can conclude that the worst-case space taken will remain constant, or O(1), because the number of alphabets is constant. The s1array and the s2 array will be of constant size.
Approach #5 of Permutation of String: Sliding Window
Let us boil down our code to one more level of optimisation! Now, did you notice one thing, every time after checking the frequency for a particular permutation of string s2, we were re-initializing our hashmaps with the frequencies of the characters in the new permutation of string s2? Don’t you think that was quite unnecessary? Because the only thing we had to do was skip a particular character of the permutation from our string s2 and add a new character in the permutation(to make it of length s1). So, this concept is used in a sliding window.
We can do the following steps to implement the sliding window logic in the code:
Algorithm:
- For the initial window in s2, we can generate the hashmap only once rather than creating it for each window that is considered. Please note, by the window, we are referring to the strings of length len(s1) in the string s2.
- Then, when we slide the window later, we will be deleting the one previous character from our window, and adding the new next character into our window.
- So, by just modifying the indices associated with those two characters, we can update the hashmap.
- Also, at each step, we will also be checking the equality of the hashmap of string s2 with the string s1.
Implementation in C++, Java and Python
Java Code:
public class Solution {
// to check if s2 contains a permutation of s1
// returns a true or false on its basis
public boolean checkInclusion(String s1, String s2) {
// if s1's length is greater than
// s2, then definitely no permutation
// of s1 will be contained in s2
// so return false
if (s1.length() > s2.length())
return false;
// s1array and s2array of size 26 to
// store the frequency of the
// 26 alphabets in the strings
int[] s1array = new int[26];
int[] s2array = new int[26];
// adding the frequencies of
// each characters in the given
// strings into their respective indexes
for (int i = 0; i < s1.length(); i++) {
s1array[s1.charAt(i) - 'a']++;
s2array[s2.charAt(i) - 'a']++;
}
for (int i = 0; i < s2.length() - s1.length(); i++) {
// compares if the both arrays
// of frequncies matches
if (matches(s1array, s2array))
return true;
s2array[s2.charAt(i + s1.length()) - 'a']++;
s2array[s2.charAt(i) - 'a']--;
}
return matches(s1array, s2array);
}
// custom match function to
// match the two arrays
public boolean matches(int[] s1array, int[] s2array) {
for (int i = 0; i < 26; i++) {
if (s1array[i] != s2array[i])
return false;
}
return true;
}
}
Python Code:
class Solution:
# to check if s2 contains a permutation of s1
# returns a true or false on its basis
def checkInclusion(self, s1, s2):
# if s1's length is greater than
# s2, then definitely no permutation
# of s1 will be contained in s2
# so return false
if len(s1) > len(s2):
return False
# s1map and s2map of size 26 to
# store the frequency of the
# 26 alphabets in the strings
s1map = [0 for _ in range(26)]
s2map = [0 for _ in range(26)]
# adding the frequencies of
# each characters in the given
# strings into their respective indexes
i = 0
while i < len(s1):
s1map[ord(s1[i]) - ord('a')] += 1
s2map[ord(s2[i]) - ord('a')] += 1
i += 1
i = 0
while i < len(s2) - len(s1):
# compares if the both arrays
# of frequncies matches
if self.matches(s1map, s2map):
return True
# stores the frequency of the
# next substring window of s2
s2map[ord(s2[i+ len(s1)]) - ord('a')] += 1
s2map[ord(s2[i]) - ord('a')] -= 1
i += 1
return self.matches(s1map, s2map)
# custom match function to
# match the two arrays
def matches(self, s1map, s2map):
for i in range(0, 26):
if s1map[i] != s2map[i]:
return False
return True
# driver code
#creating object of solution class
ob = Solution()
# calling the function
ans = ob.checkInclusion("ab","mnbac")
# displaying results
print(ans)
Output:
True
C++ Code:
// to check if s2 contains a permutation of s1
// returns a true or false on its basis
bool checkInclusion(string s1, string s2) {
// empty string is always a substring
// so return True
if(s1 == "")
return true;
// if s1 is non-empty and s2 is empty
// then definitely s2 won't contain
// permutation of s1, so return false
if(s2 == "")
return false;
int n = s1.length(), m = s2.length();
// if s1's length is greater than
// s2, then definitely no permutation
// of s1 will be contained in s2
// so return false
if(n > m)
return false;
// v1 and v2 are vectors
// of size 26 to
// store the frequency of the
// 26 alphabets in the strings
vector<int> v1(26,0), v2(26,0);
for(int i=0; i<n; i++){
v1[s1[i]-'a']++;
v2[s2[i]-'a']++;
}
for(int i=0; i<m-n; i++){
// compare if their frequencies are same
if(v1 == v2)
return true;
// store the frequency of
// the next window substring
// of string s2
v2[s2[i]-'a']--;
v2[s2[i+n]-'a']++;
}
// return True if both the vectors
// have same values (of frequencies),
// false otherwise
return v1 == v2;
}
Time Complexity Analysis
Suppose, the length of our string s1 is n1 and the string s2 is n2. Now, in this approach since we are using the sliding window technique. Firstly, we will calculate the frequency of string s1, which will take a time of O(n1).
Please note that the comparison will take place for (n2−n1) times, and every time we will send the two strings for matching, where the loop iterates 26 times so, the time taken will be 26∗(n2−n1) .
So, the overall worst case time taken will be O(n1+26∗(n2−n1)).
Space Complexity Analysis
A constant space will be used since we already know there are 26 alphabets at max, so no extra space would be required. So, we can conclude that the worst-case space taken will remain constant, or O(1) because the number of alphabets is constant.
Approach #6 of Permutation of String: Optimized Sliding Window
So, in this problem we are expected to find a substring in s2, which should be somewhat a permutation of s1, right? So, as per the definition of permutation, it is just re-arranging the letters of a string. So, we may say that we just need to find the anagrams for s1 into s2.
Let us look at the definition of anagram —
A string s is an anagram of a string t, if it follows the below conditions:
- string s must contain all the characters of string t
- The frequency of characters in s should be equal to that in p.
So, our problem boils down to finding anagram of string s1 into string s2. For this, we will follow the below steps:
Algorithm:
- Firstly, find the frequencies of each character in s1.
- After that, find all the substrings of length s1 from the string s2.
- To find all the substrings, we can use the sliding window technique, which will make the process very efficient.
Let us look at the sliding window technique for String Permutation problem with an example: Say we have the below two strings:
s1 = "xyz"
s2 = "mzxyq"
- Let us take two pointers ii and jj.
- At the beginning, the i and j point to starting position of the string s2.
s2 = m z x y q
^
i, j
- Move “j” until j – i == len(s1)
s2 = m z x y q
^ ^
i j
- Now, you can see that the current substring we are getting when j – i == len(s1) = 3, is ‘mxz’, which is not the anagram of ‘xyz’. Hence, we move to our next substring or increment i by 1.
s2 = m z x y q
^ ^
i j
- Please note, since j is at the 3rd index, and i is at the 1st index, the difference between their indexes i.e. 3−1<len(s1), hence we increment j till it becomes equal to the len(s1)
s2 = m z x y q
^ ^
i j
- Now, in our current window, the substring formed is “zxy”, which is an anagram of s1. Hence we will return a True.
- We keep moving i and j until j reaches the end of s2.
- This is how we find substring using the sliding window technique, correspondingly checking whether it is an anagram or not.
- If there is no anagram, then simply return False.
Implementation in C++, Java and Python
Java Code:
class Solution {
// to check if s2 contains a permutation of s1
// returns a true or false on its basis
public boolean checkInclusion(String s1, String s2) {
// single array to store
// frequency of 26 alphabets
int[] freq = new int[26];
// computes the frequency
// of characters in string s1
for(char c : s1.toCharArray()) freq[c - 'a']++;
int j = 0, i = 0;
int length_chars = s1.length();
while(j < s2.length()){
// decreases the frequency of
// the characters in the same frequency
// array for the string s2
if(freq[s2.charAt(j++) - 'a']-- > 0)
length_chars--;
// if length becomes 0 then
// that means the string1 had
// same character for some substring
// of string s2
if(length_chars == 0) return true;
if(j - i == s1.length() && freq[s2.charAt(i++) - 'a']++ >= 0)
length_chars++;
}
return false;
}
}
Python Code:
class Solution:
# to check if s2 contains a permutation of s1
# returns a true or false on its basis
def checkInclusion(self, s1: str, s2: str) -> bool:
# single array to store
# frequency of 26 alphabets
freq = [0] * 26
# calculates frequency of characters
# in string s1
for c in s1:
freq[ord(c) - 97] += 1
i, j, length_chars = 0, 0, len(s1)
while j < len(s2):
# decrement the frequency whenever
# some character appear in the
# string s2 which is also present
# in string s1
if freq[ord(s2[j]) - 97] > 0:
length_chars -= 1
freq[ord(s2[j]) - 97] -= 1
j += 1
# if length becomes 0 then
# that means the string1 had
# same character for some substring
# of string s2, so return true
if length_chars == 0:
return True
if j - i == len(s1):
if freq[ord(s2[i]) - 97] >= 0:
length_chars += 1
freq[ord(s2[i]) - 97] += 1
i += 1
return False
# driver code
#creating object of solution class
ob = Solution()
# calling the function
ans = ob.checkInclusion("ab","mnbac")
# displaying results
print(ans)
Output:
True
C++ Code:
class Solution {
public:
// to check if s2 contains a permutation of s1
// returns a true or false on its basis
bool checkInclusion(string s1, string s2) {
// single array to store
// frequency of 26 alphabets
int freq[26] = {0};
// computes the frequency
// of characters in string s1
for(char c : s1) freq[c - 'a']++;
int j = 0, i = 0, length_chars = s1.size();
while(j < s2.size()){
// decreases the frequency of
// the characters in the same frequency
// array for the string s2
if(freq[s2.at(j++) - 'a']-- > 0)
length_chars--;
// if length becomes 0 then
// that means the string1 had
// same character for some substring
// of string s2
if(length_chars == 0) return true;
if(j - i == s1.size() && freq[s2.at(i++) - 'a']++ >= 0)
length_chars++;
}
return false;
}
};
Time Complexity Analysis
The time complexity for the above solution will be simply O(N) because we are simply iterating over the whole string length, and trying to find out whether any anagram exists or not.
Space Complexity Analysis
The space taken for the above approach is also constant. So, overall space complexity = O(1).
Conclusion
In this problem, we had to find a substring in a string s2, which is one of the Permutation of String in s1. Let us look into the approach we learned for this:
- We looked into the Brute-force approach for Permutation of String problem, which was majorly generating all the permutations and then comparing.
- We also looked into the approach which used backtracking for Permutation of String.
- We used the hashmap approach to hash all the values of the strings and then compare them with the other string.
- Later we used the sliding window approach for Permutation of String problem, to slide through the string and compare the frequency of the string at each window size.
- The best of all the approaches for the above Permutation of String problem was the optimised sliding window approach where we used only one frequency table and updated the frequency of the characters for both the strings simultaneously, thereby cutting off any extra space. The time complexity also was linear for this approach, i.e. O(N).