Overview
Prim’s algorithm and Kruskal’s algorithm are greedy algorithms used to find the minimum spanning tree in a weighted graph. Prim’s and Kruskal’s algorithms have many use cases they are used in solving traveling salesman problems, LAN networks, TV networks, and in general for any network where we need to find the least cost subset of this network such that any two nodes are connected.
Scope
- This article gives a brief introduction to Prim’s algorithm and Kruskal’s algorithm.
- It explains Prim’s and Kruskal’s algorithms with corresponding examples.
- It also explains the key differences between Prim’s and Kruskal’s algorithms and similarities as well.
- We learn about some of the use cases of Prim’s and Kruskal’s algorithms in real-life scenarios like designing a LAN network.
What is Prim’s Algorithm in MST?
Prim’s algorithm is used to find the minimum spanning tree for a given weighted graph. Given a weighted graph of n nodes, prim’s algorithm is used to find the tree having n nodes and $n-1$ edges such that the sum of weights of these $n-1$ edges is the minimum of all possible trees.
Spanning Tree(ST):
A spanning tree of a weighted graph with $N$ nodes is a subgraph that includes all vertices of the graph with the minimum possible number of edges i.e. there is a unique path between any two nodes of the subgraph. There can be more than one spanning tree.
Minimum Spanning tree(MST):
The minimum spanning tree of a weighted graph having $N$ nodes is the spanning tree having the minimum sum of weights of all edges.
In the example below given a graph and its spanning trees
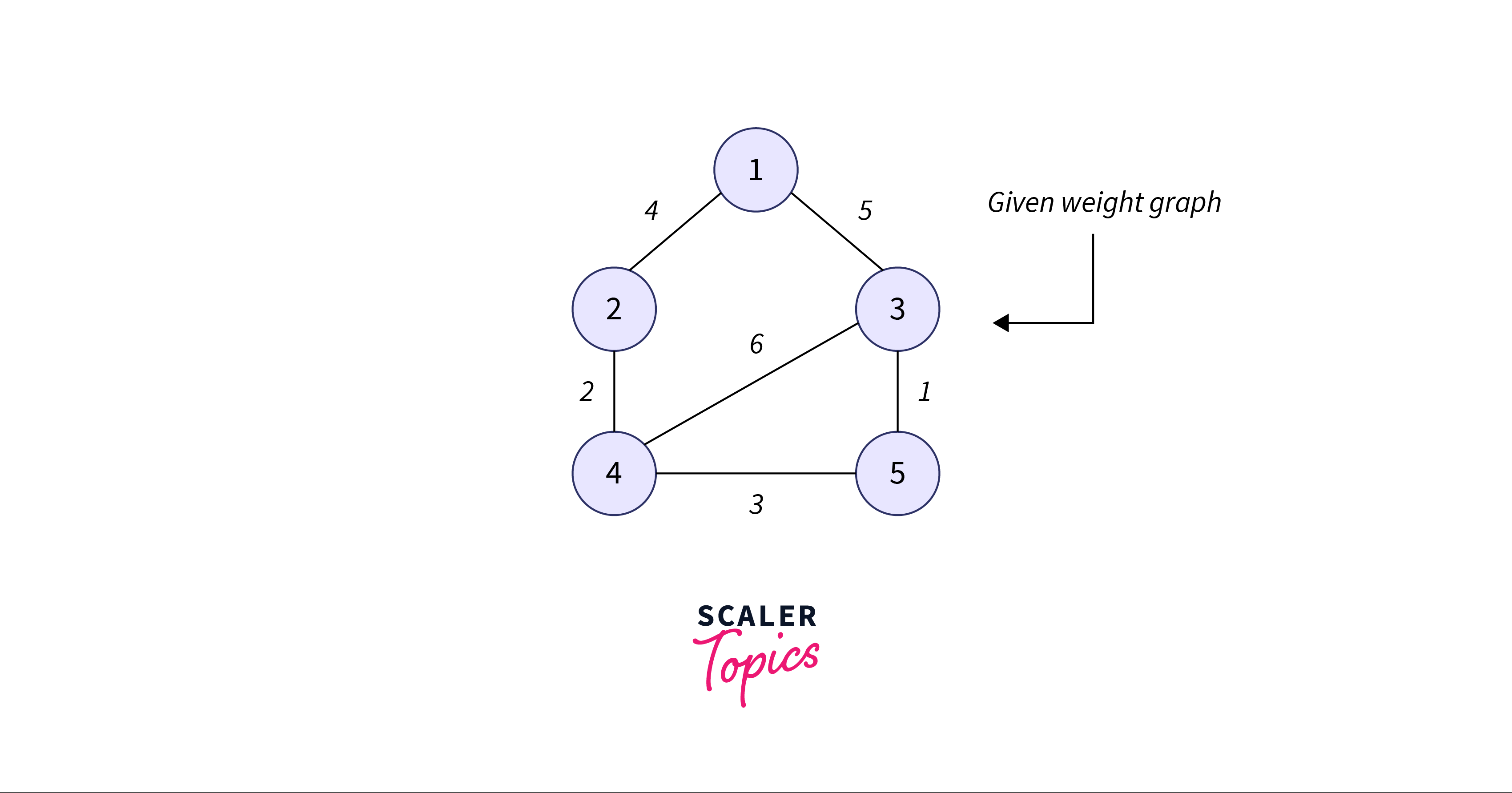
The spanning trees of the above-weighted graph are shown below
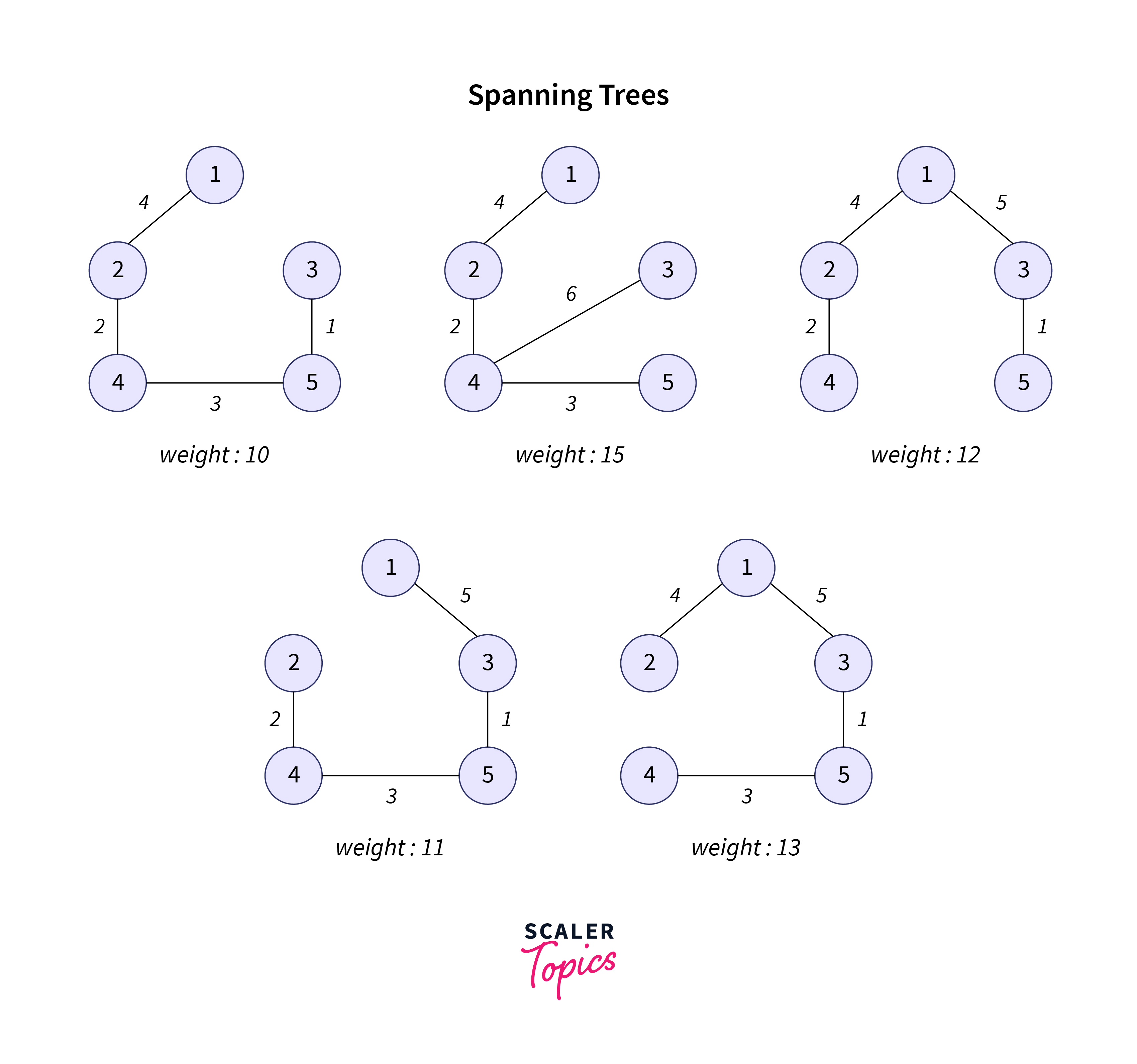
The first spanning tree has the least weight i.e. 10 and hence is the minimum spanning tree.
Prim’s algorithm:
Prim’s algorithm is used to find the minimum spanning tree.
It is a greedy algorithm that constructs the minimum spanning tree by selecting the most optimal edge at that point.
To read more about prim’s algorithm and its implementation click here Prim’s algorithm
What is the Kruskal Algorithm in MST?
Kruskal’s algorithm is another greedy algorithm besides prim’s which is used to find the minimum spanning tree from a given graph.
The main idea of Kruskal’s algorithm is as follows:
Given a weighted graph with $N$ vertices and $E$ edges, the idea is to sort all the edges in increasing order of their weights, then we select the first $N-1$ edges such that they do not form a cycle within them.
It is guaranteed that those selected $N-1$ edges will construct the minimum spanning tree because there is no other way to include even smaller weight edges as we already considered the smallest weight $N-1$ edges.
To read more about Krushkal’s algorithm click here Krushkal’s algorithm
Examples
Let’s go through examples of Prim’s and Krushkal’s algorithm one by one.
Prim’s Algorithm
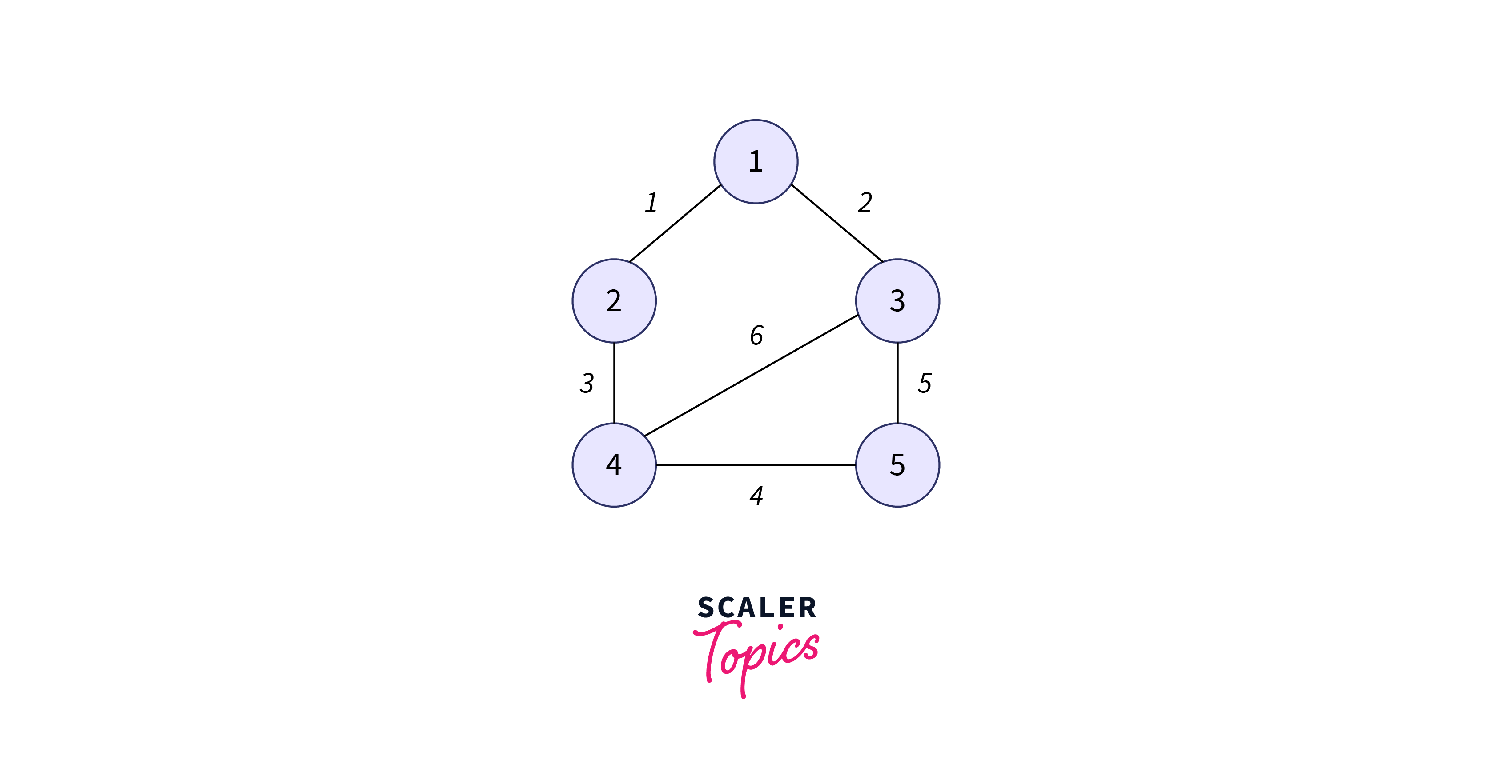
Suppose you are given a weight graph as shown below, the task is to find the minimum spanning tree using Prim’s algorithm, and list out all steps for finding the minimum spanning tree of the given graph.
Below are the steps of Prim’s algorithm:
1) Start with any node in the graph and mark it visited and include it in the MST.
2) Iterate over all adjacent vertices of the chosen vertex which are not included in the MST and update their values and parent.
3) Repeat the above two steps until all the nodes are included in the MST.
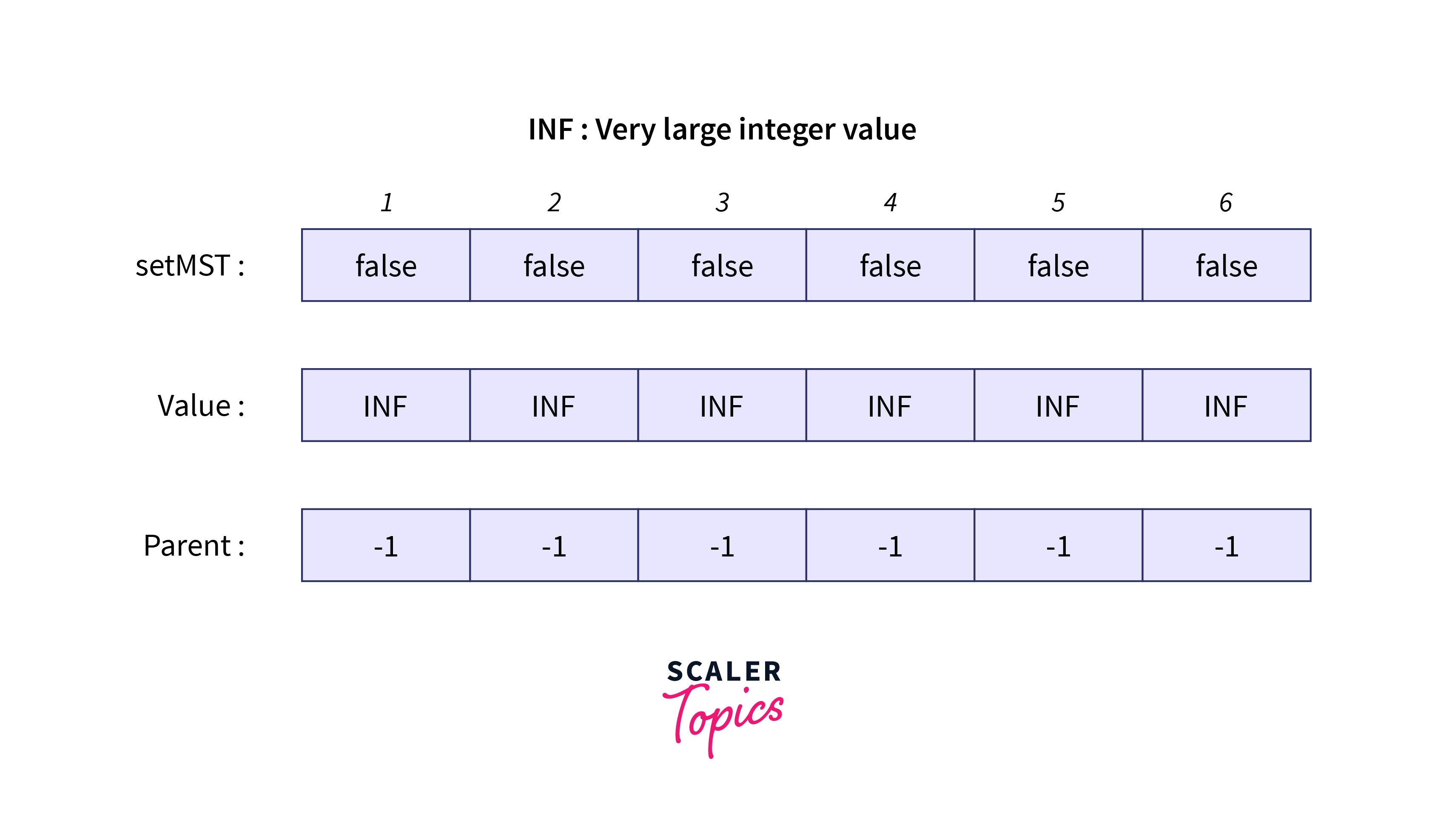
To implement the above steps of the algorithm we need three arrays:
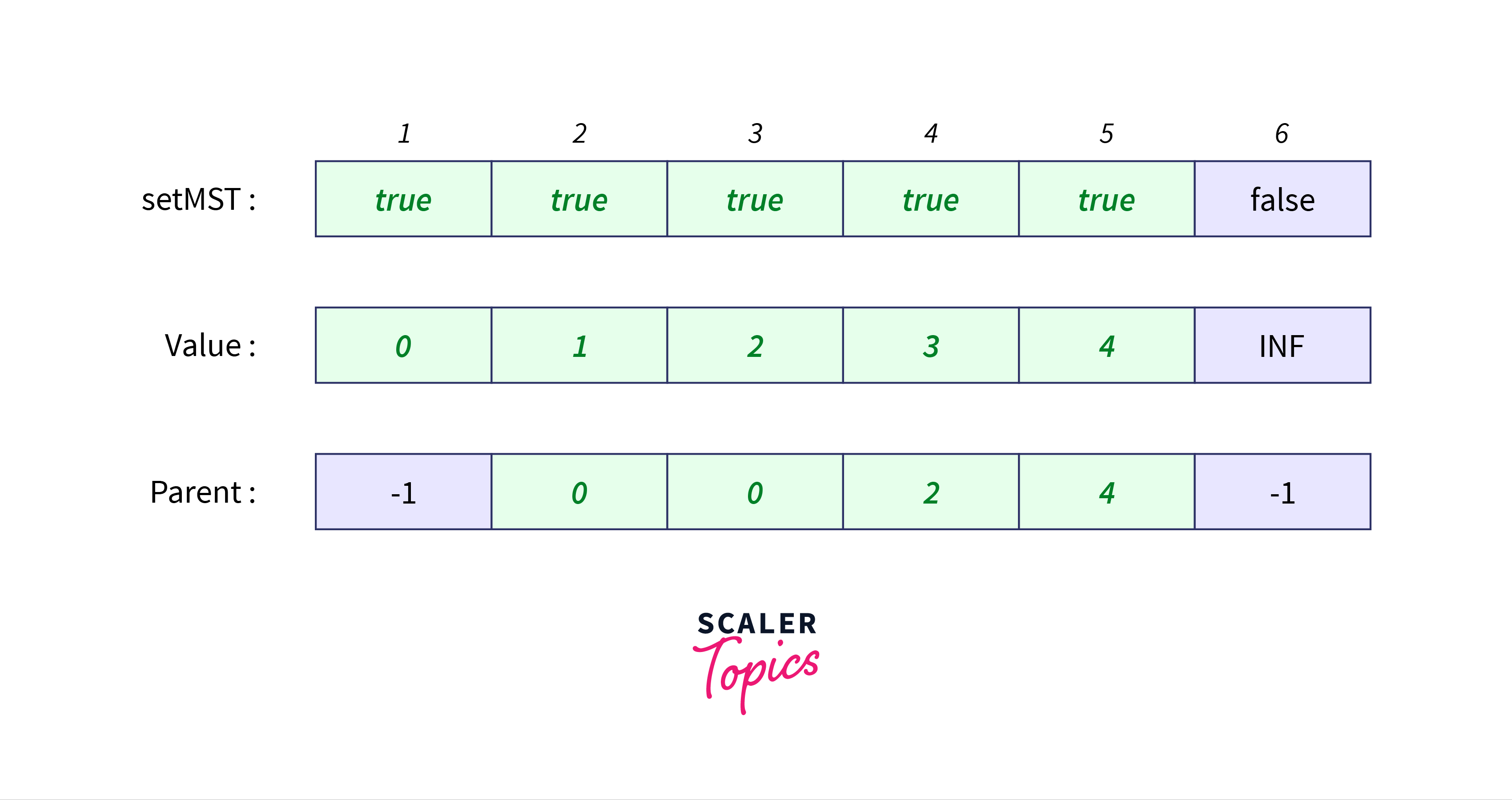
setMST[N]: A boolean array that keeps track of the nodes included in the MST.
value[N]: An integer array that keeps track of the minimum edge weight for a particular node.
parent[N]: An integer array that stores the parent of each node, the parent of starting node is set to -1.
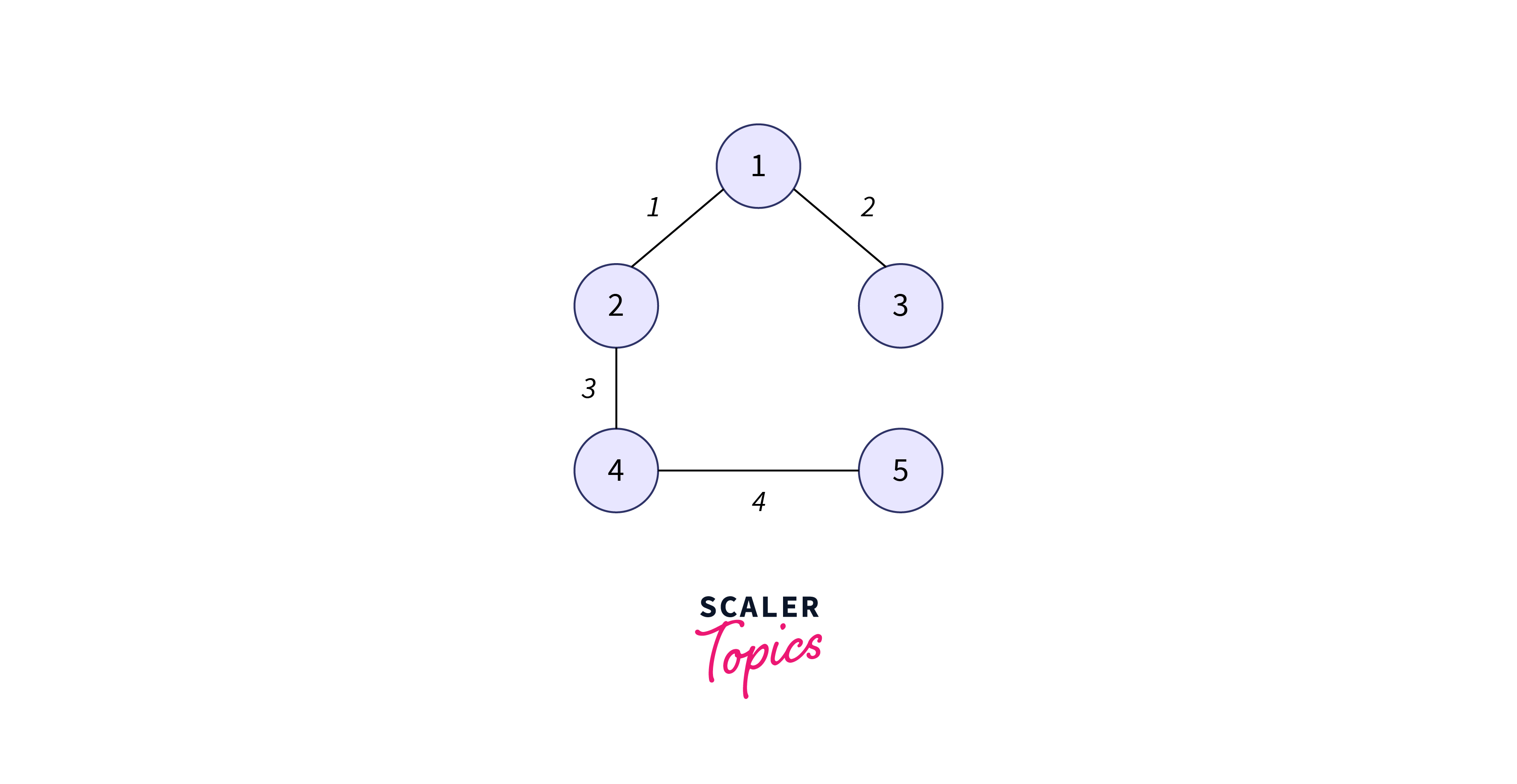
Let’s start simulating the algorithm for the above graph:
Initially, the status of the above-mentioned arrays is as follows:
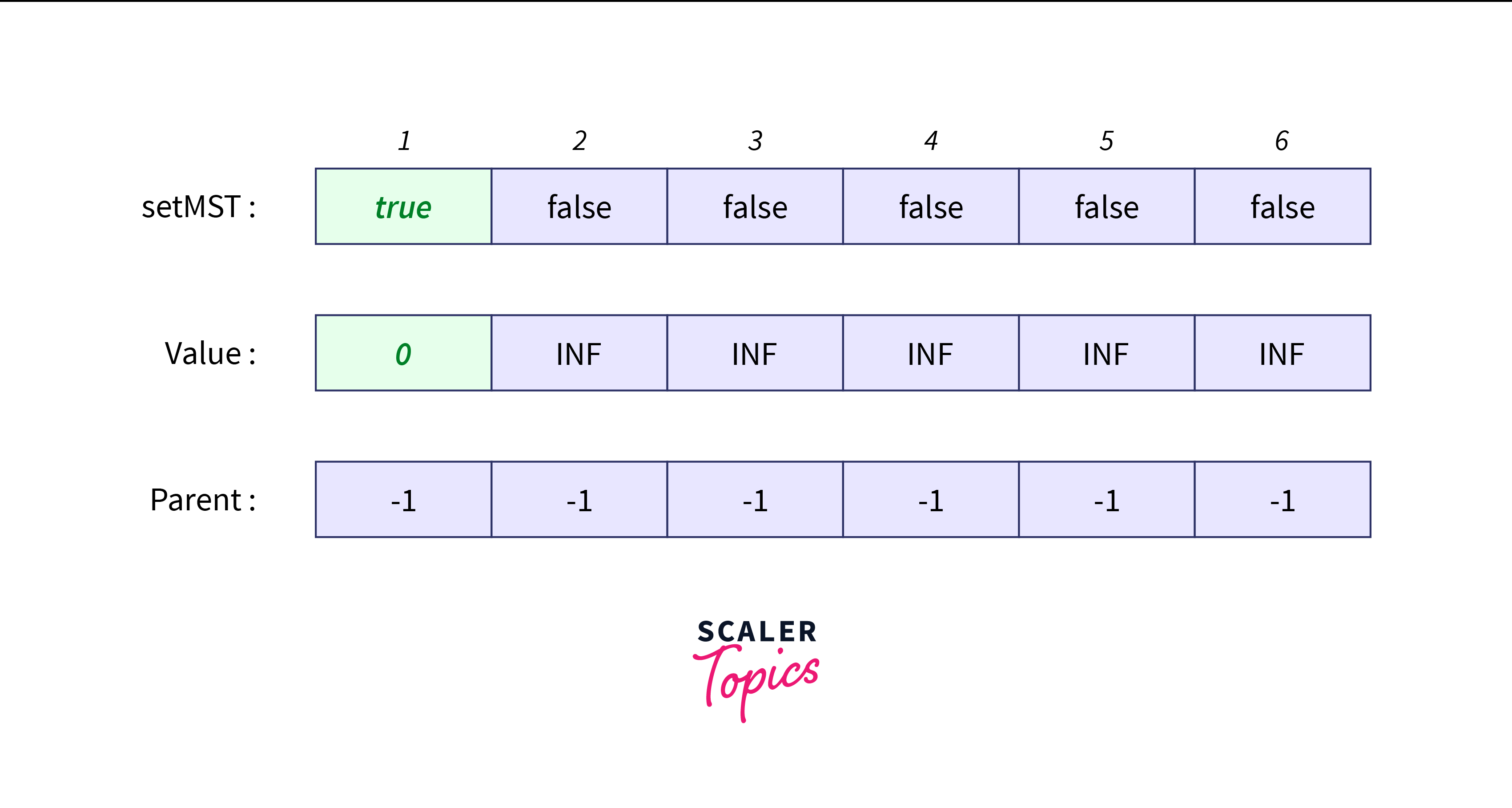
First of all, we pick an arbitrary vertex in the graph that says 1.
The arrays will be as follows

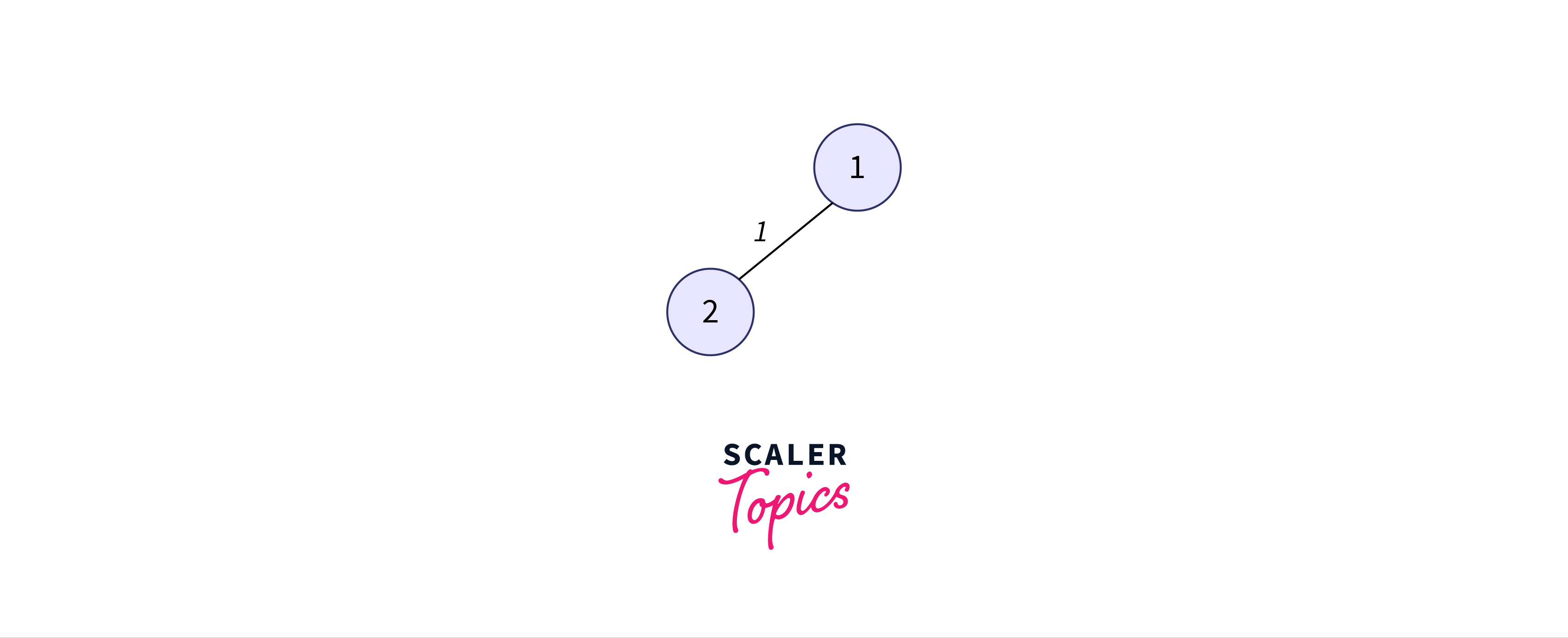
Now, we select the edge with the least weight out of all edges going out of node 1.
The arrays will be updated as follows:
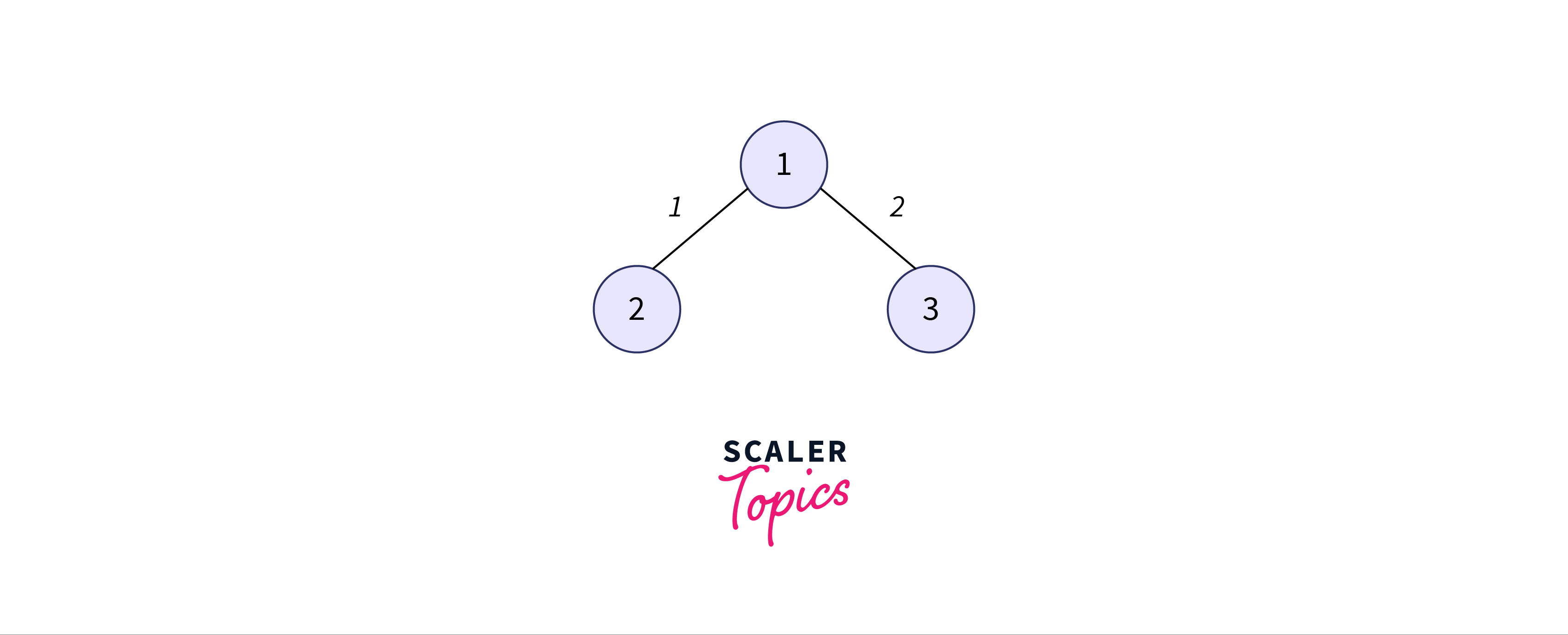
Next, we have edges $1-3$ and $2-4$ out of which we select $1-3$ because it has the least weight.
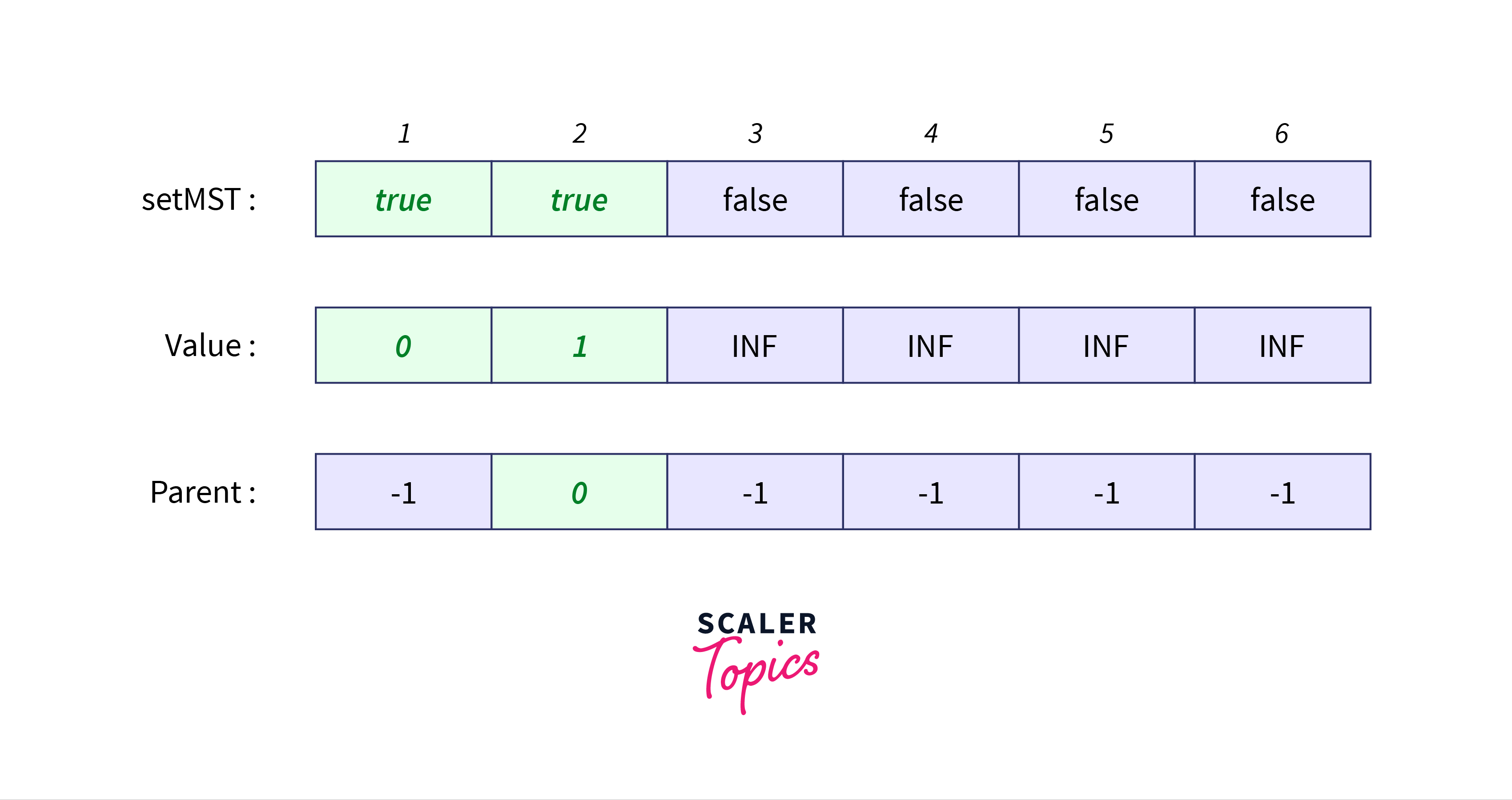
The arrays will be updated as follows:
Next, we have edges $2-4$, $3-4$, and $3-5$ out of which $2-4$ is chosen as it has the least weight.
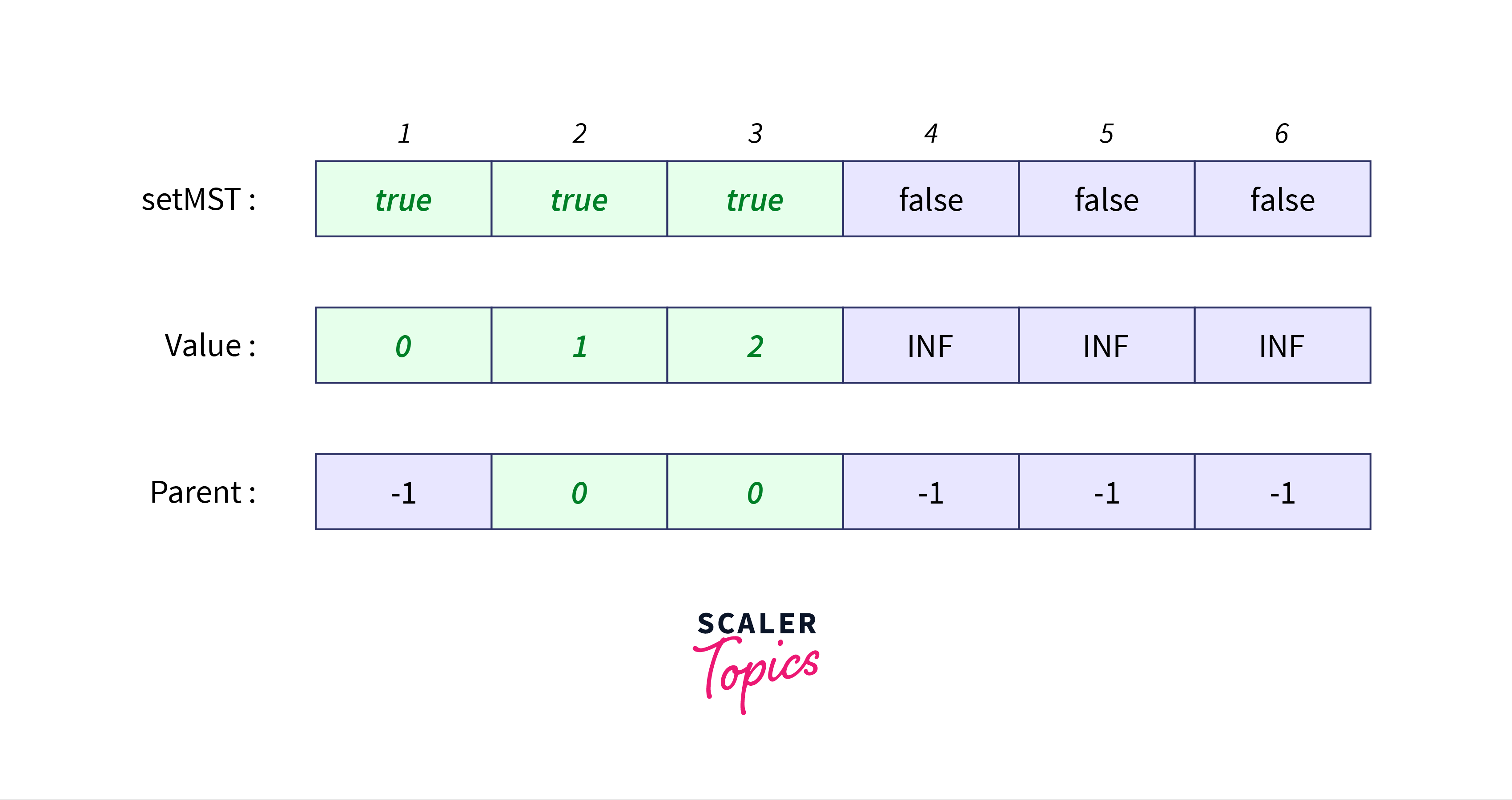
The corresponding arrays will be updated as follows:

Next, we have edges $3-4$, $3-5$, and $4-5$ and we shall select the edge $4-5$.
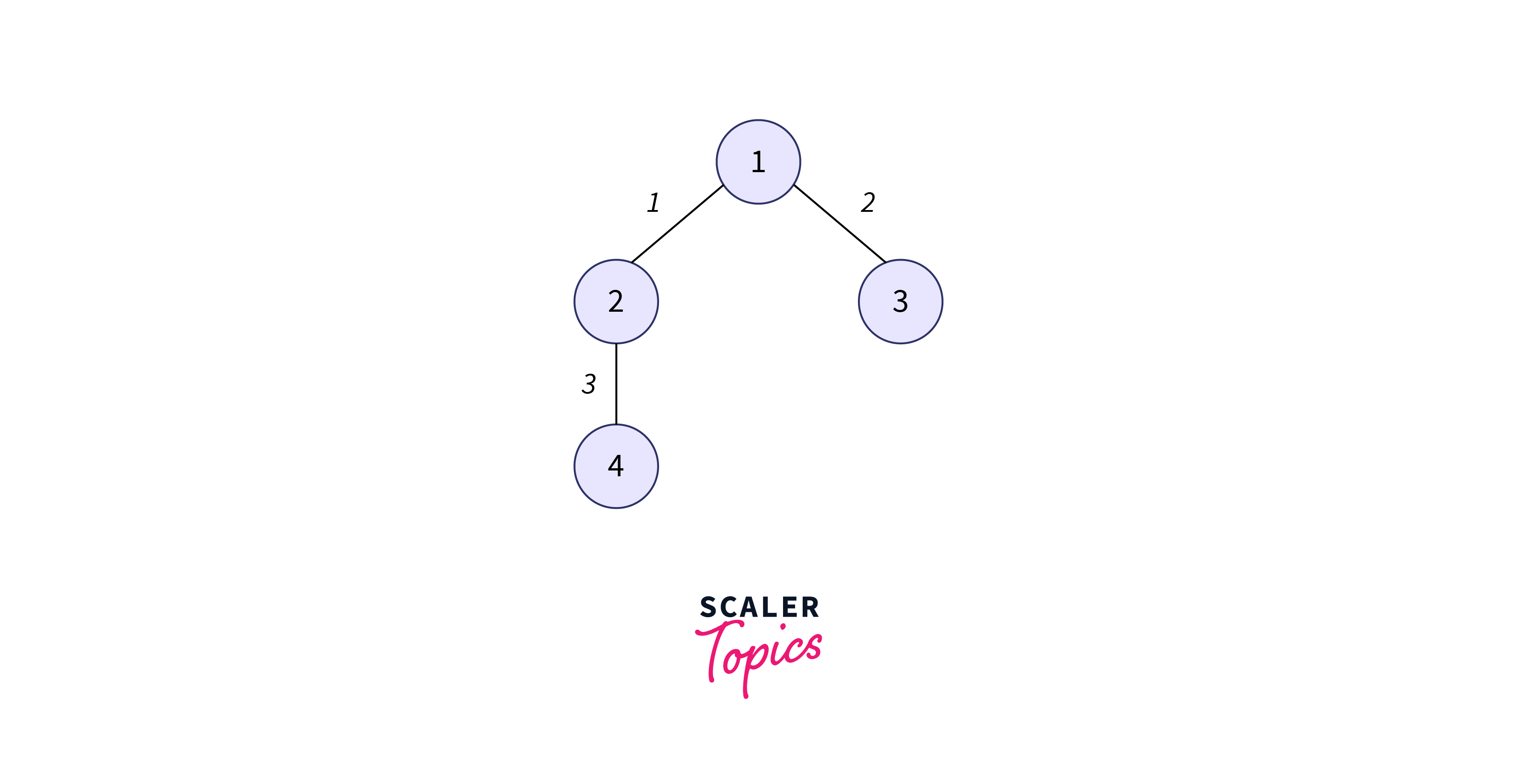
The corresponding arrays will be updated as follows:
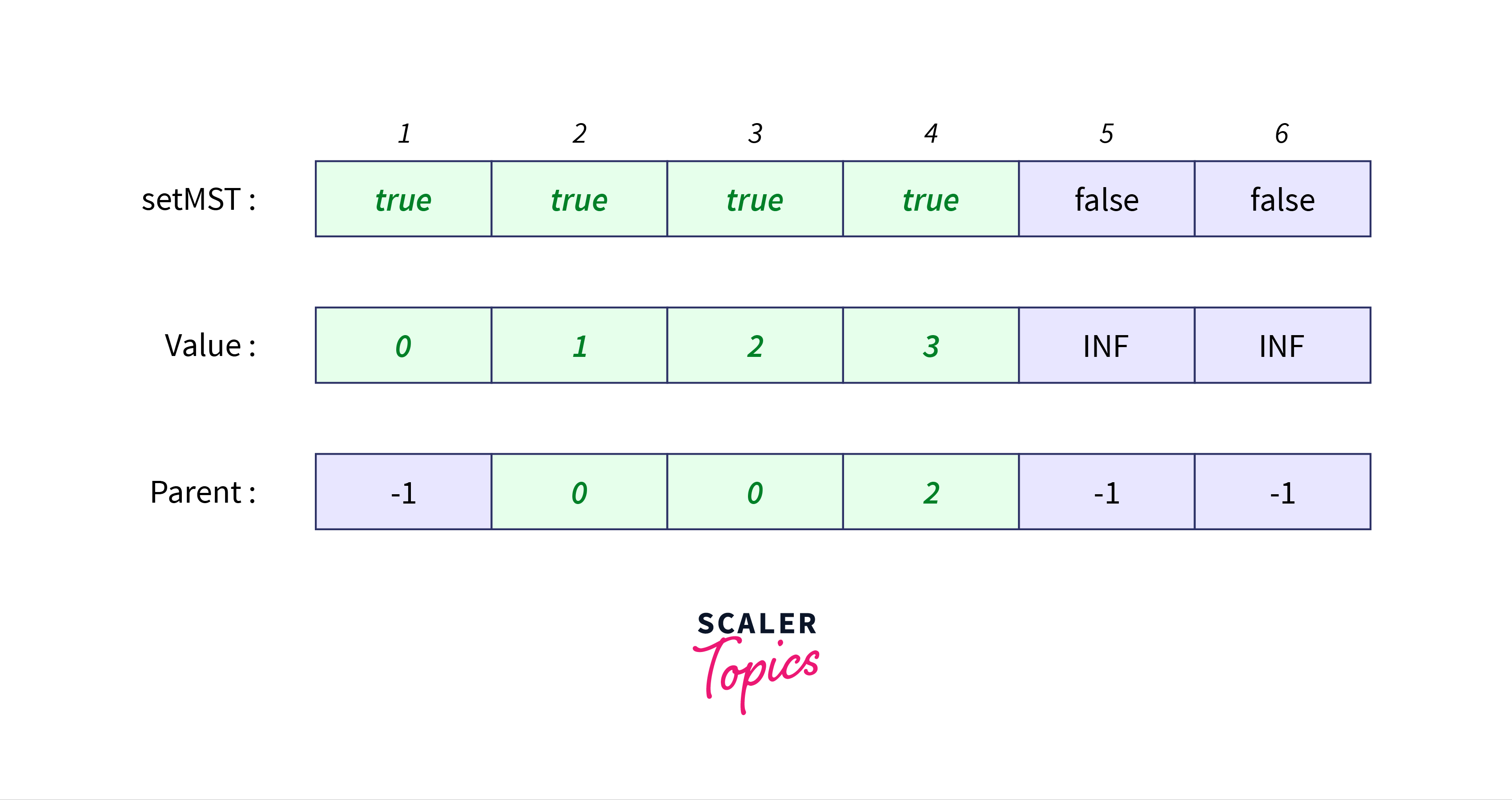
Now, we have covered all the vertices and this must be the minimum spanning tree for the above example with weight equal to the sum of elements of array value i.e. $0 + 1 + 2 + 3 + 4 = 10$ which is indeed the answer.
Kruskal Algorithm
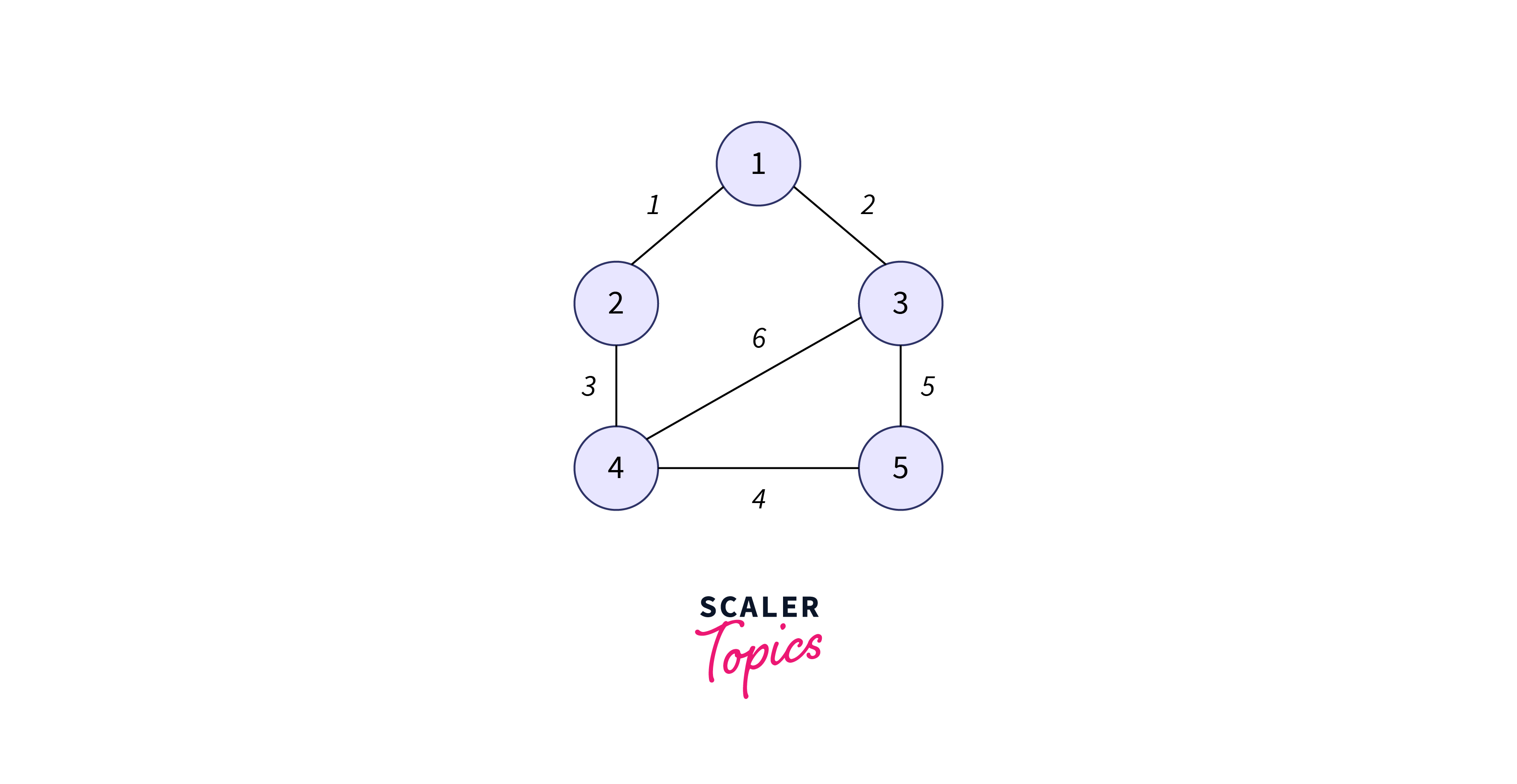
Suppose you are given a weight graph as shown below, the task is to find the minimum spanning tree using Kruskal’s algorithm, and list out all steps for finding the minimum spanning tree of the given graph.
Below are the steps of Kruskal’s algorithm:
1) Sort all the edges in increasing order of their weight.
2) Select the first $N-1$ edges such that they do not form any cycle within them.
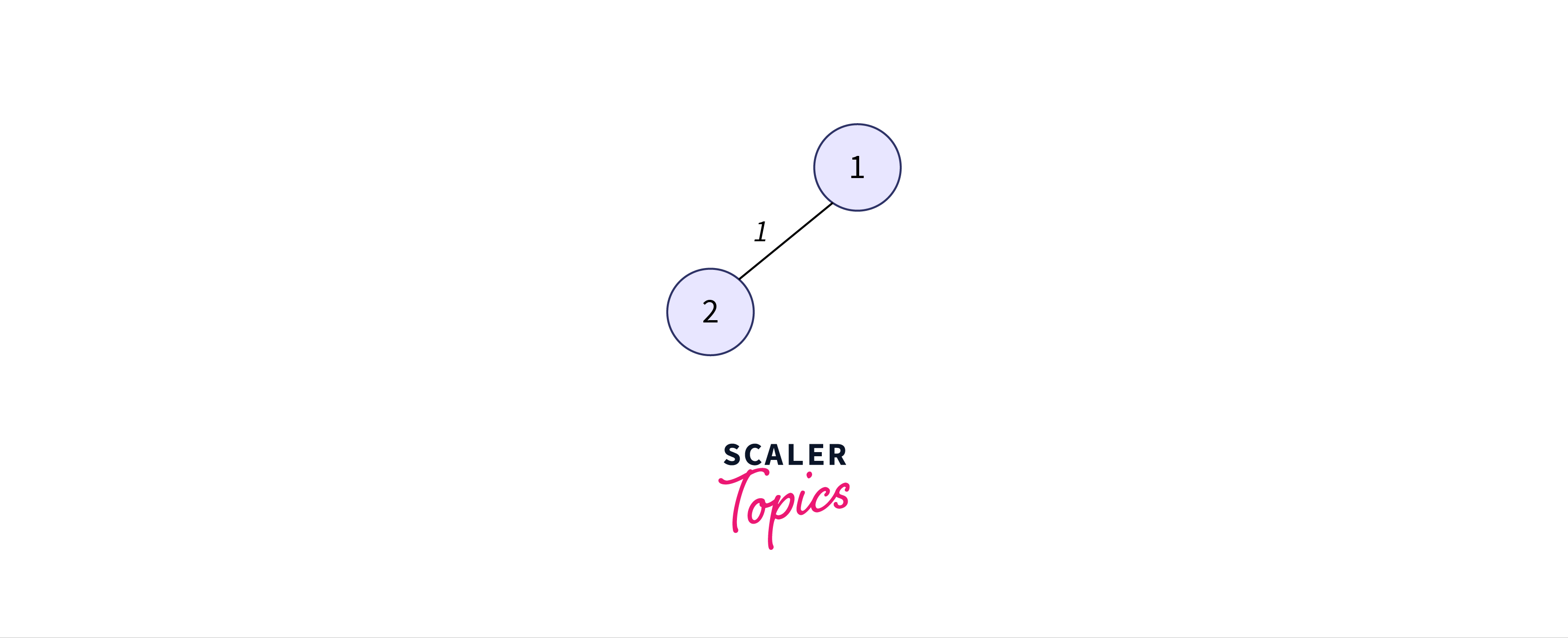
Let’s see the simulation of prim’s algorithm:
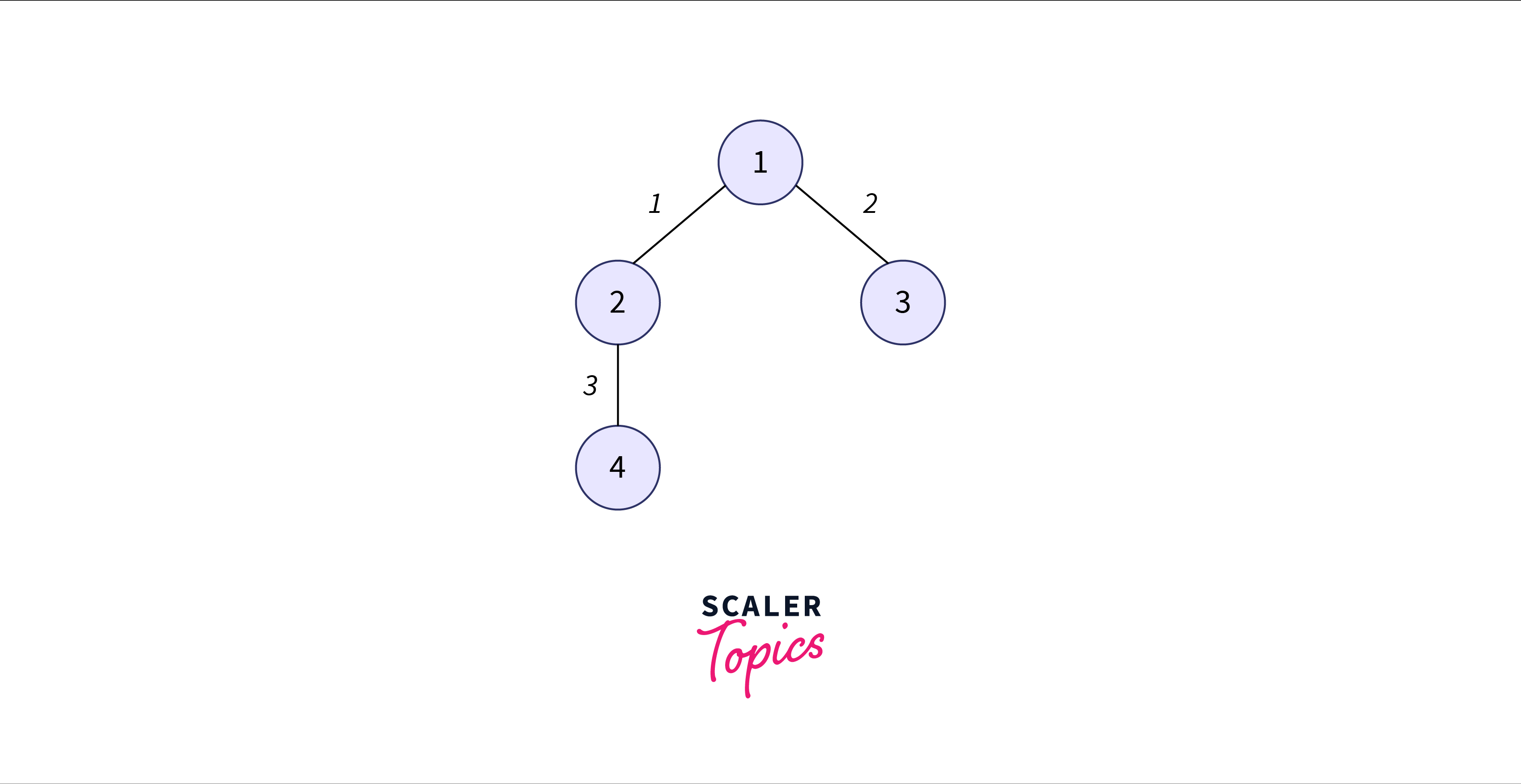
We start from the lowest-weight edge
Now, we choose the second-lowest weight edge.
Next, we choose the third-lowest weight edge such that it does not form a cycle.
Now, we choose the fourth-lowest weight edge such that it does not form a cycle.
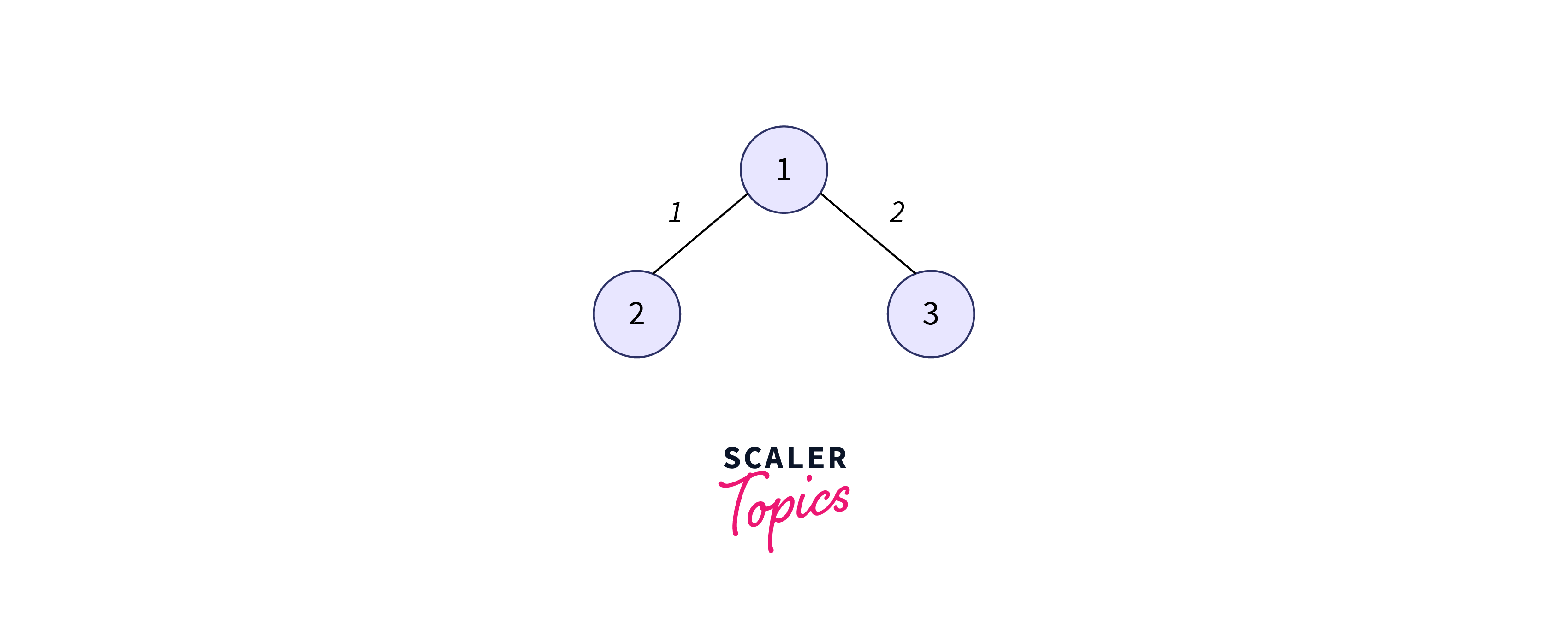
Here, we have selected all the vertices, therefore, this is the minimum spanning tree and the sum of the edge weights is $1 + 2 + 3 + 4 = 10$.
Key Differences between Prims and Kruskal Algorithm
Although both prim’s and Kruskal’s algorithms are greedy algorithms used to find the minimum spanning tree for a given weighted graph there are few differences between prim’s and Kruskal’s algorithm in terms of time, space, and working mechanisms.
1) In prim’s algorithm, we choose the nodes greedily i.e. the node is chosen at a point such that the edge weight for this node is minimum while in the case of Krushkal’s algorithm we choose the minimum weight edges greedily.
2) In Kruskal’s algorithm we sort the edges by weight in increasing order and then select the $N-1$ edges without cycle having minimum weight but in the case of Prim’s algorithm, we choose the vertices considering the edge weights, and even if the number of edges goes high it still stays efficient. In the case of dense graphs, Prim’s algorithm is better.
3) Time complexity for the Prim’s algorithm is $O(N^2)$ while for Krushkal it is $O(ElogN)$.
4) Prim’s algorithm only works on a connected graph because we need to select the adjacent node for a selected node with minimum weight, while Krushkal can work for the disconnected component as well.
Prim’s Vs Kruskal’s Algorithm
Prim’s and Kruskal’s algorithm besides having similarities also has a lot of differences in terms of their use cases, complexity, and other factors like speed.
Following are the key differences between Prim’s and Kruskal’s algorithms in table format.
Conclusion
- We conclude that Prim’s and Kruskal’s algorithms are greedy algorithms used for finding the minimum spanning tree of a given weighted graph.
- Prim’s algorithm adds nodes while Kruskal’s algorithm adds edges which calculates the minimum spanning tree.
- Prim’s algorithm runs faster in the case of dense graphs while Kruskal runs faster in the case of sparse graphs.
- Prim’s algorithm is a little complex in implementation as compared to Kruskal’s algorithm.
- Space complexity of Prim’s algorithm is relatively higher than Kruskal’s algorithm.
FAQs
Q. Why does Prim’s algorithm is faster on denser graphs while Kruskal’s algorithm on sparse graphs?
A: Prim’s algorithm is faster on dense graphs because it just traverses the adjacent nodes for each node and it does not have to sort the edges as in the case of Kruskal, therefore Prim’s algorithm is faster in calculating the minimum spanning tree for dense graphs.
Kruskal Algorithm is faster in the case of sparse graphs because for sparse graphs the number of edges is smaller and hence sorting the edges is more efficient than selecting an adjacent node for each node.