Pattern Searching with Rabin-Karp Algorithm

The Rabin-Karp algorithm uses a hash function to search for and match patterns in text. Instead of going through every character in the initial phase as the Naive String Matching Algorithm does, it filters out the characters that don’t match before comparing.

What is the Rabin-Karp Algorithm?

The M-character subsequences of text to be compared and the pattern is both given hash values by the Rabin-Karp string matching method. The algorithm will decide the hash value for the following M-character sequence if the values are unequal. The method will examine the pattern and the M-character sequence if the hash values are equal. Thus, character matching is only necessary when the hash values match, resulting in a single comparison for each text subsequence.

Example

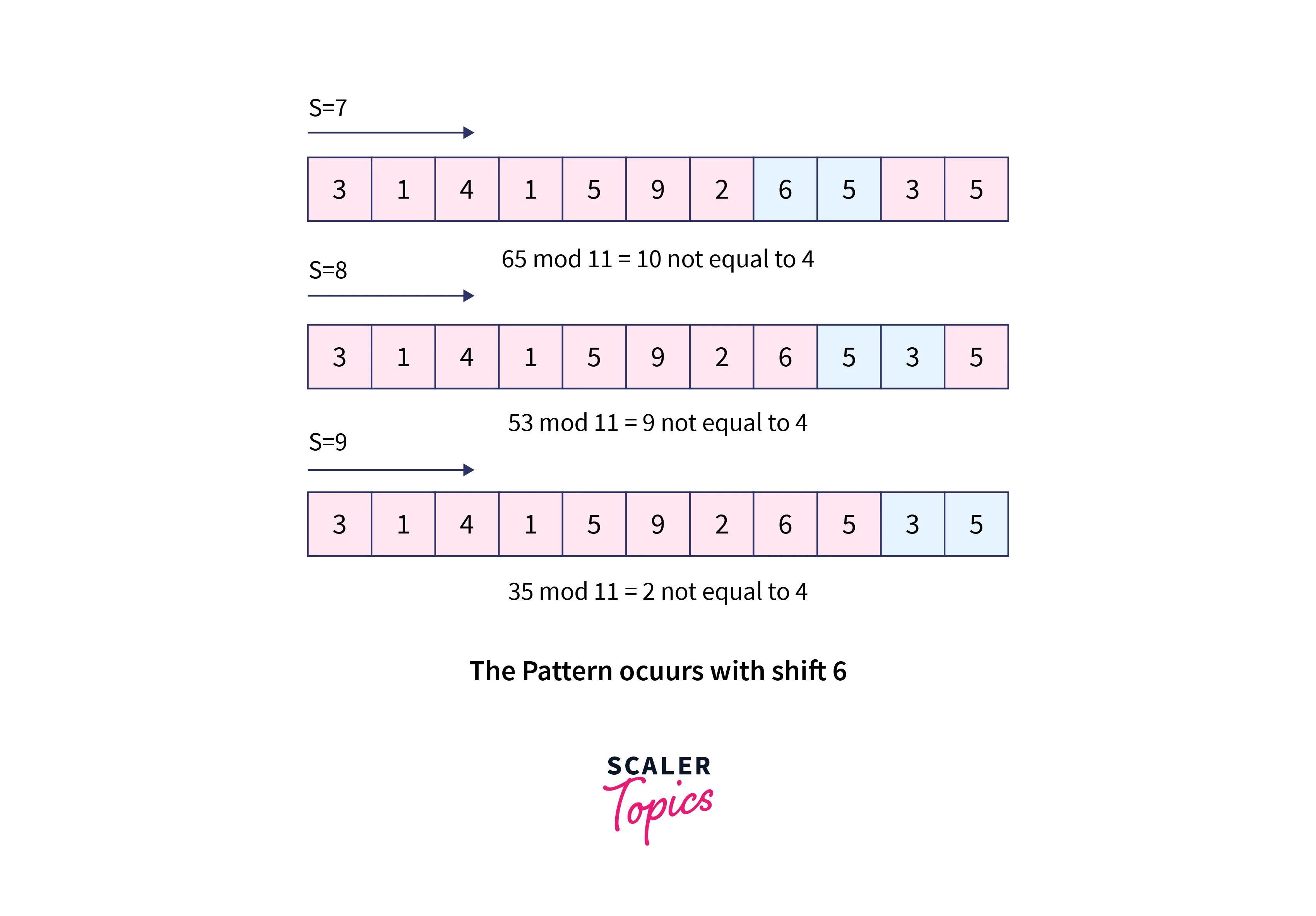
How many false positives does the Rabin-Karp matcher find while matching strings with working module q = 11 and text T = 31415926535?

T = 31415926535.......  
  P = 26  
 Here T.Length = 11 so Q = 11      
 And P mod Q = 26 mod 11 = 4  
Now find the exact match of P mod Q...  

How does it Work?

A string of characters is chosen, and its capacity to contain the necessary text is examined. Character matching is done if the possibility is discovered.

Let’s break down the algorithm using the stages below:

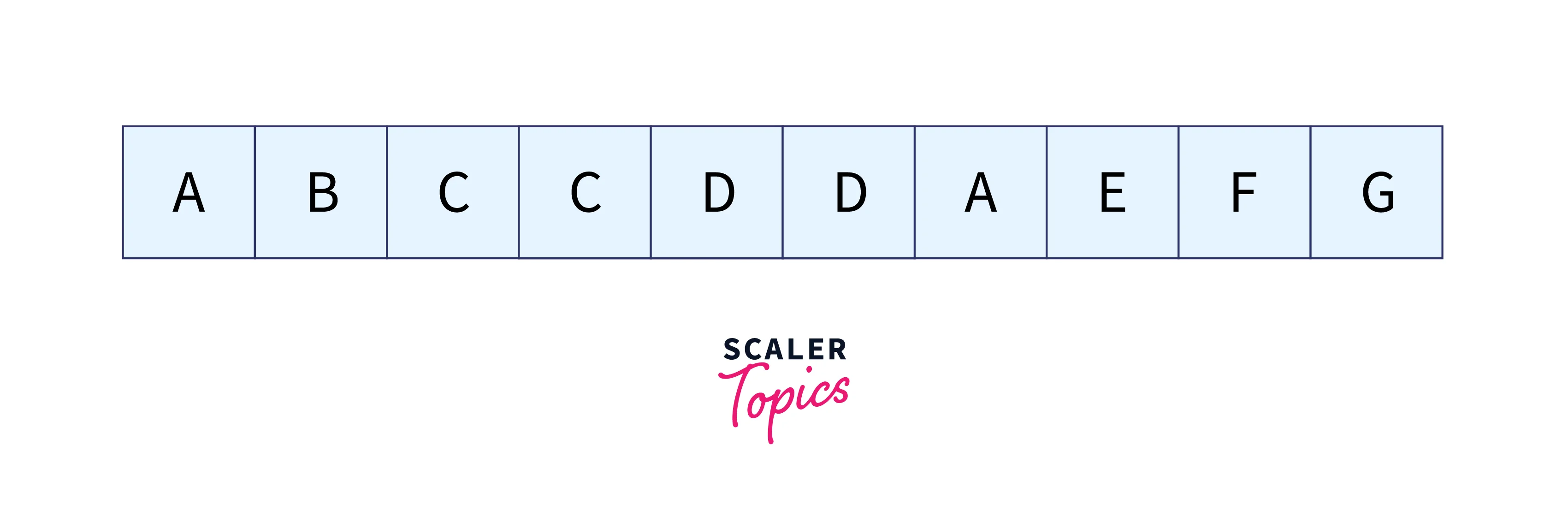
Let the text be:

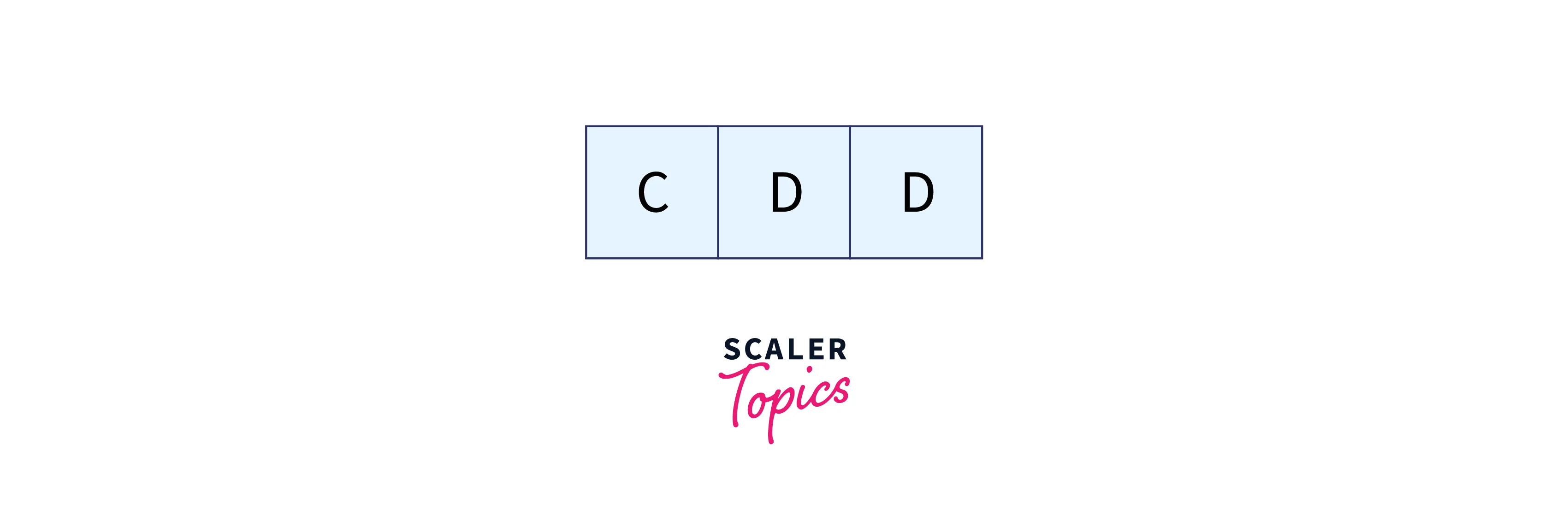
And the above text’s search term should be:

Let’s give each character we use in the problem a numerical value(v)/weight. Only the first ten alphabets—A to J—have been used here.

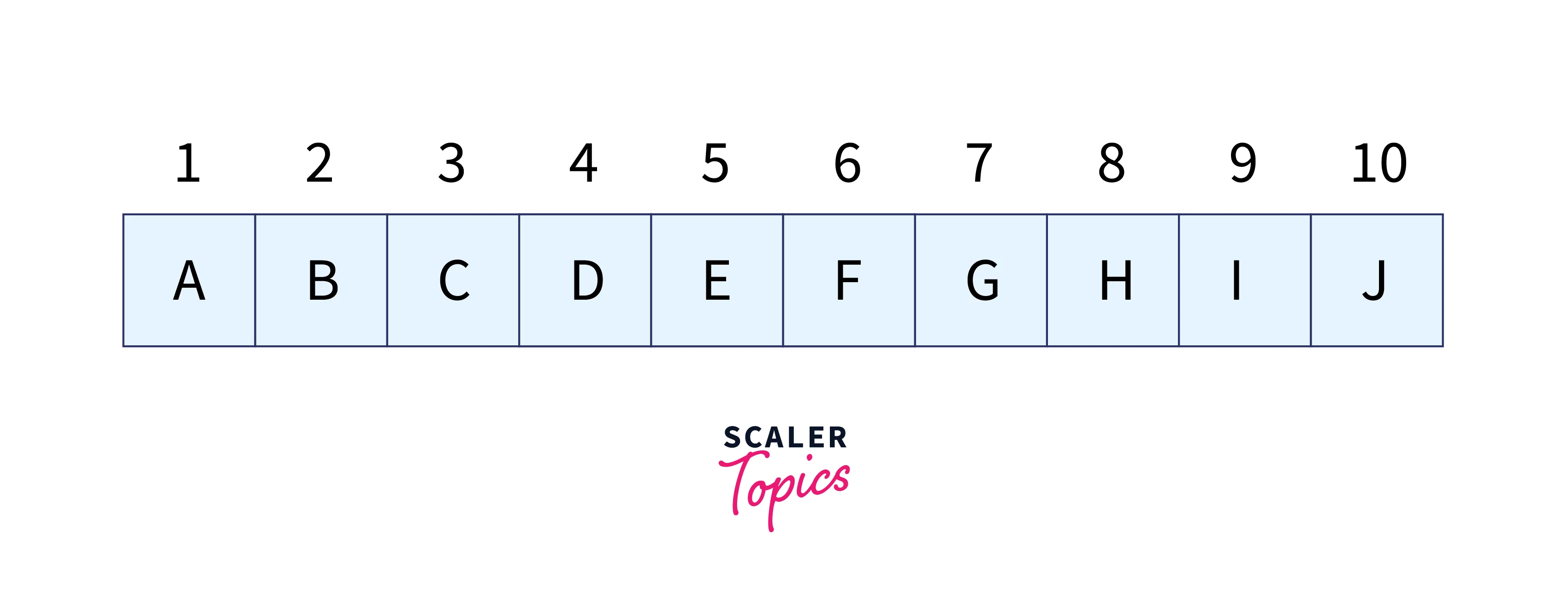
Let n represent the pattern’s length and m represent the text’s length. Here, n is 3, and m is 10.

Let d represent the overall character count for the input set. We used the input set “A, B, C,…, J” in this case. So, d = 10. For d, any appropriate value may be used.

Let’s determine the pattern’s hash value.

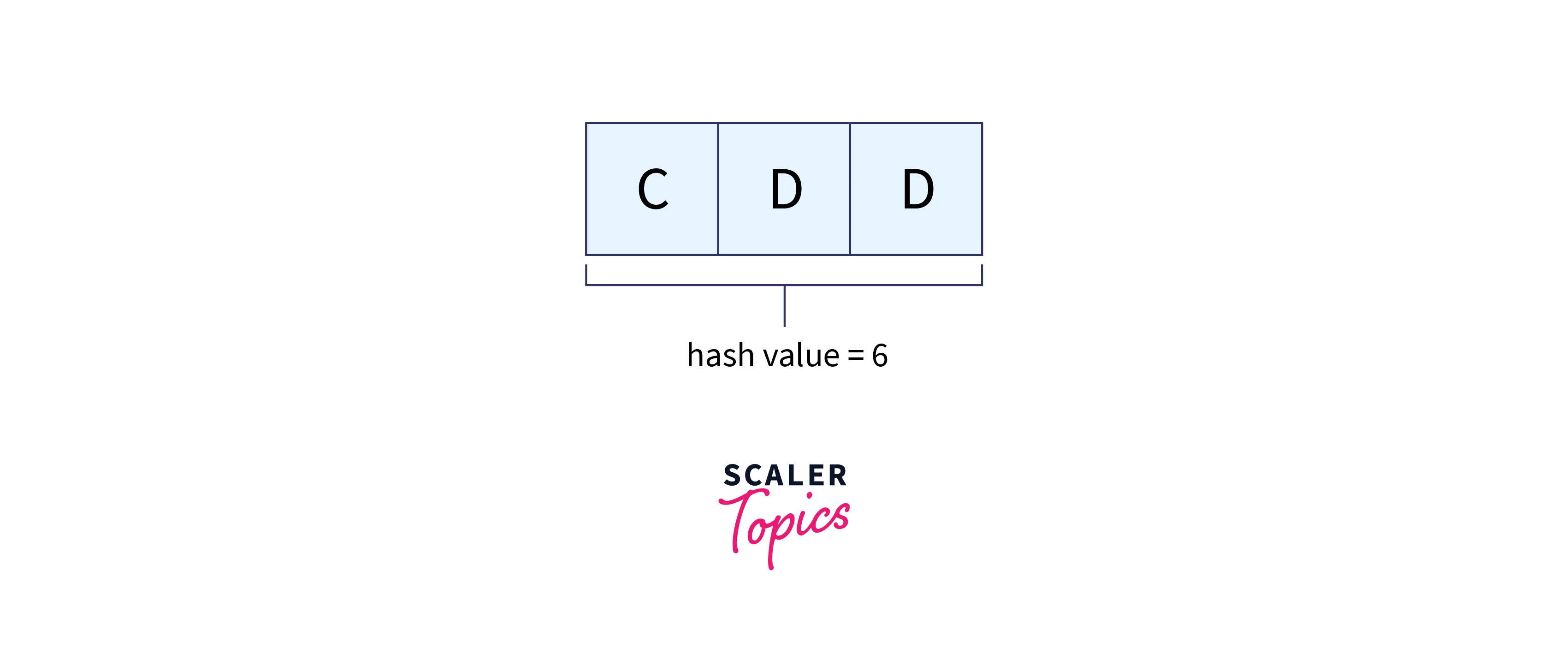
hash value for pattern(p) = Σ(v * dm-1) mod 13 
                      = ((3 * 102) + (4 * 101) + (4 * 100)) mod 13 
                      = 344 mod 13 
                      = 6

Choose a prime integer (in this case, 13) for the computation above so that we can complete all of the calculations using single-precision arithmetic.

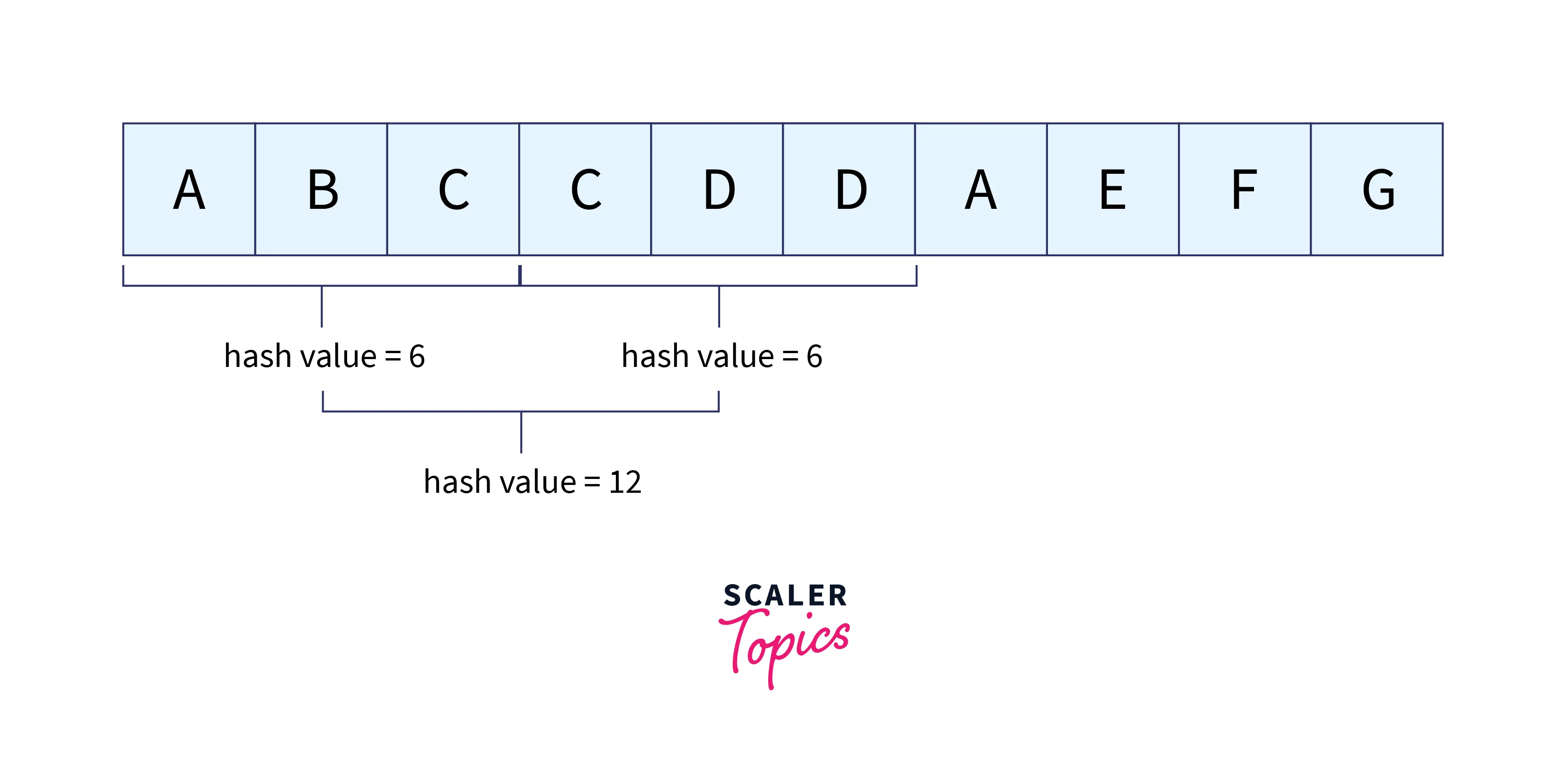
Determine the hash value for the m-character text window.

For the first window ABC,
hash value for text(t) = Σ(v * dn-1) mod 13 
                  = ((1 * 102) + (2 * 101) + (3 * 100)) mod 13 
                  = 123 mod 13  
                  = 6

Compare the pattern’s hash value to the text’s hash value. Character matching is carried out if they match. Consider character matching between ABC and CDD since the hash value of the first window (i.e. t) in the instances above matches with p. Go to the next window since they don’t match. By removing the first term and adding the following term, we arrive at the hash value for the following window, as shown below.

t = ((1 * 102) + ((2 * 101) + (3 * 100)) * 10 + (3 * 100)) mod 13 
  = 233 mod 13  
  = 12

We use the previous hash value in the manner described below to streamline this procedure.

t = ((d * (t - v[character to be removed] * h) + v[character to be added] ) mod 13  
  = ((10 * (6 - 1 * 9) + 3 )mod 13  
  = 12
Where, h = dm-1 = 103-1 = 100.

For BCC, t=12(≠6). Therefore, go for the next window. After a few searches, we will get the match for the window CDA in the text.

n = t.length
m = p.length
h = dm-1 mod q
p = 0
t0 = 0
for i = 1 to m
    p = (dp + p[i]) mod q
    t0 = (dt0 + t[i]) mod q
for s = 0 to n - m
    if p = ts
        if p[1.....m] = t[s + 1..... s + m]
            print "pattern found at position" s
    If s < n-m
        ts + 1 = (d (ts - t[s + 1]h) + t[s + m + 1]) mod q

Approach

Follow the instructions below to solve the problem:

The Naive String Matching algorithm gradually shifts the pattern. Characters at the current shift are checked individually after each slide, and if they all match, the match is printed.

The Rabin-Karp algorithm slides the pattern one by one, just like the Naive Algorithm. The Rabin Karp algorithm, in contrast to the Naive approach, compares the pattern’s hash value to the hash value of the currently selected substring of text and only begins matching individual characters if the hash values match. Therefore, the following strings require hash values to be calculated via the Rabin-Karp algorithm.

• Its own pattern
• All the substrings of the text of length m

We require a hash function that has the following property to efficiently calculate hash values for all text substrings of size m:

• The next shift’s hash value must be efficiently computed from the previous shift’s hash value and the next letter in the text, or we can say that hash(txt[s+1.. s+m]) must be efficiently computed from hash(txt[s.. s+m-1]) and txt[s+m].
• To put it another way, hash(txt[s+1.. s+m]) = rehash(txt[s+m], hash(txt[s.. s+m-1])) and Rehash needs to run in O(1) time.

Note: Rabin and Karp’s hash function generates an integer value. The integer value for a string is the numeric value of a string. For instance, “122” will have the numeric value of 122 if all the characters are in the range of 1 to 10.

Input:  txt[] = “THIS IS A TEST TEXT”, pat[] = “TEST”
Output: Pattern found at index 10
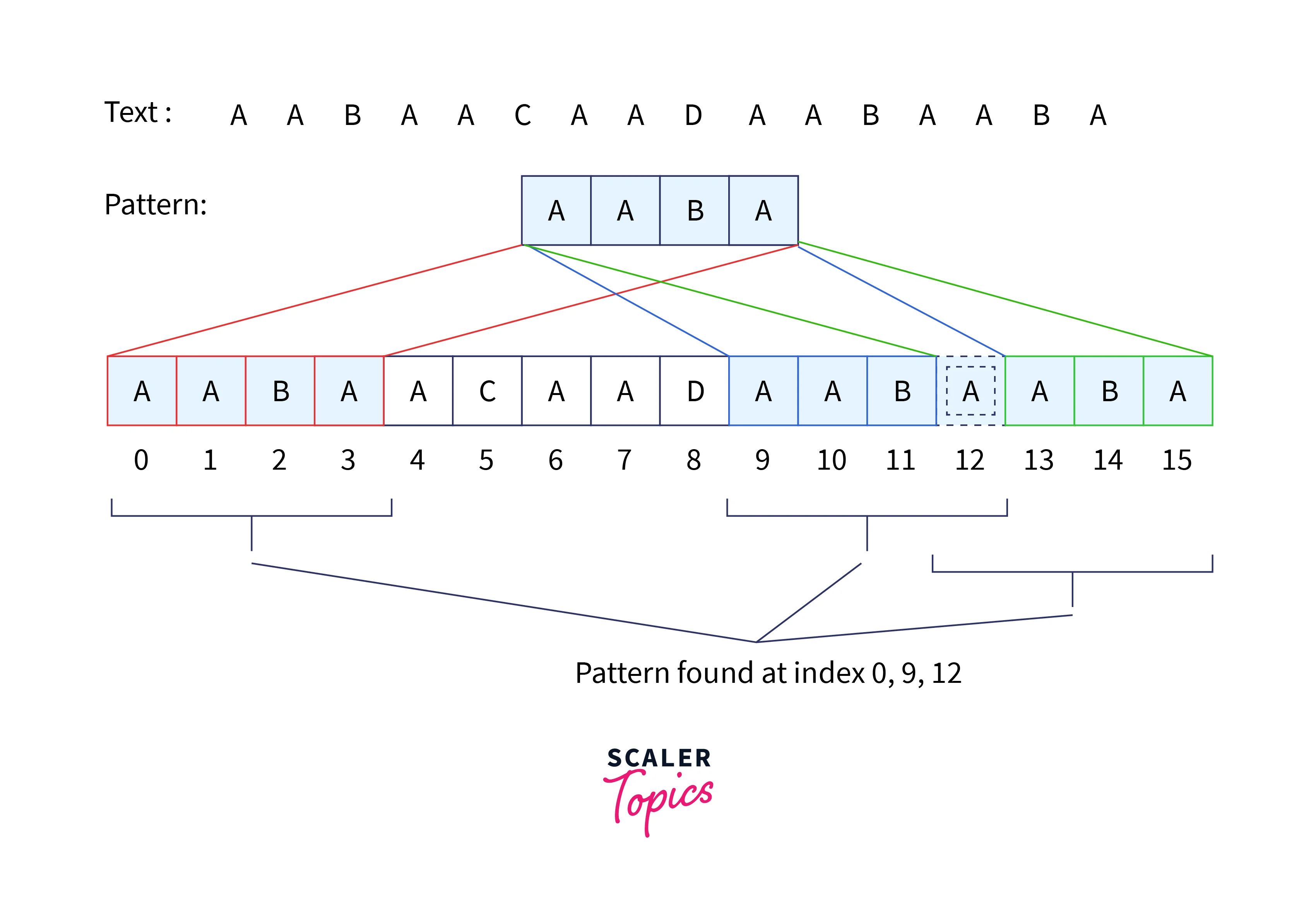
Input:  txt[] =  “AABAACAADAABAABA”, pat[] =  “AABA”
Output: Pattern found at index 0
              Pattern found at index 9
              Pattern found at index 12

Implementation of the Rabin Karp Algorithm Approach

To put this concept into practice, follow these instructions:

• First, determine the pattern’s hash value.
• Iterate beginning at the start of the string:
• Find the hash value of the current m-character substring.
• If the current substring’s hash value and the pattern’s hash value are the same, see if the substring matches the pattern.
• Save the starting index as a valid response if they are identical. If not, move on to the following substrings.
• As the necessary response, give the starting indices.

The application of the aforementioned strategy is seen below:

C++

#include <iostream>
#include <cstring>
#include <climits>
using namespace std;

#define ALPHABET_SIZE 256

void rabinKarpSearch(const char pattern[], const char text[], int prime)
{
    int patternLength = strlen(pattern);
    int textLength = strlen(text);
    int i, j;
    int patternHash = 0;
    int textHash = 0;
    int h = 1;

    for (i = 0; i < patternLength - 1; i++)
        h = (h * ALPHABET_SIZE) % prime;

    for (i = 0; i < patternLength; i++) {
        patternHash = (ALPHABET_SIZE * patternHash + pattern[i]) % prime;
        textHash = (ALPHABET_SIZE * textHash + text[i]) % prime;
    }

    for (i = 0; i <= textLength - patternLength; i++) {
        if (patternHash == textHash) {
            for (j = 0; j < patternLength; j++) {
                if (text[i + j] != pattern[j]) {
                    break;
                }
            }

            if (j == patternLength)
                cout << "Pattern found at index " << i << endl;
        }

        if (i < textLength - patternLength) {
            textHash = (ALPHABET_SIZE * (textHash - text[i] * h) + text[i + patternLength]) % prime;

            if (textHash < 0)
                textHash = (textHash + prime);
        }
    }
}

int main()
{
    char text[] = "SCALER ACADEMY";
    char pattern[] = "SCALER";
    int prime = INT_MAX;

    rabinKarpSearch(pattern, text, prime);
    return 0;
}

Output:

Pattern found at index 0

Java

public class RabinKarpAlgorithm {
    public final static int d = 256;

    static void search(String pat, String txt, int q) {
        int M = pat.length();
        int N = txt.length();
        int i, j;
        int p = 0;
        int t = 0;
        int h = 1;

        for (i = 0; i < M - 1; i++)
            h = (h * d) % q;

        for (i = 0; i < M; i++) {
            p = (d * p + pat.charAt(i)) % q;
            t = (d * t + txt.charAt(i)) % q;
        }

        for (i = 0; i <= N - M; i++) {
            if (p == t) {
                for (j = 0; j < M; j++) {
                    if (txt.charAt(i + j) != pat.charAt(j))
                        break;
                }

                if (j == M)
                    System.out.println("Pattern found at index " + i);
            }

            if (i < N - M) {
                t = (d * (t - txt.charAt(i) * h) + txt.charAt(i + M)) % q;

                if (t < 0)
                    t = (t + q);
            }
        }
    }

    public static void main(String[] args) {
        String txt = "EXAMPLE TEXT FOR TESTING";
        String pat = "TEXT";
        int q = 101;

        search(pat, txt, q);
    }
}

Output:

Pattern found at index 8

Python

# Implementation of the Rabin-Karp Algorithm based on CLRS book
# d represents the size of the character set in the input alphabet
d = 256

def rabin_karp_search(pattern, text, prime):
    pattern_length = len(pattern)
    text_length = len(text)
    pattern_hash = 0
    text_hash = 0
    h = 1

    for i in range(pattern_length - 1):
        h = (h * d) % prime

    for i in range(pattern_length):
        pattern_hash = (d * pattern_hash + ord(pattern[i])) % prime
        text_hash = (d * text_hash + ord(text[i])) % prime

    for i in range(text_length - pattern_length + 1):
        if pattern_hash == text_hash:
            match = True
            for j in range(pattern_length):
                if text[i + j] != pattern[j]:
                    match = False
                    break
            if match:
                print("Pattern found at index " + str(i))

        if i < text_length - pattern_length:
            text_hash = (d * (text_hash - ord(text[i]) * h) + ord(text[i + pattern_length])) % prime
            if text_hash < 0:
                text_hash += prime

# Driver Code
if __name__ == '__main__':
    text = "SCALER ACADEMY"
    pattern = "ACADEMY"
    prime_number = 101

    # Calling the function
    rabin_karp_search(pattern, text, prime_number)

Output:

Pattern found at index 7

C#

using System;

public class PlagiarismFreeCode {
    public readonly static int AlphabetSize = 256;

    static void RabinKarpSearch(string pattern, string text, int prime)
    {
        int patternLength = pattern.Length;
        int textLength = text.Length;
        int i, j;
        int patternHash = 0;
        int currentTextHash = 0;
        int h = 1;

        for (i = 0; i < patternLength - 1; i++)
            h = (h * AlphabetSize) % prime;

        for (i = 0; i < patternLength; i++)
        {
            patternHash = (AlphabetSize * patternHash + pattern[i]) % prime;
            currentTextHash = (AlphabetSize * currentTextHash + text[i]) % prime;
        }

        for (i = 0; i <= textLength - patternLength; i++)
        {
            if (patternHash == currentTextHash)
            {
                for (j = 0; j < patternLength; j++)
                {
                    if (text[i + j] != pattern[j])
                        break;
                }

                if (j == patternLength)
                    Console.WriteLine("Pattern found at index " + i);
            }

            if (i < textLength - patternLength)
            {
                currentTextHash = (AlphabetSize * (currentTextHash - text[i] * h) + text[i + patternLength]) % prime;

                if (currentTextHash < 0)
                    currentTextHash = (currentTextHash + prime);
            }
        }
    }

    public static void Main()
    {
        String text = "SAMPLE TEXT FOR TESTING";
        String pattern = "TEXT";

        int prime = 101;

        RabinKarpSearch(pattern, text, prime);
    }
}

Output:

Pattern found at index 7

Rabin Karp Algorithm Time Complexity

Time Complexity:

The Rabin-Karp method has an O(n+m) average and best-case running time but an O(nm) worst-case running time. The worst-case scenario for the Rabin-Karp algorithm is when all characters in the pattern and text are identical, and all of the substrings in the text match the pattern’s hash value.

Auxiliary Space: O(1)

FAQs

Q. What are the limitations of the Rabin-Karp algorithm?

A. Spurious Hit makes the algorithms’ worst-case complexity higher. A spurious hit occurs when the hash value of the pattern matches the hash value of the string, but the string differs from the pattern. We use modulus to lessen Spurious Hit.

Q. Which specific circumstances call for a Rabin-Karp algorithm to perform better?

A. When a vast text is being searched for, and several pattern matches are being found, such as when looking for plagiarism, the Rabin-Karp algorithm performs better. Additionally, Boyer-Moore performs better with somewhat large patterns, a medium-sized alphabet, and a wide vocabulary.

Q. How does the Rabin-Karp algorithm improve?

A. Rabin-Karp enhances this concept by taking advantage of the fact that comparing the hashes of two strings can be done in linear time and is far more effective than comparing the individual characters of those strings to discover a match. Consequently, a best-case runtime complexity of O(n+m) is provided.

Q. Which algorithm for pattern search is the quickest?

A. The Boyer-Moore technique has a smaller constant factor than many other string search algorithms because it skips over portions of the text using information obtained during the preprocessing step. The algorithm generally operates more quickly than the pattern length does.

Conclusion

• The Rabin-Karp algorithm is a string matching algorithm used to search for a pattern within a text efficiently.
• It employs hashing techniques to compare the hash values of the pattern and substrings of the text, reducing the number of character comparisons.
• Rabin-Karp is especially useful for multiple pattern searches within a text.
• Hash collisions are handled by rechecking characters individually when hash values match, ensuring accuracy.
• This algorithm is employed in various applications, including plagiarism detection, data deduplication, and substring search in large datasets.
• Rabin-Karp’s ability to perform pattern searches in linear time complexity makes it a valuable tool for efficient string matching.