Preorder to Postorder Traversal

Problem Statement

Given an array that represents the preorder traversal of a binary search tree, write a program to find the postorder traversal of the BST.

Example

The preorder of a BST is given below:
preorder[] = {10, 5, 8, 25, 47}
The postorder for the example will be:
postorder[] = {8, 5, 47, 25, 10}

Example Explanation

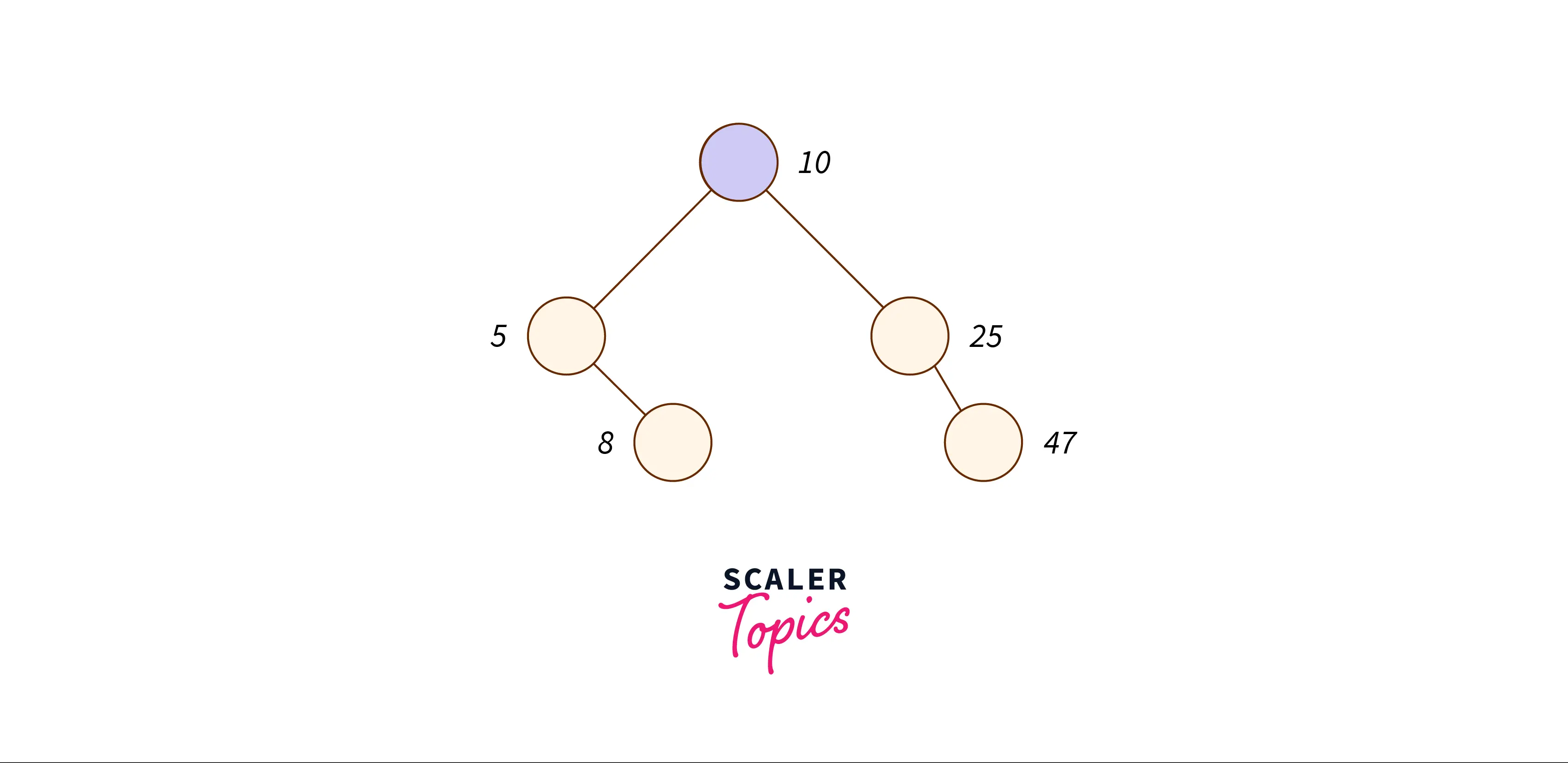
Input/Output

Input
An array of size N represents the preorder traversal of a BST.

Output
The postorder traversal of the given BST.

Constraints

$1 <= N <= 10^{3}$

$1 <= arr[i] <= 10^{4}$

Algorithm 1 – Simple Approach

• Step 1 – Construct a Binary Search Tree from the given preorder traversal using the function ‘constructBST’.
• Step 2 – Perform postorder traversal on the constructed BST.

Code Implementation

C++

/* C++ program for finding postorder traversal of BST from preorder traversal */
#include <bits/stdc++.h>
using namespace std;
/* A binary tree node has val, a pointer to the left child, and a pointer to the right child */
class node {
public:
    int val;
    node* left;
    node* right;
};
/* Function to create a node */
node* newNode(int val){
    node* temp = new node();
    temp->val = val;
    temp->left = temp->right = NULL;
    return temp;
}
/* Recursive function to create a Binary Search Tree using its preorder traversal */
node* constructBST(int pre[], int* preIndex, int low, int high, int size){
    if (*preIndex >= size || low > high)
        return NULL;
    /* The node at preIndex from pre[] is made the root, and preIndex is incremented. */
    node* root = newNode(pre[*preIndex]);
    *preIndex = *preIndex + 1;
    /* return if subarray has only one element */
    if (low == high)
        return root;
    /* Search for the first element greater than  root */
    int i;
    for (i = low; i <= high; ++i)
        if (pre[i] > root->val)
            break;
    /* Using an index of elements found in preorder, divide the preorder array into Left subtree and right subtree */
    root->left = constructBST(pre, preIndex, *preIndex, i - 1, size);
    root->right = constructBST(pre, preIndex, i, high, size);
    return root;
}
// Function to find postorder traversal
void PostOrder(node* head){
    node* temp = head;
    unordered_set<node*> visited;
    while (temp && visited.find(temp) == visited.end()) {
        // Visited left subtree
        if (temp->left && visited.find(temp->left) == visited.end())
            temp = temp->left;
        // Visited right subtree
        else if (temp->right && visited.find(temp->right) == visited.end())
            temp = temp->right;
        // Print node
        else {
            printf("%d ", temp->val);
            visited.insert(temp);
            temp = head;
        }
    }
}
// Driver code
int main(){
    int N=5, preIndex=0;
    int preorder[5] = {10, 5, 8, 25, 47};

    cout<<"Input: Preorder traversal of the BST: ";
    for(int i=0;i<N;i++)
        cout << preorder[i] << " ";
    cout << endl;

    node* root = constructBST(preorder, &preIndex, 0, N - 1, N);
    cout << "Output: Postorder traversal of the BST: ";
    PostOrder(root);
    return 0;
}

Java

/* Java program for finding postorder traversal of BST from preorder traversal */
import java.io.*;
import java.util.*;
/* A binary tree node has val, the pointer to the left child, and a pointer to the right child */
/* Function to create a node */
class Node {
    int data;
    Node left, right;
    Node(int d){
        data = d;
        left = right = null;
    }
}
class Main {
    static class INT {
        int index;
        INT(int d) { index = d; }
    }
    /* Recursive function to create a Binary Search Tree using its preorder traversal */
    Node constructBST(int pre[], INT preIndex,
                        int low, int high, int size){
        // Base case
        if (preIndex.index >= size || low > high) {
            return null;
        }
        /* The node at preIndex from pre[] is made the root, and preIndex is incremented. */
        Node root = new Node(pre[preIndex.index]);
        preIndex.index = preIndex.index + 1;
        /* return if subarray has only one element */
        if (low == high) {
            return root;
        }
        /* Search for the first element greater than  root */
        int i;
        for (i = low; i <= high; ++i) {
            if (pre[i] > root.data) {
                break;
            }
        }
        /* Using the index of elements found in preorder, divide the preorder array into Left subtree and right subtree */
        root.left = constructBST(pre, preIndex, preIndex.index, i - 1, size);
        root.right = constructBST(pre, preIndex, i, high, size);
        return root;
    }
    // Function to find postorder traversal
    void postOrder(Node head){
    Node temp = head;   
    HashSet<Node> visited = new HashSet<>();
    while ((temp != null  && !visited.contains(temp))){
        // Visited left subtree
        if (temp.left != null &&
         !visited.contains(temp.left))
            temp = temp.left;
         // Visited right subtree
        else if (temp.right != null &&
        !visited.contains(temp.right))
            temp = temp.right;
         // Print node
        else{
            System.out.printf("%d ", temp.data);
            visited.add(temp);
            temp = head;
        }
    }
}
    // Driver code
    public static void main(String[] args){
        Main tree = new Main();
        int N = 5;
        // int[] preorder = new int[5];  
        int[] preorder = {10, 5, 8, 25, 47};  


        System.out.print("Input: Preorder traversal of the BST: ");  
        for(int i=0; i<N; i++) {
            System.out.printf("%d ", preorder[i]);
        }
        System.out.printf("\n");

        INT preIndex = new INT(0);
        Node root = tree.constructBST(preorder, preIndex, 0, N-1, N);
        System.out.print("Output: Postorder traversal of the BST: ");  
        tree.postOrder(root);
    }
}

Python

# Python program for finding postorder traversal of BST from preorder traversal
"""A binary tree node has val, pointer to left child and a pointer to the right child"""
class Node():
    # Function to create a node
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None
# function to create a Binary Search Tree using its preorder traversal.
def constructBST(preorder, low, high):
    if(low > high):
        return None
    # The node at preIndex from pre[] is made the root, and  preIndex is incremented
    root = Node(preorder[constructBST.preIndex])
    constructBST.preIndex += 1
    # return if subarray has only one element 
    if low == high:
        return root
    r_root = -1
    # Search for the first element greater than the root
    for i in range(low, high+1):
        if (preorder[i] > root.val):
            r_root = i
            break
    # If no elements are greater than the current root, all elements are assigned as left children of the root
    if r_root == -1:
        r_root = constructBST.preIndex + (high - low)
    # Using an index of elements found in preorder, divide the preorder array into the Left subtree and right subtree
    root.left = constructBST(preorder, constructBST.preIndex, r_root-1)
    root.right = constructBST(preorder, r_root, high)
    return root

# Function to find postorder traversal 
def PostOrder(head):
    temp = head
    visited = set()
    while (temp and temp not in visited):
        # Visited left subtree
        if (temp.left and temp.left not in visited):
            temp = temp.left
        # Visited right subtree
        elif (temp.right and temp.right not in visited):
            temp = temp.right
        # Print node
        else:
            print(temp.val, end = " ")
            visited.add(temp)
            temp = head
# Driver code
if __name__ == '__main__':
    N= 5
    preorder = [10, 5, 8, 25, 47] 
    print("Input: Preorder traversal of the BST:", end=" ")
    print(*preorder)

    constructBST.preIndex =0 #static variable of constructBST
    root = constructBST(preorder, 0, N-1)
    print("Output: Postorder traversal of the BST:", end=" ")
    PostOrder(root)

Output

Input: Preorder traversal of the BST: 10 5 8 25 47
Output: Postorder traversal of the BST: 8 5 47 25 10

Time Complexity

Time Complexity to construct BST is O($N^2$).
Time complexity to find out the postorder traversal of the constructed BST is O(N) where N is no of the nodes in a binary tree.
Thus, the overall time complexity of converting preorder to postorder traversal using this approach will be O($N^2$).

Space Complexity

The space complexity of this approach is O(N) where N is the extra space required for the set visited.

Algorithm 2 – Efficient Approach

In this approach of converting preorder to postorder traversal construction of a tree is avoided.

• The preorder array is traversed to maintain a range in which the current element should lie.
• In preorder traversal, the first element or root is stored as it lies in the initial range.
• Next, recursive calls are made for the left and right subtrees respectively. Then, the value of the root is printed.
  • For left subtree range is minval to root->data.
  • For right subtree range is root->data to maxval.
  • If the element considered lies outside the range specified, then it does not belong to a current subtree. Such recursive calls are returned until the correct position of that element is not found.

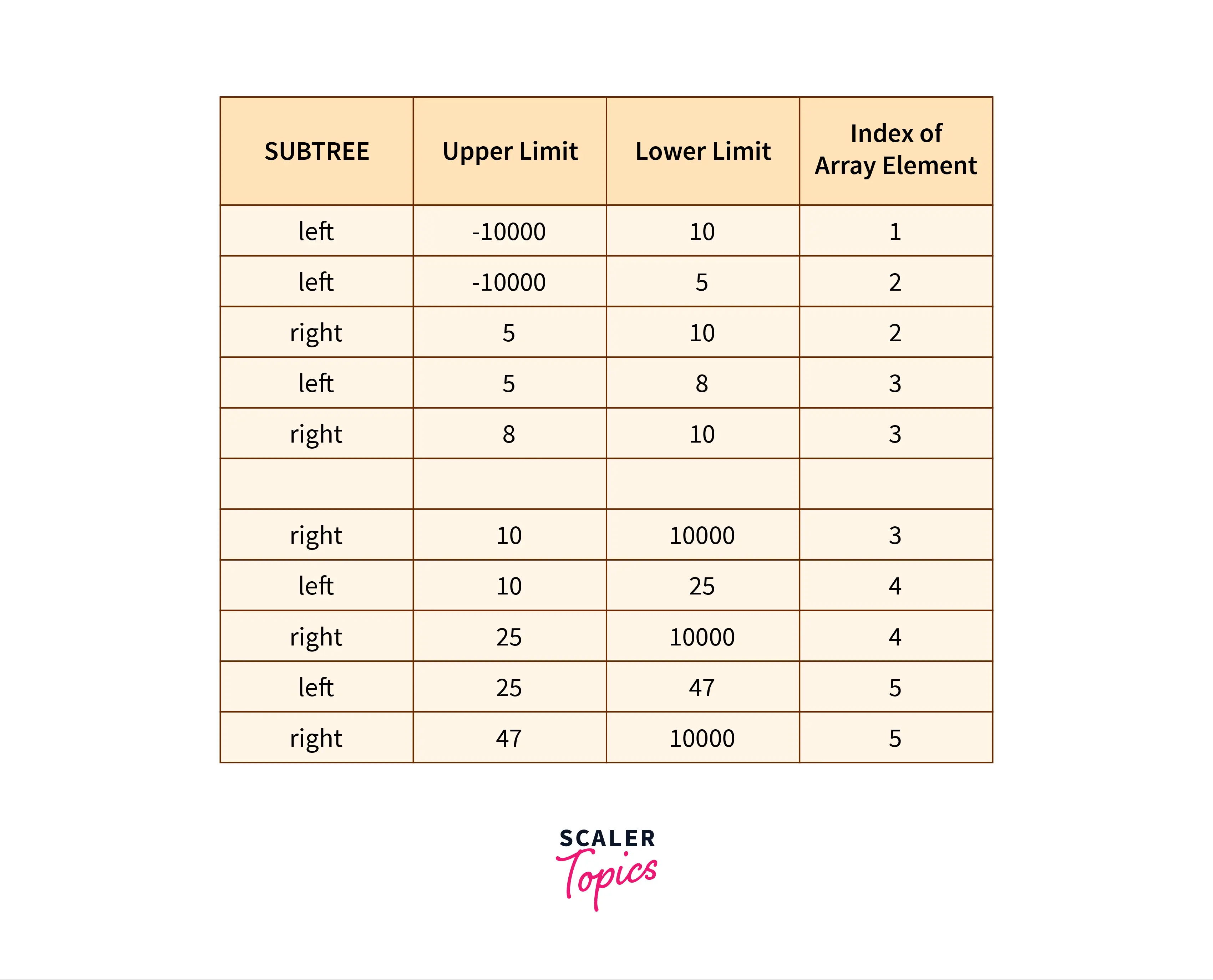
Code Implementation

C++

/* C++ program for finding postorder traversal of BST from preorder traversal */
#include <bits/stdc++.h>
using namespace std;

/* Function to find postorder traversal from preorder traversal.*/
void PostOrder(int pre[], int size, int minval, int maxval, int& preIndex){
    /* Return if all elements are added to the postorder array.*/
    if (preIndex == size)
        return;
    /* If the array element does not lie in the range specified, then it is not part of the current subtree. */ 
    if (pre[preIndex] < minval || pre[preIndex] > maxval)
        return;
    /* Store current value, to be printed later, after printing left and right subtree. */
    int val = pre[preIndex];
    preIndex+=1;
    /* All elements within minval and val are present in the left subtree. */
    PostOrder(pre, size, minval, val, preIndex);
    /* All elements within val and maxval are present in the right subtree. */
    PostOrder(pre, size, val, maxval, preIndex);
    cout << val << " ";
}

// Driver code
int main(){
    int N=5, preorderIndex=0;
    int preorder[5] = {10, 5, 8, 25, 47};

    cout<<"Input: Preorder traversal of the BST: ";
    for(int i=0;i<N;i++)
        cout << preorder[i] << " ";
    cout << endl;

    cout << "Output: Postorder traversal of the BST: ";
    PostOrder(preorder, N, -10000, 10000, preorderIndex);
    return 0;
}

Java

// Java program for finding postorder traversal of BST from preorder traversal
import java.io.*;
import java.util.*;
class Main {
    static class INT {
        int data;
        INT(int d) { data = d; }
    }
    /* Function to find postorder traversal from preorder traversal. */
    static void PostOrder(int pre[], int size, int minval, int maxval, INT preIndex){
        /* Return if all elements are added to the postorder array.*/
        if (preIndex.data == size)
            return;
        /* If the array element does not lie in the range specified, then it is not part of the current subtree. */
        if (pre[preIndex.data] < minval|| pre[preIndex.data] > maxval) {
            return;
        }
        /* Store current value, to be printed later, after printing left and right subtree. */
        int val = pre[preIndex.data];
        preIndex.data++;
        /* All elements within minval and val are present in the left subtree. */
        PostOrder(pre, size, minval, val, preIndex);
        /* All elements within val and maxval are present in the right subtree. */
        PostOrder(pre, size, val, maxval, preIndex);

        System.out.print(val + " ");
    }
    // Driver code
    public static void main(String args[]){
        Main tree = new Main();
        int N = 5;
        // int[] preorder = new int[5];  
        int[] preorder = {10, 5, 8, 25, 47};  


        System.out.print("Input: Preorder traversal of the BST: ");  
        for(int i=0; i<N; i++) {
            System.out.printf("%d ", preorder[i]);
        }
        System.out.printf("\n");

        INT preIndex = new INT(0);

        System.out.print("Output: Postorder traversal of the BST: ");  
        PostOrder(preorder, N, -10000, 10000, preIndex);
    }
}

Python

"""Python3 program for finding postorder traversal of BST from preorder traversal"""
# Function to find postorder traversal from preorder traversal.
def PostOrder(pre, size, minval, maxval, preIndex):
    # Return if all elements are added to the postorder array.
    if (preIndex[0] == size):
        return
    # If the array element does not lie in the range specified, then it is not part of the current subtree.
    if (pre[preIndex[0]] < minval or pre[preIndex[0]] > maxval):
        return
    # Store current value, to be printed later, after printing left and right subtree.
    val = pre[preIndex[0]]
    preIndex[0] += 1
    # All elements within minval and val are present in the left subtree.
    PostOrder(pre, size, minval, val, preIndex)
    # All elements within val and maxval are present in the right subtree.
    PostOrder(pre, size, val, maxval, preIndex)
    print(val, end=" ")

# Driver Code
if __name__ == '__main__':
    N= 5
    preorder = [10, 5, 8, 25, 47] 
    print("Input: Preorder traversal of the BST:", end=" ")
    print(*preorder)
    preorderIndex =[0]

    print("Output: Postorder traversal of the BST:", end=" ")
    PostOrder(preorder, N, -10000, 10000, preorderIndex)

Output

Input: Preorder traversal of the BST: 10 5 8 25 47
Output: Postorder traversal of the BST: 8 5 47 25 10

Time Complexity

Since every node is traversed once, the time complexity for this approach is O(N), where N is the number of nodes.

Space Complexity

Due to the use of a call stack, the time complexity of this approach is O(N).

Algorithm 3 – Using Iteration and Recursion

The conversion of preorder to postorder traversal can also be done using iteration and recursion.

• Step 1 – Preorder can be represented as root -> left -> right and postOrder can be represented as left -> right -> root.
• Step 2 – A loop is used, and the last element of the left group is taken as the pivot element. The pivot is the point from which the array will be rotated. It is found by finding the index of the smallest element greater than the root.
• Step 3 – Consider the left section as elements from index 1 to index before pivot.
• Step 4 – Consider the right section as elements in between the last index and pivot.
• Step 5 – Repeat step 4 recursively till both the left and right sections have at most 1 element. Print the only element in the section.
• Step 6 – Finally, print the element at index 0.

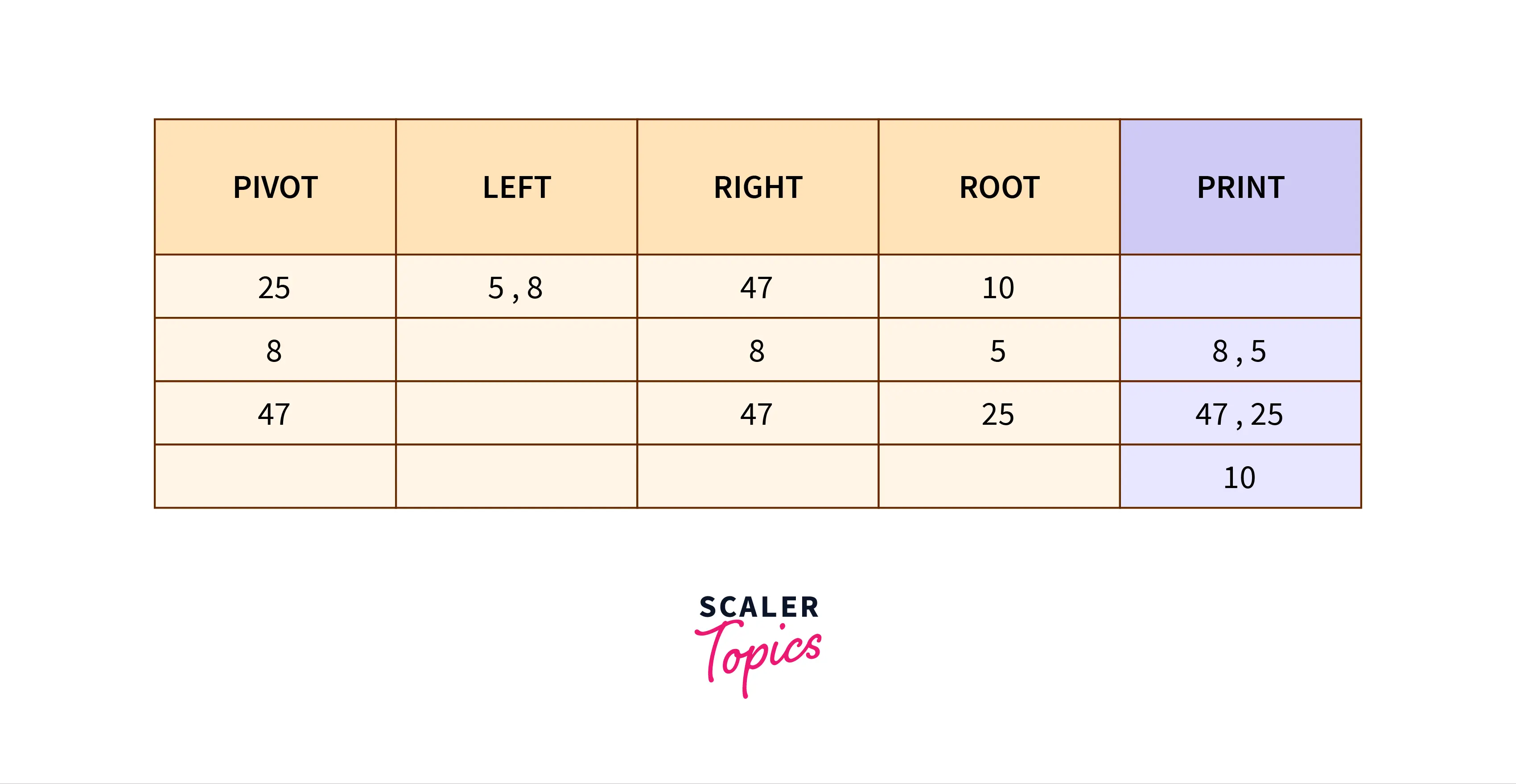
Code Implementation

C++

/* C++ program for finding postorder traversal of BST from preorder traversal */
#include <bits/stdc++.h>
using namespace std;
/* Function to find postorder traversal from preorder traversal.*/
void PostOrder(int pre[], int size){
   int pivot = 0;
   for(int i = 1; i < size; i++){
      if (pre[0] <= pre[i]) {
         pivot = i;
         break;
      }
   }
   /* left subtree */
    if(pivot==0){
        for(int i = size - 1; i >= 0; i--)
            cout<<pre[i]<< " ";
        return;
    }
    int slicedpre[pivot];
    int j=0, i=0;
    for (i=1; i<pivot; i++){
        slicedpre[j]=pre[i];
        j++;
        }
    if (j>1)
        PostOrder(slicedpre, j);
    if (j==1){
        cout<<pre[pivot-1]<<" ";
    }
    /* right subtree */
    int slicepre[size-pivot];
    j=0;
    i=0;
    for (i=pivot; i<size; i++){
        slicepre[j]=pre[i];
        j++;
        }
    if (j>1)
        PostOrder(slicepre, j);
    if (j==1){
        cout<<pre[size-1]<<" ";
    }
   cout << pre[0]<<" ";
}
// Driver code
int main(){
    int N=5, preorderIndex=0;
    int preorder[5] = {10, 5, 8, 25, 47};

    cout<<"Input: Preorder traversal of the BST: ";
    for(int i=0;i<N;i++)
        cout << preorder[i] << " ";
    cout << endl;

    cout << "Output: Postorder traversal of the BST: ";
    PostOrder(preorder, N);
    return 0;
}

Java

/* Java program for finding postorder traversal of BST from preorder traversal */
import java.io.*;
import java.util.*;
class Main {
    static class INT {
        int data;
        INT(int d) { data = d; }
    }
    /* Function to find postorder traversal from preorder traversal. */
    static void PostOrder(int pre[], int size){
       int pivot = 0;
       for(int i = 1; i < size; i++){
          if (pre[0] <= pre[i]) {
             pivot = i;
             break;
          }
       }
       /* left subtree */
       if(pivot==0){
            for(int i = size - 1; i >= 0; i--)
                System.out.print(pre[i]+" ");
            return;
        }
        int slicedpre[] =  new int[pivot];;
        int j=0, i=0;
        for (i=1; i<pivot; i++){
            slicedpre[j]=pre[i];
            j++;
            }
        if (j>1)
            PostOrder(slicedpre, j);
        if (j==1){
            System.out.print(pre[pivot-1]+" ");
        }
        /* right subtree */
        int slicepre[] = new int[size-pivot];
        j=0;
        i=0;
        for (i=pivot; i<size; i++){
            slicepre[j]=pre[i];
            j++;
        }
        if (j>1)
            PostOrder(slicepre, j);
        if (j==1){
            System.out.print(pre[size-1]+" ");
        }
    System.out.print(pre[0]+ " ");
}
    // Driver code
    public static void main(String args[]){
        int N = 5;
        // int[] preorder = new int[5];  
        int[] preorder = {10, 5, 8, 25, 47};  


        System.out.print("Input: Preorder traversal of the BST: ");  
        for(int i=0; i<N; i++) {
            System.out.printf("%d ", preorder[i]);
        }
        System.out.printf("\n");

        INT preIndex = new INT(0);

        System.out.print("Output: Postorder traversal of the BST: ");  
        PostOrder(preorder, N);
    }
}

Python

"""Python3 program for finding postorder traversal of BST from preorder traversal """
# Function to find postorder traversal from preorder traversal.
def PostOrder(pre, size):
    pivot = 0
    for i in range(1, size):
        if (pre[0] <= pre[i]):
            pivot = i
            break
    #left subtree
    if len(pre[1:pivot])>1:
        PostOrder(pre[1:pivot], len(pre[1:pivot]))
    if len(pre[1:pivot])==1:
        print(pre[pivot-1], end= " ")
    if pivot==0:
        for i in range(size-1, -1, -1):
            print(pre[i], end= " ")
        return
    # right subtree
    if len(pre[pivot:size])>1:
        PostOrder(pre[pivot:size], len(pre[pivot:size]))
    if len(pre[pivot:size])==1:
        print(pre[size-1], end= " ")
    print(pre[0], end=" ")

# Driver Code
if __name__ == '__main__':
    N= 5
    preorder = [10, 5, 8, 25, 47] 
    print("Input: Preorder traversal of the BST:", end=" ")
    print(*preorder)

    print("Output: Postorder traversal of the BST:", end=" ")
    PostOrder(preorder ,N)

Output

Input: Preorder traversal of the BST: 10 5 8 25 47
Output: Postorder traversal of the BST: 8 5 47 25 10

Time Complexity

For the execution of this approach, the array consisting of the preorder traversal elements is traversed to find the pivot in O(N).
The rotation also takes O(N) time causing the overall time complexity for the Preorder function to be O(N). However, since the function is called recursively the overall time complexity will be O($N^2$).

Space Complexity

The Preorder function is called recursively which creates a new array every time it is called. Hence, the overall space complexity for this approach will be O($N^2$).

Conclusion

• The traversal in which at first the root node is visited, followed by the left sub-tree, and after that right sub-tree is visited is called preorder traversal.
• The traversal in which at first the left sub-tree is visited, followed by the right sub-tree, and finally the root is called postorder traversal.
• Approach 1 – In this approach of conversion of preorder to postorder traversal, a BST is created.
  • Time Complexity – O($N^2$)
  • Space Complexity – O(n)
• Approach 2 – Traversing the preorder array with a limit on values to separate values of the left and right subtree.
  • Time Complexity – O(n)
  • Space Complexity – O(n)
• Approach 3 – Using a loop to calculate the pivot element where preorder is root -> left -> right and postorder is left -> right -> root. In this approach iteration and recursion are used.
  • Time Complexity – O($N^2$)
  • Space Complexity – O($N^2$)

FAQ

Q. What is Preorder Traversal?

A. The process of visiting the root node first, followed by the left sub-tree and finally, the right sub-tree is known as preorder traversal. It can be represented as –
$root → left → right$

Q. What is Postorder Traversal?

A. The process of visiting the left sub-tree and followed by the right sub-tree and finally the root is known as postorder traversal. It can be represented as –
$left → right → root$