Problem Statement
The problem states that we are given a text string (let’s say text) having the length n and a pattern string (let’s say pattern) having the length m. We need to write a function that takes these two strings (pattern, and text) and prints all the occurrences of the pattern string in the text string.
Note:
- We can assume that the value of m will always be less than the value of n.
- We can assume 0-based indexing.
Refer to the Example and Example Explanation sections for more details and the Approach section to understand the working of the naive string matching algorithm.
Example
Example 1: The input string is:
"Welcome to Scaler Topics"
The input pattern is:
"Scaler"
Output: The pattern was found at index: 11.
Example 2: The input string is:
"Hello, World!"
The input pattern is:
"World!"
Output:
The pattern was found at index: 7.
Example Explanation
Before getting into various approaches to the Naive String Matching Algorithm, let us briefly discuss strings in brief.
A string is an immutable data type that is used to store the sequence of characters. Strings are one of the most widely used data types of any programming language. A string can be easily created using quotes (either single quotes or double quotes).
Example:
string = "Scaler Topics"
or Example:
string = 'Scaler Topics'
Now, let us take a few examples to understand the algorithm i.e. naive string matching algorithm.
In the example above, the input string is “Hello World! and the pattern that needs to be searched is “World!”. We can see that the size of the pattern is 6 (i.e. m) and the size of the input text is 12 (i.e. n).
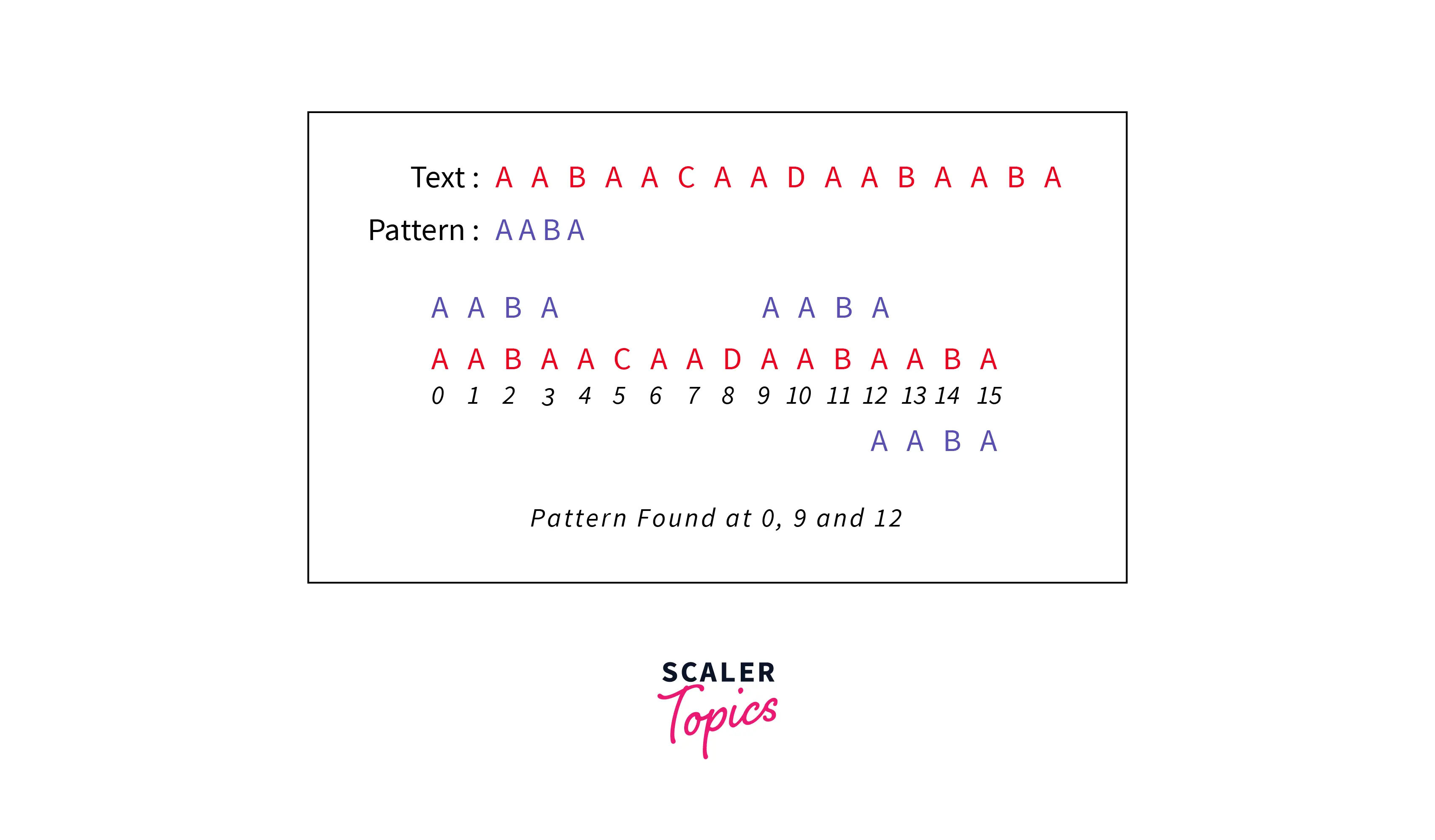
We can start searching for the pattern in the input text by sliding the pattern over the text one by one and checking for a match.
So, we would start searching from the first index and slowly move our pattern window from index-0 to index-6. At index-6, we can see that both the W’s are matching. So, we will search the entire pattern in the window starting with index-6.
Hence, we will find a match and return the starting index of the pattern as the answer.
For better clarity of the window search, please refer to the image provided below.
Best Case
The best case in the naive string matching algorithm is when the required pattern is found in the first searching window only.
For example, the input string is: “Scaler Topics” and the input pattern is “Scaler. We can see that if we start searching from the very first index, we will get the matching pattern from index-0 to index-5. So, we would return 0 as the answer.
In the best-case scenarios, we have only searched a smaller section of the entire string. We need not traverse the entire input string.
Note: In the best case, we need to perform the O(1 + m)a number of comparisons, m for comparing the pattern string in the window and 11 comparison for the first character of the input string text with the pattern string’s first character. Here, m is the size of the input pattern string.
Worst Case
The worst case in the naive string-matching algorithm is when the required pattern cannot be found in the entire input string.
For example, the input string is: “Scaler Topics” and the input pattern is “InterviewBit. We can see that if we start searching from the very first index and traverse the entire input string but we cannot find any matching.
In the worst-case scenario, we need to traverse the entire input string.
Note: In the worst case, we need to perform the O(m*(n-m+1)) number of comparisons, where n is the size of the input string and m is the size of the input pattern string.
Features
String searching algorithms like the naive string matching algorithm are widely used algorithms in computer science. They are extensively used to search strings and patterns in notepad/word files or browsers or databases, etc. They are used in search engines to search for matching results.
Input/Output
The input text is:
"Welcome to Scaler Topics"
The input pattern is:
"Scaler"
Output:
The pattern was found at index: 11.
Example 2: The input text is:
"Hello, World!"
The input pattern is:
"World!"
Output: The pattern was found at index: 7.
Constraints
- 1 <= n <= 30
- 1 <= m <= 30
In some problems, you may find the number of test cases represented by t. So, we only need to call the searchPattern() function t-times.
Algorithm 1 – Naive Pattern Searching
One approach to search a certain pattern in the input string can be using two loops (nested loops). We will use all the possible placements of the pattern string in the input text and check whether the current positioning matches the input pattern or not. If the current positioning matches with the input pattern then we would return the first index of the matching window (of input text). If all the possible positioning does not match with the input string then we would return −1.
Note: This approach tests all the possible placements of input pattern [1…….m] relative to input text [1……n]. We then try to shift s = 0, 1…….n-m, successively and for each shift s, we will compare both the input and pattern string.
Refer to the next sub-section to learn the understanding pseudo-code of the naive string-matching algorithm.
Algorithm
The pseudo-code for the same:
- We will initialize an outer loop that will run from i = 0 to i less than or equal to (n-m). Since, after the index n-m, our searching space (or searching window) will exceed the length of the input string.
- After the outer loop, we will initialize an inner loop that will run from j = 0 to j less than m as this inner loop will range from 0 to the size of the input pattern.
- Now, first we would check if the current input text character matches with the current input pattern character or not.
- If a match is not found, we would break from the loop, and the inner loop will move one index far and start searching in the next window.
- If a match is found, we would try to match the entire input pattern with the current window of the input text.
- If we have traversed the entire searching window in the input text and we have found our pattern string, we would print the result.
- Else, we would search in the next window.
Please check the code implementation section for more clarity.
Code Implementation
Let us the code implementation of the same in various languages:
C++ Code:
#include <bits/stdc++.h>
using namespace std;
// a function that prints occurrences of pattern[] in text[]
void searchPattern(string pattern, string text, int m, int n) {
// Outer loop will help to traverse the entire input text string
for (int i = 0; i <= n - m; i++) {
int j;
// Traversing the entire pattern string and checking if the current character matches or not.
for (j = 0; j < m; j++)
if (text[i + j] != pattern[j])
break;
/*
If we have traversed the entire searching space and did not break, it means we have found our pattern in the string starting from the index-i
*/
if (j == m)
{
cout << "The pattern was found at the index: " << i << endl;
return;
}
}
cout << "No match found!" << endl;
}
/* The main function */
int main() {
string text = "Scaler Topics";
string pattern = "Topics";
searchPattern(pattern, text, pattern.size(), text.size());
return 0;
}
Java Code:
public class Test {
// a function that prints occurrences of pattern[] in text[]
static void searchPattern(String pattern, String text, int m, int n) {
// Initializing the pointers that will point to the input text and pattern
int i = 0, j = n - 1;
for (i = 0, j = n - 1; j < m;) {
/*
If we have traversed the entire searching space and did not break, it means we have found our pattern in the string starting from the index-i
*/
if (text.equals(pattern.substring(i, j + 1))) {
System.out.println("The pattern was found at the index: " + i);
return;
}
i++;
j++;
}
System.out.println("No match found!");
}
public static void main(String[] args) {
String text = "Scaler Topics";
String pattern = "Topics";
searchPattern(pattern, text, pattern.length(), text.length());
}
}
Python Code:
# a function that prints occurrences of pattern[] in the text[]
def searchPattern(pattern, text, m, n):
# Outer loop will help to traverse the entire input text string
for i in range(n - m + 1):
j = 0
# Traversing the entire pattern string and checking if the current character matches or not.
while(j < m):
if (text[i + j] != pattern[j]):
break
j += 1
"""
If we have traversed the entire searching space and did not break, it means we have found our pattern in the string starting from the index-i
"""
if (j == m):
print("The pattern was found at the index:", i)
return
print("No match found!")
# The main function
if __name__ == '__main__':
text = "Scaler Topics"
pattern = "Topics"
searchPattern(pattern, text, len(pattern), len(text))
Output
The pattern was found at the index: 7
In the naive string matching algorithm, we are traversing the entire input string text until we found a match with the input pattern. For searching the pattern, we are searching the window size of m if the first character of the window matches the input string text.
Time complexity
In the naive string matching algorithm, the time complexity of the algorithm comes out to be O(n-m+1), where n is the size of the input string and m is the size of the input pattern string.
Space complexity
In the naive string matching algorithm, the space complexity of the algorithm comes out to be O(1).
Algorithm 2 – Alternate Approach – using 2 pointers
Another approach to the string pattern searching problem can be using two-pointers. We can use the degenerating property which means patterns having the same sub-patterns appearing in the pattern more than once.
Whenever we detected a mismatch, we can already sense or see the characters that will be present in the next search window. We can use this information and this information will help us to avoid searching for repeated characters present commonly in the various windows.
Algorithm
The pseudo-code for the same:
- We would initialize two pointers i and j. i will point to the input text string and j will point to the input pattern string
- Start comparing the pattern with the text of the current window.
- We will keep incrementing both the pointer (i and j) until both the string matches.
- When a mismatch is encountered:
- We already know that the character of the pattern from index-0 to index-j – 1 matches with the text string from index i – j to index i – 1. Apart from this, we also know that the pattern[0.. j-1] is both a proper suffix and a proper prefix.
- So, we do not need to match both these character sequences because these two (proper suffix and proper prefix) will always match.
- We would then perform the same algorithm for the next window but in the new window, we already know about the proper prefix and proper suffix.
Note:
- Proper Prefix: A proper prefix of the string will be a subset of the string using only the beginning portion of the pattern. A subset is any possible combination of the original set (string).
- Proper Suffix: A proper suffix of a string would be a subset of the pattern with elements taken only starting from the last character.
We would also store the longest proper prefix inside a string (namely – longestProperPrefSuf) which is also a suffix so that the processing becomes easier.
Code Implementation
Let us the code implementation of the same in various languages:
C++ Code:
#include <bits/stdc++.h>
using namespace std;
// A function that will compute the longest possible proper prefix and proper suffix
void computeLongestProperPrefixSuffix(string pat, int m, int *longestProperPrefSuf) {
// length of the previous longest prefix suffix
int length = 0;
longestProperPrefSuf[0] = 0;
// calculating the longest possible proper prefix and proper suffix for i = 1 to m-1
int i = 1;
while (i < m) {
if (pat[i] == pat[length]) {
// if matches increment the length
length++;
longestProperPrefSuf[i] = length;
i++;
}
else {
// if the length is not zero, redefining the length of the longestProperPrefSuf
if (length != 0)
length = longestProperPrefSuf[length - 1];
else {
// when the length is 0
longestProperPrefSuf[i] = 0;
i++;
}
}
}
}
// a function that prints occurrences of pattern[] in text[]
void searchPattern(string pattern, string text, int m, int n) {
/*
defining array that will store the longest possible proper prefix and proper suffix.
*/
int longestProperPrefSuf[m];
// calculating the longest possible proper prefix and proper suffix
computeLongestProperPrefixSuffix(pattern, m, longestProperPrefSuf);
// initializing both the pointers.
int i = 0;
int j = 0;
while ((n - i) >= (m - j)) {
// increment the pointer until the match is found.
if (pattern[j] == text[i]) {
j++;
i++;
}
// If the match is completely found.
if (j == m) {
cout << "The pattern was found at the index: " << i - j << endl;
return;
j = longestProperPrefSuf[j - 1];
}
// when mismatch after j matches
else if (i < n && pattern[j] != text[i]) {
if (j != 0)
j = longestProperPrefSuf[j - 1];
else
i = i + 1;
}
}
cout << "No match found!" << endl;
}
/* The main function */
int main() {
string text = "Scaler Topics";
string pattern = "Topics";
searchPattern(pattern, text, pattern.size(), text.size());
return 0;
}
Java Code:
public class Test {
// A function that will compute the longest possible proper prefix and proper suffix
static void computeLongestProperPrefixSuffix(String pat, int m, int longestProperPrefSuf[]) {
// length of the previous longest prefix suffix
int length = 0;
longestProperPrefSuf[0] = 0;
// calculating the longest possible proper prefix and proper suffix for i = 1 to m-1
int i = 1;
while (i < m) {
if (pat.charAt(i) == pat.charAt(length)) {
// if matches increment the length
length++;
longestProperPrefSuf[i] = length;
i++;
} else {
// if the length is not zero, redefining the length of the longestProperPrefSuf
if (length != 0)
length = longestProperPrefSuf[length - 1];
else {
// when the length is 0
longestProperPrefSuf[i] = 0;
i++;
}
}
}
}
// a function that prints occurrences of pattern[] in text[]
static void searchPattern(String pattern, String text, int m, int n) {
/*
defining array that will store the longest possible proper prefix and proper suffix.
*/
int longestProperPrefSuf[] = new int[m];
// calculating the longest possible proper prefix and proper suffix
computeLongestProperPrefixSuffix(pattern, m, longestProperPrefSuf);
// initializing both the pointers.
int i = 0;
int j = 0;
while ((n - i) >= (m - j)) {
// increment the pointer until the match is found.
if (pattern.charAt(j) == text.charAt(i)) {
j++;
i++;
}
// If the match is completely found.
if (j == m) {
System.out.println("The pattern was found at the index: " + (i - j));
j = longestProperPrefSuf[j - 1];
}
// when mismatch after j matches
else if (i < n && pattern.charAt(j) != text.charAt(i)) {
if (j != 0)
j = longestProperPrefSuf[j - 1];
else
i = i + 1;
}
}
System.out.println("No match found!");
}
public static void main(String[] args) {
String text = "Scaler Topics";
String pattern = "Topics";
searchPattern(pattern, text, pattern.length(), text.length());
}
}
Python Code:
# A function that will compute the longest possible proper prefix and proper suffix
def computeLongestProperPrefixSuffix(pattern, m, longestProperPrefSuf):
# length of the previous longest prefix suffix
length = 0
longestProperPrefSuf[0]
# calculating the longest possible proper prefix and proper suffix for i = 1 to m-1
i = 1
while i < m:
if pattern[i] == pattern[length]:
# if matches increment the length
length += 1
longestProperPrefSuf[i] = length
i += 1
else:
# if the length is not zero, redefining the length of the longestProperPrefSuf
if length != 0:
length = longestProperPrefSuf[length-1]
else:
# when the length is 0
longestProperPrefSuf[i] = 0
i += 1
# a function that prints occurrences of pattern[] in text[]
def searchPattern(pattern, text, m, n):
# defining array that will store the longest possible proper prefix and proper suffix.
longestProperPrefSuf = [0]*m
# calculating the longest possible proper prefix and proper suffix
computeLongestProperPrefixSuffix(pattern, m, longestProperPrefSuf)
# initializing both the pointers.
i = 0
j = 0
while (n - i) >= (m - j):
# increment the pointer until the match is found.
if pattern[j] == text[i]:
i += 1
j += 1
# If the match is completely found.
if j == m:
print("The pattern was found at the index: " + str(i-j))
return
j = longestProperPrefSuf[j-1]
# when mismatch after j matches
elif i < n and pattern[j] != text[i]:
if j != 0:
j = longestProperPrefSuf[j-1]
else:
i += 1
print("No match found!")
# The main function
if __name__ == '__main__':
text = "Scaler Topics"
pattern = "Topics"
searchPattern(pattern, text, len(pattern), len(text))
Output
The pattern was found at the index: 7
In this algorithm, we are calculating the longestProperPrefSuf first, then utilizing it to get the desired answer.
Time complexity
In the two-pointer algorithm, the time complexity of the algorithm comes out to be O(n), where n is the size of the input string.
Space complexity
In the two-pointer algorithm, we are creating an array for proper prefixes or suffixes, the space complexity of the algorithm comes out to be O(m), where m is the size of the input pattern string.
Advantages & Disadvantages of Naive String Matching Algorithm
Let us first discuss some of the advantages of the naive string-matching algorithm.
- In the naive string matching algorithm, we do not need any extra space to find the starting index of the pattern in the string.
- In the naive string matching algorithm, we can perform the checking and comparison in any direction (from left to right or from right to left).
- In the two-pointer approach, we need to create a proper suffix or proper prefix array. In the naive string-matching algorithm, we do not require any pre-processing.
The only disadvantage of the naive string matching algorithm is that it is an inefficient searching algorithm as it requires O(n-m+1) time complexity, where n is the size of the input string and m is the size of the input pattern string.
Conclusion
- The naive string matching algorithm uses two loops (nested loops). It uses all the possible placements of the pattern string in the input text and checks whether the current positioning matches the input pattern or not.
- In the naive string matching algorithm, we do not need any extra space to find the starting index of the pattern in the string.
- In the naive string matching algorithm, we can perform the checking and comparison in any direction (from left to right or from right to left).
- In the two-pointer approach, we need to create a proper suffix or proper prefix array. In the naive string-matching algorithm, we do not require any pre-processing.
- Another approach to the string pattern searching problem can be using two pointers. We can use the degenerating property which means patterns having the same sub-patterns appearing in the pattern more than once.
- In the naive string matching algorithm, the time complexity of the algorithm comes out to be O(n-m+1), where n is the size of the input string and m is the size of the input pattern string.
- In the naive string matching algorithm, the space complexity of the algorithm comes out to be O(1).
- In the two-pointer algorithm, the time complexity of the algorithm comes out to be O(n), where n is the size of the input string.
- In the two-pointer algorithm, the space complexity of the algorithm comes out to be O(m), where m is the size of the input pattern string.