October 7, 2024

Postorder Traversal without Recursion

Problem Statement

Given a tree, we need to traverse the tree in a post-order traversal way and print the nodes of the tree in the post-order traversal order. The traversal should be done without using recursion.

In order to proceed with the problem, we need to understand how post-order traversal is done over the tree.

How is Post Order Traversal Done?

In post-order traversal without recursion, traversal is done in the following order :

Firstly, the left subtree is visited.
Secondly, the right subtree is visited.
And lastly the root is visited.

As trees are nonlinear data structures so the traversal is not similar to linear data structures like arrays, linked lists, etc. In a binary tree, there can be more than one next node from the current node of the tree.

Let’s see with an Example how post-order traversal is done.

Example

Let’s represent a tree and do post-order traversal on it.

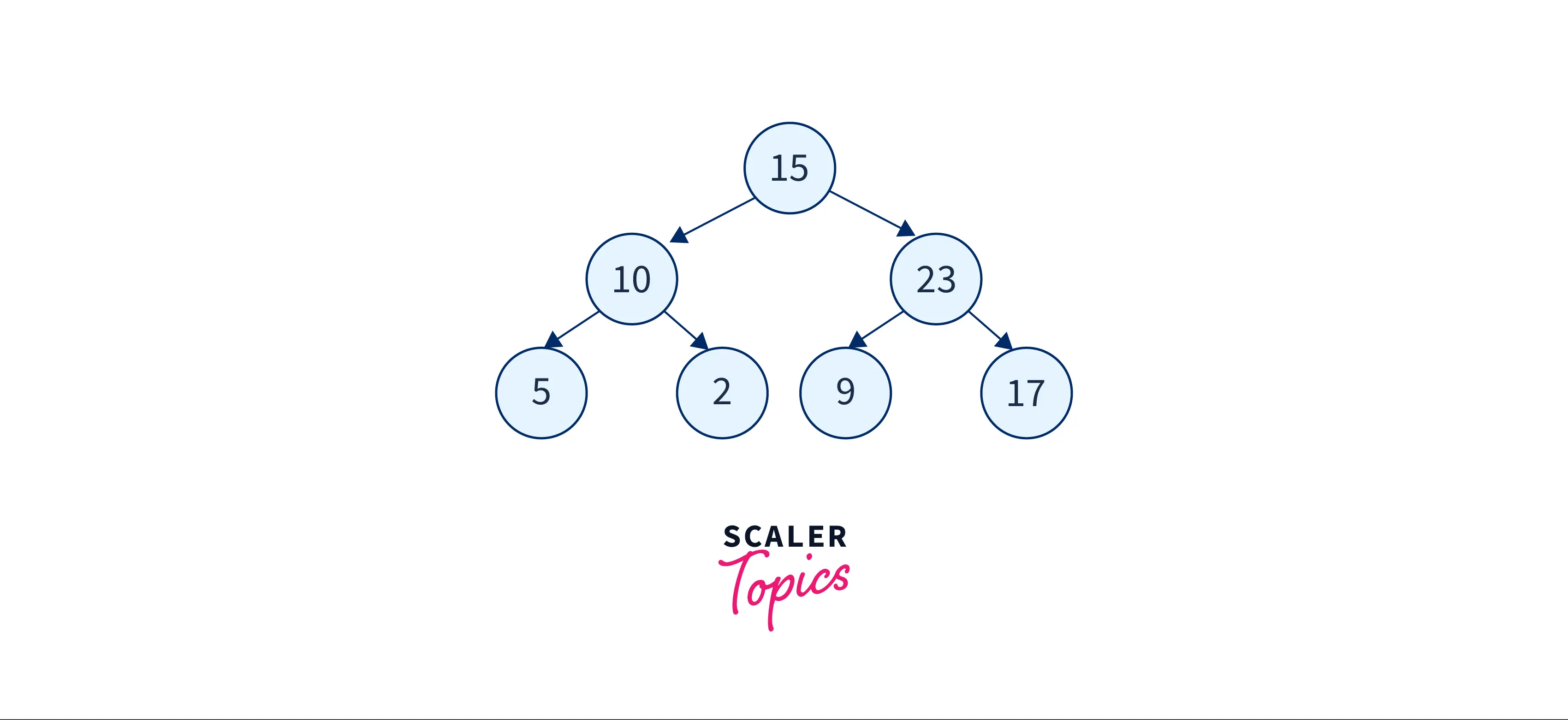
post-order traversal

The output of the post-order traversal

5 2 10 9 17 23 15

Let’s understand in steps how the post-order traversal is done in the above tree example.

Example Explanation

Let’s understand how post-order traversal is done using two stacks by traversing on the tree shown below.

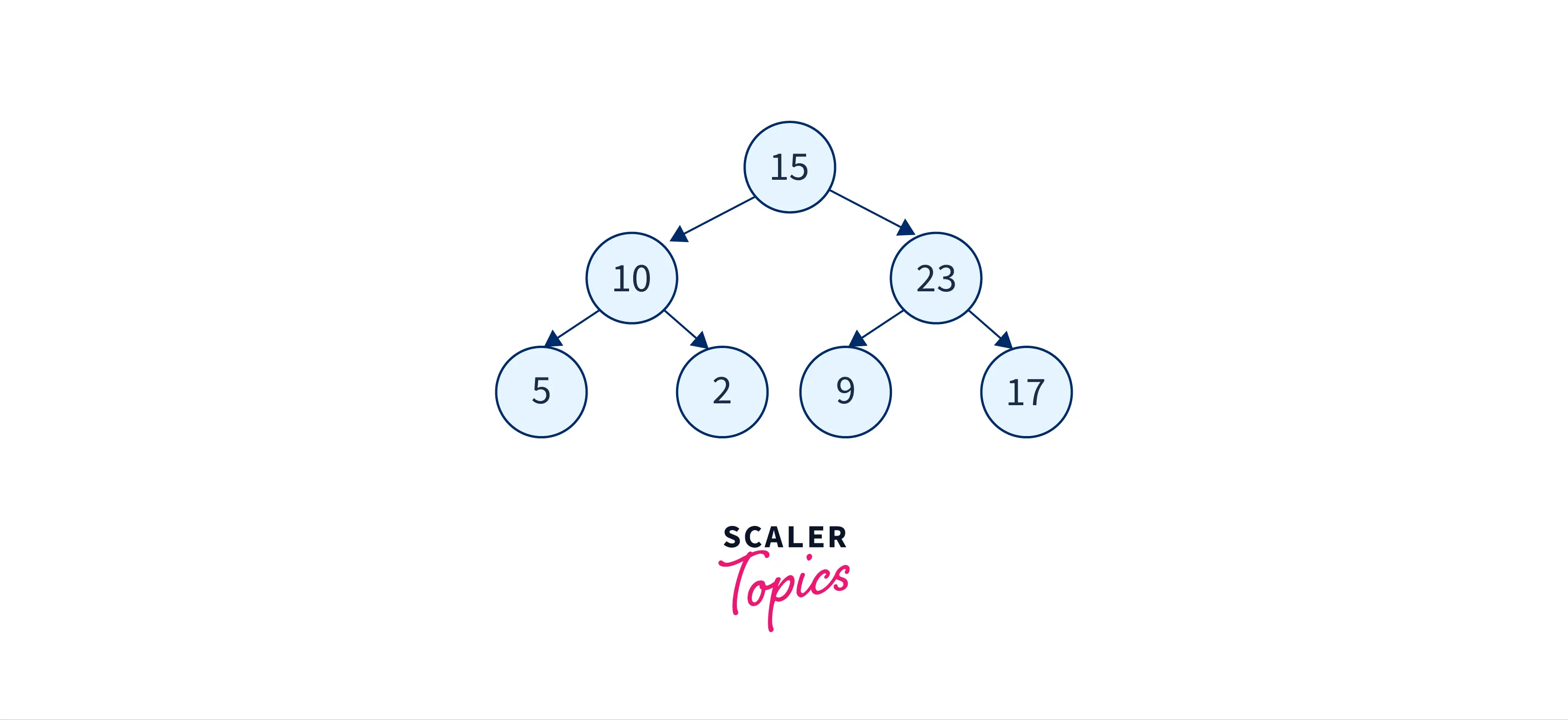
two stacks

Following are the steps are taken to get post order traversal in the tree

push 15 to the first stack First stack – 15 Second stack – Empty
pop 15 from the first stack and push it to the second stack and then push left and right child of 15 to the first stack First stack – 10 23 Second stack – 15
pop top node from first stack i.e 23 and push it to second stack and then push its left and right node to first stack First stack – 10 9 17 Second stack – 15 23
pop top node from first stack i.e 17 and push it to second stack and then push its left and right node to first stack. If it does not have a left or right child then don’t push anything to the second stack. First stack – 10 9 Second stack – 15 23 17
pop top node from first stack i.e 9 and push it to second stack and then push its left and right node to first stack. If it does not have a left or right child then don’t push anything to the second stack. First stack – 10 Second stack – 15 23 17 9
pop top node from first stack i.e 10 and push it to second stack and then push its left and right node to first stack. If it does not have a left or right child then don’t push anything to the second stack. First stack – 5 2 Second stack – 15 23 17 9 10
pop top node from first stack i.e 2 and push it to second stack and then push its left and right node to first stack. If it does not have a left or right child then don’t push anything to the second stack. First stack – 5 Second stack – 15 23 17 9 10 2
pop top node from first stack i.e 2 and push it to second stack and then push its left and right node to first stack. If it does not have a left or right child then don’t push anything to the second stack. First stack – Empty Second stack – 15 23 17 9 10 2 5
If the first stack becomes empty then pop the nodes of the second stack which will give the post-order traversal.
Result – 5 2 10 9 17 23 15

Input/Output

Input

Output

5 2 10 9 17 23 15

Constraints

The constraint for post-order traversal without recursion are :

1 <= number of nodes <= 10^5
-10^9 <= node value <= 10^9

Algorithm 1- Iterative Approach – Using Two Stacks

Algorithm

In this algorithm, we use two stacks to store the nodes of the binary tree. Let’s see how the algorithm works:

Start from the root node and push the root node to the first stack
While the first stack is not empty repeat the below two steps

From the first stack pop a node and push that node to the second stack
If there is a left and right node of the popped stack then push the left and right node of the popped stack to the first stack

Once the first stack is empty print the nodes in the second stack. It will be post-order traversal order.

Implementation in C++

#include <bits/stdc++.h>
using namespace std;


struct Node {

	int data;
	Node *left, *right;
};

//  create a new node 
Node* createNode(int data)
{
	Node* node = new Node;
	node->data = data;
	node->left = node->right = NULL;
	return node;
}
// An iterative function to do post order
// traversal of a given binary tree
void postOrderTraversal(Node* root)
{
	if (root == NULL)
		return;

	// define two stacks - stack1 and stack2
	stack<Node *> stack1, stack2;

	// start from root node and push to first stack
	stack1.push(root);
	Node* node;

	// Repeat untill first stack is not empty
	while (!stack1.empty()) {
		// pop node from stack1 and push to stack2
		node = stack1.top();
		stack1.pop();
		stack2.push(node);

		// push left and right node of popped stack
		if (node->left)
			stack1.push(node->left);
		if (node->right)
			stack1.push(node->right);
	}

	// if stack is empty print the nodes in stack2
	while (!stack2.empty()) {
		node = stack2.top();
		stack2.pop();
		cout << node->data << " ";
	}
}

// main function
int main()
{
	// build the tree with creteNode function
	Node* root = NULL;
	root = createNode(15);
	root->left = createNode(10);
	root->right = createNode(23);
	root->left->left = createNode(5);
	root->left->right = createNode(2);
	root->right->left = createNode(9);
	root->right->right = createNode(17);

	postOrderTraversal(root);

	return 0;
}

Implementation in Java

import java.util.*;
public class Main {

	static class node {
		int data;
		node left, right;

		public node(int data)
		{
			this.data = data;
		}
	}

	// define two stacks to use in  traversal
	static Stack<node> stack1, stack2;

	static void postOrderTraversal(node root)
	{
		// Create two stacks
		stack1 = new Stack<>();
		stack2 = new Stack<>();

		if (root == null)
			return;

		// start from root node and push it to stack1
		stack1.push(root);

		// repeat untill first stack is not empty
		while (!stack1.isEmpty()) {
			// pop node from stack1 and push to stack2
			node temp = stack1.pop();
			stack2.push(temp);

			// push left and right node of popped node
			if (temp.left != null)
				stack1.push(temp.left);
			if (temp.right != null)
				stack1.push(temp.right);
		}

		// if stack1 is empty print all nodes of stack2
		while (!stack2.isEmpty()) {
			node temp = stack2.pop();
			System.out.print(temp.data + " ");
		}
	}

	public static void main(String[] args)
	{
		// create a tree

		node root = null;
		root = new node(15);
		root.left = new node(10);
		root.right = new node(23);
		root.left.left = new node(5);
		root.left.right = new node(2);
		root.right.left = new node(9);
		root.right.right = new node(17);

		postOrderTraversal(root);
	}
}

Implementation in Python


# python program for pist order traversal in iterative manner

# class to define node
class Node:
	
	# constructor to create node
	def __init__(self, data):
		self.data = data
		self.left = None
		self.right = None

# function to do post-order traversal in an iterative manner
def postOrderTraversal(root):

	if root is None:
		return	
	
	# define tow stack to use - stack1 and stack2
	stack1 = []
	stack2 = []
	
	# start from root node and push to stack1
	stack1.append(root)
	
	# Repeat untill stack1 is empty
	while stack1:
		
		# pop node from stack1 and push to stack2
		node = stack1.pop()
		stack2.append(node)
	
		# push left and right node of popped node
		if node.left:
			stack1.append(node.left)
		if node.right:
			stack1.append(node.right)

		# if stack1 is empty print all nodes of stack2
	while stack2:
		node = stack2.pop()
		print(node.data,end=" ")

# program to run traversal function
root = Node(15)
root.left = Node(10)
root.right = Node(23)
root.left.left = Node(5)
root.left.right = Node(2)
root.right.left = Node(9)
root.right.right = Node(17)
postOrderTraversal(root)

Output

5 2 10 9 17 23 15

Time Complexity: As in the post-order traversal every node is iterated and pushed to the stack so the time taken to do traversal on every node of the tree is O(n), where n is the number of nodes in the tree.
Space Complexity: The extra space used in the post-order traversal of the two stacks. In the worst case, the stack will contain all the nodes of the stack so the size of the stack should be equal to the number of nodes in the tree. So, space complexity = O(n), where n is the number of nodes in the tree.

Algorithm 2- Iterative Approach – Using One Stack

Algorithm: In this method, we will reduce the space complexity from two stacks to one stack. Let’s see how the algorithm works in steps :

Create an empty stack
Repeat the below steps while the root is not NULL
1. Push the right root child and then push the root node.
2. Set root as root’s left child.
pop the node from the stack and set it as the root node
1. If popped node has a right child and the right child node is present at the top of the stack then pop the right child node and push the root node to the stack and set root as the root’s right child
2. Else print the root node and set the root to NULL.
Repeat the above two steps until the stack is not empty.

Implementation in C++ :

// program to implement post order traversal iteratively using one stack
#include <bits/stdc++.h>
using namespace std;

// structure of a node of a tree
struct Node {
	int data;
	struct Node *left, *right;
};

// function to create new node
struct Node* newNode(int data)
{
	struct Node* node = new Node;
	node->data = data;
	node->left = node->right = NULL;
	return node;
}

// function to do post-order traversal
vector<int> postOrderTraversal(struct Node* root)
{
	vector<int> postOrderTraversalNodesList;
	// Check if tree is empty
	if (root == NULL)
		return postOrderTraversalNodesList;
	stack<Node*> stack1;
	stack1.push(root);
	Node* prev = NULL;
	while (!stack1.empty()) {
		auto current = stack1.top();
		if (prev == NULL || prev->left == current
			|| prev->right == current) {
			if (current->left)
				stack1.push(current->left);
			else if (current->right)
				stack1.push(current->right);
			else {
				stack1.pop();
				postOrderTraversalNodesList.push_back(current->data);
			}
		}

		else if (current->left == prev) {
			if (current->right)
				stack1.push(current->right);
			else {
				stack1.pop();
				postOrderTraversalNodesList.push_back(current->data);
			}

		}
		else if (current->right == prev) {
			stack1.pop();
			postOrderTraversalNodesList.push_back(current->data);
		}
		prev = current;
	}
	return postOrderTraversalNodesList;
}

// main funtion to run the program
int main()
{
	// make a tree to traverse
	struct Node* root = NULL;
	root = newNode(15);
	root->left = newNode(10);
	root->right = newNode(23);
	root->left->left = newNode(5);
	root->left->right = newNode(2);
	root->right->left = newNode(9);
	root->right->right = newNode(17);
	printf("Post order traversal: ");
	printf("[");
	vector<int> postOrderTraversalNodesList = postOrderTraversal(root);
	for (auto it : postOrderTraversalNodesList)
		cout << it << " ";
	printf("]");
	return 0;
}

Implementation in Java

// program for iterative post-order traversal

import java.util.ArrayList;
import java.util.Stack;

// node class for a binary tree
class Node {
	int data;
	Node left, right;

	Node(int item)
	{
		data = item;
		left = right;
	}
}

class BinaryTree {
	Node root;
	ArrayList<Integer> postOrderTraversalNodesList = new ArrayList<Integer>();

	// function to do post-order traversal
	ArrayList<Integer> postOrderTraversal(Node node)
	{
		Stack<Node> stack1 = new Stack<Node>();

		// empty tree check
		if (node == null)
			return postOrderTraversalNodesList;
		stack1.push(node);
		Node prev = null;
		while (!stack1.isEmpty()) {
			Node current = stack1.peek();
			if (prev == null || prev.left == current || prev.right == current) {
				if (current.left != null)
					stack1.push(current.left);
				else if (current.right != null)
					stack1.push(current.right);
				else {
					stack1.pop();
					postOrderTraversalNodesList.add(current.data);
				}
			}
			else if (current.left == prev) {
				if (current.right != null)
					stack1.push(current.right);
				else {
					stack1.pop();
					postOrderTraversalNodesList.add(current.data);
				}
			}
			else if (current.right == prev) {
				stack1.pop();
				postOrderTraversalNodesList.add(current.data);
			}

			prev = current;
		}

		return postOrderTraversalNodesList;
	}
}

class Main{
    // main function to run the program
	public static void main(String args[])
	{
		BinaryTree tree = new BinaryTree();

		// Let us create trees shown in above diagram
		tree.root = new Node(15);
		tree.root.left = new Node(10);
		tree.root.right = new Node(23);
		tree.root.left.left = new Node(5);
		tree.root.left.right = new Node(2);
		tree.root.right.left = new Node(9);
		tree.root.right.right = new Node(17);

		ArrayList<Integer> resultantList = tree.postOrderTraversal(tree.root);

		System.out.print(
			"Post order traversal :");
		System.out.println(resultantList);
	}
}

Implementation in Python

# program to iteratively perform post order traversal

# array to store the post order traversed nodes
result = []

# class for binary tree
class Node:
	
	# define a constructor to create new node
	def __init__(self, data):
		self.data = data
		self.left = None
		self.right = None

def peek(stack):
	if len(stack) > 0:
		return stack[-1]
	return None
# function to do post order traversal of tree
def postOrderTraversal(root):
		
	# check if root node is null
	if root is None:
		return

	stack1 = []
	
	while(True):
		
		while (root):
			# push right node and then root
			if root.right is not None:
				stack1.append(root.right)
			stack1.append(root)

			# rott is set to root left child
			root = root.left
		
		# Ppop item from stack and set as root
		root = stack1.pop()

		if (root.right is not None and
			peek(stack1) == root.right):
			stack1.pop() 
			stack1.append(root) 
			root = root.right 
		else:
			result.append(root.data)
			root = None

		if (len(stack1) <= 0):
				break

# program to create tree and run post order traversal on it
root = Node(15)
root.left = Node(10)
root.right = Node(23)
root.left.left = Node(5)
root.left.right = Node(2)
root.right.left = Node(9)
root.right.right = Node(17)

print("Post Order traversal: ")
postOrderTraversal(root)
print(result)

Output

Post order traversal :[5, 2, 10, 9, 17, 23, 15]

Time complexity : The traversal is done iteratively over all the nodes of the tree so, the time taken to do traversal on each and every node is O(n), where n is the number of nodes in the tree.
Space complexity : The algorithm uses only single stack which can store all the nodes in the worst case. so, the space required in this algorithm is O(n).

Algorithm 3- Iterative Approach – Using Stack and Hashing

Algorithm: In this method, we will use stack and unordered map for hashing. Let’s understand the step-by-step algorithm.

Create an unordered map for marking the visited nodes while traversing and create a stack to find the post-order traversal.
Firstly, push the root node in the stack and then repeat the below steps until the stack is not empty.
Mark the current node(node on top of stack) as visited in the hash table.
Check if the left child of the current node is not Null, if yes then push the left child node to the stack.
If a left child is not present check for the right child. If the right child is present then push it to the stack.
If the current node has no left or right child node then simply pop the node from the stack and store it in the result list.
As the stack gets empty the nodes in our result list will give the post-order traversal.

Implementation in C++ :


// program for post order traversal iteratively using stack and hashing
#include <bits/stdc++.h>
using namespace std;
#define MAX_HEIGHT 100000

// Tree Node
struct Node {
	int data;
	Node* left;
	Node* right;
};

//function to create node
Node* createNode(int val)
{
	Node* tempNode = new Node;
	tempNode->data = val;
	tempNode->left = NULL;
	tempNode->right = NULL;

	return tempNode;
}

// Function to Build Tree
Node* buildTreeFromString(string str)
{
	
	if (str.length() == 0 || str[0] == 'N')
		return NULL;

	vector<string> ip;

	istringstream iss(str);
	for (string str; iss >> str;)
		ip.push_back(str);

	//tree root creation
	Node* root = createNode(stoi(ip[0]));

	// push to queue
	queue<Node*> queue;
	queue.push(root);

	int i = 1;
	while (!queue.empty() && i < ip.size()) {
		
		Node* currNode = queue.front();
		queue.pop();
		string currVal = ip[i];
		if (currVal != "N") {
			currNode->left = createNode(stoi(currVal));
			queue.push(currNode->left);
		}

		//  right child
		i++;
		if (i >= ip.size())
			break;
		currVal = ip[i];

		if (currVal != "N") {

			currNode->right = createNode(stoi(currVal));

			queue.push(currNode->right);
		}
		i++;
	}

	return root;
}

//for post order traversal
vector<int> postOrder(Node* node)
{
	stack<Node*> stack1;

	// vector to store nodes in post order traversal
	vector<int> result;

    // unordered map for hashing
	unordered_map<Node*, int> visited;

	// initially push root node in starting
	stack1.push(node);

    // repeat untill stack is empty
    while (!stack1.empty()) {

		// top onode in stack is marked visited
		visited[stack1.top()] = 1;

	    // left child present and not visited then push to stack
		if (stack1.top()->left != 0) {
			if (!visited[stack1.top()->left]) {
				stack1.push(stack1.top()->left);
				continue;
			}
		}

	    // if right child present and not visited push to stack
		if (stack1.top()->right != 0) {
			if (!visited[stack1.top()->right]) {
				stack1.push(stack1.top()->right);
				continue;
			}
		}
		result.push_back(stack1.top()->data);

		// Remove the top node from the stack
		stack1.pop();
	}
	return result;
}


int main() {
	// Constructing the tree as shown in above diagram
	string nodes = "15 10 23 5 2 9 17";
	Node* root = buildTreeFromString(nodes);

	vector<int> result;

	result = postOrder(root);

	for (int i = 0; i < result.size(); i++)
		cout << result[i] << " ";

	cout << endl;

	return 0;
}

Implementation in Java

import java.util.Stack;

class Node{
	int data;
	Node left, right;

	Node(int item){
		data = item;
		left = right;
	}
}

class PostOrder{
	Node root;
	
	public void postOrderTraversal(Node root) {
		Stack<Node> stack1 = new Stack<>();
		
		while(true) {
			while(root != null) {
				stack1.push(root);
				stack1.push(root);
				root = root.left;
			}
			
			if(stack1.empty()) 
			    return;
			
			root = stack1.pop();
			
			if(!stack1.empty() && stack1.peek() == root){
			    root = root.right;
			} 
			else{
				System.out.print(root.data + " "); 
				root = null;
			}
		}
	}
}

class Main{
    public static void main(String args[]) {
	    PostOrder tree = new PostOrder();

		tree.root = new Node(15);
		tree.root.left = new Node(10);
		tree.root.right = new Node(23);
		tree.root.left.left = new Node(5);
		tree.root.left.right = new Node(2);
		tree.root.right.left = new Node(9);
		tree.root.right.right = new Node(17);
		tree.postOrderTraversal(tree.root);
	}
}

Implementation in Python

class Node:

	def __init__(self, x):
		
		self.data = x
		self.right = None
		self.left = None
        
def postOrderTraversal(root):
	
	stack1 = []
	
	while(True):
		while(root != None):
			stack1.append(root)
			stack1.append(root)
			root = root.left

		if (len(stack1) == 0):
			return
		
		root = stack1.pop()

		if (len(stack1) > 0 and stack1[-1] == root):
			root = root.right
		else:
			print(root.data, end = " ")
			root = None

if __name__ == '__main__':
	
	root = Node(15)
	root.left = Node(10)
	root.right = Node(23)
	root.left.left = Node(5)
	root.left.right = Node(2)
	root.right.left = Node(9)
	root.right.right = Node(17)
	postOrderTraversal(root)

Output

5 2 10 9 17 23 15

Time complexity : As in this algorithm we are traversing over each node of the tree and then marking it visited in the hashmap. So, the time required to traverse all the nodes of the tree will be O(n) Space complexity : Extra space of the stack and hashmap is used to store the nodes and mark visited nodes so the space complexity of the algorithm will be O(n)

Algorithm 4- Using No Stacks (Morris Traversal)

In this algorithm we will not use any extra space for post order traversal. Lets understand this algorithm.

Instead of using stacks to remember our way back up the tree, we are going to modify the tree to create upwards links. The idea is based on Threaded Binary Tree.

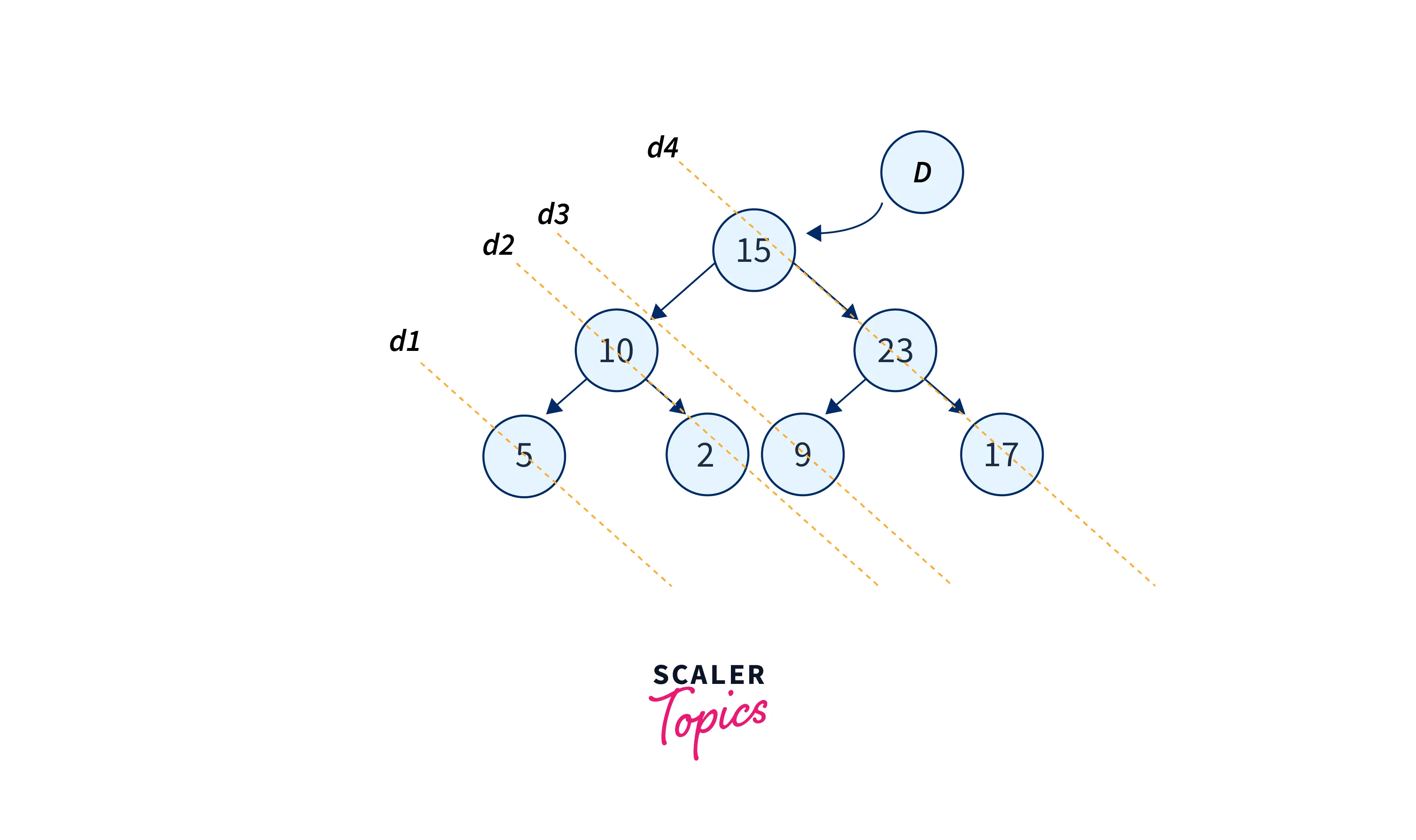
Morris Traversal

The diagonal d1, d2,d3, and d4 shown in the figure above are first reversed, then printed, and then re-reversed.

We reverse each diagonal shown in the picture (d1-d4), print it, and re-reverse it.

Create a temp or dummy node and make the left node of the temp node point to the root node of the tree.
Set the dummy node as the root node.
Repeat till root is not null.
1. If the root has a left child node then find the inorder predecessor i.e. rightmost node of its left node. Then make it point to root.
2. If it is already pointing to the root i.e it is already traversed then reverse the direction from left to the root node and print the nodes.
If a left child is null do the same above steps with the right child.

Implementation in C++

// morris traversal in cpp
#include <bits/stdc++.h>
using namespace std;

struct TreeNode {
	int key;
	TreeNode* left;
	TreeNode* right;

	TreeNode(int data)
	{
		key = data;
		left = NULL;
		right = NULL;
	}
};

void printPostOrderTraversal(vector<int>& result)
{
	for (auto x : result) {
		cout << x << " ";
	}
}

// PostorderTraversal without recursion
vector<int> postorderTraversal(TreeNode* root)
{
	vector<int> res;
	TreeNode* current = root;

	while (current != NULL) {

		if (current->right == NULL) {
			res.push_back(current->key);
			current = current->left;
		}
		else {
			TreeNode* predecessor = current->right;
			while (predecessor->left != NULL
				&& predecessor->left != current) {
				predecessor = predecessor->left;
			}

			if (predecessor->left == NULL) {
				res.push_back(current->key);
				predecessor->left = current;
				current = current->right;
			}
			else {
				predecessor->left = NULL;
				current = current->left;
			}
		}
	}
	reverse(res.begin(), res.end());
	return res;
}
// main program
int main()
{
	TreeNode* root = new TreeNode(15);
	root->left = new TreeNode(10);
	root->right = new TreeNode(23);
	root->right->left = new TreeNode(9);
	root->right->right = new TreeNode(17);
    root->left->left = new TreeNode(5);
    root->left->right = new TreeNode(2);

	vector<int> result = postorderTraversal(root);

	printPostOrderTraversal(result);
	return 0;
}

Implementation in Java

// morris traversal for post order in java
import java.util.*;

class Main{

    static class TreeNode {
    	int key;
    	TreeNode left;
    	TreeNode right;
    
    	TreeNode(int data){
    		key = data;
    		left = null;
    		right = null;
    	}
    };
    
    
    static void printPostOrderTraversal(Vector<Integer> result){
    	for (int x : result) {
    		System.out.print(x+ " ");
    	}
    }
    
    // Postorder traversal
    static Vector<Integer> postorderTraversal(TreeNode root){
    	Vector<Integer> res = new Vector<>();
    	TreeNode current = root;
    
    	while (current != null){
    	
    		if (current.right == null) {
    			res.add(current.key);
    			current = current.left;
    		}
    		else {
    			TreeNode predecessor = current.right;
    			while (predecessor.left != null
    				&& predecessor.left != current) {
    				predecessor = predecessor.left;
    			}
    			if (predecessor.left == null) {
    				res.add(current.key);
    				predecessor.left = current;
    				current = current.right;
    			}
    			else {
    				predecessor.left = null;
    				current = current.left;
    			}
    		}
    	}
    
    	Collections.reverse(res);
    	return res;
    }
    
    // main program
    public static void main(String[] args){
    	TreeNode root = new TreeNode(15);
    	root.left = new TreeNode(10);
    	root.right = new TreeNode(23);
    	root.right.left = new TreeNode(9);
    	root.right.right = new TreeNode(17);
        root.left.left = new TreeNode(5);
        root.left.right = new TreeNode(2);
    	Vector<Integer> result = postorderTraversal(root);
    
    	printPostOrderTraversal(result);
    }
}

Implementation in Python

class TreeNode:
	def __init__(self, d):
		self.key = d
		self.left = None
		self.right = None

def printPostOrderTraversal(result) :
	
	for x in result:
		print(x,end=" ")
	
#Postorder traversal without recursion
def postorderTraversal(root) :

	res=[]
	current = root

	while current != None :
	
		if current.right == None :
			res.append(current.key)
			current = current.left
		
		else :
			predecessor = current.right
			while predecessor.left != None and predecessor.left != current :
					predecessor = predecessor.left
			
			if predecessor.left == None:
				res.append(current.key)
				predecessor.left = current
				current = current.right
	
			else :
				predecessor.left = None
				current = current.left
			
	res.reverse()
	return res

# main driver code
if __name__ == '__main__':
	root = TreeNode(15)
	root.left = TreeNode(10)
	root.right = TreeNode(23)
	root.right.left = TreeNode(9)
	root.right.right = TreeNode(17)
	root.left.left = TreeNode(5)
	root.left.right = TreeNode(2)
	
	result = postorderTraversal(root)
	
	printPostOrderTraversal(result)

Output

5 2 10 9 17 23 15

Time complexity : As in morris algorithm we traverse each and every node of the tree for checking the conditions of morris traversal. The time complexity of the algorithm is O(N) Space complexity : Since we use a vector to store the post order traversal of the Tree, the sapce complexity of the algorithm is O(N)

Conclusion

In post-order traversal first left subtree is visited then right subtree and then the root.
Time complexity of doing post-order traversal using two stacks is O(n) and space complexity is also O(n).
Time complexity of doing post-order traversal using one stack is O(n) and space complexity is also O(n).
Time complexity of doing post-order traversal using stacks and hashing is O(n) and space complexity is also O(n).
Time complexity of doing post-order traversal using no stacks is O(n) and space complexity is also O(n).

Author

Rohan Singh

View all posts

Postorder Traversal without Recursion

Problem Statement

How is Post Order Traversal Done?

Example

Example Explanation

Input/Output

Constraints

Algorithm 1- Iterative Approach – Using Two Stacks

Algorithm 2- Iterative Approach – Using One Stack

Algorithm 3- Iterative Approach – Using Stack and Hashing

Algorithm 4- Using No Stacks (Morris Traversal)

Conclusion

Author

Latest articles

Largest Number Formed from an Array

Fundamentals of Enhanced Interior Gateway Routing Protocol

What is Network Hub?

Largest Number Formed from an Array

Fundamentals of Enhanced Interior Gateway Routing Protocol

What is Network Hub?

Postorder Traversal without Recursion

Problem Statement

How is Post Order Traversal Done?

Example

Example Explanation

Input/Output

Constraints

Algorithm 1- Iterative Approach – Using Two Stacks

Algorithm 2- Iterative Approach – Using One Stack

Algorithm 3- Iterative Approach – Using Stack and Hashing

Algorithm 4- Using No Stacks (Morris Traversal)

Conclusion

Author

Latest articles

Largest Number Formed from an Array

Fundamentals of Enhanced Interior Gateway Routing Protocol

What is Network Hub?

Featured articles

Largest Number Formed from an Array

Fundamentals of Enhanced Interior Gateway Routing Protocol

What is Network Hub?