Problem Statement
Given a linked list, check whether the linked list is having a loop or not(detect loop in linked list). A cycle exists in a linked list if it contains a node that may be accessed again by following the next pointer.
Example
Input:
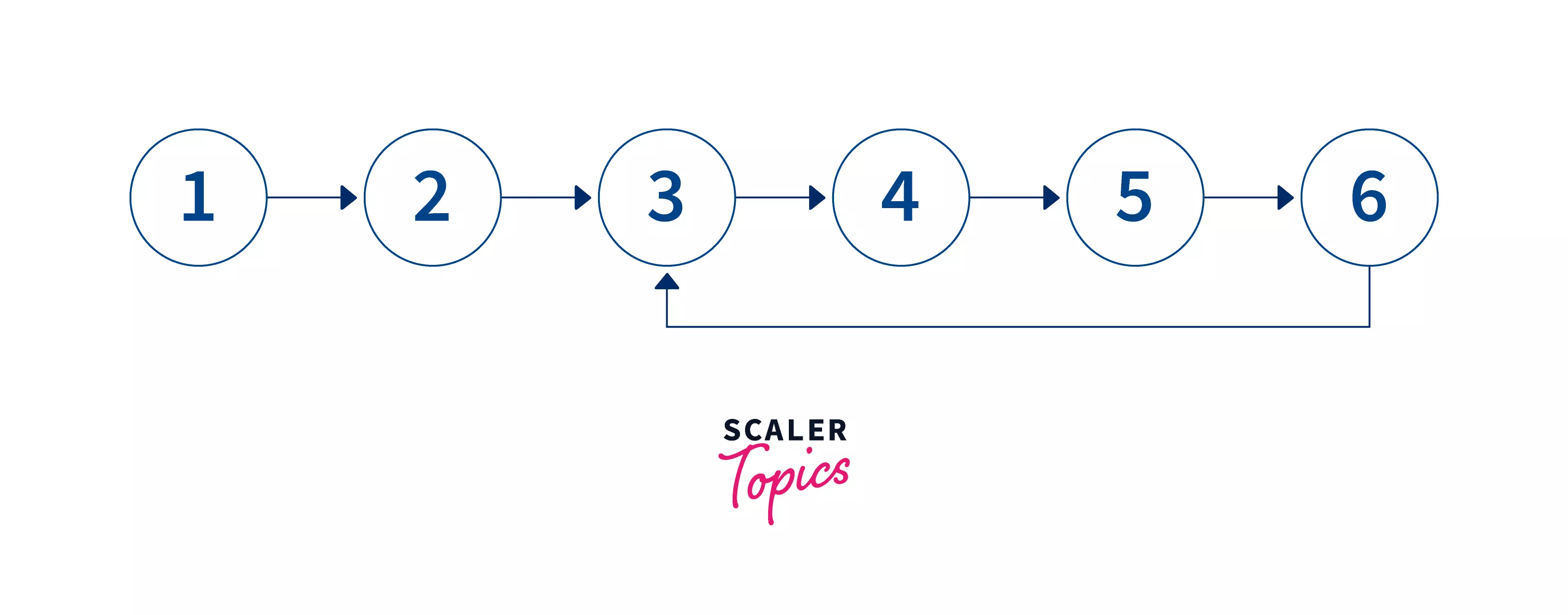
Output: True
Explanation: linked list is having 6 nodes and the next pointer of the last node is pointing to the 3rd node which indicates the loop in the linked list.
Input:
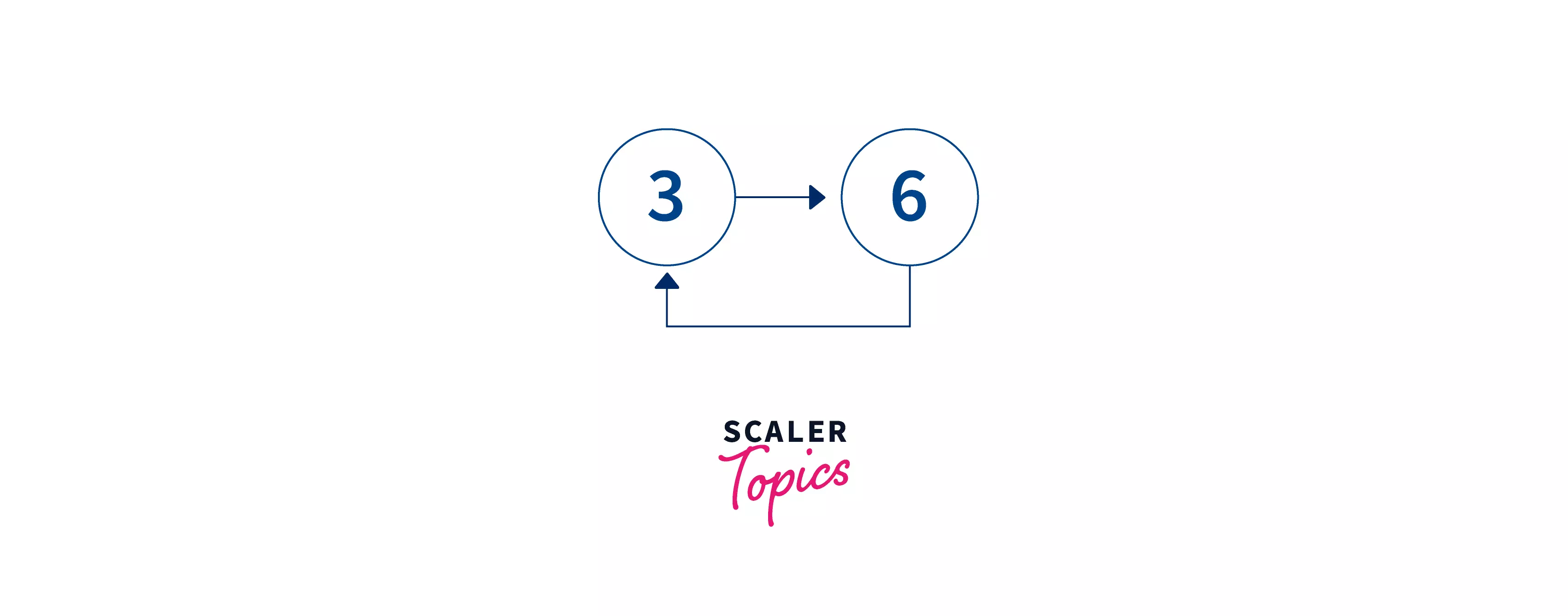
Output: True
Constraints
1<=length of linked list<=10000 1<=Data of Node<=1000
Approach 1: HashSet Approach
We can detect loop in linked list using the HashSet Approach. Traverse the linked list one by one, adding node addresses to a HashMap as you go. If NULL is reached at any point, return False as the end of linked list is reached and it doesn’t have any loop. If any previously node address is pointed by the current node, just return True.
Complexity Analysis
Time Complexity: O(N) => Only one traversal of loop is needed. Space Complexity: O(N) => N space for storing N nodes in HashMap.
C++ Implementation
bool hasLoop(Node* head) {
Node* temp = head;
set<Node*> hashSet;
while (temp != null) {
if (hashSet.find(temp) != hashSet.end()) {
return true;
}
hashSet[temp]++;
temp = temp->next;
}
return false;
}
Java Implementation
public boolean hasLoop(ListNode head) {
Set<ListNode> hashSet = new HashSet<>();
while (head != null) {
if (hashSet.contains(head)) {
return true;
}
hashSet.add(head);
head = head.next;
}
return false;
}
Python Implementation
def hasLoop(head):
temp = head
hashSet = set()
while temp is not None:
if temp in hashSet:
return True
hashSet.add(temp)
temp = temp.next
return False
Approach 2: Modifying the Linked List Data Structure
We can detect loop in linked list by modifying the Linked List Data Structure. This approach removes the space required for storing values in hashmap, By modifying the linked list data structure. The linked list definition will contain a flag variable that marks the visited node:
- Traverse the Linked list.
- For every node make the flag variable one.
- If the already existing node is accessed return true.
- if null or the end of the linked list is reached return false
Complexity Analysis
Time Complexity: O(N) => Only one traversal of loop is needed. Space Complexity: O(1)
C++ Implementation
/* Link list node definition */
struct Node {
int data;
struct Node* next;
int vis;
};
bool hasLoop(struct Node* head){
while (head != NULL) {
// If vis is 1 then it is already visited, return true
if (head->vis == 1)
return true;
// If we are seeing the node first time, vis = 1
head->vis = 1;
head = head->next;
}
return false;
}
Java Implementation
// Link list node definition
static class Node
{
int data;
Node next;
int vis;
};
static boolean hasLoop(Node head)
{
while (head != null)
{
// If vis is 1 then it is already visited, return true
if (head.vis == 1)
return true;
// If we are seeing the node first time, vis = 1
head.vis = 1;
head = head.next;
}
return false;
}
Python Implementation
# Link list node definition
class Node:
def __init__(self):
self.data = 0
self.next = None
self.vis = 0
def hasLoop(head):
while (head != None):
# If vis is 1 then it is already visited, return true
if (head.vis == 1):
return True;
# If we are seeing the node first time, vis = 1
head.vis = 1;
head = head.next;
return False;
Approach 3: Floyd’s Cycle
We can detect loop in linked list using the Floyd’s Cycle. This is the fastest method for detecting a loop in a linked list:
- Traverse the linked list using two pointers, a fast pointer, and a slow pointer starting from the first node.
- Now in a loop move the fast pointer by 2 nodes and the slow pointer by 1 node.
- If both the pointers point to a same node then loop is detected and return true, else if fast pointer details the end of the linked list return false
Complexity Analysis
Time Complexity: O(N) => Only one traversal of loop is needed. Space Complexity: O(1)
C++ Implementation
bool hasLoop(Node* head)
{
Node *slow = head, *fast = head;
while (slow && fast && fast->next) {
slow = slow->next;
fast = fast->next->next;
if (slow == fast) {
return true;
}
}
return false;
}
Java Implementation
static boolean hasLoop(Node head)
{
Node slow = head, fast = head;
while (slow != null && fast != null && fast.next != null) {
slow = slow.next;
fast = fast.next.next;
if (slow == fast) {
return true;
}
}
return false;
}
Python Implementation
def hasLoop(head):
slow = head
fast = head
while(slow and fast and fast.next):
slow = slow.next
fast = fast.next.next
if slow == fast:
return True
return False
Approach 4: Marking visited nodes without modifying the linked list data
We can detect loop in linked list by marking visited nodes without modifying the linked list data. A temporary node is created in this method. Each node that is traversed has its next pointer set to this temporary node:
- The next pointer of a node is used as a visited flag to indicate whether or not the node has been visited.
- Every node is examined to see if the next node is pointing to a temporary node.
- In the case of the loop’s first node, this condition will be true the second time we traverse it, indicating that the loop exists.
Complexity Analysis
Time Complexity: O(N) => Only one traversal of loop is needed. Space Complexity: O(1)
C++ Implementation
bool hasLoop(Node* head)
{
// Temporary node
Node* temp = new Node;
while (head != NULL) {
// If End is reached return false
if (head->next == NULL) {
return false;
}
// if next is pointing to temp loop exists
if (head->next == temp) {
return true;
}
// Store the pointer to the next node
Node* next = head->next;
// Make next point to temp
head->next = temp;
// Getting the next node in the list
head = next;
}
return False;
}
Java Implementation
static boolean hasLoop(Node head)
{
// Creating a temporary node
Node temp = new Node();
while (head != null) {
// If End is reached return false
if (head.next == null) {
return false;
}
// if next is pointing to temp loop exists
if (head.next == temp) {
return true;
}
// Store the pointer to the next node
Node nex = head.next;
// Make next point to temp
head.next = temp;
// Getting the next node in the list
head = nex;
}
return false;
}
Python Implementation
def hasLoop(head):
# Creating a temporary node
temp = ""
while (head != None):
# If End is reached return false
if (head.next == None):
return False
# if next is pointing to temp loop exists
if (head.next == temp):
return True
# Store the pointer to the next node
nex = head.next
# Make next point to temp
head.next = temp
# Geting the next node in the list
head = nex
return False
Approach 5: Store length
we can detect loop in linked list by storing length. Two pointers are formed in this method: the first (which always points to the head) and the last. When the last pointer moves, we calculate the number of nodes between the first and last nodes and check whether the current number of nodes is greater than the previous number of nodes; if it is, we move the last pointer; otherwise, we’ve reached the end of the loop, and we return output accordingly.
Complexity Analysis
Time Complexity: O(N^2) => traversal of pointers * traversal for distance at every iteration. Space Complexity: O(1)
C++ Implementation
int distance(Node* start, Node* end)
{
Node* temp = start;
// initializing the counter variable by 0
int count = 0;
// Counting the distance
while (temp != end) {
count += 1;
temp = temp->next;
}
return count + 1;
}
bool hasLoop(Node* head)
{
// Creating a temporary node
Node* temp = new Node;
Node *first, *last;
first = head;
last = head;
int currentLength = 0;
// prev_length stores no of nodes between previous position of first and last
int previousLength = -1;
while (currentLength > previousLength && last != NULL) {
// set the value of previousLength to current length
previousLength = currentLength;
// currentLength between the first and last node passed in distance function
currentLength = distance(first, last);
// Increment last node
last = last->next;
}
if (last == NULL) {
// Return false if last node is reached
return false;
}
else {
return true;
}
}
Java Implementation
static int distance(Node start, Node end)
{
Node temp = start;
// initializing the counter variable by 0
int count = 0;
// Counting the distance
while (temp != end) {
count += 1;
temp = temp.next;
}
return count + 1;
}
static boolean hasLoop(Node head)
{
// Create a temporary node
Node temp = new Node();
Node first, last;
first = head;
last = head;
int currentLength = 0;
// prev_length stores no of nodes between previous position of first and last
int previousLength = -1;
while (currentLength > previousLength && last != null) {
// set the value of previousLength to current length
previousLength = currentLength;
// currentLength between the first and last node passed in distance function
currentLength = distance(first, last);
// Increment last node
last = last.next;
}
if (last == null)
{
// Return false if last node is reached
return false;
}
else
{
return true;
}
}
Python Implementation
def distance(first, last):
# counts no of nodes between first and last
counter = 0
temp = first
while (temp != last):
counter = counter + 1
temp = temp.next
return counter + 1
def detectLoop(head):
# Create a temporary node
temp = ""
first = head;
last = head;
current_length = 0
# prev_length stores no of nodes between previous position of first and last
prev_length = -1
while (current_length > prev_length and last != None) :
# set prev_length to current length then update the current length
prev_length = current_length
# distance is calculated
current_length = distance(first, last)
# last node points the next node
last = last.next;
if (last == None) :
return False
else :
return True
Conclusion
- A cycle exists in a linked list if it contains a node that may be accessed again by following the next pointer.
- We can follow many approaches for detecting the loop in a linked list:
- Approach 1: HashSet Approach
- Approach 2: modifying the linked list data structure
- Approach 3: Floyd’s Cycle
- Approach 4: Marking visited nodes without modifying the linked list data structure
- Approach 5: Store length