Counting Sort Algorithm

Counting Sort Algorithm is a sorting algorithm that works best when you have a small range of numbers to sort. Instead of comparing elements like in other sorting methods, it counts how many times each number appears and then puts them in order based on that count. This makes it really fast when the range of numbers is not too big compared to the total number of items to be sorted.

Working of counting Sort Algorithm

1. Determine the maximum element, denoted as “max,” from the provided array.

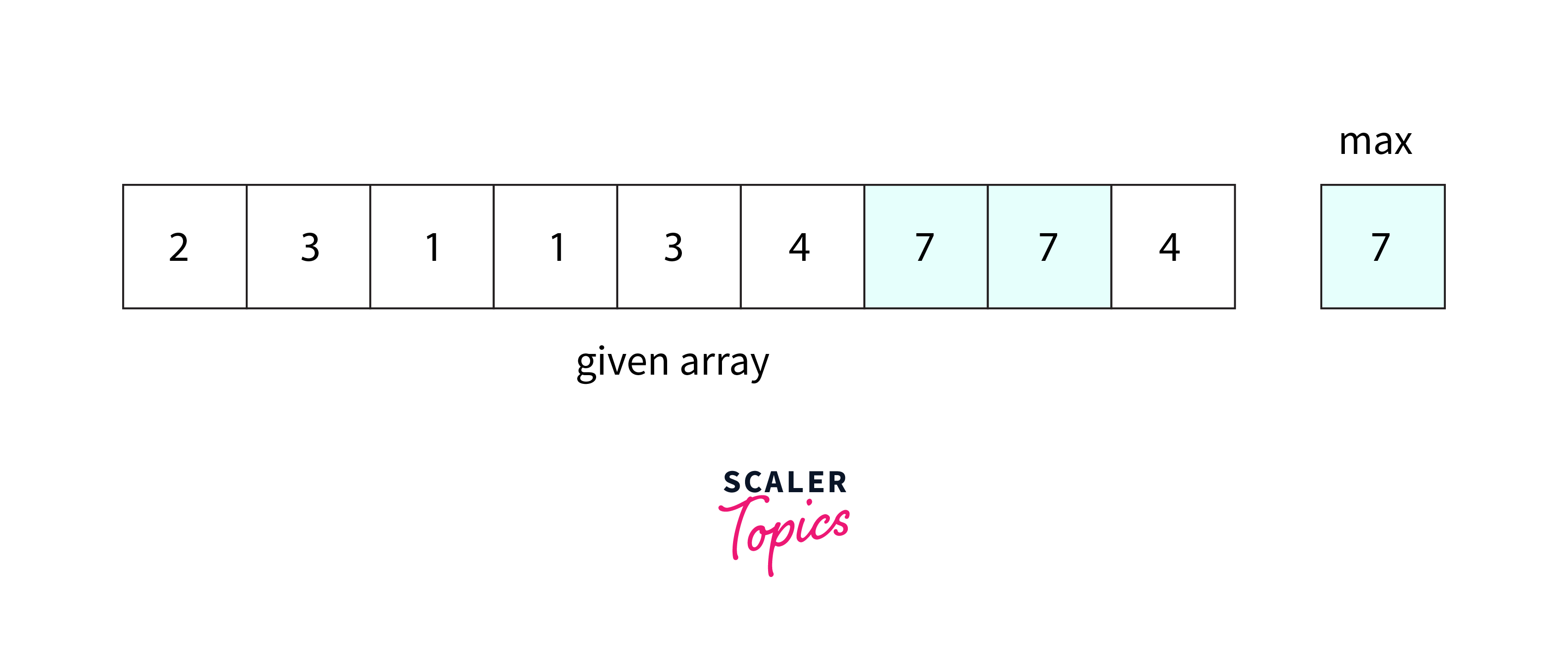
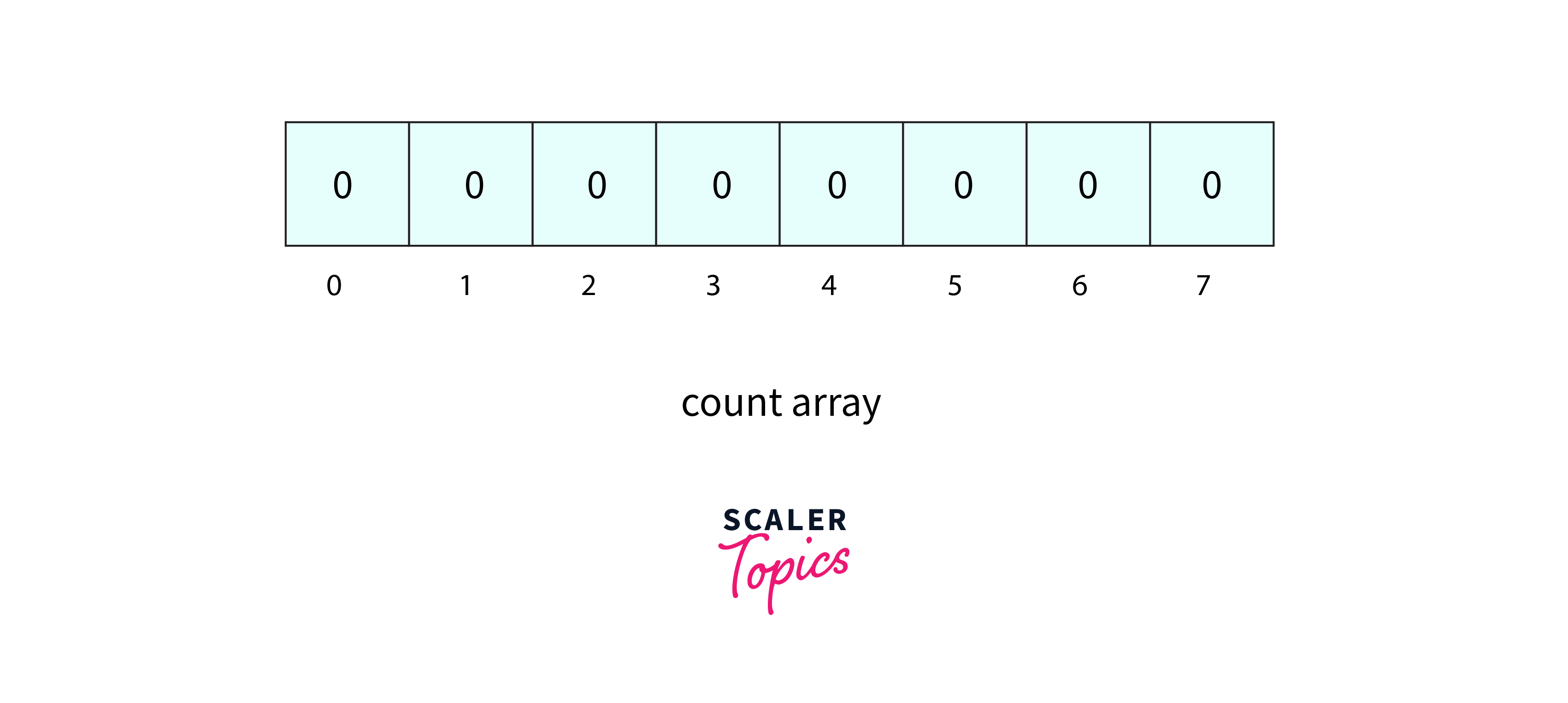
2. Create an array of length “max+1” with all elements initialized to 0. This array serves the purpose of storing the count of each element present in the given array.

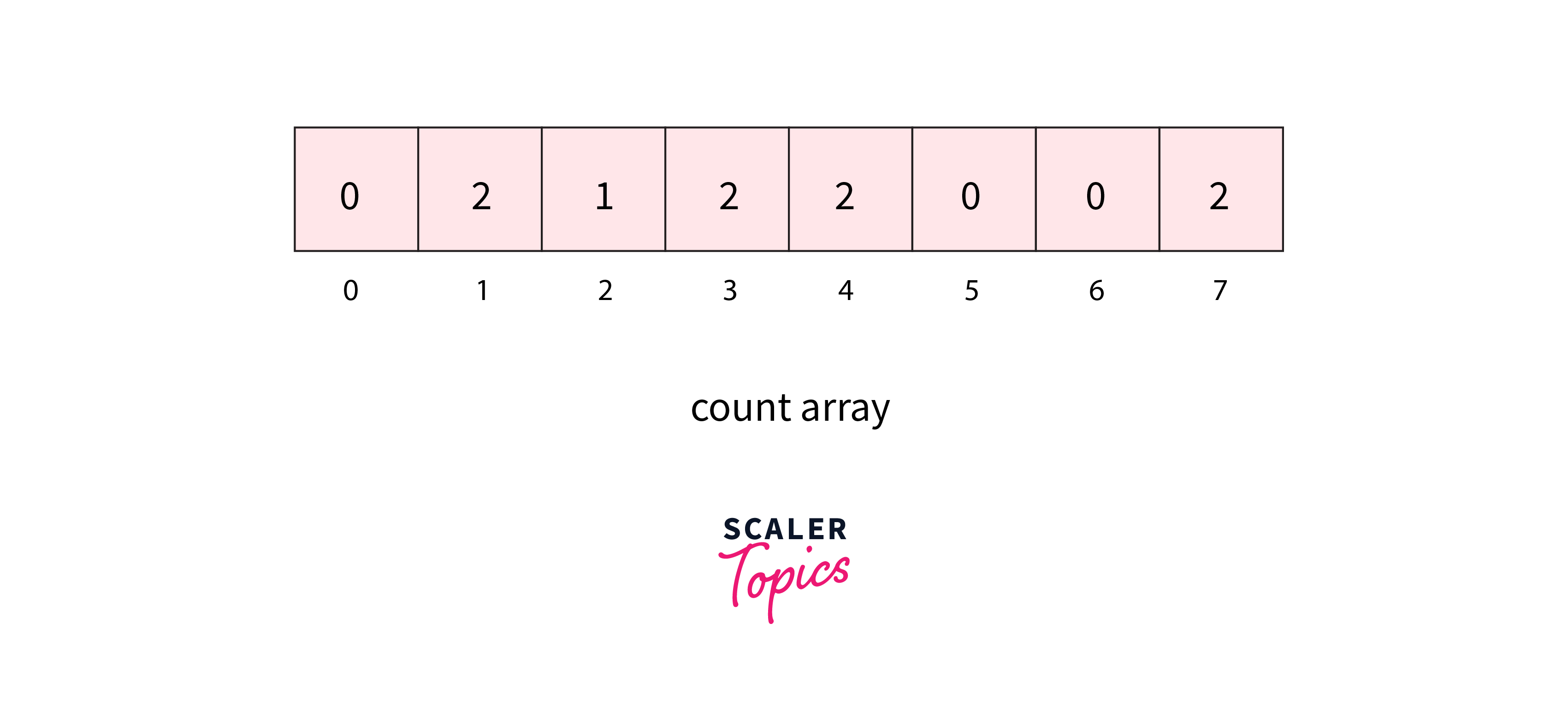
3. Assign the count of each element to their corresponding index in the count array.

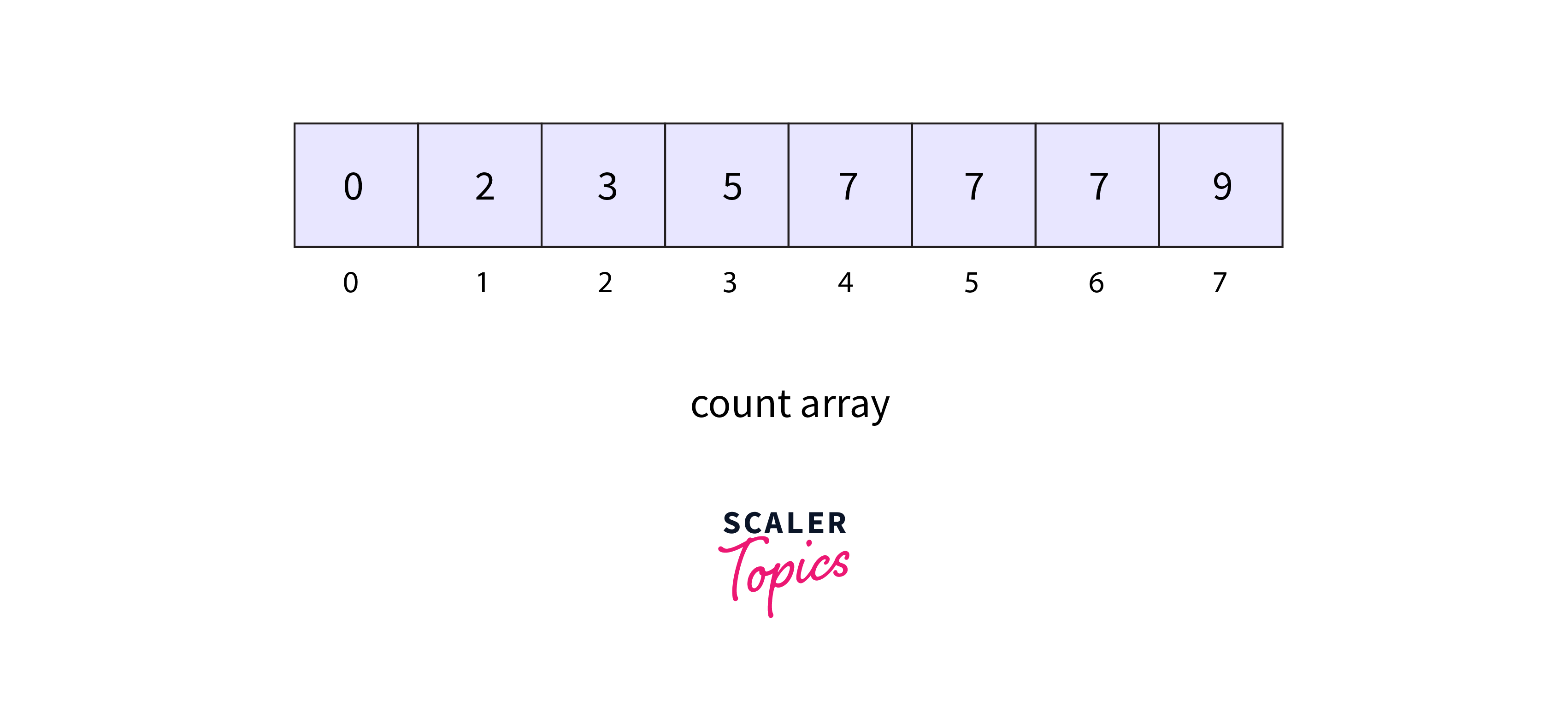
4. Calculate the cumulative sum of the elements in the count array. This cumulative sum assists in correctly positioning the elements in the sorted array.

5. Determine the index of each element from the original array in the count array, yielding the cumulative count. Place each element at the calculated index position in the sorted array, as illustrated in the figure below.

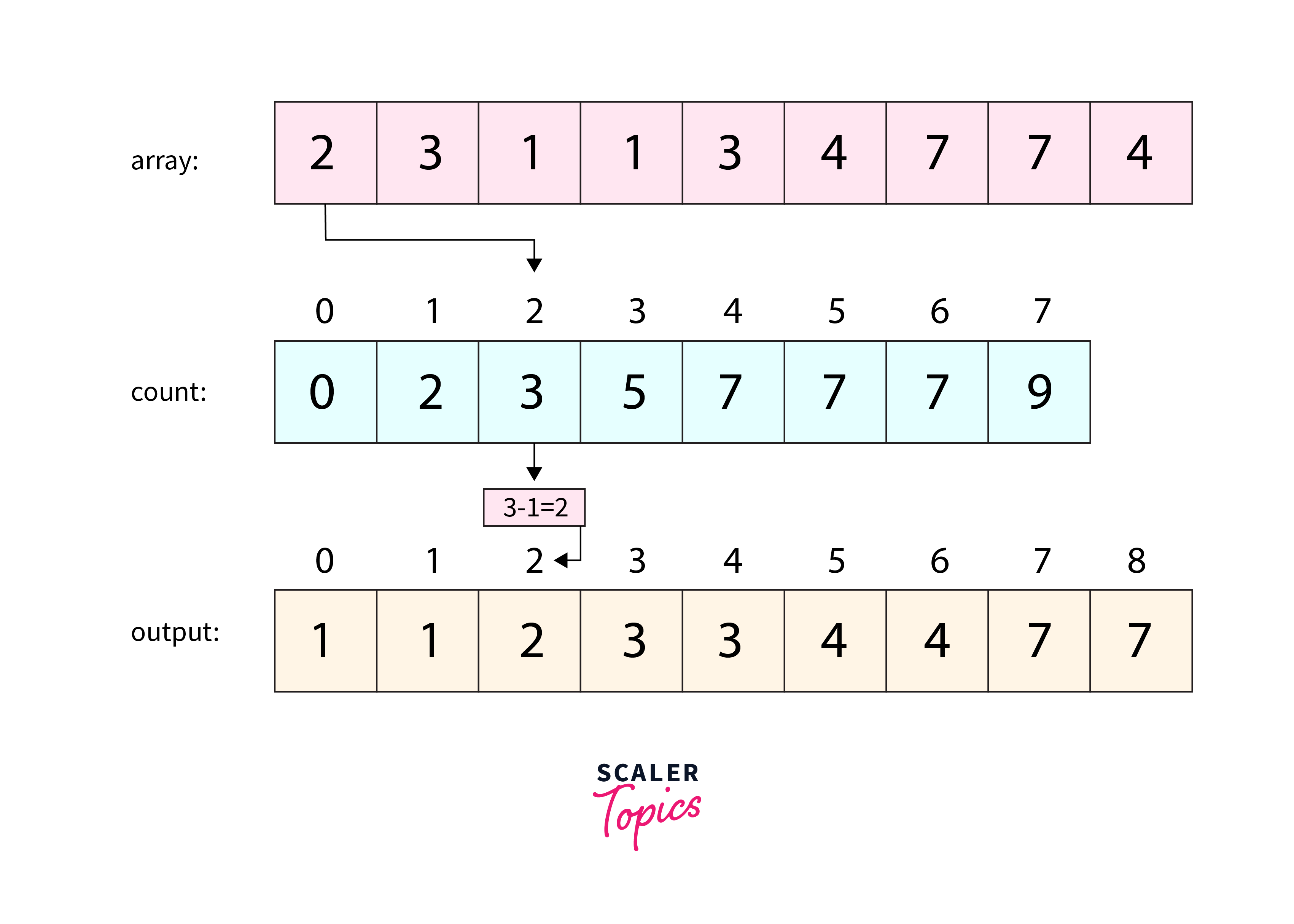
6. Once each element is correctly positioned, decrement its count by one in the count array.

Implementation of counting sort Algorithm

Counting sort in Java

public static void main(String[] args) {
        int[] arr = new int[] { 8,14,3,10,6,2,8,5,9};
        System.out.print("Original array: ");
        print(arr);
        countingSort(arr);
        System.out.print("Sorted array: ");
        print(arr);
    }
    private static int maximum(int[] arr) {
        int n = arr.length;
        int max = Integer.MIN_VALUE;
        for (int i = 0; i < n; ++i) {
            max = Math.max(max, arr[i]);
        }
        return max;
    }
    private static void countingSort(int[] arr) {
        int n = arr.length;
        int max = maximum(arr);
        int[] count = new int[max + 1];
        for (int i = 0; i < n; ++i) {
            count[arr[i]]++;
        }
        int lastIndex = 0;
        for (int i = 0; i <= max; ++i) {
            while (count[i]-- > 0) {
                arr[lastIndex++] = i;
            }
        }
    }
    private static void print(int[] arr) {
        int n = arr.length;
        for (int i = 0; i < n; ++i) {
            System.out.print(arr[i] + " ");
        }
        System.out.println();
    }

Output:

Original array: 8 14 3 10 6 2 8 5 9 
Sorted array: 2 3 5 6 8 8 9 10 14

Counting sort in C/C++

void print(int arr[], int n)
{
    for (int i = 0; i < n; ++i)
    {
        printf("%d ", arr[i]);
    }
    printf("\n");
}
int maximum(int a, int b)
{
    return a >= b ? a : b;
}
int maximum(int arr[], int n)
{
    int max = INT_MIN;
    for (int i = 0; i < n; ++i)
    {
        max = maximum(max, arr[i]);
    }
    return max;
}
void countingSort(int arr[], int n)
{
    int max = maximum(arr, n);
    int count[max + 1];
    for (int i = 0; i <= max; ++i)
    {
        count[i] = 0;
    }
    for (int i = 0; i < n; ++i)
    {
        count[arr[i]]++;
    }
    int lastIndex = 0;
    for (int i = 0; i <= max; ++i)
    {
        while (count[i]--)
        {
            arr[lastIndex++] = i;
        }
    }
}
int main()
{
    int arr[] = {8,14,3,10,6,2,8,5,9};
    int n = sizeof(arr) / sizeof(arr[0]);
    printf("Original array: ");
    print(arr, n);
    countingSort(arr, n);
    printf("Sorted array: ");
    print(arr, n);
    return 0;
}

Output:

Original array: 8 14 3 10 6 2 8 5 9
Sorted array: 2 3 5 6 8 8 9 10 14

Counting sort in Python

def countingSort(arr):
    max = maximum(arr)
    count = [0] * (max + 1)
    for e in arr:
        count[e] += 1
    lastIndex = 0
    for i in range(0, max+1):
        while count[i] > 0:
            arr[lastIndex] = i
            lastIndex += 1
            count[i] -= 1
def maximum(arr):
    res = -sys.maxsize-1
    for e in arr:
        res = max(res, e)
    return res
def printArray(arr):
    for e in arr:
        print(e, end=" ")
    print()
arr = [8,14,3,10,6,2,8,5,9]
print("Original array: ", end=" ")
printArray(arr)
countingSort(arr)
print("Sorted array: ", end=" ")
printArray(arr)

Output:

Original array: 8 14 3 10 6 2 8 5 9
Sorted array: 2 3 5 6 8 8 9 10 14

Complexity Analysis of Counting Sort Algorithm

Time Complexity of Counting Sort Algorithm

The time complexity of the algorithm is O(N+M), where N denotes the size of the input array and M is the size of the count array. This holds true for worst-case, average-case, and best-case scenarios.

Space Complexity of Counting Sort Algorithm

The Space Complexity is O(N+M), accounting for the space used by the output array and the count array.

Applications of Counting Sort Algorithm

1. Counting sort Algorithm is employed for sorting arrays containing smaller integers with numerous repetitions.
2. It’s chosen when achieving linear time complexity is crucial for efficient sorting operations.
3. Its effectiveness lies in efficiently handling scenarios where elements have limited range and frequent repetitions.

Advantage of Counting Sort Algorithm

1. Counting sort outperforms comparison-based sorting algorithms, like merge sort and quicksort, for inputs with a range comparable to the input size.
2. It offers simplicity in implementation, making it straightforward to code.
3. Counting sort maintains stability, preserving the original order of elements with equal values in the sorted output.

Disadvantage of Counting Sort Algorithm

1. Counting sort is incompatible with decimal values, limiting its applicability in sorting operations involving non-integer data.
2. Its efficiency diminishes significantly when sorting a large range of values, rendering it inefficient for such scenarios.
3. As a non-in-place sorting algorithm, counting sort necessitates additional space to store auxiliary data, impacting its memory usage compared to in-place algorithms.

Conclusion

1. Counting Sort Algorithm provides an efficient means of sorting arrays with small integer values and numerous repetitions.
2. Its linear time complexity makes it ideal for scenarios where achieving fast sorting operations is crucial.
3. Counting Sort maintains stability, preserving the original order of elements with equal values.
4. Despite its effectiveness, Counting Sort is limited by its inability to handle decimal values and its decreased efficiency with large range inputs.
5. Nevertheless, its simplicity in implementation and ability to handle repetitive elements efficiently contribute to its practical significance.
6. Careful consideration of the input data characteristics is essential to determine Counting Sort’s suitability for specific sorting tasks.

Thanks for reading. May the code be with you 🙂

Code with Precision! Enroll in Scaler Academy’s Online DSA Certification Course and Master Efficient Algorithms.