Quicksort is a prominent divide-and-conquer-based sorting algorithm renowned for its efficiency. Operating by selecting a pivot and partitioning the array around this pivot, Quicksort places the pivot in its correct sorted position. This technique achieves an average of nlogn comparisons for sorting n elements, making it notably swift.
The algorithm’s essence lies in its divide-and-conquer approach: it breaks down tasks into smaller subproblems, resolves them, and amalgamates the solutions. Initially, a pivot element is chosen, leading to the array’s partitioning into sub-arrays. One sub-array encompasses values less than or equal to the pivot, while the other contains values greater than it. Recursively, Quicksort sorts these sub-arrays. This partitioning and sorting continue until individual elements remain in each sub-array.
For students and professionals, understanding Quicksort’s fundamentals becomes pivotal, given its frequent examination appearances and its reputation as a rapid and efficient sorting method.
Working of Quick Sort Algorithm
Recall the list/array that had the elements – 10,8,5,15,610,8,5,15,6 in it. To sort these elements in ascending order using quick sort, let us follow the under-given steps –
Step – 1:
Select the pivot element, here for the sake of simplicity, we are selecting the rightmost element as the pivot.
Step – 2:
Rearrange the elements of the array in a way that all the elements smaller than the pivot are on its left and that all the greater ones are on the right. They need not be sorted. After the rearrangement, the array would look like this –
Here, 6 is our pivot element, and all the elements greater than itself are on the right side, while the elements smaller than the pivot is on its left side.
Now let us understand how did this rearrangement happen –
- Take two pointer variables that point to the left & right of the array (with pivot excluded). Let’s call them left & right respectively.
- Under a loop, increment the left pointer until a value greater than pivot is found. In this case, since 10 is already greater than 6, we move to step c.
- Under the same loop, increment the right pointer until a value smaller than pivot is found. Here, a value smaller than pivot is 5.
- Now since the conditions given in steps b and c are simultaneously fulfilled, swap the value at index left with the value at index right of the given array. This helps us move the elements smaller than the pivot element to the left of it, and the greater ones to the right of it.
Here, 5 & 10 are swapped. - Repeat steps b, c and d until the left index is greater than the right index.
- Here, the execution of the loop is stopped because left > right. Now, swap the value at pivot with the value at the index left or right.
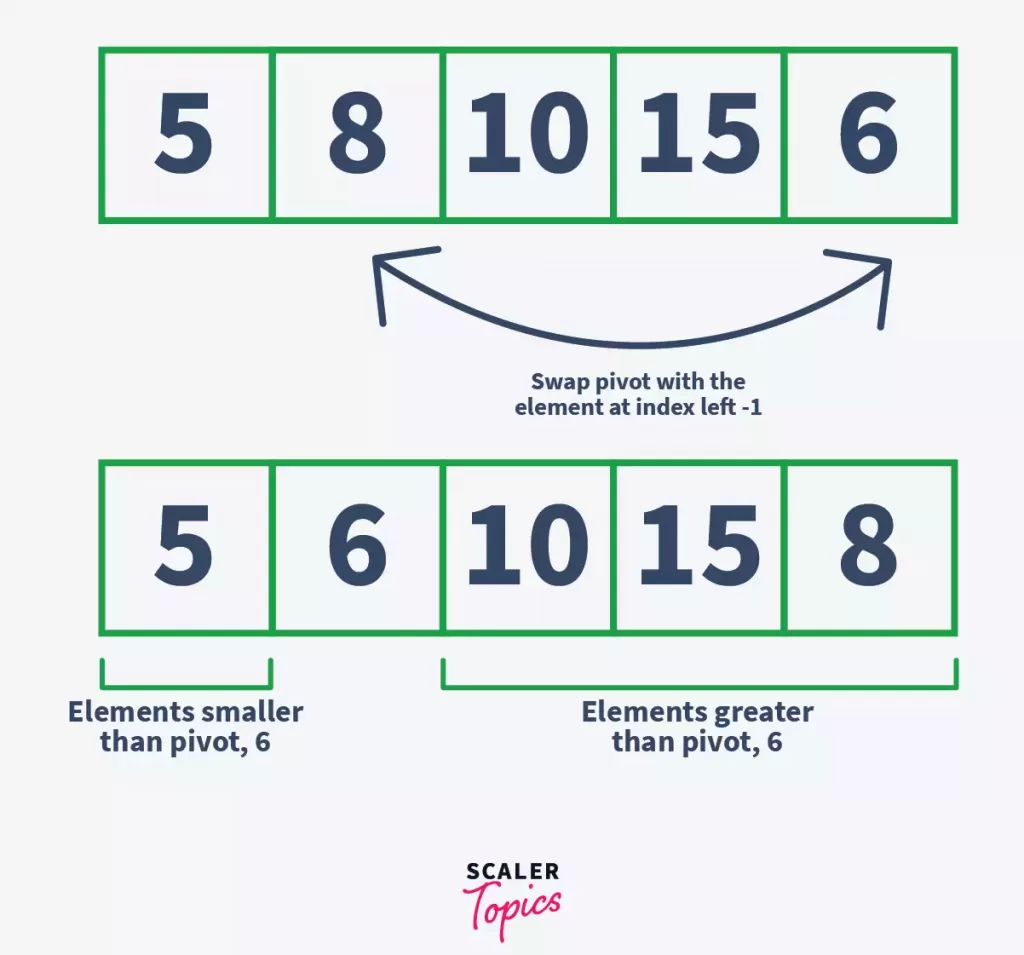We have placed 6 after 5, and before 10, 15, and 8. This way, we have placed 6 (pivot element) at such a position that elements smaller than it is on its left, and the elements greater than it is on its right. Notice that 6 is at its correct sorted position now.
Step – 3:
In this step, the sublist is divided into two parts – sublist before the pivot element, and sublist after the pivot element.
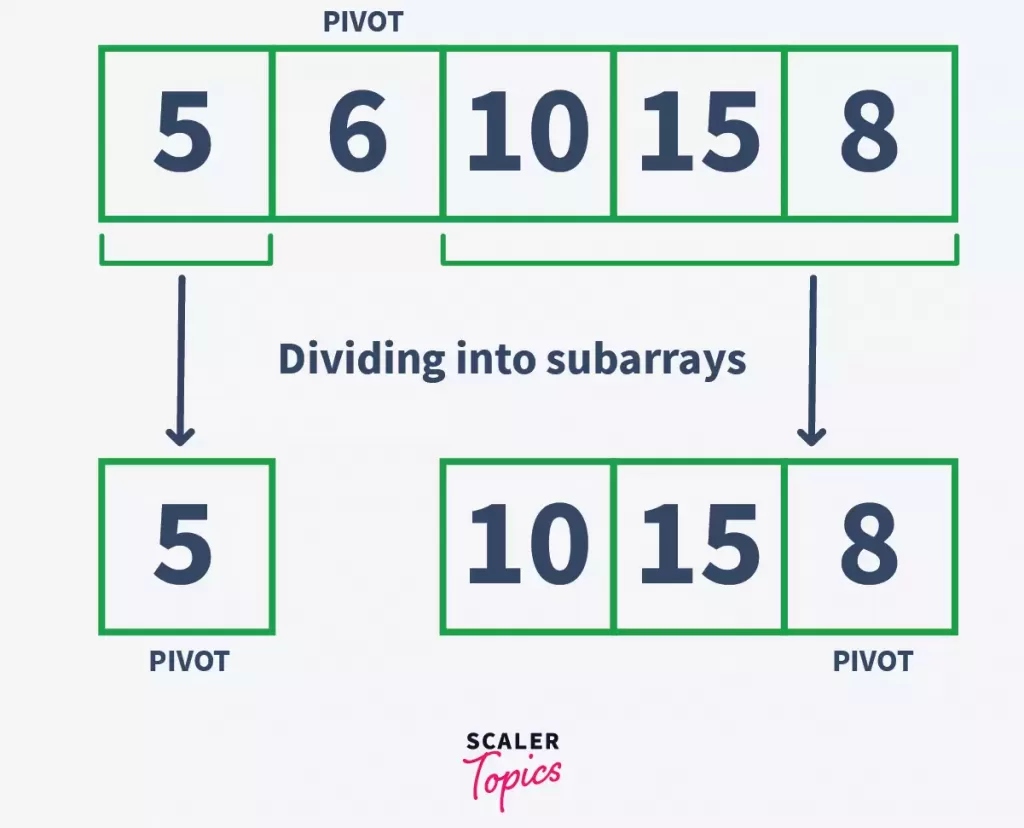
Step – 4:
Repeat the above-given steps recursively until all the elements of the array are at their correct sorted position.
The following diagram shows the working of the quick sort algorithm.
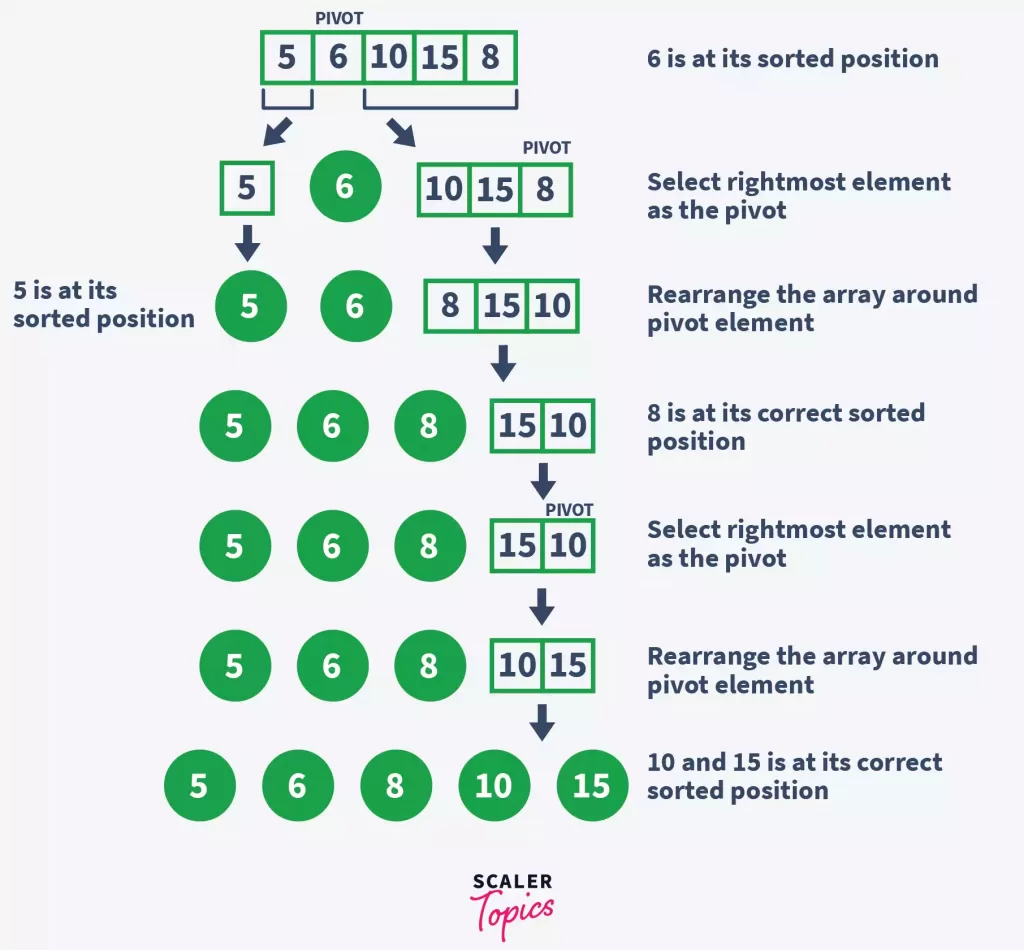
We have sorted the array using the quick sort algorithm. Let’s write some code to implement the algorithm.
Pseudocode for Quick Sort Algorithm
1. Pseudocode for Partitioning/Creating Subarrays –
//low and high are the lowest & highest index of the array/subarray respectively
function partition(array, low, high) {
// selecting the rightmost element as pivot
pivot = array[high]
//setting the left pointer to point at the lowest index initially
left = low
//setting the left pointer to point at the lowest index initially
right = high - 1;
//running a loop till left is smaller than right
while(left <= right)
//incrementing the value of left until the value at left'th
//index is smaller than pivot
while(array[left] < pivot)
left = left + 1
end while
//decrementing the value of right until the value at right'th
//index is greater than pivot
while(array[right] > pivot)
right = right - 1
end while
if(left < right)
//swapping the elements at left & right index
swap(array[left], array[right])
end if
end while
// swapping pivot with the element where left and right meet
swap(array[left], array[high])
// return the partition point
return left
end function
2. Pseudocode for Quick Sort Function
quickSort(array, low, high) {
if low < high
// since this function returns the point where the array is
//partitioned, it is used to track the subarrays/partitions in the
// array
pi = partition(array, low, high)
// recursively calling the function on left subarray
quickSort(array, low, pi - 1)
// recursively calling the function on right subarray
quickSort(array, pi + 1, high)
end if
end quicksort function
Implementation of Quick Sort
1. C Program for Quick Sort
// function to swap the elements
void swap(int *a, int *b) {
int temp = *a;
*a = *b;
*b = temp;
}
// finding the partition point & rearranging the array
int partition(int array[], int low, int high) {
// selecting the rightmost element as pivot
int pivot = array[high];
//setting the left pointer to point at the lowest index initially
int left = low;
//setting the left pointer to point at the lowest index initially
int right = high - 1;
//running a loop till left is smaller than right
while(left <= right){
//incrementing the value of left until the value at left'th index is smaller than pivot
while(array[left] < pivot){
left++;
}
//decrementing the value of right until the value at right'th index is greater than pivot
while(array[right] > pivot){
right--;
}
if(left < right){
//swapping the elements at left & right index
swap(&array[left], &array[right]);
}
}
// swapping pivot with the element where left and right meet
swap(array[left], array[high]);
// return the partition point
return (left);
}
void quickSort(int array[], int low, int high) {
if (low < high) {
// since this function returns the point where the array is partitioned, it is used to track the subarrays/partitions in the array
int pi = partition(array, low, high);
// recursively calling the function on left subarray
quickSort(array, low, pi - 1);
// recursively calling the function on right subarray
quickSort(array, pi + 1, high);
}
}
2. C++ Program for Quick Sort
// finding the partition point & rearranging the array
int partition(int array[], int low, int high) {
// selecting the rightmost element as pivot
int pivot = array[high];
//setting the left pointer to point at the lowest index initially
int left = low;
//setting the left pointer to point at the lowest index initially
int right = high - 1;
//running a loop till left is smaller than right
while(left <= right){
//incrementing the value of left until the value at left'th index is smaller than pivot
while(array[left] < pivot){
left++;
}
//decrementing the value of right until the value at right'th index is greater than pivot
while(array[right] > pivot){
right--;
}
if(left < right){
//swapping the elements at left & right index
swap(array[left], array[right]);
}
}
// swapping pivot with the element where left and right meet
swap(array[left], array[high]);
// return the partition point
return (left);
}
void quickSort(int array[], int low, int high) {
if (low < high) {
// since this function returns the point where the array is partitioned, it is used to track the subarrays/partitions in the array
int pi = partition(array, low, high);
// recursively calling the function on left subarray
quickSort(array, low, pi - 1);
// recursively calling the function on right subarray
quickSort(array, pi + 1, high);
}
}
3. Python Program for Quick Sort
# Quick sort in Python
# finding the partition point & rearranging the array
def partition(array, low, high):
# selecting the rightmost element as pivot
pivot = array[high];
# setting the left pointer to point at the lowest index initially
left = low;
#setting the left pointer to point at the lowest index initially
right = high - 1;
#running a loop till left is smaller than right
while (left <= right):
#incrementing the value of left until the value at left'th
# index is smaller than pivot
while (array[left] < pivot):
left = left + 1
#decrementing the value of right until the value at right'th
#index is greater than pivot
while (array[right] > pivot):
right = right - 1;
if (left < right):
#swapping the elements at left & right index
array[left], array[right] = array[right], array[left]
#swapping pivot with the element where left and right meet
array[left], array[high] = array[high], array[left]
# return the partition point
return left
# function to perform quicksort
def quickSort(array, low, high):
if low < high:
# since this function returns the point where the array is
#partitioned, it is used to track the subarrays/partitions in the
#array
pi = partition(array, low, high)
# recursively calling the function on left subarray
quickSort(array, low, pi - 1)
# recursively calling the function on right subarray
quickSort(array, pi + 1, high)
4. Java Program for Quick Sort
class Quicksort {
// method to find the partition position
static int partition(int array[], int low, int high) {
// selecting the rightmost element as pivot
int pivot = array[high];
//setting the left pointer to point at the lowest index initially
int left = low;
//setting the left pointer to point at the lowest index initially
int right = high - 1;
//running a loop till left is smaller than right
while(left <= right){
//incrementing the value of left until the value at left'th
//index is smaller than pivot
while(array[left] < pivot){
left++;
}
//decrementing the value of right until the value at right'th
//index is greater than pivot
while(array[right] > pivot){
right--;
}
if(left < right){
//swapping the elements at left & right index
int temp = array[left];
array[left] = array[right];
array[right] = temp;
}
}
// swapping pivot with the element where left and right meet
int temp = array[left];
array[left] = array[high];
array[high] = temp;
// return the partition point
return (left);
}
static void quickSort(int array[], int low, int high) {
if (low < high) {
// since this function returns the point where the array is
//partitioned, it is used to track the subarrays/partitions in
//the array
int pi = partition(array, low, high);
// recursively calling the function on left subarray
quickSort(array, low, pi - 1);
// recursively calling the function on right subarray
quickSort(array, pi + 1, high);
}
}
}
Complexity Analysis of Quick Sort
1. Quick Sort Time Complexity
Best-Case:
The best-case occurs when the pivot is almost in the middle of the array, and the partitioning is done in the middle. So, let us assume that we have a total of n elements in the array, and we are dividing the array from the middle.
In this case, with each partition, we will have at most n/2 elements. And we have to perform the partition until only one element is left in each subarray. The following is the tree representation of the given condition
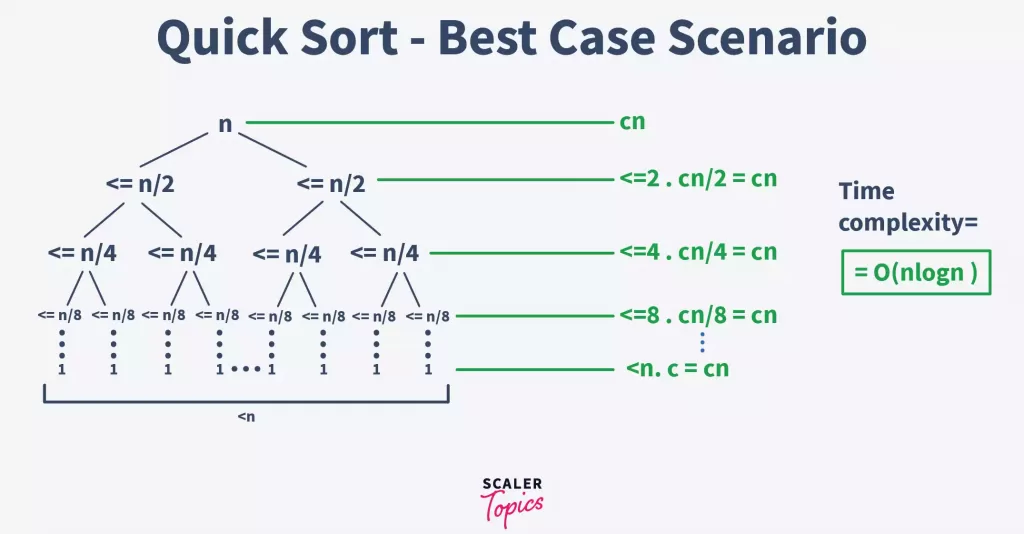
Notice that the above-given tree is a binary tree. And for a binary tree, we can know that its height is equal to logn. Therefore, the complexity of this part is O(logn).
Also, the time complexity of the partition() function would be equal to O(n). This is because, under the function, we are iterating over the array to swap rearranging the array around the pivot element.
Therefore, from the above results, we can conclude that the best-case time complexity for the quick sort algorithm is O(nlogn).
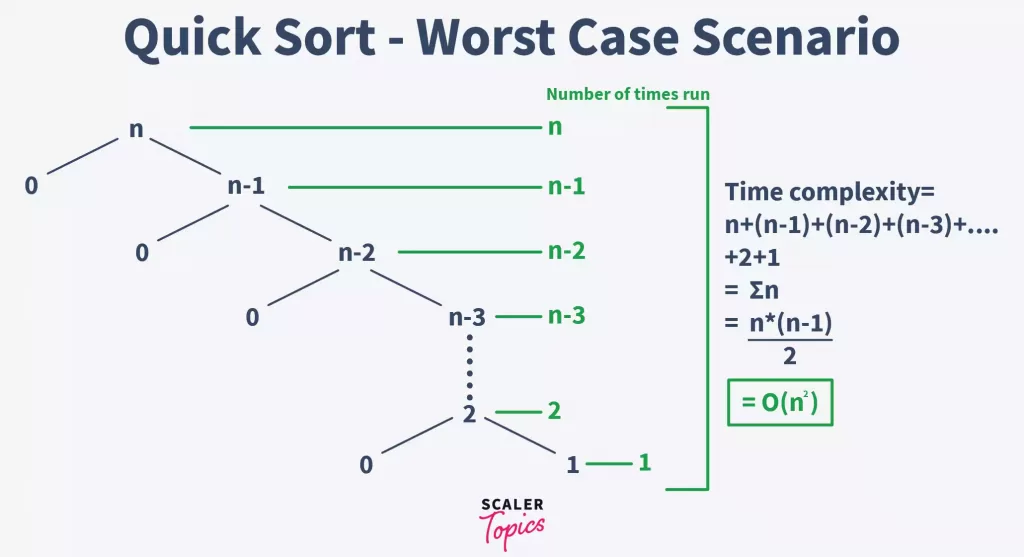
Worst Case:
The Worst-case occurs when either of the two partitions is unbalanced. This generally happens when the greatest or smallest element is selected as the pivot.
In this case, the pivot lies at the extreme of the array, and one subarray is always empty while the other contains n – 1 elements.
This way, in the first call, the array is divided into two subarrays of 0 & n – 1 elements respectively. For the second call, the array with n – 1 elements is divided into two subarrays of 0 & n – 2 elements respectively. This continues till only one element is left.
The time complexity, in this case, would be the sum of all the complexities at each step.
T(quicksort) = T(n) + T(n – 1) + T(n – 2) + …….. + 2 + 1
T(quicksort) = O((n * (n – 1))/2)
T(quicksort) = &O(n ^ 2)&
The following is the tree representation of this condition –
2. Quick Sort Space Complexity
In quick sort, the time complexity is calculated on the basis of space used by the recursion stack. In the worst case, the space complexity is O(n) because in the worst case, n recursive calls are made. And, the average space complexity of a quick sort algorithm is equal to O(logn).
From sorting to searching, Java DSA is essential. Join our free Java DSA course and become a proficient programmer in these core concepts.
Conclusion
- Quick Sort method sorts the elements using the Divide and Conquer approach.
- It has an average O(nLogn) complexity.
- It can be implemented in both recursive and iterative ways.
- Quick Sort is in-place, cache-friendly, and also a tail-recursive algorithm
Takeaways
Quicksort partitions an array and then calls itself recursively twice to sort the two resulting subarrays.
Complexity of Quick sort
- Time complexity – O(nlog(n))
- Space complexity – O(n)
FAQs
Q: Where is Quick Sort Used?
A: Quick sort is used in separating the Nth smallest or the largest element from an array. Being a fast sorting algorithm, quick sort is used by various departments in information retrieval. It is used for numerical computing where the efficient algorithms use priority queues and in turn quick sort for achieving accuracy. It is used where fast searching and/or sorting is the priority.
Q: Is Quick Sort a Stable Algorithm?
A: An algorithm is called stable if the relative order of two equal elements is preserved. Therefore, quick sort is not a stable algorithm because ordering is done on the basis of the pivot’s position.
Q: Why Quick Sort Runs Faster Than Merge Sort?
A: Quick sort is an in-place algorithm. But in merge sort, a new temporary array is required to merge the sorted subarrays. Therefore, quick sort is faster than merge sort.
Moreover, in quick sort, the worst case can be avoided by randomly choosing an element as the pivot, and performing sorting around it. Thus, a properly implemented quick sort has a time complexity of O(nlogn) in the average case.
Q: Why Quick Sort is Preferred for Array?
A: Quick sort is cache-friendly, which means it does not create unnecessary buffers in the cache memory and slows the system down. It is because, when used for arrays, quick sort has a good locality of reference
