A* Algorithm in AI

Search algorithms retrieve elements from data structures, essential for accessing specific items. Pathfinding, integral to this, determines optimal routes from one point to another. The A* algorithm stands out in artificial intelligence and computer science, efficiently finding optimal paths. Understanding A* is vital due to its pivotal role across various applications.

What is A* Algorithm in AI?

A* Search algorithm is a searching algorithm that searches for the path with the least cost between the initial and final state. It is one of the best and most popular methods out there, that are used in path-finding in graphs.

To relate the path with least-cost in real-life like Maps, games, etc. Like we can consider a 2-Dimensional board containing a source cell (colored green), destination cell (colored blue), and some obstacles (colored red).

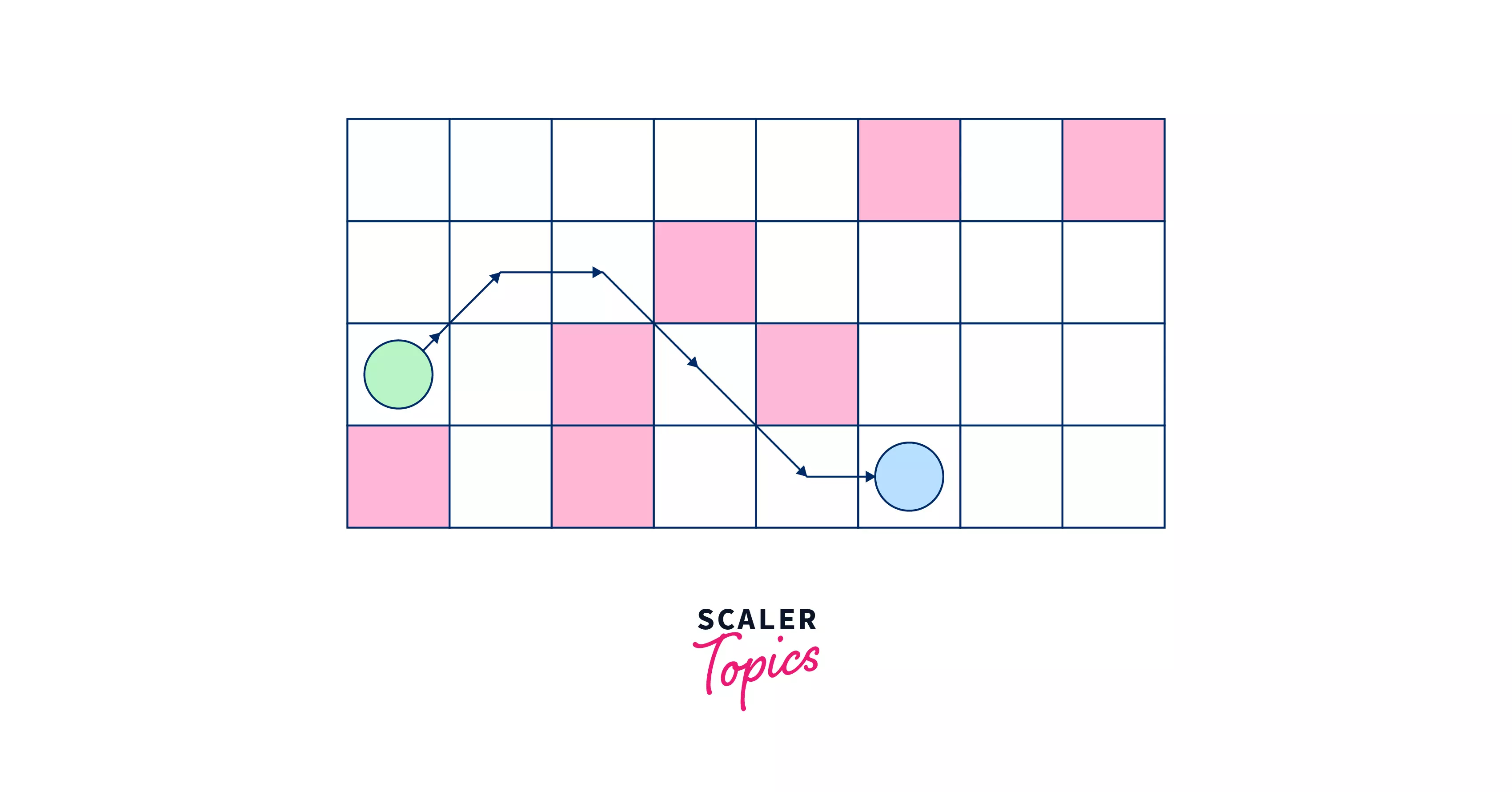
Why A* Algorithm in AI?

Informally speaking,A*algorithm unlike other searching techniques is “intelligent”. It is because it searches for the shorter paths rather than searching for longer paths first, that makes it optimal as well as a complete algorithm.

Here optimal means, it is sure that A* search algorithm will find the shortest path (if it exists) for a given graph/board and completeness means if the solution exists then it is guaranteed that the algorithm will find the solution in a finite amount of time.

Now the question would arise, why would one use the A* search algorithm over other popular algorithms like Dijkstra’s algorithm.

It is because Dijkstra’s algorithm always proceeds with the path with the least cost without even considering whether the taken path will lead us close to the destination or not.

On the other hand, theA* algorithm takes the most optimal path from its current position to reach closer to the destination.

How Does theA* Algorithm in AI Work?

Before continuing with the actual working of the A* algorithm let’s have a look at some key terms:

• $g$ — It is the cost incurred in moving from the initial cell (src) to the current cell. In the case of a board cost is nothing but the number of cells that have been visited since leaving the source cell.
• $h$ — It is known as the heuristic value, it is the estimated cost of reaching the final cell (dest cell) from the current cell. Note that, $h$ is not the actual value but an estimation so we must take care that $h$ is not overestimated.
• $f$ — It is the sum of the values of $g$ and $h$. Hence, $$f=g+h$$

To make the decision (where to go in the next step), the algorithm takes the $f’s$ value into account. Greedily, it selects the minimum possible $f$ value to process the current cell.

What is a Heuristic Function?

Heuristic function (or simply heuristic) is nothing but a shortcut to solve a given problem (by making approximations) when either the exact solution is non-existing or it takes huge time to find the same.

You will always see the terms admissibility and consistency associated with heuristics, let us understand what they are –

• Admissibility – A heuristic function is said to be admissible if it never overestimates the cost/price of reaching the target. In other words, it can be said that the estimated cost should be less than or equal to the lowest possible cost.
• Consistency – In searching related problems, a heuristic function is said to be consistent if its estimate to reach the target is always less than or equal to the sum of estimated cost from any of its neighboring points and the cost of reaching that neighbor from current position.

As described above, it is the estimated cost of reaching the final cell (dest cell) from any given cell. Its value is denoted by $h$, to find its value we make an approximation with the help of basic mathematical knowledge.

Mathematical tools we use to approximate the distance are –

• Manhattan Distance — It is the sum of absolute values of the difference between coordinates of the current node (say $cur$) and the destination node (say $dest$).
  It is defined as –
  $$h= \mid cur.x-dest.x\mid+\mid cur.y-dest.y\mid$$
  It is taken into account when we are allowed to move in only four directions (North, South, East, and West) from the current node.
• Diagonal Distance — Here we calculate the cost (number of steps) required if we can’t take a diagonal and then we subtract steps that can be saved by using the diagonal from it.

$\Delta x=\mid cur.x – dest.x \mid $
$\Delta y=\mid cur.y – dest.y \mid $
$h = D_1\times(\Delta x + \Delta y) + (D_2-2\times D_1)\times min(\Delta x, \Delta y)$

There are $min(\Delta x, \Delta y)$ diagonal steps, and each step costs us $D_2$ but on the other hand, it saves $2\times D_1$ non-diagonal steps. To keep things simple we take the values of $D_1$ and $D_2$ to be $1$.

It is taken into account when we are allowed to move in 8 directions (just like the King in chess) from the current node.

Example of A* Algorithm

Let’s assume we have the following board for the example with the green-colored cell as the source node and the blue-colored cell as the destination node, given that it is prohibited to pass any red filled cell.

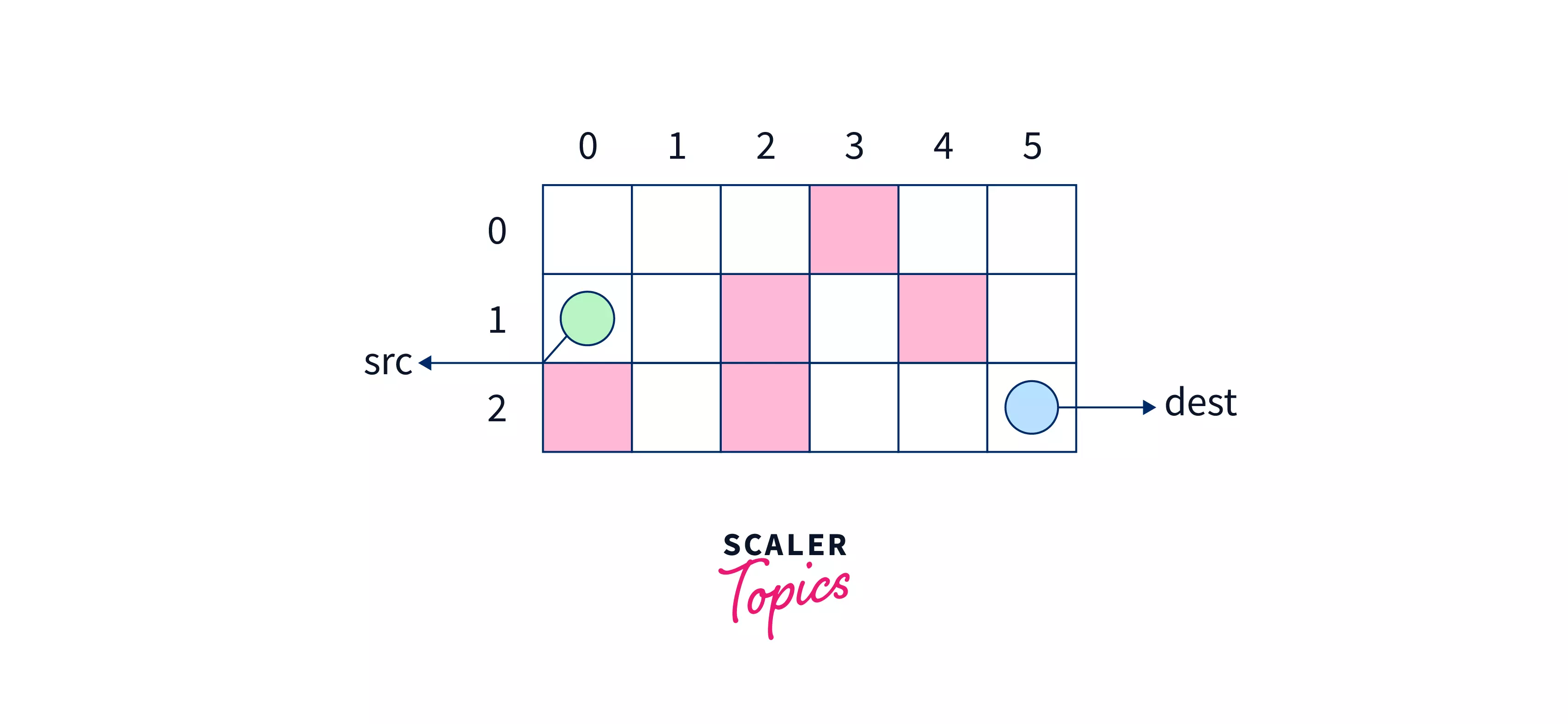
Here we are assuming that we can move in any of the 8 possible directions $i.e.$ left-right, up-down, and diagonally upward/downwards. Let’s assume the start node to be $(1,0)$ and the destination cell to be $(2,5)$.

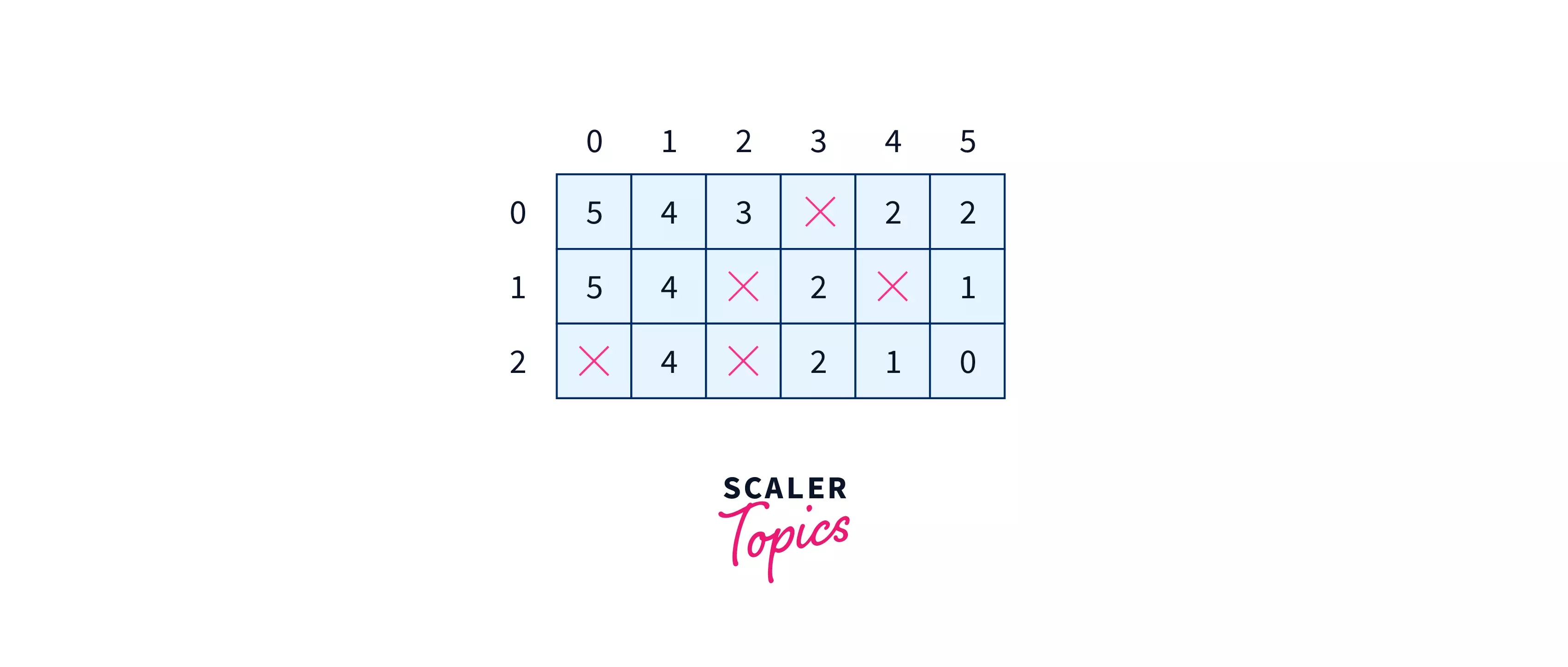
So we will be using Diagonal distance for the heuristic value. The heuristic values of all the cells to the destination will be calculated using the formulae –
$$h=\Delta x + \Delta y – min(\Delta x,\Delta y)$$

The heuristic values when calculated will be like –

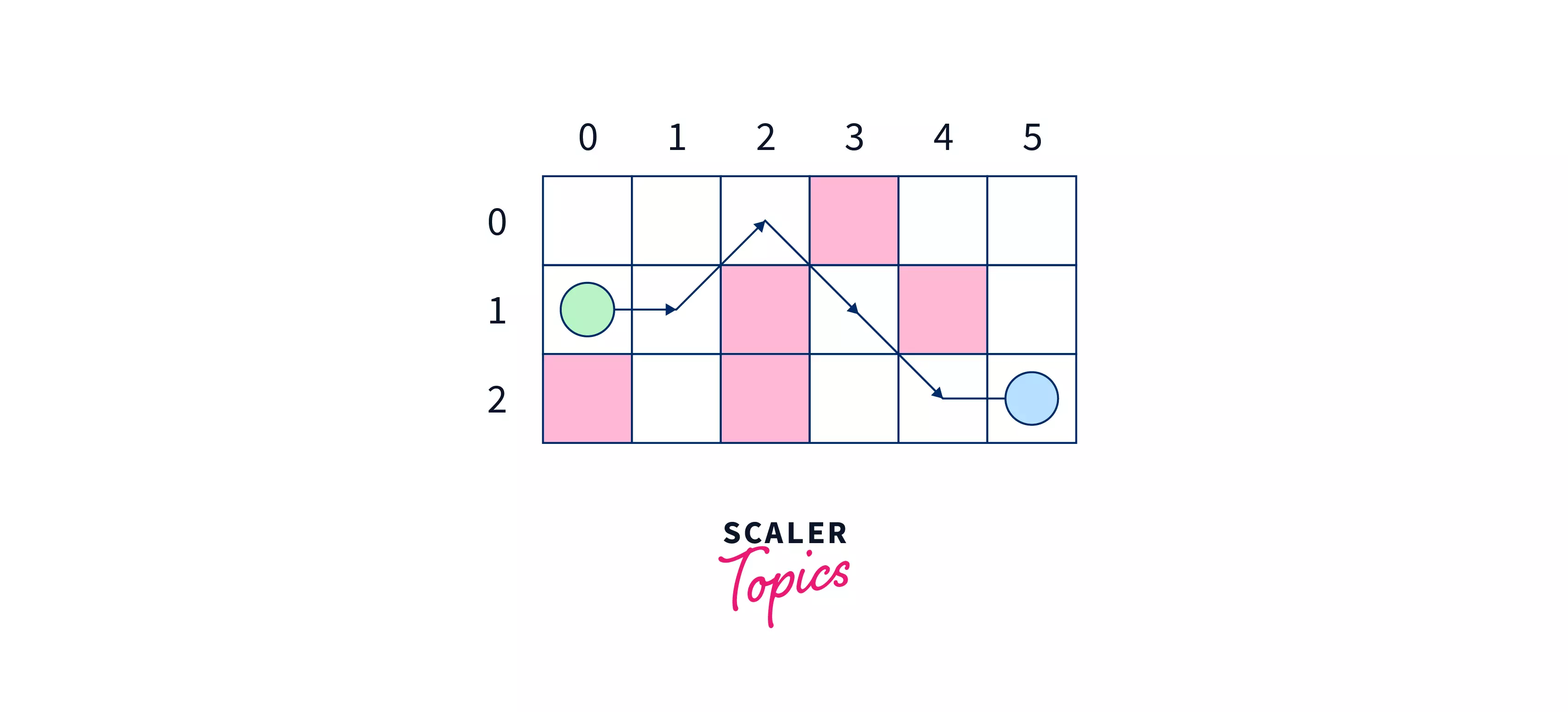
So steps involved in finding the path with minimum cost from the source node to the destination node will be –

• Step 1 – From cell $(0,0)$ we search for cell with the least heuristic value. We have three choices $i.e.$ $(0,1),$ $(1,1),$ and $(2,1)$ with heuristic values as $4$. We can pick any one of them, let’s say we picked $(1,1)$.
  Since we are moving at each step, therefore we will increase the value of $g$ after each step.
• Step 2 – From cell $(1,1)$ we again search for the cell with the least $h$ value. So, we are left with only one choice $i.e.$ cell $(0,2)$ so we jump to it, and increase the value of $g$ by 1.
• Step 3 – Again at this cell, we have only one choice $i.e.$ to go to cell $(1,3)$.
• Step 4 – We search for all the adjacent cells of $(1,3)$ with the minimum $h$ value. It is nothing but the cell $(2,4)$. So jump to this cell.
• Step 5 – We again repeat the process of searching the adjacents, after which we will get cell $(2,5)$ with the least $h$ value. So, we will jump to it, and since it is the destination node our process is complete with a cost of $g$ which is $5$.

Implementation

Steps to implement the code –

• Initialize two lists of Node type (say openList and closedList)
• Add src node in openList.
• Till openList is not empty do the following
  • Find the node in the openList with the least f value (say x)
  • Remove x from openList
  • Find and add all the 8 successors of x and add them to openList.
  • For each of the successors (say y) do the following –
    • If y is the destination then stop the search.
    • Otherwise, calculate g and h for y.
      y.g = x.g + distance between y and x (it is 1 in our case)
      y.h = distance between destination and y (Here we will be using Euclidean distance for the same).
      y.f = y.g + y.h
    • If a node with the same position as y and lower f is present in openList then skip this successor.
    • Else If a node with the same position as y exists in closedList with smaller f than y.f skip this successor.
    • Otherwise, add rhe node (y) to the openList.
  • Push x is the closedList.

Implementing A* Algorithm in Java

import java.util.*;
public class Main{
    // A Node class for A* Pathfinding
    static class Node{
        
        Node parent;
        int position[];
        int f,g,h;
        // Constructor for Node class.
        Node(Node parent, int position[]){
            this.parent=parent;
            this.position=position;
            this.f=this.g=this.h=0;
        }
        // Comparator for Node class
        boolean equals(Node temp){
            return this.position[0]==temp.position[0]&&
            this.position[1]==temp.position[1];
        }
    }
    // Boolean function to check if 
    // a move is valid or not.
    private static boolean notValid(int nodePosition[], 
                                    int n, int m){
        return nodePosition[0]>n-1||nodePosition[0]<0 ||
        nodePosition[1]>m-1||nodePosition[1]<0;
    }
    // A* algorithm function
    private static List<int[]> A_star(int board[][], 
                                int src[], int dest[]){
        /* This function returns a list of
        tuples representing the path from the given 
        src node to the given dest node in the given board */
        
        // Creating the src and dest node
        // with parent as None.
        Node srcNode=new Node(null, src);
        Node destNode=new Node(null, dest);
        
        // Initializing both openList and 
        // closedList as empty list.
        List<Node> openList=new ArrayList<>();
        List<Node> closedList=new ArrayList<>();
        
        // Append srcNode in openList. 
        openList.add(srcNode);
        
        // Iterate until we reach the 
        // dest Node. 
        while(openList.size()>0){
            // Get the current node
            Node currentNode=openList.get(0);
            int currentIndex=0;
            
            // Iterate over the openList to find 
            // node with least 'f'. 
            for(int i=0;i<openList.size();i++)
                if(openList.get(i).f<currentNode.f){
                    currentNode=openList.get(i);
                    currentIndex=i;
                }
                
            // Pop the found node off openList,
            // and add it to the closedList.
            openList.remove(currentIndex);
            closedList.add(currentNode);
            
            // If reached the dest.
            if(currentNode.equals(destNode)){
                // Initializng the 'path' list. 
                List<int[]> path=new ArrayList<>();
                Node current=currentNode;
                
                // Adding currentposition in path 
                // and the moving to its parent until 
                // we reach None (parent of src). 
                while(current!=null){
                    path.add(current.position);
                    current=current.parent;
                }
                // Returning the reversed path (to make
                // it src -> dest, instead of dest -> src).
                Collections.reverse(path);
                return path;
            }
            // Generate children
            List<Node> children=new ArrayList<>();
            int dirs[][]=new int[][]{
                {0,-1}, {0,1}, {-1,0}, {1,0},
                {-1,-1}, {-1,1}, {1,-1}, {1,1}
            };
            // Iterate over neighouring cells.
            for(int newPosition[]:dirs){
                // Find the position of new Node.
                int nodePosition[]=new int[]{
                  currentNode.position[0]+newPosition[0],
                  currentNode.position[1]+newPosition[1]
                };
                
                // If the new position is not valid (lies outside board)
                // then do not proceed ahead with this node. Also if the  
                // new position contains obstacle, we can't proceed.
                if(notValid(nodePosition, board.length,board[0].length)||
                        board[nodePosition[0]][nodePosition[1]]!=0){
                    continue;
                }
                // Append the node in children list.
                children.add(new Node(currentNode, nodePosition));
            }
            // Iterate over children list.
            for(Node child: children){
                // If the child is in closedList
                for(Node closedChild:closedList)
                    if(closedChild.equals(child))
                        continue;
                    
                // Assign the values of f, g, and h.
                child.g=currentNode.g+1;
                child.h=(int)((Math.pow(child.position[0]-
                    destNode.position[0],2) + (Math.pow(child.position[1]-
                        destNode.position[1],2))));
                child.f=child.g+child.h;
                
                // If the Child is present in OpenList. 
                for(Node openNode:openList){
                    if(child.equals(openNode) && child.g>openNode.g)
                        continue;
                }
                // Append the child at the last of open list
                openList.add(child);
            }
            
            if(openList.size()>board.length*board.length*
            board[0].length*board[1].length)
                break;
        }
        return new ArrayList<>();
    }
    public static void main(String args[]){
        int board[][]=new int[][]{
          {0, 0, 0, 1, 0, 0},
          {0, 0, 1, 0, 1, 0},
          {1, 0, 1, 0, 0, 0}
        };
        int src[]=new int[]{1,0};
        int dest[]=new int[]{2,5};
        
        List<int[]> pathSrcToDest=A_star(board,src,dest);
        for(int i=0;i<pathSrcToDest.size();i++){
            System.out.print("("+pathSrcToDest.get(i)[0]+
            ", "+pathSrcToDest.get(i)[1]+") ");
        }
    }
}

Implementing A* Algorithm in Python

class Node():
    """A Node class for A* Pathfinding"""
    # Constructor for Node class.
    def __init__(self, parent=None, position=None):
        self.parent = parent
        self.position = position

        self.g = self.h = self.f = 0
    # Comparator for Node class
    def __eq__(self, temp):
        return self.position == temp.position

# Boolean function to check if 
# a move is valid or not.
def notValid(nodePosition,n,m):
    return nodePosition[0] > n-1 or nodePosition[0] < 0 \
    or nodePosition[1] > m-1 or nodePosition[1] < 0

# A* algorithm function
def A_Star(board, src, dest):
    """This function returns a list of
    tuples representing the path from the given 
    src node to the given dest node in the given board"""
    # Creating the src and dest node
    # with parent as None.
    srcNode = Node(None, src)
    destNode = Node(None, dest)
    

    # Initializing both openList and 
    # closedList as empty list.
    openList = []
    closedList = []

    # Append srcNode in openList. 
    openList.append(srcNode)

    # Iterate until we reach the 
    # dest Node. 
    while len(openList) > 0:

        # Get the current node
        currentNode = openList[0]
        currentIndex = 0
        # Iterate over the openList to find 
        # node with least 'f'. 
        for index, item in enumerate(openList):
            if item.f < currentNode.f:
                currentNode = item
                currentIndex = index

        # Pop the found node off openList,
        # and add it to the closedList. 
        openList.pop(currentIndex)
        closedList.append(currentNode)

        # If reached the dest.
        if currentNode == destNode:
            # Initializng the 'path' list. 
            path = []
            current = currentNode
            # Adding currentposition in path 
            # and the moving to its parent until 
            # we reach None (parent of src). 
            while current is not None:
                path.append(current.position)
                current = current.parent
            # Returning the reversed path (to make
            # it src -> dest, instead of dest -> src.
            return path[::-1] 

        # Generate children
        children = []
        dirs=((0, -1), (0, 1), (-1, 0), (1, 0),
        (-1, -1), (-1, 1), (1, -1), (1, 1))
        # Iterate over neighouring cells.
        for newPosition in dirs: 

            # Find the position of new Node.
            nodePosition = (currentNode.position[0] + newPosition[0], 
            currentNode.position[1] + newPosition[1])

            # If the new position is not valid (lies outside the board)
            # then do not proceed ahead with this node.
            if(notValid(nodePosition,len(board),
            len(board[len(board)-1]))==True):
                continue
            # Also if the new position contains obstacle, 
            # we can't go ahead.
            if (board[nodePosition[0]][nodePosition[1]] != 0):
                continue
            # Append the node in children list.
            children.append(Node(currentNode, nodePosition))

        # Iterate over children list.
        for child in children:
            
            # If the child is in closedList
            for closedChild in closedList:
                if closedChild == child:
                    continue
            
            # Assign the values of f, g, and h.
            child.g = currentNode.g + 1
            child.h = ((child.position[0] - destNode.position[0]) ** 2) \
            + ((child.position[1] - destNode.position[1]) ** 2)
            child.f = child.g + child.h

            # If the Child is present in OpenList. 
            for openNode in openList:
                if child == openNode and child.g > openNode.g:
                    continue

            # Append the child at the last of open list
            openList.append(child)
        if (len(openList) > len(board)**2*len(board[0])**2): 
            return None

def main():
    board = [
                [0, 0, 0, 1, 0, 0],
                [0, 0, 1, 0, 1, 0],                
                [1, 0, 1, 0, 0, 0]
            ]

    src = (1, 0)
    dest = (2, 5)

    pathSrcToDest = A_Star(board, src, dest)
    print(pathSrcToDest)


if __name__ == '__main__':
    main()

Output –

[(1, 0), (1, 1), (0, 2), (1, 3), (2, 4), (2, 5)]

Complexity Analysis

• Time Complexity – In the worst situation, we may require to traverse through all the edges to reach the destination. Hence in the worst case, the time complexity will be $O(E)\simeq O(V^2)$.
• Space Complexity – In the worst scenario, we may have all the vertices (nodes) in openList which will make the worst case space complexity be $O(V)$.

Conclusion

• A* Algorithm in AI can be used to find the minimum cost path in 1 source – 1 destination type problems efficiently.
• It is extensively used in Tower Defense games (where we need to attack the enemy’s territory surpassing all obstacles placed by him/her).
• Be careful in choosin the heuristic function, on choosing the wrong one A*algorithm might produce the wrong outputs.