Best First Search is a heuristic search algorithm that selects the most promising node for expansion based on an evaluation function. It prioritizes nodes in the search space using a heuristic to estimate their potential. By iteratively choosing the most promising node, it aims to efficiently navigate towards the goal state, making it particularly effective for optimization problems.
Best First Search Algorithm
Best First Search is a heuristic search algorithm that explores a graph by expanding the most promising node first, according to a specified evaluation function. It continuously selects nodes based on their estimated cost to reach the goal, typically using a priority queue. BFS is suitable for finding paths in graphs and optimization problems where informed decision-making is crucial.
Here’s a concise explanation of the Best First Search algorithm in step-by-step form:
- Start with an initial node and add it to the open list.
- While the open list is not empty.
- Select the node with the lowest estimated cost (based on a heuristic function) from the open list.
- If the selected node is the goal, return the solution.
- Otherwise, expand the selected node by generating its successors.
- Evaluate each successor node using the heuristic function and add them to the open list.
- If the open list becomes empty without reaching the goal, the search fails.
What is a Heuristic Function?
Heuristic function (or simply heuristic) is nothing but a shortcut to solve a given problem (by making approximations) when either the exact solution is non-existing or it takes huge time to find the same. You will always see the terms admissibility and consistency associated with heuristics, let us understand what they are –
- Admissibility – A heuristic function is said to be admissible if it never overestimates the cost/price of reaching the target. In other words, it can be said that the estimated cost should be less than or equal to the lowest possible cost.
- Consistency – In searching related problems, a heuristic function is said to be consistent if its estimate to reach the target is always less than or equal to the sum of estimated cost from any of its neighboring points and the cost of reaching that neighbor from current position.
Majorly we have two types of best first search algorithms –
- Greedy Best First Search
- A* Search Algorithm
Approach 1: Greedy Best First Search Algorithm
In the greedy best first algorithm, we select the path that appears to be the most promising at any moment. Here, by the term most promising we mean the path from which the estimated cost of reaching the destination node is the minimum.
To decide which path is the most promising we will use the heuristics function (say h(n)) where h(i) denotes the estimated cost of reaching the destination node from the ith node. Note that, the value of h(dest) will be 0 because no cost is incurred to reach the destination if we are already there.
Algorithm
The algorithm of the greedy best first search algorithm is as follows –
- Define two empty lists (let them be openList and closeList).
- Insert src in the openList.
- Iterate while the open list is not empty, and do the following –
- Find the node with the least h value that is present in openList (let it be node).
- Remove the node from the openList, and insert it in the closeList.
- Check for all the adjacents nodes of the node, if anyone of them equals the dest. If yes, then terminate the search process as we’ve reached the destination.
- Otherwise, find all the adjacents of the node that are neither present in openList nor closeList and insert them in the openList.
- If we have reached here, it means there is no possible path between src and dest.
Dry Run
Let’s say we have the following graph, in which src and dest nodes are highlighted, and heuristic values for each of the nodes are written against them in the form of the table.
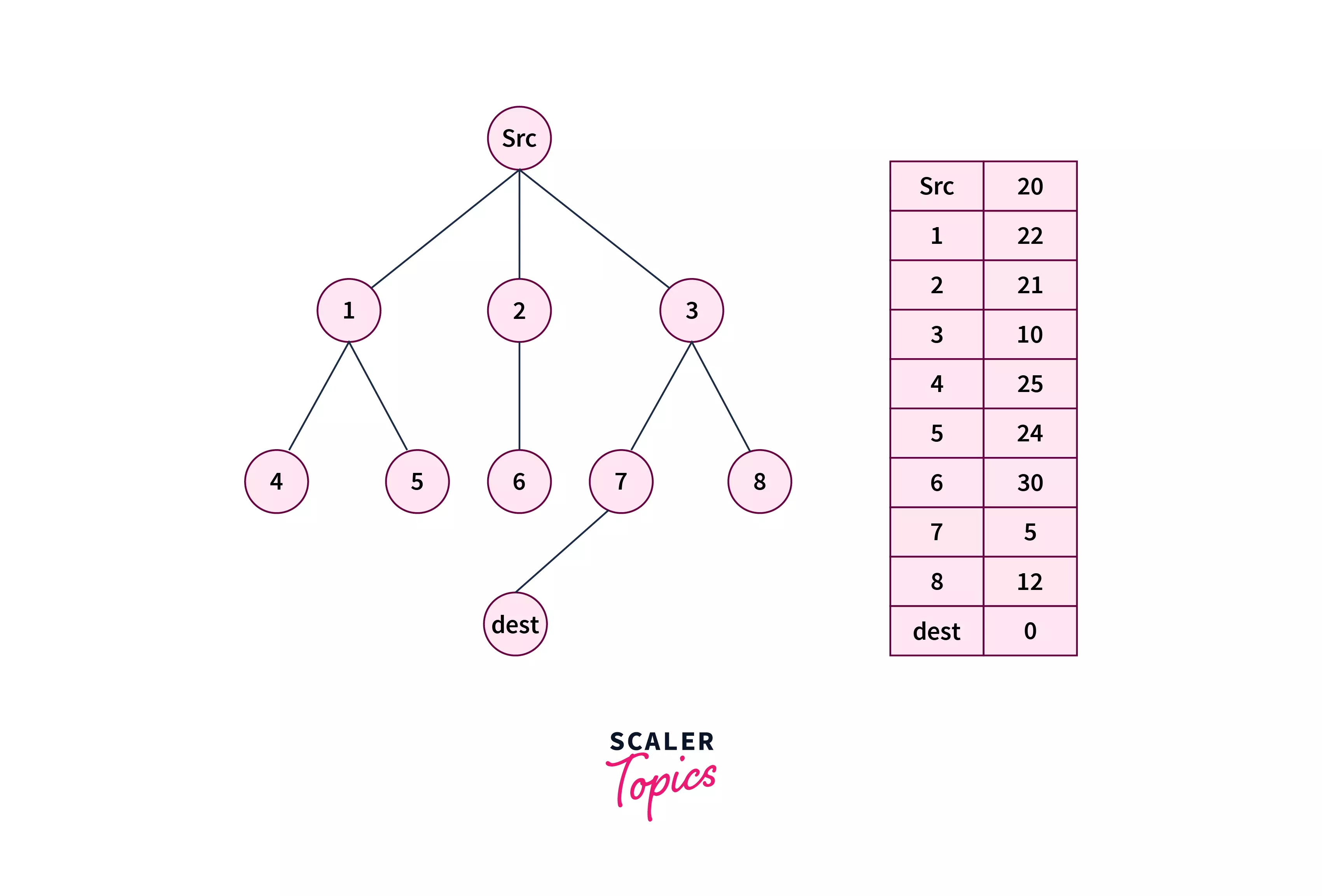
- Step 1 – Initialize two empty lists i.e.i.e. openList and closeList.
- Step 2– Insert src in the openList, after which we have – openList = [src] closeList = []
- Step 3 – (Iterating while the open list is not empty) –
- Iteration 1 –
- After this operation we will have – openList = [1, 2, 3] closeList = [src]
- Iteration 2 –
- After this operation we will have – openList = [1, 2, 7, 8] closeList = [src, 3]
- Iteration 3 –
- Upon exploring the adjacents of node 7 we found that dest is one of them. Hence, we return that search result in success, and print the path src→3→7→dest.
- Iteration 1 –
Java Implementation
import java.util.*;
public class Main{
// A Node class for GBFS Pathfinding
static class Node{
int v, weight;
Node(int v, int weight){
this.v=v;
this.weight=weight;
}
}
// pathNode class will help to store
// the path from src to dest.
static class pathNode{
int node;
pathNode parent;
pathNode(int node, pathNode parent){
this.node=node;
this.parent=parent;
}
}
// Function to add edge in the graph.
static void addEdge(int u, int v, int weight){
// Add edge u -> v with weight weight.
adj.get(u).add(new Node(v, weight));
}
// Declaring the adjacency list;
static List<List<Node>> adj;
// Greedy best first search algorithm function
private static List<Integer> GBFS(int h[]
, int V, int src, int dest){
/* This function returns a list of
integers that denote the shortest
path found using the GBFS algorithm.
If no path exists from src to dest, we will return an empty list.
*/
// Initializing openList and closeList.
List<pathNode> openList = new ArrayList<>();
List<pathNode> closeList = new ArrayList<>();
// Inserting src in openList.
openList.add(new pathNode(src, null));
// Iterating while the openList
// is not empty.
while(!openList.isEmpty()){
pathNode currentNode = openList.get(0);
int currentIndex = 0;
// Finding the node with the least 'h' value.
for(int i = 0; i < openList.size(); i++){
if(h[openList.get(i).node] <
h[currentNode.node]){
currentNode = openList.get(i);
currentIndex = i;
}
}
// Removing the currentNode from
// the openList and adding it in
// the closeList.
openList.remove(currentIndex);
closeList.add(currentNode);
// If we have reached the destination node.
if(currentNode.node == dest){
// Initializing the 'path' list.
List<Integer> path = new ArrayList<>();
pathNode cur = currentNode;
// Adding all the nodes in the
// path list through which we have
// reached to dest.
while(cur != null){
path.add(cur.node);
cur = cur.parent;
}
// Reversing the path, because
// currently it denotes path
// from dest to src.
Collections.reverse(path);
return path;
}
// Iterating over adjacents of 'currentNode'
// and adding them to openList if
// they are neither in openList or closeList.
for(Node node: adj.get(currentNode.node)){
for(pathNode x : openList){
if(x.node == node.v) continue;
}
for(pathNode x : closeList){
if(x.node == node.v) continue;
}
openList.add(new pathNode(node.v, currentNode));
}
}
return new ArrayList<>();
}
public static void main(String args[]){
// Initializing the adjacency list.
adj=new ArrayList<>();
/* Making the following graph
src = 0
/ | \
/ | \
1 2 3
/\ | /\
/ \ | / \
4 5 6 7 8
/
/
dest = 9
*/
// Total number of vertices.
int V = 10;
for(int i = 0; i < V; i++)
adj.add(new ArrayList<>());
addEdge(0, 1, 2);
addEdge(0, 2, 1);
addEdge(0, 3, 10);
addEdge(1, 4, 3);
addEdge(1, 5, 2);
addEdge(2, 6, 9);
addEdge(3, 7, 5);
addEdge(3, 8, 2);
addEdge(7, 9, 5);
// Defining the heuristic values for each node.
int h[] = {20, 22, 21, 10,
25, 24, 30, 5, 12, 0};
List<Integer> path = GBFS(h, V, 0, 9);
for(int i = 0; i < path.size() - 1; i++){
System.out.print(path.get(i)+" --> ");
}
System.out.println(path.get(path.size()-1));
}
}
Output:
0 --> 3 --> 7 --> 9
C++ Implementation
#include<bits/stdc++.h>
using namespace std;
// A Node class for GBFS Pathfinding
class Node{
public:
int v, weight;
Node(int V, int Weight){
v=V;
weight=Weight;
}
};
// pathNode class will help to store
// the path from src to dest.
class pathNode{
public:
int node;
pathNode *parent;
pathNode(int Node){
node=Node;
parent=NULL;
}
pathNode(int Node, pathNode *Parent){
node=Node;
parent=Parent;
}
};
// Declaring the adjacency list;
static vector<vector<Node*>> adj;
// Function to add edge in the graph.
void addEdge(int u, int v, int weight){
// Add edge u -> v with weight weight.
adj[u].push_back(new Node(v, weight));
}
// Greedy best first search algorithm function
vector<int> GBFS(int h[], int V,
int src, int dest){
/* This function returns a list of
integers that denote the shortest
path found using the GBFS algorithm.
If no path exists from src to dest, we will return an empty list.
*/
// Initializing openList and closeList.
vector<pathNode*> openList;
vector<pathNode*> closeList;
// Inserting src in openList.
openList.push_back(new pathNode(src));
// Iterating while the openList
// is not empty.
while(!openList.empty()){
pathNode *currentNode = openList[0];
int currentIndex = 0;
// Finding the node with the least 'h' value.
for(int i = 0; i < openList.size(); i++){
if(h[openList[i]->node] <
h[currentNode->node]){
currentNode = openList[i];
currentIndex = i;
}
}
// Removing the currentNode from
// the openList and adding it in
// the closeList.
openList.erase(openList.begin() + currentIndex);
closeList.push_back(currentNode);
// If we have reached the destination node.
if(currentNode->node == dest){
// Initializing the 'path' list.
vector<int> path;
pathNode *cur = currentNode;
// Adding all the nodes in the
// path list through which we have
// reached to dest.
while(cur != NULL){
path.push_back(cur->node);
cur = cur->parent;
}
// Reversing the path, because
// currently it denotes path
// from dest to src.
reverse(path.begin(), path.end());
return path;
}
// Iterating over adjacents of 'currentNode'
// and adding them to openList if
// they are neither in openList or closeList.
for(Node *node: adj[currentNode->node]){
for(pathNode *x : openList){
if(x->node == node->v) continue;
}
for(pathNode *x : closeList){
if(x->node == node->v) continue;
}
openList.push_back(new pathNode(node->v, currentNode));
}
}
return vector<int>();
}
int main(){
/* Making the following graph
src = 0
/ | \
/ | \
1 2 3
/\ | /\
/ \ | / \
4 5 6 7 8
/
/
dest = 9
*/
// Total number of vertices.
int V = 10;
adj.resize(V);
addEdge(0, 1, 2);
addEdge(0, 2, 1);
addEdge(0, 3, 10);
addEdge(1, 4, 3);
addEdge(1, 5, 2);
addEdge(2, 6, 9);
addEdge(3, 7, 5);
addEdge(3, 8, 2);
addEdge(7, 9, 5);
// Defining the heuristic values for each node.
int h[] = {20, 22, 21, 10,
25, 24, 30, 5, 12, 0};
vector<int> path = GBFS(h, V, 0, 9);
for(int i = 0; i < path.size() - 1; i++){
cout << path[i] << " --> ";
}
cout << path[path.size()-1] << endl;
return 0;
}
Output:
0 --> 3 --> 7 --> 9
Python Implementation
# A Node class for GBFS Pathfinding
class Node:
def __init__(self, v, weight):
self.v=v
self.weight=weight
# pathNode class will help to store
# the path from src to dest.
class pathNode:
def __init__(self, node, parent):
self.node=node
self.parent=parent
# Function to add edge in the graph.
def addEdge(u, v, weight):
# Add edge u -> v with weight weight.
adj[u].append(Node(v, weight))
# Declaring the adjacency list
adj = []
# Greedy best first search algorithm function
def GBFS(h, V, src, dest):
"""
This function returns a list of
integers that denote the shortest
path found using the GBFS algorithm.
If no path exists from src to dest, we will return an empty list.
"""
# Initializing openList and closeList.
openList = []
closeList = []
# Inserting src in openList.
openList.append(pathNode(src, None))
# Iterating while the openList
# is not empty.
while (openList):
currentNode = openList[0]
currentIndex = 0
# Finding the node with the least 'h' value
for i in range(len(openList)):
if(h[openList[i].node] < h[currentNode.node]):
currentNode = openList[i]
currentIndex = i
# Removing the currentNode from
# the openList and adding it in
# the closeList.
openList.pop(currentIndex)
closeList.append(currentNode)
# If we have reached the destination node.
if(currentNode.node == dest):
# Initializing the 'path' list.
path = []
cur = currentNode
# Adding all the nodes in the
# path list through which we have
# reached to dest.
while(cur != None):
path.append(cur.node)
cur = cur.parent
# Reversing the path, because
# currently it denotes path
# from dest to src.
path.reverse()
return path
# Iterating over adjacents of 'currentNode'
# and adding them to openList if
# they are neither in openList or closeList.
for node in adj[currentNode.node]:
for x in openList:
if(x.node == node.v):
continue
for x in closeList:
if(x.node == node.v):
continue
openList.append(pathNode(node.v, currentNode))
return []
# Driver Code
""" Making the following graph
src = 0
/ | \
/ | \
1 2 3
/\ | /\
/ \ | / \
4 5 6 7 8
/
/
dest = 9
"""
# The total number of vertices.
V = 10
## Initializing the adjacency list
for i in range(V):
adj.append([])
addEdge(0, 1, 2)
addEdge(0, 2, 1)
addEdge(0, 3, 10)
addEdge(1, 4, 3)
addEdge(1, 5, 2)
addEdge(2, 6, 9)
addEdge(3, 7, 5)
addEdge(3, 8, 2)
addEdge(7, 9, 5)
# Defining the heuristic values for each node.
h = [20, 22, 21, 10, 25, 24, 30, 5, 12, 0]
path = GBFS(h, V, 0, 9)
for i in range(len(path) - 1):
print(path[i], end = " -> ")
print(path[(len(path)-1)])
Output:
0 --> 3 --> 7 --> 9
Complexity Analysis
- Time Complexity – In the worst situation, we may require to traverse through all the edges to reach the destination. Hence in the worst case, the time complexity will be O(ElogV).
- Space Complexity – In the worst scenario, we may have all the vertices (nodes) in openList which will make the worst case space complexity O(V).
Approach 2: A* Search Algorithm
What is A* Search Algorithm?
A* Search algorithm is a searching algorithm that searches for the path with the least cost between the initial and final state. It is one of the best and most popular methods out there, that are used in path-finding in graphs.
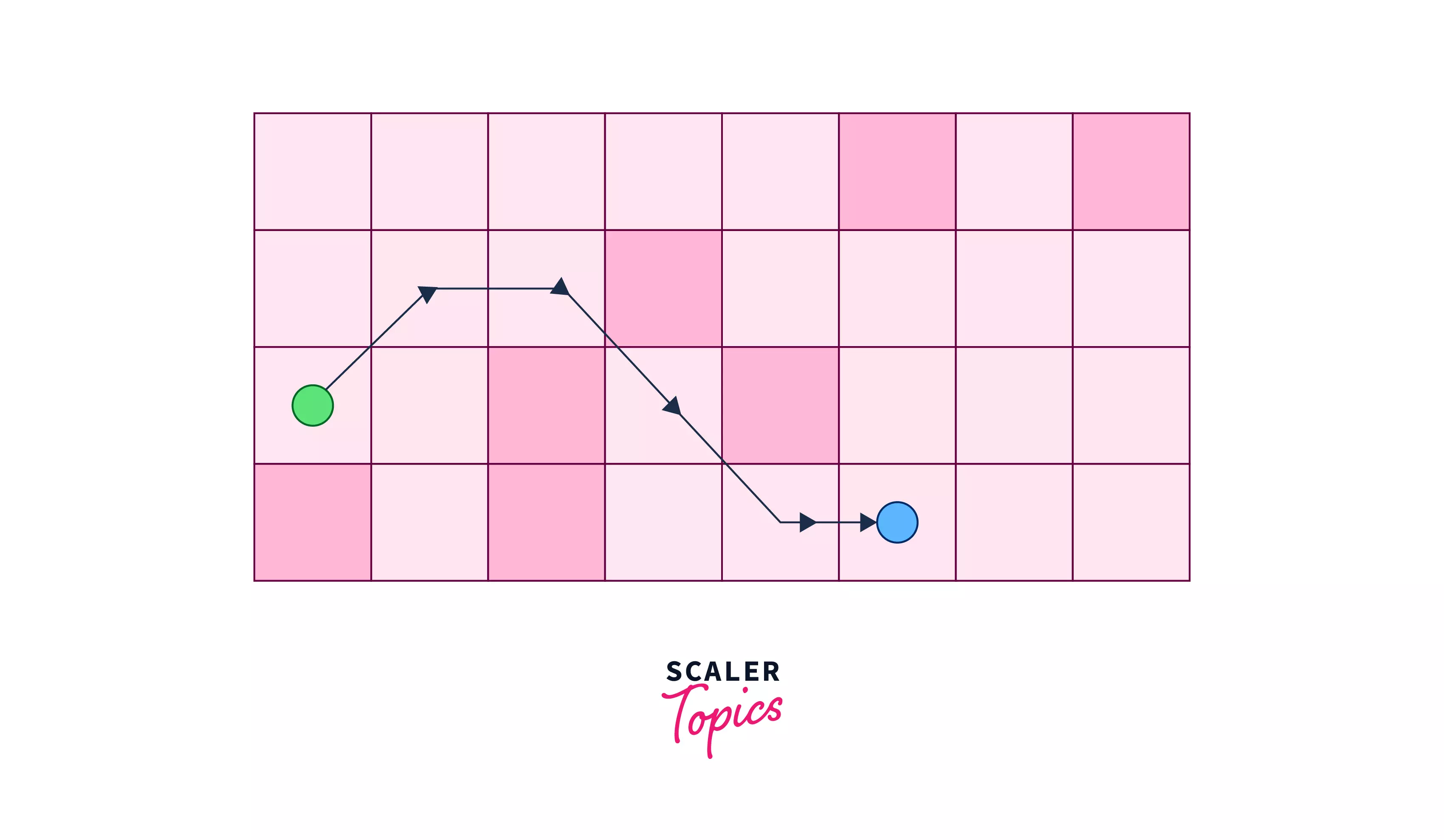
Consider a 2-dimensional board containing a source cell (colored green), a destination cell (colored blue), and some obstacles (colored red).
How Does the A* Algorithm Work?
Before continuing with the actual working of the A* algorithm let’s have a look at some key terms:
- g – It is the cost incurred in moving from the initial cell (src) to the current cell.
- h – It is known as the heuristic value, it is the estimated cost of reaching the final cell (dest cell) from the current cell.
- f – It is the sum of the values of gg and hh. Hence,f=g+h
To make the decision (where to go in the next step), the algorithm takes the f′s value into account. Greedily, it selects the minimum possible ff value to process the current cell.
Example of A* Algorithm
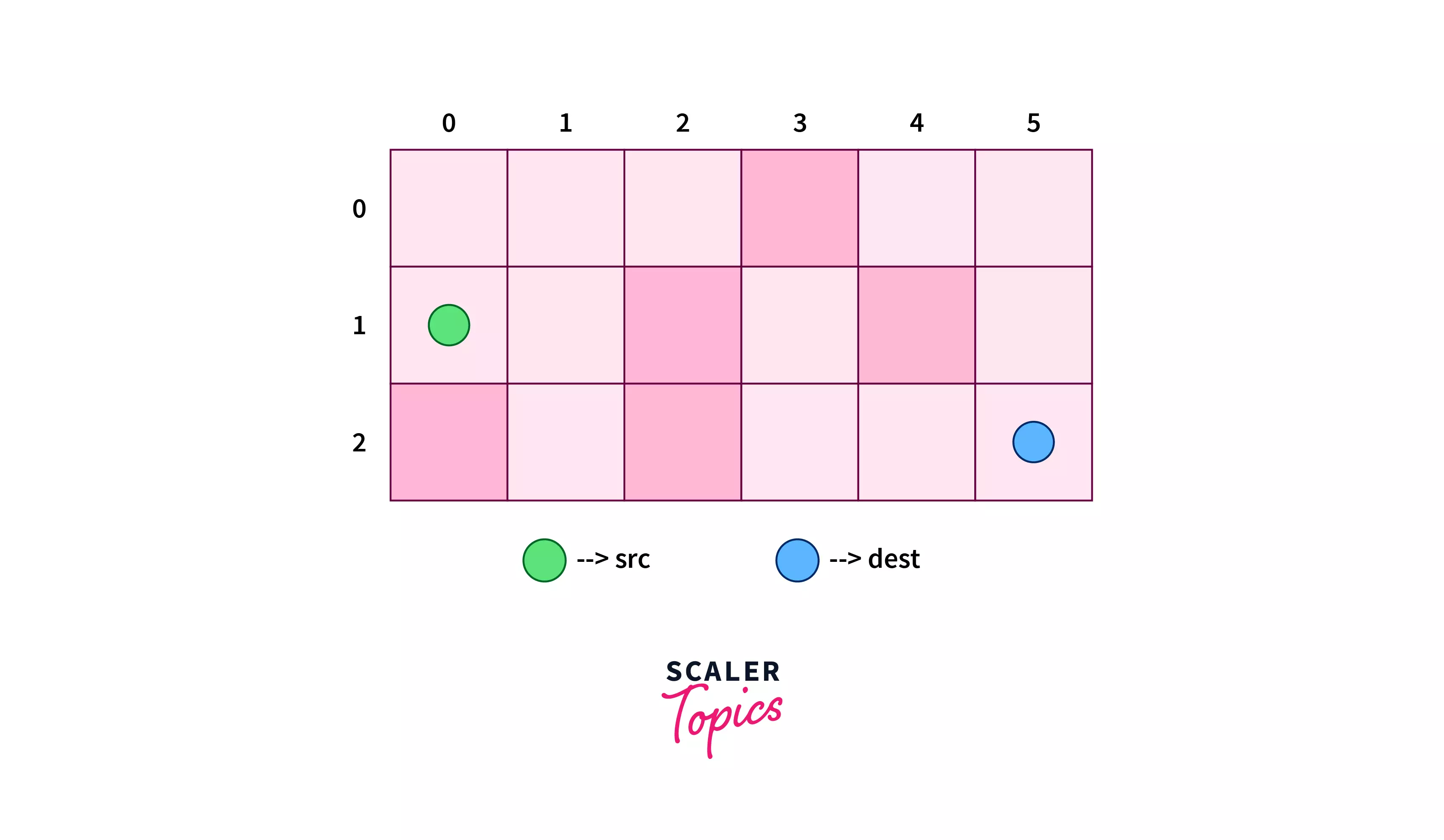
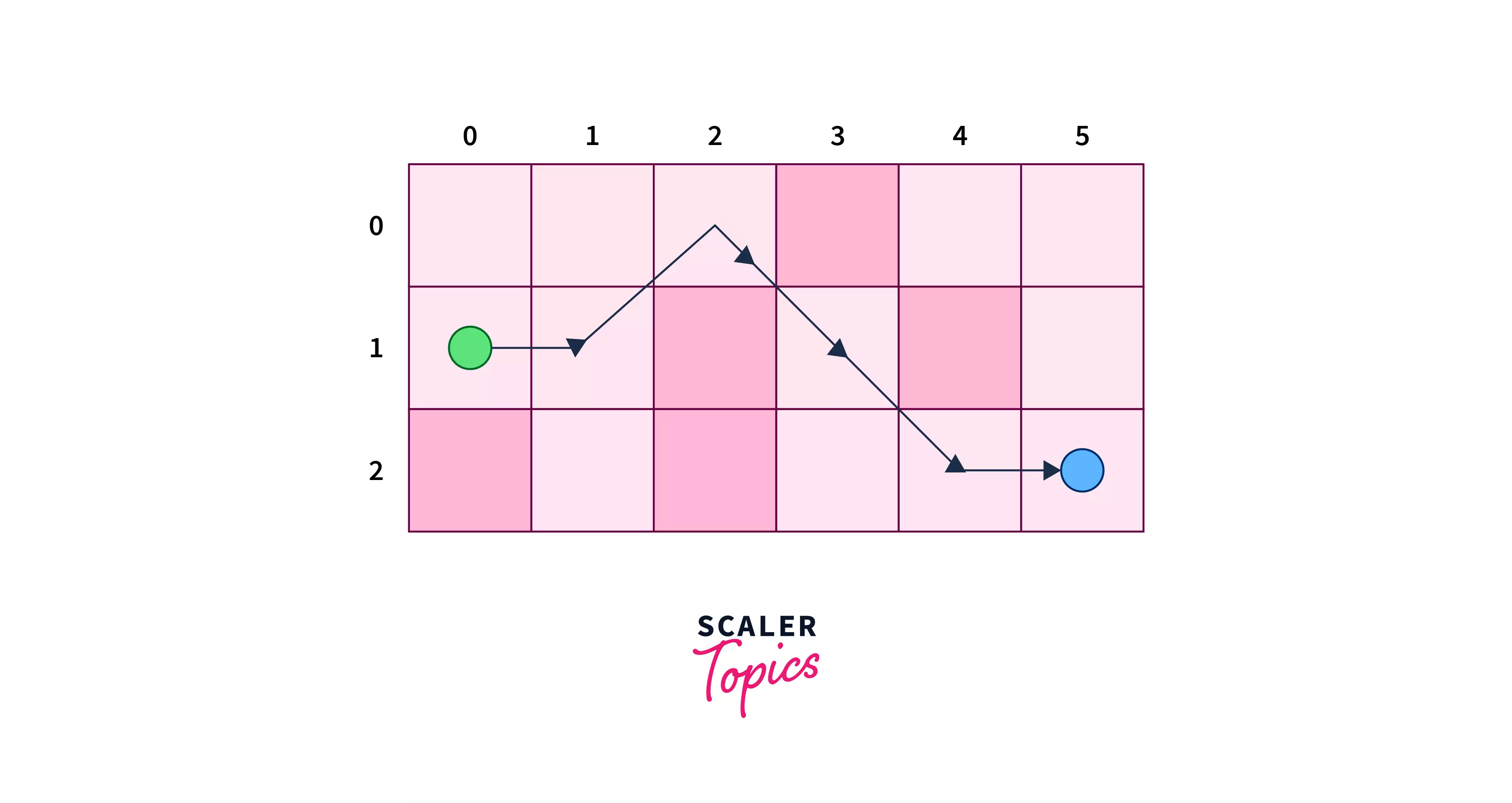
Let’s assume we have the following board for the example with the green-colored cell as the source node and the blue-colored cell as the destination node, given that it is prohibited to pass any red-filled cell.
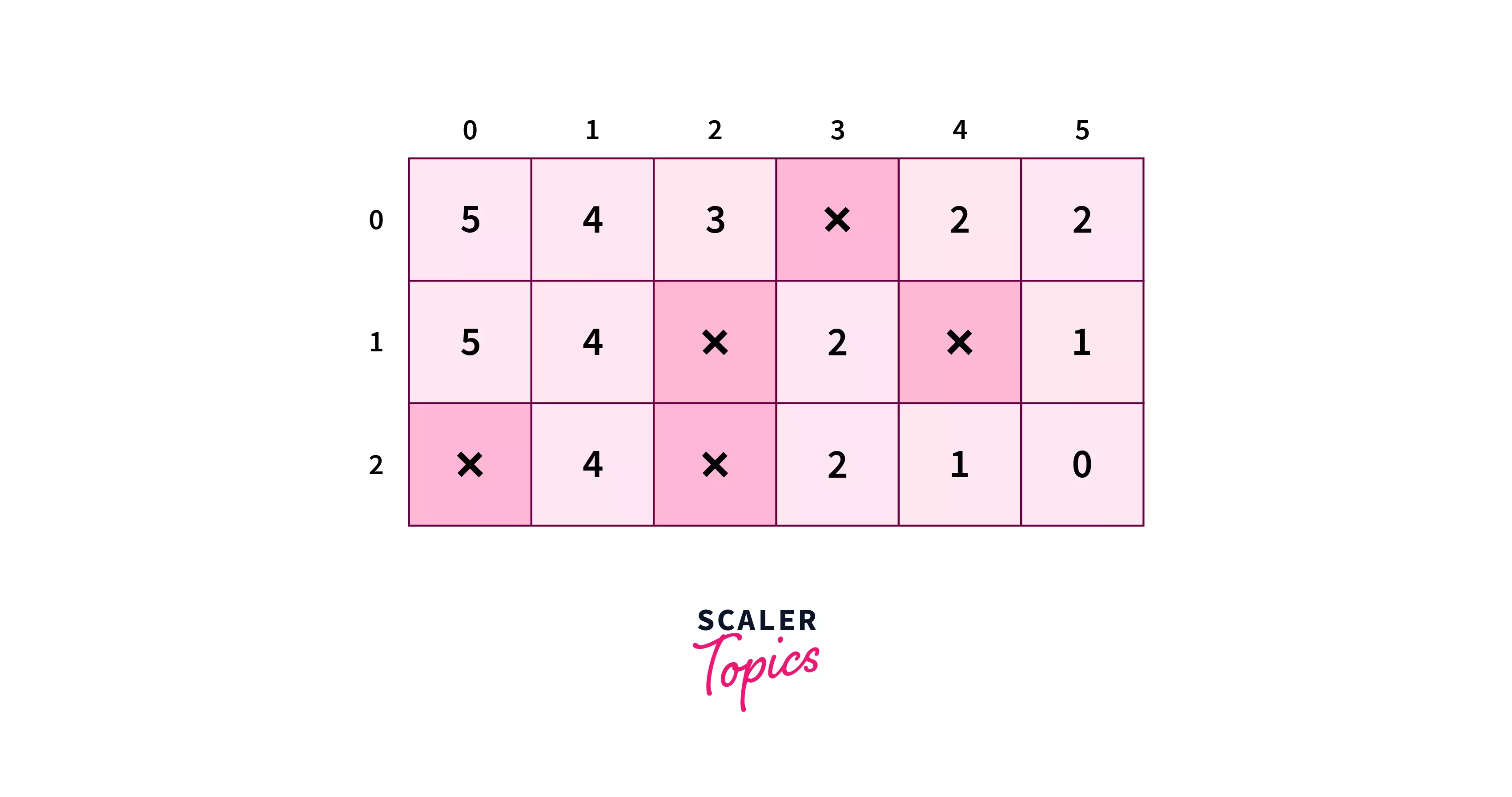
The heuristic values when calculated will be like –
h=Δx+Δy−min(Δx,Δy)
So steps involved in finding the path with minimum cost from the source node to the destination node will be –
- Step 1 – From the cell (0,0)(0,0) we search for the cell with the least heuristic value. We have three choices i.e.i.e. (0,1),(0,1), (1,1),(1,1), and (2,1)(2,1) with heuristic values as 44. We can pick any one of them, let’s say we picked (1,1)(1,1). Since we are moving at each step, therefore we will increase the value of gg after each step.
- Step 2 – From cell (1,1)(1,1), we jump to (0,2)(0,2).
- Step 3 – Again at this cell, we have only one choice i.e.i.e. to go to cell (1,3)(1,3).
- Step 4 – From cell (1,3)(1,3), we jump to (2,4)(2,4).
- Step 5 – Finally we reach at the cell (2,5)(2,5).
Implementation
Steps to implement the code –
- Initialize two lists of Node type (say openList and closedList)
- Add src node in openList.
- Till openList is not empty do the following
- Find the node in the openList with the least f value (say x)
- Remove x from openList
- Find and add all the 8 successors of x and add them to openList.
- For each of the successors (say y) do the following –
- If y is the destination then stop the search.
- Otherwise, calculate g and h for y. y.g = x.g + distance between y and x (it is 1 in our case) y.h = distance between destination and y (Here we will be using Euclidean distance for the same). y.f = y.g + y.h
- If a node with the same position as y and lower f is present in openList then skip this successor.
- Else If a node with the same position as y exists in closedList with smaller f than y.f skip this successor.i6
- Otherwise, add the node (y) to the openList.
- Push x is the closedList.
Implementing A* Algorithm in Java
import java.util.*;
public class Main{
// A Node class for A* Pathfinding
static class Node{
Node parent;
int position[];
int f,g,h;
// Constructor for Node class.
Node(Node parent, int position[]){
this.parent=parent;
this.position=position;
this.f=this.g=this.h=0;
}
// Comparator for Node class
boolean equals(Node temp){
return this.position[0]==temp.position[0]&&
this.position[1]==temp.position[1];
}
}
// Boolean function to check if
// a move is valid or not.
private static boolean notValid(int nodePosition[],
int n, int m){
return nodePosition[0]>n-1||nodePosition[0]<0 ||
nodePosition[1]>m-1||nodePosition[1]<0;
}
// A* algorithm function
private static List<int[]> A_star(int board[][],
int src[], int dest[]){
/* This function returns a list of
tuples representing the path from the given
src node to the given dest node in the given board */
// Creating the src and dest node
// with the parent as null.
Node srcNode=new Node(null, src);
Node destNode=new Node(null, dest);
// Initializing both openList and
// closedList as empty list.
List<Node> openList=new ArrayList<>();
List<Node> closedList=new ArrayList<>();
// Append srcNode in openList.
openList.add(srcNode);
// Iterate until we reach the
// dest Node.
while(openList.size()>0){
// Get the current node
Node currentNode=openList.get(0);
int currentIndex=0;
// Iterate over the openList to find
// node with least 'f'.
for(int i=0;i<openList.size();i++)
if(openList.get(i).f<currentNode.f){
currentNode=openList.get(i);
currentIndex=i;
}
// Pop the found node off openList,
// and add it to the closedList.
openList.remove(currentIndex);
closedList.add(currentNode);
// If reached the dest.
if(currentNode.equals(destNode)){
// Initializng the 'path' list.
List<int[]> path=new ArrayList<>();
Node current=currentNode;
// Adding current position in path
// and the moving to its parent until
// we reach None (parent of src).
while(current!=null){
path.add(current.position);
current=current.parent;
}
// Returning the reversed path (to make
// it src -> dest, instead of dest -> src).
Collections.reverse(path);
return path;
}
// Generate children
List<Node> children=new ArrayList<>();
int dirs[][]=new int[][]{
{0,-1}, {0,1}, {-1,0}, {1,0},
{-1,-1}, {-1,1}, {1,-1}, {1,1}
};
// Iterate over neighouring cells.
for(int newPosition[]:dirs){
// Find the position of new Node.
int nodePosition[]=new int[]{
currentNode.position[0]+newPosition[0],
currentNode.position[1]+newPosition[1]
};
// If the new position is not valid (lies outside board)
// then do not proceed ahead with this node. Also if the
// new position contains obstacle, we can't proceed.
if(notValid(nodePosition, board.length,board[0].length)||
board[nodePosition[0]][nodePosition[1]]!=0){
continue;
}
// Append the node in children list.
children.add(new Node(currentNode, nodePosition));
}
// Iterate over children list.
for(Node child: children){
// If the child is in closedList
for(Node closedChild:closedList)
if(closedChild.equals(child))
continue;
// Assign the values of f, g, and h.
child.g=currentNode.g+1;
child.h=(int)((Math.pow(child.position[0]-
destNode.position[0],2) + (Math.pow(child.position[1]-
destNode.position[1],2))));
child.f=child.g+child.h;
// If the Child is present in OpenList.
for(Node openNode:openList){
if(child.equals(openNode) && child.g>openNode.g)
continue;
}
// Append the child at the last of open list
openList.add(child);
}
if(openList.size()>board.length*board.length*
board[0].length*board[1].length)
break;
}
return new ArrayList<>();
}
public static void main(String args[]){
int board[][]=new int[][]{
{0, 0, 0, 1, 0, 0},
{0, 0, 1, 0, 1, 0},
{1, 0, 1, 0, 0, 0}
};
int src[]=new int[]{1,0};
int dest[]=new int[]{2,5};
List<int[]> pathSrcToDest=A_star(board,src,dest);
for(int i=0;i<pathSrcToDest.size();i++){
System.out.print("("+pathSrcToDest.get(i)[0]+
", "+pathSrcToDest.get(i)[1]+") ");
}
}
}
Output:
(1, 0) (1, 1) (0, 2) (1, 3) (2, 4) (2, 5)
Implementing A* Algorithm in C++
#include<bits/stdc++.h>
using namespace std;
int **board;
// A Node class for A* Pathfinding
class Node{
public:
Node *parent;
vector<int> position;
int f,g,h;
// Constructor for Node class.
Node(Node *Parent, vector<int> Position){
parent=Parent;
position=Position;
f=g=h=0;
}
// Comparator for Node class
bool equals(Node *temp){
return position[0]==temp->position[0]&&
position[1]==temp->position[1];
}
};
// Boolean function to check if
// a move is valid or not.
bool notValid(vector<int> nodePosition,
int n, int m){
return nodePosition[0]>n-1||nodePosition[0]<0 ||
nodePosition[1]>m-1||nodePosition[1]<0;
}
// A* algorithm function
vector<vector<int>> A_star(vector<vector<int>> board,
vector<int> src, vector<int> dest){
/* This function returns a list of
tuples representing the path from the given
src node to the given dest node in the given board */
// Creating the src and dest node
// with the parent as null.
Node *srcNode=new Node(nullptr, src);
Node *destNode=new Node(nullptr, dest);
// Initializing both openList and
// closedList as empty list.
vector<Node*> openList;
vector<Node*> closedList;
// Append srcNode in openList.
openList.push_back(srcNode);
// Iterate until we reach the
// dest Node.
while(openList.size()>0){
// Get the current node
Node *currentNode=openList[0];
int currentIndex=0;
// Iterate over the openList to find
// node with least 'f'.
for(int i=0;i<openList.size();i++)
if(openList[i]->f<currentNode->f){
currentNode=openList[i];
currentIndex=i;
}
// Pop the found node off openList,
// and add it to the closedList.
openList.erase(openList.begin() + currentIndex);
closedList.push_back(currentNode);
// If reached the dest.
if(currentNode->equals(destNode)){
// Initializng the 'path' list.
vector<vector<int>> path;
Node *current=currentNode;
// Adding current position in path
// and the moving to its parent until
// we reach None (parent of src).
while(current!=nullptr){
path.push_back(current->position);
current=current->parent;
}
// Returning the reversed path (to make
// it src -> dest, instead of dest -> src).
reverse(path.begin(), path.end());
return path;
}
// Generate children
vector<Node*> children;
vector<vector<int>> dirs={
{0,-1}, {0,1}, {-1,0}, {1,0},
{-1,-1}, {-1,1}, {1,-1}, {1,1}
};
// Iterate over neighouring cells.
for(vector<int> newPosition: dirs){
// Find the position of new Node.
vector<int> nodePosition={
currentNode->position[0]+newPosition[0],
currentNode->position[1]+newPosition[1]
};
// If the new position is not valid (lies outside board)
// then do not proceed ahead with this node. Also if the
// new position contains obstacle, we can't proceed.
if(notValid(nodePosition, board.size(),board[0].size())||
board[nodePosition[0]][nodePosition[1]]!=0){
continue;
}
// Append the node in children list.
children.push_back(new Node(currentNode, nodePosition));
}
// Iterate over children list.
for(Node *child: children){
// If the child is in closedList
for(Node *closedChild:closedList)
if(closedChild->equals(child))
continue;
// Assign the values of f, g, and h.
child->g=currentNode->g+1;
child->h=(int)((pow(child->position[0]-
destNode->position[0],2) + (pow(child->position[1]-
destNode->position[1],2))));
child->f=child->g+child->h;
// If the Child is present in OpenList.
for(Node *openNode:openList){
if(child->equals(openNode) && child->g>openNode->g)
continue;
}
// Append the child at the last of open list
openList.push_back(child);
}
if(openList.size()>board.size()*board.size()*
board[0].size()*board[1].size())
break;
}
return vector<vector<int>>();
}
int main(){
vector<vector<int>> board={
{0, 0, 0, 1, 0, 0},
{0, 0, 1, 0, 1, 0},
{1, 0, 1, 0, 0, 0}
};
vector<int> src={1,0};
vector<int> dest={2,5};
vector<vector<int>> pathSrcToDest=A_star(board,src,dest);
for(int i=0;i<pathSrcToDest.size();i++){
cout << "(" << pathSrcToDest[i][0] <<
", " << pathSrcToDest[i][1] << ") ";
}
cout<<endl;
return 0;
}
Output:
(1, 0) (1, 1) (0, 2) (1, 3) (2, 4) (2, 5)
Implementing A* Algorithm in Python
class Node():
"""A Node class for A* Pathfinding"""
# Constructor for Node class.
def __init__(self, parent=None, position=None):
self.parent = parent
self.position = position
self.g = self.h = self.f = 0
# Comparator for Node class
def __eq__(self, temp):
return self.position == temp.position
# Boolean function to check if
# a move is valid or not.
def notValid(nodePosition,n,m):
return nodePosition[0] > n-1 or nodePosition[0] < 0 \
or nodePosition[1] > m-1 or nodePosition[1] < 0
# A* algorithm function
def A_Star(board, src, dest):
"""This function returns a list of
tuples representing the path from the given
src node to the given dest node in the given board"""
# Creating the src and dest node
# with parent as None.
srcNode = Node(None, src)
destNode = Node(None, dest)
# Initializing both openList and
# closedList as empty list.
openList = []
closedList = []
# Append srcNode in openList.
openList.append(srcNode)
# Iterate until we reach the
# dest Node.
while len(openList) > 0:
# Get the current node
currentNode = openList[0]
currentIndex = 0
# Iterate over the openList to find
# node with least 'f'.
for index, item in enumerate(openList):
if item.f < currentNode.f:
currentNode = item
currentIndex = index
# Pop the found node off openList,
# and add it to the closedList.
openList.pop(currentIndex)
closedList.append(currentNode)
# If reached the dest.
if currentNode == destNode:
# Initializng the 'path' list.
path = []
current = currentNode
# Adding currentposition in path
# and the moving to its parent until
# we reach None (parent of src).
while current is not None:
path.append(current.position)
current = current.parent
# Returning the reversed path (to make
# it src -> dest, instead of dest -> src.
return path[::-1]
# Generate children
children = []
dirs=((0, -1), (0, 1), (-1, 0), (1, 0),
(-1, -1), (-1, 1), (1, -1), (1, 1))
# Iterate over neighouring cells.
for newPosition in dirs:
# Find the position of new Node.
nodePosition = (currentNode.position[0] + newPosition[0],
currentNode.position[1] + newPosition[1])
# If the new position is not valid (lies outside the board)
# then do not proceed ahead with this node.
if(notValid(nodePosition,len(board),
len(board[len(board)-1]))==True):
continue
# Also if the new position contains obstacle,
# we can't go ahead.
if (board[nodePosition[0]][nodePosition[1]] != 0):
continue
# Append the node in children list.
children.append(Node(currentNode, nodePosition))
# Iterate over the children list.
for child in children:
# If the child is in closedList
for closedChild in closedList:
if closedChild == child:
continue
# Assign the values of f, g, and h.
child.g = currentNode.g + 1
child.h = ((child.position[0] - destNode.position[0]) ** 2) \
+ ((child.position[1] - destNode.position[1]) ** 2)
child.f = child.g + child.h
# If the Child is present in OpenList.
for openNode in openList:
if child == openNode and child.g > openNode.g:
continue
# Append the child at the last of open list
openList.append(child)
if (len(openList) > len(board)**2*len(board[0])**2):
return None
def main():
board = [
[0, 0, 0, 1, 0, 0],
[0, 0, 1, 0, 1, 0],
[1, 0, 1, 0, 0, 0]
]
src = (1, 0)
dest = (2, 5)
pathSrcToDest = A_Star(board, src, dest)
print(pathSrcToDest)
if __name__ == '__main__':
main()
Output:
[(1, 0), (1, 1), (0, 2), (1, 3), (2, 4), (2, 5)]
Complexity Analysis
- Time Complexity – The time it takes for the A* search algorithm to find a solution depends on how many options each step has (the branching factor) and how deep the solution is. We express this time complexity as O(bd), where b is the branching factor and d is the depth of the solution.
- Space Complexity – In the worst scenario, we may have all the vertices (nodes) in openList which will make the worst case space complexity be O(bd).
Conclusion
- Best First Search (BFS) efficiently navigates search spaces using heuristic evaluation.
- Greedy Best First Search prioritizes paths based solely on heuristic estimates, sacrificing optimality for speed.
- A Algorithm* combines actual and estimated costs, ensuring optimality in pathfinding tasks.
- Greedy BFS is simpler and faster but may not always find the optimal solution.
- A* guarantees optimality by considering both current and estimated costs.
- The choice between Greedy BFS and A* depends on the balance between solution quality and computational efficiency.