Problem Statement
We need to print the bottom view of binary tree, i.e., all the bottommost nodes from left to right in a binary tree.
The 3D projection of a binary tree will have different views from different angles. In our case, we’ll print the bottom view of the binary tree.
It’s better to visualize them with horizontal distance (like an x-axis). The root node will be located at the horizontal distance or hd 0. The left child will have hd-1 of its parent and the child will have hd+1 of its parent. The bottommost nodes at each horizontal distance will be present in our output.
Note: Let’s also assume that each child node makes a 45-degree angle with its parent node.
Let’s look at this simple example of what the bottom view really looks like.
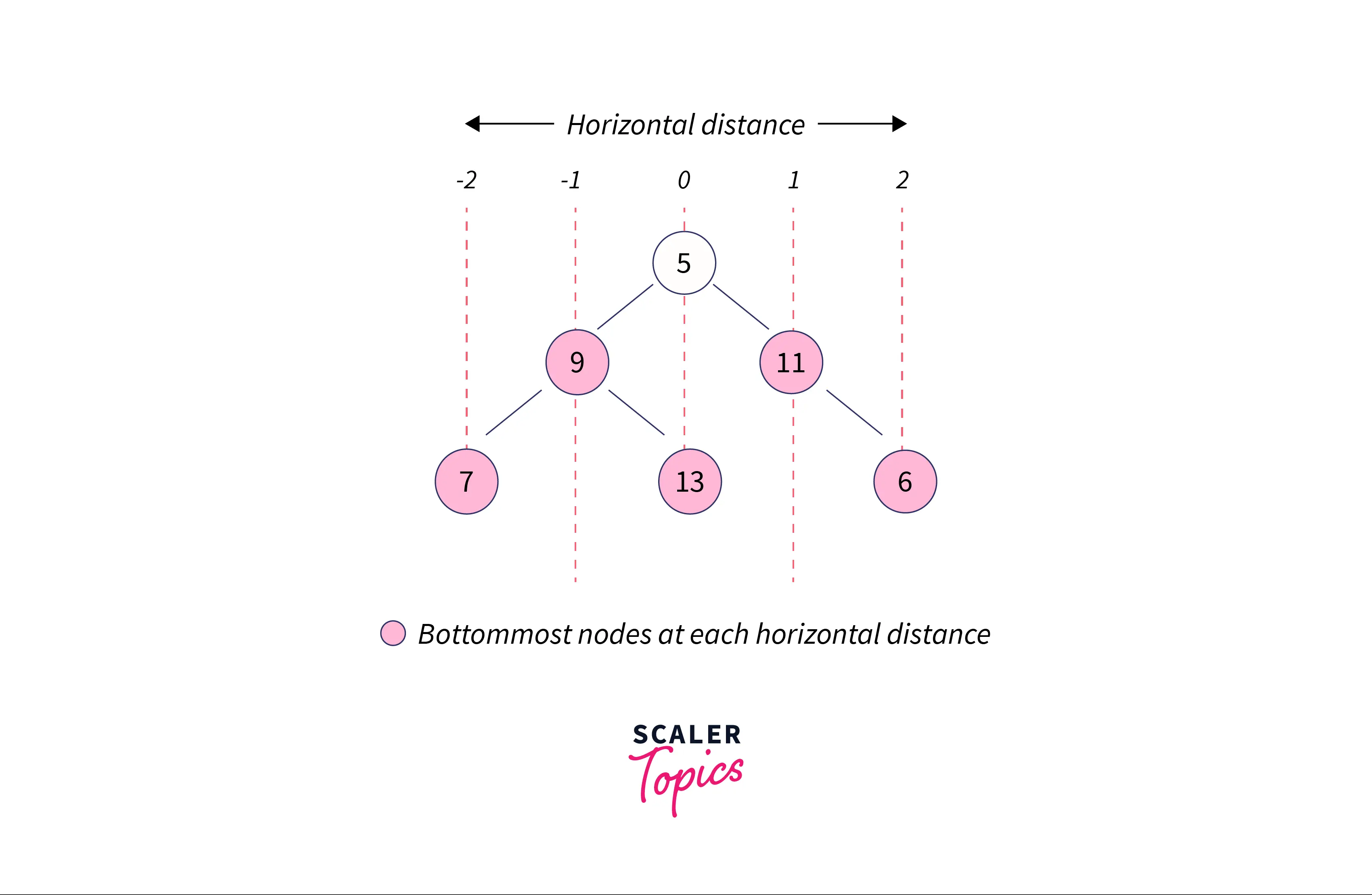
The bottom view of this binary tree will be 7 9 13 11 6.
Example
Note: To avoid confusion, level and height are the same thing in our topic of discussion.
Now, we’ll again assume the same above example because we haven’t discussed the height which will be used in our algorithm.
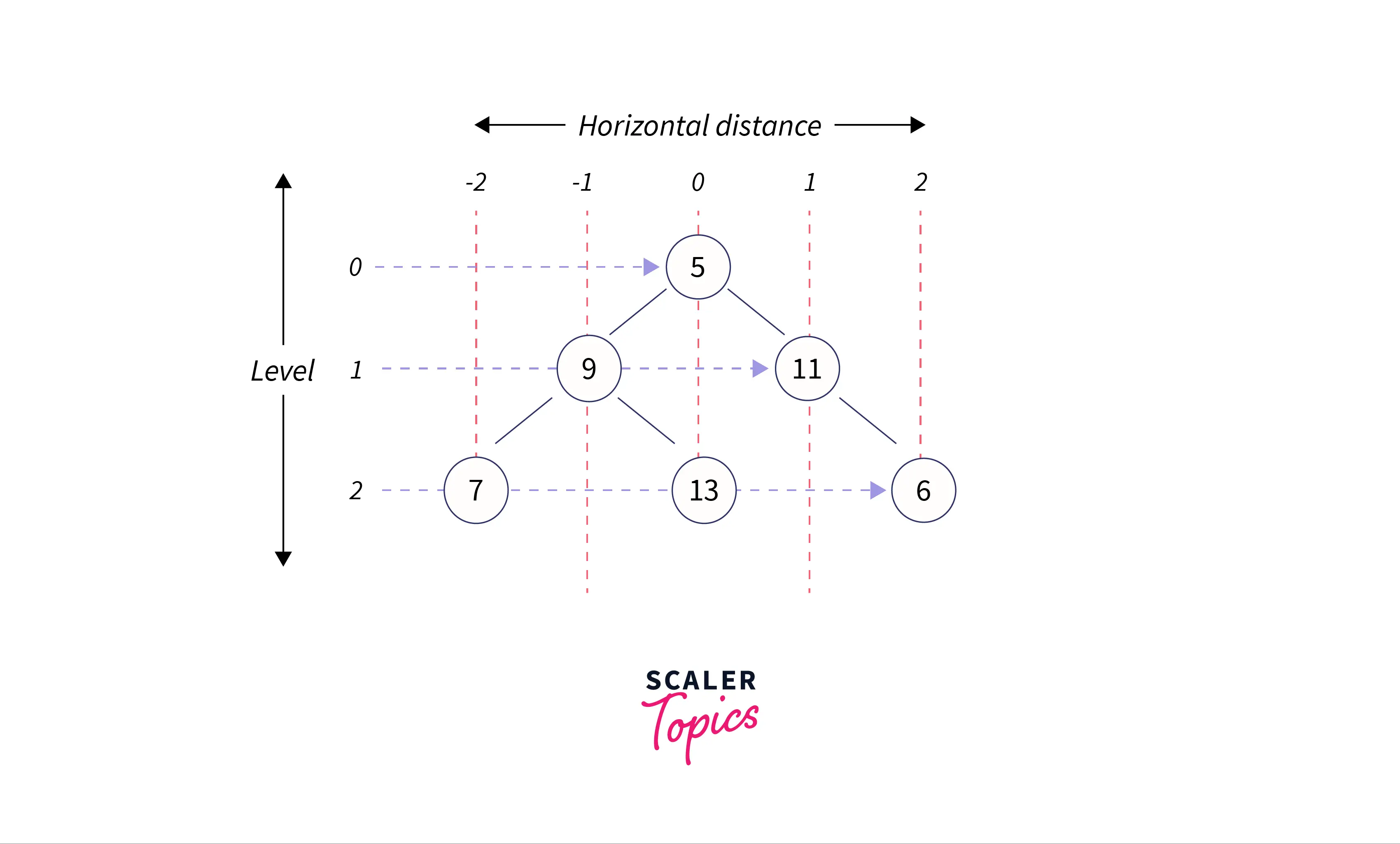
In this case, we’ll get the output as 7 9 13 11 6.
But how about a different scenario. What if there are two child nodes at the same level and horizontal distance?
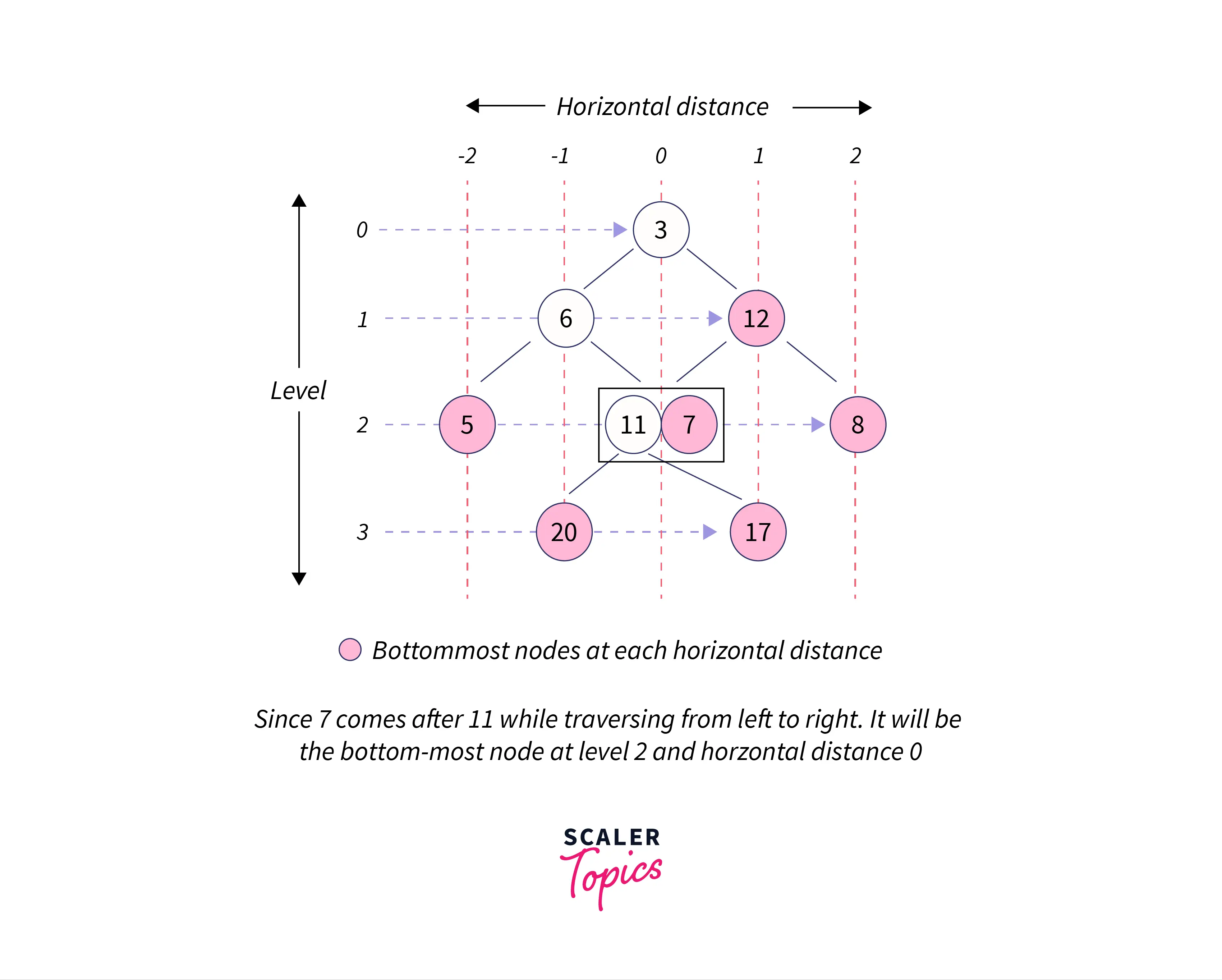
Example Explanation
Just like the x-axis, the root node is present at the origin (with horizontal distance, say hd, being 0) and at height 0. The immediate child nodes of the root node will be at height 1 with the left child node having a horizontal distance of hd-1 and the right child node having a horizontal distance of hd+1.
And if there are two nodes present at the same height as well as horizontal distance, the bottom-most node will be the one that comes later while traversing from left to right.
Constraints
Although we are not making any assumptions for the input nodes because they are hard-coded, let us assume that:
-10^9 <= node's value <= 10^9
Approach 1 – HashMap & Recursion
We discussed how horizontal distance as well as levels in the above example. What if we start traversing the parent nopde and then its left and right child nodes one by one. As we go down at each of the horizontal distance axis vertically, we’ll keep on updating our bottommost nodes. In this case, we’ll start with the parent node (which has horizontal distance, hd, 0) and then traverse through its left and right child nodes. Since we want only the bottom-most nodes at each horizontal distance, we’ll traverse through every node until we reach the maximum height where we’ll have all the bottommost nodes of the tree.
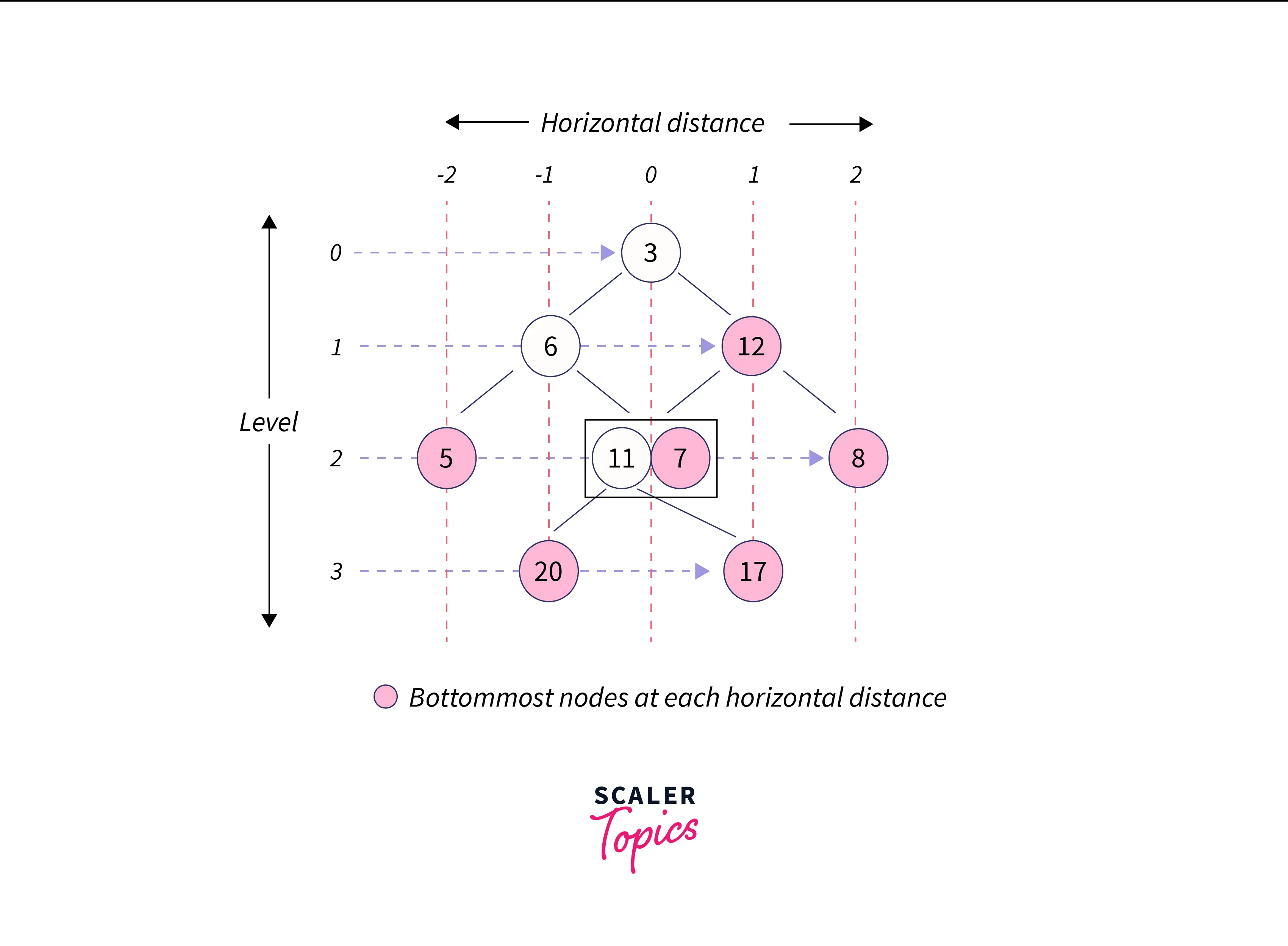
Technically, we’ll need a TreeMap that stores and sorts the entries based on their keys.
At height 0 and hd 0, we’ll store the parent node in the map with its hd being the key and an array as the value that contains both height and data of the node. We’ll traverse through its left and right child nodes and update the TreeMap if there’s already a key present in the map. It recursively goes on until
we traverse each node in the tree.
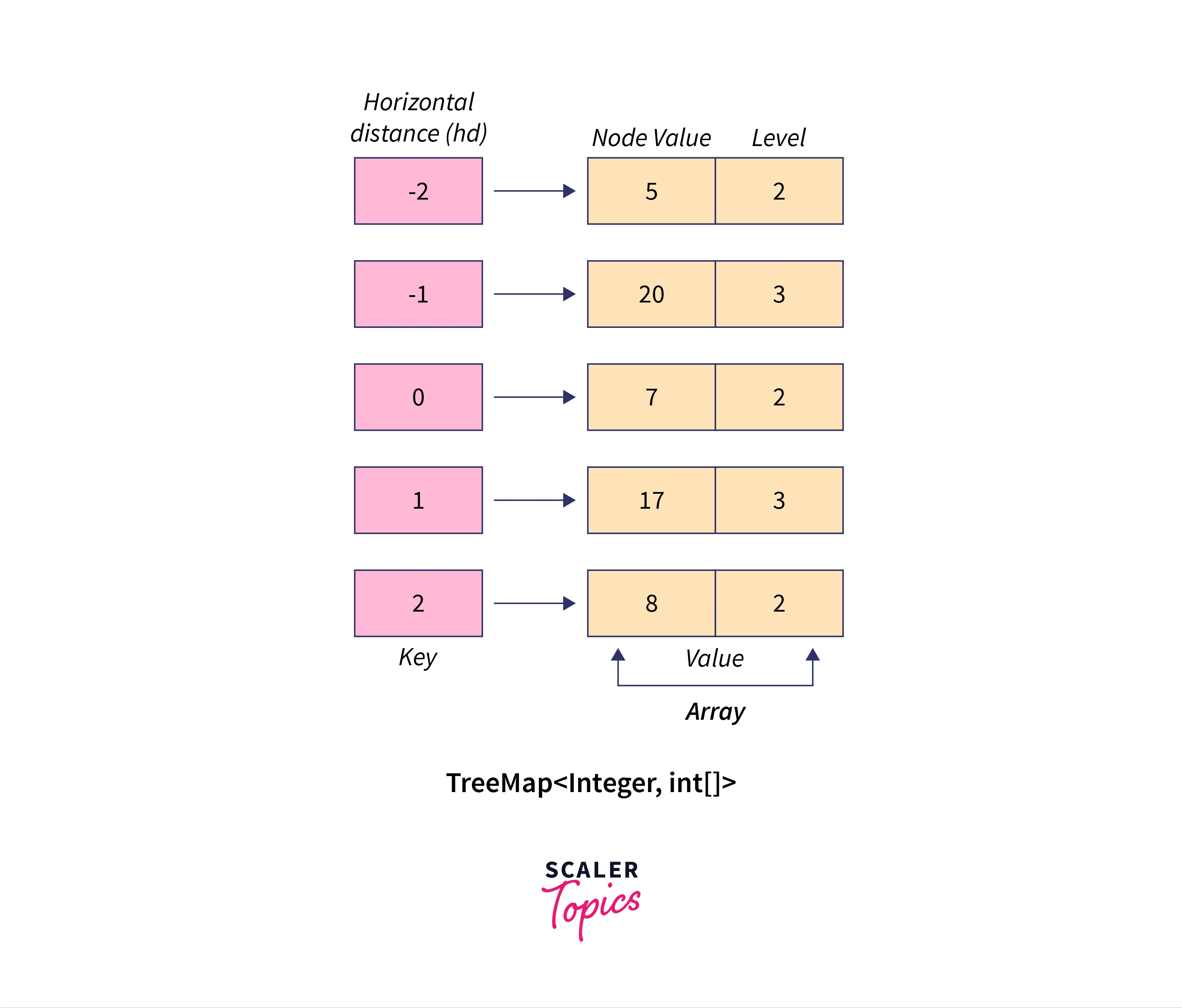
Algorithm
- Create a hashmap/treemap that stores the horizontal distance as the key and an array containing the node’s value and its height as the value of the map.
- We’ll perform the preorder traversal on the binary tree. (We need to traverse the parent node before traversing its left and right child nodes. This can be performed with preorder traversal).
- If we reach a node having the horizontal distance that already exists as key in the map and a height greater than that of the previous node, we need to update this key with the new node and its height.
- Else, we’ll put a new key (horizontal distance) with the current node’s value and its height.
Eventually, we’ll end up getting the bottom-most nodes of the binary tree.
Code Implementation
C++
#include <bits/stdc++.h>
#include <map>
using namespace std;
//Create new nodes with the class Node
struct Node{
/* class Node contains:
->node's value
->horizontal distance (hd)
->left and right child node
*/
int val; //node's value
int hd; //horizontal distance
// Left and right child nodes
Node * left;
Node * right;
//Constructor
Node(int data){
val = data;
hd = INT_MAX;//hd will be updated later
left = NULL;
right = NULL;
}
};
void bottomViewHelper(Node * node, int height, int hd, map <int, pair <int, int>> & map){
//A base case that returns when there's no node
if (node == NULL)
return;
//If any node for the current horizontal distance already exists, and
// the current node's height is greater than that of previous one
//we'll update it with the current node's value and height
if (map.find(hd) == map.end()){
map[hd] = make_pair(node -> val, height);
}
else{
//when the horizontal distance is not present in the map,
//we'll simply add the current one
pair < int, int > p = map[hd];
//if height is greater
if (p.second <= height){
map[hd].first = node -> val; //putting new node's value
map[hd].second = height; //updating height
}
}
//Recursively call left child node
bottomViewHelper(node -> left, height + 1, hd - 1, map);
//Recursively call right child node
bottomViewHelper(node -> right, height + 1, hd + 1, map);
}
void bottomView(Node * root){
//Key -> horizontal distance,
//value -> {node's value, height}
map < int, pair < int, int > > m;
//Calling helper method
bottomViewHelper(root, 0, 0, m);
//Printing the bottom-most nodes of the binary tree
map < int, pair < int, int > > ::iterator iter;
for (iter = m.begin(); iter != m.end(); ++iter){
pair < int, int > p = iter -> second;
cout << p.first << " ";
}
}
int main(){
//Create a binary tree
Node * root = new Node(3);
root -> left = new Node(6);
root -> right = new Node(12);
root -> left -> left = new Node(5);
root -> left -> right = new Node(11);
root -> right -> left = new Node(7);
root -> right -> right = new Node(8);
root -> left -> right -> left = new Node(20);
root -> left -> right -> right = new Node(17);
cout << "The bottom view of the binary tree is: ";
bottomView(root);
return 0;
}
Java
import java.util.*;
class Main{
//Create new nodes with the class Node
static class Node
{
/* class Node contains:
->node's value
->horizontal distance (hd)
->left and right child node
*/
int val; //node's value
int hd; //horizontal distance
// Left and right child nodes
Node left;
Node right;
//Constructor
public Node(int val)
{
this.val = val;
this.hd = Integer.MAX_VALUE; //hd will be updated later
this.left = null;
this.right = null;
}
}
static void bottomViewHelper(Node node, int height, int hd, TreeMap<Integer, int[]> map)
{
//A base case that returns when there's no node
if(node == null) return;
//If any node for the current horizontal distance already exists, and
// the current node's height is greater than that of previous one
//we'll update it with the current node's value and height
if(map.containsKey(hd) == true)
{
int[] existing = map.get(hd);
//if height is greater
if(existing[1] <= height)
{
existing[0] = node.val; //putting new node's value
existing[1] = height; //updating height
}
map.put(hd, existing); //update and add to the map
}else
{
//when the horizontal distance is not present in the map,
//we'll simply add the current one
map.put(hd, new int[]{node.val, height}); //add to the map
}
//Recursively call left child node
bottomViewHelper(node.left, height+1, hd-1, map);
//Recursively call right child node
bottomViewHelper(node.right, height+1, hd+1, map);
}
static void bottomView(Node root)
{
//TreeMap
//Key -> horizontal distance,
//value -> {node's value, height}
TreeMap<Integer, int[]> map = new TreeMap<>();
//Calling helper method
bottomViewHelper(root, 0, 0, map);
//Printing the bottom-most nodes of the binary tree
for(int arrays[]: map.values())
{
System.out.print(arrays[0] + " ");
}
}
public static void main(String[] args)
{
//Create a binary tree
Node root = new Node(3);
root.left = new Node(6);
root.right = new Node(12);
root.left.left = new Node(5);
root.left.right = new Node(11);
root.right.left = new Node(7);
root.right.right = new Node(8);
root.left.right.left = new Node(20);
root.left.right.right = new Node(17);
System.out.print("The bottom view of the binary tree is: ");
bottomView(root);
}
}
Python
# View of Binary Tree
class Node:
#class Node contains:
#->node's value
#->horizontal distance (hd)
#->left and right child node
def __init__(self, val = None,
left = None,
right = None):
self.data = val #node's value
# Left and right child nodes
self.left = left
self.right = right
def bottomViewHelper(node, d, hd, height):
# A base case that returns when there's no node
if node is None:
return
# if horizontal distance is already present in the dictionary, then it should be updated with new node data & height
if hd in d:
if height >= d[hd][1]:
d[hd] = [node.data, height]
else: # else the new horizontal distance will be inserted in the dictionary with new node data & height
d[hd] = [node.data, height]
bottomViewHelper(node.left, d, hd - 1, height + 1)
bottomViewHelper(node.right, d, hd + 1, height + 1)
def bottomView(root):
# Creating a dictionary
# key -> horizontal distance
# value -> pair of node's value and height
d = dict()
bottomViewHelper(root, d, 0, 0)
for i in sorted(d.keys()):
print(d[i][0], end = " ")
if __name__ == '__main__':
# Create a binary tree
root = Node(3);
root.left = Node(6);
root.right = Node(12);
root.left.left = Node(5);
root.left.right = Node(11);
root.right.left = Node(7);
root.right.right = Node(8);
root.left.right.left = Node(20);
root.left.right.right = Node(17);
print("The bottom view of the binary tree is: ", end=" ")
bottomView(root)
Output
The bottom view of the binary tree is: 5 20 7 17 8
Time Complexity
Since we are visiting each node in the tree once, the time complexity will be: O(N * logN), where N is the number of nodes of the binary tree
Space Complexity
We have used a map in our code to store all the nodes of the tree. If there are N nodes in a tree, the space complexity will be: O(N), where N is the number of nodes
Approach 2 – Queue
Note: We’re calling the horizontal distance as hd in this approach too.
We already know that the sole purpose of a queue is to have First-in-First-out (FIFO) sequence. So, we can insert the parent node first in the queue along with the horizontal distance (hd=0). Following it will be the insertion of its left and right child node with their horizontal distances, hd-1, and hd+1 respectively. If you look clearly, this is exacly like Breadth First Search (BFS) where each node is visited and then all its adjacent nodes will be added to the queue.
We need to maintain a TreeMap to contain the key-value pairs in the sorted order of keys.
Now, whether we just need to put the horizontal distance as the key and node’s value(or data) as the value here. If it’s a new horizontal distance, it will be simply inserted. Or if this horizontal distance already exists as a key, it will be updated with its value. This would go on until each of the keys has got the values of the bottom-most nodes.
Algorithm
- Create a class for the node of the Tree and a class Pair that comprises a node and its level.
- We’ll begin with the parent node with a horizontal distance which will be inserted into a queue.
- We need to perform the level order traversal (also known as Breadth First Search).
- A TreeMap will be used to sort the entries according to their keys. The horizontal distance will be the key whereas the node’s value will be the value of the keys in the map.
- Once we get a new horizontal distance, we’ll insert it into the queue. Each of these nodes will have a node’s value and horizontal distance (hd).
- If the horizontal distance already exists in the map, then it will be updated with the new node’s value whose height is greater than that of its previous one.
Code Implementation
C++
#include<bits/stdc++.h>
using namespace std;
//Create new nodes with the class Node
struct Node{
/* class Node contains:
->node's value
->horizontal distance (hd)
->left and right child node
*/
int val; //node's value
int hd; //horizontal distance
// Left and right child nodes
Node *left;
Node *right;
// Constructor
Node(int data){
val = data;
hd = INT_MAX;
left = NULL;
right = NULL;
}
};
void bottomView(Node *root){
if (root == NULL)
return;
int hd = 0; //horizontal distance (initialized to 0)
map<int, int> mp;
///Creating queue of the type Node
queue<Node *> q;
root->hd = hd;
q.push(root); //adding root to the queue
while (!q.empty()){
Node *temp = q.front();
q.pop(); //remove element from the queue
hd = temp->hd;
//Inserts a new key or updates the existing key with the new value
mp[hd] = temp->val;
if (temp->left != NULL){
temp->left->hd = hd-1;
q.push(temp->left);
}
if (temp->right != NULL){
temp->right->hd = hd+1;
q.push(temp->right);
}
}
//Using iterator to iterate through the values of the treemap
for (auto i = mp.begin(); i != mp.end(); ++i)
cout << i->second << " ";
}
int main(){
//Create a binary tree
Node * root = new Node(3);
root -> left = new Node(6);
root -> right = new Node(12);
root -> left -> left = new Node(5);
root -> left -> right = new Node(11);
root -> right -> left = new Node(7);
root -> right -> right = new Node(8);
root -> left -> right -> left = new Node(20);
root -> left -> right -> right = new Node(17);
cout << "The bottom view of the binary tree is: ";
bottomView(root);
return 0;
}
Java
import java.util.*;
//Create new nodes with the class Node
class Node{
/* class Node contains:
->node's value
->left and right child node
*/
int val; //node's value
// Left and right child nodes
Node left;
Node right;
//Constructor
public Node(int data){
val = data;
left = null;
right = null;
}
}
public class Main{
//Creating a pair class for node, and
//horizontal distance (initialized to 0)
static class Pair{
Node node;
int hd = 0;
}
public static void bottomView(Node root){
//Creating queue of the type Pair
Queue<Pair> queue = new LinkedList<>();
Pair p = new Pair();
p.node = root;
p.hd = 0;
queue.add(p);
Map<Integer, Integer> map = new TreeMap<>();
while(queue.size() > 0){
Pair temp = queue.remove();
//Inserts a new key or updates the existing key with the new value
map.put(temp.hd, temp.node.val);
if(temp.node.left != null){
Pair lp = new Pair(); //lp-> left pair
lp.node = temp.node.left;
lp.hd = temp.hd - 1;
queue.add(lp);
}
if(temp.node.right != null){
Pair rp = new Pair(); //rp -> right pair
rp.node = temp.node.right;
rp.hd = temp.hd + 1;
queue.add(rp);
}
}
//Using iterator to iterate the values of the treemap
Iterator<Integer> itr = map.values().iterator();
while(itr.hasNext())
System.out.print(itr.next() + " ");
}
public static void main(String[] args){
//Create a binary tree
Node root = new Node(3);
root.left = new Node(6);
root.right = new Node(12);
root.left.left = new Node(5);
root.left.right = new Node(11);
root.right.left = new Node(7);
root.right.right = new Node(8);
root.left.right.left = new Node(20);
root.left.right.right = new Node(17);
System.out.print("The bottom view of the binary tree is: ");
bottomView(root);
}
}
Python
#Using deque to push and pop the elements
from collections import deque
#Create new nodes with the class Node
class Node:
def __init__(self, data):
# class Node contains:
# ->node's value
# ->horizontal distance (hd)
# ->left and right child node
self.val = data # node's value
self.hd = float('inf') # horizontal distance
# Left and right child nodes
self.left = None
self.right = None
# Bottom View method
def bottomView(root):
# A base case that returns when there's no node
if root is None:
return
hd = 0 # horizontal distance (initialized to 0)
# Store start and end for the range of all horizontal distances
# This doesn't require sorting
start, end = 0, 0
hd_dict = dict()
# Creating queue to store nodes
q = deque()
# Add root node with the horizontal distance (hd=0) to the queue
root.hd = hd
q.append(root)
while q:
temp = q.popleft()
# Extract the horizontal distance value
# from the dequeued tree node.
hd = temp.hd
# Updating the start and end for the range horizontal distance
start = min(start, hd)
end = max(end, hd)
# Inserts a new node or updates the existing node in the dictionary
hd_dict[hd] = temp.val
if temp.left:
temp.left.hd = hd - 1
q.append(temp.left)
if temp.right:
temp.right.hd = hd + 1
q.append(temp.right)
# Traverse the map from the start to the end
for i in range(start, end+1):
print(hd_dict[i], end = " ")
if __name__=='__main__':
# Create a binary tree
root = Node(3);
root.left = Node(6);
root.right = Node(12);
root.left.left = Node(5);
root.left.right = Node(11);
root.right.left = Node(7);
root.right.right = Node(8);
root.left.right.left = Node(20);
root.left.right.right = Node(17);
print("The bottom view of the binary tree is: ", end=" ")
bottomView(root)
Output
The bottom view of the binary tree is: 5 20 7 17 8
Time Complexity
Any comparison to insert, remove, and get an element in a TreeMap takes O(logN) time. So, for N nodes in a tree, it will be:
O(N * log N), where N is the number of nodes present in the binary tree
Space Complexity
Since we have used a map in our code, the space complexity will be: O(N), where N is the number of nodes
Conclusion
- The bottom view of a binary tree is the representation of all the bottommost nodes in a binary tree.
- We can simplify our understanding of bottommost nodes with the help of horizontal distances(hd) and the height of the successor in a binary tree.
- The bottom view of a binary tree can be found in two ways:
- HashMap and Recursion
- Queue
FAQs
Q: What is the Bottom View of a Binary Tree?
A: The bottom view of a binary tree refers to all the bottommost nodes of the binary tree. Similarly, there is a top, left, and right view of the binary tree.
Q: How can we Find the Bottom of a Binary Tree?
A: We’ve discussed two ways to find the bottom view of a binary tree:
- HashMap + Recursion, in which the preorder traversal takes place
- Queue, with the level order traversal (preorder traversal)