Problem Statement
We are provided with an input pattern and a text (or string), and we need to search and print all the occurrences of the pattern in the string.
Note: Use Boyer Moore’s algorithm for searching the pattern in the string.
- The first input is the size of the actual string i.e. n.
- The second input is the size of the pattern string i.e. m.
- The third input contains the actual string.
- The fourth input contains the pattern to be searched.
Refer to the Example and Explanation sections for more details and the Approach section to understand the working of the Boyer Moore algorithm.
Example
Let us look at some of the examples provided to search for a pattern searching using the Boyer-Mooreoore algorithm.
Example 1: text = “Scaler Topics” pattern = “Topics”
Output: Pattern found at index: 7.
Example 2: text = “he is doing what he was told to do” pattern = “he”
Output: Pattern found at index: 0. Pattern found at index: 17.
Example Explanation
Before getting into the explanation of how to search or find the occurrences of a specific pattern in a string, let us first get a brief introduction to strings.
A String is an immutable data type that is used to store the sequence of characters. Strings are one of the most widely used data types of any programming language. A string can be easily created using quotes (either single quotes or double quotes).
Now, for searching the pattern in the string, we can use the Boyer Moore pattern searching algorithm (or B-M algorithm). The intuition of the Boyer Moore algorithm is very simple, two pointers are aligned at the 0th index of the text string and the character string. The pattern string is then compared character by character with the current portion of the text string, beginning with the rightmost character.
Now, if a character does not match then the Boyer-Moore algorithm shifts the characters using two strategies simultaneously. So, we can say that the Boyer Moore algorithm is a combination of two approaches namely:
- Bad Character Heuristic, and
- Good Suffix Heuristic.
Refer to the following sections to understand both approaches.
Now, coming back to the example, the provided text is: text = “Scaler Topics” and the pattern to be searched is: pattern = “Topics”. Now, in this example, we would start the searching with the first character i.e. index-0, and the pattern is found from index-7 to index-12, but we need to print the index where the pattern occurrence starts. So, we would print index-77. Similarly in the second example: text = “he is doing what he was told to do.” pattern = “he” The first occurrence of he is found on index-0 and then again on index-17. So, we printed both indices.
Constraints
−1≤∣s∣≤105−1≤∣s∣≤105
Here, s denotes the pattern string and text string.
In some problems, you may find the number of test cases represented by t So, we only need to call the BoyerMooreAlgorithm function `to-times.
The problem is to search a pattern searching using the Boyer-Moore algorithm.
Approach 1: Bad Character Heuristic
As we have discussed earlier that the Boyer Moore algorithm matches the pattern string with the provided text. Now, if a match is found then it returns the pattern’s starting index. Otherwise, there may arise two cases:
1. When the Mismatched Character of Input Text is Present in the Pattern
In such cases, we call that character a bad character. So, when a bad character is found, we will shift the pattern until it gets aligned with the mismatched character of the text.
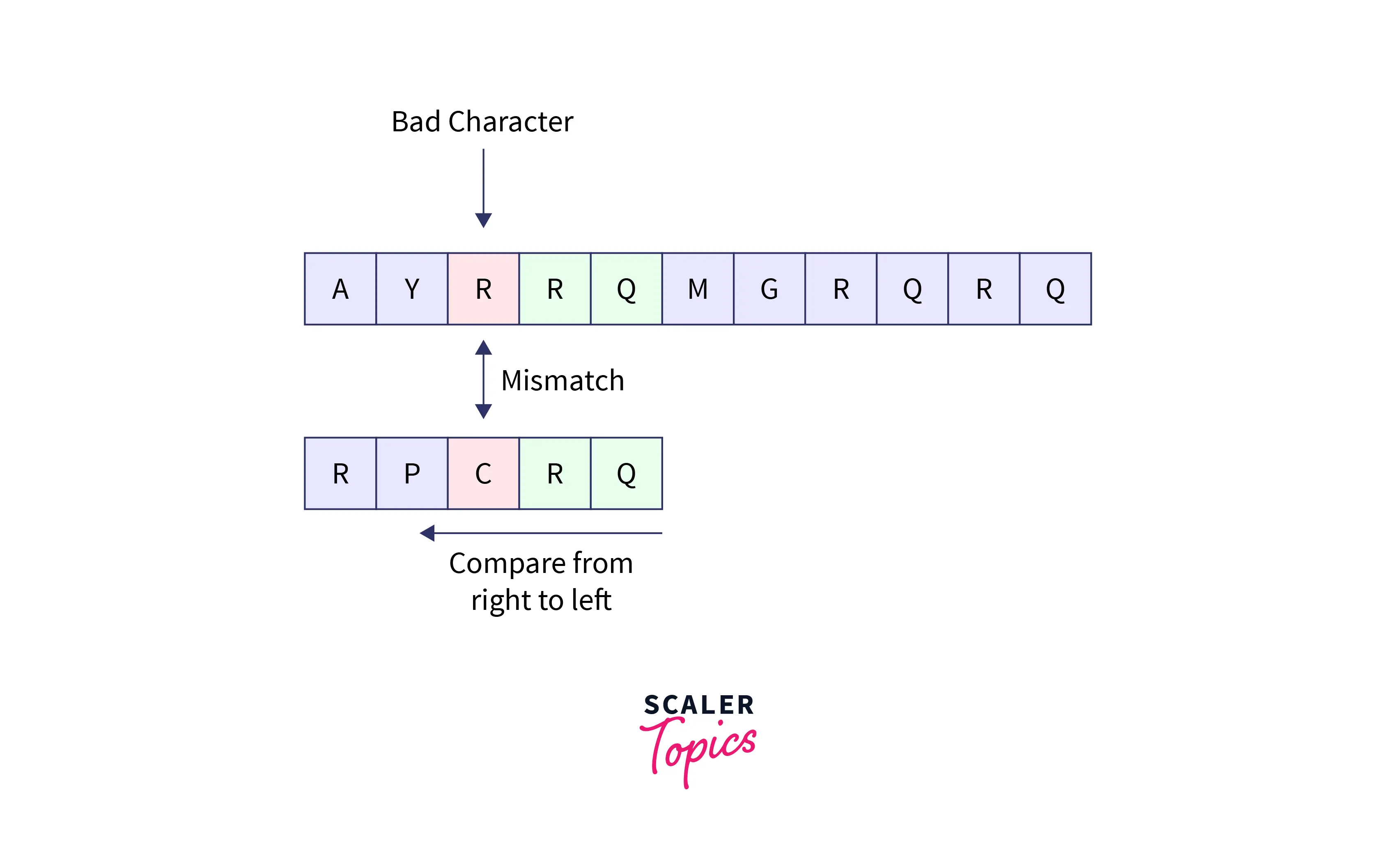
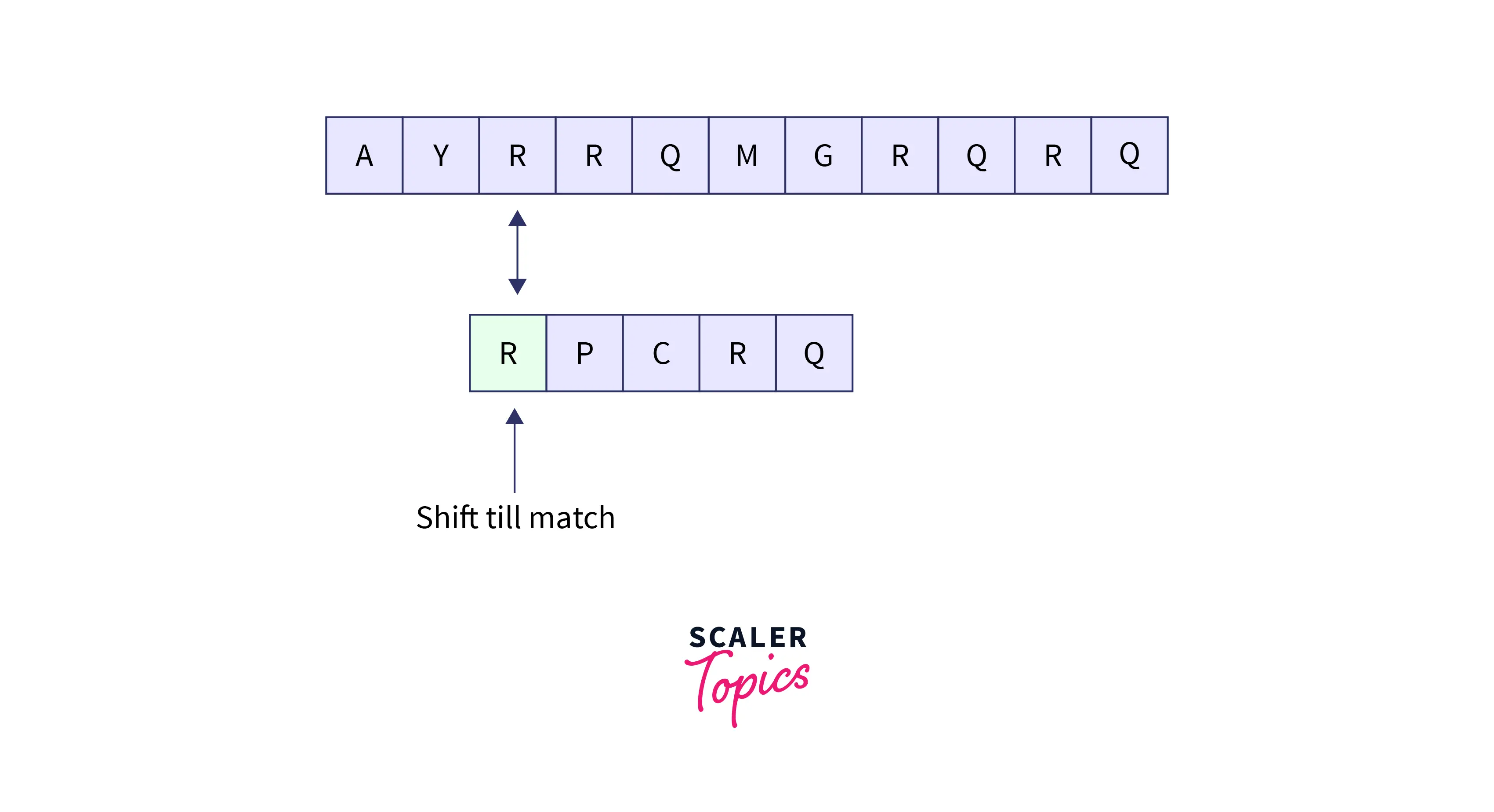
For example, let’s say that the pattern given is: RPCRQ and the input text is: AYRRQMGRQRQ. Now, we start comparing the pattern string with the input string and we have found a mismatch between the character R of the text (the bad character) and the character C of the pattern. So, we will shift the pattern string until the character R of the pattern matches the character R of the text string.
Refer to the image provided below for better visualization.
2. When the Mismatched Character of Input Text is Not Present in the Pattern
Let us take the same example as above and we have found that the mismatched character of input text is not present in the pattern.
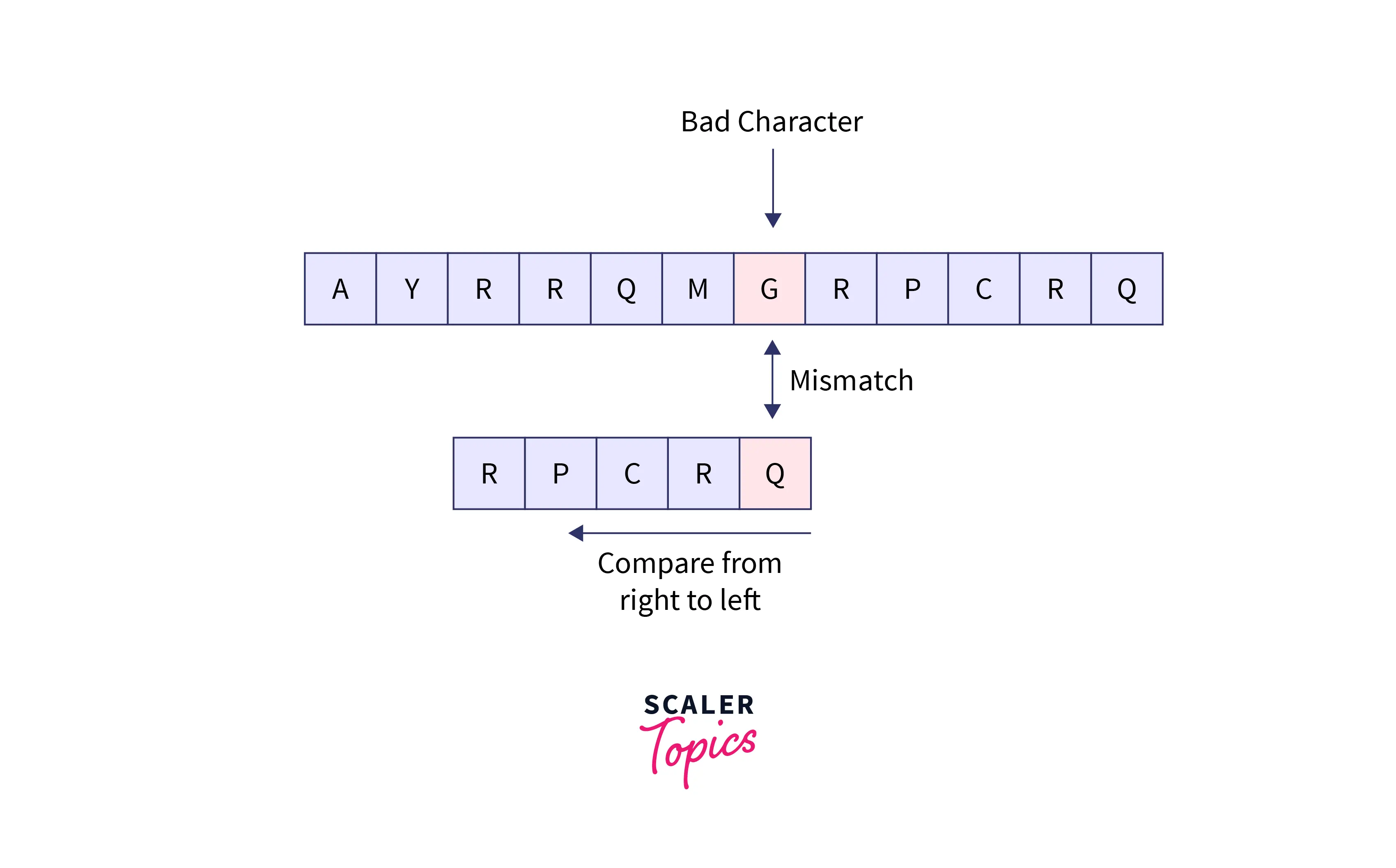
There is a mismatch between G and Q, but G is not at all present in the entire pattern string. So, we would not compare the entire pattern and we would easily shift the pattern until the character G on the input text as:
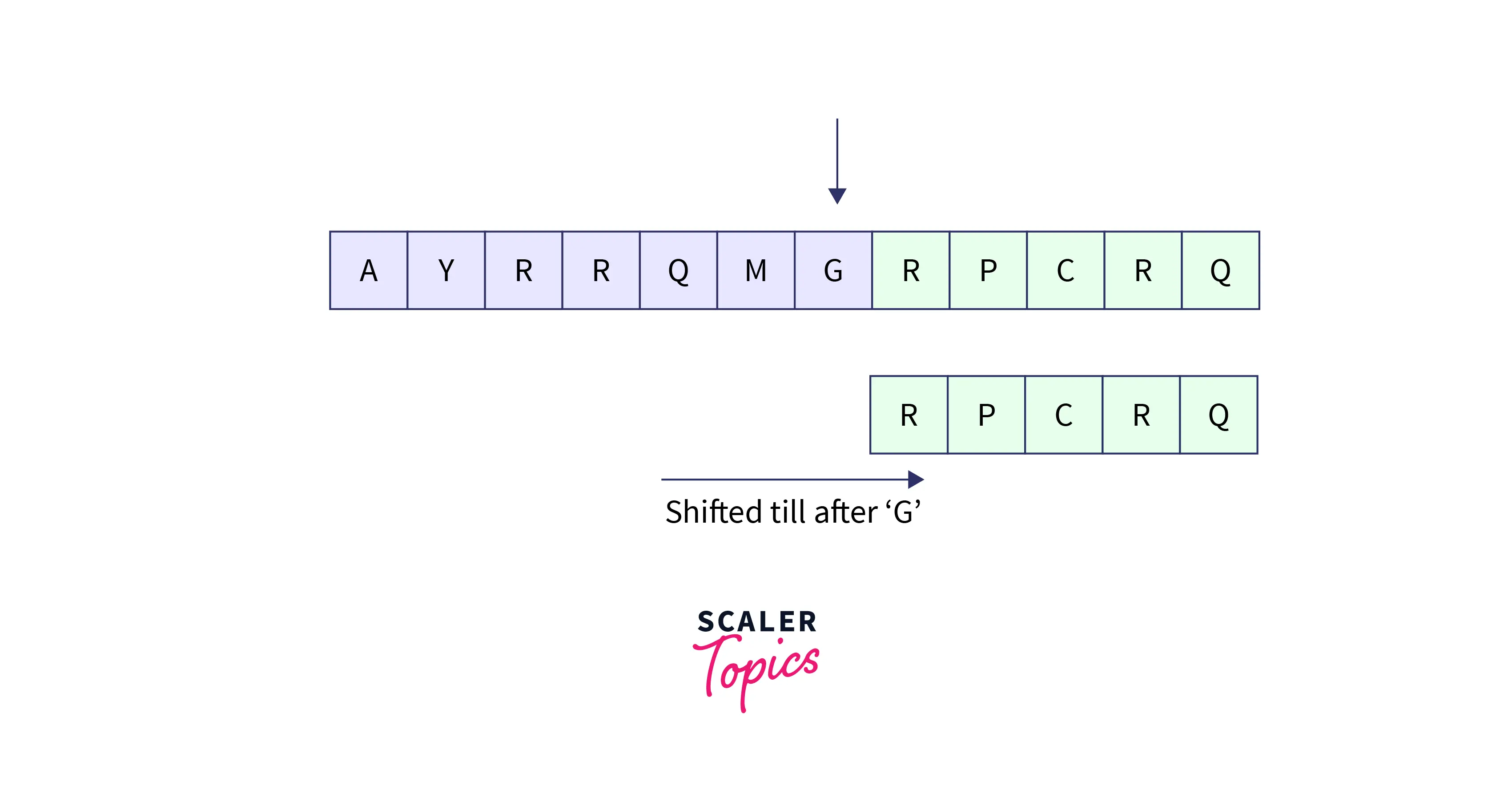
Let us implement the above algorithm for better understanding.
C++ code:
#include <bits/stdc++.h>
using namespace std;
// defining a macro
#define TOTAL_CHARACTERS 256
// The preprocessing function that fills the actual value of the last occurrence of a character
void badCharacterHeuristic(string s, int n,
int badCharacter[TOTAL_CHARACTERS]) {
// First initializing all occurrences with -1
for (int i = 0; i < TOTAL_CHARACTERS; i++)
badCharacter[i] = -1;
// Filling the actual value of the last occurrence of a character in the bad character array.
for (int i = 0; i < n; i++)
badCharacter[(int)s[i]] = i;
}
/*
A function that searches the string and returns the occurrence.
*/
void BoyerMooreAlgorithm(string text, string pattern) {
// getting the size of the pattern and the string.
int m = pattern.size();
int n = text.size();
// defining a a character array.
int badCharacter[TOTAL_CHARACTERS];
/*
Filling the badCharacter array with the current pattern using a helper function.
*/
badCharacterHeuristic(pattern, m, badCharacter);
// initially there is no shift
int shifts = 0;
// defining the boundaries of the searching
while (shifts <= (n - m)) {
int j = m - 1;
/*
If the pattern and text are matching, keep on reducing the j variable.
*/
while (j >= 0 && pattern[j] == text[shifts + j])
j--;
/*
If the pattern is present at current
shift, then j will become -1.
*/
if (j < 0) {
cout << "Pattern found at index: " << shifts << endl;
/*
Shifting the pattern so that the next character of the text is aligned with its last occurrence in the pattern.
*/
shifts += (shifts + m < n) ? m - badCharacter[text[shifts + m]] : 1;
}
/*
Shifting the pattern so that the bad character of the text is aligned with its last occurrence in the pattern. The max function helps to get the positive shift only.
*/
else
shifts += max(1, j - badCharacter[text[shifts + j]]);
}
}
int main() {
string text = "Scaler Topics";
string pattern = "Topics";
BoyerMooreAlgorithm(text, pattern);
return 0;
}
Java code:
public class Test {
static int TOTAL_CHARACTERS = 256;
// The preprocessing function that fills the actual value of the last occurrence of a character
static void badCharacterHeuristic(char s[], int n,
int badCharacter[]) {
// First initializing all occurrences with -1
for (int i = 0; i < TOTAL_CHARACTERS; i++)
badCharacter[i] = -1;
// Filling the actual value of the last occurrence of a character in the badCharacter array.
for (int i = 0; i < n; i++)
badCharacter[(int)s[i]] = i;
}
/*
A function that searches the string and returns the occurrence.
*/
static void BoyerMooreAlgorithm(char text[], char pattern[]) {
// getting the size of the pattern and the string.
int m = pattern.length;
int n = text.length;
// defining a bacCharacter array.
int badCharacter[] = new int[TOTAL_CHARACTERS];
/*
Filling the badCharacter array with the current pattern using a helper function.
*/
badCharacterHeuristic(pattern, m, badCharacter);
// initially there is no shift
int shifts = 0;
// defining the boundaries of the searching
while (shifts <= (n - m)) {
int j = m - 1;
/*
If the pattern and text are matching, keep on reducing the j variable.
*/
while (j >= 0 && pattern[j] == text[shifts + j])
j--;
/*
If the pattern is present at current
shift, then j will become -1.
*/
if (j < 0) {
System.out.println("Pattern found at index: " + shifts);
/*
Shifting the pattern so that the next character of the text is aligned with its last occurrence in the pattern.
*/
shifts += (shifts + m < n) ? m - badCharacter[text[shifts + m]] : 1;
}
/*
It is shifting the pattern so that the bad character of the text is aligned with its last occurrence in the pattern. The max function helps to get the positive shift only.
*/
else
shifts += Math.max(1, j - badCharacter[text[shifts + j]]);
}
}
public static void main(String args[]) {
char text[] = "Scaler Topics".toCharArray();
char pattern[] = "Topics".toCharArray();
BoyerMooreAlgorithm(text, pattern);
}
}
Python code:
TOTAL_CHARACTERS = 256
"""
The preprocessing function that fills the actual value of the last occurrence of a character
"""
def badCharacterHeuristic(string, size):
# First initializing all occurrences with -1
Bachar = [-1]*TOTAL_CHARACTERS
# Filling the actual value of the last occurrence of a character in the badCharacter list (array).
for i in range(size):
badChar[ord(string[i])] = i
return badChar
"""
A function that searches the string and returns the occurrence.
"""
def boyerMooreAlgorithm(text, pattern):
# getting the size of the pattern and the string.
m = len(pattern)
n = len(text)
# defining a bacCharacter array.
# Filling the badCharacter array with the current pattern using a helper function.
badCharacter = badCharacterHeuristic(pattern, m)
# initially there is no shift
shifts = 0
# defining the boundaries of the searching
while(shifts <= n-m):
j = m-1
# If the pattern and text are matching, keep on reducing the j variable.
while j >= 0 and pattern[j] == text[shifts+j]:
j -= 1
# If the pattern is present at the current shift, then j will become -1.
if j < 0:
print("Pattern found at index: ", shifts)
'''
Shifting the pattern so that the next character of the text is aligned with its last occurrence in the pattern.
'''
shifts += (m-badCharacter[ord(text[shifts+m])]
if shifts+m < n else 1)
else:
"""
Shifting the pattern so that the bad character of the text is aligned with its last occurrence in the pattern. The max function helps to get the positive shift only.
"""
shifts += max(1, j-badCharacter[ord(text[shifts+j])])
text = "Scaler Topics"
pattern = "Topics"
boyerMooreAlgorithm(text, pattern)
Output:
Pattern found at index: 7
Complexity Analysis
In this approach, we are traversing the pattern string for each portion of the text string.
Time Complexity
The time complexity of the algorithm comes out to be O (n x m), where n and m are sizes of text and pattern string respectively.
Space Complexity
Although we need to create the array for the preprocessing function the size of that array is fixed i.e. 256. We are not using any extra space apart from the preprocessing, so the space complexity of the algorithm comes out to be (O(1)).
Approach 2: Good Suffix Heuristic
Another approach for searching the pattern using the Boyer-Moore algorithm is to detect the good suffix and then do the processing. The main idea is to shift more efficiently when a mismatch occurs by aligning the overlapping parts of the pattern and the text string together.
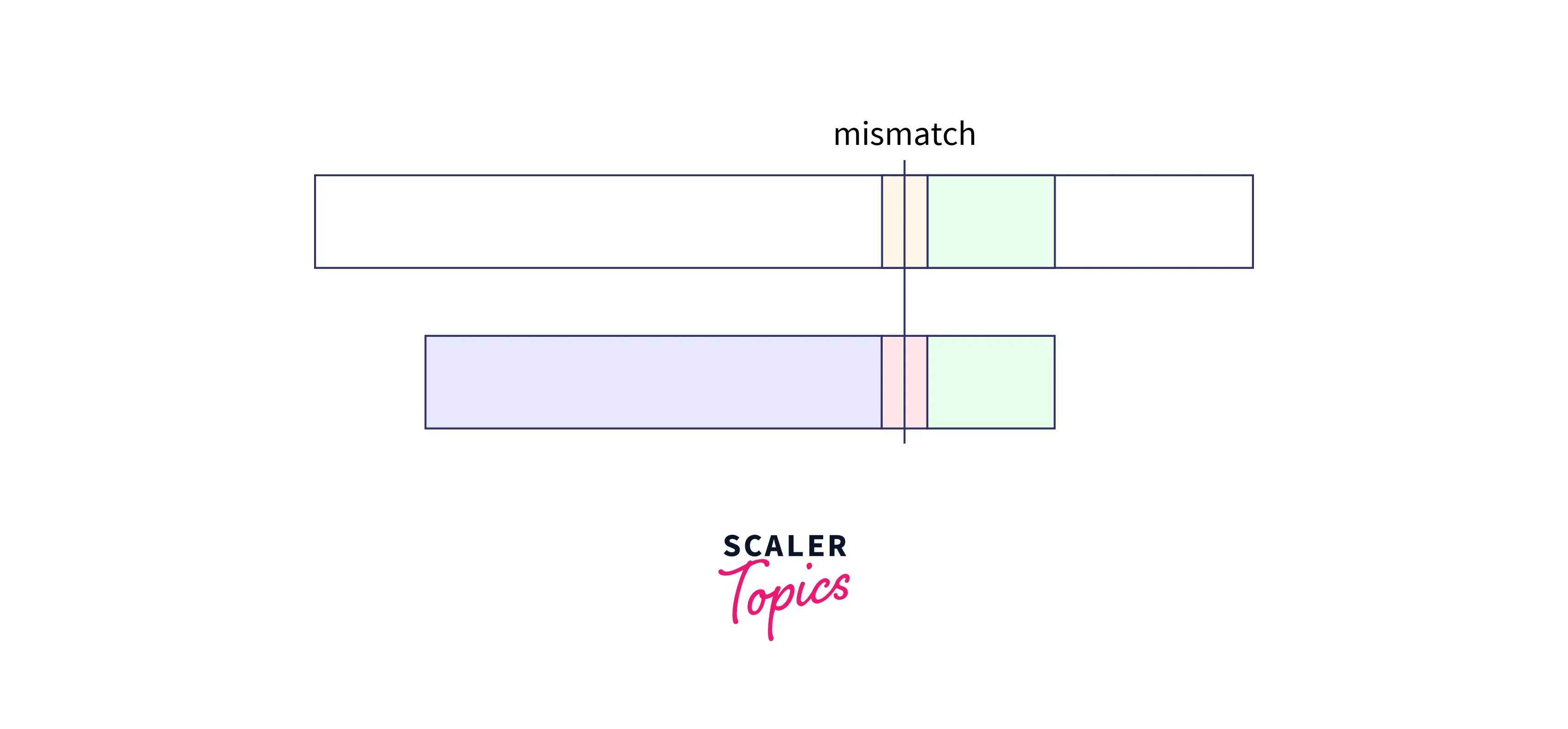
Let us learn the algorithm with an example for better visualization. We start searching from the right-hand side and suppose that we have found a part of the pattern matching. Refer to the image (green color marks match).
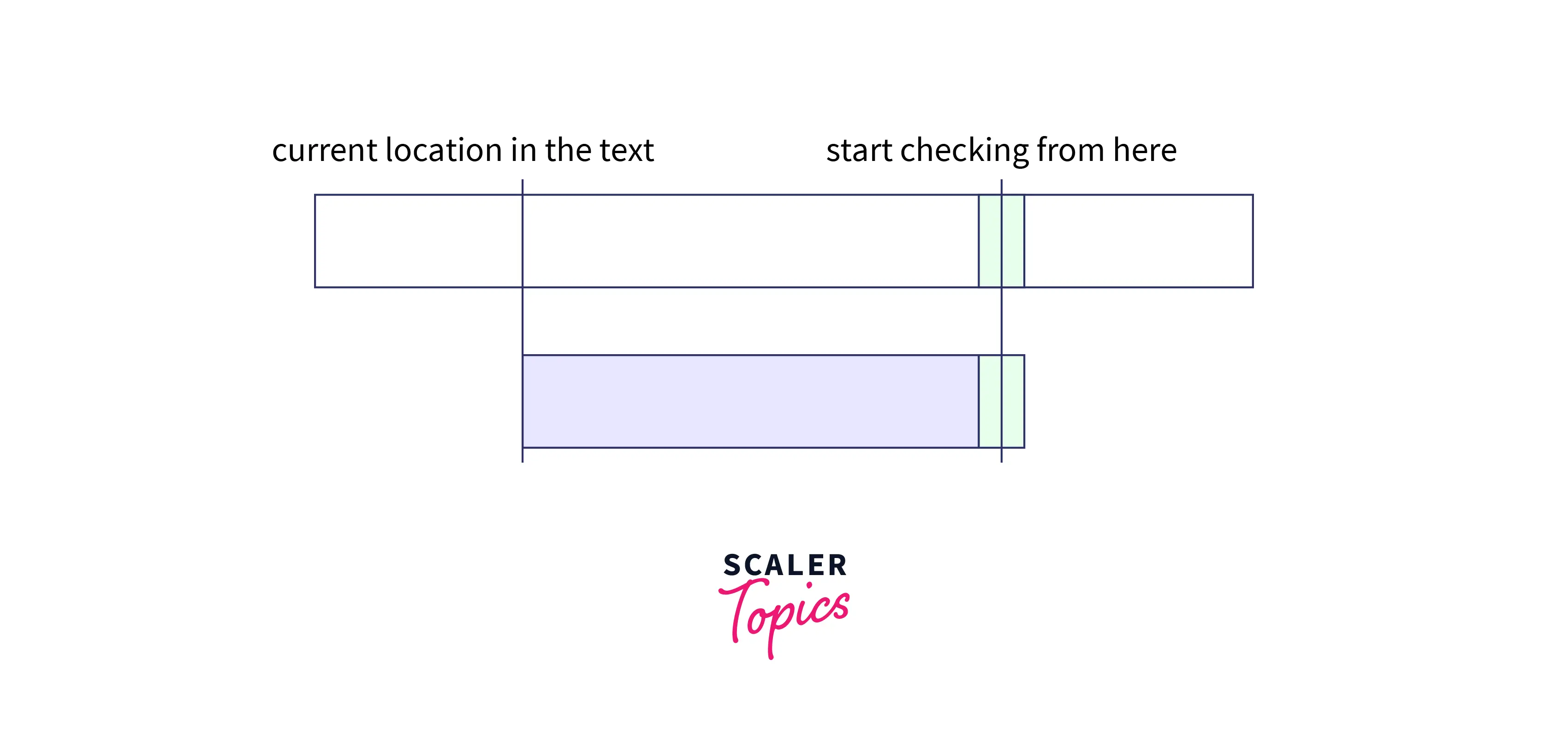
We will continue the search and as soon as we have found a mismatch, we would stop. the portion of the pattern that matched is called Good String. And a mismatch means that the current location in the text is not the suitable starting place for the target pattern.
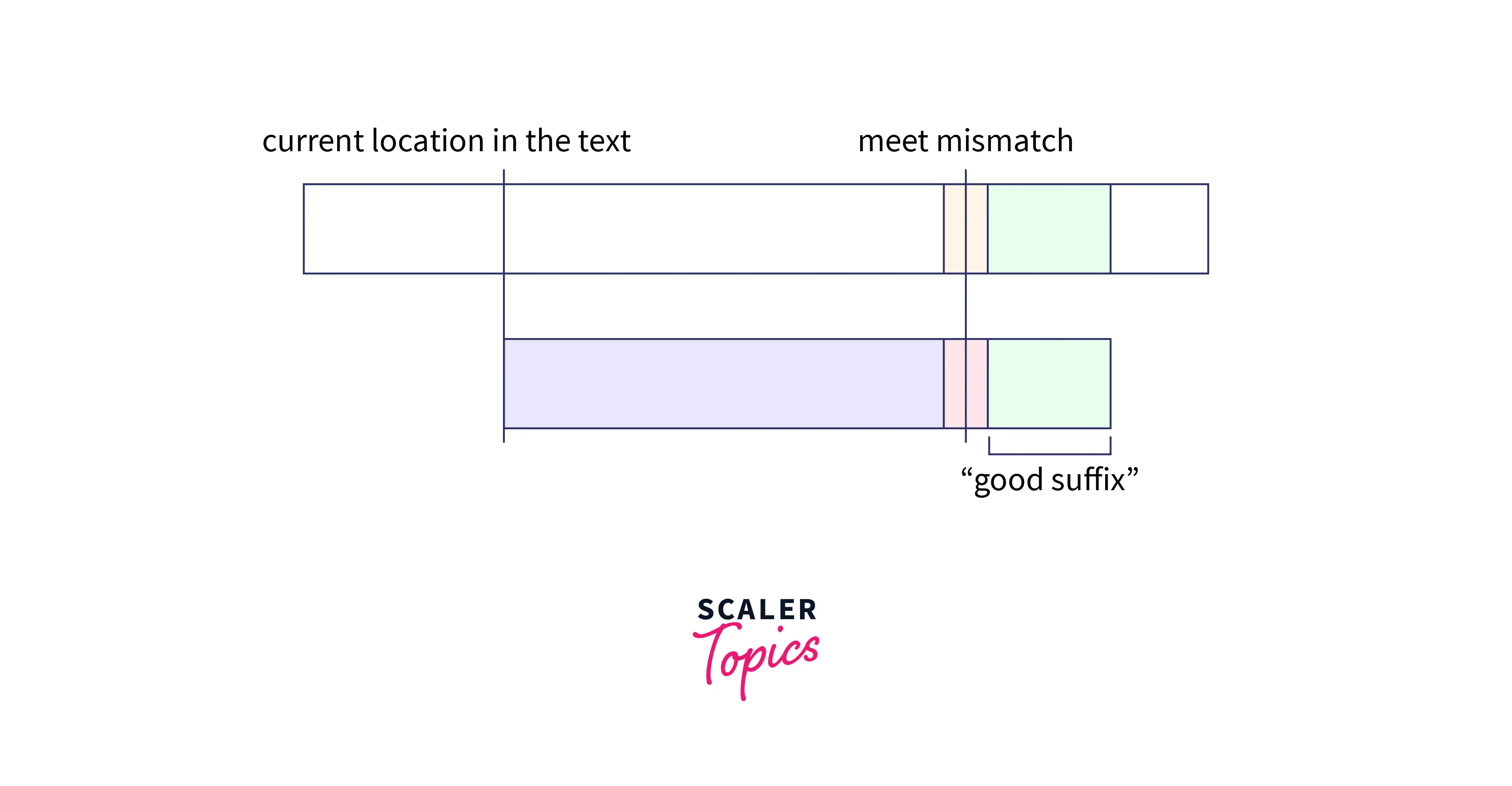
So, we should shift the pattern to find the next possible location for checking. We can use the good suffix for efficient shifting. There can be two cases if we use a good suffix for shifting.
- When the good suffix exists somewhere in the pattern itself:
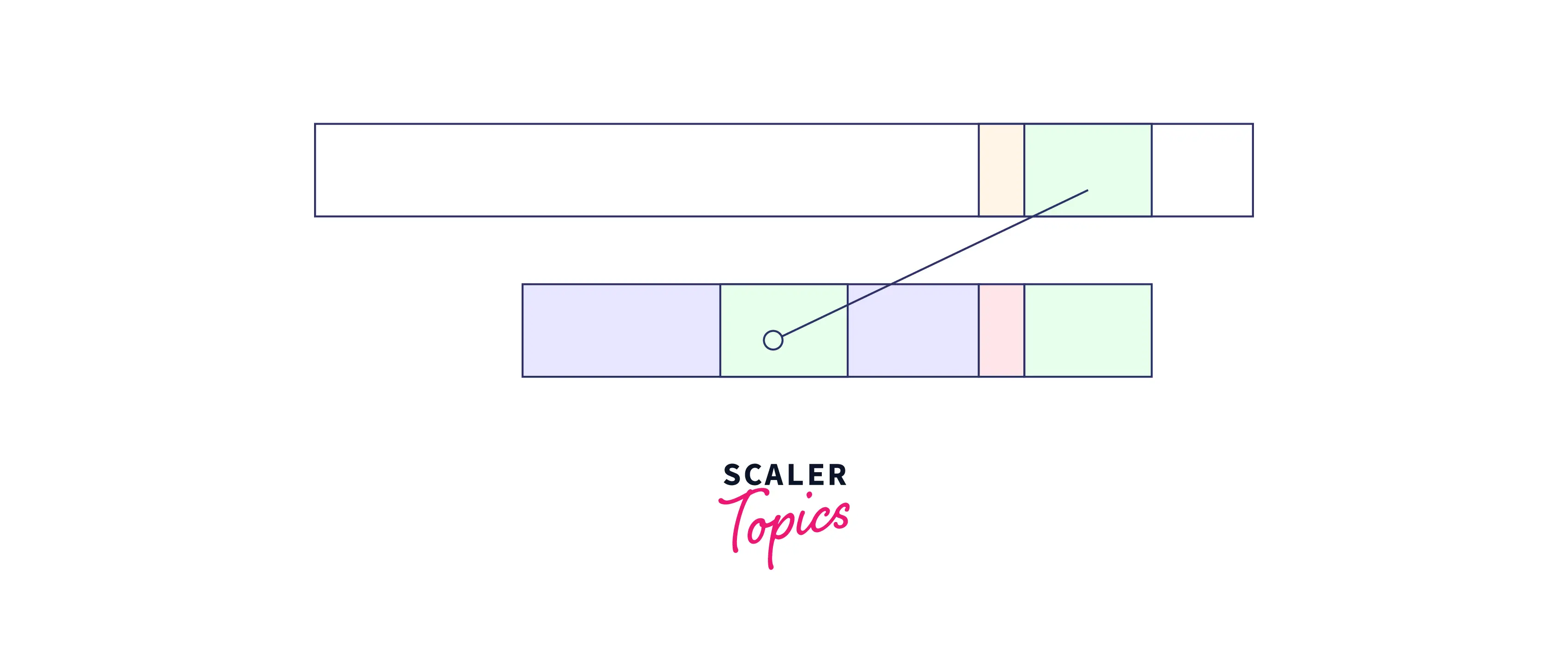
As we can see that the good string is also present somewhere else. So, shift the pattern so that the good suffix parts are aligned as:
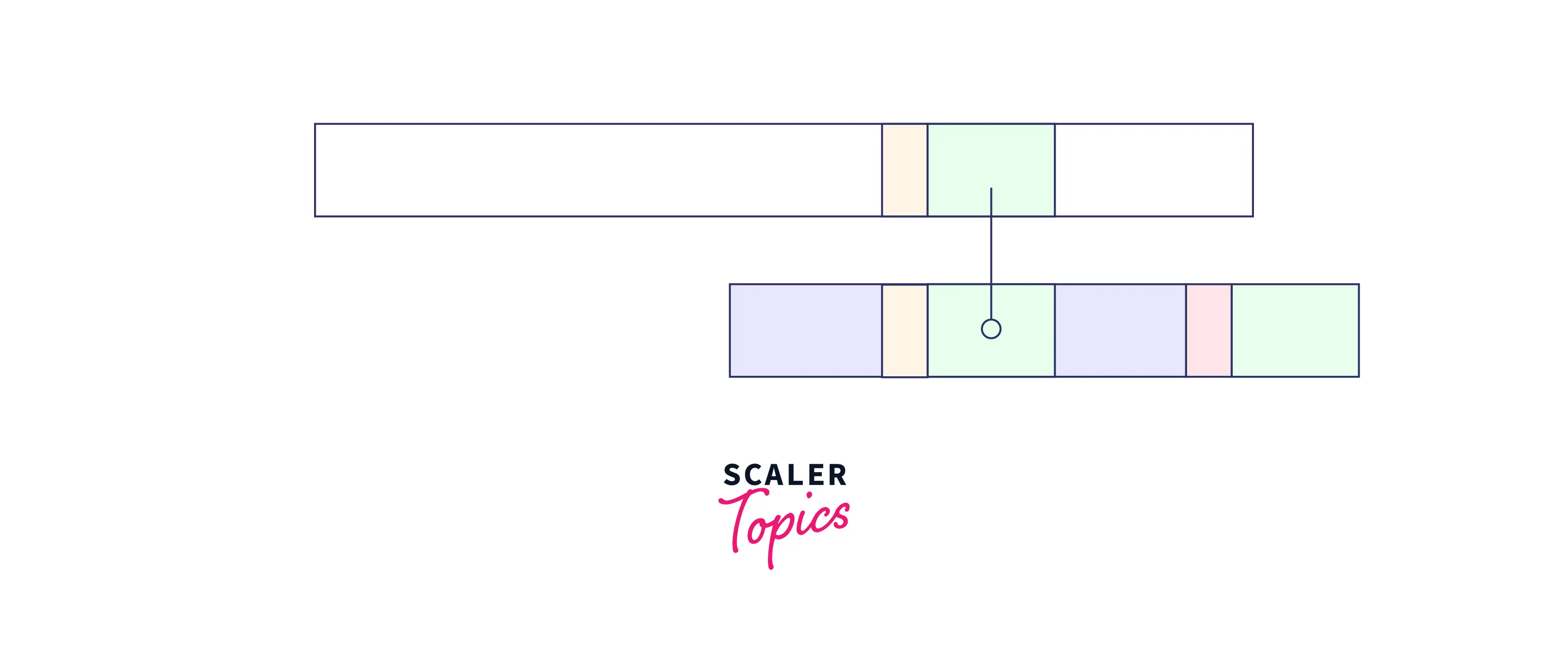
- When the partial good suffix exists as a prefix of the pattern:
As we can that there is a mismatch but we cannot find the exact match of the good string. However, if we can find the suffix of the suffix (marked in blue) in the prefix of our pattern then we can also take thfrontmp of this match in shifting. 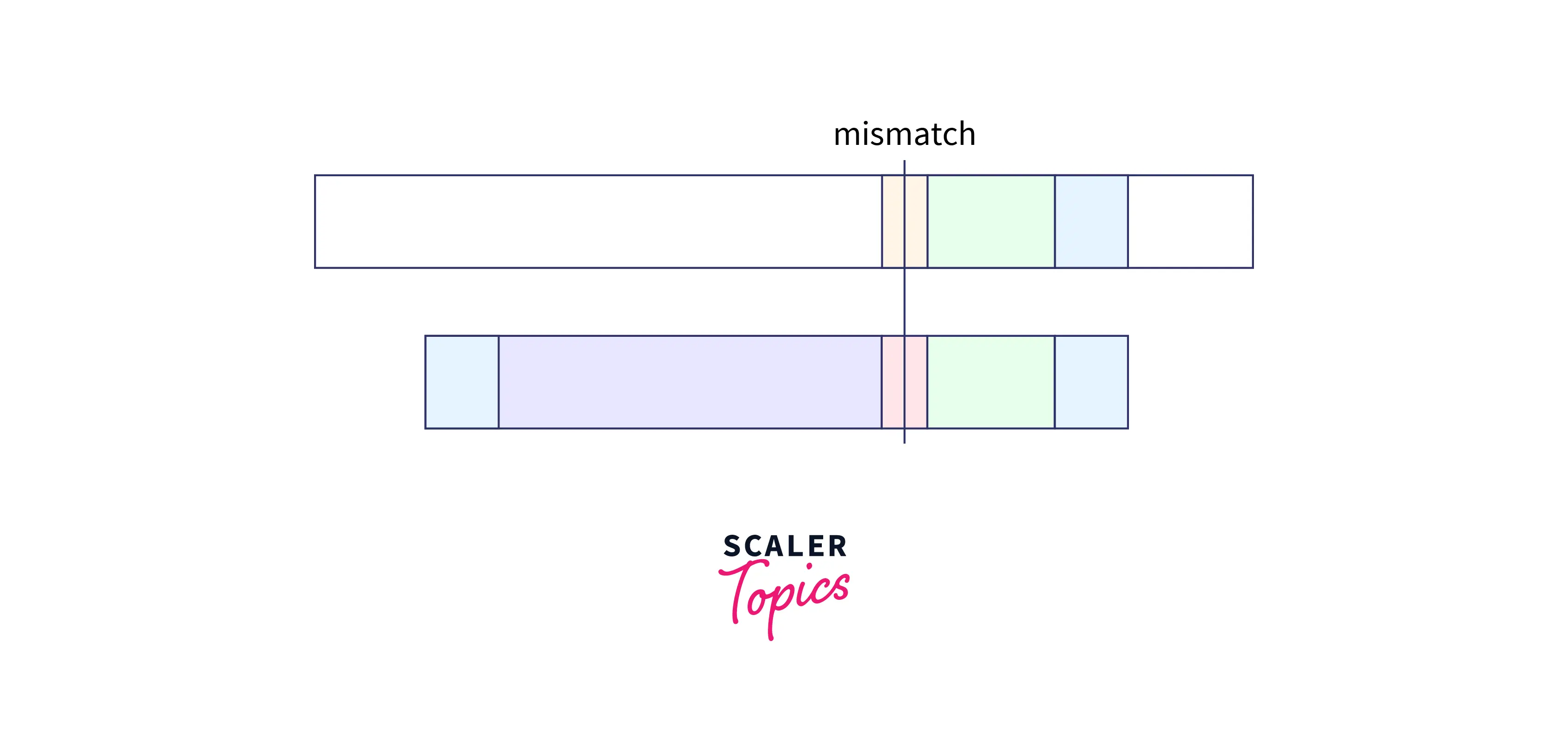
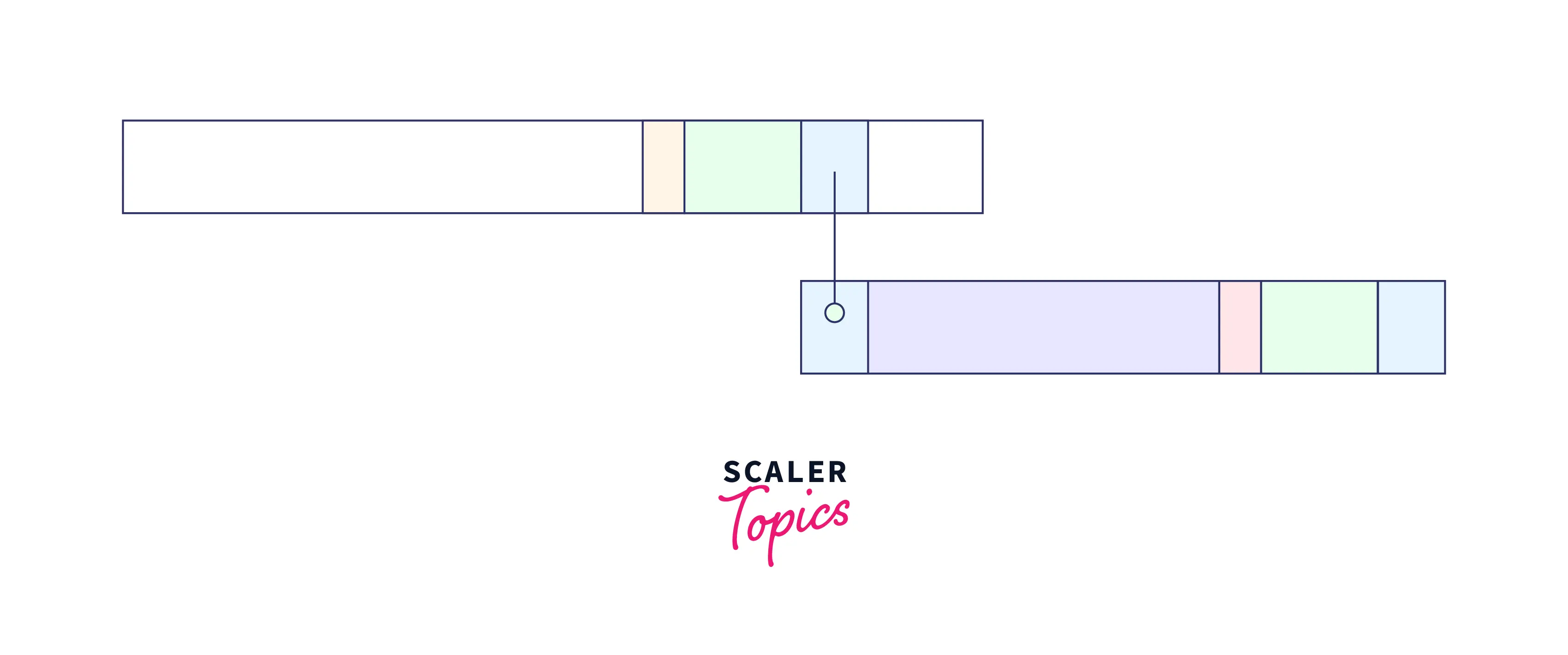
In such a case, shift the pattern so that the partial suffix is in alignment with the prefix of the pattern.
So, we can add the virtual green part rest of the good string) to the blue partial good suffix to make it a virtually complete good suffix starting at the location before the pattern.
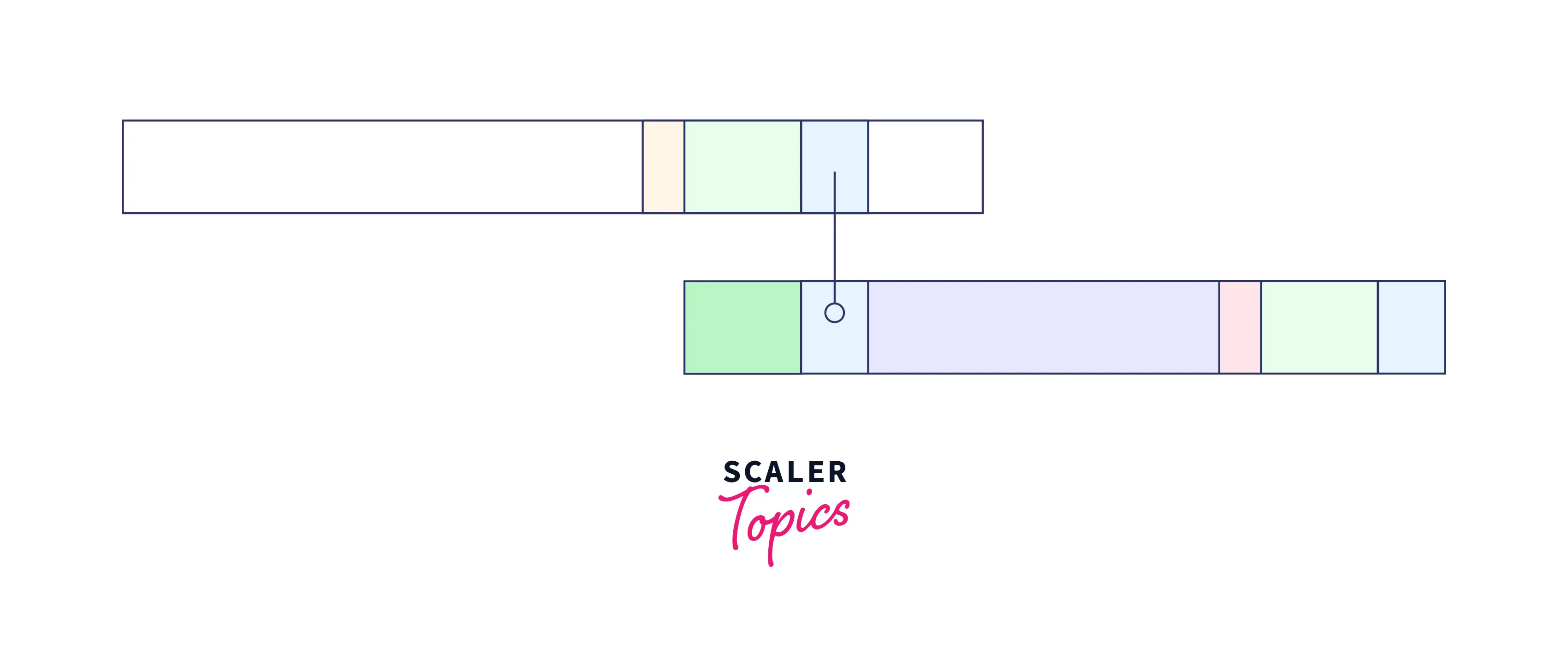
Let us implement the above algorithm for better understanding.
C++ code:
#include <bits/stdc++.h>
using namespace std;
// a function to handle the strong suffix case.
void preprocess_suffix(int *shift, int *borderPosition,
char *pattern, int m) {
int i = m, j = m + 1;
borderPosition[i] = j;
// traversing until the size of the pattern is greater than 0
while (i > 0) {
/*
If the character at position (i-1) is not the same as the character at (j-1), then continue the algorithm.
*/
while (j <= m && pattern[i - 1] != pattern[j - 1]) {
if (shift[j] == 0)
shift[j] = j - i;
// Updating the position of the next border
j = borderPosition[j];
}
/*
Since p[i-1] is matched with p[j-1] then we have found the border, then store the border.
*/
i--;
j--;
borderPosition[i] = j;
}
}
// a function to handle the prefix case.
void preprocess_prefix(int *shift, int *borderPosition,
char *pattern, int m) {
int i, j;
j = borderPosition[0];
for (i = 0; i <= m; i++) {
/*
setting the border position of the pattern's first character to all the indices in the shift array.
*/
if (shift[i] == 0)
shift[i] = j;
/* suffix becomes shorter than borderPosition[0], use the position of the next widest border as the value of j.
Now if the suffix becomes shorter than borderPosition[0], we need to use the next position of
the widest border as the new value of j.
*/
if (i == j)
j = borderPosition[j];
}
}
// A function that searches the string and returns the occurrence.
void BoyerMooreAlgorithm(char *text, char *pattern) {
// s is a shift of the pattern concerning input text.
int s = 0, j;
int m = strlen(pattern);
int n = strlen(text);
// an array to store the shifts and
// borderPosition will store the widest border of the pattern
int borderPosition[m + 1], shift[m + 1];
// initialize all occurrences of the shift to 0
for (int i = 0; i < m + 1; i++)
shift[i] = 0;
// first performing the preprocessing
preprocess_suffix(shift, borderPosition, pattern, m);
preprocess_prefix(shift, borderPosition, pattern, m);
while (s <= n - m) {
j = m - 1;
// If the pattern and text are matching, keep on reducing the j variable.
while (j >= 0 && pattern[j] == text[s + j])
j--;
// If the pattern is a represencurrentnt shift, then j will become -1.
if (j < 0) {
cout << "Pattern found at index:" << s << endl;
s += shift[0];
}
else
/*
pattern[i] != pattern[s+j] so Shifting the pattern so that the bad character of the text is aligned
*/
s += shift[j + 1];
}
}
int main() {
char text[] = "he is doing what he was supposed to do.";
char pattern[] = "he";
BoyerMooreAlgorithm(text, pattern);
return 0;
}
Java code
public class Test {
static void preprocess_suffix(int[] shift, int[] borderPosition,
char[] pattern, int m) {
int i = m, j = m + 1;
borderPosition[i] = j;
// traversing until the size of the pattern is greater than 0
while (i > 0) {
/*
If the character at position (i-1) is not the same as the character at (j-1), then continue the algorithm.
*/
while (j <= m && pattern[i - 1] != pattern[j - 1]) {
if (shift[j] == 0)
shift[j] = j - i;
// Updating the position of the next border
j = borderPosition[j];
}
/*
Since p[i-1] is matched with p[j-1] then we have found the border, then store the border.
*/
i--;
j--;
borderPosition[i] = j;
}
}
// a function to handle the prefix case.
static void preprocess_prefix(int[] shift, int[] borderPosition,
char[] pat, int m) {
int i, j;
j = borderPosition[0];
for (i = 0; i <= m; i++) {
/*
setting the border position of the pattern's first character to all the indices in the shift array.
*/
if (shift[i] == 0)
shift[i] = j;
/* suffix becomes shorter than borderPosition[0], use the position of
next widest border as the value of j.
Now if the suffix becomes shorter than borderPosition[0], we need to use the next position of
the widest border as the new value of j.
*/
if (i == j)
j = borderPosition[j];
}
}
// A function that searches the string and returns the occurrence.
static void BoyerMooreAlgorithm(char text[], char pattern[]) {
// sa s a shift of the patterconcerningto input text.
int s = 0, j;
int m = pattern.length;
int n = text.length;
// an array to store the shifts and
// borderPosition will store the widest border of the pattern
int[] borderPosition = new int[m + 1];
int[] shift = new int[m + 1];
// initialize all occurrences of shift to 0
for (int i = 0; i < m + 1; i++)
shift[i] = 0;
// first performing the preprocessing
preprocess_suffix(shift, borderPosition, pattern, m);
preprocess_prefix(shift, borderPosition, pattern, m);
while (s <= n - m) {
j = m - 1;
// If the pattern and text are matching, keep on reducing the j variable.
while (j >= 0 && pattern[j] == text[s + j])
j--;
// If the pattern is present at the current not shift, then j will become -1.
if (j < 0) {
System. out.println("Pattern found at index:" + s);
s += shift[0];
} else
/*
pattern[i] != pattern[s+j] so Shifting the pattern so that the bad character of the text is aligned.
*/
s += shift[j + 1];
}
}
public static void main(String args[]) {
char text[] = "he is doing what he was supposed to do.".toCharArray();
char pattern[] = "he".toCharArray();
BoyerMooreAlgorithm(text, pattern);
}
}
Python code:
# a function to handle the strong suffix case.
def preprocess_suffix(shift, borderPosition, pattern, m):
i = m
j = m + 1
borderPosition[i] = j
# traversing until the size of the pattern is greater than 0
while i > 0:
"""
If the character at position (i-1) is not the same as the character at (j-1), then continue the algorithm.
"""
while j <= m and pattern[i - 1] != pattern[j - 1]:
if shift[j] == 0:
shift[j] = j - i
# Updating the position of the next border
j = borderPosition[j]
"""
Since p[i-1] is matched with p[j-1] then we have found the border, then store the border.
"""
i -= 1
j -= 1
borderPosition[i] = j
# a function to handle the prefix case.
def preprocess_prefix(shift, borderPosition, pattern, m):
j = borderPosition[0]
for i in range(m + 1):
"""
setting the border position of the pattern's first character to all the indices in the shift array.
"""
if shift[i] == 0:
shift[i] = j
"""
suffix becomes shorter than borderPosition[0], use the position of the next widest border as the value of j.
Now if the suffix becomes shorter than borderPosition[0], we need to use the next position of
the widest border as the new value of j.
"""
if i == j:
j = borderPosition[j]
# A function that searches the string and returns the occurrence.
def boyerMooreAlgorithm(text, pattern):
# s is a shift of the pattern concerning input text.
s = 0
m = len(pattern)
n = len(text)
"""
an array to store the shifts and border position will store the widest border of the pattern.
initialize all occurrences of the shift to 0.
"""
shift = [0] * (m + 1)
borderPosition = [0] * (m + 1)
# first performing the preprocessing
preprocess_suffix(shift, borderPosition, pattern, m)
preprocess_prefix(shift, borderPosition, pattern, m)
while s <= n - m:
j = m - 1
"""
If the pattern and text are matching, keep on reducing the j variable.
"""
while j >= 0 and pattern[j] == text[s + j]:
j -= 1
"""
If the pattern is present at the current shift, then j will become -1.
"""
if j < 0:
print("Pattern found at index:", s)
s += shift[0]
else:
"""
pattern[i] != pattern[s+j] so Shifting the pattern so that the bad character of the text is aligned.
"""
s += shift[j + 1]
text = "he is doing what he was supposed to do."
pattern = "he"
boyerMooreAlgorithm(text, pattern)
Output:
Pattern found at index: 0
Pattern found at index: 17
Complexity Analysis
In this approach, we are traversing the pattern string and preprocessing the string to handle the strong suffix case, and prefix case.
Time Complexity
The time complexity of the algorithm comes out to be O (n x m), where n and m are sizes of text and pattern string respectively.
Space Complexity
We have used two arrays of sizes equal to the size of the pattern. So, the time complexity comes out to be [O(m) + O(m)] i.e. O(n) where n = (m+m) or twice the size of the pattern.
Conclusion
- A String is an immutable data type that is used to store the sequence of characters. Strings are one of the most widely used data types of any programming language.
- For searching the pattern in the string, we can use the Boyer-Moore pattern searching algorithm (or B-M algorithm).
- The intuition of the Boyer-Moore algorithm is very simple, two pointers are aligned at the 0th index of the text string and the character string. The pattern string is then compared character by character with the current portion of the text string, beginning with the rightmost character.
- When a character does not match then the Boyer Moore algorithm shifts the characters using two strategies simultaneously:
- Bad Character Heuristic, and
- Good Suffix Heuristic.
- In the Bad Character Heuristic approach, we are traversing the pattern string for each portion of the text string.
- In the Good Suffix Heuristic approach, we are traversing the pattern string and preprocessing the string to handle the strong suffix case, and prefix case.
- The time complexity of the Bad Character Heuristic approach, comes out to be O (nm), where n and m are sizes of text and pattern string respectively. Apart from that, we are using an array of fixed size (257) so the space complexity of the algorithm comes out to be (O(1)).
- The time complexity of the Good Suffix Heuristic approach, comes out to be O (nm), where n and m are sizes of text and pattern string respectively. We have used two arrays of sizes equal to the size of the pattern. So, the time complexity comes out to be [O(m)+ O(m)] i.e. O(n) where n = (m+m).