Chocolate Distribution Problem

Problem Statement

In the above chocolate distribution problem, you will be given an array of n integers where each value represents the number of chocolates in a packet. Each packet can have a variable number of chocolates. There are m students, the task is to distribute chocolate packets such that:

Rules :

• Each student gets only one packet.
• The difference between the number of chocolates in the packet with maximum chocolates and the packet with minimum chocolates given to the students is minimum.
• However, it is not necessary that all packets should be distributed among the children.

Input Format :

• Array Length n
• Array’s element of size n
• number of children m

Output Format :

• Return an integer containing the minimum difference between the number of chocolates in the packet with maximum chocolates and the packet with minimum chocolates.

Example

Input : arr[] = {3, 4, 1, 9, 56, 7, 9, 12}

m = 5

Output :

Minimum Difference is 6.

Explanation

Let us now understand the above example of chocolate distribution problem in detail.

• In the above example, there are eight packets and five children. The number of chocolates in each packet is 3 4 1 9 56 7 9 12 respectively.
• Let us say that the packet which contains 1, 3, 4, 7, and 9 is been distributed among the 5 children, so the difference between the number of chocolates in the packet with maximum chocolates and the packet with minimum chocolates would be 9 – 1 = 8.
• Let us say that the packet which contains 3, 4, 7, 9, and 9 is been distributed among the 5 children, so the difference between the number of chocolates in the packet with maximum chocolates and packet with minimum chocolates would be 9 – 3 = 6.
• Let us say that the packet which contains 4, 7, 9, 9, and 12 is been distributed among the 5 children, so the difference between the number of chocolates in the packet with maximum chocolates and packet with minimum chocolates would be 12 – 4 = 8.
• Let us say that the packet which contains 7, 9, 9, 12, and 56 is been distributed among the 5 children, so the difference between the number of chocolates in the packet with maximum chocolates and packet with minimum chocolates would be 56 – 7 = 49.

and so on.

So above all the assumptions we can see the minimum difference between maximum chocolates and minimum chocolates is 9 – 3 = 6 by choosing the following M packets : {3, 4, 9, 7, 9}.

Constraints

1 ≤ N ≤ 10^5

1 ≤ Ai ≤ 10^9

1 ≤ M ≤ N

Approach 1: Brute Force

Let us begin with the brute force approach of chocolate distribution problem, which is too slow but should be mentioned during the interview.

Intution : In this approach, at first, we will find all the subsets of length m (children) from the given array and then we will choose the one with the minimum difference between the lowest and the maximum value.

Algorithm :

Here is the brute force algorithm for this particular problem:

• Firstly, we are going to take a double dimension (2D) ArrayList data structure to store all the subsets of length m in it.
• Then we will follow a recursive approach to find all the subsets of size m from the given array.
• We will have a recursive function which will contains the array, index of elements inside the array starting with 0 index, double dimension (2D) ArrayList, single dimension (1D) ArrayList to store the current subset, and m (size of subset), as arguments.
• Inside the recursive function there will be a base case and recursive steps. Let us discuss them.

Recursive Steps :

//Include the element in our subset
store the element inside the 1D ArrayList.

recursiveFunction(array, index+1, 2D ArryaList, 1D ArrayList, m);

remove the last visited element from the 1D ArrayList.

//Exclude the element in our subset
recursiveFunction(array, index+1, 2D ArryaList, 1D ArrayList, m);

Explanation :

Basically, a subset of an array can be formed by choosing some (maybe 0, 1, 2, … or equal to the size of the array) elements out of all the possible array elements, in the same order in which they appear in the original array. So every element in the array has its chance of including itself or excluding itself from the subset. In the above recursive steps, we have two recursive calls, one after including the element in the subset (adding the element in the 1D ArrayList) and another after excluding the element from the subset.

Note : We are removing the last visited element from the ArrayList, because the ArrayList stores the element by reference and it will not remove the element automatically while returning, so we have to remove it manually.

But when this including and excluding of elements from the array will continue, and when will be the actual ending of this process. for that we need a base case

Base Case :

if(index == array's length){
    if(1D ArrayList size == m){
        Store the subset of 1D ArrayList inside the 
        2D ArrayList.
    }
    return;
}

Explanation :

In the above base case we can see, that when the index surpasses the length of the array, we are stopping the process. At that time we also check whether the size of the 1D ArrayList is equal to m, if it is the case, then we know we have got the subset of size m from the array. So we will store it in our 2D ArrayList and return it.

• We will use an answer variable to store the minimum difference between the lowest and the maximum value of every subset.
• Initialize the answer variable with Integer.MAX_VALUE.
• After getting all the subsets of size m of the given array in our 2D ArrayList, we will now iterate throughout the 2D ArrayList.
• While iterating we will keep storing the minimum difference between the lowest and the maximum value of every subset (1D ArrayList) from the 2D ArrayList in our answer variable.
• we print the answer.

Code

Now, let us see the code of chocolate distribution problem in different programming languages.

Code in JAVA :

// JAVA Code For Chocolate Distribution
// Problem
import java.util.*;
public class Main {
    //Recursive function to get all the
    //Subsets of size m.
    public static void subSet(int[] arr, int idx, List<List<Integer>> list, List<Integer> l, int m){
        
        //Base Case
        if(idx == arr.length){
            if(l.size() == m  ){
                list.add(new ArrayList<>(l));
            }
            return;
        }
        
        //Including the element in subset
        //Adding element in the 1D ArrayList
        l.add(arr[idx]);
        subSet(arr, idx+1, list, l, m);
        
        //Removing element from the 1D ArrayList (BackTracking)
        l.remove(l.size() - 1);
        
        //Excluding the element
        subSet(arr, idx+1, list, l, m);
    }
    
    //Minimum element from the subset
    public static int findMin(List<Integer> l){
        int min = Integer.MAX_VALUE;
        for(int i : l){
            min = Math.min(min, i);
        }
        return min;
    }
    
    //Maximum element from the subset
    public static int findMax(List<Integer> l){
        int max = Integer.MIN_VALUE;
        for(int i : l){
            max = Math.max(max, i);
        }
        return max;
    }
    
    //main function
    public static void main(String args[]) {
        
        //2D ArrayList to store all the subsets
        List<List<Integer>> list = new ArrayList<>();
        
        //1D ArrayList to store the perticular subset
        List<Integer> l = new ArrayList<>();
        
        // arr[0..n-1] represents sizes of packets
        int[] arr = {3, 4, 1, 9, 56, 7, 9, 12};
        
         //Number of students
        int m = 5;
        
        //Recursive function
        subSet(arr, 0, list, l, m);
        
        int ans = Integer.MAX_VALUE;
        
        //Finding the  minimum difference between
        //Maximum and minimum values of
        //Distribution.
        for(List<Integer> i : list){
            int min = findMin(i);
            int max = findMax(i);
            int diff = max - min;
            ans = Math.min(ans, diff);
        }
        
        //Printing the minimum difference
        System.out.println(ans);
    }
}

Output :

6

Code in Python :

# Python3 program to solve
# chocolate distribution
# problem
def findMinDiff(A,N,M):
    res = []
    
    # Initializing our minimum difference
    # to minus infinity
    minimum_difference = float('inf')
    
    # finding subset
    def findSubset(A, path, idx):
        if idx == N:
            if len(path) == M:
                res.append(path[:])
            return
        path.append(A[idx])
        findSubset(A, path, idx+1)
        path.pop()
        findSubset(A, path, idx+1)
            
    findSubset(A,[],0)
    for i in res:
        x = min(i)
        y = max(i)
        # calculating the minimum difference
        minimum_difference = min(minimum_difference, y-x)
        
    return minimum_difference

# Printing out answer
print(findMinDiff([3, 4, 1, 9, 56, 7, 9, 12],8,5))

Output :

6

Code in C++

// C++ program to solve chocolate distribution
// problem
#include<bits/stdc++.h>

using namespace std;
class Solution {
  public:
    // arr[0..n-1] represents sizes of packets
    // m is number of students.
    // Returns minimum difference between maximum
    // and minimum values of distribution.
    void findMinDiff(int ind, vector < int > & arr, vector < vector < int >> & ans, vector < int > & ds, int m) {
      if (ind == arr.size()) {
        if (ds.size() == m) {
          ans.push_back(ds);
        }
        return;
      }
      // pick up the element 
        ds.push_back(arr[ind]);
        findMinDiff(ind + 1, arr, ans, ds, m);
        ds.pop_back();
     // Don't pick up the element
      findMinDiff(ind + 1, arr, ans, ds, m);

    }
  public:
    vector < vector < int >> MinDiff(vector < int > & candidates, int m) {
      vector < vector < int >> ans;
      vector < int > ds;
      findMinDiff(0, candidates, ans, ds, m);
      return ans;
    }
};


//main function
int main() {
  Solution obj;
  // arr to store the chocolates
  vector < int > arr {3, 4, 1, 9, 56, 7, 9, 12};
  // number of children  
  int m = 5;
  // 2D vector to store the subsets of size m 
  vector < vector < int >> map = obj.MinDiff(arr, m);
  // ans to store minimum difference  
  int ans = INT_MAX	;
  for (int i = 0; i < map.size(); i++) {
      int minimum = INT_MAX;
      int maximum = INT_MIN;
    for (int j = 0; j < map[i].size(); j++){
        // Store minimum element of
        // the perticular subset
        minimum = min(minimum, map[i][j]);
        // Store maximum element of
        // the perticular subset
        maximum = max(maximum, map[i][j]);
    }
      // Store the difference between
      // the maximum and minimum element
      int diff = maximum - minimum;
      ans = min(ans, diff);
  }
  cout << "The Minimum difference is " << ans;
cout << endl;
}

Output :

The Minimum difference is 6

Complexity Analysis

This is a brute-force approach to the chocolate distribution problem, and it will have a very inefficient solution, with very high time and space complexity.

Time Complexity :

As there are two recursive calls inside the recursive function, it will take exponential O(2^n) time, also we are performing the iteration throughout the 2d ArrayList which will again take O(2^n) time as the total elements will be nearly equal to 2^n (all subsets) where n is the total element of the array.

Time Complexity : O(2^n) or exponential.

Space Complexity :

As we are taking a 2D ArrayList to store all the subsets of the array. So it will take O(2^n) space as the total subset of any array is 2^n. The recursive call will also take some space in the stack memory.

Auxilary Space Complexity : O(2^n) or exponential.

Approach 2: Efficient solution

Now let us look at the efficient solution of chocolate distribution problem, which will be much more optimal than brute force.

Intuition :

In the problem statement of chocolate distribution problem, they are asking us to get the minimum difference between the maximum and minimum chocolate given to m children. If we see the problem statement properly, we can observe that if the array is sorted, then the minimum difference of subarrays of size m can be easily found in O(n) time.

For example, Let’s assume for the given array above, the number of students is 3 (m = 3). After sorting the array, just one iteration with a window of size 3 will give us the minimum difference. Here’s how:

At first sort the array :

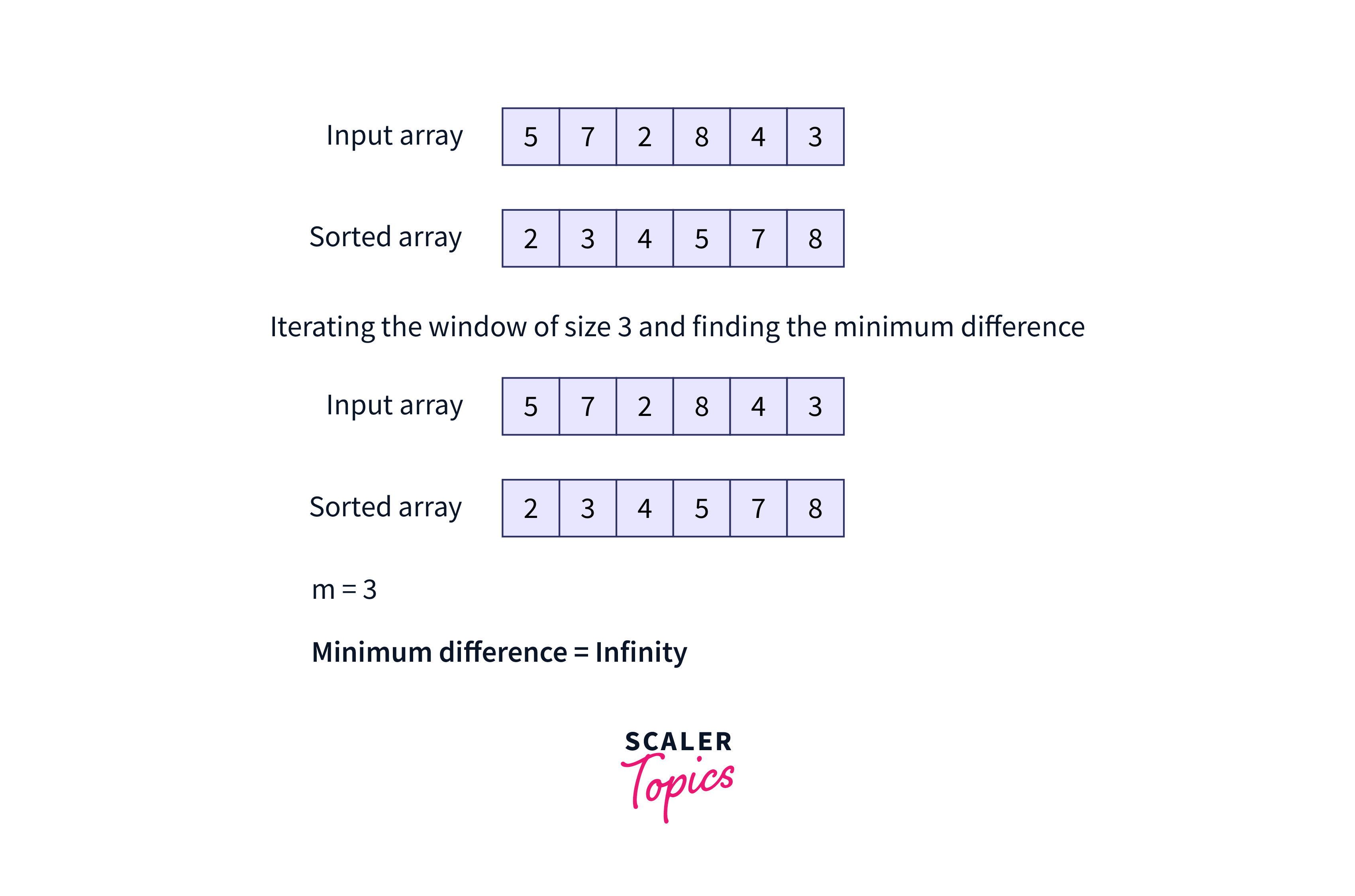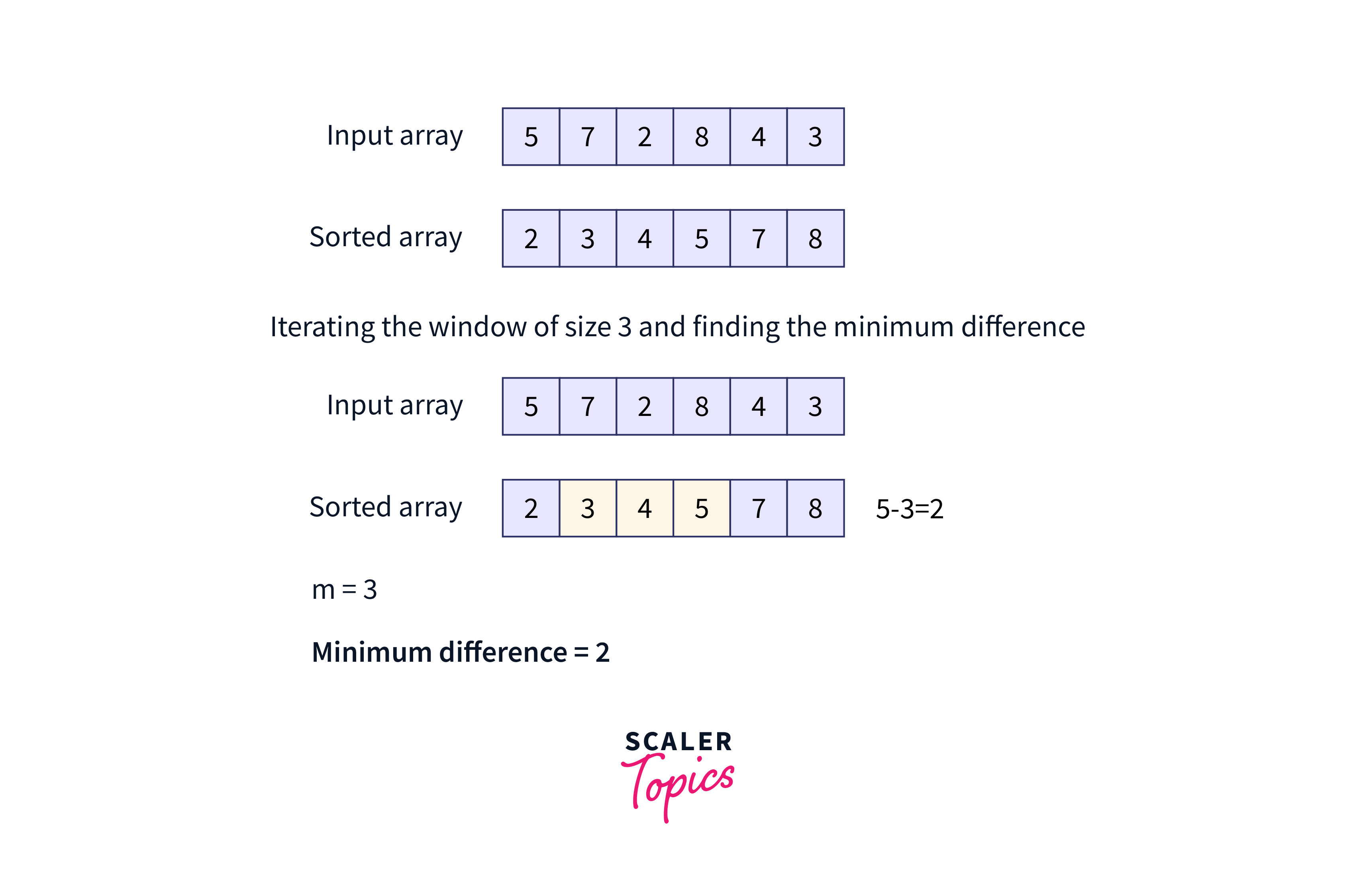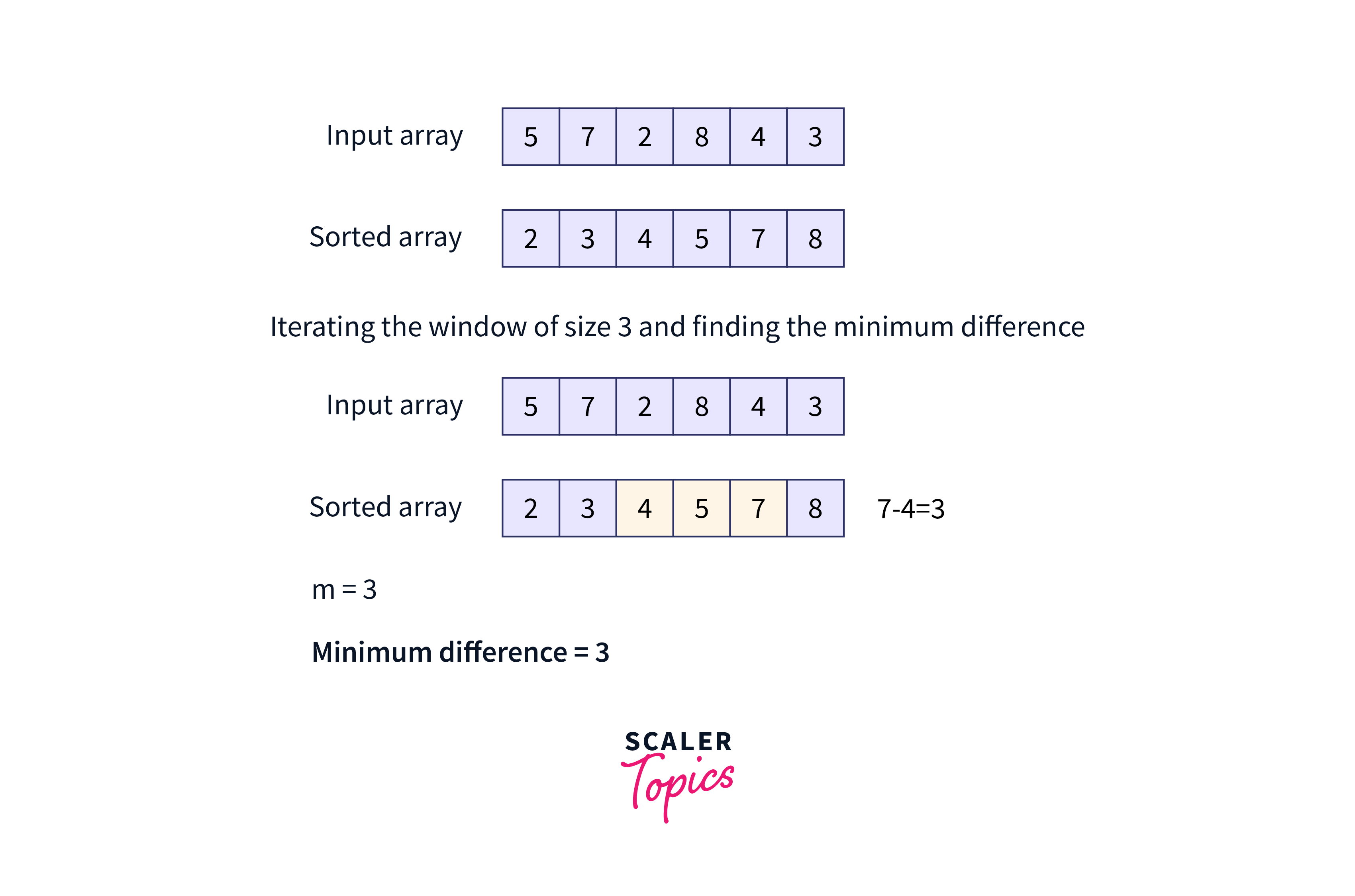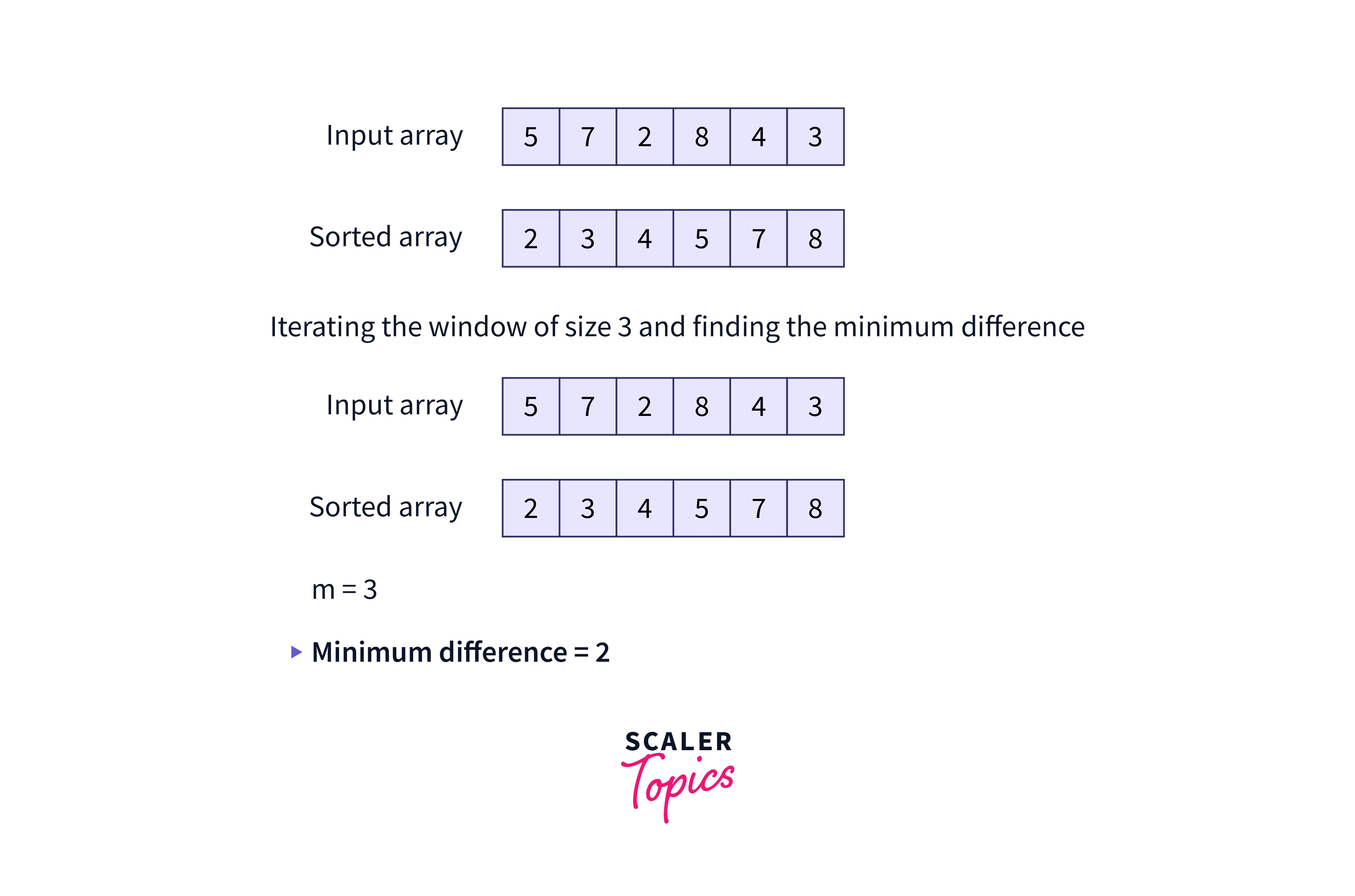
Hence, the minimum difference of subarrays of size m can be easily found in O(n) time.

Algorithm :

Here is the optimal algorithm for this particular problem:

• Firstly, we will sort the array so that it is easy to calculate the difference between the maximum and minimum chocolates.
• Then we will initialize an answer variable with Integer.MAX_VALUE (because we are supposed to find the minimum), where we will store the minimum difference.
• Then we will iterate with a window of size m, that is, from i = 0 to i = size – m (where m is the number of children).
• Then we will initialize a minimumChocolate variable to arr[i] and maximumChocolate variable to arr[i+m-1].
• Then we will initialize a difference variable which will contain the difference between the maximumChocolate and the minimumChocolate variable maximumChocolate – minimumChocolate.
• Then we will check if the difference variable is less than the answer variable.
• If it is true we will update our answer variable to the difference variable.
• After iteration is completed, we will just return the answer and that will be our required answer.

Code

Now, let us see the code of chocolate distribution problem in different programming languages.

Code in JAVA :

// JAVA Code For Chocolate Distribution
// Problem
import java.util.*;
public class Main
{
    // Function to find the minimum difference
    public static int minDifferenceFinder(int[] arr, int size, int m)
    {
        // If there are no chocolates or
        // number of students is 0
        if (m == 0 || size == 0)
            return 0;
            
        // To store the minimum difference 
        int answer = Integer.MAX_VALUE;
        
        // Sort the given packets   
        Arrays.sort(arr);
        
        // Find the subarray of size m
        // such that difference between
        // last (maximum in case of
        // sorted) and first (minimum in
        // case of sorted) elements of
        // subarray is minimum.
        for (int i=0; i<=size-m; i++)
        {
            int minimumWindow = arr[i];
            int maximumWindow = arr[i+m-1];
            int gap = maximumWindow- minimumWindow ;
            
            if(gap < answer)
            {
                answer = gap;
            }
        }
        return answer;
    }
    
    //main function
    public static void main(String[] args) 
    {
      // arr[0..n-1] represents sizes of packets    
      int[] arr = {3, 4, 1, 9, 56, 7, 9, 12};
      
      // Number of students
      int m = 5;
      
      //Length of arr
      int size = arr.length;
      
      //Print minimum difference
      System.out.println("Minimum difference is " +minDifferenceFinder(arr, size, m));
    } 
}

Output :

6

Code in Python :

# Python3 program to solve
# chocolate distribution
# problem


# arr[0..n-1] represents sizes of packets
# m is number of students.
# Returns minimum difference between maximum
# and minimum values of the distribution.
def findMinDiff(arr, n, m):

	# if there are no chocolates or number
	# of students is 0
	if (m==0 or n==0):
		return 0

	# Sort the given packets
	arr.sort()

	# Number of students cannot be more than
	# number of packets
	if (n < m):
		return -1

	# Largest number of chocolates
	min_diff = arr[n-1] - arr[0]

	# Find the subarray of size m such that
	# difference between last (maximum in case
	# of sorted) and first (minimum in case of
	# sorted) elements of subarray is minimum.
	for i in range(len(arr) - m + 1):
		min_diff = min(min_diff , arr[i + m - 1] - arr[i])
	
		
	return min_diff

# Driver Code
if __name__ == "__main__":
	arr = [3, 4, 1, 9, 56, 7, 9, 12]
	m = 5 # Number of students
	n = len(arr)
	print("The Minimum difference is", findMinDiff(arr, n, m))

Output :

The minimum difference is 6

Code in C++ :

// C++ program to solve chocolate distribution
// problem
#include <bits/stdc++.h>
using namespace std;

// arr[0..n-1] represents sizes of packets
// m is number of students.
// Returns minimum difference between maximum
// and minimum values of distribution.
int findMinDiff(int arr[], int n, int m)
{
	// if there are no chocolates or number
	// of students is 0
	if (m == 0 || n == 0)
		return 0;

	// Sort the given packets
	sort(arr, arr + n);

	// Number of students cannot be more than
	// number of packets
	if (n < m)
		return -1;

	// Largest number of chocolates
	int min_diff = INT_MAX;

	// Find the subarray of size m such that
	// difference between last (maximum in case
	// of sorted) and first (minimum in case of
	// sorted) elements of the subarray are minimum.

	for (int i = 0; i + m - 1 < n; i++) {
		int diff = arr[i + m - 1] - arr[i];
		if (diff < min_diff)
			min_diff = diff;
	}
	return min_diff;
}

int main()
{
	int arr[] = { 3, 4, 1, 9, 56, 7, 9, 12 };
	int m = 5; // Number of students
	int n = sizeof(arr) / sizeof(arr[0]);
	cout << "The Minimum difference is "
		<< findMinDiff(arr, n, m);
	return 0;
}

Output :

The minimum difference is 6

Complexity Analysis

This is the most optimal approach, and it will have a very efficient solution, with very less time and space complexity.

Time Complexity

As we are sorting the array at first, which will take O(nlogn) time which will overshadow the linear iteration of the sorted array which will take O(n) time. Hence, the time complexity is O(nlogn).

Time Complexity : O(nlogn).

Space Complexity

Assuming we are using an in-place sorting algorithm, Hence, the space complexity will be constant O(1).

Space Complexity : O(1).

Conclusion

In this article, we learned about the problem, the chocolate distribution problem. Let us recap the points we discussed throughout the article:

• Basically, in the chocolate distribution problem, we will be given an array and number of children, and we have to find the difference between the number of chocolates in the packet with maximum chocolates and the packet with minimum chocolates given to the students is minimum.
• Firstly, we applied the brute force approach in which we will find all the subsets of size m (number of children) from the array, and iterate over them, and find the minimum difference.
• In the brute force approach, the time complexity will be exponential O(2^n), and also the space complexity will be exponential O(2^n). This approach is very inefficient and slow.
• Then, we applied the optimal approach, in which we will use the sorting technique.
• At first, we will sort the given array, then we will iterate over the array with a window of size m (number of children) and keep storing the minimum difference.
• In the optimal approach, the time complexity will be only O(nlogn) and the space complexity will be O(1). This approach is very efficient and fast.

Frequently Asked Questions

1. How should we approach a problem like this? 
   Answer : Firstly, you need to understand the problem properly. Then think of a algorithm for this problem. Then begin with the Brute Force approach. Later, try to optimise your code.
2. What is the minimisation problem? 
   Answer : Finding the minimum possible value for the given function.
3. Which is the best sorting algorithm? 
   Answer : Merge Sort algorithm is the best sorting algorithm.