Divide and Conquer Algorithm

Divide and Conquer is a fundamental algorithmic technique in computer science, where a problem is divided into smaller, more manageable sub-problems, solved individually, and then combined to form the final solution. Divide and conquer algorithm approach not only simplifies complex problems but also enhances computational efficiency.

How Does the Divide and Conquer Algorithm Work?

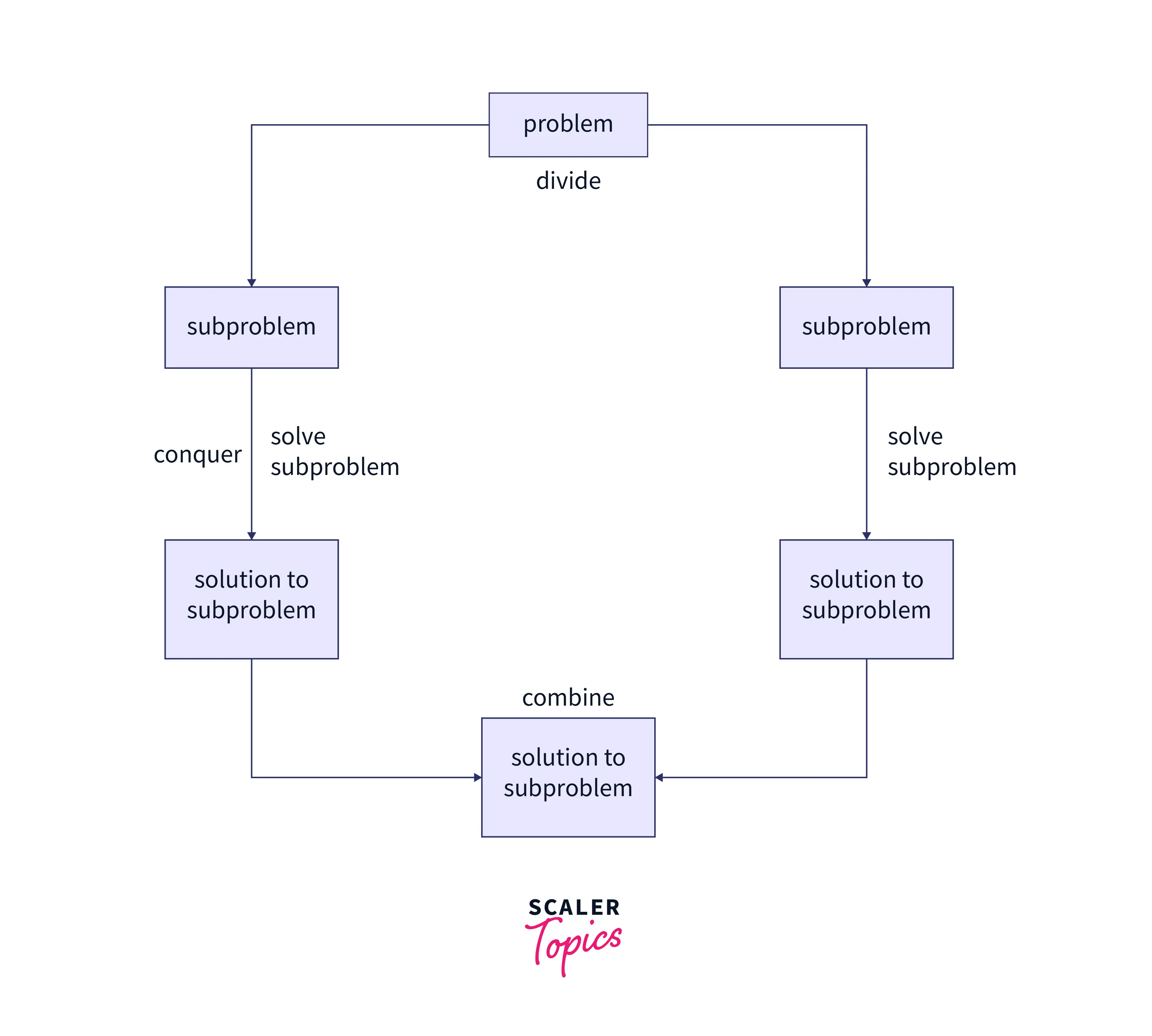
The divide and conquer strategy encompasses three main steps:

• Divide: The original problem is divided into smaller sub-problems that are similar to the original but simpler to solve.
• Conquer: These sub-problems are tackled recursively until they become simple enough to be solved directly.
• Combine: The solutions to the sub-problems are then combined to create a solution to the original problem.

This method is particularly effective for problems that can be broken down into similar, smaller problems, allowing for a more straightforward and efficient resolution. The entire process can be illustrated with the help of the diagram given below :

For example, we will be considering the following unsorted array of integers.

The output of the algorithm will be a sorted array with the values arranged in increasing order.

As we read earlier, the first step of the algorithm will be to divide the problem at hand into atomic sub-problems. In merge sort, we keep dividing the initial array (and thereafter the sub-arrays) into two halves recursively till the subarrays are no longer divisible, i.e., the size of the sub-arrays is one. This process can be visualized as follows :

Divide the original array into two parts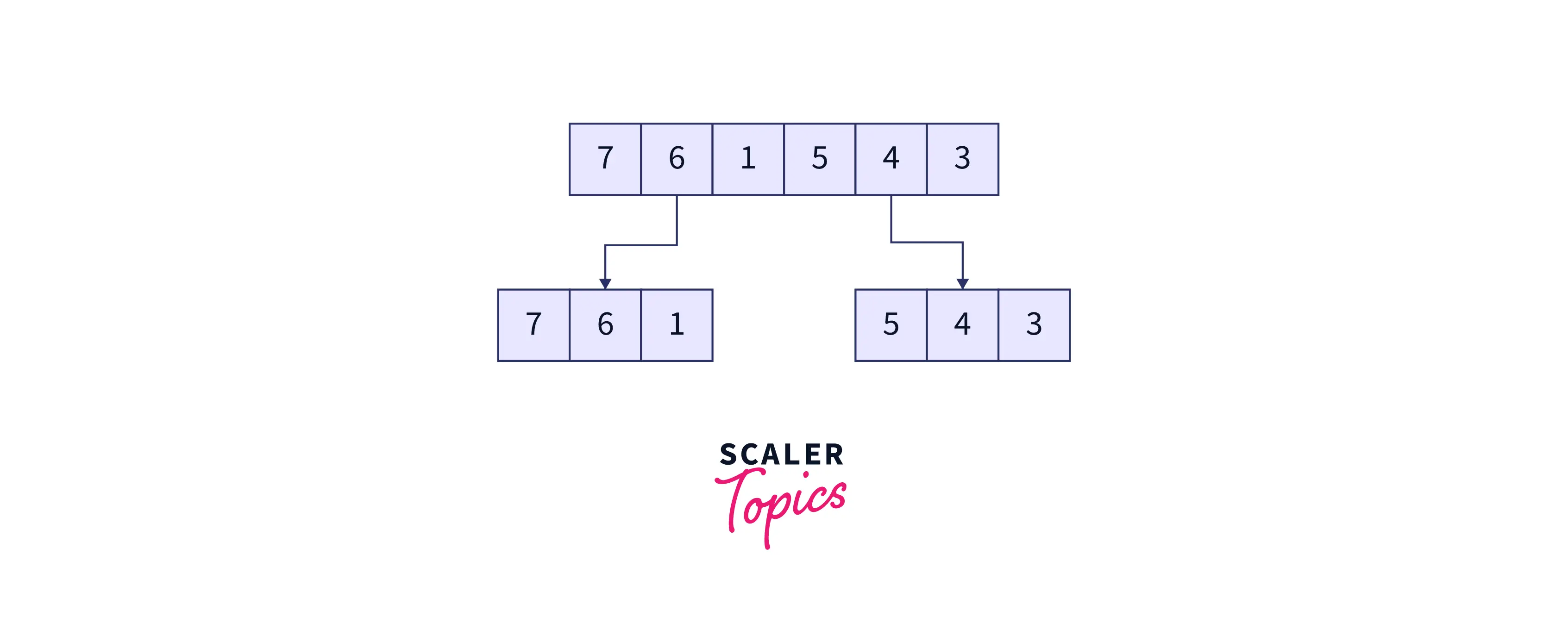

Divide the two sub-arrays, and hence the subsequent sub-arrays further until the size of all the sub-arrays equals one.

The resultant sub-arrays will be as follows. 

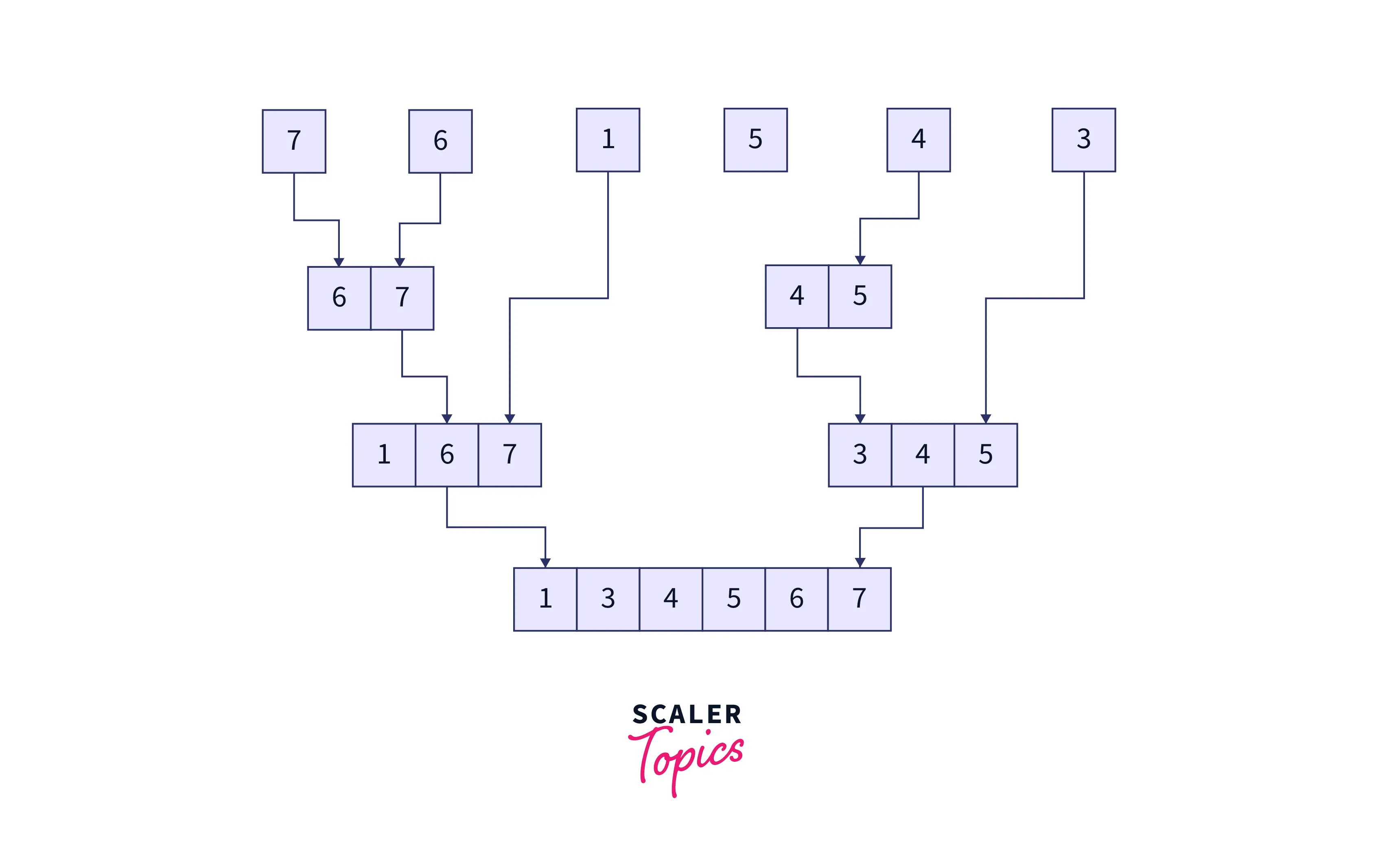
1. Now, we enter the conquer step of the algorithm where, as per the definition, these sub-arrays will be sorted individually. However, in practice, an array of sizes does not need any sorting. So this step is complete by default.
2. Finally, we arrive at the merge stage of the merge sort algorithm. Here, we will recursively combine the subarrays in a sorted manner until we are left with just one array.
   Here’s how the merging is done. We take two sorted subarrays, with a pointer at the left end of both subarrays. We keep adding whichever value (as denoted by both the pointers) is the smallest, to the solution array (and hence incrementing the pointers) until all the elements in both the subarrays are traversed. The following graphic explains the merge step.

This final array will be the required, sorted array. 

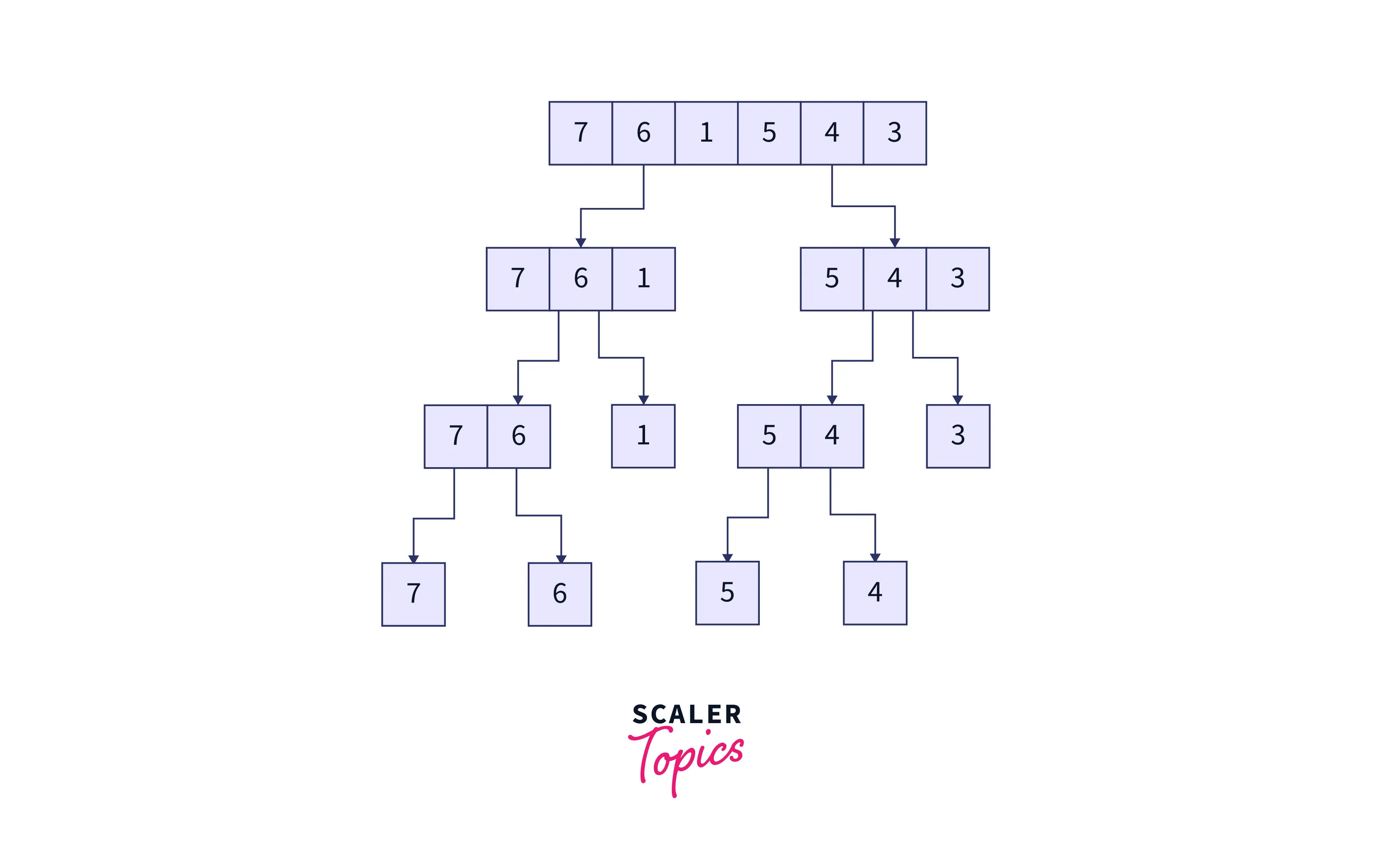
Merge sort has primarily three kinds of operation, as we discussed earlier.

• Divide operation :
  The divide operation is a constant time operation (O(1))(O(1)) regardless of the size of the subarray since we are just finding the middle index of the subarray (mid=(start+end)/2)(mid=(start+end)/2) and thereafter dividing the subarray into two parts based on this middle index. During the entire divide operation, we keep on dividing the initial array into 2 subarrays at each level, till we get subarrays of size 1. In total, there are going to be approximate log2nlog2n levels of division operations.
• Conquer operation :
  As we discussed earlier, upon breaking down the initial array to sub-arrays of size 1, these sub-arrays get sorted by default. Hence, the conquer operation has a constant time complexity of O(1)O(1).
• Merge operation :
  The merging operation at each level, where we sort and merge 2 subarrays at a time recursively, is a linear time operation, i.e., O(n)O(n). As we discussed earlier, since there are log2nlog2n levels in the division process, the merge step, on average, will take around n.log2nn.log2n steps.

Therefore, considering all three kinds of operations, merge sort results out to be an O(nlog2n)O(nlog2n) operation.

Comparing this to insertion sort or bubble sort, both of which have a quadratic time complexity of O(n2)O(n2), merge sort proves to be a relatively faster sorting algorithm, especially for large input sizes.

Thus, we understood how the divide and conquer algorithm works in practice. Next, let us compare the divide and conquer approach against the dynamic programming approach for problem-solving.

Difference Between Divide and Conquer and Dynamic Programming

When it comes to how a problem is tackled during problem-solving, both the divide and conquer as well as the dynamic programming algorithms share a common characteristic:

Before solving it, the initial problem is atomized into smaller sub-problems, and then the final output is generated in a bottom-up approach where the individual sub-problems are solved and their resultant outputs are merged into the final solution.

However, the difference between these two algorithmic approaches only becomes evident after the atomization or division step. The difference lies in how the sub-problems are solved and merged into the final solution.

• Divide and conquer algorithms are often used as single-shot solutions where we don’t require re-calculations on the same problem or sub-problem data. As a result, storing the keys of the individual sub-problems will just result in the wastage of memory resources.
• On the other hand, we use dynamic programming algorithms when we tend to require the solution of the same sub-problems multiple times in the future. Thus saving the output for future reference will save some computation resources and help eliminate redundancy.

Let us take an example that will help us visualize the difference better. We will consider a problem where we want to find the nth Fibonacci number in the Fibonacci sequence.

Divide and conquer algorithm :

fib(n):
    if n < 2, return n
    else , return fib(n - 1) + fib(n - 2)

The above-given solution is based on the divide-and-conquer algorithmic approach. For every nth Fibonacci number in the Fibonacci sequence, we keep breaking it down as the sum of (n−1)th(n−1)th and (n−2)th(n−2)th Fibonacci numbers. This breakdown keeps occurring recursively until we reach the base case (i.e.(i.e.,index n=0n=0 or n=1)n=1). After reaching the base cases, we keep solving the individual subproblems and merging their solutions till we get the final solution, which is the nth Fibonacci number. The following example for deriving the 4th Fibonacci number will help us understand things better.

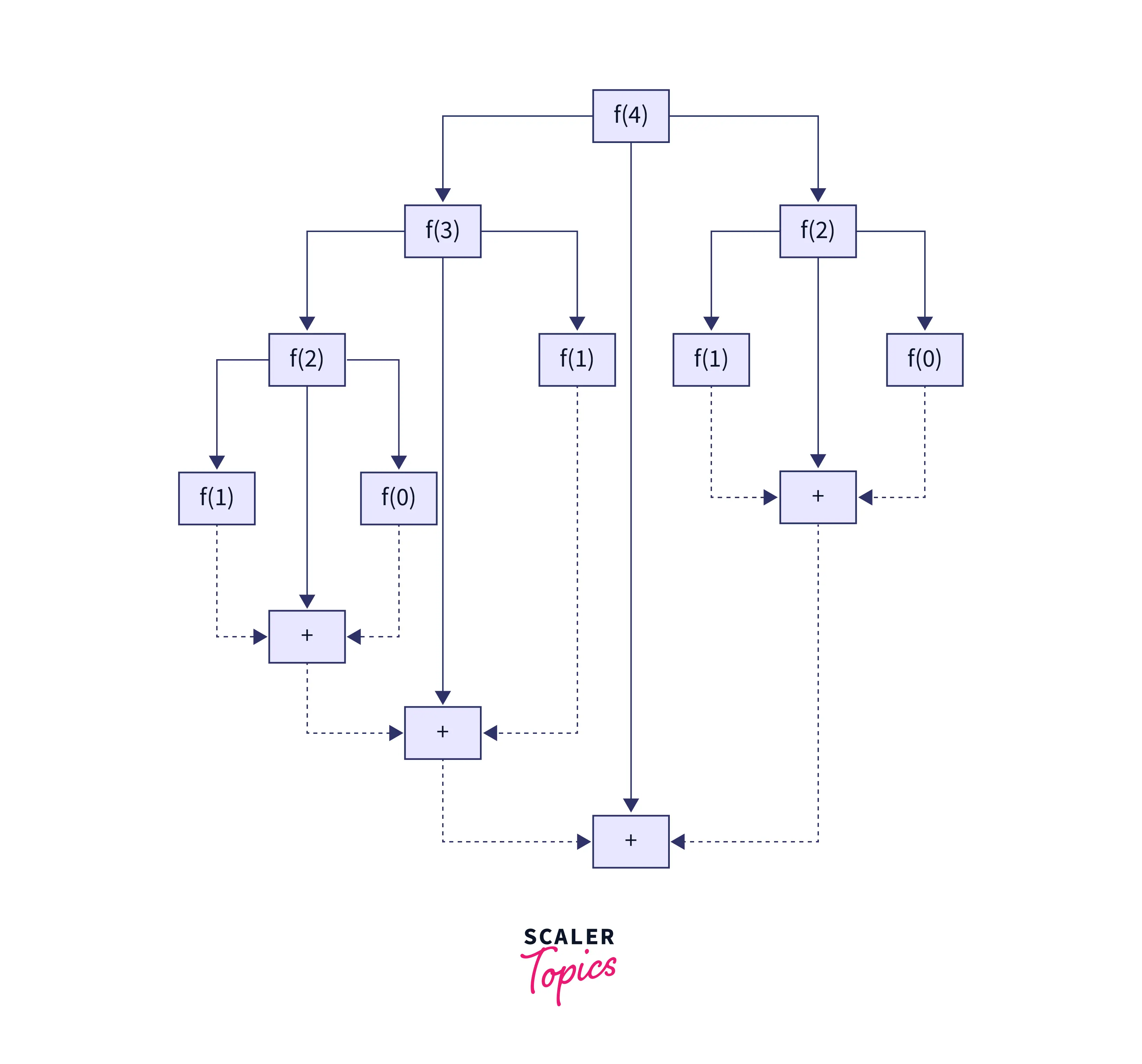
As you can see in the solution above, we aren’t storing any individual sub-problem results.

Dynamic programming algorithm :

memory = [ ]
fib(n):
    if n in memory: return memory[n]
    else,
        If n < 2, f = n
        else , f = f(n - 1) + f(n - 2)
        memory [n] = f
        return f

In the solution given above, we are storing the result of each sub-problem in the memory array. These stored solutions can then be referenced and reused in the future as we are further solving the problem. This saves us some repeated calculations down the line.

So now that we know how the divide and conquer algorithms work and how they differ from dynamic programming algorithms, let us now take a look at the advantages that the divide and conquer algorithms provide over the other classes of algorithms.

Advantages of Divide and Conquer Algorithms

Let’s discuss some advantages of divide-and-conquer algorithms.

• For sorting the values in an array, merge sort and quicksort are two of the fastest known sorting algorithms with the average-case time complexity of O(nlog2n) . Both these algorithms are based on the divide and conquer algorithmic approach.
• The brute force approach of matrix multiplication is an O(n3) operation, which is computationally very expensive. On the other hand, using a divide and conquer approach for the same (eg.- by using Strassen’s matrix multiplication), this time complexity can be reduced to O(n2.8074) .
• For other problems too like the famous Tower of Hanoi or searching an element within a sorted array, the divide and conquer approach is known to give the optimal solution.
• Divide and conquer algorithms are known for making efficient use of memory caches, and are suitable for multi-processing systems.

Finally, now that we are well aware of some of the advantages of the divide-and-conquer paradigm, we’ll go ahead and take a look at the application of these algorithms in the field of computer science.

Application of Divide and Conquer Algorithms

Here are some of the most common applications of the divide-and-conquer algorithmic approach.

• Binary Search
  Binary search is a search-based algorithm that follows the divide and conquers approach and can be used for searching a target element within a sorted array.
• Merge Sort
  Earlier, we saw the working of merge sort, which is a divide and conquer-based sorting algorithm, with the worst-case time complexity of O(nlog2n).
• Quick Sort
  Quick sort, as we saw earlier, is another divide-and-conquer-based sorting algorithm that is often regarded as one of the fastest sorting algorithms, especially for large array sizes.
• Strassen’s Matrix Multiplication :
  While dealing with matrix multiplication for large matrix sizes, Strassen’s matrix multiplication algorithm tends to be significantly faster as compared to the standard matrix multiplication algorithm.
• Karatsuba Algorithm :
  The Karatsuba algorithm is a highly efficient algorithm for the multiplication of n-bit numbers. It is a divide and conquers algorithm that performs the multiplication operation with a time complexity of O(n1.59) as compared to the O(n2) of the brute force approach.

Apart from the above-mentioned algorithms, there exist several other algorithms within the divide and conquer paradigm too that can be used to solve a multitude of problem types.

Conclusion

• Divide and Conquer is an approach for problem-solving, which involves breaking down a given problem into smaller sub-problems and then individually solving these sub-problems before merging them into the final solution.
• Divide and conquer algorithms are somewhat similar to dynamic programming algorithms, but here we do not store the result of individual sub-problem solutions. On the contrary, dynamic programming algorithms keep a track of these individual solutions for future reference.
• Real-life examples like Binary Search, Merge Sort, Quick Sort, and Strassen’s Matrix Multiplication show that divide and conquer can be an effective technique in solving those problems.