Doubly Linked List

A Doubly Linked List enhances the standard Linked List by allowing bidirectional navigation. Each node points to both the next and the previous node, enabling efficient forward and backward traversal. This structure contrasts with Single Linked Lists, where movement is restricted to one direction, making it challenging to access previous elements without iterating from the start.

What is Doubly Linked List?

Doubly Linked List is a Data Structure, which is a variation of the Linked List, in which the transversal is easily possible in both directions, forward and backwards, as compared to the Singly Linked List, or simply called a Linked List.
You might be aware of the tabs on Windows/Mac. You can loop over all the opened applications and switch between them in both directions.
This can be thought of as all these applications being linked via a Doubly Linked List data structure, and you can switch to the applications on both sides of the current application.

So if a Linked List ⇒ A → B → C
Then a Doubly Linked List ⇒ A ⇆ B ⇆ C

Representation of Doubly Linked List in Data Structure

The Doubly Linked List has 3 parts: Value, Next pointer, and the Previous pointer.

The Previous pointer is the fundamental difference between the Doubly Linked List and the Linked List, which enables one to transverse back also in the Doubly Linked List.

As per the above illustration, following are the important points to be considered.

• Each Doubly Linked List Element contains pointers to next and Previous Elements and the data field.
• The First Element will have its Previous pointer as Null, to mark the start of the List.
• The Last Element will have its Next pointer as Null, to mark the end of the List.

The memory representation in a Doubly Linked List is not necessarily contiguous, as illustrated below:

In this diagram, -1 represents the NULL value, indicating the start or end of the list. For example, the first node (A) has its previous address as -1, and the last node (D) has its next address as -1, forming the structure -1 ← A ⇆ B ⇆ C ⇆ D → -1.

Insertion Operation In Doubly Linked List

Insertion at the Beginning

1. Start with the initial doubly linked list: A ⇆ B ⇆ C.
2. Insert X to become the first element: X ⇆ A ⇆ B ⇆ C.
3. Change X.previous to NULL and X.next to point to the original head (A).
4. Set A.previous to X to link A back to the new head.
5. Update Head to point to X, making X the new first element of the list.

Code

    // Adding a node at the front of the list
    public void insertFront(int newValue) {

       // Create New Node and put data in it.
       Node newNode = new Node(newValue);

       // Update next of the new node as head and previous as NULL.
       newNode.next = head; // i.e. X.next = A. Head points to A yet.

       // Since X = first Node, so its prev should point to NULL.
       newNode.previous = null; 

       // Change prev of head node to new node
       // Head points to A, so change A Previous to be X.
       if (head != null)
           head.previous = newNode;

       // Since X and A pointers are altered, we can not point Head to X which is the new start of the DLL.
       head = newNode;
    }

Insertion in Between Nodes

Insert After a Node

1. Start with the current doubly linked list: B ⇆ C ⇆ D ⇆ E.
2. To insert X after C, change the list to: B ⇆ C ⇆ X ⇆ D ⇆ E.
3. Adjust C.next to point to X.
4. Change D.prev to point to X.
5. Set X.prev to C and X.next to D, linking X correctly between C and D.

Code

    // Given a node as previousNode, insert a new node after it.
public void InsertAfter(Node previousNode, int newValue) {

   // Check if the given prev_node is NULL
   if (previousNode == null) {
       System.out.println("The given previous node cannot be NULL ");
       return;
   }

   // Create New Node and put data in it.
   Node newNode = new Node(newValue);

   // Make next of new node as next of previous node
   // X --> C.next i.e. X --> D
   newNode.next = previousNode.next;

   // Make the next of previousNode as newNode
   // C --> X
   previousNode.next = newNode;

   // Make previousNode as previous of newNode
   // C <-- X
   newNode.previous = previousNode;

   // Change the previous of D to point to X.
   // newNode.next = D, D.previous = X OR set X <-- D
   if (newNode.next != null)
       newNode.next.previous = newNode;
}

Insert Before a Node

1. Starting point: B ⇆ C ⇆ D ⇆ E.
2. Goal: Insert X before C to get B ⇆ X ⇆ C ⇆ D ⇆ E.
3. Change C.prev (previously pointing to B) to point to X.
4. If C was the first node (no B), update Head to point to X.
5. Configure X’s pointers: X.prev points to B, and X.next points to C.

Code

void insertBefore(Node head, Node nextNode, int newValue) {

    // Check if the given nextNode is NULL
    if (nextNode == null) {
        System.out.print("The given next node cannot be NULL");
        return;
    }

    // Create New Node and put data in it.
    Node newNode = new Node(newValue);

    // Make prev of new node as prev of nextNode
    // C.Prev <-- X OR B <-- X
    newNode.previous = nextNode.previous;

    // Make the prev of nextNode as newNode
    // X <-- C
    nextNode.previous = newNode;

    // Make nextNode as next of newNode
    // X --> C
    newNode.next = nextNode;

    // Change next of newNode's previous node
    // X.previous = B so B.next = X i.e. B --> X
    if (newNode.previous != null)
        newNode.previous.next = newNode;
    else
        // If the prev of newNode is NULL, it will be the new head node
        head = newNode;

 }

Insertion at the End

1. Initial state: A ⇆ B ⇆ C.
2. Insert X at the end: A ⇆ B ⇆ C ⇆ X.
3. Update C.next from Null to X.
4. Set X.prev to C and X.next to Null.

Code:

// Add a node to the end
void insertAtEnd(int newValue) {
   // Create New Node and put data in it.
   Node newNode = new Node(newValue);

   // Since this Node = Last Node, its Next needs to be Null.
   newNode.next = null;

   // If the Linked List is empty, then make this new Node as head
   if (head == null) {
       newNode.previous = null;
       head = newNode;
       return;
   }

   Node last = head;
   // Else traverse till the last node
   while (last.next != null)
       last = last.next;

   // Change the next of last node
   // C --> X
   last.next = newNode;

   // Make last node as previous of new node
   // C <-- X
   newNode.previous = last;
}

Deletion Operation In Doubly Linked List

Deletion at the Beginning

1. Start with the doubly linked list A ⇆ B ⇆ C.
2. Identify the node to delete, which is the head node A.
3. Update the head to point to A.next, making B the new head.
4. Adjust B.previous to point to Null, disconnecting A from the list.
5. The deletion of A is confirmed with the head now pointing to B, and B having no previous node.

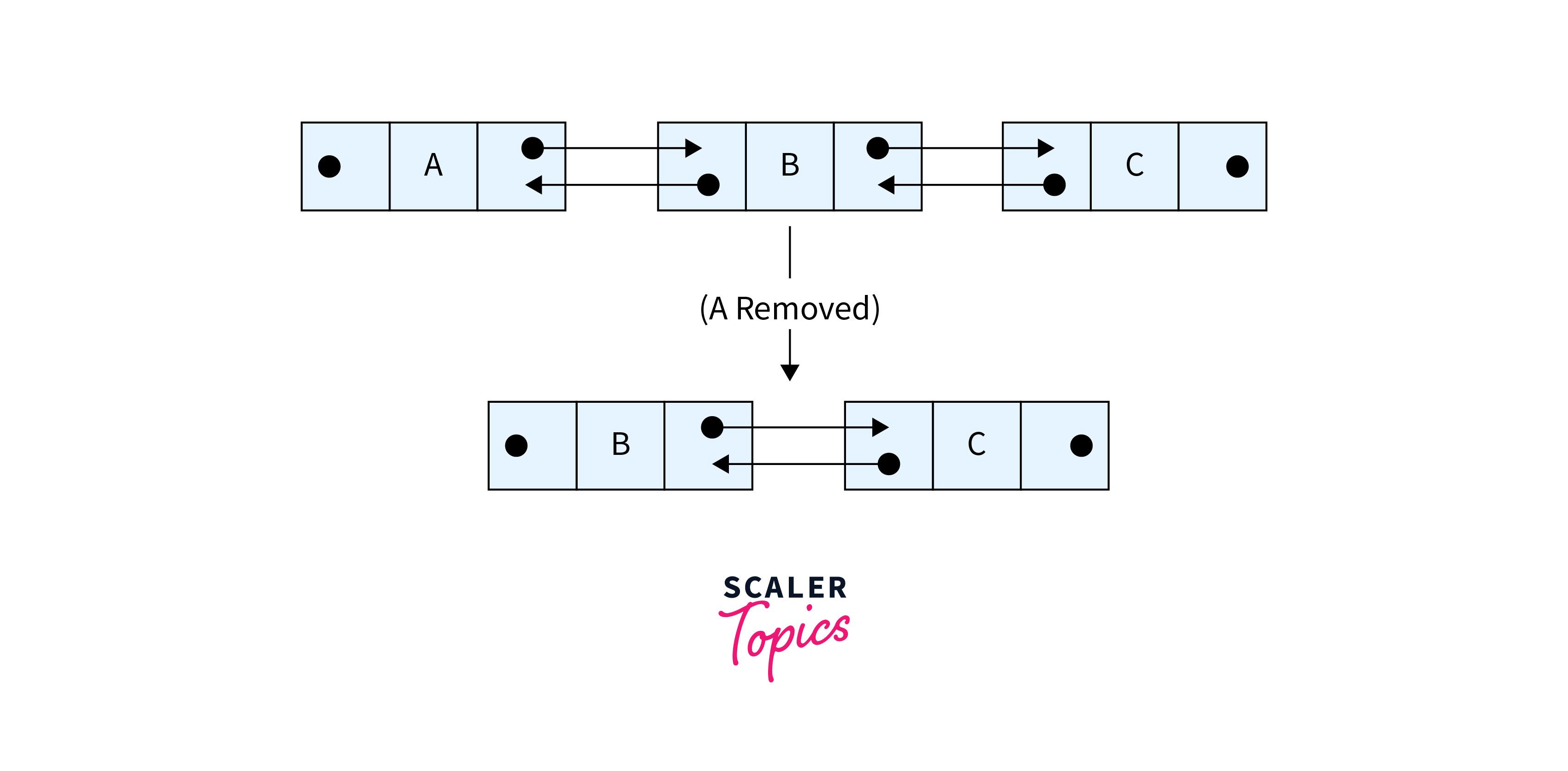
Deletion of the Inner Node

1. Start with the doubly linked list A ⇆ B ⇆ C.
2. Identify the inner node to delete, for example, B.
3. Update A.next to point to C, skipping over B.
4. Change C.previous to point to A, disconnecting B from C.
5. By updating these pointers, B is effectively removed from the list, resulting in A ⇆ C.

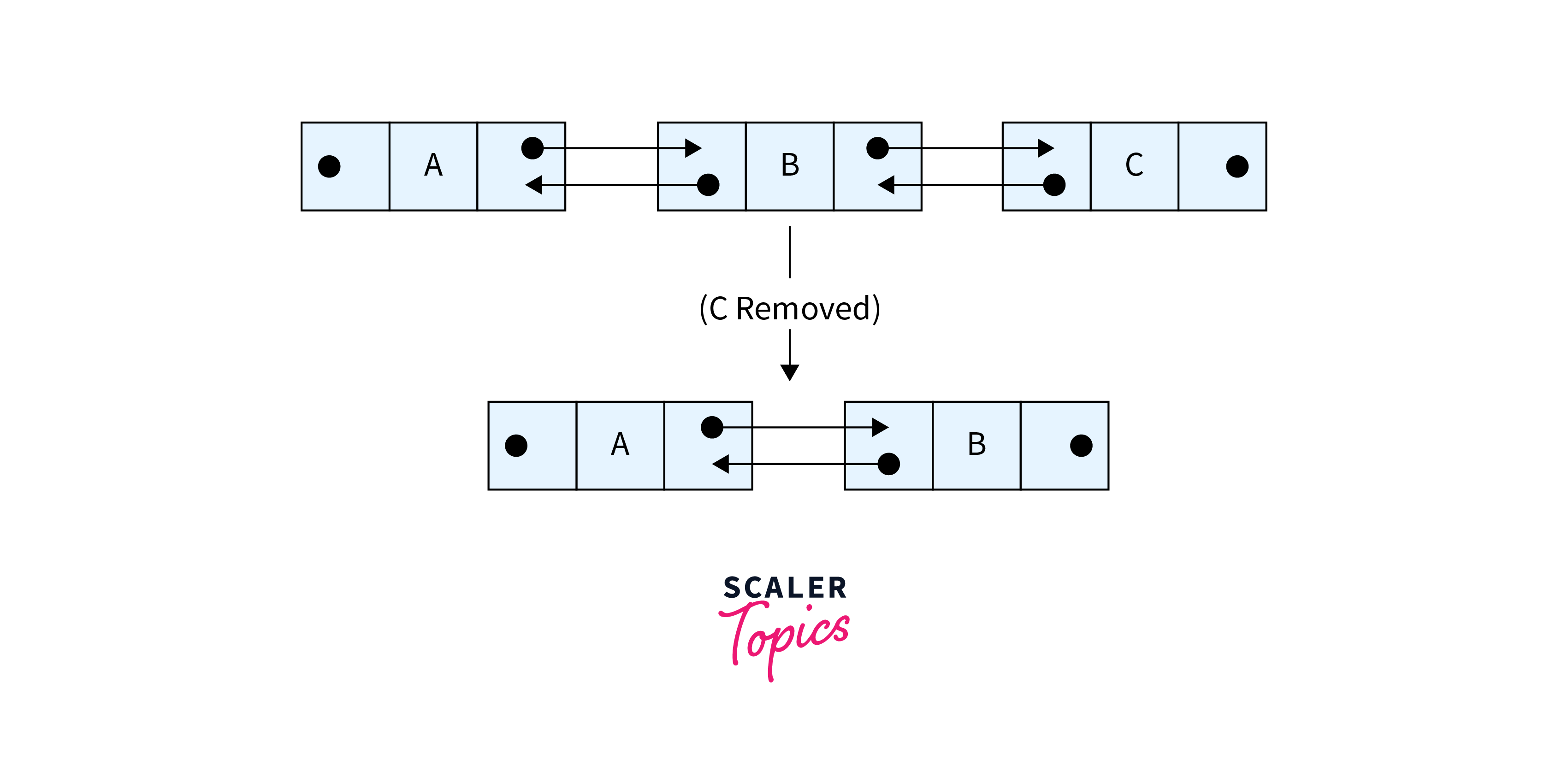
Deletion at the End

1. Begin with a doubly linked list, for instance, A ⇆ B ⇆ C.
2. Identify the node at the end to delete, which is C.
3. Change B.next, which previously pointed to C, to Null, indicating the end of the list.
4. Since C is the last node, there’s no C.next to update.
5. With B.next now pointing to Null, C is effectively removed from the list, leaving A ⇆ B as the updated list.

Code

void deleteNode(Node nodeToDelete) {

   // If the DLL is Empty or the NodeToDelete is Null, then there is nothing to do.
   if (head == null || nodeToDelete == null) {
       return;
   }

   // If node to be deleted is head node of the list
   // Head now points to the next of nodeToDelete meaning nodeToDelete is not a part of DLL anymore.
   if (head == nodeToDelete) {
       head = nodeToDelete.next;
   }

   // If nodeToDelete is NOT the last node:
   // A --> B --> C, Delete B, then A <-- C
   if (nodeToDelete.next != null) {
       nodeToDelete.next.previous = nodeToDelete.previous;
   }

   // If nodeToDelete is NOT the first node
   // A --> B --> C, Delete B, then A --> C
   if (nodeToDelete.previous != null) {
       nodeToDelete.previous.next = nodeToDelete.next;
   }

}

Doubly Linked List Code Implementation

#include <iostream>
using namespace std;

// Define the Node structure
struct Node {
    int data;
    Node* prev;
    Node* next;

    // Constructor to create a new node
    Node(int data) : data(data), prev(NULL), next(NULL) {}
};

// Class for Doubly Linked List
class DoublyLinkedList {
public:
    Node* head; // Head pointer for the list

    // Constructor to create an empty list
    DoublyLinkedList() : head(NULL) {}

    // Function to insert a node at the front of the list
    void insertAtFront(int data) {
        Node* newNode = new Node(data);
        newNode->next = head;
        if (head != NULL) {
            head->prev = newNode;
        }
        head = newNode;
    }

    //insert a node at the end of the list
    void insertAtEnd(int data) {
        Node* newNode = new Node(data);
        if (head == NULL) {
            head = newNode;
            return;
        }
        Node* temp = head;
        while (temp->next != NULL) {
            temp = temp->next;
        }
        temp->next = newNode;
        newNode->prev = temp;
    }

    //  insert a node after a given node
    void insertAfter(Node* prevNode, int data) {
        if (prevNode == NULL) {
            cout << "Previous node cannot be NULL" << endl;
            return;
        }
        Node* newNode = new Node(data);
        newNode->next = prevNode->next;
        prevNode->next = newNode;
        newNode->prev = prevNode;
        if (newNode->next != NULL) {
            newNode->next->prev = newNode;
        }
    }

    // Function to delete a node from the front of the list
    void deleteFromFront() {
        if (head == NULL) return;
        Node* temp = head;
        head = head->next;
        if (head != NULL) {
            head->prev = NULL;
        }
        delete temp;
    }

    // Function to delete a node from the end
    void deleteFromEnd() {
        if (head == NULL) return;
        if (head->next == NULL) {
            delete head;
            head = NULL;
            return;
        }
        Node* temp = head;
        while (temp->next != NULL) {
            temp = temp->next;
        }
        temp->prev->next = NULL;
        delete temp;
    }

    // Function to delete a specific node
    void deleteNode(Node* delNode) {
        if (head == NULL || delNode == NULL) return;
        if (head == delNode) {
            head = delNode->next;
        }
        if (delNode->next != NULL) {
            delNode->next->prev = delNode->prev;
        }
        if (delNode->prev != NULL) {
            delNode->prev->next = delNode->next;
        }
        delete delNode;
    }

    // Function to print the list
    void printList() {
        Node* temp = head;
        while (temp != NULL) {
            cout << temp->data << " ";
            temp = temp->next;
        }
        cout << endl;
    }
};

int main() {
    DoublyLinkedList dll;

    // Insertions
    dll.insertAtEnd(1);
    dll.insertAtFront(2);
    dll.insertAtEnd(3);
    dll.insertAfter(dll.head->next, 4);

    cout << "List after insertions: ";
    dll.printList();

    // Deletions
    dll.deleteFromFront();
    cout << "List after deleting from front: ";
    dll.printList();

    dll.deleteFromEnd();
    cout << "List after deleting from end: ";
    dll.printList();

    dll.deleteNode(dll.head->next); // Assuming this node exists
    cout << "List after deleting a specific node: ";
    dll.printList();

    return 0;
}

Doubly Linked List Complexity Analysis

For Insertion operations in a doubly linked list, the complexities are as follows:

• Time Complexity: O(1) or O(n)
• Auxiliary Space: O(1)

For Deletion operations in a doubly linked list, the complexities are as follows:

• Time Complexity: O(1)
• Auxiliary Space: O(1)

Advantages of Doubly Linked List Compared to Singly Linked List

• Doubly linked lists allow bidirectional traversal, making operations like reverse traversal more efficient.
• Deletion of a node in a doubly linked list is more efficient as it does not require traversal from the head to find the previous node.
• It’s easier to insert or delete nodes from both ends of the list, as both head and tail pointers are maintained.
• Doubly linked lists facilitate the implementation of more complex data structures like linked lists with parent pointers, which are useful in hierarchical structures such as trees.
• They provide better flexibility for certain algorithms and operations, such as those needing to frequently access previous and next elements.

Disadvantages of Doubly Linked List Compared to Singly Linked List

• Doubly linked lists consume more memory per node as they require an extra pointer to store the address of the previous node.
• Operations like insertion and deletion involve updating more pointers, increasing the complexity and potential for errors.
• The extra pointer in each node can lead to higher overhead in terms of memory management and allocation, especially in systems with limited memory resources.
• Traversing and modifying a doubly linked list can be slightly slower due to the additional pointer operations involved.
• The increased complexity in managing two pointers per node can make the code more complex and harder to understand, especially for beginners.

Applications of Doubly Linked List

• Navigation systems that require forward and backward traversal, such as web browser history or a music playlist.
• Implementing complex data structures like linked lists, stacks, queues, and their variations.
• Creating a base for advanced data structures like Fibonacci heaps, or for algorithms requiring quick insertion and deletion from both ends, like the LRU cache.
• Facilitating undo functionality in applications by allowing backward traversal to previous states.
• Managing windows in software applications where users can easily switch between currently open windows or tabs.

Conclusion

• As we have seen, the doubly linked list can transverse in both directions using an extra pointer “previous”.
• Since the doubly linked list has an extra pointer, it has some downsides like:
  • storing this pointer over the Singly Linked list takes extra memory.
  • Every operation(insert/delete, etc.) has an extra overhead of managing the previous pointer.
• On the other hand, we can see that with an extra pointer, we can transverse in both directions, which finds its applications in many systems.