Expression Tree

This article mainly explains Expression trees. Expression trees are binary trees where the internal nodes denote operators (“+”, “-“, “/”, “*”,”^”) whereas the leaf nodes denote operands. These expression trees are used to implement or represent various kinds of expressions like infix, postfix, and prefix expressions.

What is the Expression Tree?

Expression trees are the binary trees that are used to express various expressions like infix, postfix, and prefix expressions. The internal nodes of this expression tree consist of operators like +, -, \*,/,^, etc. And the external nodes(leaf nodes) of the Expression tree contain the operands, on which operations are performed. The leaves of an Expression tree always contain the operands that can be of any data type like character, integer, double, etc.

The below-given image is an example of the Expression tree:

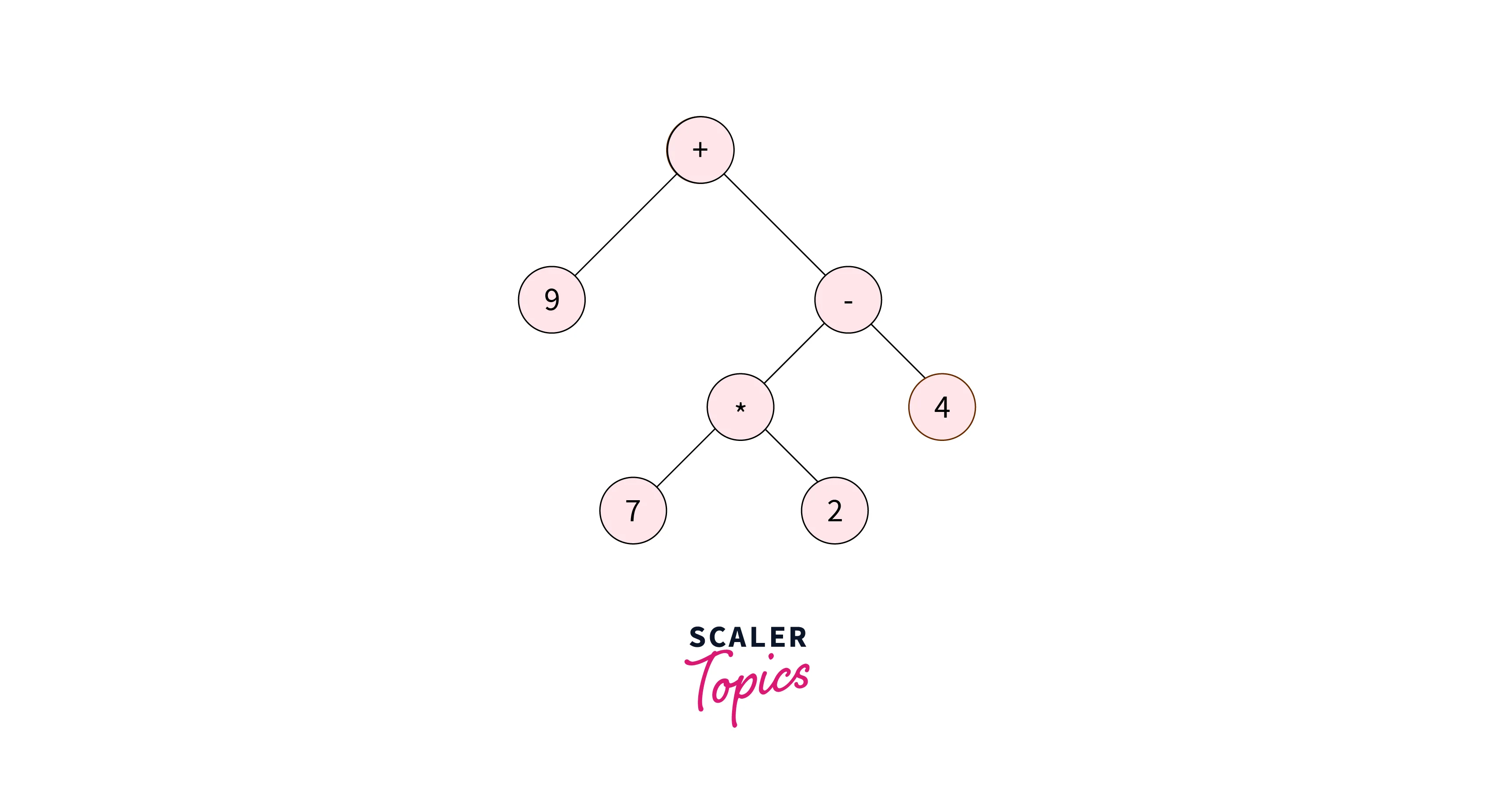
The below article clearly explains how the Expression tree is formed from the given expression.

Evaluating the Expression Represented by an Expression Tree

For evaluation of the expression which is represented by an Expression tree, we use recursion. We follow a preorder traversal, to find the value of the expression. Firstly the left subtree is processed and then the right subtree of the root node is processed in the recursion. Below are the steps to be followed to evaluate an expression from the expression tree:

Assume that ExpTree is the root of the Expression tree which is given. Following are the steps involved in

 If  ExpTree is not null then we need to check for:
      If ExpTree.val is an operand:
          return ExpTree.val

      // If ExpTree.val is an operator,
      // Solve for the value of expression represented by ExpTree.left
      Left = Solve_Exp(ExpTree.left)

      // Solve for the value of expression represented by ExpTree.right
      Right = Solve_Exp(ExpTree.right)

      // Apply ExpTree.val between these two values and return the answer
     return Calculate_Exp(Left, Right, ExpTree.value)

Let’s understand more about how the expression is evaluated for the below image:

Consider this is the tree and the expression obtained is evaluated as:

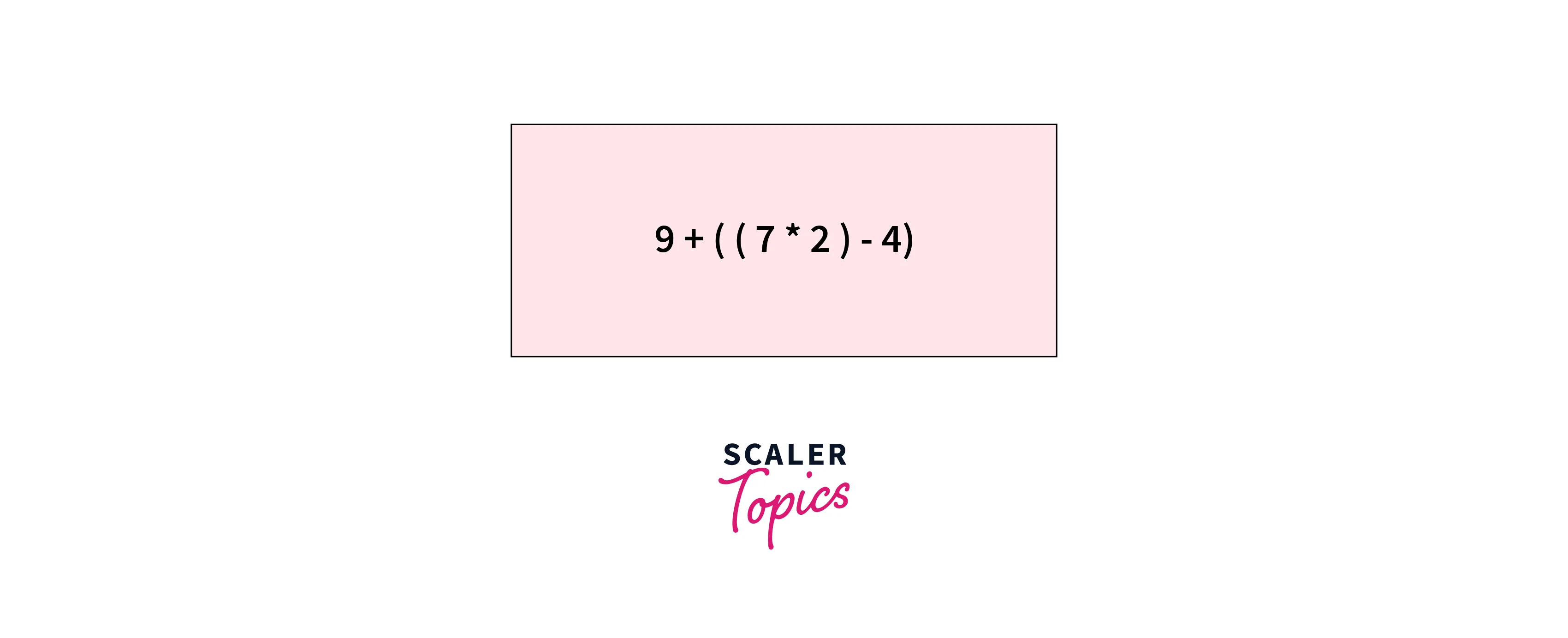
This expression is formed for the Expression tree present in the first image.

How to Construct an Expression Tree?

• After understanding the basic definition of Expression trees, let’s understand the steps needed for the construction of the Expression tree using the given input expression. During the construction of the Expression tree, we use Stack (Stack is a data structure based on the Last In First Out Principle).
• The given expression can be of any type like infix, postfix, etc. The most interesting fact about the Expression tree is that when we perform the postorder traversal on the Expression tree, we get the postfix expression, for the preorder traversal on the Expression tree we get the prefix expression, and similarly, inorder traversal gives the infix expression.
• For the construction of the Expression tree from the given input expression we use stack data structure which handles elements in a Last In First Out manner. Stack helps in storing the root of the Expression tree until that point and adding nodes to the Expression tree once it goes into the next character of the given expression.

Algorithm:

Below is the algorithm to be followed for the construction of the Expression tree from the given expression using stack data structure:

We need to traverse through the given expression using a for loop on it, then follow the below steps for every character in the given expression:

• If the character is an operand then we need to push that character into the stack.
• If the character is an operator then pop two nodes from the stack and make them the children of the present operator, first popped node should be on the left side and the second popped node should be on the right side of the operator.
• At last, we need to push this modified node into the stack again. The below image clearly explains the above step:

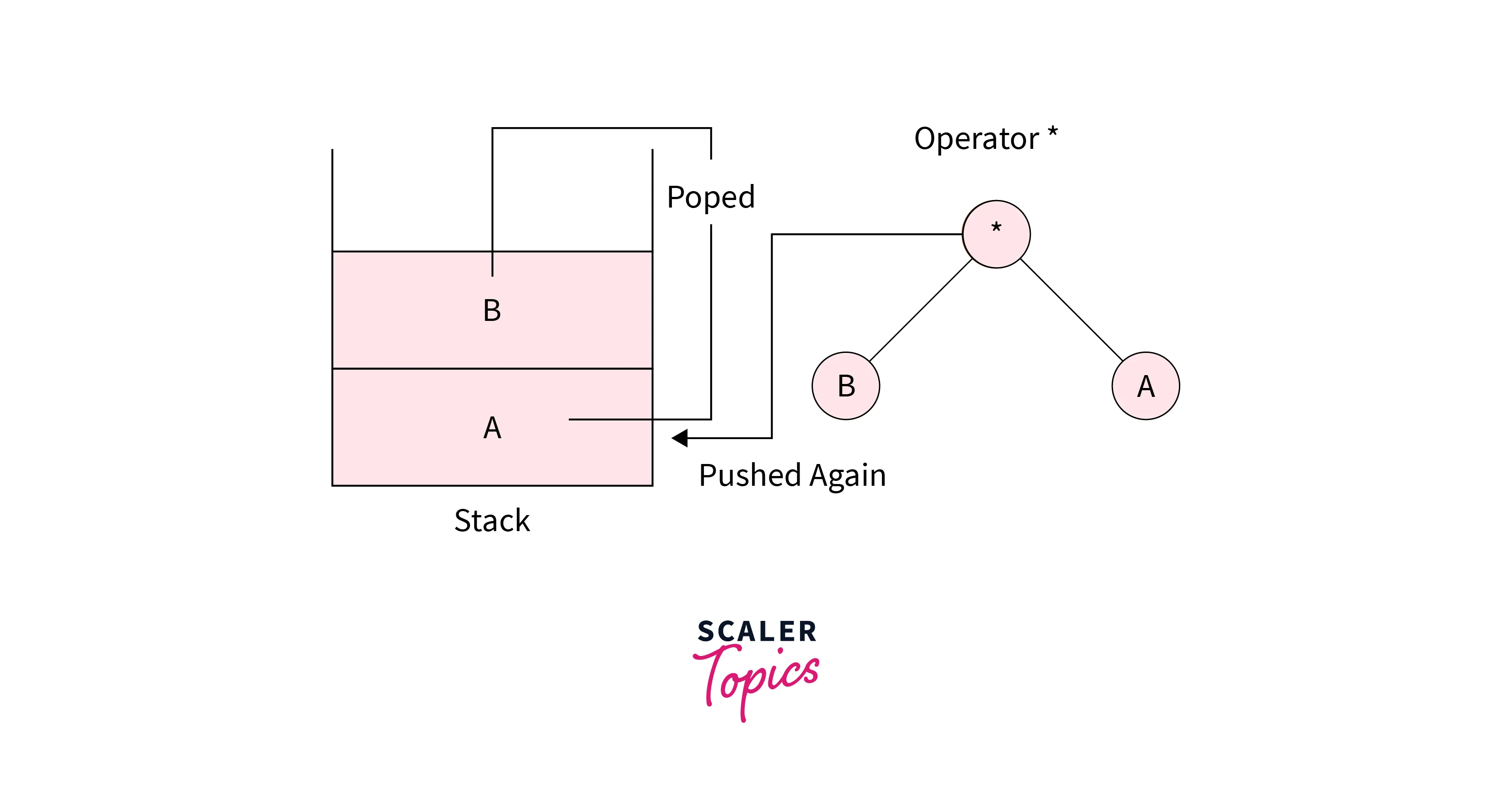
At any instant, the stack stores the root nodes of the subtrees of the final Expression tree. These nodes are combined as an operator arrives in the expression and the root node of a larger subtree is pushed into the stack. This continues till the expression is over.

At the end of traversal on the given expression, the stack contains only one node which is the root node of the Expression tree formed from the given expression. The root of the Expression tree is always an operator, and generally, the operator with the least precedence is present as the root of the Expression tree.

Example:

For a better understanding of the above algorithm, let’s look at the below-given infix expression and convert it into the Expression tree.

Input:

Expression: F A ^ B \* C / D - E +

The steps to be followed for the construction of the Expression tree are:

Start traversing the given expression using a for loop:

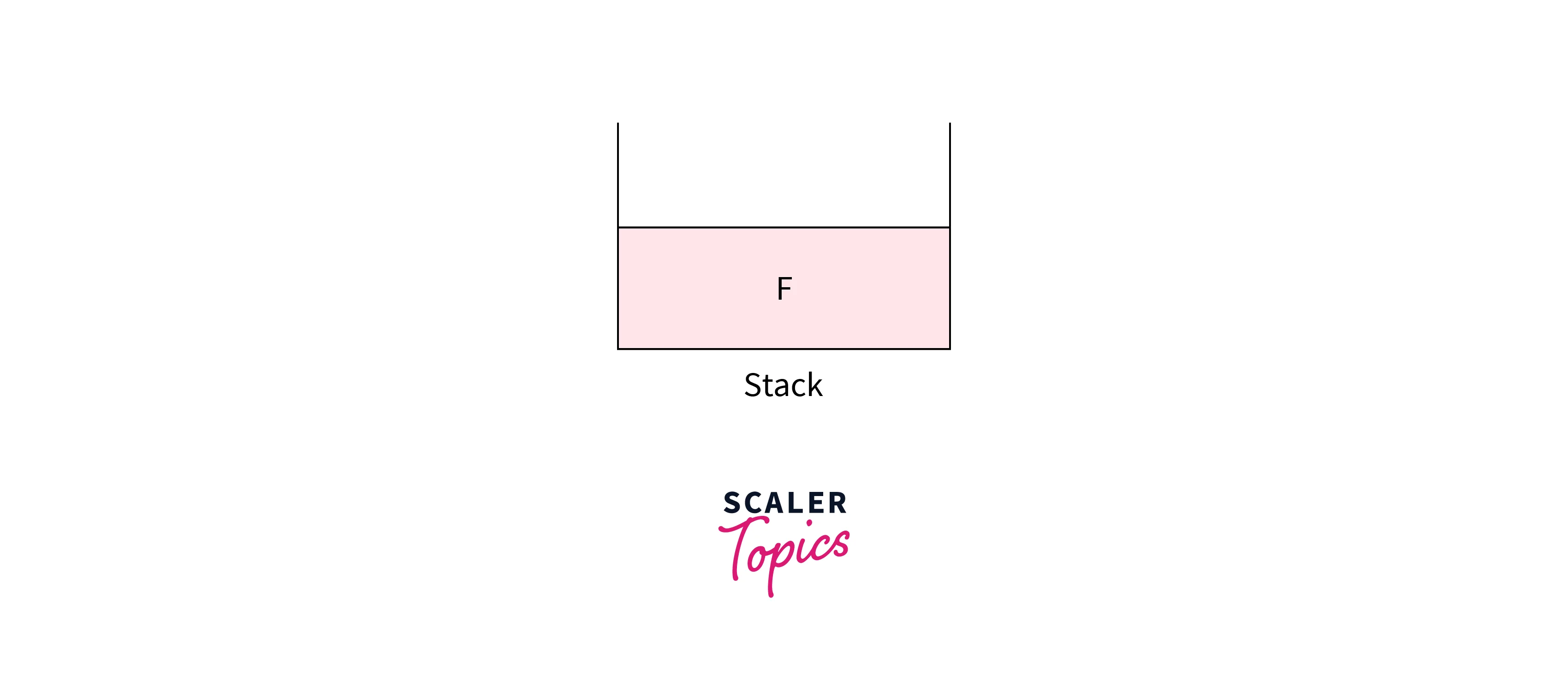
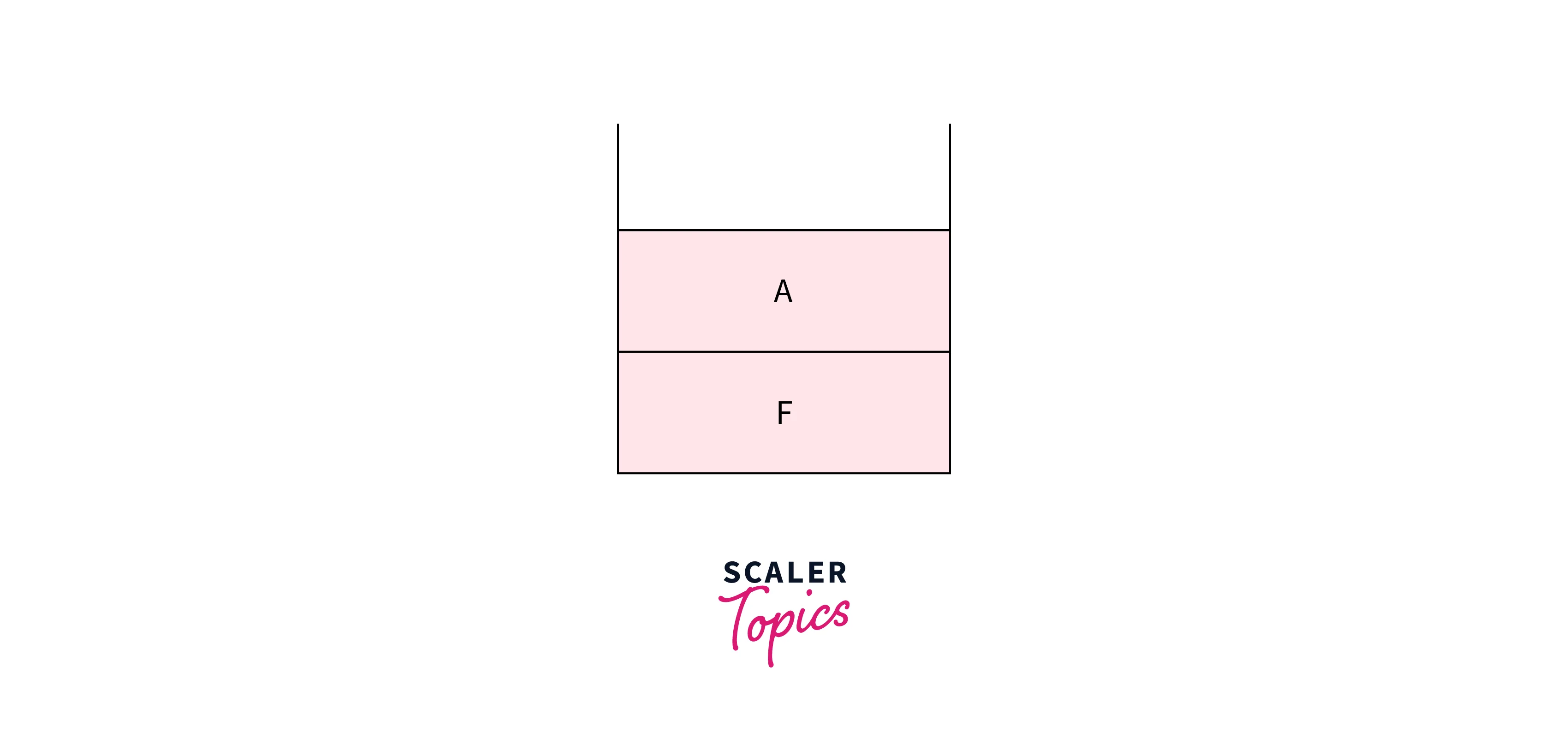
Firstly operand F is present, create a Tree node using F as data and push this node into the stack as shown in the below image. We are storing only the root of the tree formed until now in the stack. For a clear understanding, the below images below elaborately show the root of the subtree formed till now. 

Now operand A is encountered. Create a node with value A and push it in the stack as shown in the below image. 

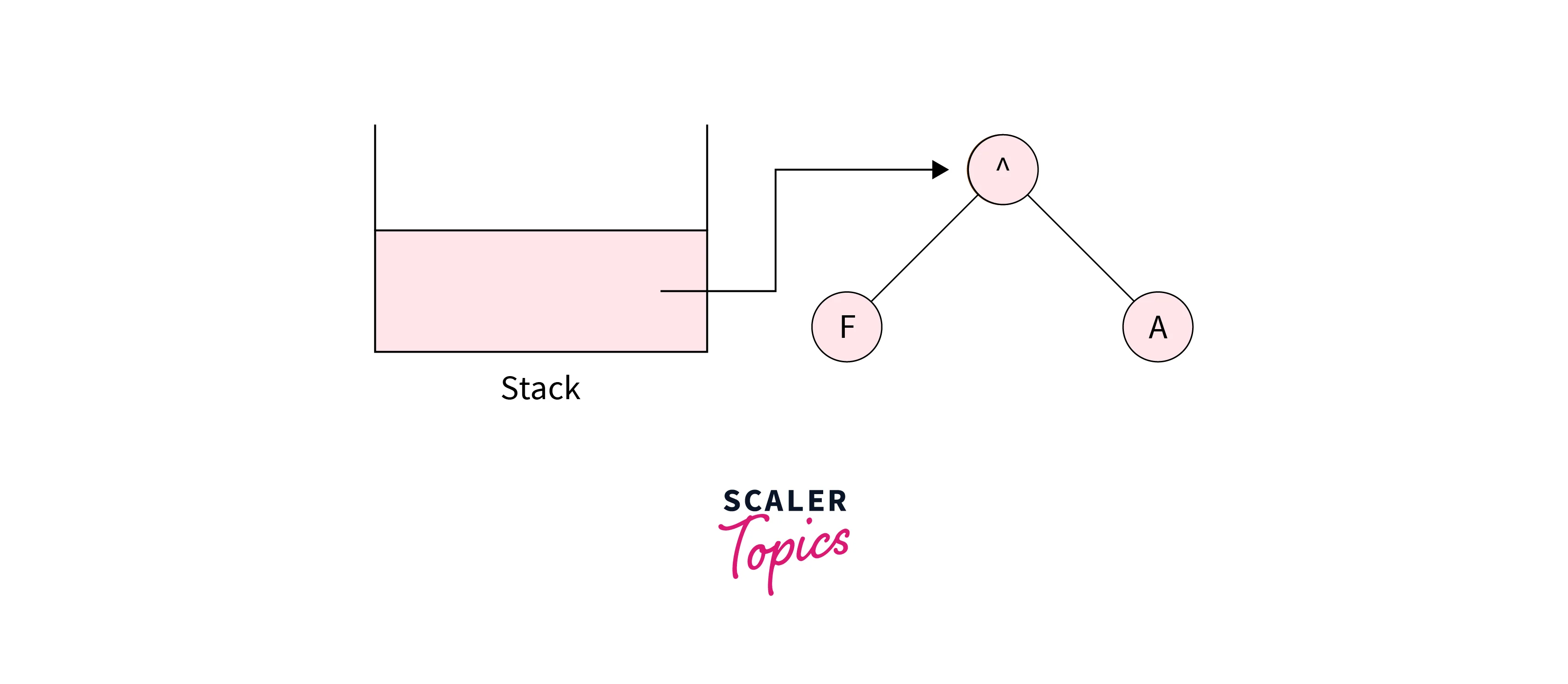
For “^”, firstly create the node with value “^”, and we need to pop two nodes from the stack and make them the children of the newly formed node “^”.

Push this newly formed node into the stack as shown in the below image: 

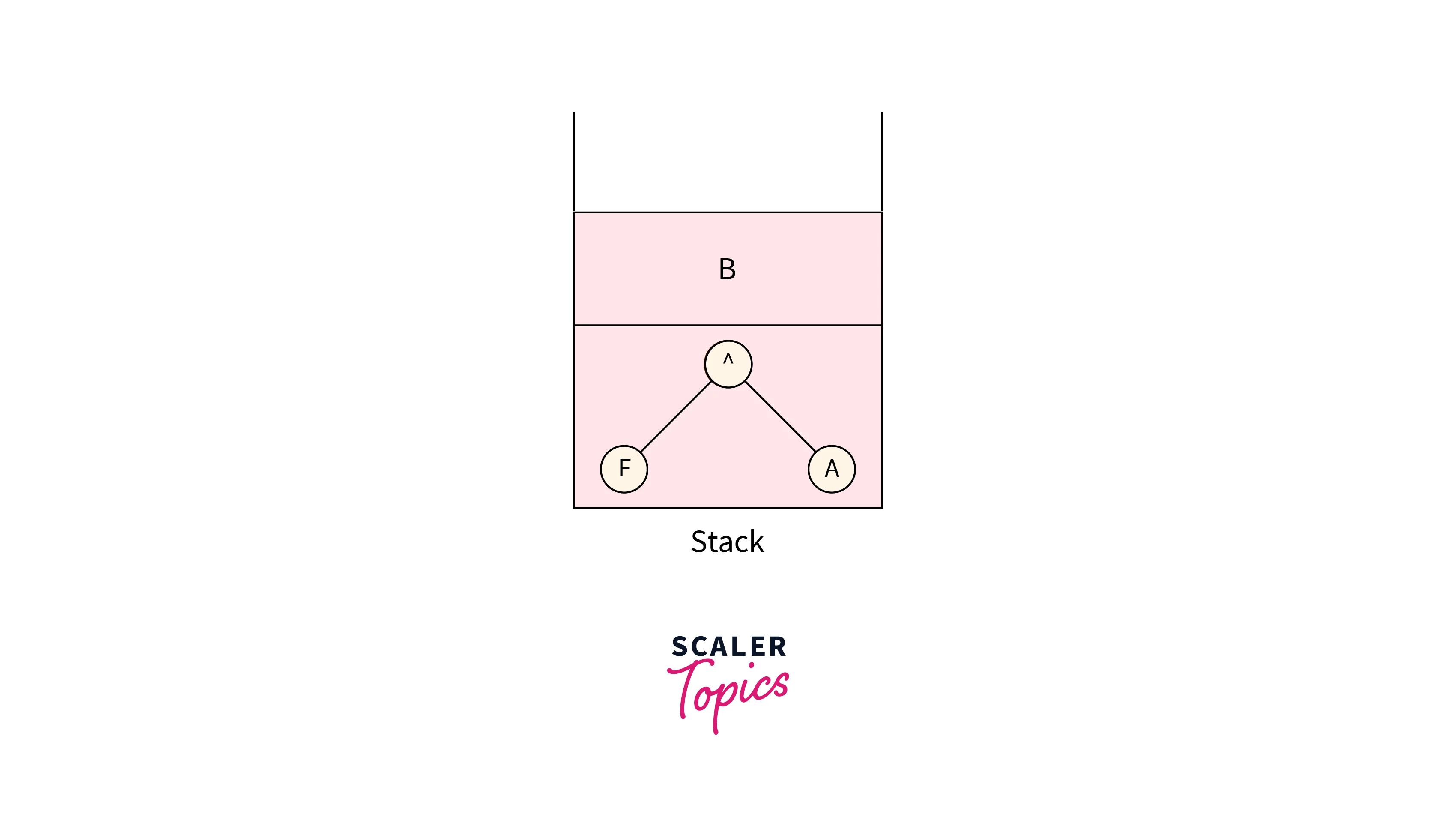
Push the operand B into the stack by creating a node with B as data. Now nodes present in the stack are shown in the below image: 

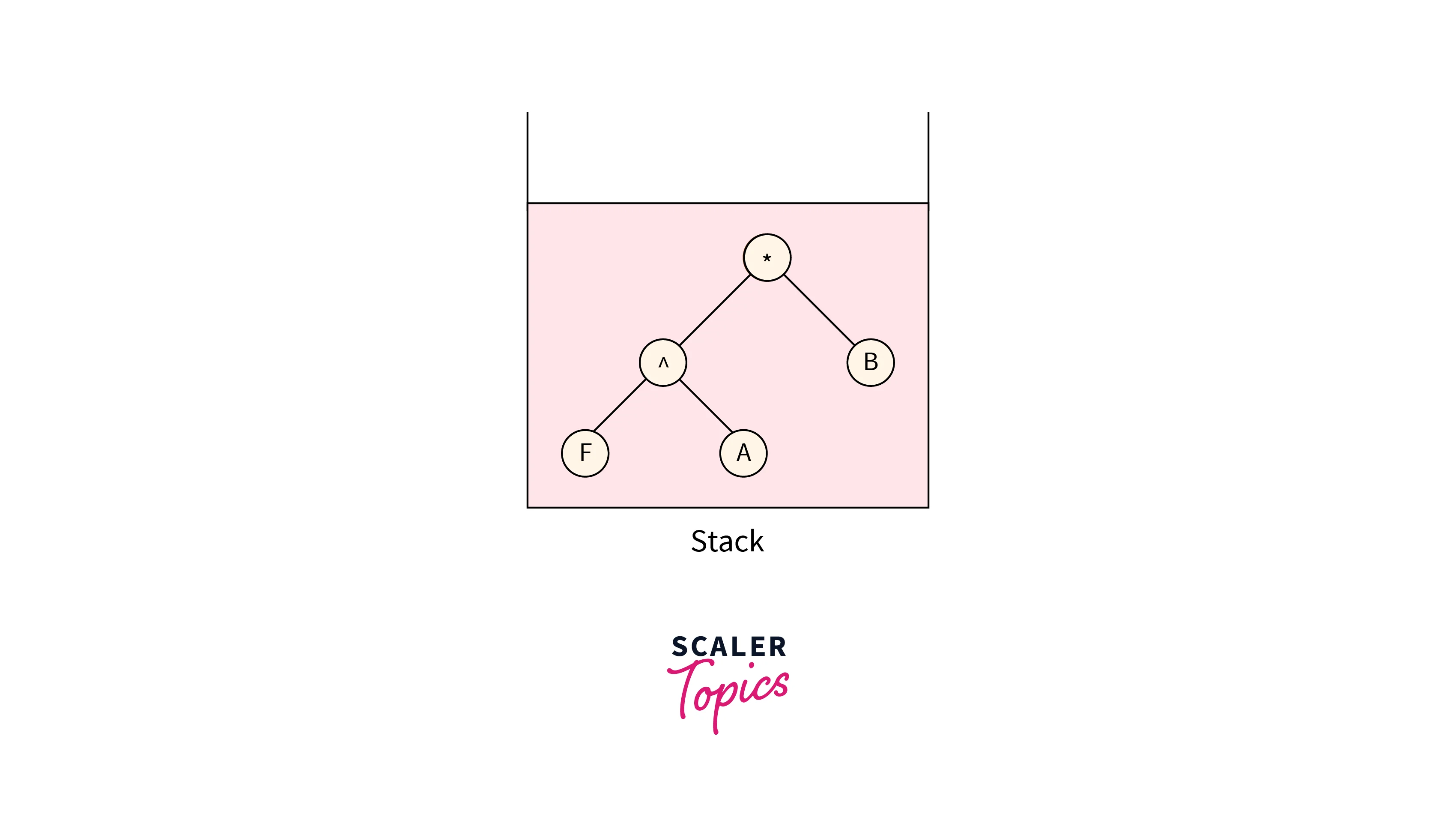
The next character which is present is “*”, forming a node with “*”. Pop two nodes from the stack and, make them the children nodes for the “*” node, which is shown in the below image. And push this newly formed node into the stack. 

The next character which is encountered is C, create a Tree node with C as data and push it into the stack which is shown in the below image: 

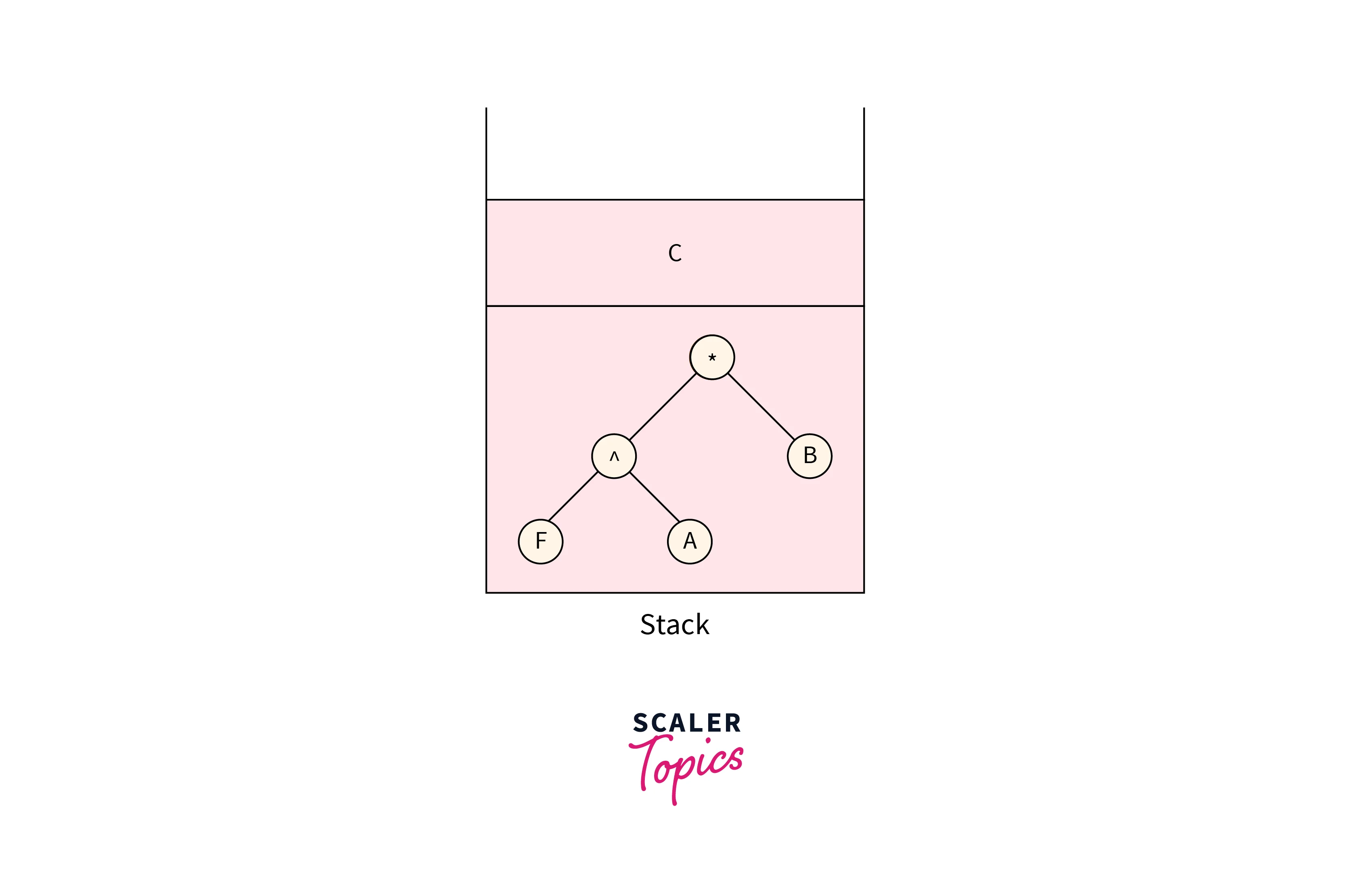
For the next character, form a node “/” and pop two nodes from the stack and make them children nodes for the newly formed node and push this node into the stack which is shown in the below image:

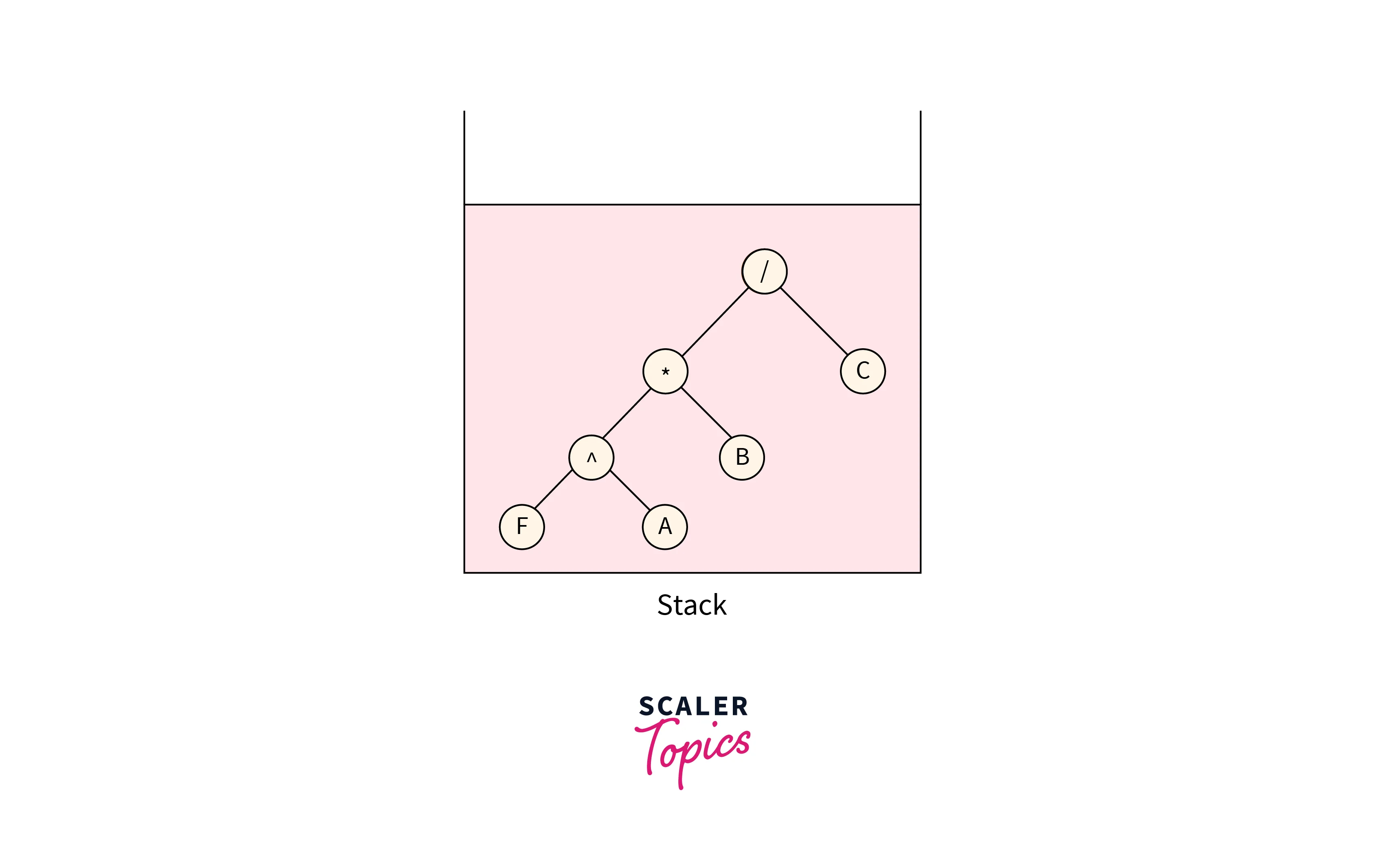
The next character is D, make a corresponding tree node and push it into the stack as shown in the below image: 

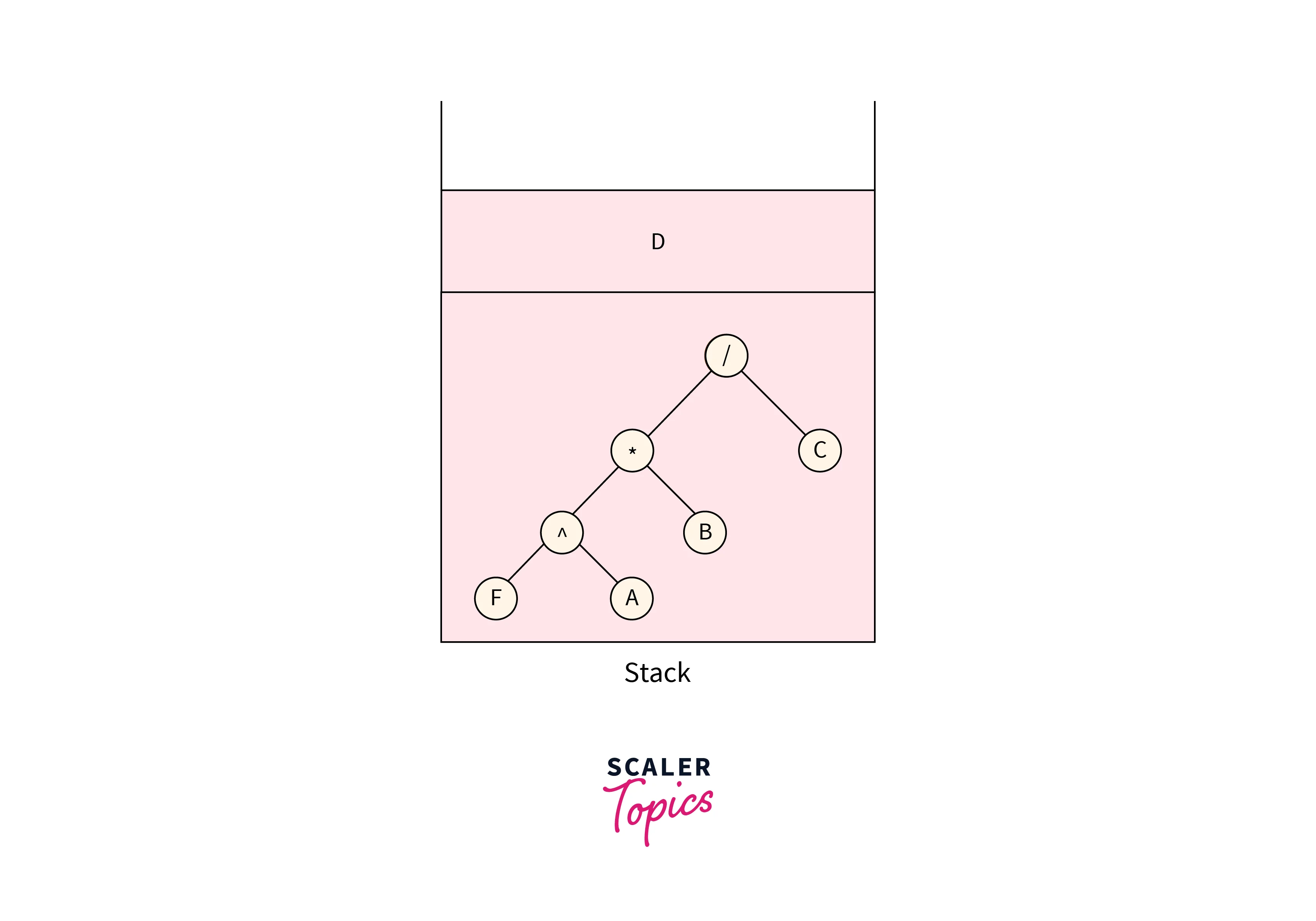
The next character is “-“, make a tree node and pop two elements from the stack and make them the child nodes for the newly formed node, and push this node into the stack which is shown in the below image: 

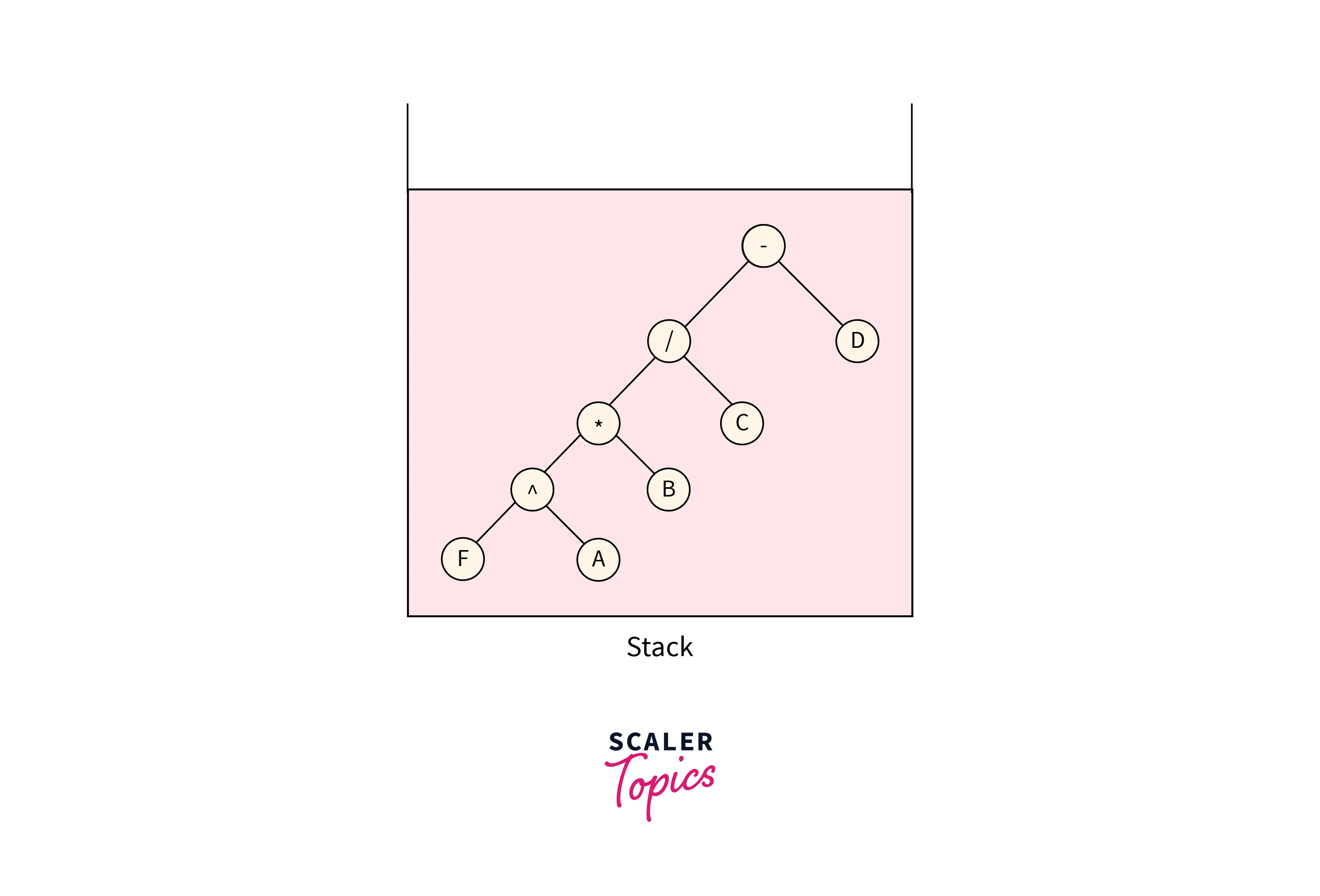
The next character is an operand E, make the corresponding tree node with value E and push it into the stack which is shown in the below image: 

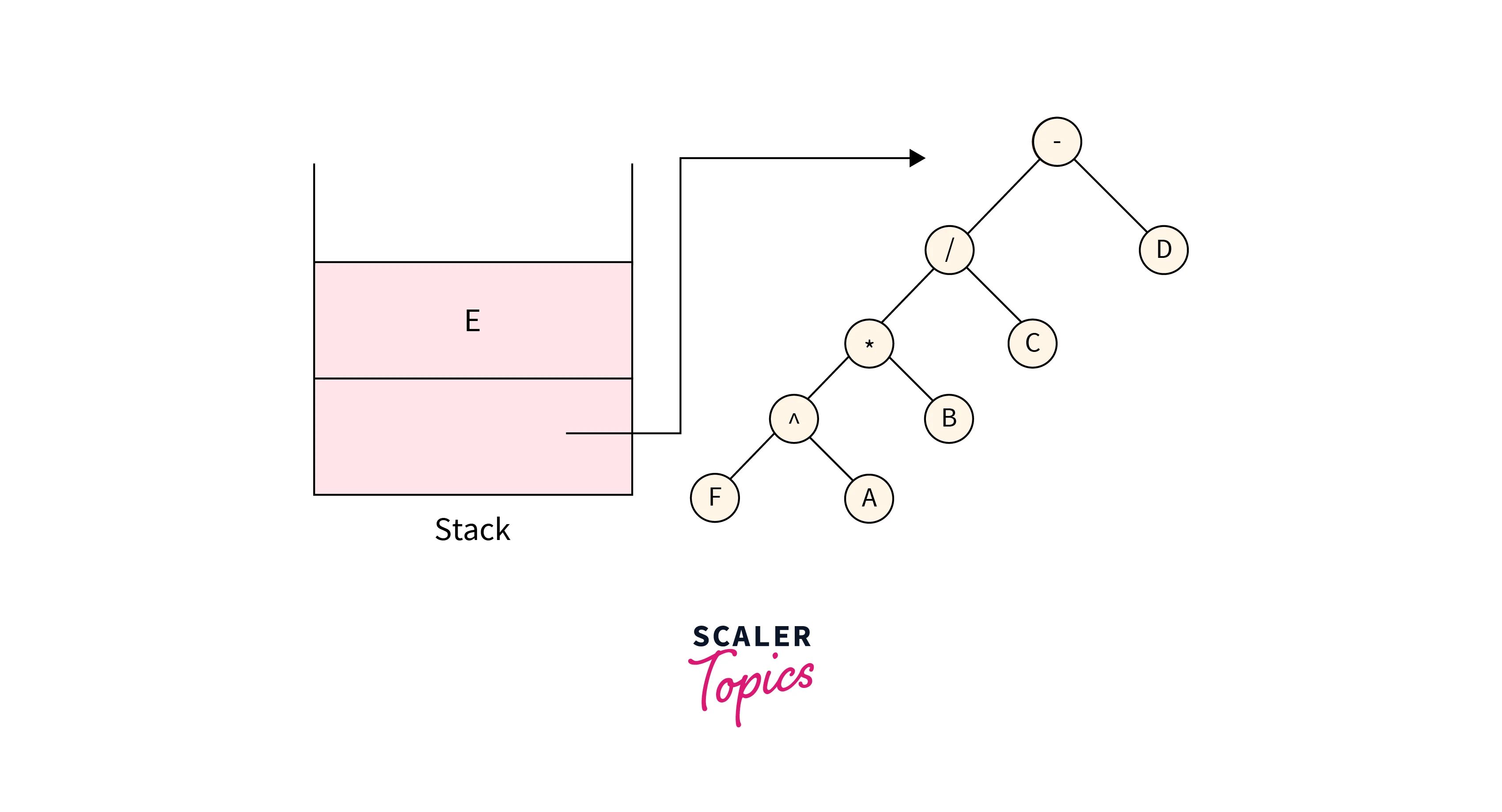
The last character from the given expression is an operator “+”, so make a tree node with “+” and pop two elements from the stack and make them the children nodes of the newly formed tree and push this node in the stack which is shown in the below image: 

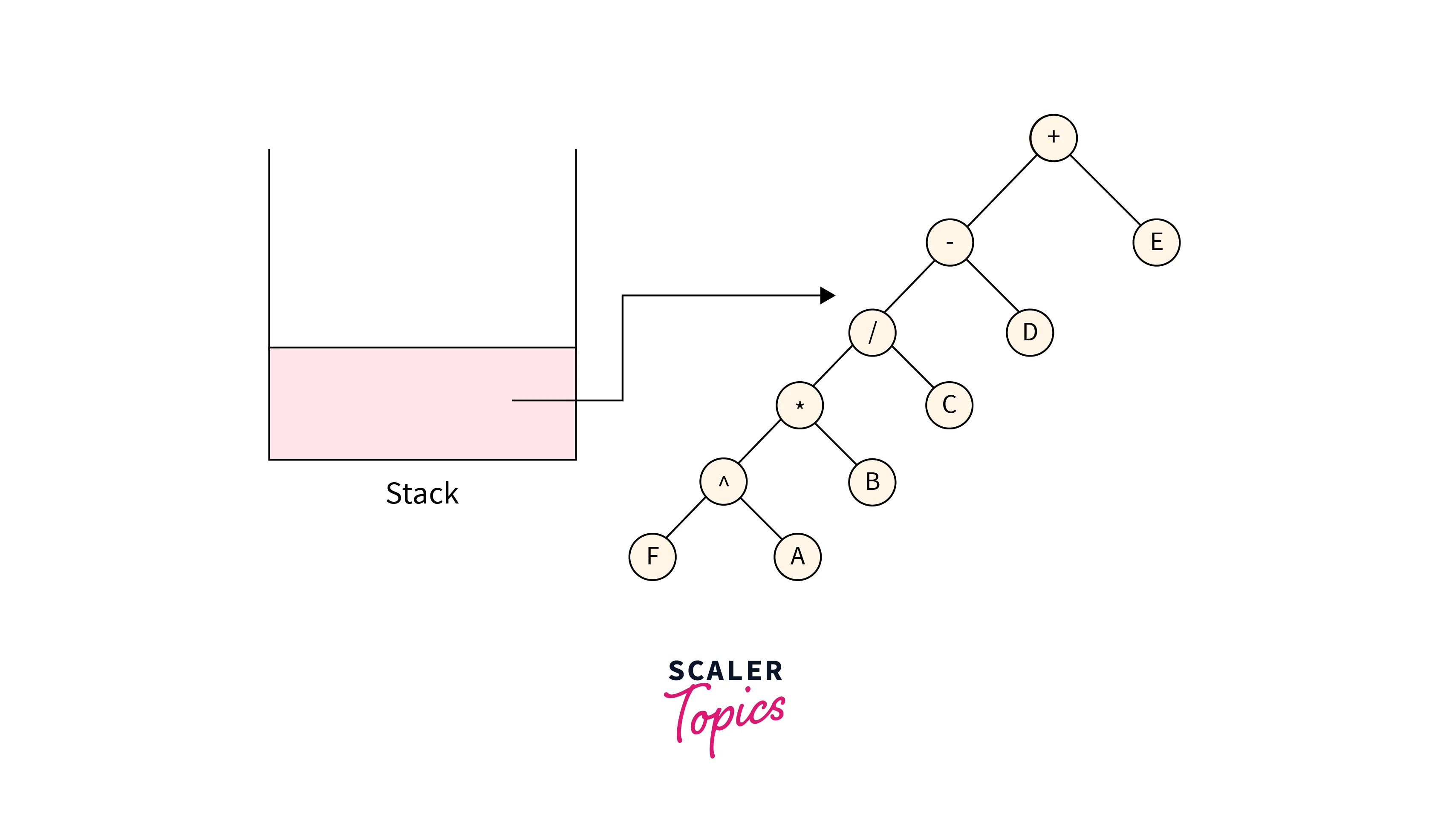
Finally the stack contains only one node which is the root node of the Expression tree representing the given expression. The Expression tree formed as shown in the below image: 

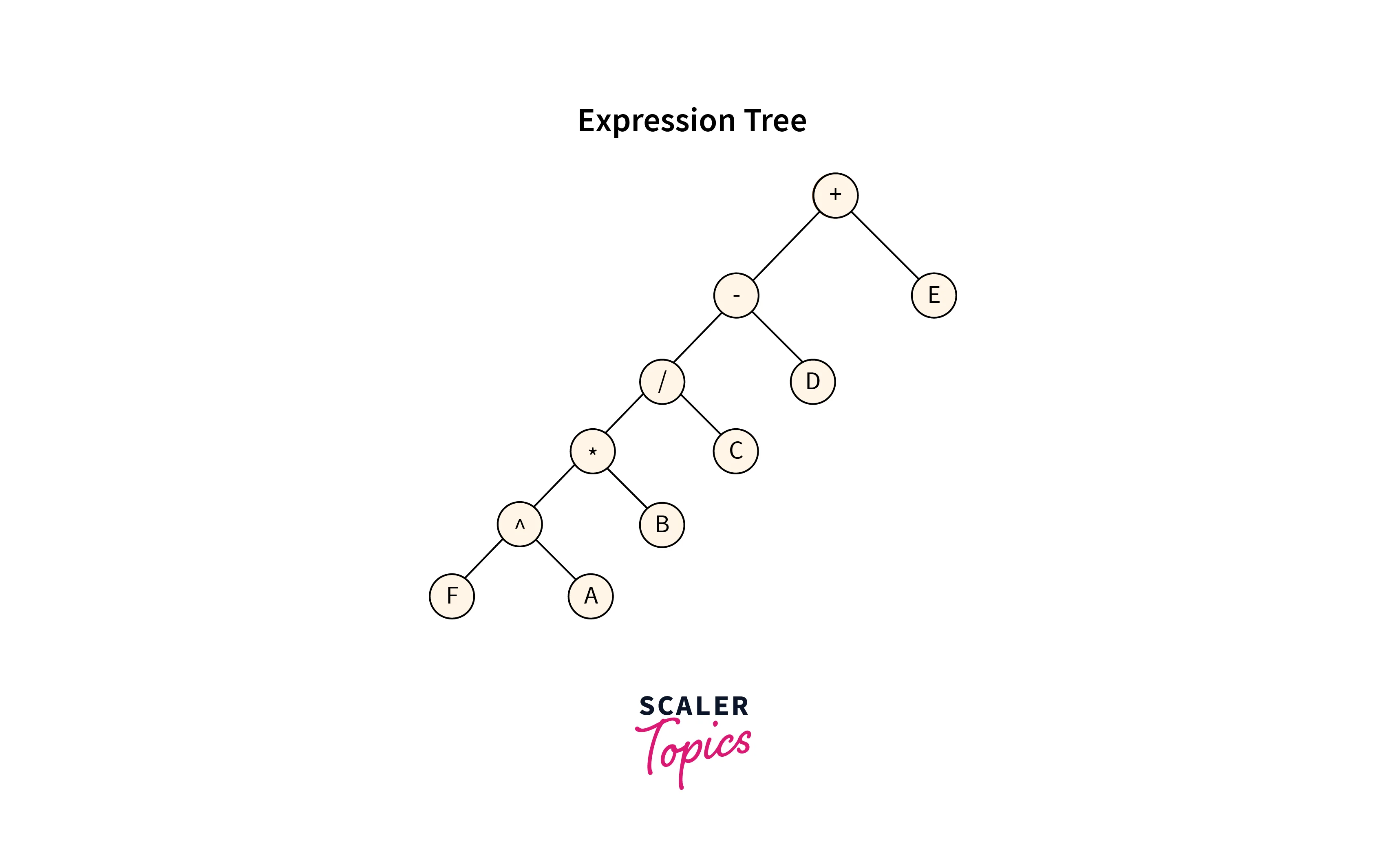
Implementation

Below is the implementation for the construction of the Expression tree from the given expression:

C++ implementation: for the construction of the Expression tree using the above-discussed algorithm.

// C++ program for constructing the expression tree using the given expression.
#include <bits/stdc++.h>
using namespace std;
// Representation of tree node
class Node
{
    // a tree node has data, left and right.
public:
    char data;
    Node *left;
    Node *right;
    Node *next = NULL;

    Node(char ch)
    {
        // constructor for the tree node
        this->data = ch;
        left = NULL;
        right = NULL;
    }

    // creating the instance of the node
    Node()
    {
        left = NULL;
        right = NULL;
    }
    // initiating the stack and expression_tree using the property of friend class
    friend class Stack;
    friend class Expression_tree;
};

// Class which represents the stack used while traversing the nodes
class Stack
{
    Node *head = NULL;
    // constructor of the stack class
public:
    // method which pushes the nodes in the stack
    void push_node(Node *);

    // method which pops the nodes from the stack
    Node *pop_node();
    friend class Expression_tree;
};
// class which represents the expression tree
class Expression_tree
{
public:
    // method which is used for printing the inorder traversal for the constructed tre
    void inorder_traversal(Node *head)
    {
        // base case
        if (head == NULL)
            return;
        else
        {
            // recursively call the function in an inorder fashion
            inorder_traversal(head->left);
            cout << head->data << "  ";
            inorder_traversal(head->right);
        }
    }
};
// method which pops the top element from the stack
Node *Stack::
    pop_node()
{
    // popping the top node
    Node *ptr = head;
    head = head->next;
    return ptr;
}

// method which is used for pushing elements into the stack
void Stack::
    push_node(Node *node)
{
    // base case when the node is the first node in the expression tree
    if (head == NULL)
    {
        head = node;
    }
    // push the nodes into the stacks in a LIFO manner
    else
    {
        node->next = head;
        head = node;
    }
}

// Driver code
int main()
{
    // given expression is as follows: "BAC^/D-E+""
    string expression = "BAC^/D-E+";
    // creating a stack
    Stack st;
    // initiating the expression tree
    Expression_tree et;
    Node *operand_1, *operand_2, *opt;
    // get the size of the input expression
    int len = expression.length();
    // traversing through the complete expression
    for (int i = 0; i < len; i++)
    {
        // Check if the character is an operator
        if (expression[i] == '-' || expression[i] == '+' || expression[i] == '^' || expression[i] == '*' || expression[i] == '/')
        {
            // create the tree node using the operator
            opt = new Node(expression[i]);

            // pop two elements from the stack
            operand_1 = st.pop_node();
            operand_2 = st.pop_node();

            // make them the children node for the newly formed node
            opt->left = operand_2;
            opt->right = operand_1;

            // push this node into the stack
            st.push_node(opt);
        }
        // if the current character is an operand make a node and
        // push it into the stack
        else
        {
            opt = new Node(expression[i]);
            st.push_node(opt);
        }
    }
    // printing the inorder traversal of the formed Expression tree
    et.inorder_traversal(opt);
    return 0;
}

Output:

B / A ^ C - D + E

Java implementation: for the construction of the Expression tree using the above-discussed algorithm.

// Java program for constructing the expression tree
// from the given expression.
import java.util.Stack;

// Representation of tree node
class Node {
  // a tree node has data, left and right.
  char data;
  Node left;
  Node right;

  // constructor for the tree node
  public Node(char data) {
    this.data = data;
    left = null;
    right = null;
  }
}

// Main class which has all the methods
public class Solution {

  // To check whether a character is an operator or not
  public static boolean is_Operator(char c) {
    // operators include "+ - * / ^"
    if (c == '/' || c == '+' || c == '-' || c == '*' || c == '^') {
      return true;
    }
    return false;
  }

  // To print the inorder traversal for the constructed Expression tree
  public static void inorder_traversal(Node head) {
    // base case
    if (head == null) return;

    // recursively call the method in the given manner
    inorder_traversal(head.left);
    System.out.print(head.data + " ");
    inorder_traversal(head.right);
  }

  // Method which is used for the creation of the expression Tree
  public static Node expression_Tree(String expression) {
    //initialize a stack for keeping track of the nodes
    Stack<Node> stc = new Stack<Node>();
    Node x, y, z;

    // traversing the given expression
    for (int i = 0; i < expression.length(); i++) {
      // if the current character is an operand
      // make a node and push it into the stack
      if (!is_Operator(expression.charAt(i))) {
        // create the tree node using the operator
        z = new Node(expression.charAt(i));
        stc.push(z);
      } else {
        // Create the tree node using the operator
        // Pop two elements from the stack
        z = new Node(expression.charAt(i));
        x = stc.pop();
        y = stc.pop();

        // make them the children node for the newly formed node
        z.left = y;
        z.right = x;

        // push this node into the stack
        stc.push(z);
      }
    }
    z = stc.pop();
    return z;
  }

  // Driver Code
  public static void main(String[] args) {
    // given expression is as follows: "BAC^/D-E+""
    String expression = "BAC^/D-E+";

    Node temp = expression_Tree(expression);
    // printing the inorder traversal of the formed Expression tree
    inorder_traversal(temp);
  }
}

Output:

B / A ^ C - D + E

Explanation:

From the given expression the expression tree is constructed using the stack data structure. After the formation of the Expression tree, inorder traversal is performed and output is obtained by printing its inorder traversal.

Applications of the Expression Tree

Below mentioned are a few applications of the Expression Tree:

• Expression tree is very helpful for evaluating the expressions, as it simplifies calculations by forming a tree.
• Expression trees also help in enforcing the associativity of each operator in the given expression. For instance, the + operator is the left-associative, and / is the right-associative.
• Expression trees are also very helpful for computing the infix expression, postfix expression, and prefix expression.

Conclusion

• This article explains the concept of the Ean xpression tree and the process of construction of an expression tree.
• The following observations from the formed EXpression tree are as follows:
  • The operator which is present in the depth of the expression tree is considered to be having the highest priority. The greater the depth, the higher the priority.
  • Operands are always the leaf nodes of Expression Trees.
  • At any point, the stack stores the roots of subtrees of the final expression tree.
• The main use of these expression trees is that it is used to evaluate, analyze and modify the various expressions efficiently.
• Expression trees also help in enforcing the associativity of each operator in the given expression. Using expression trees we can enforce that the “+” operator is the left-associative and “/” is the right-associative.