Flattening a Linked List

Problem Statement

Given a Linked List of size N, where every node of the linked list has either of the two pointer or can have both pointer.

1. Pointer to the next node – next pointer
2. bottom pointer to a sub-linked list – bottom pointer

The sublinked(vertical linked list) and the horizontal linked list is in sorted order.
Flatten this linked list such that all the nodes appear in a single level(horizontally) and the node elements are in sorted order.

Example

number of nodes in the horizontal linked list(head nodes) = $4$

Array of number of nodes in every sublinked list to the bottom including head node = $[4,2,1,3]$

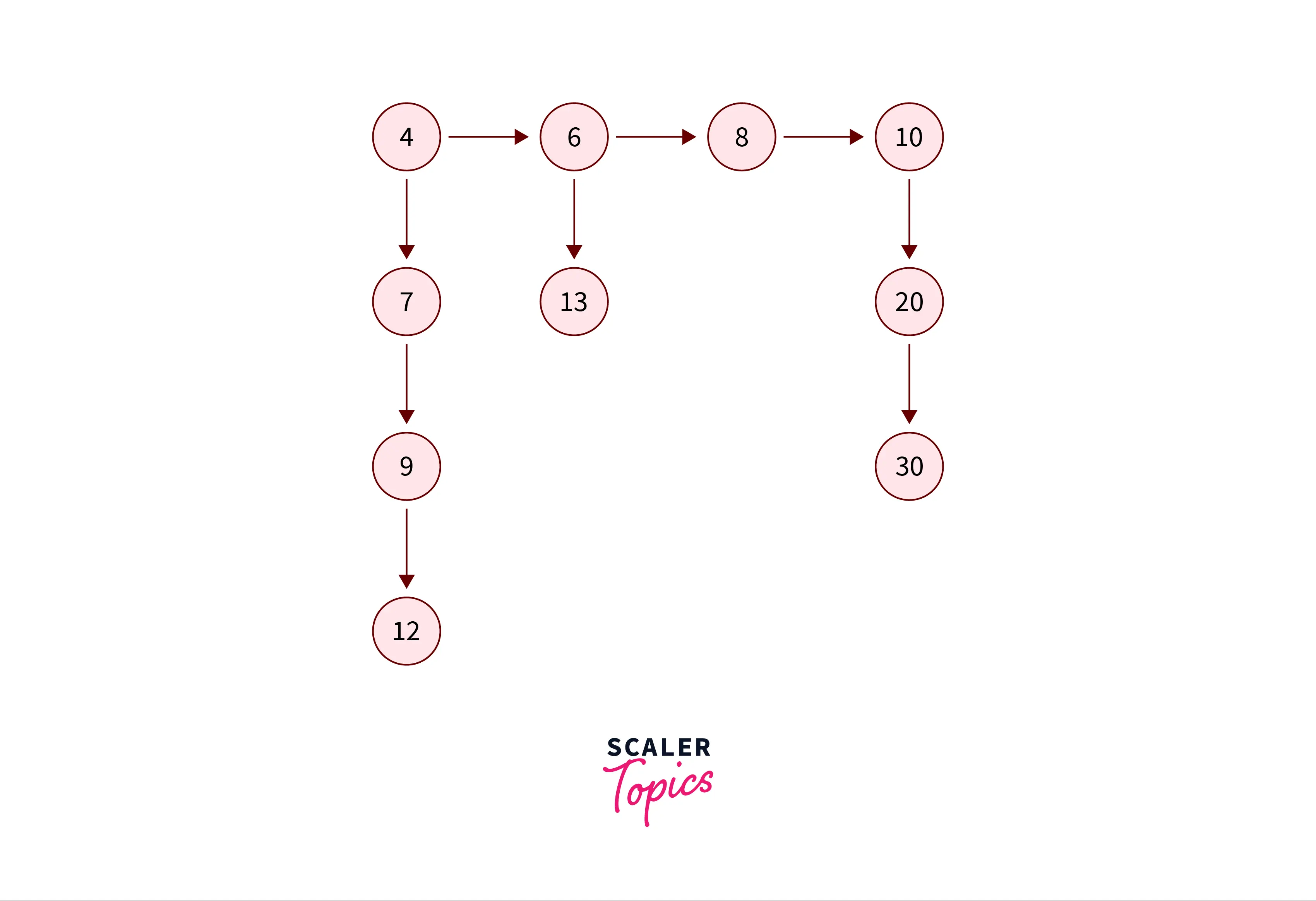
After flatteneing the linked list, the linked list should look like :

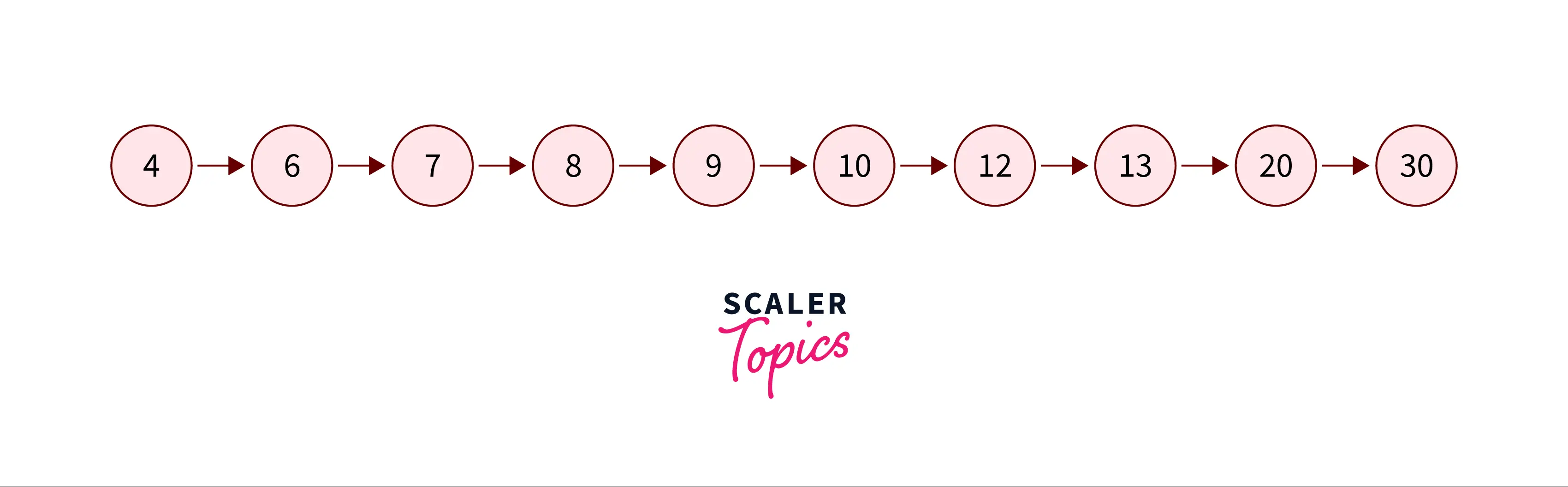
The elements of the flattened linked list are :

$[4,6,7,8,9,10,12,13,20,30]$

Example Explanation

In the example below lets understand the initial structure of linked list and the final structure after merging of linked list.

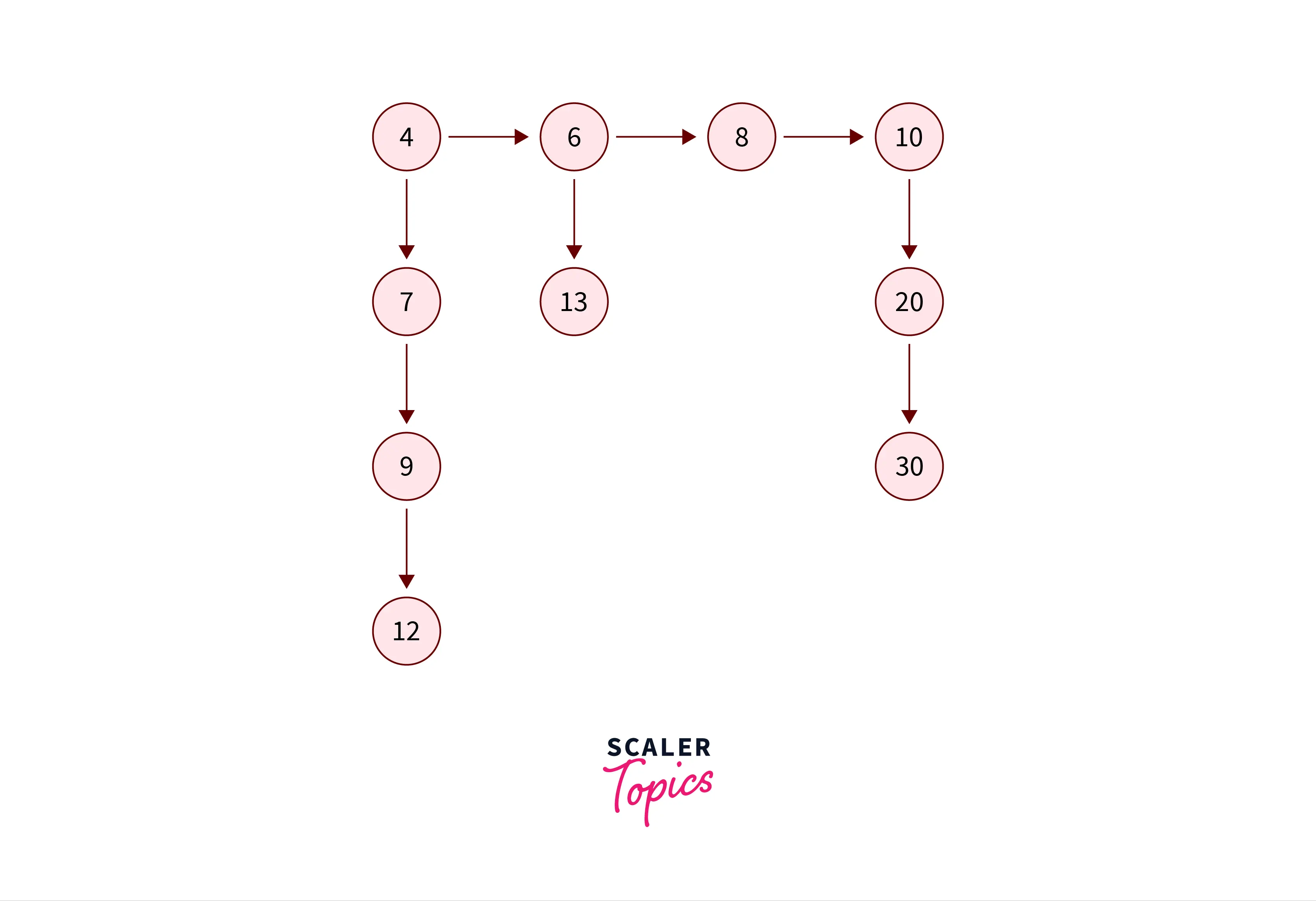
In the above linked list diagram we can see there is a single horizontal linked list and some vertical sub-linked list connected to the bottom pointer of the nodes of horizontal linked list.

The node of the horizontal linked list (4->6->8->10) have two pointer. One pointer(next pointer) points to the next node in the horizontal linked list itself and the second pointer (bottom pointer) points to the vertical sublinked list atted to each node of the horizontal linked list.

The bottom pointer of node with data = 4 is pointing to 7->9->12 (vertical sub linked list). The vertical sublinked list is in sorted order.

The bottom pointer of node with data = 6 is pointing to 13. (vertical sublinked list).The vertical sublinked list is in sorted order.

The bottom pointer of node with data = 8 points to NULL, which means there is no vertical sublinked list underneath node with data = 8.The vertical sublinked list is in sorted order.

The bottom pointer of node with data = 10 points to 20->30 . (vertical sublinked list).The vertical sublinked list is in sorted order.

When all the elemnts of the horizontal and vertical sub-linked list are merged to a single linked list . The linked then looks like :

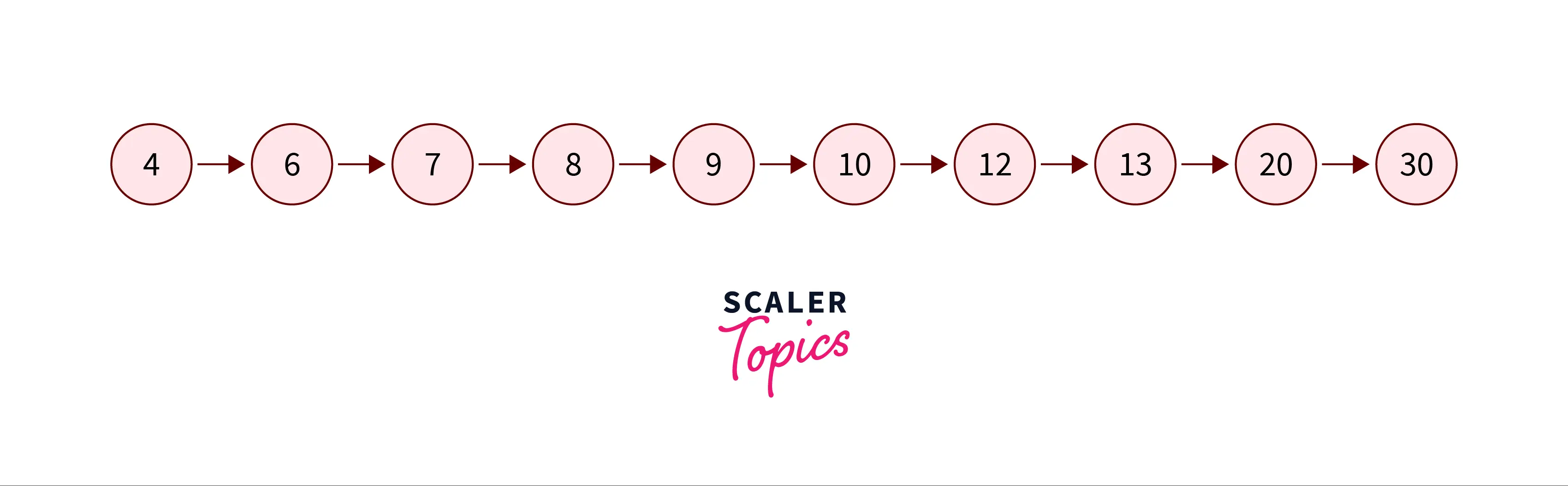
All the elements in the above flattened Linked list lt is in sorted order. Flattening of the linked list can be done by two methods which are explained further in this article.

Approach 1 : Merging in Merge Sort Algorithm

As each sub-list in the linked list is in sorted order we can use merge sort on the sub list to merge all the sublist to a single list.

The steps used in this algorithm are :

1. create a dummy node with two pointer. one pointer is used to keep track of the dummy node and the second pointer is used to move ahaed as we merge the linked list.
2. Choose any two sub-linked list and iterate through the list and merge them using merge algorithm of merge sort.
3. Return the final list after all sub-list are merged to a single list.

Implementation in C++

// C++ program for flattening a Linked List
#include <bits/stdc++.h>
using namespace std;


class Node
{
    public:
        int data;
        Node *next, *bottom;
};

Node* head = NULL;

// A function to merge two sorted linked lists
Node* merge(Node* l1, Node* l2)
{

    // If first linked list is empty then return the second list

    if (l1 == NULL)
        return l2;

    // If the second linked list is empty then return the first list
    if (l2 == NULL)
        return l1;

    // Compare the data members of the two linked
    // lists and put the larger one in the result
    Node* result;

    if (l1->data < l2->data)
    {
        result = l1;
        result->bottom = merge(l1->bottom, l2);
    }

    else
    {
        result = l2;
        result->bottom = merge(l1, l2->bottom);
    }
    result->next = NULL;
    return result;
}

Node* flattenList(Node* root)
{

    // Base Cases
    if (root == NULL || root->next == NULL)
        return root;

    // Recur for list on right
    root->next = flattenList(root->next);

    // Now merge
    root = merge(root, root->next);

    // Return the root
    return root;
}

// function to insert a node at the beginning of the linked list
Node* push(Node* head_ref, int data)
{

    // Allocate the Node & Put in the data
    Node* new_node = new Node();

    new_node->data = data;
    new_node->next = NULL;

    // Make next of new Node as head
    new_node->bottom = head_ref;

    // Move the head to point to the new Node
    head_ref = new_node;

    return head_ref;
}

void printList()
{
    Node* temp = head;
    while (temp != NULL)
    {
        cout << temp->data << " ";
        temp = temp->bottom;
    }
    cout << endl;
}

// Driver code
int main()
{

    /* Let us create the following linked list
        4 -> 6 -> 8 -> 10
        |    |         |
        V    V         V
        7   13        20
        |             |
        V             V
        9            30
        |       
        V          
        12            
    */
    head = push(head, 12);
    head = push(head,  9);
    head = push(head, 7);
    head = push(head, 4);

    head->next = push(head->next, 13);
    head->next = push(head->next, 6);

    head->next->next = push(head->next->next, 8);

    head->next->next->next = push(head->next->next->next, 30);
    head->next->next->next = push(head->next->next->next, 20);
    head->next->next->next = push(head->next->next->next, 10);


    // Flatten the list
    head = flattenList(head);

    printList();
    return 0;
}

Implementation in Java :

// Java program for flattening a Linked List
class LinkedList
{
    Node head; // head of list

    /* Linked list Node*/
    class Node
    {
        int data;
        Node next, bottom;
        Node(int data)
        {
            this.data = data;
            next = null;
            bottom = null;
        }
    }

    // A function to merge two sorted linked lists
    Node merge(Node l1, Node l2)
    {
        // if first linked list is empty then return the second list
        if (l1 == null)  return l2;

        // if the second linked list is empty then return the first list
        if (l2 == null)  return l1;

        // compare the data members of the two linked lists
        // and put the larger one in the result
        Node result;

        if (l1.data < l2.data)
        {
            result = l1;
            result.bottom = merge(l1.bottom, l2);
        }

        else
        {
            result = l2;
            result.bottom = merge(l1, l2.bottom);
        }

        result.next = null;
        return result;
    }

    Node flattenList(Node root)
    {
        // Base Cases
        if (root == null || root.next == null)
            return root;

        // recur for list on right
        root.next = flattenList(root.next);

        // now merge
        root = merge(root, root.next);

        // return the root
        return root;
    }

    /*function to insert a node at beginning of the
    linked list */
    Node push(Node head_ref, int data)
    {
        /* Allocate the Node &
                Put in the data*/
        Node new_node = new Node(data);

        /*  Make next of new Node as head */
        new_node.bottom = head_ref;

        /*  Move the head to point to the new Node */
        head_ref = new_node;

        /* return to link it back */
        return head_ref;
    }

    void printList()
    {
        Node temp = head;
        while (temp != null)
        {
            System.out.print(temp.data + " ");
            temp = temp.bottom;
        }
        System.out.println();
    }
} 

public class Main{
    /* Driver program to test above functions */
    public static void main(String args[])
    {
        LinkedList L = new LinkedList();

        /* Let us create the following linked list
        4 -> 6 -> 8 -> 10
        |    |         |
        V    V         V
        7   13        20
        |             |
        V             V
        9            30
        |       
        V          
        12  
        */

        L.head = L.push(L.head, 12);
        L.head = L.push(L.head, 9);
        L.head = L.push(L.head, 7);
        L.head = L.push(L.head, 4);

        L.head.next = L.push(L.head.next, 13);
        L.head.next = L.push(L.head.next, 6);

        L.head.next.next = L.push(L.head.next.next, 8);

        L.head.next.next.next = L.push(L.head.next.next.next, 30);
        L.head.next.next.next = L.push(L.head.next.next.next, 20);
        L.head.next.next.next = L.push(L.head.next.next.next, 10);

        // flatten the list
        L.head = L.flattenList(L.head);

        L.printList();
    }
} 

Implementation in python :

# Python program for flattening a Linked List
class Node():
    def __init__(self,data):
        self.data = data
        self.next = None
        self.bottom = None

class LinkedList():
    def __init__(self):

        # the head of list
        self.head = None

    # function to insert a node at beginning of the linked list
    def push(self,head_ref,data):

        # Allocate the Node &
        # Put in the data
        new_node = Node(data)

        # Make next of new Node as head
        new_node.bottom = head_ref

        #  Move the head to point to the new Node
        head_ref = new_node

        # return to link it back
        return head_ref

    def printList(self):

        temp = self.head
        while(temp != None):
            print(temp.data,end=" ")
            temp = temp.bottom

        print()

    # An utility function to merge two sorted linked lists
    def merge(self, l1, l2):
        # if the first linked list is empty then return the second list
        if(l1 == None):
            return l2

        # if the second linked list is empty then return the first list
        if(l2 == None):
            return l1

        # compare the data members of the two linked lists
        # and put the larger one in the result
        result = None

        if (l1.data < l2.data):
            result = l1
            result.bottom = self.merge(l1.bottom,l2)
        else:
            result = l2
            result.bottom = self.merge(l1,l2.bottom)

        result.next = None
        return result

    def flattenList(self, root):

        # Base Case
        if(root == None or root.next == None):
            return root
        # recur for the list on the right

        root.next = self.flattenList(root.next)

        # now merge
        root = self.merge(root, root.next)

        # return the root

        return root

# Driver program to test above functions
L = LinkedList()

'''
Let us create the following linked list
        4 -> 6 -> 8 -> 10
        |    |         |
        V    V         V
        7   13        20
        |       |
        V           V
        9       30
        |       
        V          
        12  
'''
L.head = L.push(L.head, 12);
L.head = L.push(L.head, 9);
L.head = L.push(L.head, 7);
L.head = L.push(L.head, 4);

L.head.next = L.push(L.head.next, 13);
L.head.next = L.push(L.head.next, 6);

L.head.next.next = L.push(L.head.next.next, 8);


L.head.next.next.next = L.push(L.head.next.next.next, 30);
L.head.next.next.next = L.push(L.head.next.next.next, 20);
L.head.next.next.next = L.push(L.head.next.next.next, 10);


# flatten the list
L.head = L.flattenList(L.head);

L.printList()

Output of the code :

4,6,7,8,9,10,12,13,20,30

Time complexity :

• If we consider each vertical linked list of size O(M) in the worst case, then in this method we are merging two vertical sub-linked list at a time.
• Time taken to merge two linked list of size M = $O(M+M) =O(2M)$
• Similarly, time taken to merge another linked list of size M with linked list of size 2M = $O(M+2M)=O(3M)$
• Similarly, time taken to merge another linked list of size M with linked list of size $3M = O(M+3M) =O(4M)$.
• This process will take place N times where N is the no of nodes in the horizontal linked list.
  So, the total time taken till all the nodes are merged = $O(2M+3M+4M+5M+…N * M )$
  $= O(2+3+4+5+6…+N)* M$
  $=O(N* ( N + 1 ) / 2)* M$
  $= O(N * N * M)$

Note : sum of $2+3+4+5+6+….N =$ $(N(N+1)/2)-1$

Space Complexity :

• As recursion is taking place in this algorithm and the size of the recursive stack will be $O(NM)$ where, $(NM)$ is the total no of elements in the flattend list. So, the space complexity will be O(N*M)

Approach 2 : Using Priority Queue

We can build min-heap from the element of the linked list and extract min element from the min heap by using Extractmin property of min heap.

The steps involved in this Priority queue method are :

1. All the nodes are pushed to priority queue using next pointer untill we encounter NULL.
2. The minimum element from the queue is extracted using ExtractMin property and if the bottom pointer of that element is not pointing to any NULL value then push the element pointed by bottom pointer to the priority queue.
3. Else the element found by ExtractMin operation is printed and the size of the priority queue decreases.

Implementation in C++

#include <bits/stdc++.h>
using namespace std;

struct Node {
    int data;
    struct Node* next;
    struct Node* bottom;

    Node(int x){
        data = x;
        next = NULL;
        bottom = NULL;
    }
};

void flattenList(Node* root);

int main(void){
    Node* head=new Node(4);
    head->bottom=new Node(7);
    head->bottom->bottom=new Node(9);
    head->bottom->bottom->bottom=new Node(12);

    head->next=new Node(6);
    head->next->bottom=new Node(13);

    head->next->next=new Node(8);

    head->next->next->next=new Node(10);
    head->next->next->bottom=new Node(20);
    head->next->next->bottom->bottom=new Node(30);

    flattenList(head);
    cout << endl;
    return 0;
}


// comparator operator
struct mycomp{
    bool operator()(Node* l1, Node* l2){
        return l1->data > l2->data;
    }
};

void flattenList(Node* root){
    priority_queue<Node*, vector<Node*>, mycomp> p;

    //pushing main link nodes into priority_queue.
    while (root!=NULL) {
        p.push(root);
        root = root->next;
    }

    while (!p.empty()) {
        //extracting min
        auto k = p.top();
        p.pop();
        //printing least element
        cout << k->data << " ";
        if (k->bottom)
            p.push(k->bottom);
    }
}

Implementation in Java :

import java.util.PriorityQueue;
import java.util.Comparator;

/* Linked list Node*/
class Node{
    int data;
    Node next, bottom;
    Node(int data){
        this.data = data;
        next = null;
        bottom = null;
    }
}

class FlattenLinkedList {

    Node head; // head of list

    void flattenList(Node root) {
        // Creating a priority queue with custom comparator
        PriorityQueue<Node> pq = new PriorityQueue<Node>(new Comparator<Node>() {
            public int compare(Node n1, Node n2) {
                return n1.data - n2.data;
            }
        });

        // Pushing main link nodes into priority queue
        while (root != null) {
            pq.offer(root);
            root = root.next;
        }

        // Extracting min and printing least element
        while (!pq.isEmpty()) {
            Node curr = pq.poll();
            System.out.print(curr.data + " ");

            if (curr.bottom != null) {
                pq.offer(curr.bottom);
            }
        }
    }
}

public class Main{
    public static void main (String args[]) {
        // This code builds the flattened linked list
        // of the first picture in this article
        Node head = new Node(4);
        head.bottom = new Node(7);
        head.bottom.bottom = new Node(9);
        head.bottom.bottom.bottom = new Node(12);

        head.next = new Node(6);
        head.next.bottom = new Node(13);

        head.next.next = new Node(8);

        head.next.next.next = new Node(10);
        head.next.next.next.bottom = new Node(20);
        head.next.next.next.bottom.bottom = new Node(30);

        FlattenLinkedList list = new FlattenLinkedList();
        list.flattenList(head);
    }
}

Implementation in python :

import queue

class Node():
    def __init__(self, data):
        self.data = data
        self.next = None
        self.bottom = None

    def __lt__(self, other):
        return self.data < other.data

class LinkedList():
    def __init__(self):
        # the head of the list
        self.head = None

    def flattenList(self, root):
        p = queue.PriorityQueue()
        # pushing main link nodes into priority_queue
        while root:
            p.put(root)
            root = root.next

        while not p.empty():
            # extracting min
            k = p.get()
            # printing least element
            print(k.data, end=" ")
            if k.bottom:
                p.put(k.bottom)

        print("\n")

# this code builds the flattened linked list
# of the first picture in this article
head = Node(4)
head.bottom = Node(7)
head.bottom.bottom = Node(9)
head.bottom.bottom.bottom = Node(12)

head.next = Node(6)
head.next.bottom = Node(13)

head.next.next = Node(8)

head.next.next.next = Node(10)
head.next.next.next.bottom = Node(20)
head.next.next.next.bottom.bottom = Node(30)

l = LinkedList()
l.flattenList(head)

Output of the min heap code :

4 6 7 8 9 10 12 13 20 30

Time complexity :

Total no of elements present in the min heap is equal to the total number of nodes in the linked list = N * M. where N is the number of nodes in horizontal linked list and M is the size of each verical sub-linked list in worst case.
So, time taken to extract one min element from the $min heap = O(log N)$.
So, time taken to extract all N*M elements from the $min heap = O(N * M * logN)$

Space complexity :

The space required to store the elements of horizontal linked list in the priority $queue = O(N)$. So, the space required is $O(N)$.

Conclusion

• Flatteneing a linked list is a problem in which all the nodes of a bigger linked list is combined to form a single horizontal linked list.
• Merge algorithm of merge sort can be used to merge every sublist untill all the elements are merged into a single linked list.
• priority queue and Extract min operation on mean heap is used to solve the problem of flattening a linked list.
• Time complexity of merge algorithm used to flatten a linked list is $O(N * N * M)$
• Time complexity of the algorithm to flatten a linked list using priority queue is $O(N * M * logN)$