The main purpose of the flood fill algorithm is to trace out the bounded area with the same color. In this article, we will learn the working and implementation of the flood fill algorithm.
Takeaways
Flood fill is an algorithm mainly used to determine a bounded area connected to a given node in a multi-dimensional array.
Problem Statement:
You are given a integer matrix mat[][] of size n*n which represents an area where each cell is connected to adjacent cells by an undirected edge, where mat[i][j] represents the color of cell (i,j). also a source cell (x,y) and a target color C is given , you are supposed to replace the color of the region connected to cell (x,y) with color C.
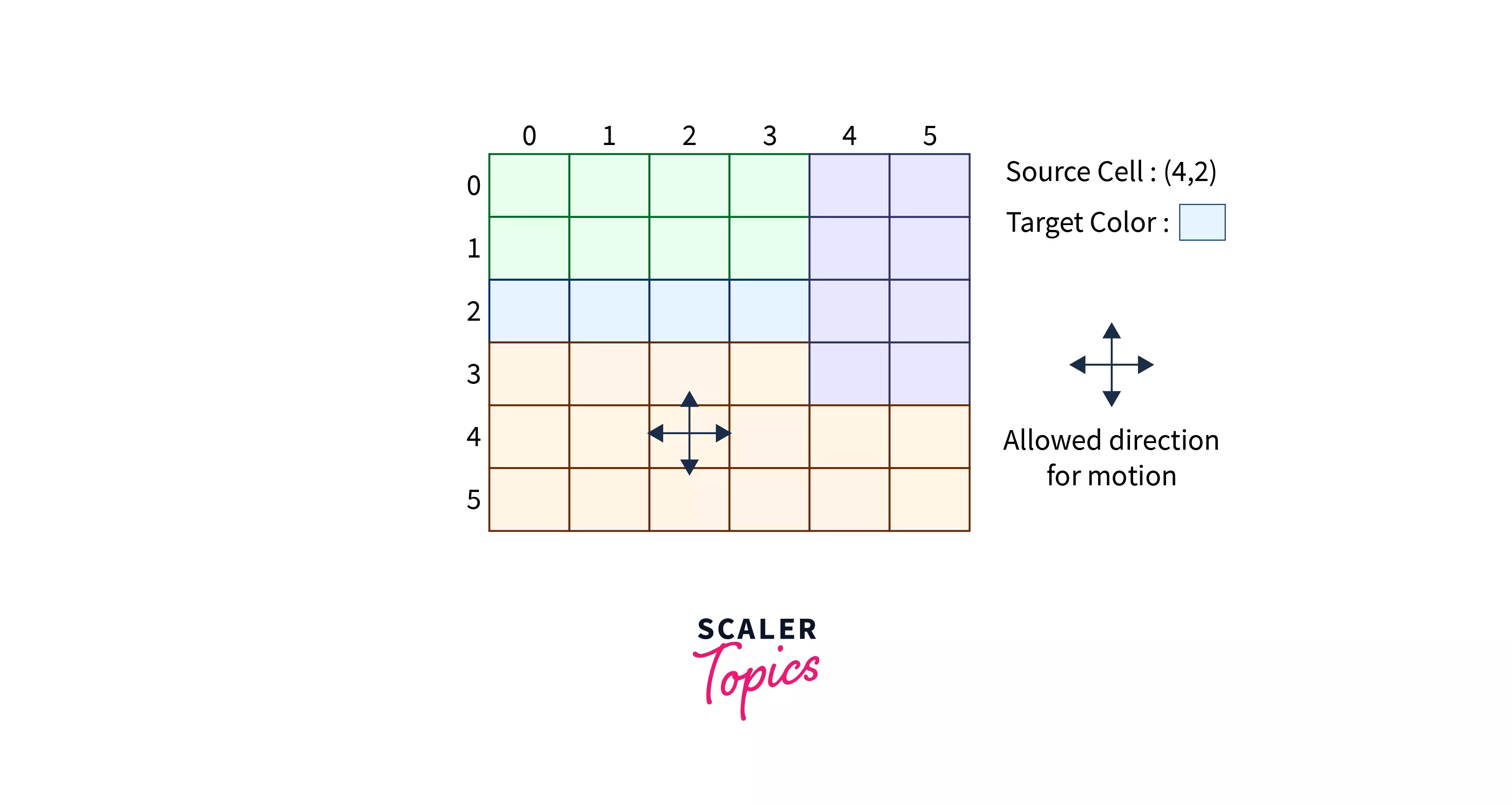
In the above scenario, all cells which are of the same color as cell (4,2) will be colored in the same target color.
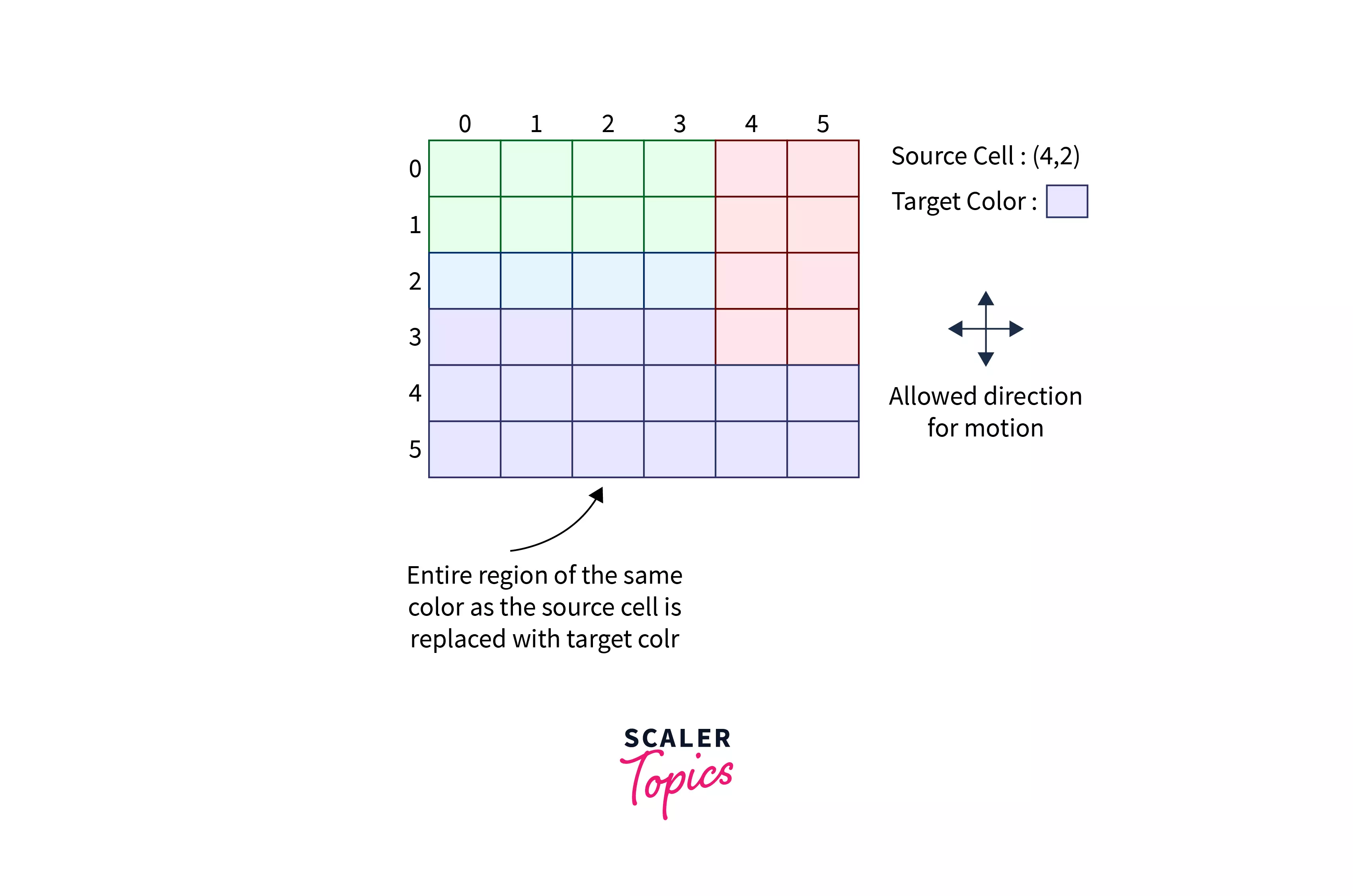
Assume that each color is represented by an integer number, then it is just a matrix of integers where each integer represents a particular color, and we need to replace the integer of the target cell (x,y) along with its neighbors which contain the integer number by the integer C.
Example:
Input: mat[][] = {
{1,1,1,1,2,2},
{1,1,1,1,2,2},
{3,3,3,3,2,2},
{4,4,4,4,2,2},
{4,4,4,4,4,4},
{4,4,4,4,4,4}
}
x = 4,y=3,C=5
Output:
1 1 1 1 2 2
1 1 1 1 2 2
3 3 3 3 2 2
5 5 5 5 2 2
5 5 5 5 5 5
5 5 5 5 5 5
Explanation:
In the above example, the source cell is (4,3) where we replaced the colors of all neighbor cells of this cell having color same as this color i.e. 4 with color 5.
How does Flood Fill Algorithm Works?
Let’s build an intuition on how to solve this problem.
First of all, it is given that we can move to left, right, up, and down from the current cell and our target is to change the color of all the connected cells having the color as the color of the source cell to the given color C, since we need to check all the neighbor cells,Breadth-first search quickly comes into the mind where we can start the BFS from the source cell and visit the entire valid region while the motion is only constrained to adjacent four directions.
So in each move (left, right, up, down), we are checking the validity of the new cell by checking whether it has the same color as the source cell had then we replace the color of that cell otherwise we skip that cell, in this way the entire region with the same color is visited and its color is changed to C.
Breadth-first Search Approach:
- Create an empty queue of pairs to store the cells say que.
- Initialize the queue qu with the source cell coordinates i.e. (x,y) and change its color to target color C.
- Iterate until the queue que is not empty and pop the front cell of the queue.
- For each popped cell check for the valid adjacent cells i.e. in four directions (right,left,up,down) if they have the same color then push them into the queue.
- For the valid adjacent cells, also change their color to C.
Let’s see the implementation of the above approach:
#include<bits/stdc++.h>
using namespace std;
//Dimensions of the matrix
const int N = 6,M=6;
// Function to return true if the given cell is valid
bool isValid(int mat[N][M], int x, int y, int currC, int C){
if(x < 0 || x >= N || y < 0 || y >= M || mat[x][y] != currC || mat[x][y] == C)
return false;
return true;
}
// flood Fill Function.
void floodFillAlgorithm(int mat[N][M], int x, int y, int currC, int C){
// create a queue
queue<pair<int,int>>que;
// push the starting pair into the queue
pair<int,int>p(x,y);
que.push(p);
// Iterate while not empty
while(!que.empty()){
// Dequeue the front node.
pair<int,int>currPair = que.front();
que.pop();
// current coordintes
int currX = currPair.first;
int currY = currPair.second;
// check for the upper adjacent cell
if(isValid(mat, currX-1, currY, currC, C)){
mat[currX-1][currY] = C;
p.first = currX-1;
p.second = currY;
que.push(p);
}
// Check for the lower adjacent cell
if(isValid(mat,currX+1,currY,currC, C)){
mat[currX+1][currY] = C;
p.first = currX+1;
p.second = currY;
que.push(p);
}
// Check for the left adjacent cell
if(isValid(mat,currX,currY-1,currC, C)){
mat[currX][currY-1] = C;
p.first = currX;
p.second = currY-1;
que.push(p);
}
// Check for the right adjacent cell
if(isValid(mat,currX,currY+1,currC,C)){
mat[currX][currY+1] = C;
p.first = currX;
p.second = currY+1;
que.push(p);
}
}
}
//Driver program
int main(){
// Given matrix
int mat[N][M] = {
{1,1,1,1,2,2},
{1,1,1,1,2,2},
{3,3,3,3,2,2},
{4,4,4,4,2,2},
{4,4,4,4,4,4},
{4,4,4,4,4,4}
};
// Source cell coordinates
int x=4;
int y = 3;
// New color
int C = 5;
// source cell color
int currC = mat[x][y];
// Call the algorithm
floodFillAlgorithm(mat,x,y,currC,C);
//Print the result matrix
for(int i=0;i<N;i++){
for(int j=0;j<M;j++){
cout << mat[i][j] << " ";
}
cout << "\n";
}
}
Output:
1 1 1 1 2 2
1 1 1 1 2 2
3 3 3 3 2 2
5 5 5 5 2 2
5 5 5 5 5 5
5 5 5 5 5 5
In the above implementation, we just implemented simple BFS and we painted the given region with single color C, Now let’s jump into the complexity analysis of the above code
Complexity Analysis
Time Complexity: O(N*M), due to traversal of each and every cell of the matrix. Space Complexity: O(N*M)
Since we know that the solution of the problem involves the traversal of the enclosed region, we may also use depth-first search for that.
Depth-first Search Approach:
Since we know that the solution of the problem involves the traversal of the enclosed region, we may also use depth-first search for that.
- First of all replace the color of the source node with C.
- After that, explore all of the 4 adjacent cells recursively and replace their color with C if they are found valid.
- A valid adjacent cell is the one that has the same color as the source cell.
Let’s see the implementation of the above algorithm:
#include<bits/stdc++.h>
using namespace std;
// Dimensions of the matrix:
const int N = 6, M=6;
// Direction vectors
int row[] = {-1,0,1,0};
int col[] = {0,1,0,-1};
//Function to validate the given cell
bool isValid(int mat[][M], int x, int y, int currC, int C){
if(x >= N || x < 0 || y <0 || y >= M || mat[x][y] != currC || mat[x][y] == C)return false;
return true;
}
// Flood fill recursive function
void floodfill(int mat[][M], int x, int y, int currC, int C){
// Target color is same as the replacement
if(currC == C)return;
// Replace the current pixel color with replacement
mat[x][y]=C;
for(int i=0;i<4;i++){
if(isValid(mat,x+row[i],y+col[i],currC, C))
floodFill(mat,x+row[i],y+col[i],currC,C);
}
}
//Driver program
int main(){
// Given matrix
int mat[N][M] = {
{1,1,1,1,2,2},
{1,1,1,1,2,2},
{3,3,3,3,2,2},
{4,4,4,4,2,2},
{4,4,4,4,4,4},
{4,4,4,4,4,4}
};
// Source cell coordinates
int x=4;
int y = 3;
// New color
int C = 5;
// source cell color
int currC = mat[x][y];
// Call the algorithm
floodFill(mat,x,y,currC,C);
//Print the result matrix
for(int i=0;i<N;i++){
for(int j=0;j<M;j++){
cout << mat[i][j] << " ";
}
cout << "\n";
}
}
Output:
1 1 1 1 2 2
1 1 1 1 2 2
3 3 3 3 2 2
5 5 5 5 2 2
5 5 5 5 5 5
5 5 5 5 5 5
Let’s understand the time and space complexity of the above code:
Complexity Analysis
Let’s understand the time and space complexity of the above code:
- Time complexity = O(N * M), as each cell of the matrix is visited once, performing constant-time operations.
- Space complexity = O(N * M), where N and M are the dimensions of the input matrix.
Conclusion:
- The flood fill algorithm is a versatile technique used for filling connected regions of a grid with a specified color.
- It can be applied in various scenarios such as computer graphics, image processing, and game development.
- Implemented using either Depth-First Search (DFS) or Breadth-First Search (BFS), the algorithm offers an efficient solution with a time complexity of O(N * M) and a space complexity of O(N * M) in the worst case, where N and M are the dimensions of the grid.
- The choice between DFS and BFS depends on factors such as the nature of the grid and the desired order of traversal.
- DFS may be preferred for simplicity and ease of implementation.
- BFS may be more suitable for finding the shortest path or when memory usage is a concern.
- There are uses of flood fill algorithm in computer graphics, image processing, and game development.