Hamiltonian Cycle

What is Hamiltonian Cycle?

Hamiltonian Cycle or Circuit is a path in an undirected graph that visits all the vertices in the graph exactly once and terminates back at the starting node.

Problem Statement

Given an undirected graph, our task is to determine whether the graph contains a Hamiltonian cycle or not.

Example

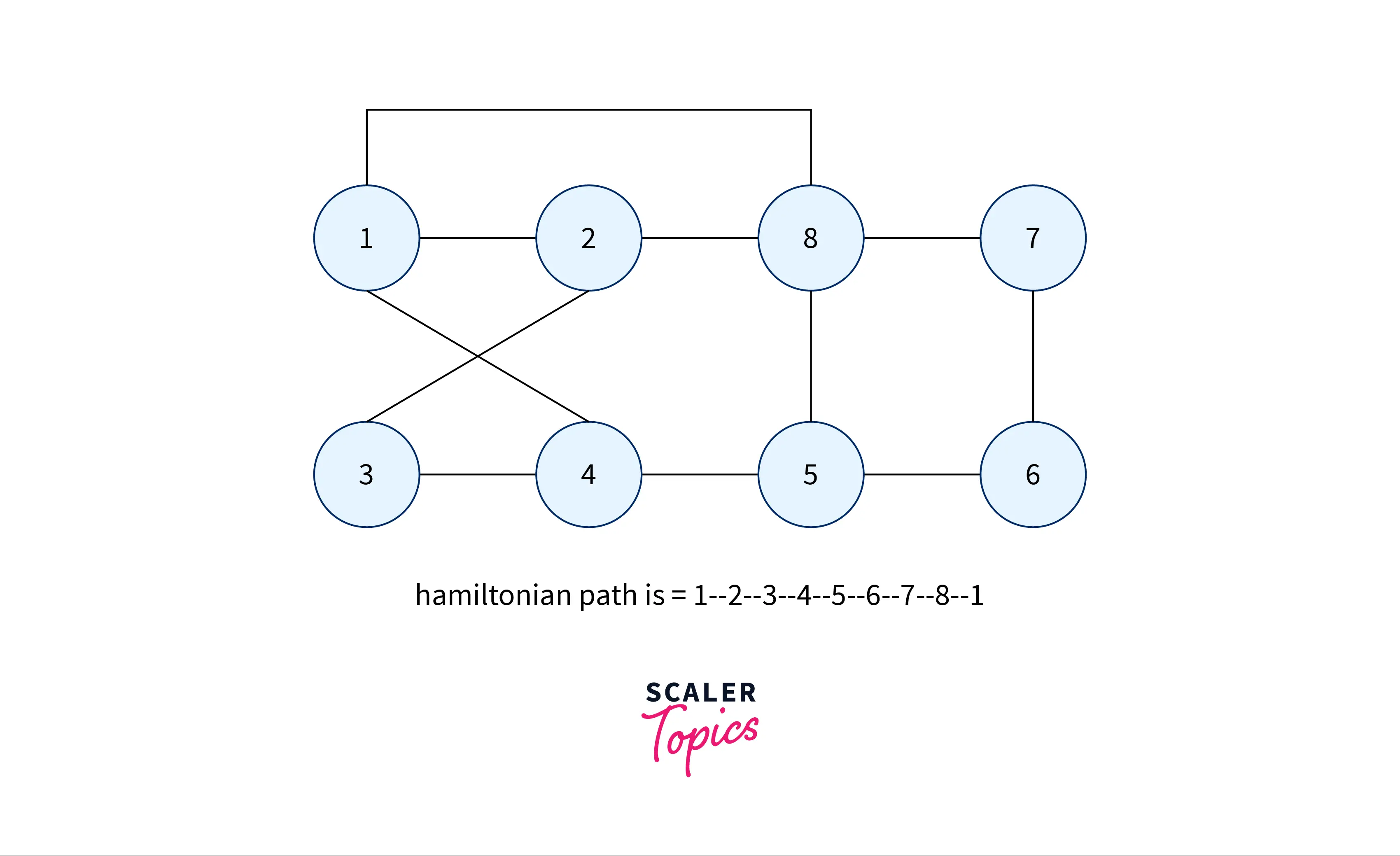
Explanation

In the above example, we are given an undirected having 8 vertices. We start traversing from vertex 1 and are able to visit every vertex exactly once and return back to vertex 1 which is the starting vertex.

Input/ Output

Input is the adjacency matrix of a graph G(V, E), where V is the number of Vertices and E is the number of Edges. An adjacency matrix represents the adjacency of two vertices in constant time.

In Output, we have to Return True (boolean value) along with the path if the graph contains a Hamiltonian cycle, otherwise returns False.

Constraints

• The graph is undirected.
• The task is to determine the presence of a Hamiltonian cycle in the graph.
• A Hamiltonian cycle is a cycle that visits every vertex exactly once and returns to the starting vertex.

Approach – Naive Algorithm

In this approach, we will use Dynamic Programming and Bit Masking techniques to check whether there exists a Hamiltonian Cycle or not.

Algorithm
1. Initialize a boolean matrix dp[][] having dimension $N*2^{N}$, where dp[j][i] represents whether there exists a path for the given subset or not.
2. For the base case, update dp[i][1 << i] = true, for i in range [0, N – 1].
3. Iterate over the range [1, $2^{N}$ – 1] using and perform the following steps:
– All the vertices with bits set in mask i, are included in the subset.
– Iterate over the range [1, N] using the variable j that will represent the end vertex of the hamiltonian path of current subset mask i and perform the following steps:
– If the value of i and $2^{j}$ is true, then iterate over the range [1, N] using the variable k and if the value of dp$[k][i^{2^{j}}]$ is true, then mark dp[j][i] is true and break out of the loop.
– Otherwise, continue to the next iteration.
4. Iterate over the range using the variable i and if the value of dp[i][$2^{N}$ – 1] is true, then there exists a hamiltonian path ending at vertex i.

Implementation
Let us now see the implementation of the Hamiltonian Cycle using the naive approach in the following Graph in C++:

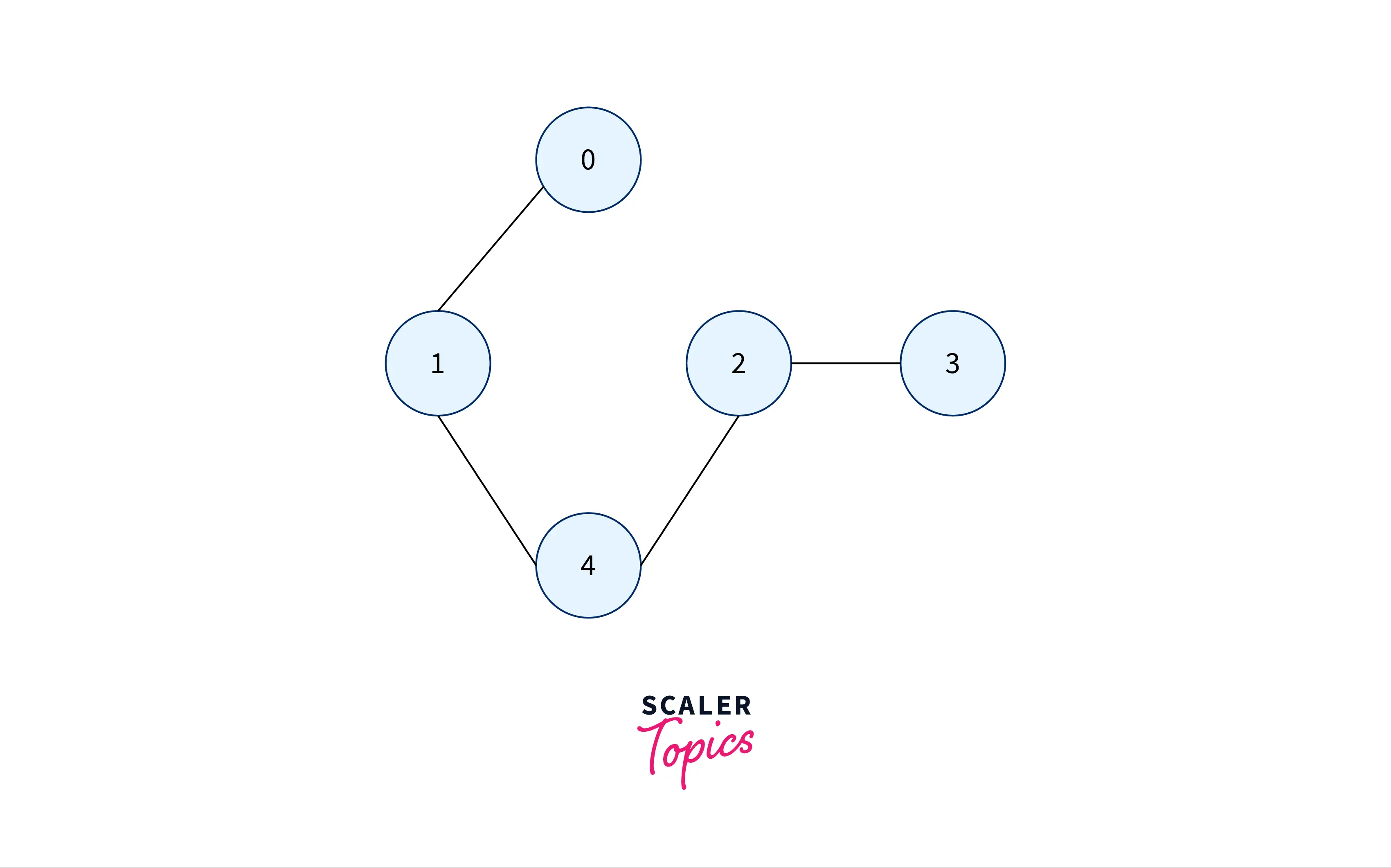
#include <bits/stdc++.h>
    using namespace std;
    const int N = 5;

    // function to check whether there exists a Hamiltonian Path or not
    bool hamiltonianCycle(vector<vector<int> >& adj, int N) {

        int dp[N][(1 << N)];

        // initializing the dp table
        memset(dp, 0, sizeof dp);

        // set all dp[i][(1 << i)] to true
        for (int i = 0; i < N; i++)
            dp[i][(1 << i)] = true;

        // iterate over each subset of vertices
        for (int i = 0; i < (1 << N); i++) {

            for (int j = 0; j < N; j++) {

                // if the jth nodes is included in the current subset
                if (i & (1 << j)) {

                    // find K, neighbour of j also present in the current subset
                    for (int k = 0; k < N; k++) {

                        if (i & (1 << k) && adj[k][j] && j != k && dp[k][i ^ (1 << j)]) {

                            // update dp[j][i] to true
                            dp[j][i] = true;
                            break;
                        }
                    }
                }
            }
        }

        // traverse the vertices
        for (int i = 0; i < N; i++) {

            // if hamiltonian path exists
            if (dp[i][(1 << N) - 1])
                return true;
        }

        // else, return false
        return false;
    }

    int main() {
        vector<vector<int> > adj = { { 0, 1, 1, 1, 0 },
                                     { 1, 0, 1, 0, 1 },
                                     { 1, 1, 0, 1, 1 },
                                     { 1, 0, 1, 0, 0 } };
        int N = adj.size();

        // calling the function
        if (hamiltonianCycle(adj, N))
            cout << "Hamiltonian Cycle exists";
        else
            cout << "Hamiltonian Cycle does not exist";

        return 0;
    }

Output:

Hamiltonian Cycle exists

Let us now see the implementation of the Hamiltonian Cycle using the naive approach of the above-shown graph in Java:

    import java.io.*;
    import java.lang.*;
    import java.util.*;

    class Main{

        // function to check whether there exists a Hamiltonian Path or not
        static boolean hamiltonianCycle(int adj[][], int N) {
            // initializing the dp table
            boolean dp[][] = new boolean[N][(1 << N)];

            // set all dp[i][(1 << i)] to true
            for(int i = 0; i < N; i++)
                dp[i][(1 << i)] = true;

            // iterate over each subset of vertices
            for(int i = 0; i < (1 << N); i++) {
                for(int j = 0; j < N; j++) {

                    // if the jth nodes is included in the current subset
                    if ((i & (1 << j)) != 0) {

                        // find K, neighbour of j also present in the current subset
                        for(int k = 0; k < N; k++) {

                            if ((i & (1 << k)) != 0 && adj[k][j] == 1 && j != k && dp[k][i ^ (1 << j)]) {

                                // update dp[j][i] to true
                                dp[j][i] = true;
                                break;
                            }
                        }
                    }
                }
            }

            // traverse the vertices
            for(int i = 0; i < N; i++) {

                // if hamiltonian path exists
                if (dp[i][(1 << N) - 1])
                    return true;
            }

            // else, return false
            return false;
        }

        public static void main(String[] args) {
            int adj[][] = { { 0, 1, 1, 1, 0 },
                            { 1, 0, 1, 0, 1 },
                            { 1, 1, 0, 1, 1 },
                            { 1, 0, 1, 0, 0 } };
            int N = adj.length;

            // calling the function
            if (hamiltonianCycle(adj, N))
                System.out.println("Hamiltonian Cycle exists");
            else
                System.out.println("Hamiltonian Cycle does not exist");
            }
        }    

Output:

Hamiltonian Cycle exists

Let us now see the implementation of the Hamiltonian Cycle using the naive approach of the above-shown graph in Python:

# function to check whether there exists a Hamiltonian Path or not
def hamiltonianCycle(adj, N):

    # initializing the dp table
    dp = [[False for i in range(1 << N)]
                for j in range(N)]

    # set all dp[i][(1 << i)] to true
    for i in range(N):
        dp[i][1 << i] = True

    # iterate over each subset of vertices
    for i in range(1 << N):
        for j in range(N):

            # if the jth nodes is included in the current subset
            if ((i & (1 << j)) != 0):

                # find K, neighbour of j also present in the current subset
                for k in range(N):
                    if ((i & (1 << k)) != 0 and adj[k][j] == 1 and j != k and dp[k][i ^ (1 << j)]):

                        # update dp[j][i] to true
                        dp[j][i] = True
                        break

    # traverse the vertices
    for i in range(N):

        # if hamiltonian path exists
        if (dp[i][(1 << N) - 1]):
            return True

    # else, return false
    return False

adj = [ [ 0, 1, 1, 1, 0 ] ,
        [ 1, 0, 1, 0, 1 ],
        [ 1, 1, 0, 1, 1 ],
        [ 1, 0, 1, 0, 0 ] ]

N = len(adj)

if (hamiltonianCycle(adj, N)):
    print("Hamiltonian Cycle exists")
else:
    print("Hamiltonian Cycle does not exist")

Output:

Hamiltonian Cycle exists

Let us now see the implementation of the Hamiltonian Cycle using the naive approach of the above-shown graph in Java:

    import java.io.*;
    import java.lang.*;
    import java.util.*;

    class Main{

        // function to check whether there exists a Hamiltonian Path or not
        static boolean hamiltonianCycle(int adj[][], int N) {
            // initializing the dp table
            boolean dp[][] = new boolean[N][(1 << N)];

            // set all dp[i][(1 << i)] to true
            for(int i = 0; i < N; i++)
                dp[i][(1 << i)] = true;

            // iterate over each subset of vertices
            for(int i = 0; i < (1 << N); i++) {
                for(int j = 0; j < N; j++) {

                    // if the jth nodes is included in the current subset
                    if ((i & (1 << j)) != 0) {

                        // find K, neighbour of j also present in the current subset
                        for(int k = 0; k < N; k++) {

                            if ((i & (1 << k)) != 0 && adj[k][j] == 1 && j != k && dp[k][i ^ (1 << j)]) {

                                // update dp[j][i] to true
                                dp[j][i] = true;
                                break;
                            }
                        }
                    }
                }
            }

            // traverse the vertices
            for(int i = 0; i < N; i++) {

                // if hamiltonian path exists
                if (dp[i][(1 << N) - 1])
                    return true;
            }

            // else, return false
            return false;
        }

        public static void main(String[] args) {
            int adj[][] = { { 0, 1, 1, 1, 0 },
                            { 1, 0, 1, 0, 1 },
                            { 1, 1, 0, 1, 1 },
                            { 1, 0, 1, 0, 0 } };
            int N = adj.length;

            // calling the function
            if (hamiltonianCycle(adj, N))
                System.out.println("Hamiltonian Cycle exists");
            else
                System.out.println("Hamiltonian Cycle does not exist");
            }
        }    

Output:

Hamiltonian Cycle exists

Let us now see the implementation of the Hamiltonian Cycle using the naive approach of the above-shown graph in Python:

# function to check whether there exists a Hamiltonian Path or not
def hamiltonianCycle(adj, N):

    # initializing the dp table
    dp = [[False for i in range(1 << N)]
                for j in range(N)]

    # set all dp[i][(1 << i)] to true
    for i in range(N):
        dp[i][1 << i] = True

    # iterate over each subset of vertices
    for i in range(1 << N):
        for j in range(N):

            # if the jth nodes is included in the current subset
            if ((i & (1 << j)) != 0):

                # find K, neighbour of j also present in the current subset
                for k in range(N):
                    if ((i & (1 << k)) != 0 and adj[k][j] == 1 and j != k and dp[k][i ^ (1 << j)]):

                        # update dp[j][i] to true
                        dp[j][i] = True
                        break

    # traverse the vertices
    for i in range(N):

        # if hamiltonian path exists
        if (dp[i][(1 << N) - 1]):
            return True

    # else, return false
    return False

adj = [ [ 0, 1, 1, 1, 0 ] ,
        [ 1, 0, 1, 0, 1 ],
        [ 1, 1, 0, 1, 1 ],
        [ 1, 0, 1, 0, 0 ] ]

N = len(adj)

if (hamiltonianCycle(adj, N)):
    print("Hamiltonian Cycle exists")
else:
    print("Hamiltonian Cycle does not exist")

Output:

Hamiltonian Cycle exists

• Time Complexity Time Complexity for finding the Hamiltonian Cycle using the naive approach is $O(N*2^{N})$, where N is the number of vertices in the graph.
• ### Space Complexity
  Since we are using the boolean matrixdp[][] as an auxiliary space, the space complexity for finding the Hamiltonian Cycle using the naive approach is $O(N*2^{N})$.

Approach – Backtracking

The optimal Approach for this problem will be to solve it using the concept of backtracking. The following algorithm demonstrates the working of the backtracking approach:

Algorithm

1. Create an empty path array and add vertex 0 to it.
2. Start adding other vertices by checking if they have been added previously or not.
3. We can check this by creating a visiting array to check if the vertex has already been visited or is adjacent to the previously added vertex.
4. If any such vertex is found, add it to the path array and backtrack from there.
5. If no such vertex is found we return False.

Implementation
Let us now see the implementation of the Hamiltonian Cycle of the following two Graphs in C++:

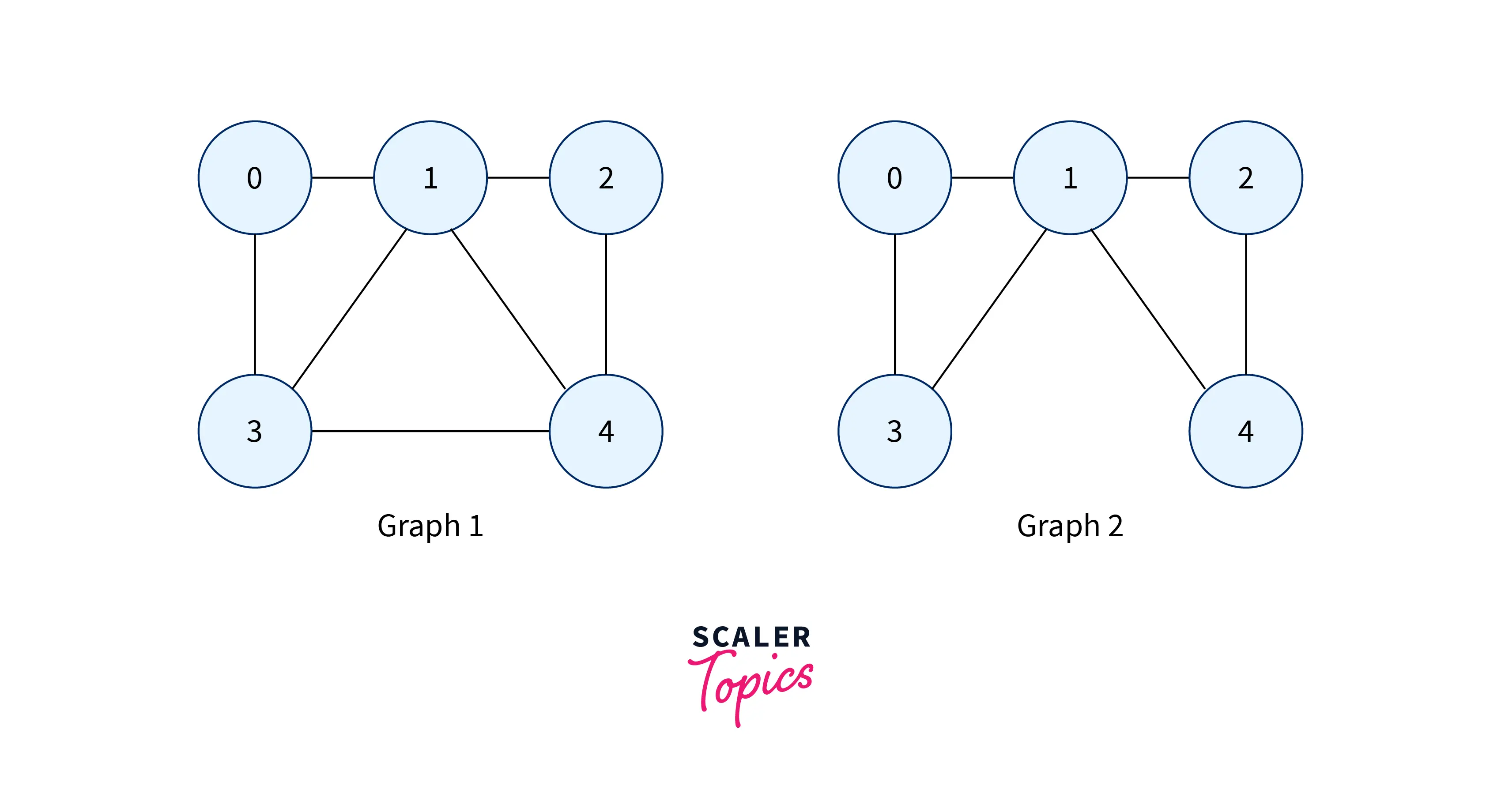
    #include <bits/stdc++.h>
    using namespace std;

    // number of vertices
    #define V 5

    /* function to check if the vertex v can be added
    in the Hamiltonian Cycle constructed so far */
    bool check(int v, bool graph[V][V], int path[], int pos) {

        /* checking if this vertex is an adjacent
        vertex of the previously added vertex */
        if (graph [path[pos - 1]][ v ] == 0)
            return false;

        // checking if the vertex has already been included
        for (int i = 0; i < pos; i++)
            if (path[i] == v)
                return false;

        return true;
    }

    // utility function to print the cycle 
    void printCycle(int path[])
    {
        cout << "Hamiltonian Cycle exists: ";
        for (int i = 0; i < V; i++)
            cout << path[i] << " ";

        // printing the starting vertex again to show a cycle
        cout << path[0] << " ";
        cout << endl;
    }

    // recursive function to check if hamiltonian cycle exists or not 
    bool hamiltonianUtil(bool graph[V][V], int path[], int pos) {

        // if all vertices are included in Hamiltonian Cycle 
        if (pos == V) {

            // if there is exists an edge from the last included vertex to the first vertex
            if (graph[path[pos - 1]][path[0]] == 1)
                return true;
            else
                return false;
        }

        // traversing for different vertices as a next vertex in Hamiltonian Cycle. 
        for (int v = 1; v < V; v++)
        {
            // checking if this vertex can be added to Hamiltonian Cycle 
            if (check(v, graph, path, pos))
            {
                path[pos] = v;

                // recursive to construct rest of the path 
                if (hamiltonianUtil (graph, path, pos + 1) == true)
                    return true;

                // if adding vertex v doesn't lead to a solution, then remove it 
                path[pos] = -1;
            }
        }

        // if no vertex can be added to Hamiltonian Cycle constructed so far, then return false 
        return false;
    }

    // this function finds the Hamiltonian Cycle problem using Backtracking
    bool hamiltonianCycle(bool graph[V][V])
    {
        int *path = new int[V];
        for (int i = 0; i < V; i++)
            path[i] = -1;

        // put vertex 0 as the first vertex in the path
        path[0] = 0;
        if (hamiltonianUtil(graph, path, 1) == false )
        {
            cout << "\nHamiltonian Cycle does not exist";
            return false;
        }

        printCycle(path);
        return true;
    }

    int main() {
        bool graph1[V][V] = {{0, 1, 0, 1, 0},
                            {1, 0, 1, 1, 1},
                            {0, 1, 0, 0, 1},
                            {1, 1, 0, 0, 1},
                            {0, 1, 1, 1, 0}};

        // print the cycle
        hamiltonianCycle(graph1);

        bool graph2[V][V] = {{0, 1, 0, 1, 0},
                            {1, 0, 1, 1, 1},
                            {0, 1, 0, 0, 1},
                            {1, 1, 0, 0, 0},
                            {0, 1, 1, 0, 0}};

        // print the cycle
        hamiltonianCycle(graph2);

        return 0;
    }

Output:

Hamiltonian Cycle exists 0 1 2 4 3 0 

Hamiltonian Cycle does not exist

Let us now see the implementation of the Hamiltonian Cycle in the above shown Graphs in Java:

    class Main {
        // number of vertices
        final int V = 5;
        int path[];

        /* function to check if the vertex v can be added
        in the Hamiltonian Cycle constructed so far */
        boolean check(int v, int graph[][], int path[], int pos) {

            /* checking if this vertex is an adjacent
            vertex of the previously added vertex */
            if (graph[path[pos - 1]][v] == 0)
                return false;

            // checking if the vertex has already been included
            for (int i = 0; i < pos; i++)
                if (path[i] == v)
                    return false;

            return true;
        }

        // recursive function to check if hamiltonian cycle exists or not 
        boolean hamiltonianUtil(int graph[][], int path[], int pos) {

            // if all vertices are included in Hamiltonian Cycle
            if (pos == V) {
                // if there is exists an edge from the last included vertex to the first vertex
                if (graph[path[pos - 1]][path[0]] == 1)
                    return true;
                else
                    return false;
            }

            // traversing for different vertices as a next vertex in Hamiltonian Cycle.
            for (int v = 1; v < V; v++) {
                // checking if this vertex can be added to Hamiltonian Cycle
                if (check(v, graph, path, pos)) {
                    path[pos] = v;

                    // recursive to construct rest of the path
                    if (hamiltonianUtil(graph, path, pos + 1) == true)
                        return true;

                    // if adding vertex v doesn't lead to a solution, then remove it
                    path[pos] = -1;
                }
            }

            // if no vertex can be added to Hamiltonian Cycle constructed so far, then return false
            return false;
        }

        // this function finds the Hamiltonian Cycle problem using Backtracking. 
        int hamiltonianCycle(int graph[][]) {
            path = new int[V];
            for (int i = 0; i < V; i++)
                path[i] = -1;

            // put vertex 0 as the first vertex in the path
            path[0] = 0;
            if (hamiltonianUtil(graph, path, 1) == false)
            {
                System.out.println("\nHamiltonian Cycle does not exist");
                return 0;
            }

            printCycle(path);
            return 1;
        }

        // utility function to print the cycle
        void printCycle(int path[]) {

            System.out.print("Hamiltonian Cycle exists: ");
            for (int i = 0; i < V; i++)
                System.out.print(" " + path[i] + " ");

            // printing the starting vertex again to show a cycle
            System.out.println(" " + path[0] + " ");
        }

        public static void main(String args[]) {
            Main hamiltonian = new Main();
            int graph1[][] = {{0, 1, 0, 1, 0},
                {1, 0, 1, 1, 1},
                {0, 1, 0, 0, 1},
                {1, 1, 0, 0, 1},
                {0, 1, 1, 1, 0},
            };

            // print the cycle
            hamiltonian.hamiltonianCycle(graph1);

            int graph2[][] = {{0, 1, 0, 1, 0},
                {1, 0, 1, 1, 1},
                {0, 1, 0, 0, 1},
                {1, 1, 0, 0, 0},
                {0, 1, 1, 0, 0},
            };

            // print the cycle
            hamiltonian.hamiltonianCycle(graph2);
        }
    }

Output:

Hamiltonian Cycle exists 0 1 2 4 3 0 

Hamiltonian Cycle does not exist

Let us now see the implementation of the Hamiltonian Cycle above shown in two Graphs in Python:

class Graph():
    def __init__(self, vertices):
        self.graph = [[0 for column in range(vertices)]
                            for row in range(vertices)]
        self.V = vertices

    ''' function to check if the vertex v can be added
        in the Hamiltonian Cycle constructed so far '''
    def check(self, v, pos, path):
        # checking if this vertex is an adjacent
        # vertex of the previously added vertex
        if self.graph[ path[pos-1] ][v] == 0:
            return False

        # checking if the vertex has already been included
        for vertex in path:
            if vertex == v:
                return False

        return True

    # recursive function to check if hamiltonian cycle exists or not 
    def hamiltonianUtil(self, path, pos):

        # if all vertices are included in Hamiltonian Cycle
        if pos == self.V:
            # if there is exists an edge from the last included vertex to the first vertex
            if self.graph[ path[pos-1] ][ path[0] ] == 1:
                return True
            else:
                return False

        # traversing for different vertices as a next vertex in Hamiltonian Cycle.
        for v in range(1,self.V):

            # checking if this vertex can be added to Hamiltonian Cycle
            if self.check(v, pos, path) == True:

                path[pos] = v

                # // recursive to construct rest of the path
                if self.hamiltonianUtil(path, pos+1) == True:
                    return True

                # if adding vertex v doesn't lead to a solution, then remove it
                path[pos] = -1

        # if no vertex can be added to Hamiltonian Cycle constructed so far, then return false
        return False

    # this function finds the Hamiltonian Cycle problem using Backtracking.
    def hamiltonianCycle(self):
        path = [-1] * self.V

        # put vertex 0 as the first vertex in the path
        path[0] = 0

        if self.hamiltonianUtil(path,1) == False:
            print ("Hamiltonian Cycle does not exist\n")
            return False

        self.printCycle(path)
        return True

    # utility function to print the cycle
    def printCycle(self, path):
        print ("Hamiltonian Cycle exists",end=" ")
        for vertex in path:
            print (vertex, end = " ")
        # printing the starting vertex again to show a cycle
        print (path[0], "\n")

g1 = Graph(5)
g1.graph = [ [0, 1, 0, 1, 0], [1, 0, 1, 1, 1],
            [0, 1, 0, 0, 1,],[1, 1, 0, 0, 1],
            [0, 1, 1, 1, 0], ]

# print the cycle
g1.hamiltonianCycle();

g2 = Graph(5)
g2.graph = [ [0, 1, 0, 1, 0], [1, 0, 1, 1, 1],
        [0, 1, 0, 0, 1,], [1, 1, 0, 0, 0],
        [0, 1, 1, 0, 0], ]

# print the cycle
g2.hamiltonianCycle();

Output:

Hamiltonian Cycle exists 0 1 2 4 3 0 

Hamiltonian Cycle does not exist

In the above implementation, the hamiltonianCycle function solves the Hamiltonian Cycle problem using Backtracking. It mainly utilizes hamiltonianUtil() function to solve the problem. It returns False if there is no Hamiltonian Cycle possible, otherwise, returns true and prints the cycle.

Time Complexity
Time Complexity for finding the Hamiltonian Cycle using the Backtracking approach is O(N!), where N is the number of vertices in the graph.

Space Complexity
Since we are not using any auxiliary space, the space complexity for finding the Hamiltonian Cycle using the Backtracking approach is O(1).

Conclusion

• Hamiltonian Cycleis a path in an undirected graph that visits all the vertices in the graph exactly once and terminates back at the starting node.
• Naive Approach has the following Complexities:
  • Time Complexity: $O(N*2^{N})$, where N is the number of vertices
  • Space Complexity: $O(N*2^{N})$
• Backtracking Approach has the following Complexities:
  • Time Complexity: O(N!), where N is the number of vertices
  • Space Complexity: O(1)
• The Hamiltonian cycle problem is a combination of both decision and an optimization problem.