Intersection of Two Linked Lists

Implement a program to detect the intersection point of two linked lists, where one list accidentally merges with the other, forming an inverted Y-shaped structure.

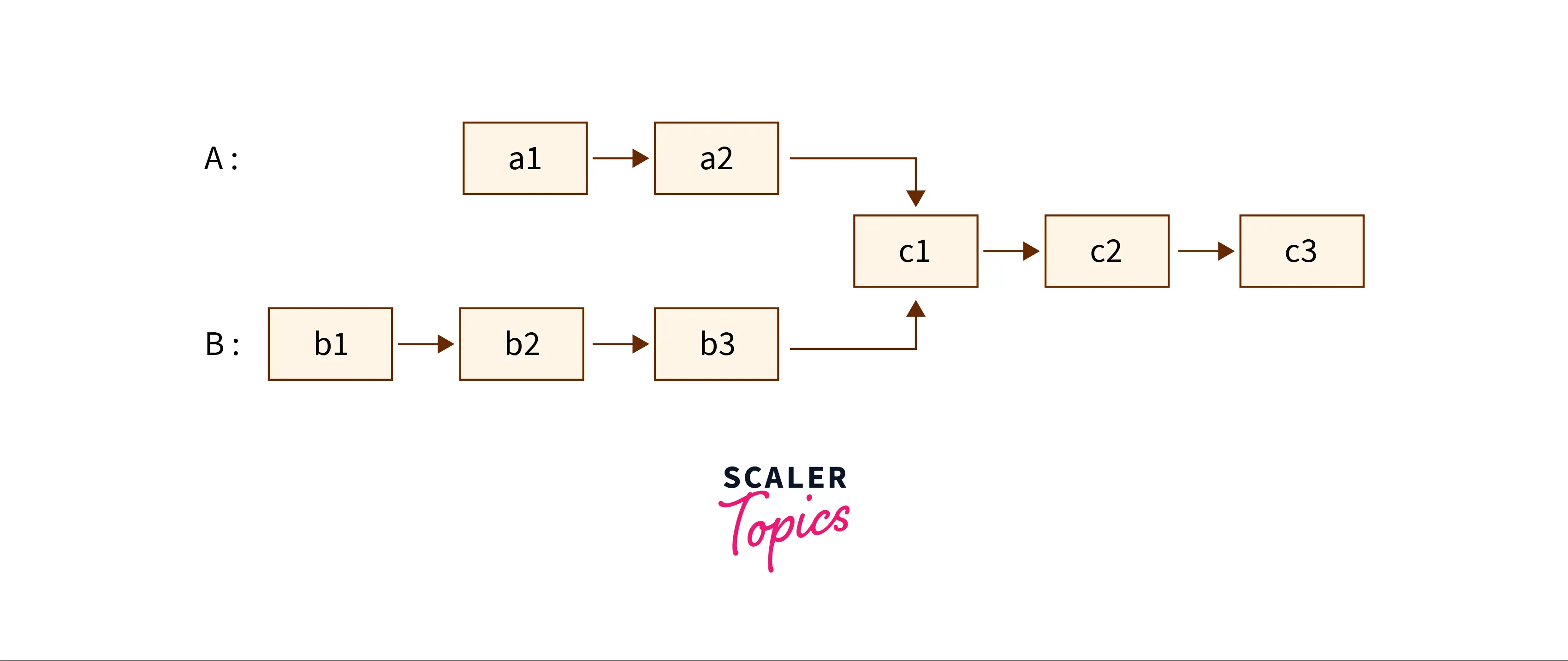
For example, the following two linked lists have common nodes starting from c1. Thus, c1 is the intersection point of two linked lists.

Approach 1: Using Two Nested Loops

Utilize two nested for loops, where the outer loop iterates over each node of the first list, and the inner loop iterates over each node of the second list. Within the inner loop, check if any nodes from the second list match the current node of the first linked list.

Code Implementation

C++ Code

#include <iostream>
using namespace std;

// Definition of a Linked List Node
struct Node {
    int data;
    Node* next;
};

// Function to insert a new node at the beginning of a linked list
void push(Node*& head, int data) {
    // Create a new node
    Node* newNode = new Node;
    newNode->data = data;
    newNode->next = head;
    head = newNode;
}

// Function to detect the intersection point of two linked lists
Node* findIntersection(Node* first, Node* second) {
    // Pointer to traverse the first linked list
    Node* x = first;

    // Traverse through the first linked list using x
    while (x != nullptr) {
        // Pointer to traverse the second linked list
        Node* y = second;

        // Traverse through the second linked list using y
        while (y != nullptr) {
            // If there is a point of intersection, return the common node
            if (x == y)
                return x;
            y = y->next;
        }
        x = x->next;
    }

    // If there is no intersecting node
    return nullptr;
}

int main() {
    // Construct the first linked list
    Node* first = nullptr;
    int firstListValues[] = {7, 4, 9, 2, 5, 3, 8};
    int firstListLength = sizeof(firstListValues) / sizeof(firstListValues[0]);
    for (int i = firstListLength - 1; i >= 0; i--) {
        push(first, firstListValues[i]);
    }

    // Construct the second linked list
    Node* second = nullptr;
    int secondListValues[] = {1, 6, 10, 5, 3, 8};
    int secondListLength = sizeof(secondListValues) / sizeof(secondListValues[0]);
    for (int i = secondListLength - 1; i >= 0; i--) {
        push(second, secondListValues[i]);
    }

    // Link the fifth node of the first linked list to the fourth node of the second linked list
    Node* currentFirst = first;
    for (int i = 0; i < 4; i++) {
        currentFirst = currentFirst->next;
    }

    Node* currentSecond = second;
    for (int i = 0; i < 3; i++) {
        currentSecond = currentSecond->next;
    }

    currentFirst->next = currentSecond;

    // Find the intersection point
    Node* intersectionNode = findIntersection(first, second);

    // Print the result
    if (intersectionNode) {
        cout << "Intersection point is " << intersectionNode->data << endl;
    } else {
        cout << "Lists do not intersect." << endl;
    }

    return 0;
}

Java Code

class Main {
    // Definition of a Linked List Node
    static class ListNode {
        int value;
        ListNode next;
    }
    
    // Function to create a new node with the given value
    // and add it to the front of the list
    public static ListNode addNodeToFront(ListNode head, int value) {
        // Create a new node
        ListNode newNode = new ListNode();
        newNode.value = value;
        newNode.next = head;
 
        return newNode;
    }
    
    // Function to detect the intersection point of two linked lists
    private static ListNode findIntersectionPoint(ListNode list1, ListNode list2) {
        ListNode current1 = list1;
        
        // Traverse through the first linked list
        while (current1 != null) {
            ListNode current2 = list2;
            
            // Traverse through the second linked list
            while (current2 != null) {
                // If both linked lists point to the same node
                if (current1 == current2) {
                    return current1;
                }
                current2 = current2.next;
            }
            current1 = current1.next;
        }
        
        // If there is no intersecting node
        return null;
    }
 
    public static void main(String[] args) {
        // Construct the first linked list
        Node first = new Node(-1); // Dummy node
        int[] firstListValues = {7, 4, 9, 2, 5, 3, 8};
        for (int i = firstListValues.length - 1; i >= 0; i--) {
            push(first, firstListValues[i]);
        }

        // Construct the second linked list
        Node second = new Node(-1); // Dummy node
        int[] secondListValues = {1, 6, 10, 5, 3, 8};
        for (int i = secondListValues.length - 1; i >= 0; i--) {
            push(second, secondListValues[i]);
        }

        // Link the fifth node of the first linked list to the fourth node of the second linked list
        Node currentFirst = first;
        for (int i = 0; i < 4; i++) {
            currentFirst = currentFirst.next;
        }

        Node currentSecond = second;
        for (int i = 0; i < 3; i++) {
            currentSecond = currentSecond.next;
        }

        currentFirst.next = currentSecond;

        // Find the intersection point
        Node intersectionNode = findIntersection(first, second);

        // Print the result
        if (intersectionNode != null) {
            System.out.println("Intersection point is " + intersectionNode.data);
        } else {
            System.out.println("Lists do not intersect.");
        }
    }
}

Python Code

class Node:
    def __init__(self, data):
        self.data = data
        self.next = None

def push(head, data):
    node = Node(data)
    node.next = head
    return node

def intersectionPoint(list1, list2):
    firstTemp = list1
    while firstTemp:
        temp = list2
        while temp:
            if firstTemp == temp:
                return firstTemp
            temp = temp.next
        firstTemp = firstTemp.next
    return None

if __name__ == "__main__":
    first = None
    first_list_values = [7, 4, 9, 2, 5, 3, 8]
    for value in reversed(first_list_values):
        first = push(first, value)

    # Construct the second linked list
    second = None
    second_list_values = [1, 6, 10, 5, 3, 8]
    for value in reversed(second_list_values):
        second = push(second, value)

    # Link the fifth node of the first linked list to the fourth node of the second linked list
    current_first = first
    for _ in range(4):
        current_first = current_first.next

    current_second = second
    for _ in range(3):
        current_second = current_second.next

    current_first.next = current_second

    # Find the intersection point
    intersection_node = find_intersection(first, second)

    # Print the result
    if intersection_node:
        print("Intersection point is", intersection_node.data)
    else:
        print("Lists do not intersect.")

Output

Intersection point is 3

Complexity Analysis

Time Complexity

The time complexity of the algorithm is O(m * n), where m and n denotes the count of nodes in the given two linked lists.

Space Complexity

The space complexity is O(1), as we do not use any extra space.

Approach 2: Using Hashing

To find the intersection point of two linked lists, we iterate over one list and store its nodes in a hash set. Then, we traverse the other list and check if each node is in the set. If we find a common node, it’s the intersection point. Otherwise, there’s no intersection.

Code Implementation

Let’s look at the code implementation of the above approach in C++, Python, and Java.

C++ Code

#include <iostream>
#include <unordered_set>
using namespace std;
 
// Definition of a Linked List Node
struct ListNode
{
    int value;
    ListNode* next;
};
 
// Function to create a new node with the given value
// and add it to the front of the list
void addNodeToFront(ListNode*& head, int value)
{
    // Create a new node from heap
    ListNode* newNode = new ListNode;
 
    newNode->value = value;
    newNode->next = head;
    head = newNode;
}
 
// Function to detect the intersection point of two linked lists using hashing
ListNode* findIntersectionPoint(ListNode* first, ListNode* second)
{
    // Maintain a set to store list nodes
    unordered_set<ListNode*> nodes;
 
    // Traverse the first linked list and insert the address of each node into the set
    while (first)
    {
        nodes.insert(first);
        first = first->next;
    }
 
    // Now traverse the second linked  list and search the first node that is
    // already present in the above set
    while (second)
    {
        // Return the node if it is found in the set
        if (nodes.find(second) != nodes.end()) {
            return second;
        }
        second = second->next;
    }
 
    // We reach here if the lists do not intersect
    return nullptr;
}
 
int main()
{
    // Construct the first linked list
    Node* first = nullptr;
    int firstListValues[] = {7, 4, 9, 2, 5, 3, 8};
    int firstListLength = sizeof(firstListValues) / sizeof(firstListValues[0]);
    for (int i = firstListLength - 1; i >= 0; i--) {
        push(first, firstListValues[i]);
    }

    // Construct the second linked list
    Node* second = nullptr;
    int secondListValues[] = {1, 6, 10, 5, 3, 8};
    int secondListLength = sizeof(secondListValues) / sizeof(secondListValues[0]);
    for (int i = secondListLength - 1; i >= 0; i--) {
        push(second, secondListValues[i]);
    }

    // Link the fifth node of the first linked list to the fourth node of the second linked list
    Node* currentFirst = first;
    for (int i = 0; i < 4; i++) {
        currentFirst = currentFirst->next;
    }

    Node* currentSecond = second;
    for (int i = 0; i < 3; i++) {
        currentSecond = currentSecond->next;
    }

    currentFirst->next = currentSecond;

    // Find the intersection point
    Node* intersectionNode = findIntersection(first, second);

    // Print the result
    if (intersectionNode) {
        cout << "Intersection point is " << intersectionNode->data << endl;
    } else {
        cout << "Lists do not intersect." << endl;
    }

    return 0;
}

Java Code

```java
import java.util.HashSet;

class Main {
    // Definition of a Linked List Node
    static class ListNode {
        int data;
        ListNode next;
    }

    // Function to create a new node with given values
    // and add it to the front of the list
    public static ListNode addNodeToFront(ListNode head, int data) {
        // Create a new linked list node
        ListNode newNode = new ListNode();
        newNode.data = data;
        newNode.next = head;
        return newNode;
    }

    // Function to detect the intersection point of two linked lists using hashing
    private static ListNode findIntersectionPoint(ListNode list1, ListNode list2) {
        // Maintain a set to store list nodes
        HashSet<ListNode> nodes = new HashSet<>();

        // Traverse the first list and insert the nodes into the set
        ListNode temp = list1;
        while (temp != null) {
            nodes.add(temp);
            temp = temp.next;
        }

        // Traverse the second list and find the intersection point
        temp = list2;
        while (temp != null) {
            if (nodes.contains(temp)) {
                return temp; // Return the intersection point
            }
            temp = temp.next;
        }

        // Return null if no intersection point is found
        return null;
    }

    public static void main(String[] args) {
        // Construct the first linked list
        Node first = new Node(-1); // Dummy node
        int[] firstListValues = {7, 4, 9, 2, 5, 3, 8};
        for (int i = firstListValues.length - 1; i >= 0; i--) {
            push(first, firstListValues[i]);
        }

        // Construct the second linked list
        Node second = new Node(-1); // Dummy node
        int[] secondListValues = {1, 6, 10, 5, 3, 8};
        for (int i = secondListValues.length - 1; i >= 0; i--) {
            push(second, secondListValues[i]);
        }

        // Link the fifth node of the first linked list to the fourth node of the second linked list
        Node currentFirst = first;
        for (int i = 0; i < 4; i++) {
            currentFirst = currentFirst.next;
        }

        Node currentSecond = second;
        for (int i = 0; i < 3; i++) {
            currentSecond = currentSecond.next;
        }

        currentFirst.next = currentSecond;

        // Find the intersection point
        Node intersectionNode = findIntersection(first, second);

        // Print the result
        if (intersectionNode != null) {
            System.out.println("Intersection point is " + intersectionNode.data);
        } else {
            System.out.println("Lists do not intersect.");
        }
    }
}

Python Code

```python
# Definition of a Linked List Node
class ListNode:
    def __init__(self, data):
        self.data = data
        self.next = None

# Function to add a new node with the given data to the front of the list
def add_node_to_front(head, data):
    new_node = ListNode(data)
    new_node.next = head
    return new_node

# Function to detect the intersection point of two linked lists using hashing
def find_intersection_point(list1, list2):
    # Maintain a set to store list nodes
    nodes = set()

    # Traverse the first list and insert the nodes into the set
    temp = list1
    while temp:
        nodes.add(temp)
        temp = temp.next

    # Traverse the second list and find the intersection point
    temp = list2
    while temp:
        if temp in nodes:
            return temp  # Return the intersection point
        temp = temp.next

    # Return None if no intersection point is found
    return None

# Main function
if __name__ == "__main__":
    first = None
    first_list_values = [7, 4, 9, 2, 5, 3, 8]
    for value in reversed(first_list_values):
        first = push(first, value)

    # Construct the second linked list
    second = None
    second_list_values = [1, 6, 10, 5, 3, 8]
    for value in reversed(second_list_values):
        second = push(second, value)

    # Link the fifth node of the first linked list to the fourth node of the second linked list
    current_first = first
    for _ in range(4):
        current_first = current_first.next

    current_second = second
    for _ in range(3):
        current_second = current_second.next

    current_first.next = current_second

    # Find the intersection point
    intersection_node = find_intersection(first, second)

    # Print the result
    if intersection_node:
        print("Intersection point is", intersection_node.data)
    else:
        print("Lists do not intersect.")

Output

Intersection point is 3

Complexity Analysis

Time Complexity

The time complexity of the above method is O(m+n) as the linked lists get traversed once.

Space Complexity

The space complexity of the above method is O(m) as the nodes of the first linked list is get stored in the hash table.

Approach 3: Using Difference in Node Count

In this approach to find the intersection of linked lists, we use the difference in the count of nodes. Both the linked lists get traversed to find their lengths. We get the longer linked list by counting the difference in the number of nodes which is k. The longer linked list gets traversed until both the linked lists have the same number of nodes. We move through the linked lists at an equal speed until they reach the intersection point.

Steps Involved :

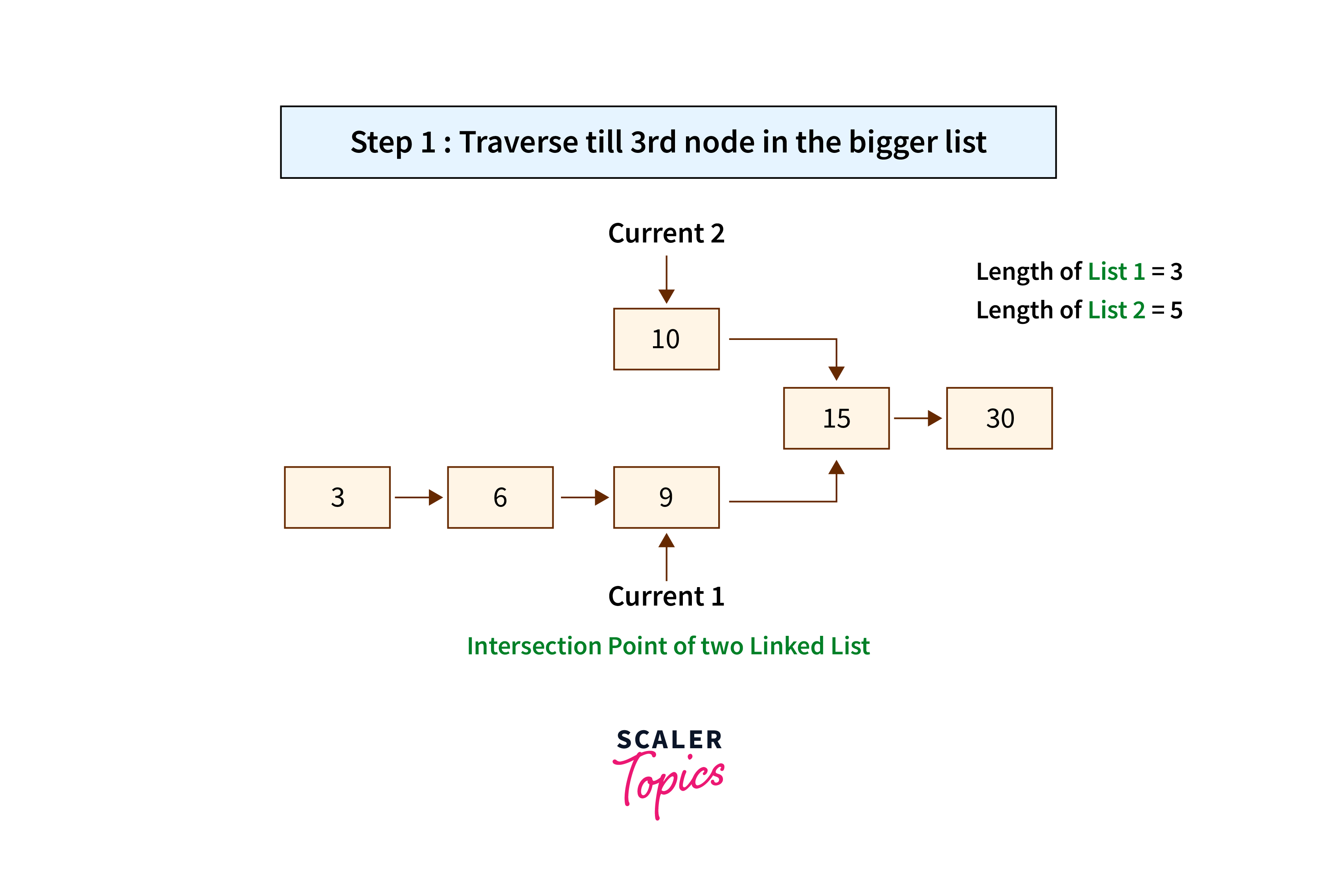
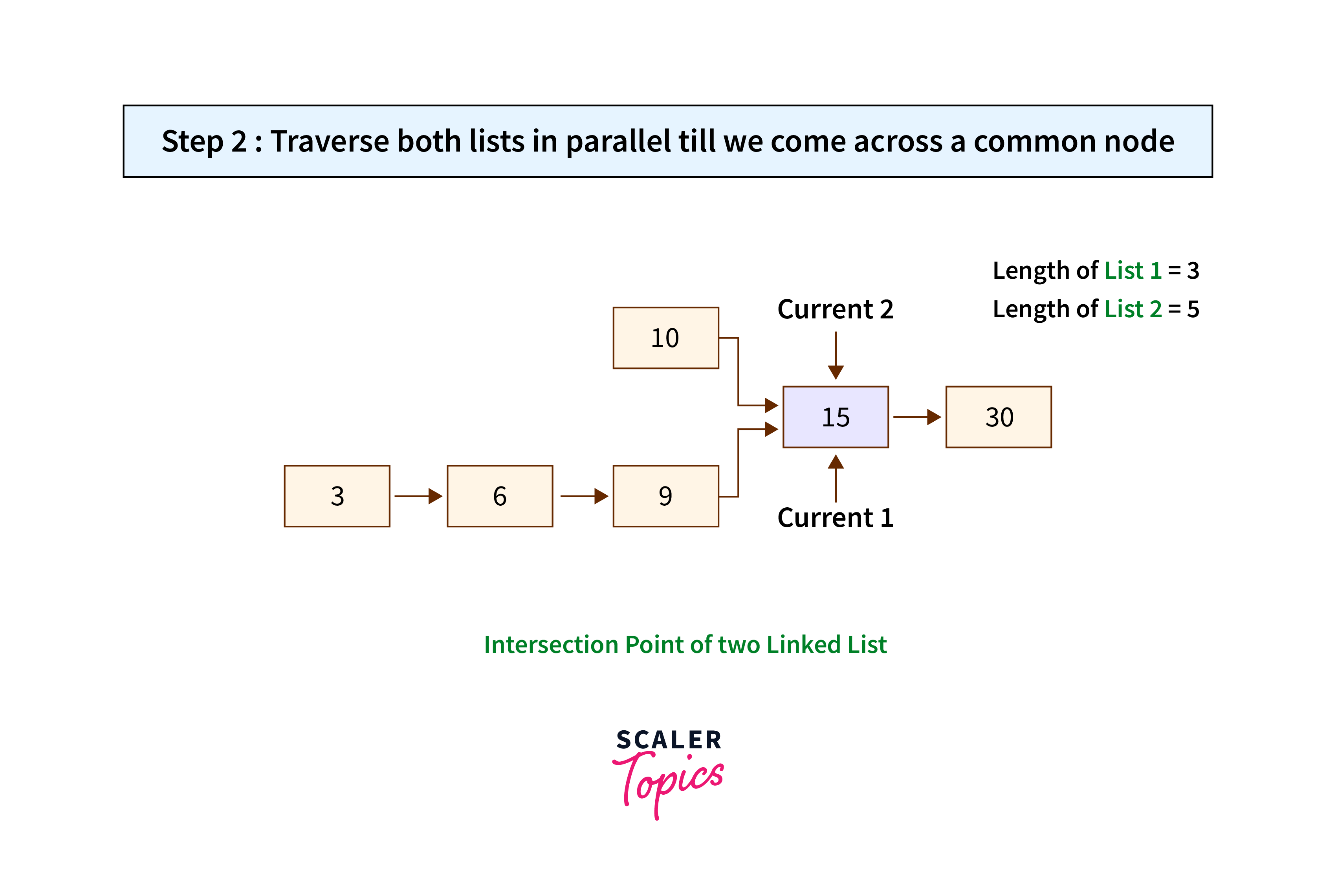
• Traverse both linked lists and keep a count on the number of nodes. Let the number of nodes in the first linked list be c1 and the second c2.
• Check which one is larger and calculate the difference d = abs(c1 – c2) in the number of nodes of the linked lists.
• Make sure that the longer linked list is the first one. Swap the linked lists whenever required.
• Traverse the longer list till d nodes as both the linked lists will be left with an equal number of nodes.
• Traverse the linked lists simultaneously and compare the address of each node until they reach the intersection point.
• Return the common node present at the point of intersection. If there is no common node, return null.

Code Implementation

C++ Code

#include <iostream>
using namespace std;
 
// Definition of a Linked List Node
struct Node
{
    int data;
    Node* next;
};
 
// Function to create a new node with the given values and
// adds it to the front of the linked list
void insertFront(Node*& head, int data)
{
    // Create a new node
    Node* newNode = new Node;
    newNode->data = data;
    newNode->next = head;
    head = newNode;
}
 
// Utility function to find the length of a linked list
int length(Node* head)
{
    int len = 0;
    Node* curr=head;
    for (; curr != nullptr; curr = curr->next) {
        len++;
    }
    return len;
}
 
// Function to detect the intersection point of two linked lists.
// Assumes that the first list contains `k` nodes more than the second list
Node* findIntersectionPoint(Node* first, Node* second, int k)
{
    // Advance the longer list by `k` nodes
    for (int i = 0; i < k && first; i++) {
        first = first->next;
    }
 
    // Move both lists simultaneously until they meet
    while (first && second)
    {
        // If both lists meet at any node, return that node as the intersection point
        if (first == second) {
            return first;
        }
 
        // Move to the next node in both lists
        first = first->next;
        second = second->next;
    }
 
    // Return null if the lists do not intersect
    return nullptr;
}
 
// Function to detect the intersection point of given two lists
Node* findIntersection(Node* first, Node* second)
{
    // Find the difference in the number of nodes between both lists
    int diff = length(first) - length(second);
 
    // If the first list is shorter, swap the lists
    if (diff < 0) {
        swap(first, second);
    }
 
    // Find and return the intersection node
    return findIntersectionPoint(first, second, abs(diff));
}
 
int main()
{
    // Construct the first linked list
    Node* first = nullptr;
    int firstListValues[] = {7, 4, 9, 2, 5, 3, 8};
    int firstListLength = sizeof(firstListValues) / sizeof(firstListValues[0]);
    for (int i = firstListLength - 1; i >= 0; i--) {
        push(first, firstListValues[i]);
    }

    // Construct the second linked list
    Node* second = nullptr;
    int secondListValues[] = {1, 6, 10, 5, 3, 8};
    int secondListLength = sizeof(secondListValues) / sizeof(secondListValues[0]);
    for (int i = secondListLength - 1; i >= 0; i--) {
        push(second, secondListValues[i]);
    }

    // Link the fifth node of the first linked list to the fourth node of the second linked list
    Node* currentFirst = first;
    for (int i = 0; i < 4; i++) {
        currentFirst = currentFirst->next;
    }

    Node* currentSecond = second;
    for (int i = 0; i < 3; i++) {
        currentSecond = currentSecond->next;
    }

    currentFirst->next = currentSecond;

    // Find the intersection point
    Node* intersectionNode = findIntersection(first, second);

    // Print the result
    if (intersectionNode) {
        cout << "Intersection point is " << intersectionNode->data << endl;
    } else {
        cout << "Lists do not intersect." << endl;
    }

    return 0;
}

Java Code

class Main {
    // Node class for a linked list
    static class Node {
        int data;
        Node next;
    }
    
    // Function to insert a new node at the beginning of the list
    public static Node insertAtBeginning(Node head, int data) {
        Node newNode = new Node();
        newNode.data = data;
        newNode.next = head;
        return newNode;
    }
    
    // Function to detect the intersection point of two linked lists
    public static Node findIntersection(Node list1, Node list2) {
        // Traverse the first list and mark each node as visited
        while (list1 != null) {
            list1.data = -list1.data; // Mark visited nodes by negating data
            list1 = list1.next;
        }
        
        // Traverse the second list and find the first visited node
        while (list2 != null) {
            // If a visited node is found, return it as the intersection point
            if (list2.data < 0)
                return list2;
            list2 = list2.next;
        }
        
        // If no intersection is found, return null
        return null;
    }
    
    public static void main(String[] args) {
        // Construct the first linked list
        Node first = new Node(-1); // Dummy node
        int[] firstListValues = {7, 4, 9, 2, 5, 3, 8};
        for (int i = firstListValues.length - 1; i >= 0; i--) {
            push(first, firstListValues[i]);
        }

        // Construct the second linked list
        Node second = new Node(-1); // Dummy node
        int[] secondListValues = {1, 6, 10, 5, 3, 8};
        for (int i = secondListValues.length - 1; i >= 0; i--) {
            push(second, secondListValues[i]);
        }

        // Link the fifth node of the first linked list to the fourth node of the second linked list
        Node currentFirst = first;
        for (int i = 0; i < 4; i++) {
            currentFirst = currentFirst.next;
        }

        Node currentSecond = second;
        for (int i = 0; i < 3; i++) {
            currentSecond = currentSecond.next;
        }

        currentFirst.next = currentSecond;

        // Find the intersection point
        Node intersectionNode = findIntersection(first, second);

        // Print the result
        if (intersectionNode != null) {
            System.out.println("Intersection point is " + intersectionNode.data);
        } else {
            System.out.println("Lists do not intersect.");
        }
    }
}

Python Code

# Node class for a linked list
class Node:
    def __init__(self, data):
        self.data = data
        self.next = None

# Function to insert a new node at the starting of the list
def insert_at_beginning(head, data):
    new_node = Node(data)
    new_node.next = head
    return new_node

# Function to detect the intersection point of two linked lists
def find_intersection(list1, list2):
    # Traverse the first list and mark each node as visited
    while list1:
        list1.data = -list1.data  # Mark visited nodes by negating data
        list1 = list1.next
        
    # Traverse the second list and find the first visited node
    while list2:
        # If a visited node is found, return it as the intersection point
        if list2.data < 0:
            return list2
        list2 = list2.next
        
    # If no intersection is found, return None
    return None

# Construct the first linked list
first = None
first_list_values = [7, 4, 9, 2, 5, 3, 8]
for value in reversed(first_list_values):
    first = push(first, value)

# Construct the second linked list
second = None
second_list_values = [1, 6, 10, 5, 3, 8]
for value in reversed(second_list_values):
    second = push(second, value)

# Link the fifth node of the first linked list to the fourth node of the second linked list
current_first = first
for _ in range(4):
    current_first = current_first.next

current_second = second
for _ in range(3):
    current_second = current_second.next

current_first.next = current_second

# Find the intersection point
intersection_node = find_intersection(first, second)

# Print the result
if intersection_node:
    print("Intersection point is", intersection_node.data)
else:
    print("Lists do not intersect.")

Output

Intersection point is 3

Complexity Analysis

Time Complexity

The time complexity of the above method is O(m+n) as both the linked lists get traversed one by one, where m is the length of the first linked list and n of the second linked list.

Space Complexity

The space complexity of the above method is O(1).

Approach 4: Using Two Pointer Technique

In this approach to find the intersection of two linked lists, we use the two-pointer technique. We take two pointers pointing to the head node of both the linked lists. Each pointer reaching the end of the linked list gets reassigned to the head of the other linked list. It makes the two pointers at a distance equal to the intersection point. When both pointers reach a common node and are not null, it is said to be the intersection point.

Steps Involved

• Initialize two pointers – head1 pointing to the head of the first linked list and head2 pointing to the head of the second linked list.
• Advance through both the linked lists until it reaches the end.
• When head1 points to the end of the first linked list, it gets assigned to the head of the second linked list.
• When head2 points to the end of the second linked list, it gets assigned to the head of the first linked list.
• When both pointers point to a common node and are not null, we get the intersection point of the linked lists and return it.

Code Implementation

C++ Code

#include <iostream>
using namespace std;
 
// Definition of a Linked List Node
struct Node
{
    int data;
    Node* next;
};
 
// Function to insert a new node with the given data at the front of the list
void insertAtFront(Node*& head, int data)
{
    // Create a new node and link it to the front of the list
    Node* newNode = new Node;
    newNode->data = data;
    newNode->next = head;
    head = newNode;
}
 
// Function to find the point of intersection between two linked lists
Node* findIntersectionPoint(Node* list1, Node* list2)
{
    // Initialize two pointers to traverse the lists
    Node *ptr1 = list1, *ptr2 = list2;
 
    // Traverse both lists until they meet at the intersection point
    while (ptr1 != ptr2)
    {
        // If one list reaches the end, redirect it to the beginning of the other list
        if (ptr1 == nullptr) {
            ptr1 = list2;
        }
        else {
            ptr1 = ptr1->next;
        }
 
        if (ptr2 == nullptr) {
            ptr2 = list1;
        }
        else {
            ptr2 = ptr2->next;
        }
    }
 
    // Return the intersection point
    return ptr1;
}
 
int main()
{
    // Construct the first linked list
    Node* first = nullptr;
    int firstListValues[] = {7, 4, 9, 2, 5, 3, 8};
    int firstListLength = sizeof(firstListValues) / sizeof(firstListValues[0]);
    for (int i = firstListLength - 1; i >= 0; i--) {
        push(first, firstListValues[i]);
    }

    // Construct the second linked list
    Node* second = nullptr;
    int secondListValues[] = {1, 6, 10, 5, 3, 8};
    int secondListLength = sizeof(secondListValues) / sizeof(secondListValues[0]);
    for (int i = secondListLength - 1; i >= 0; i--) {
        push(second, secondListValues[i]);
    }

    // Link the fifth node of the first linked list to the fourth node of the second linked list
    Node* currentFirst = first;
    for (int i = 0; i < 4; i++) {
        currentFirst = currentFirst->next;
    }

    Node* currentSecond = second;
    for (int i = 0; i < 3; i++) {
        currentSecond = currentSecond->next;
    }

    currentFirst->next = currentSecond;

    // Find the intersection point
    Node* intersectionNode = findIntersection(first, second);

    // Print the result
    if (intersectionNode) {
        cout << "Intersection point is " << intersectionNode->data << endl;
    } else {
        cout << "Lists do not intersect." << endl;
    }

    return 0;
}

Java Code

class LinkedListIntersection {
    // Definition of a Linked List Node
    static class Node {
        int data;
        Node next;
    }
    
    // Method to insert a new node with the given data at the front of the list
    public static Node insertAtFront(Node head, int data) {
        // Create a new node and link it to the front of the list
        Node newNode = new Node();
        newNode.data = data;
        newNode.next = head;
        return newNode;
    }
    
    // Method to find the intersection point of two linked lists
    public static Node findIntersectionPoint(Node list1, Node list2) {
        // Initialize two pointers to traverse the lists
        Node pointer1 = list1, pointer2 = list2;
        
        // Traverse both lists until they meet at the intersection point
        while (pointer1 != pointer2) {
            // When the first list reaches its own end, redirect it to the head of the second list
            if (pointer1 == null) {
                pointer1 = list2;
            } else {
                pointer1 = pointer1.next;
            }
 
            // When the second list reaches its own end, redirect it to the head of the first list
            if (pointer2 == null) {
                pointer2 = list1;
            } else {
                pointer2 = pointer2.next;
            }
        }
 
        // Return the intersection point
        return pointer1;
    }
 
    public static void main(String[] args) {
        // Construct the first linked list
        Node first = new Node(-1); // Dummy node
        int[] firstListValues = {7, 4, 9, 2, 5, 3, 8};
        for (int i = firstListValues.length - 1; i >= 0; i--) {
            push(first, firstListValues[i]);
        }

        // Construct the second linked list
        Node second = new Node(-1); // Dummy node
        int[] secondListValues = {1, 6, 10, 5, 3, 8};
        for (int i = secondListValues.length - 1; i >= 0; i--) {
            push(second, secondListValues[i]);
        }

        // Link the fifth node of the first linked list to the fourth node of the second linked list
        Node currentFirst = first;
        for (int i = 0; i < 4; i++) {
            currentFirst = currentFirst.next;
        }

        Node currentSecond = second;
        for (int i = 0; i < 3; i++) {
            currentSecond = currentSecond.next;
        }

        currentFirst.next = currentSecond;

        // Find the intersection point
        Node intersectionNode = findIntersection(first, second);

        // Print the result
        if (intersectionNode != null) {
            System.out.println("Intersection point is " + intersectionNode.data);
        } else {
            System.out.println("Lists do not intersect.");
        }
    }
}

Python Code

# Definition of a Linked List Node
class ListNode:
    def __init__(self, data, next=None):
        self.data = data
        self.next = next
 
 
# Function to detect the intersection point of two linked lists
def find_intersection_point(first, second):
    x = first
    y = second
 
    # increase both pointers until they meet at a common node
    while x != y:
 
        # When the first list reaches its own end, redirect it to the
        # the head of the second list
        if x is None:
            x = second
        else:
            x = x.next
 
        # When the second list reaches its own end, redirect it to the
        # the head of the first list
        if y is None:
            y = first
        else:
            y = y.next
 
    # return the common node
    return x
 
 
if __name__ == '__main__':
 
    # Construct the first linked list
    first = None
    first_list_values = [7, 4, 9, 2, 5, 3, 8]
    for value in reversed(first_list_values):
        first = push(first, value)

    # Construct the second linked list
    second = None
    second_list_values = [1, 6, 10, 5, 3, 8]
    for value in reversed(second_list_values):
        second = push(second, value)

    # Link the fifth node of the first linked list to the fourth node of the second linked list
    current_first = first
    for _ in range(4):
        current_first = current_first.next

    current_second = second
    for _ in range(3):
        current_second = current_second.next

    current_first.next = current_second

    # Find the intersection point
    intersection_node = find_intersection(first, second)

    # Print the result
    if intersection_node:
        print("Intersection point is", intersection_node.data)
    else:
        print("Lists do not intersect.")

Output

Intersection point is 3

Complexity Analysis

Time Complexity

The time complexity to find the intersection point of two linked lists using the two-pointer technique is O(m+n).

Space Complexity

The algorithm has a space complexity of O(1), indicating that it uses a constant amount of extra space regardless of the size of the input linked lists.

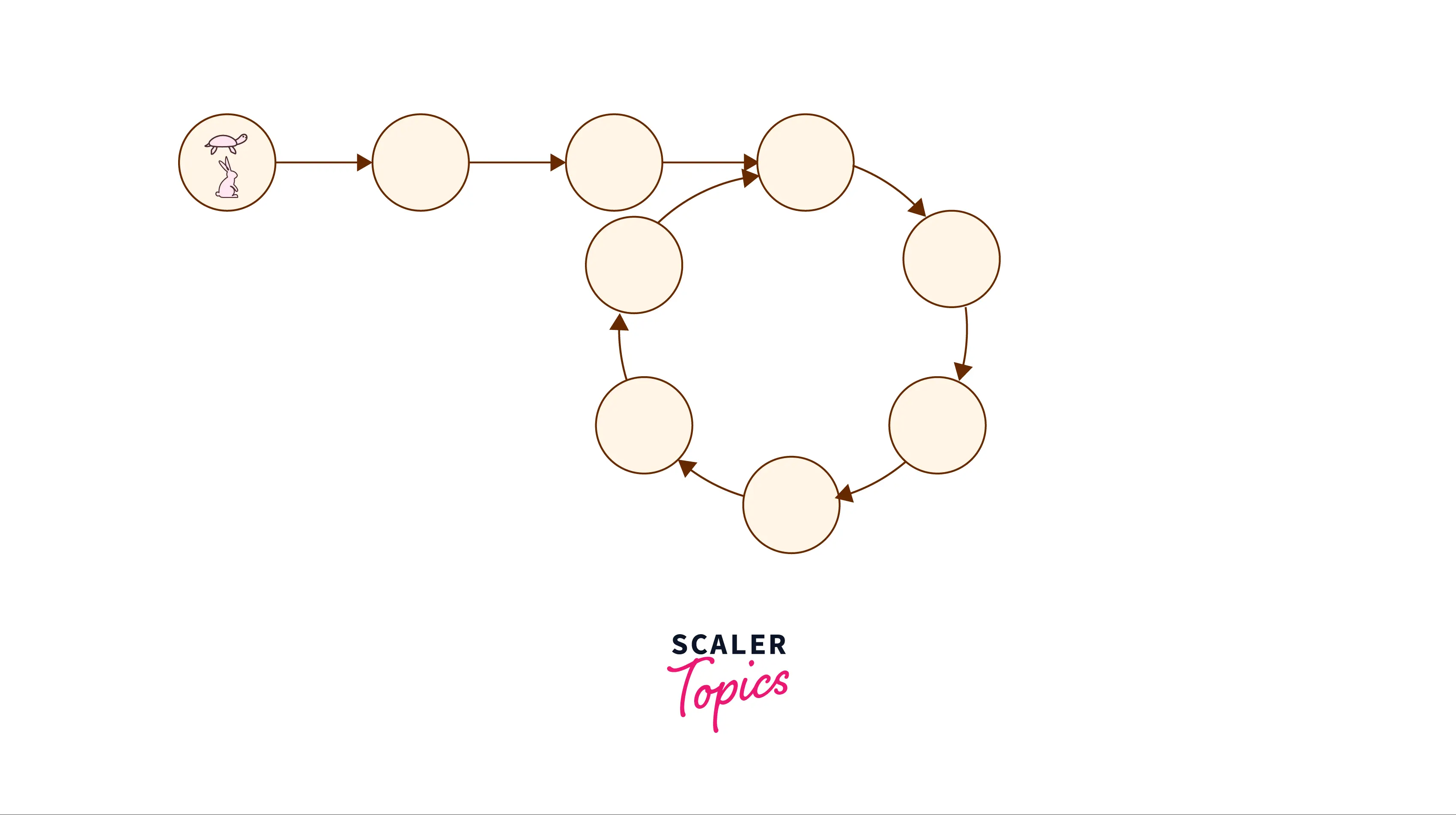
Approach 5: Making Loop in the First List

This approach uses Floyd’s Cycle Detection Algorithm. This approach converts the first linked list to a circular linked list by connecting the tail node to the head node. Two pointers point to the head node and the kth node from the head, which is the total number of nodes in the loop of the circular linked list. The pointers move at the same speed until the intersection of the two linked lists is reached.

Steps Involved

• Traverse the first linked list and take a count of the nodes.
• Convert it into a circular linked list by joining the head node to the tail node.
• Since the length of the loop formed by the first linked list is already known, traverse the same number of nodes in the second linked list and keep a pointer at it.
• Set another pointer at the beginning of the second linked list.
• Move the pointers simultaneously until they reach a common node.
• Return the value of the node at the point of intersection.
• Remove the cycle from the first linked list.

Code Implementation

Let’s look at the code implementation of the above approach in C++, Python, and Java.

C++ Code

#include <iostream>
#include <unordered_set>
using namespace std;
 
// Definition of a Linked List Node
struct ListNode
{
    int data;
    ListNode* next;
};
 
// Function to create a new node with the given values and
// push it onto the front of the list
void addNodeToFront(ListNode*& headRef, int data)
{
    // Create a new node from the heap
    ListNode* newNode = new ListNode;
 
    newNode->data = data;
    newNode->next = headRef;
    headRef = newNode;
}
 
// Function to find the starting node of a cycle in a linked list
// identified by the `cycleNode`. Returns the starting node of the cycle.
ListNode* findCycleStart(ListNode* cycleNode, ListNode* head)
{
    // Find the count of total nodes involved in the cycle and store it in variable `k`
    int k = 1;
    ListNode* ptr = cycleNode;
    while (ptr->next != cycleNode) {
        k++;
        ptr = ptr->next;
    }
 
    // Get the pointer to the k'th node from the head
    ListNode* current = head;
    for (int i = 0; i < k; i++) {
        current = current->next;
    }
 
    // Simultaneously advance the `head` and `current` pointers
    // at the same speed until they meet at the same point
    while (current != head)
    {
        current = current->next;
        head = head->next;
    }
 
    // `current` now points to the starting node of the circular loop
    return current;
}
 
// Function to detect a cycle in a list using
// Floyd’s cycle detection algorithm
ListNode* detectCycle(ListNode* head)
{
    // Take two pointers – `slow` and `fast`
    ListNode *slow = head, *fast = head;
 
    while (fast && fast->next)
    {
        // Advance slow by one pointer
        slow = slow->next;
 
        // Advance fast by two pointers
        fast = fast->next->next;
 
        // If they meet at any node, the linked list contains a cycle
        if (slow == fast) {
            return slow;
        }
    }
 
    // Return null if the list does not contain any cycle
    return nullptr;
}
 
// Function to detect the intersection point of two linked lists
ListNode* findIntersection(ListNode* first, ListNode* second)
{
    ListNode* previous = nullptr;       // Previous pointer
    ListNode* current = first;          // Main pointer
 
    // Traverse the first list
    while (current)
    {
        // Update the previous pointer to current node and
        // advance the main pointer to the next node
        previous = current;
        current = current->next;
    }
 
    // Create a cycle in the first list
    if (previous) {
        previous->next = first;
    }
 
    // Find a pointer to the loop node using the given second list
    ListNode* cycleNode = detectCycle(second);
 
    // Find the intersection node
    ListNode* intersectionNode = nullptr;
    if (cycleNode) {
        intersectionNode = findCycleStart(cycleNode, second);
    }
 
    // Remove the cycle in the first list before exiting
    if (previous) {
        previous->next = nullptr;
    }
 
    // Return the intersection node
    return intersectionNode;
}
 
int main()
{
    // Construct the first linked list
    Node* first = nullptr;
    int firstListValues[] = {7, 4, 9, 2, 5, 3, 8};
    int firstListLength = sizeof(firstListValues) / sizeof(firstListValues[0]);
    for (int i = firstListLength - 1; i >= 0; i--) {
        push(first, firstListValues[i]);
    }

    // Construct the second linked list
    Node* second = nullptr;
    int secondListValues[] = {1, 6, 10, 5, 3, 8};
    int secondListLength = sizeof(secondListValues) / sizeof(secondListValues[0]);
    for (int i = secondListLength - 1; i >= 0; i--) {
        push(second, secondListValues[i]);
    }

    // Link the fifth node of the first linked list to the fourth node of the second linked list
    Node* currentFirst = first;
    for (int i = 0; i < 4; i++) {
        currentFirst = currentFirst->next;
    }

    Node* currentSecond = second;
    for (int i = 0; i < 3; i++) {
        currentSecond = currentSecond->next;
    }

    currentFirst->next = currentSecond;

    // Find the intersection point
    Node* intersectionNode = findIntersection(first, second);

    // Print the result
    if (intersectionNode) {
        cout << "Intersection point is " << intersectionNode->data << endl;
    } else {
        cout << "Lists do not intersect." << endl;
    }

    return 0;
}

Java Code

```java
class LinkedListIntersection {
    // Definition of a Linked List Node
    static class ListNode {
        int value;
        ListNode next;
    }
    
    // Function to add a node with the given value to the front of a linked list
    public static ListNode addToFront(ListNode head, int value) {
        ListNode node = new ListNode();
        node.value = value;
        node.next = head;
        return node;
    }

    // Search the starting node of the loop in a list pointed by `head`.
    // The `loopNode` points to one of any nodes in the cycle
    public static ListNode findLoopStart(ListNode loopNode, ListNode head) {
        // Find the total count of nodes involved in the loop and store the count in variable `k`
        int k = 1;
        for (ListNode ptr = loopNode; ptr.next != loopNode; ptr = ptr.next) {
            k++;
        }

        // Get pointer to the k'th node from the head of the list
        ListNode current = head;
        for (int i = 0; i < k; i++) {
            current = current.next;
        }

        // Simultaneously move the `head` and `current` pointers
        // at the same speed until they meet
        while (current != head) {
            current = current.next;
            head = head.next;
        }

        // `current` now points to the starting node of the loop
        return current;
    }

    // Function to detect a cycle in a list using
    // Floyd’s cycle detection algorithm
    public static ListNode detectCycle(ListNode head) {
        // Take two pointers – `slow` and `fast`
        ListNode slow = head, fast = head;
        while (fast != null && fast.next != null) {
            // Advance slow by one pointer
            slow = slow.next;

            // Advance fast by two pointers
            fast = fast.next.next;

            // If they meet at any node, the list surely contains a cycle
            if (slow == fast) {
                return slow;
            }
        }

        // Return null if list does not have a cycle
        return null;
    }

    // Function to detect the intersection point of two linked lists
    public static ListNode findIntersection(ListNode first, ListNode second) {
        ListNode previous = null;       // Previous pointer
        ListNode current = first;       // Main pointer

        // Traverse the first list
        while (current != null) {
            // Update previous pointer to the current node and
            // advance the main pointer to the next node
            previous = current;
            current = current.next;
        }

        // Create a cycle in the first list
        if (previous != null) {
            previous.next = first;
        }

        // Now find a pointer to the loop node using the second list
        ListNode slow = detectCycle(second);

        // Find the intersection node
        ListNode address = null;
        if (slow != null) {
            address = findLoopStart(slow, second);
        }

        // Remove the cycle in the first list before exiting
        if (previous != null) {
            previous.next = null;
        }

        // Return the intersection node
        return address;
    }

    public static void main(String[] args) {
        // Construct the first linked list
        Node first = new Node(-1); // Dummy node
        int[] firstListValues = {7, 4, 9, 2, 5, 3, 8};
        for (int i = firstListValues.length - 1; i >= 0; i--) {
            push(first, firstListValues[i]);
        }

        // Construct the second linked list
        Node second = new Node(-1); // Dummy node
        int[] secondListValues = {1, 6, 10, 5, 3, 8};
        for (int i = secondListValues.length - 1; i >= 0; i--) {
            push(second, secondListValues[i]);
        }

        // Link the fifth node of the first linked list to the fourth node of the second linked list
        Node currentFirst = first;
        for (int i = 0; i < 4; i++) {
            currentFirst = currentFirst.next;
        }

        Node currentSecond = second;
        for (int i = 0; i < 3; i++) {
            currentSecond = currentSecond.next;
        }

        currentFirst.next = currentSecond;

        // Find the intersection point
        Node intersectionNode = findIntersection(first, second);

        // Print the result
        if (intersectionNode != null) {
            System.out.println("Intersection point is " + intersectionNode.data);
        } else {
            System.out.println("Lists do not intersect.");
        }
    }
}

Python Code

class LinkedListIntersection:
    # Definition of a Linked List Node
    class ListNode:
        def __init__(self, data, next=None):
            self.data = data
            self.next = next
    
    # Get the starting node of the loop in a linked list pointed by `head`.
    # The `loop_node` points to one of any nodes in cycle
    @staticmethod
    def remove_cycle(loop_node, head):
        # Find the total number of nodes involved in the loop and store the count in variable `k`.
        k = 1
        ptr = loop_node
        while ptr.next is not loop_node:
            k += 1
            ptr = ptr.next
        
        # Get pointer to k'th node from the head
        curr = head
        for _ in range(k):
            curr = curr.next
        
        # Simultaneously advance the `head` and `curr` pointers
        # at the same speed until they meet at a point
        while curr is not head:
            curr = curr.next
            head = head.next
        
        # `curr` points to the starting node of the loop
        return curr
    
    # Function to detect a cycle in a lisusing
    # Floyd’s cycle detection algorithm
    @staticmethod
    def identify_cycle(head):
        # Take two pointers – `slow` and `fast`
        slow = fast = head
    
        while fast and fast.next:
            # Advance slow by one pointer
            slow = slow.next
    
            # Advance fast by two pointers
            fast = fast.next.next
    
            # If they meet at any node, the linked list surely contains a cycle
            if slow == fast:
                return slow
    
        # Return None if the list does not contain a cycle
        return None
    
    # Function to detect the intersection point of two linked lists
    @staticmethod
    def find_intersection(first, second):
        prev = None  # Previous pointer
        curr = first  # Main pointer
    
        # Traverse the first list
        while curr:
            # Update previous pointer to the current node and
            # advance the main pointer to the next node
            prev = curr
            curr = curr.next
    
        # Create a cycle in the first list
        if prev:
            prev.next = first
    
        # Now find a pointer to the loop node using the second list
        slow = LinkedListIntersection.identify_cycle(second)
    
        # Find the intersection node
        addr = None
        if slow:
            addr = LinkedListIntersection.remove_cycle(slow, second)
    
        # Remove the cycle in the first list before exiting
        if prev:
            prev.next = None
    
        # Return the intersection node
        return addr
    
if __name__ == '__main__':
 
    # Construct the first linked list
    first = None
    first_list_values = [7, 4, 9, 2, 5, 3, 8]
    for value in reversed(first_list_values):
        first = push(first, value)

    # Construct the second linked list
    second = None
    second_list_values = [1, 6, 10, 5, 3, 8]
    for value in reversed(second_list_values):
        second = push(second, value)

    # Link the fifth node of the first linked list to the fourth node of the second linked list
    current_first = first
    for _ in range(4):
        current_first = current_first.next

    current_second = second
    for _ in range(3):
        current_second = current_second.next

    current_first.next = current_second

    # Find the intersection point
    intersection_node = find_intersection(first, second)

    # Print the result
    if intersection_node:
        print("Intersection point is", intersection_node.data)
    else:
        print("Lists do not intersect.")

Output

Intersection point is 3.

Complexity Analysis

Time Complexity

The time complexity of the above method is O(m+n) as both the lists get traversed linearly, where m and n are the counts of nodes in the first and the second linked list, respectively.

Space Complexity

The space complexity of the above method is O(1), as we do not use any extra space.

Conclusion

• This article shows that we can find the intersection point of two linked lists using the following eight methods –
  1. Using Two Nested Loops
  2. Using Hashing
  3. Using Difference in Node Count
  4. Using Two Pointer Technique
  5. Making Loop in the First List
• Using the two-pointer technique, we can optimize the time complexity from O(m*n) in the nested loop approach to O(m), significantly improving the efficiency of the algorithm.
• The space complexity varies from O(m) using the hashing technique to O(1) using the other techniques.