Kosaraju Algorithm

Problem Statement

Find all strongly connected components in O(V+E) time using Kosaraju’s algorithm.

Strongly connected Component(SCC) – In a directed graph a strongly connected component is a component of the graph in which there is a path between every pair of vertices.

Example

Example of strongly connected component in a graph :

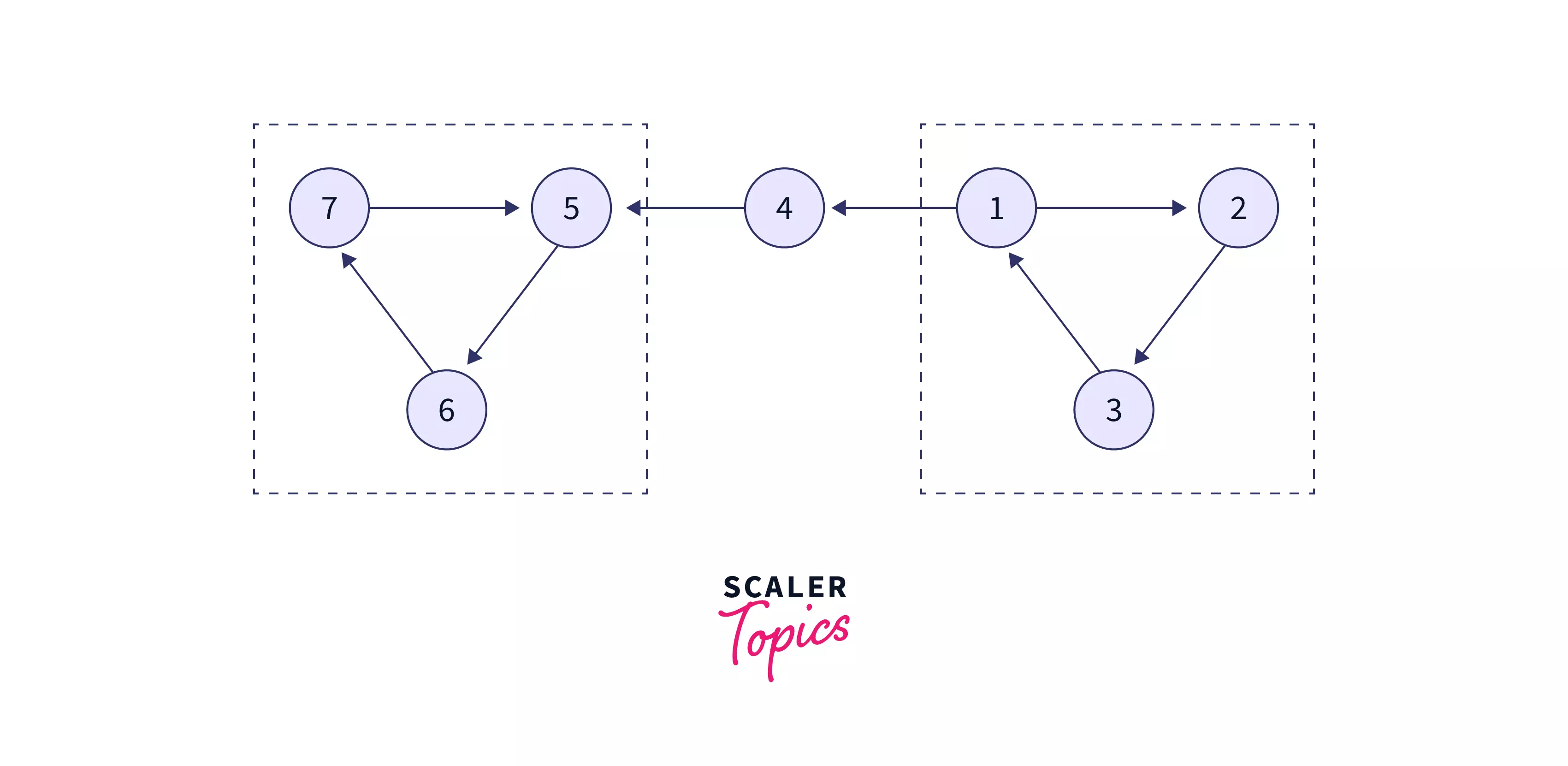
Example Explanation

In the above Example diagram the directed graph contains three strongly connected component.

1. the vertex group of (7,5,6) in which there is a path between every pair of vertices.
2. 4 – single vertex
3. The vertex group of (1,2,3) in which there is a path between every pair of vertices.

In the above example we can see that a single vertex is also considered as a strongly connected component. As kosaraju Algorithm finds the minimum number of strongly connected component in directed graph so the answer to the above example will be 3.

Input/Output

Input – Given Number of vertices = N, and number of edges of the directed graph = M and the weight of the M edges.

Output – Number of strongly connected component in the given directed graph.

Kosaraju’s Algorithm

Intution – The intution behind Koasaraju algorithm is to perform DFS in the directed graph such that one DFS call would be able visit all the vertices of a strongly connected component in the graph.

Algorithm Steps :

• Depth First traversal(DFS) is done on the graph and when DFS traversal is done recursively on adjacent vertex of the graph, the vertex are pushed to an empty stack one by one.
• Find the transpose of the graph by reversing the direction of every edge in the directed graph.
• Pop the vertex from the stack one by one and do DFS on the popped out vertex “v”. The DFS will print the stronlgy connected component of “v”.

Implementaion in C++ :

#include <bits/stdc++.h>
using namespace std;

class DirectedGraph{
	int V; // total no of vertices in graph
	list<int> *Arr; // An array of adjacency lists to represent the graph

	// function to fill the stack with vertices in correct order of finishing time
	void fillInCorrectOrder(int v, bool isVisited[], stack<int> &Stack);

	//  function to apply DFS in vertex of the graph
	void DFSOnVertex(int v, bool isVisited[]);

public:

	DirectedGraph(int V);
	void addEdgeWithWeight(int v, int w);

	// function to print the strongly connected component in graph
	void printStronglyConnectedComponent();

	// Funtion to reverse the arrow direction in the directed graph
	DirectedGraph getTranspose();
};

// function to create graph with vertex V
DirectedGraph::DirectedGraph(int V){
	this->V = V;
	Arr = new list<int>[V];
}

// A recursive function to print DFS starting from v
void DirectedGraph::DFSOnVertex(int v, bool isVisited[]){
	// Mark the current node as visited and print it
	isVisited[v] = true;
	cout << v << " ";

	list<int>::iterator it;
	for (it = Arr[v].begin(); it != Arr[v].end(); ++it){
     if (!isVisited[*it])
			DFSOnVertex(*it, isVisited);   
    }
		
}

DirectedGraph DirectedGraph::getTranspose(){
	DirectedGraph original_graph(V);
	for (int v = 0; v < V; v++){
		list<int>::iterator it;
		for(it = Arr[v].begin(); it != Arr[v].end(); ++it){
			original_graph.Arr[*it].push_back(v);
		}
	}
	return original_graph;
}

void DirectedGraph::addEdgeWithWeight(int v, int weight){
	Arr[v].push_back(weight); // push the weight to the array 
}

void DirectedGraph::fillInCorrectOrder(int v, bool isVisited[], stack<int> &Stack){
	// current node is marked visited initially
	isVisited[v] = true;

	// iterate over all the vertices and check if its visited or not.
	list<int>::iterator it;
	for(it = Arr[v].begin(); it != Arr[v].end(); ++it)
		if(!isVisited[*it])
			fillInCorrectOrder(*it, isVisited, Stack);

	// push the vertices visited in the stack
	Stack.push(v);
}

// function  to print the strongly connected components
void DirectedGraph::printStronglyConnectedComponent(){
	stack<int> Stack;

	// Mark all the vertices as not visited (For first DFS)
	bool *isVertexVisited = new bool[V];
	for(int j = 0; j < V; j++)
		isVertexVisited[j] = false;

	for(int j = 0; j < V; j++)
		if(isVertexVisited[j] == false)
			fillInCorrectOrder(j, isVertexVisited, Stack);

	// transpose of the graph
	DirectedGraph reverse_graph = getTranspose();

	// in second DFS mark all vertices as not visited
	for(int j = 0; j < V; j++)
		isVertexVisited[j] = false;

	// check for all vertices in the stack
	while (Stack.empty() == false){
		int v = Stack.top();
		Stack.pop();
		if (isVertexVisited[v] == false){
			reverse_graph.DFSOnVertex(v, isVertexVisited);
			cout << endl;
		}
	}
}

int main(){
	// Create a graph given 
	DirectedGraph original_graph(5);
	original_graph.addEdgeWithWeight(1, 0);
	original_graph.addEdgeWithWeight(0, 2);
	original_graph.addEdgeWithWeight(2, 1);
	original_graph.addEdgeWithWeight(0, 3);
	original_graph.addEdgeWithWeight(3, 4);

	cout << "SCC in the given graph \n";
	original_graph.printStronglyConnectedComponent();

	return 0;
}

Impelementation in Java :

import java.io.*;
import java.util.*;
import java.util.LinkedList;

class Graph{
	private int V; // Total no of vertices in the graph
	private LinkedList<Integer> Arr[]; // representation of graph as adjacency list

	Graph(int vertex){
		V = vertex;
		Arr = new LinkedList[vertex];
		for (int i=0; i<vertex; ++i)
			Arr[i] = new LinkedList();
	}

	//function to create graph by adding edge to the graph
	void addEdgeWithWeight(int v, int weight){ 
        Arr[v].add(weight); 
    }

	// function to apply DFS on the vertex of the graph recursively
	void DFSOnVertex(int v, boolean isVisited[]){
		// initially the current node is marked visited in the graph
		isVisited[v] = true;
		System.out.print(v + " ");

		int next;

		// check for all the vertices adjacent to the current verices
		Iterator<Integer> i =Arr[v].iterator();
		while (i.hasNext()){
			next = i.next();
			if (!isVisited[next])
				DFSOnVertex(next,isVisited);
		}
	}

	//function to create transpose of the graph 
	Graph getTranspose(){
		Graph original_graph = new Graph(V);
		for (int v = 0; v < V; v++){
			// check for all the vertex adjacent to the current vertex
			Iterator<Integer> it =Arr[v].listIterator();
			while(it.hasNext())
				original_graph.Arr[it.next()].add(v);
		}
		return original_graph;
	}

	void fillInCorrectOrder(int v, boolean isVisited[], Stack stack){
		// current node is marked visited initially
		isVisited[v] = true;

		// Recur for all the vertices adjacent to this vertex
		Iterator<Integer> it = Arr[v].iterator();
		while (it.hasNext()){
			int next = it.next();
			if(!isVisited[next])
				fillInCorrectOrder(next, isVisited, stack);
		}

		// push the vertices to the stack
		stack.push(new Integer(v));
	} 

	// funciton to print the strongly connected component in the graph
	void printStronglyConnectedComponents(){
		Stack stack = new Stack();

		// for second DFS all the vertices are marked not visited
		boolean isVertexVisited[] = new boolean[V];
		for(int j = 0; j < V; j++)
			isVertexVisited[j] = false;

		// fill the stack with vertices based on finising time
		for (int j = 0; j < V; j++)
			if (isVertexVisited[j] == false)
				fillInCorrectOrder(j, isVertexVisited, stack);

		// to create transpose of the graph
		Graph reverse_graph = getTranspose();

		// In the second DFS all the vertices are marked non visited
		for (int j = 0; j < V; j++)
			isVertexVisited[j] = false;

		// process all the vertices in the stack in order of finishing time
		while (stack.empty() == false){
			int v = (int)stack.pop();

			if (isVertexVisited[v] == false){
				reverse_graph.DFSOnVertex(v, isVertexVisited);
				System.out.println();
			}
		}
	}

	public static void main(String args[]){
		// Create a graph 
		Graph original_graph = new Graph(5);
		original_graph.addEdgeWithWeight(1, 0);
		original_graph.addEdgeWithWeight(0, 2);
		original_graph.addEdgeWithWeight(2, 1);
		original_graph.addEdgeWithWeight(0, 3);
		original_graph.addEdgeWithWeight(3, 4);

		System.out.println("SCC in the given graph \n");
		original_graph.printStronglyConnectedComponents();
	}
}

Implementaion in Python :

from collections import defaultdict

class Graph:
    def __init__(self,vertices):
        self.V= vertices #Total no of verices in the graph
        self.graph = defaultdict(list) # to store the graph in a dictionary

	# function to create graph by adding edge of the graph
    def addEdge(self,u,v):
        self.graph[u].append(v)

	# function to apply DFS on the vertex
    def DFSOnVertex(self,v,isVisited):
        # Mark the current node as visited and print it
        isVisited[v]= True
        print(v, end=" ")
        #Recur for all the vertices adjacent to this vertex
        for i in self.graph[v]:
            if isVisited[i]==False:
                self.DFSOnVertex(i,isVisited)

    def fillInCorrectOrder(self,v,isVisited, stack):
        # Mark the current node as visited
        isVisited[v]= True
        # Recur for all the vertices adjacent to this vertex
        for i in self.graph[v]:
            if isVisited[i]==False:
                self.fillInCorrectOrder(i, isVisited, stack)
        stack = stack.append(v)
	

	# function to get transpose of the graph
    def getTranspose(self):
        original_graph = Graph(self.V)

        # check and recursively cal for all the adjacent verices
        for i in self.graph:
            for j in self.graph[i]:
                original_graph.addEdge(j,i)
        return original_graph

    # function to print all strongly connected component in the graph
    def printStronglyConnectedComponents(self):
        stack = []
        # initally all the vertices are marked not visited in second DFS round
        isVisited =[False]*(self.V)
        # fill the stack with vertices in the order of finisshing time.
        for i in range(self.V):
            if isVisited[i]==False:
                self.fillInCorrectOrder(i, isVisited, stack)

        # tranpose of the graph
        gr = self.getTranspose()
        
        # initally all the vertices are marked not visited in second DFS round
        isVisited =[False]*(self.V)

        # process the vertices in the stack infincshing time order
        while stack:
            i = stack.pop()
            if isVisited[i]==False:
                gr.DFSOnVertex(i, isVisited)
                print("")

# Create a graph given 
original_graph = Graph(5)
original_graph.addEdge(1, 0)
original_graph.addEdge(0, 2)
original_graph.addEdge(2, 1)
original_graph.addEdge(0, 3)
original_graph.addEdge(3, 4)

print ("SCC in the given graph ")
original_graph.printStronglyConnectedComponents()

Output of All Above Programs:

SCC in the given graph
0 1 2 
3 
4

Time Complexity : In kosaraju algorithm mainly three steps takes place :

1. DFS is called : Time taken to perform DFS on graph represented by adjacency list is O(V+E).
2. graph represented by adjacency list is reversed: For reversing the graph represented using adjacency list we have to iterate over the adjacency list which will take O(V) time.
3. Again DFS is called : TIme taken for DFS on graph represented by adjacecny list is O(V+E)

So, the total time taken in all the three steps in kosaraju algorithm is O(V+E) +O(V) +O(V+E) = O(V+E)

So, the time comlexity of the kosaraju algorithm is O(V+E).

Space Complexity : As kosaraju algorithm uses stack to store the vertices while performing first DFS so the space used by stack is equal to size of the vertices of the graph. So, the time complexity of kosaraju’s algorithm is O(N), where N is the total no of vertices in the graph.

Strongly Connected Components Applications

1. Strongly connected components SCC are used in social media algorithms where SCC is used to know the persons with common interest and common friends.
2. Strongly connected components are used in maps algorithm to link the path with similar origin and destination.
3. Strongly connected components are also used in vehicle routing algorithms.

Conclusion

• Strongly connected components are group of vertices in a directed graph in which every vertex has a path to the other vertices in that component.
• Kosaraju algorithm is used to find the number of strongly component in a directed graph using DFS on the graph.
• SCC is used in social media applications to link people with common interest.
• SCC is used in maps algorithm
• SCC is used in vehicle routing algorithm.