The common prefix between the two most dissimilar strings is the longest common prefix for an array of strings. For instance, there is no common prefix in the array apple, ape, and zebra since the two most distinct strings in the array, “ape” and “zebra,” do not share any initial letters. In this article, we will learn about the longest common prefix.
The Problem Statement
You must locate the longest string S, which is the prefix of EVERY string in the array, given the array of strings S[]. The longest string S, which serves as the prefix of both strings S1 and S2, is the longest common prefix (LCP) for a pair of strings S1 and S2.
Using “ABC” as an example, the longest common prefix for “abcdefgh” and “abcefgh”
I’d advise you to try out this problem by yourself first instead of jumping to the solution.
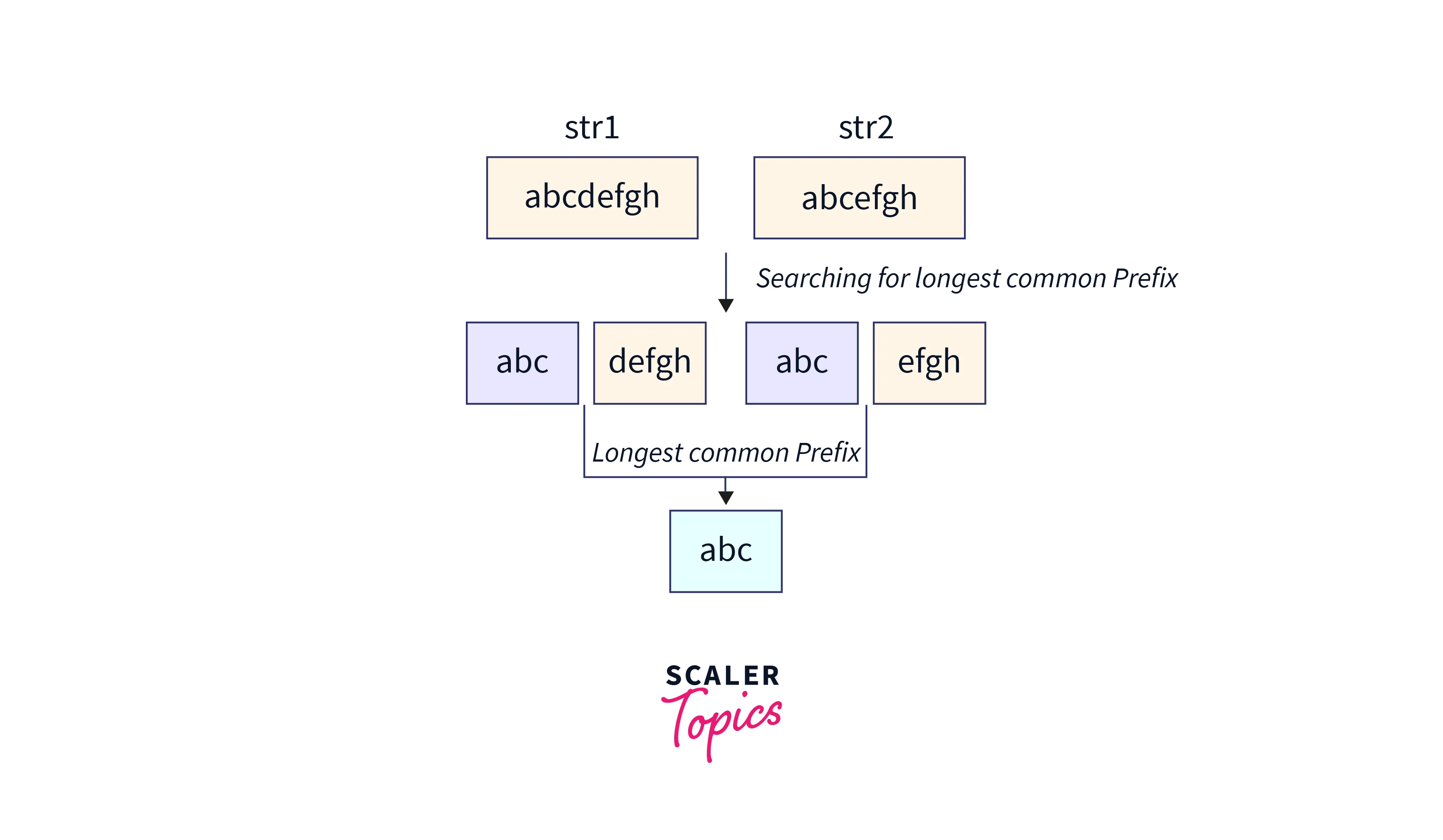
Examples
Input: S[] = {“abcdefgh”, “abcefgh”}
Output: “abc”
Input: S[] = {“abcdefgh”, “aefghijk”, “abcefgh”}
Output: “a”
Explanation: Explained in the image description above
The Binary Search Approach
The approach to solve this problem is to use the concept of Binary Search.
Algorithm:
- Consider the string with the shortest length. Let L be the length.
- Consider a variable where low=0 and high=L−1.
- Conduct a binary search:
- Split the string in half, from low to mid and from mid + 1 to high.
- Compare each character of the remaining strings at that index to the substring up to the midpoint of this smallest string.
- Update low with mid + 1 if the substring from 0 to mid – 1 is shared by all the substrings. Otherwise, update high with mid-1.
- The procedure is stopped, and the substring from 0 to mid is returned if low == high.
C++ Implementation
#include <algorithm>
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
int findMinimumLength(string words[], int count) {
int minLength = INT_MAX;
for (int i = 0; i < count; i++) {
if (words[i].length() < minLength) {
minLength = words[i].length();
}
}
return minLength;
}
bool allWordsContainPrefix(string words[], int count, string prefix,
int start, int end) {
for (int i = 0; i < count; i++) {
for (int j = start; j <= end; j++) {
if (words[i][j] != prefix[j]) {
return false;
}
}
}
return true;
}
string findLongestCommonPrefix(string words[], int count) {
int index = findMinimumLength(words, count);
string commonPrefix;
int low = 0, high = index;
while (low <= high) {
int mid = low + (high - low) / 2;
if (allWordsContainPrefix(words, count, words[0], low, mid)) {
commonPrefix = commonPrefix + words[0].substr(low, mid - low + 1);
low = mid + 1;
} else {
high = mid - 1;
}
}
return commonPrefix;
}
int main() {
string inputWords[] = {"flower", "flow", "flight"};
cout << findLongestCommonPrefix(inputWords, 3) << endl;
return 0;
}
Output:
fl
Explanation:
The provided C++ code snippet finds the longest common prefix among a given array of strings using a binary search approach. It defines functions to determine the minimum length of the strings, checks if all strings contain a specific prefix within a range, and then uses binary search to find the longest common prefix. The main function initializes an array of strings (“flower”, “flow”, “flight”), calls the prefix-finding function, and prints the resulting longest common prefix.
Java Implementation
import java.util.*;
class PrefixFinder {
public static int getMinimumLength(String[] words, int count) {
int minLength = Integer.MAX_VALUE;
for (int i = 0; i <= (count - 1); i++) {
if (words[i].length() < minLength) {
minLength = words[i].length();
}
}
return minLength;
}
public static boolean allContainPrefix(String[] words, int count, String prefix, int start, int end) {
for (int i = 0; i <= (count - 1); i++) {
String currentWord = words[i];
for (int j = start; j <= end; j++) {
if (currentWord.charAt(j) != prefix.charAt(j)) {
return false;
}
}
}
return true;
}
public static String findLongestCommonPrefix(String[] words, int count) {
int minLenIndex = getMinimumLength(words, count);
String commonPrefix = "";
int low = 0, high = minLenIndex - 1;
while (low <= high) {
int mid = low + (high - low) / 2;
if (allContainPrefix(words, count, words[0], low, mid)) {
commonPrefix = commonPrefix + words[0].substring(low, mid + 1);
low = mid + 1;
} else {
high = mid - 1;
}
}
return commonPrefix;
}
public static void main(String[] args) {
String[] wordList = {"flower", "flow", "flight"};
System.out.println(findLongestCommonPrefix(wordList, 3));
// Your additional code can be placed here
}
}
Output:
fl
Explanation:
The provided Java code defines a class named PrefixFinder that contains methods to find the longest common prefix among an array of strings using a binary search-based approach. The getMinimumLength method finds the minimum length of strings in the array, and the allContainPrefix method checks if all strings contain a given prefix within a specified character range. The findLongestCommonPrefix method performs a binary search on the length of the prefix and extends it based on whether all strings contain that prefix. In the main method, an array of strings is provided (“flower”, “flow”, “flight”), and the findLongestCommonPrefix method is called to find and print the longest common prefix among the strings.
Python Implementation
def find_shortest_length(strings):
return len(min(strings, key=len))
def all_contain_prefix(strings, prefix, start, end):
for i in range(0, len(strings)):
word = strings[i]
for j in range(start, end + 1):
if word[j] != prefix[j]:
return False
return True
def find_longest_common_prefix(strings):
shortest_length = find_shortest_length(strings)
common_prefix = ""
low, high = 0, shortest_length - 1
while low <= high:
mid = int(low + (high - low) / 2)
if all_contain_prefix(strings, strings[0], low, mid):
common_prefix = common_prefix + strings[0][low:mid + 1]
low = mid + 1
else:
high = mid - 1
return common_prefix
if __name__ == "__main__":
strings_list = ['flower', 'flow', 'flight']
print(find_longest_common_prefix(strings_list))
Output:
fl
Explanation:
The provided code defines a Python function, find_longest_common_prefix that determines the longest common prefix among a list of strings. It does so by first finding the length of the shortest string in the list. Then, it employs a binary search approach to gradually extend the common prefix, checking if all strings contain that prefix within a certain range. The code demonstrates this functionality by initializing a list of strings (‘flower’, ‘flow’, ‘flight’) and printing the longest common prefix found among them.
Time Complexity: O(K.logN) where K is the sum of all the characters in all strings.
Space Complexity: O(1)
Divide and Conquer Approach
To obtain the LCP(S1..SN), the given array of strings is split up into several smaller problems and then combined.
Divide the provided array into two halves first. Then, split the obtained left and right array into two pieces and recursively divide them until no further division is possible.
Mathematically, LCP(S1..SN) is the LCP of the array of strings, and 1 k N. LCP(S1..SN) = LCP(S1….Sk) + LCP(Sk+1…SN).
Algorithm:
- Divide the input string array into two halves iteratively.
- Find the current LCP for each division.
- Combine the LCP that was acquired from the two subarrays and return it
- LCP(S[left…mid], LCP(S[mid + 1, right])) and return it.
C++ Implementation
#include <algorithm>
#include <iostream>
#include <string>
using namespace std;
string findCommonPrefix(string first, string second) {
string prefix;
int length1 = first.length(), length2 = second.length();
for (int i = 0, j = 0; i <= length1 - 1 && j <= length2 - 1; i++, j++) {
if (first[i] != second[j])
break;
prefix.push_back(first[i]);
}
return prefix;
}
string findLongestCommonPrefix(string strings[], int start, int end) {
if (start == end)
return strings[start];
if (end > start) {
int middle = start + (end - start) / 2;
string prefix1 = findLongestCommonPrefix(strings, start, middle);
string prefix2 = findLongestCommonPrefix(strings, middle + 1, end);
return findCommonPrefix(prefix1, prefix2);
}
}
int main() {
// Your code starts here
string words[] = {"flower", "flow", "flight"};
cout << findLongestCommonPrefix(words, 0, 2) << endl;
return 0;
}
Output:
fl
Explanation:
The provided C++ code snippet finds the longest common prefix among an array of strings using a divide-and-conquer approach.
The findCommonPrefix function compares characters of two strings until a mismatch is encountered and returns the common prefix found.
The findLongestCommonPrefix function recursively divides the array of strings into smaller parts and combines the common prefixes using findCommonPrefix.
Java Implementation
import java.util.*;
import java.lang.*;
import java.io.*;
class PrefixFinder {
public static String findCommonPrefix(String str1, String str2) {
StringBuilder result = new StringBuilder();
int length1 = str1.length(), length2 = str2.length();
for (int i = 0, j = 0; i < length1 && j < length2; i++, j++) {
if (str1.charAt(i) != str2.charAt(j)) {
break;
}
result.append(str1.charAt(i));
}
return result.toString();
}
public static String findLongestCommonPrefix(String[] strings, int start, int end) {
if (start == end) {
return strings[start];
}
if (end > start) {
int mid = start + (end - start) / 2;
String prefix1 = findLongestCommonPrefix(strings, start, mid);
String prefix2 = findLongestCommonPrefix(strings, mid + 1, end);
return findCommonPrefix(prefix1, prefix2);
}
return null;
}
public static void main(String args[]) {
String words[] = {"flower", "flow", "flight"};
String longestPrefix = findLongestCommonPrefix(words, 0, words.length - 1);
System.out.println("Longest Common Prefix: " + longestPrefix);
}
}
Output:
Longest Common Prefix: fl
Explanation:
The provided Java code defines a class PrefixFinder with two main methods for finding common prefixes among strings. The findCommonPrefix method takes two strings and returns their common prefix by comparing characters one by one. The findLongestCommonPrefix method recursively divides the array of strings into halves by using int mid = start + (end – start) / 2; and finds the common prefix between pairs of divided segments.
Python Implementation
def common_prefix_util(str_1, str_2):
result = ""
length_1, length_2 = len(str_1), len(str_2)
index_1, index_2 = 0, 0
while index_1 <= length_1 - 1 and index_2 <= length_2 - 1:
if str_1[index_1] != str_2[index_2]:
break
result += str_1[index_1]
index_1, index_2 = index_1 + 1, index_2 + 1
return result
def longest_common_prefix(strings, low, high):
if low == high:
return strings[low]
if high > low:
middle = low + (high - low) // 2
sub_str_1 = longest_common_prefix(strings, low, middle)
sub_str_2 = longest_common_prefix(strings, middle + 1, high)
return common_prefix_util(sub_str_1, sub_str_2)
if __name__ == "__main__":
# Your code logic here
input_strings = ['flower', 'flow', 'flight']
print(longest_common_prefix(input_strings, 0, 2))
Output:
fl
Explanation:
The provided code defines two functions for finding the longest common prefix among a given array of strings. The common_prefix_util function compares characters of two input strings and builds the common prefix until a mismatch is found. The longest_common_prefix function utilizes a divide-and-conquer approach by recursively splitting the array of strings into smaller sub-arrays by using middle = low + (high – low) // 2, and finding the common prefix between them using the common_prefix_util function.
Time Complexity: O(K) where K is the sum of all the characters in all strings.
Space Complexity: O(MlogN), as there are log N recursive calls, and each needs a space of M.
Horizontal Scanning Approach
The objective is to discover the longest common prefix by horizontally scanning each letter in the array of strings one at a time. You can get the LCP by doing the following:
LCP(S1…SN) = LCP(S1, S2, S3,…., SN)
Algorithm:
- From S1 through SN, iterate through the string one at a time.
- For each iteration till ith index, the LCP(S1…Si) can be obtained.
- End the loop and return the empty string if the LCP is empty.
- Otherwise, keep going, and you can get the LCP(S1…SN) after scanning N strings.
C++ Implementation
#include <iostream>
#include <string>
#include <vector>
using namespace std;
string findLongestCommonPrefix(vector<string>& words) {
if (words.empty()) {
return "";
}
string prefix = words[0];
for (int i = 1; i < words.size(); ++i) {
string currentWord = words[i];
if (currentWord.empty() || prefix.empty()) {
return "";
}
int minLength = min(prefix.size(), currentWord.size());
for (int k = 0; k < minLength; ++k) {
if (currentWord[k] != prefix[k]) {
prefix = prefix.substr(0, k);
break;
}
}
}
return prefix;
}
int main() {
vector<string> words = {"flow", "flower", "flight"};
cout << findLongestCommonPrefix(words) << endl;
return 0;
}
Output:
fl
Explanation:
The provided code is a C++ program that finds the longest common prefix among a vector of strings. It iterates through the words, comparing each character of the current word with the corresponding character of the prefix. If a mismatch is encountered, the prefix is truncated to exclude the differing character. This process continues for all words.
Java Implementation
import java.util.*;
class UniquePrefixFinder {
public String findLongestCommonPrefix(String[] words) {
if (words.length == 0) return "";
String commonPrefix = words[0];
for (int i = 1; i < words.length; i++) {
while (words[i].indexOf(commonPrefix) != 0) {
commonPrefix = commonPrefix.substring(0, commonPrefix.length() - 1);
if (commonPrefix.isEmpty()) return "";
}
}
return commonPrefix;
}
public static void main(String args[]) {
UniquePrefixFinder finder = new UniquePrefixFinder();
String inputWords[] = {"flower", "flow", "flight"};
System.out.println(finder.findLongestCommonPrefix(inputWords));
}
}
Output:
fl
Explanation:
The provided Java code defines a class UniquePrefixFinder that contains a method findLongestCommonPrefix to discover the longest common prefix among an array of strings. It starts with the first word and iteratively shortens the common prefix by removing characters from the end until it matches the beginning of all other words.
Python Implementation
def find_longest_common_prefix(strings):
if "" in strings or not strings:
return ""
prefix = strings[0]
for i in range(1, len(strings)):
while prefix != "":
try:
if str.index(str(strings[i]), prefix) == 0:
break
else:
prefix = prefix[:-1]
except:
prefix = prefix[:-1]
return prefix
if __name__ == "__main__":
input_strings = ['flower', 'flow', 'flight']
print(find_longest_common_prefix(input_strings))
Output:
fl
Explanation:
The provided code defines a function find_longest_common_prefix that takes a list of strings as input and finds the longest common prefix among them using a character-by-character approach. It initializes the prefix with the first string and iterates through the rest of the strings, gradually reducing its length until a match is found at the beginning of each string or the prefix becomes empty.
Time Complexity: O(N) where N is the size of the array S[].
Space Complexity: O(1), as no extra space is used.
Vertical Scanning Approach
The objective is to traverse each string’s ith index, scanning and comparing each character from top to bottom.
When the LCP string is quite short, this method is effective. As a result, we are not required to do K comparisons.
Algorithm:
- From S1 through SN, iterate through the string one at a time.
- Start comparing the 0th index, 1st index … ith index simultaneously for each string.
- If any characters in the ith index do not match, stop the algorithm and return LPS(1,i).
- Otherwise, keep going, and you can get the LCP(S1…SN) after scanning N strings.
C++ Implementation
#include <iostream>
#include <vector>
#include <string>
using namespace std;
string findLongestCommonPrefix(vector<string> words) {
if (words.empty()) {
return "";
}
for (int charIndex = 0; charIndex < words[0].length(); charIndex++) {
char currentChar = words[0][charIndex];
for (int wordIndex = 1; wordIndex < words.size(); wordIndex++) {
if (charIndex == words[wordIndex].length() || words[wordIndex][charIndex] != currentChar) {
return words[0].substr(0, charIndex);
}
}
}
return words[0];
}
int main() {
vector<string> inputWords = {"flower", "flow", "flight"};
cout << "Longest Common Prefix: " << findLongestCommonPrefix(inputWords) << endl;
return 0;
}
Output:
Longest Common Prefix: fl
Explanation:
The provided C++ code snippet defines a function findLongestCommonPrefix that takes a vector of strings as input and calculates the longest common prefix among them. It iterates character by character through the first string and compares the corresponding characters with the same position in the other strings. If a mismatch is found or the end of any string is reached, it returns the common prefix found so far.
Java Implementation
import java.util.*;
import java.lang.*;
import java.io.*;
class Solution {
public String findLongestCommonPrefix(String[] words) {
if (words == null || words.length == 0) return "";
for (int i = 0; i < words[0].length(); i++) {
char currentChar = words[0].charAt(i);
for (int j = 1; j < words.length; j++) {
if (i == words[j].length() || words[j].charAt(i) != currentChar)
return words[0].substring(0, i);
}
}
return words[0];
}
public static void main(String args[]) {
// Your code starts here
Solution solution = new Solution();
String words[] = {"flower", "flow", "flight"};
System.out.println(solution.findLongestCommonPrefix(words));
}
}
Output:
fl
Explanation:
The provided Java code defines a class named Solution with a method findLongestCommonPrefix, which calculates the longest common prefix among an array of strings. It iterates through characters at each position in the first string and compares them with the corresponding positions in the other strings. If a mismatch is found or if the end of any string is reached, it returns the common prefix found so far.
Python Implementation
def find_longest_common_prefix(strings):
if len(strings) == 0:
return ""
for i in range(len(strings[0])):
current_char = strings[0][i]
for j in range(len(strings)):
if i == len(strings[j]) or strings[j][i] != current_char:
return strings[0][0:i]
return strings[0]
if __name__ == "__main__":
input_strings = ['flower', 'flow', 'flight']
print(find_longest_common_prefix(input_strings))
Output:
fl
Explanation:
The given Python code defines a function find_longest_common_prefix that takes a list of strings as input and finds the longest common prefix among them. It iterates through the characters at each position in the first string and compares them with the corresponding positions in the other strings. If a mismatch is found or the end of any string is reached, it returns the common prefix found up to that point.
Time Complexity: O(K)O(K) where K is the sum of all the characters in all strings.
Space Complexity: O(1)O(1), as no extra space is used.
FAQs
Q.What time and space complexity makes it possible to find the longest prefix string?
A.Using the horizontal and vertical scanning approach, the best time complexity is O(N)O(N), and the best space complexity is O(1)O(1).
Q. Is the binary search approach superior to the others?
A. No, the complexity of the binary search is O(K*logN). As a result, there are more effective strategies.
Q.Why is finding the LCP important in programming?
A. Finding the LCP is essential in various string matching and comparison tasks, such as searching for similar words, sorting strings, and identifying common substrings.
Conclusion
- The common prefix between the two most dissimilar strings is the longest common prefix for an array of strings.
- For instance, there is no common prefix in the array “apple”, “ape”, and “zebra” since the two most distinct strings in the array, “ape” and “zebra,” do not share any initial letters.
- The solution typically involves iterating through the characters of the strings and comparing them to identify the common prefix.
- There are various approaches to solving this problem, such as the horizontal scanning method or the divide-and-conquer approach, each with its trade-offs in terms of time complexity and code simplicity.
I hope you understood the longest common prefix and different strategies explained in this article.