Problem Statement
Given a string ‘S’, your objective is to identify the length of the longest palindromic subsequence. In simpler terms, you’re tasked with finding the longest sequence of characters in ‘S’ that can be read the same forwards and backwards, but not necessarily in consecutive order.
Example
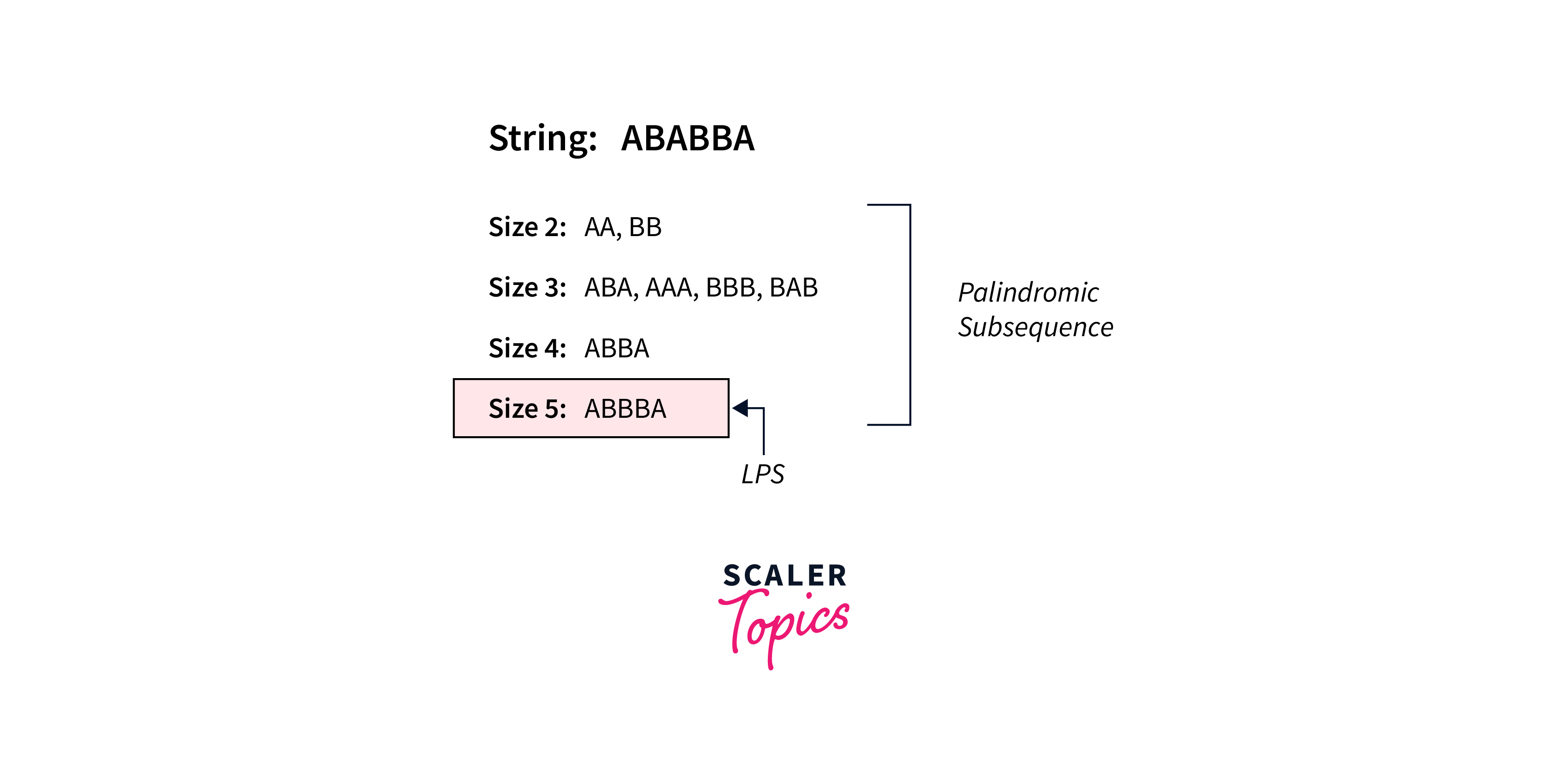
Input: string: 'ABABBA'
Output: 5
Approach-1: Using Recursive Solution
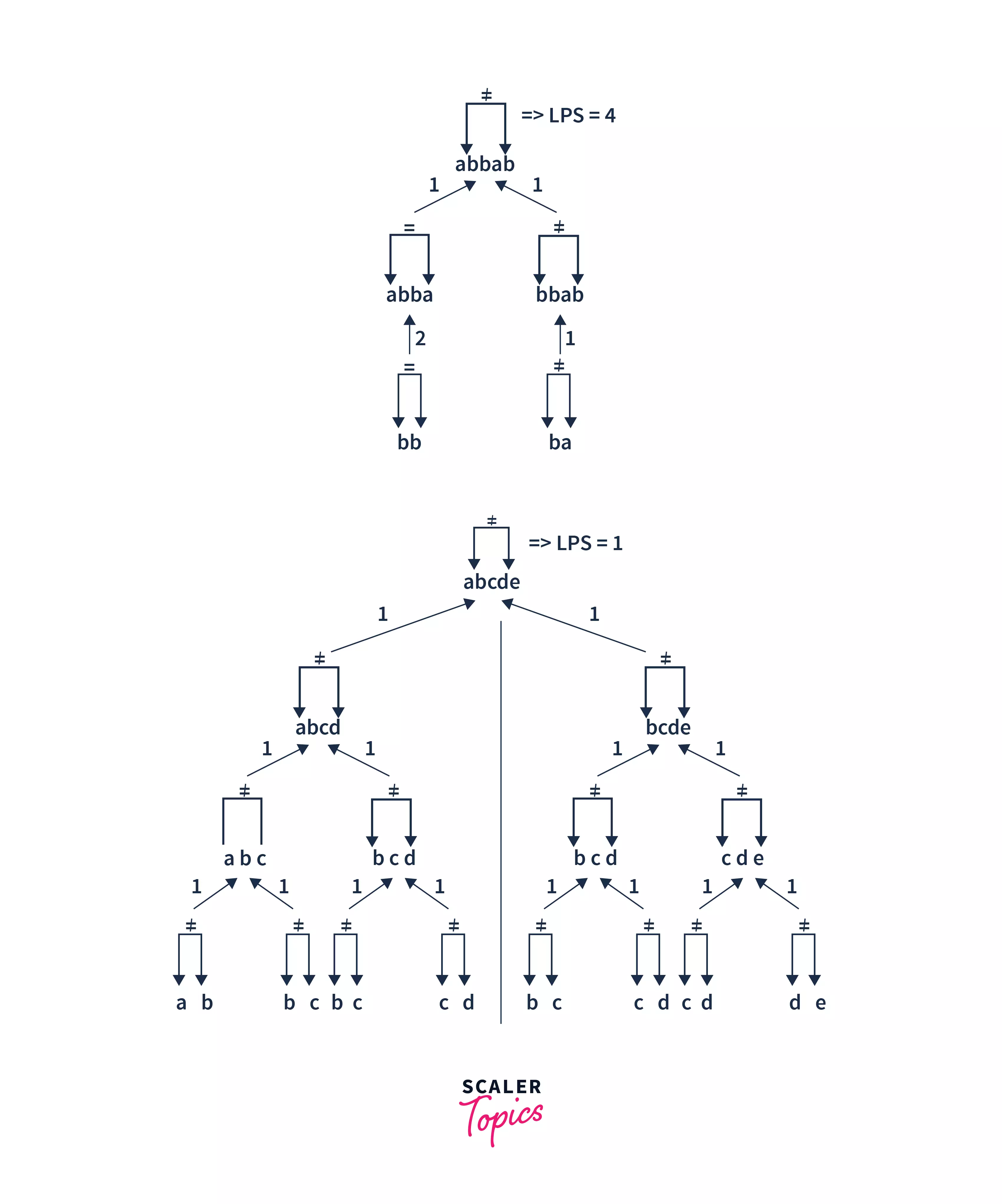
- Base case: If a single character is considered, it’s always a palindrome of length 1.
- If the first and last characters are different: In this case, the length of the LPS is the maximum of either excluding the first character or excluding the last character.
- If there are only 2 characters and both are the same: In this scenario, the length of the LPS is 2.
- If the first and last characters are the same: Here, we add 2 to the length of the LPS of the substring excluding the first and last characters.
Dry Run:
Code Implementation
C++:
#include<bits/stdc++.h>
using namespace std;
// Function to find the length of LPS
int LPS (string s, int low, int high){
// Base case 1: String of length 1.
if(low == high)
return 1;
// Base case 2: String of length 2.
if(high - low == 1){
// If both characters are equal
if(s[low] == s[high])
return 2;
// Otherwise
else
return 1;
}
// If s[low] and s[high] are equal
if(s[low] == s[high])
return 2 + LPS (s, low + 1, high - 1);
// Otherwise
return max( LPS (s, low, high - 1),
LPS(s, low + 1, high));
}
// Main function
int main(){
// Trying for string "abbab"
string s = "abbab";
int len = LPS (s, 0, s.length() - 1);
cout << "Length of LPS of " << s
<< " is " << len << endl;
// Trying for string "abaaba"
s = "abaaba";
len = LPS (s, 0, s.length() - 1);
cout << "Length of LPS of " << s
<< " is " << len << endl;
return 0;
}
Java:
// Main class
public class Main{
// Function to find the length of LPS
private static int LPS (char s[], int low, int high){
// Base case 1: String of length 1.
if(low == high)
return 1;
// Base case 2: String of length 2.
if(high - low == 1){
// If both characters are equal
if(s[low] == s[high])
return 2;
// Otherwise
else
return 1;
}
// If s[low] and s[high] are equal
if(s[low] == s[high])
return 2 + LPS (s, low + 1, high - 1);
// Otherwise
return Math.max( LPS (s, low, high - 1),
LPS(s, low + 1, high));
}
// Main function
public static void main(String args[]){
// Trying for string "abbab"
String s = "abbab";
int len = LPS (s.toCharArray(), 0, s.length() - 1);
System.out.println("Length of LPS of "+s+" is "+len);
// Trying for string "abaaba"
s = "abaaba";
len = LPS (s.toCharArray(), 0, s.length() - 1);
System.out.println("Length of LPS of "+s+" is "+len);
}
}
Python:
# Function to find the length of LPS
def LPS (s, low, high):
# Base case 1: String of length 1.
if(low == high):
return 1
# Base case 2: String of length 2.
if(high - low == 1):
# If both characters are equal
if(s[low] == s[high]):
return 2
# Otherwise
else:
return 1
# If s[low] and s[high] are equal
if(s[low] == s[high]):
return 2 + LPS (s, low + 1, high - 1)
# Otherwise
return max( LPS (s, low, high - 1),
LPS(s, low + 1, high))
# Driver code
# Trying for string "abbab"
s = "abbab"
lpsLen = LPS (s, 0, len(s) - 1)
print("Length of LPS of ", s, " is ", lpsLen)
# Trying for string "abaaba"
s = "abaaba"
lpsLen = LPS (s, 0, len(s) - 1)
print("Length of LPS of ", s, " is ", lpsLen)
Output :
Length of LPS of abbab is 4
Length of LPS of abaaba is 6
Complexity Analysis
- Time Complexity – Since we are recurring for each subsequence of string $s$, the overall time complexity is equal to the number of possible subsequences which is nothing but $O(2^n)$.
- Space Complexity – Though we are not using any auxiliary data structure, due to multiple sub-problems the maximum height of the recursive stack can reach up to $n$, hence overall space complexity is $O(n)$.
Approach-2: Memoization Technique
- Create a Memoization Table: Initialize a 2D memoization table dp of size n x n. Initialize all values in dp to -1 initially.
- Modify the Recursive Function: Modify the recursive function to check the memoization table before making recursive calls. If the value for the current indices (i, j) is already computed, return the stored value from the memoization table.
Code Implementation
C++:
#include<bits/stdc++.h>
using namespace std;
// Declaring the dp table.
int **dp;
// Function to initialize the dp table
void initializeDPTable (int n){
dp = new int*[n];
for(int i = 0; i < n; i++){
dp[i] = new int[n];
for(int j = 0; j < n; j++)
dp[i][j] = -1;
}
}
// Function to find length of LPS
int LPS (string s, int low, int high){
// If answer for s[low...high] has
// already been calculated.
if(dp[low][high] != -1)
return dp[low][high];
int ans = 0;
// Base case 1: String of length 1.
if(low == high)
ans = 1;
// Base case 2: String of length 2.
else if(high - low == 1){
// If both characters are equal
if(s[low] == s[high])
ans = 2;
// Otherwise
else
ans = 1;
}
// If s[low] and s[high] are equal
else if(s[low] == s[high])
ans = 2 + LPS (s, low + 1, high - 1);
// Otherwise
else
ans = max( LPS (s, low, high - 1),
LPS(s, low + 1, high));
// Store the answer in dp table and return it.
dp[low][high] = ans;
return dp[low][high];
}
// Main function
int main(){
// Trying for string "abbab"
string s = "abbab";
initializeDPTable(s.length());
int len = LPS (s, 0, s.length() - 1);
cout << "Length of LPS of " << s
<< " is " << len << endl;
// Trying for string "abaaba"
s = "abaaba";
initializeDPTable(s.length());
len = LPS (s, 0, s.length() - 1);
cout << "Length of LPS of " << s
<< " is " << len << endl;
return 0;
}
Java:
// Main class
public class Main{
// Declaring the dp table.
static int dp[][];
// Function to initialize the dp table
static void initializeDPTable (int n){
dp = new int[n][n];
for(int i = 0; i < n; i++)
for(int j = 0; j < n; j++)
dp[i][j] = -1;
}
// Function to find length of LPS
private static int LPS (char s[], int low, int high){
// If answer for s[low...high] has
// already been calculated.
if(dp[low][high] != -1)
return dp[low][high];
int ans = 0;
// Base case 1: String of length 1.
if(low == high)
ans = 1;
// Base case 2: String of length 2.
else if(high - low == 1){
// If both characters are equal
if(s[low] == s[high])
ans = 2;
// Otherwise
else
ans = 1;
}
// If s[low] and s[high] are equal
else if(s[low] == s[high])
ans = 2 + LPS (s, low + 1, high - 1);
// Otherwise
else
ans = Math.max( LPS (s, low, high - 1),
LPS(s, low + 1, high));
// Store the answer in dp table and return it.
dp[low][high] = ans;
return dp[low][high];
}
// Main function
public static void main(String args[]){
// Trying for string "abbab"
String s = "abbab";
initializeDPTable(s.length());
int len = LPS (s.toCharArray(), 0, s.length() - 1);
System.out.println("Length of LPS of "+s+" is "+len);
// Trying for string "abaaba"
s = "abaaba";
initializeDPTable(s.length());
len = LPS (s.toCharArray(), 0, s.length() - 1);
System.out.println("Length of LPS of "+s+" is "+len);
}
}
Python:
# DP table
dp = []
# Function to find length of LPS
def LPS (s, low, high):
# If answer to s[low...high] has
# already been calculated.
if(dp[low][high] != -1):
return dp[low][high]
ans = 0
# Base case 1: String of length 1.
if(low == high):
ans = 1
# Base case 2: String of length 2.
elif(high - low == 1):
# If both characters are equal
if(s[low] == s[high]):
ans = 2
# Otherwise
else:
ans = 1
# If s[low] and s[high] are equal
elif(s[low] == s[high]):
ans = 2 + LPS (s, low + 1, high - 1)
# Otherwise
else:
ans = max( LPS (s, low, high - 1),
LPS(s, low + 1, high))
# Store the answer in dp table and return it.
dp[low][high] = ans;
return dp[low][high];
# Driver code
# Trying for string "abbab"
s = "abbab"
n = len(s)
dp = [[-1 for i in range(n)] for j in range(n)]
lpsLen = LPS (s, 0, len(s) - 1)
print("Length of LPS of ", s, " is ", lpsLen)
# Trying for string "abaaba"
s = "abaaba"
n = len(s)
dp = [[-1 for i in range(n)] for j in range(n)]
lpsLen = LPS (s, 0, len(s) - 1)
print("Length of LPS of ", s, " is ", lpsLen)
Output:
Length of LPS of abbab is 4
Length of LPS of abaaba is 6
Complexity Analysis
- Time Complexity – The time complexity of memoization code has now been reduced to $O(n^2)$ from $O(2^n)$, due to which the problem becomes
solvableas per the given constraints of the question. - Space Complexity – As we are using an auxiliary 2-D array of dimension $n\times n$ due to which the space complexity becomes $O(n\times n) = O(n^2)$.
Approach-3: Using the Tabulation Technique of Dynamic Programming
We will define our DP state $i.e.$ dp[i][j] which denotes the length of the LPS of the string $s[i…j]$. Then we will see the state transitions –
$$
dp[i][j] = \begin{cases}
2 + dp[i+1][j-1], & \text{If s[i] == s[j]}\
max (dp[i+1][j], \space dp[i][j-1]), & \text{Otherwise}
\end{cases}
$$
Algorithm
Now we will use the gap strategy to fill the dp table step-by-step using the following logic.
Let $s$ be the string of length $n$, we will start filling the dp table for all substring with gap 0 then with gap 1, and so on till the gap of $n-1$. Here $gap=k$ means all substring with gap $k$ $i.e$ $s[i…j]$ such that $j-i=k$.
- Declare a 2-D array $dp$ of size $n\times n$.
- Iterate for $gap = 0$ to $gap = n-1$ and do the following –
- Declare a variable say $i$ and initialize it to 0.
- Iterate for $j=gap$ to $j=n-1$ and do the following –
- Fill the dp[i][j] as per the state transitions described above.
- Increment i by 1, $i.e.$
i++ - Now dp[0][n-1] will contain the length of the LPS for string $s[0…n-1]$ $i.e.$ original string. Hence, we will return it as the answer.
Code Implementation
C++:
#include<bits/stdc++.h>
using namespace std;
// Function to find length of LPS
int LPS (string s, int n){
// Declare the dp table.
int dp[n][n];
// Iterate from gap = 0 to gap = n - 1
for (int gap = 0; gap < n; gap++){
// Iterate from i = 0, j = gap to j = n - 1
for (int i = 0, j = gap; j < n; j++, i++){
// If gap = 0
if (gap == 0)
dp[i][j] = 1;
// If gap is 1
else if (gap == 1){
if (s[i] == s[j])
dp[i][j] = 2;
else
dp[i][j] = 1;
}
else{
if (s[i] == s[j])
dp[i][j] = 2 + dp[i+1][j-1];
else
dp[i][j] = max (dp[i+1][j], dp[i][j-1]);
}
}
}
// Return the answer i.e. dp[0][n-1]
return dp[0][n-1];
}
// Main function
int main(){
// Trying for string "abbab"
string s = "abbab";
int len = LPS (s, s.length());
cout << "Length of LPS of " << s
<< " is " << len << endl;
// Trying for string "abaaba"
s = "abaaba";
len = LPS (s, s.length());
cout << "Length of LPS of " << s
<< " is " << len << endl;
return 0;
}
Java:
// Main class
public class Main{
// Function to find length of LPS
private static int LPS (char s[], int n){
// Declare the dp table.
int dp[][] = new int[n][n];
// Iterate from gap = 0 to gap = n - 1
for (int gap = 0; gap < n; gap++){
// Iterate from i = 0, j = gap to j = n - 1
for (int i = 0, j = gap; j < n; j++, i++){
// If gap = 0
if (gap == 0)
dp[i][j] = 1;
// If gap is 1
else if (gap == 1){
if (s[i] == s[j])
dp[i][j] = 2;
else
dp[i][j] = 1;
}
else{
if (s[i] == s[j])
dp[i][j] = 2 + dp[i+1][j-1];
else
dp[i][j] = Math.max (dp[i+1][j], dp[i][j-1]);
}
}
}
// Return the answer i.e. dp[0][n-1]
return dp[0][n-1];
}
// Main function
public static void main(String args[]){
// Trying for string "abbab"
String s = "abbab";
int len = LPS (s.toCharArray(), s.length());
System.out.println("Length of LPS of "+s+" is "+len);
// Trying for string "abaaba"
s = "abaaba";
len = LPS (s.toCharArray(), s.length());
System.out.println("Length of LPS of "+s+" is "+len);
}
}
Python:
# DP table
dp = []
# Function to find length of LPS
def LPS (s, n):
dp = [[0 for i in range(n)] for j in range(n)]
# Iterate from gap = 0 to gap = n - 1
for gap in range(n):
# Iterate from i = 0, j = gap to j = n - 1
for i, j in zip (range(n), range(gap, n)):
# If gap = 0
if (gap == 0):
dp[i][j] = 1
# If gap is 1
elif (gap == 1):
if (s[i] == s[j]):
dp[i][j] = 2
else:
dp[i][j] = 1
# Otherwise
else:
if (s[i] == s[j]):
dp[i][j] = 2 + dp[i+1][j-1]
else:
dp[i][j] = max (dp[i+1][j], dp[i][j-1])
# Return the answer i.e. dp[0][n-1]
return dp[0][n-1]
# Driver code
# Trying for string "abbab"
s = "abbab"
n = len(s)
dp = [[-1 for i in range(n)] for j in range(n)]
lpsLen = LPS (s, len(s))
print("Length of LPS of ", s, " is ", lpsLen)
# Trying for string "abaaba"
s = "abaaba"
n = len(s)
dp = [[-1 for i in range(n)] for j in range(n)]
lpsLen = LPS (s, len(s))
print("Length of LPS of ", s, " is ", lpsLen)
Output:
Length of LPS of abbab is 4
Length of LPS of abaaba is 6
Complexity Analysis
- Time Complexity – In the first iteration the inner loop runs for $n$ time, in the second iteration it runs for $n-1$ time, and similarly in the $(n-1)^{th}$ iteration inner loop runs for 1 time.
Hence the total number of executions of the inner loop is $n + (n-1) + (n-2)+…+1$ which is an order of $n^2$ and hence the time complexity is $O(n^2)$. - Space Complexity – We have used a 2-D array of dimension $n\times n$ due to which the space complexity is $O(n^2)$.
Explore Scaler Topics Data Structures Tutorial and enhance your DSA skills with Reading Tracks and Challenges.
Conclusion
- Problem Definition: The Longest Palindromic Subsequence (LPS) problem involves finding the length of the longest subsequence in a given string that reads the same forwards and backwards.
- Naive Approach: A naive solution of longest palindromic subsequence problem involves generating all possible subsequences of the given string and checking each one for palindromic properties. However, this approach is exponential in time complexity.
- Dynamic Programming: By applying dynamic programming techniques to longest palindromic subsequence problem, it can be efficiently solved. This involves breaking down the problem into smaller subproblems and storing their solutions to avoid redundant computations.
- Memoization Technique: Memoization involves storing the results of previously computed subproblems to avoid recalculating them. This significantly reduces the time complexity by eliminating redundant recursive calls.
- Tabulation Technique: Another dynamic programming approach involves filling up a table iteratively, bottom-up, starting from smaller subproblems to larger ones. This method further enhances efficiency by eliminating recursion overhead of longest palindromic subsequence problem.
- Complexity Analysis: Both memoization and tabulation techniques achieve a time complexity of O(n^2) and a space complexity of O(n^2), making the problem solvable within reasonable time and space constraints for large inputs.