Longest Palindromic Substring

Problem Statement

The Longest Palindrome in a String in one of the most classic problems in DSA. The problem statement goes like this:

Given a string, find the maximum length substring of it that is a palindrome.

Input: String

Output: String

Before we move on to examples and the solution to this problem, make a note of the definition of ‘substring’ and ‘palindrome’. A word – ‘scaler’ can have the following substrings – ‘sca’, ‘ler’, ‘aler’ since all these characters are present in continuity in our string. However, the strings – ‘sclr’ or ‘cer’ are not substrings since the characters do not have a continuous presence in the string. A palindrome is a set of characters that is the same when read from left to right as well as from right to left. For example – ‘12321’ or ‘malayalam’ etc.

Examples

1. string = findnitianhere Longest Palindrome in the String = indni Length of the longest palindrome = 5

2. string = abcbedrardea Longest Palindrome in the String = edrarde Length of the longest palindrome = 7

Examples Explanation

1. In the first string, the only palindrome present is the substring ‘indni’ and the length of this palindrome is 5.
2. In this string, there are two palindromes – ‘bcb’ and ‘edrarde’ and the longest palindromic substring is ‘edrarde’. And the length of this substring is 7.

Constraints

1. The length of the string ranges between 1 and 1000 both inclusive 1 <= length(string) <= 1000
2. The string contains only digits and English alphabets.

Approach 1 – Brute Force / Naive Approach

The first approach that comes to mind is the naive or brute force approach. Naturally, in this method, you would traverse the string, and find every substring and check if it is a palindrome.

To do this, we would require 3 for loops. The first two loops would find every substring of the given string, and the third loop would check if the substring is a palindrome or not. At the same time, we would keep check of the length of the substring, if it is a palindrome, so as to return the longest palindromic substring.

A point that is worthy of noting here, is that every substring of length ‘1’ is a palindrome.

So what we’re going to do is, initially, keep a variable that stores the current maximum length of the palindrome that we have seen, and another variable that just stores the length of our input string. Now, to check if a string is a palindrome, one helpful way is to reverse it and compare it with the original string, or substring in this case.

Here’s how this algorithm looks:

function longestPalindrome(String s):
	length <- length of string s
	// since all substrings of length 1 are palindromes, current max length of existing palindrome in the string is 1
	maxlength <- 1
	i <- 0
	while i < n do:
		j <- i
		while j < n do:
			// set flag for this substring to be a palindrome initially, change to 0 if substring is not palindrome
			ispalindrome <- 1
			k <- i
			while k < j do:
				// checking if substring is palindrome 
				if s[k] is not equal to s[j - (k - i)] then:
					ispalindrome <- 0
				k <- k + 1
		        if ispalindrome is 1 and j - i + 1 is greater than maxlength then:
			        index <- i
			        maxlength <- j - i + 1
			j <- j + 1
		i <- i + 1
	// declare answer as empty string
	ans <- ""
	i <- 0
	wile i < index + maxlength do:
		ans <- ans + s[i]
		i <- i + 1
	return ans

Code Implementation

C++:

#include<bits/stdc++.h>

using namespace std;

string longestPalindrome(string s) {
	int length = s.size();
	int index  = -1;
	int maxlength = 0;
	// looping over the string for substrings
	for (int i = 0; i < length; i++) {
		for (int j = i; j < length; j++) {
			int isPalindrome = 1;
			// checking if string is palindrome
			for (int k = i; k <= j; k++) {
				if (s[k] != s[j - (k - i)]) {
					isPalindrome = 0;
				}
			}
			if (isPalindrome == 1 && j - i + 1 > maxlength) {
				index = i;
				maxlength = j - i + 1;
			}
		}
	}
	// return the substring from updated index till length maxlength
	string ans = "";
	for (int i = index; i < index + maxlength; i++) {
		ans += s[i];
	}
	return ans;
}

int main(){
	string word = "findnitianhere";
	cout << longestPalindrome(word) << endl;
	return 0;
}

Output:

indni

Java:

class Main{
    public static String longestPalindrome(String s) {
    	int n = s.length();
    	int index  = -1;
    	int maxlength = 0;
    	// looping over the string for substrings
    	for (int i = 0; i < n; i++) {
    		for (int j = i; j < n; j++) {
    			int isPalindrome = 1;
    			// checking if string is palindrome
    			for (int k = i; k <= j; k++) {
    				if (s.charAt(k) != s.charAt(j - (k - i))) {
    					isPalindrome = 0;
    				}
    			}
    			if (isPalindrome == 1 && j - i + 1 > maxlength) {
    				index = i;
    				maxlength = j - i + 1;
    			}
    		}
    	}
    	// return the substring from updated index till length maxlength
    	String ans = "";
    	for (int i = index; i < index + maxlength; i++) {
    		ans += s.charAt(i);
    	}
    	return ans;
    }
    
    public static void main(String[] args){
    	String word = new String("findnitianhere");
    	System.out.println(longestPalindrome(word));
    }
};

Output:

indni

Python:

def longestPalindrome(s: str) -> str:
	length = len(s)
	index = -1
	maxlength = 0
	# looping over the string for substrings
	for i in range(length):
		for j in range(i, length):
			ispalindrome = 1
			# checking if string is a palindrome
			for k in range(0, ((j - i) // 2) + 1):
				if s[i + k] != s[j - k]:
					ispalindrome = 0
			# if the string is palindrome update maximum length 
			if ispalindrome != 0 and j - i + 1 > maxlength:
				index = i
				maxlength = j - i + 1
	# return the substring from updated index till length maxlength
	return s[index:index + maxlength]

if __name__ == "__main__":
	word = "abcbedrardea"
	print(longestPalindrome(word))

Output:

edrarde

Time Complexity

Time Complexity: O(n³), where n is the length of the string. The reason for such a high time complexity is the three nested loops in the code.

Space Complexity

Space Complexity: O(1) We are not making the use of any extra space.

Approach 2 – Dynamic Programming

To understand the concept of dynamic programming in detail, and solve basic problems, refer to this article on 1 dimensional dynamic programming and this article for this problem. Moving on to our problem, it can be solved using a more optimized version of the previous approach which is dynamic programming. To re-iterate, dynamic programming solves problems by breaking down the big problem into smaller sub problems, and using the results of the computations performed on the subproblems. The results of the smaller subproblems are stored and utilized.

In this case, how would we do it? Let’s say the longest palindrome in our string is abcdedcba. If we already know that ‘ded’ is a palindrome, it is sure that ‘cdedc’ is also a palindrome since the first and last alphabets of the new string are the same. And similarly, if we know that ‘cdedc’ is a palindrome, it is not tough to find out that ‘bcdedcb’ and ‘abcdedcba’ are also palindromes. Do you see how this is going?

Keeping this in mind, we’re going to have a function P(i, j) such that: 

Which can also be written as:

— which is nothing but the condition discussed above – ‘ded’ is a palindrome, and so is ‘cdedc’ since the first and last characters are same.

Hence, the base cases are:

Using the above observations, we can yield a very straightfoward dynamic programming solution. In this approach we will first initialize the one letter, and two letter palindromes (both letters are same – ‘aa’ or ‘ee’) and then grow by finding all the 3 letter palindromes and so on.

The traditional approach of a dynamic programming solution is to create a table. In this table, every row and column represents the slicing indices on the string, both inclusive. For example, if we have a string ‘babad’ then the value of dp[2][3] will represent s[2:3] (similar to python syntax) i.e. ba.

Steps to solving the problem:

• Create a boolean table (dp) of size n * n (n is length of input string) that will be filled in the bottom-up manner.
• If the value at dp[i][j] is True, then the sliced substring s[i] is a palindrome. If the value at dp[i][j] is False, then the sliced substring s[i] is not a palindrome.
• Now, to fill in the values in the table, we will make use of the base case note that we made. The value at dp[i][j] will be filled according to dp[i + 1][j – 1] and the characters in the string at s[i] and s[j]. If dp[i + 1][j – 1] is True, and if s[i] == s[j], then dp[i][j] will also be true, else False.
• Initially we would be filling up the palindromes of length 1 and 2, i.e. single characters and repeating characters.

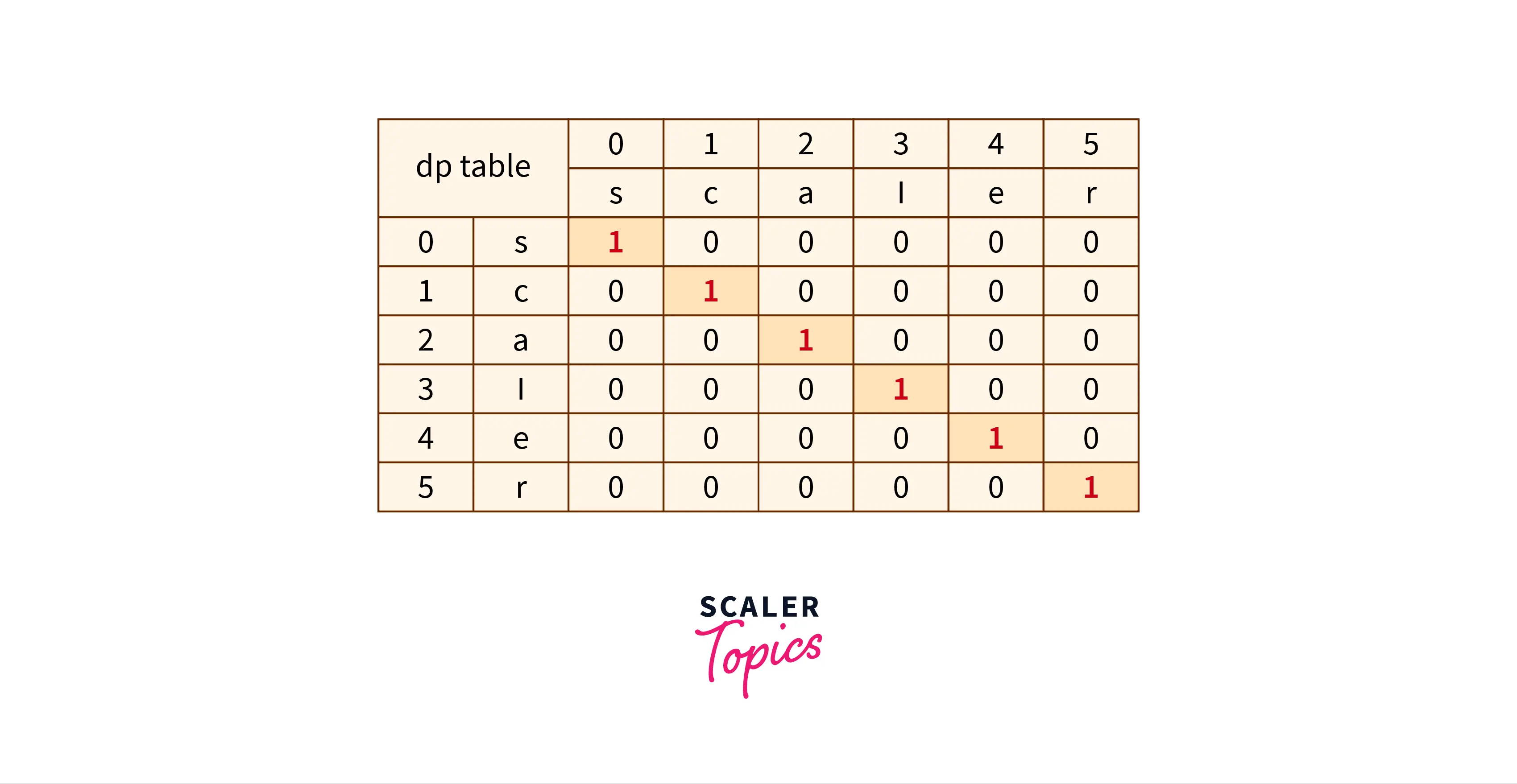
Since the string ‘scaler’ has no palindromes, this is what the table would like.

Let’s now try implementing this approach in code and discuss the time and space complexities.

Code Implementation

C++

#include <bits/stdc++.h>
using namespace std;

string longest_palindrome(string s){
	int length = s.length();
	// creating boolean table
	bool dp[length][length];
	// setting values to 0
	memset(dp, 0, sizeof(dp));
	int max_pal_length = 1;
	// setting the value of substrings of length 1 to True in dp table (i.e. same character)
	for (int i = 0; i < length; i++){
		dp[i][i] = true;
	}
	// for substrings of length 2
	int start = 0;
	for (int j = 0; j < length - 1; j++){
		// checking if there are 2 consecutive characters that are same
		if (s[j] == s[j + 1]){
			dp[j][j + 1] = true;
			start = j;
			max_pal_length = 2;
		}
	}
	// now for longer length palindromes
	for (int k = 3; k <= length; ++k) {
        // Fix the starting index
        for (int i = 0; i < length - k + 1; ++i) {
            // Get the end index of the substring from start index i and length k
            int j = i + k - 1;
 
            // check the sub-string from ith index to the jth index if s[i+1] to s[j-1] is a palindrome
            if (dp[i + 1][j - 1] && s[i] == s[j]) {
                dp[i][j] = true;
				// if current palindrome length is larger than previous largest length, update the maximum length
                if (k > max_pal_length) {
                    start = i;
                    max_pal_length = k;
                }
            }
        }
    }
    // return longest palindromic substring
    return s.substr(start, max_pal_length);
}

int main(){
	string word = "findnitianhere";
	cout << longest_palindrome(word) << endl;
	return 0;
}

Output:

indni

Java:

class Main{
    public static String longest_palindrome(String s){
    	int length = s.length();
    	// creating boolean table
    	boolean dp[][] = new boolean[length][length];
    	int max_pal_length = 1;
    	// setting the value of substrings of length 1 to True in dp table (i.e. same character)
    	for (int i = 0; i < length; i++){
    		dp[i][i] = true;
    	}
    	// for substrings of length 2
    	int start = 0;
    	for (int j = 0; j < length - 1; j++){
    		// checking if there are 2 consecutive characters that are same
    		if (s.charAt(j) == s.charAt(j + 1)){
    			dp[j][j + 1] = true;
    			start = j;
    			max_pal_length = 2;
    		}
    	}
    	// now for longer length palindromes
    	for (int k = 3; k <= length; ++k) {
            // Fix the starting index
            for (int i = 0; i < length - k + 1; ++i) {
                // Get the end index of the substring from start index i and length k
                int j = i + k - 1;
     
                // check the sub-string from ith index to the jth index if s[i+1] to s[j-1] is a palindrome
                if (dp[i + 1][j - 1] && s.charAt(i) == s.charAt(j)) {
                    dp[i][j] = true;
    				// if current palindrome length is larger than previous largest length, update the maximum length
                    if (k > max_pal_length) {
                        start = i;
                        max_pal_length = k;
                    }
                }
            }
        }
        // return longest palindromic substring
        return s.substring(start, start + max_pal_length);
    }
    
    public static void main(String[] args){
    	String word = "findnitianhere";
    	System.out.println(longest_palindrome(word));
    }
};

Output:

indni

Python:

def longest_palindrome(s) :
    length = len(s)
    dp = [[0 for x in range(length)] for y in range(length)]
    max_pal_length = 1
    i = 0
    while (i < length) :
        dp[i][i] = True
        i += 1
    # check for sub-string of longer lengths than 1.
    start = 0
    i = 0
    while i < length - 1 :
        if (s[i] == s[i + 1]) :
            dp[i][i + 1] = True
            start = i
            max_pal_length = 2
        i += 1
    k = 3
    while k <= length:
        # Fix the start index
        i = 0
        while i < (length - k + 1) :
            j = i + k - 1
            if (dp[i + 1][j - 1] and s[i] == s[j]):
                dp[i][j] = True
                if (k > max_pal_length):
                    start = i
                    max_pal_length = k
            i += 1
        k += 1
    return s[start: start + max_pal_length]

if __name__ == "__main__":
	word = "abcbedrardea"
	print(longest_palindrome(word))

Output:

edrarde

Time Complexity

Time complexity of this approach: O(n²) where n is the length of the string. The time complexity of this approach is better than the naive or brute force solution, but is still not the most optimal solution since we require 2 nested traverals of the string.

Space Complexity

Space complexity of this approach: O(n²) where n is the length of the string. In the dynamic programming approach we store the results of the sub problems in a table of size n * n and hence the space complexity of this approach is O(n²).

Approach 3 (Optimal Approach) – Expand around Centre

To understand the optimal approach, we must first make an important observation, that is, every palindrome mirrors around its centre.

For example, for the palindrome – ‘abccba’:

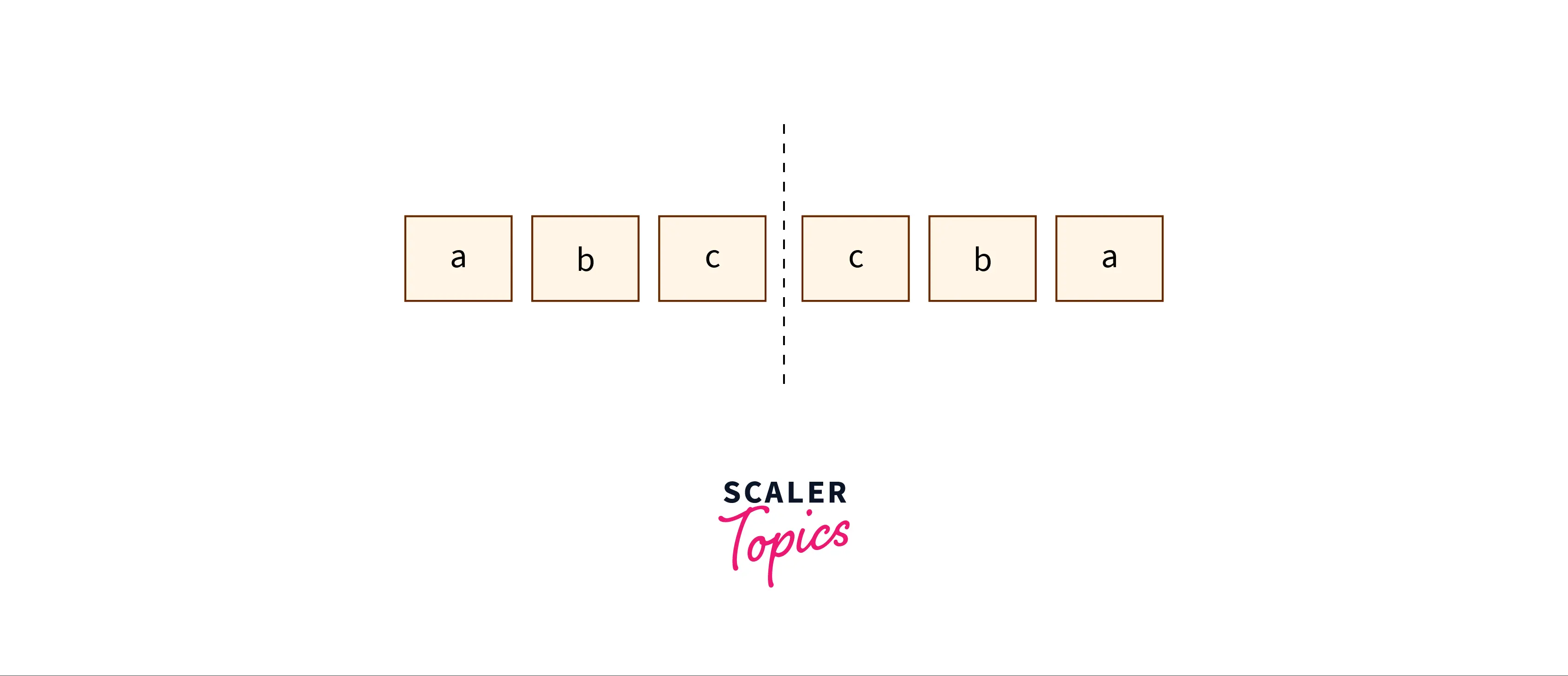
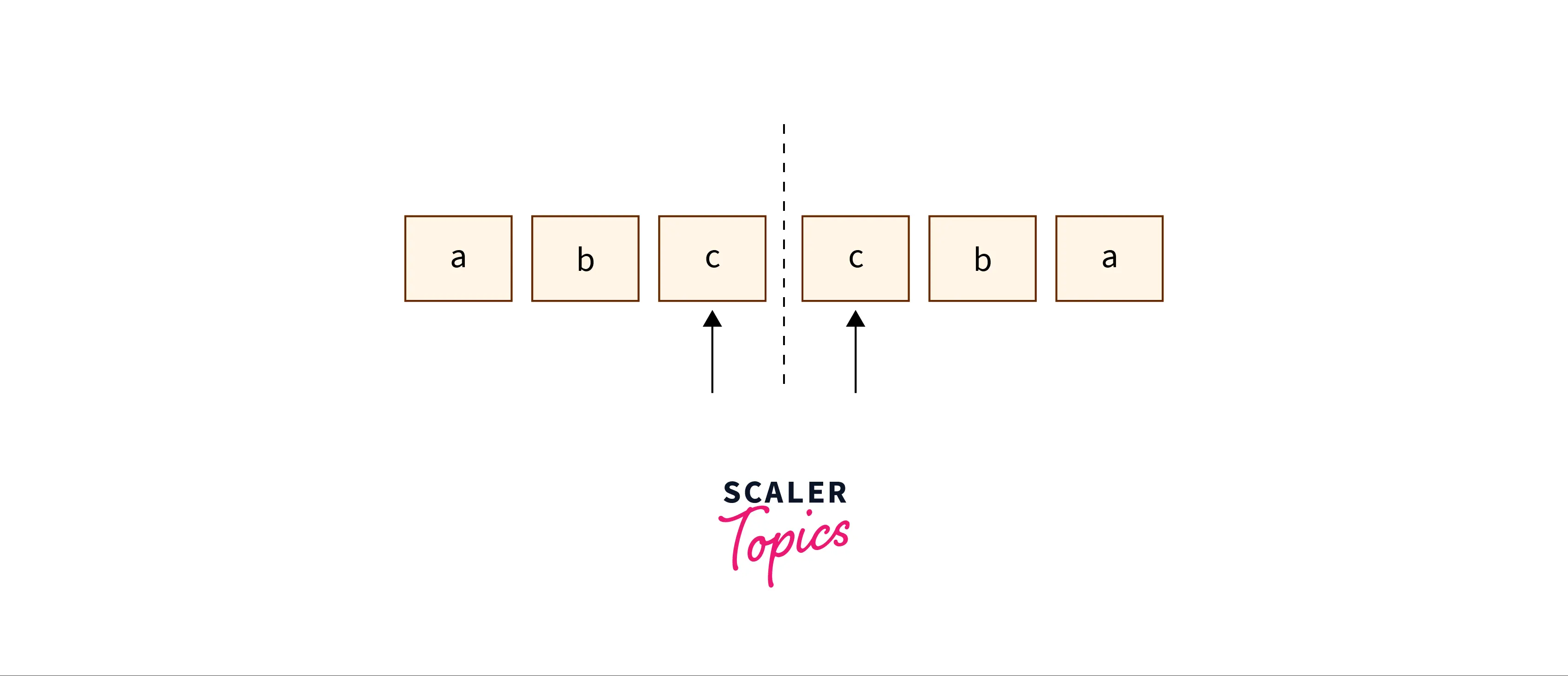
This means that a palindrome can be expanded around its centre.

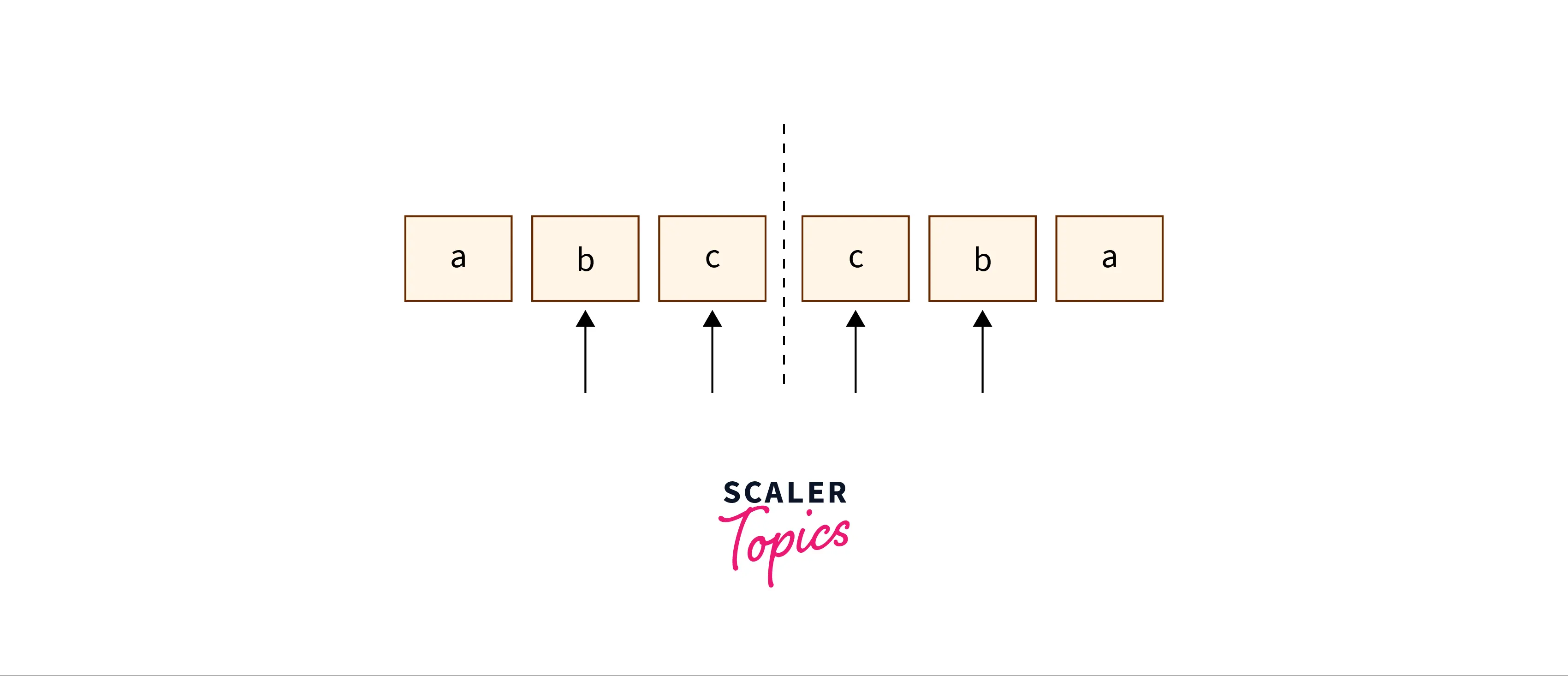
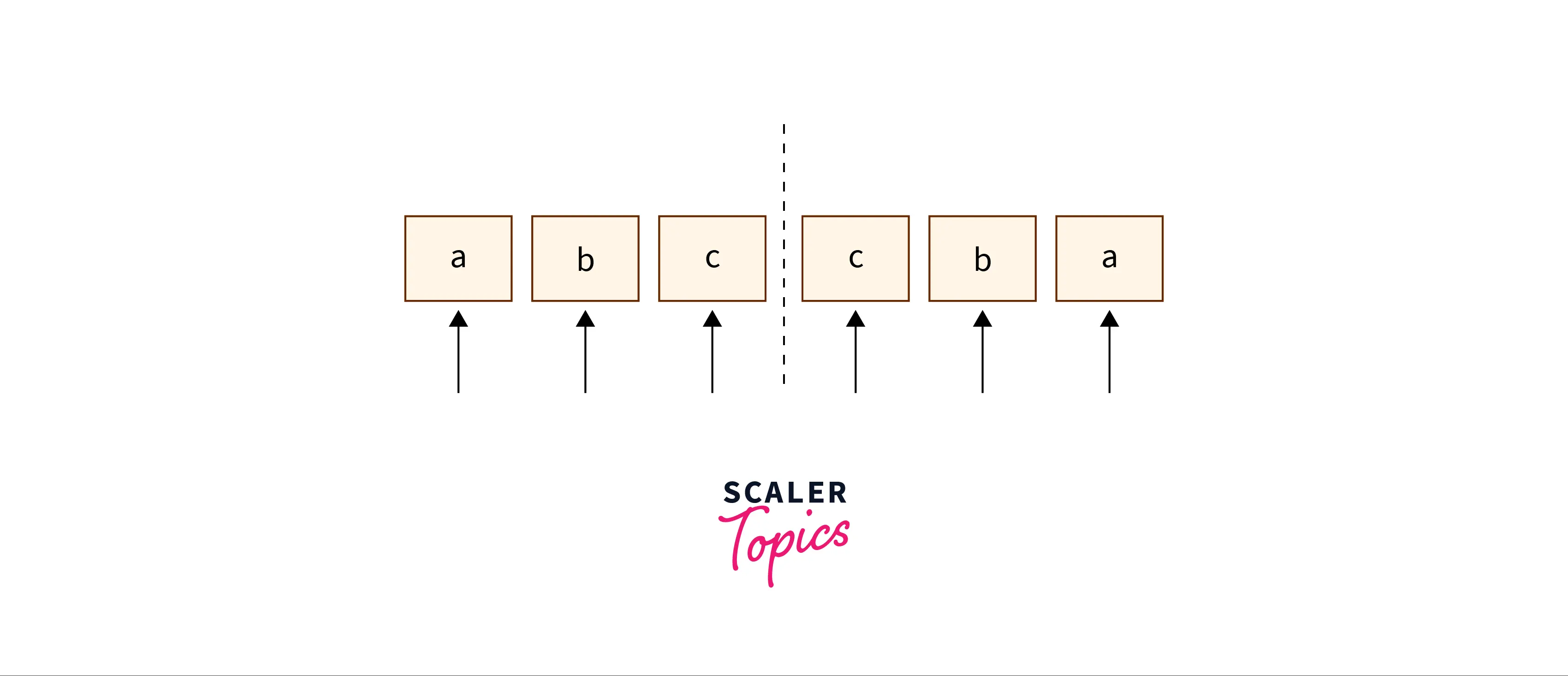
In the complete string, there are only 2n – 1 such centres available for expansion, where n is the length of the string. Why? This is because the centre around which the palindrome is mirrored, can be between two letters, and can also be a particular letter. The case of the mirror being a character in the string, is for odd length palindromes as – ‘aba’ and the case of the mirror being between characters is for even length palindromes as given in the images above.

So what is the approach to solve this problem? We’re going to consider every index of the string as the middle point or the centre of a possible palindrome and expand around it. We will expand till we find same characters.

Algorithm

Here’s the algorithm to solve the problem:

• Traverse the string and consider every index as the centre around which the palindrome is mirrored. We will encounter two cases (in both the cases, i is the loop variabe):
  • Case 1: The length of the palindromic substring is even:
    • If the palindrome is of even length, we will assign 2 pointers namely left and right pointers and initialize them with values i – 1 and i which is centre and then expand left and right in both directions, till the condition s[left] == s[right] is satisfied.
  • Case 2: The length of the palindromic substring is odd:
    • If the palindromic substring is of odd length, the centre is likely to be a particular character. In which case, we will assign the same left and right pointers and initialize them with values i – 1 and i + 1 with i as the centre. Post that, we will again expand around the centre till the condition s[left] == s[right] is satisfied.
• While this is done, we will maintain the length of the longest palindromic substring encountered and the substring, and return it.

Code Implementation

C++:

#include <bits/stdc++.h>
using namespace std;

int expand_around_center(string s, int left, int right) {
	int L = left, R = right;
	while (L >= 0 && R < s.size() && s[L] == s[R]) {
		L--;
		R++;
	}
	return R - L - 1;
}

string longest_palindrome(string s) {
	// if length of string is less than 1 return empty string
	if (s.length() < 1) return "";
	int start = 0, end = 0;
	for (int i = 0; i < s.size(); i++) {
		int len1 = expand_around_center(s, i, i);
		int len2 = expand_around_center(s, i, i + 1);
		int len = max(len1, len2);
		if (len > end - start) {
			start = i - (len - 1) / 2;
			end = i + len / 2;
		}
	}
	// return longest palindromic substring
	return s.substr(start, end - start + 1);
}

int main(){
	string word = "findnitianhere";
	cout << longest_palindrome(word) << endl;
	return 0;
}

Output:

indni

Java:

class Main{
    public static int expand_around_center(String s, int left, int right) {
    	int L = left, R = right;
    	while (L >= 0 && R < s.length() && s.charAt(L) == s.charAt(R)) {
    		L--;
    		R++;
    	}
    	return R - L - 1;
    }
    
    public static String longest_palindrome(String s) {
    	// if length of string is less than 1 return empty string
    	if (s == null || s.length() < 1) return "";
    	int start = 0, end = 0;
    	for (int i = 0; i < s.length(); i++) {
    		int len1 = expand_around_center(s, i, i);
    		int len2 = expand_around_center(s, i, i + 1);
    		int len = Math.max(len1, len2);
    		if (len > end - start) {
    			start = i - (len - 1) / 2;
    			end = i + len / 2;
    		}
    	}
    	// return longest palindromic substring
    	return s.substring(start, end + 1);
    }
    
    public static void main(String[] args){
    	String word = "findnitianhere";
    	System.out.println(longest_palindrome(word));
    }
};

Output:

indni

Python:

def longest_palindrome(s):
    res = ""
    for i in range(len(s)):
        # odd case, like "aba"
        tmp = expand(s, i, i)
        if len(tmp) > len(res):
            res = tmp
        # even case, like "abba"
        tmp = expand(s, i, i + 1)
        if len(tmp) > len(res):
            res = tmp
    return res
 
# get the longest palindrome, l, r are the middle indexes   
# from inner to outer
def expand(s, left, right):
    while left >= 0 and right < len(s) and s[left] == s[right]:
        left -= 1; right += 1
    return s[left + 1 : right]

if __name__ == "__main__":
	word = "abcbedrardea"
	print(longest_palindrome(word))

Output:

edrarde

Time Complexity

The time complexity of this approach is: O(n²) Expansion around a particular palindrome, in the worst case would take O(n) time and hence, the overall time complexity of this approach would be O(n²).

Space Complexity

Space complexity of this approach: O(1) In this approach we are not making the use of any extra space and hence, the space complexity is linear.

Approach 4 – Manachar Algorithm

For a detailed solution, to this problem using the manacher’s algorithm, it is strongly recommended that you refer to this post by scaler topics. Manachar’s algorithm can be used to solve the current problem at hand with a linear time complexity.

Manacher’s algorithm is essentially designed to find the palindromic substrings that have odd lengths only. To use it for even lengths as well, we can tweak the input string by inserting a character such as – “#” at the beginning and each alternate position after that (for example, changing a string “abcaac” to “#a#b#c#a#a#c#”).

Algorithm

Here’s the algorithm that solves the problem at hand:

• Create an array or a list (sChars) of length strLen which is 2∗n+3 (n being the length of the given string), to modify the given string.
• Assign the first and last element of sChars to be “@” and “$”, respectively.
• Fill the blank spaces in sChars by characters of the given string and “#” alternatively.
• Declare the following variables
  • maxLen = 0, which is the variable that stores the current maximum detected length of the palindromic substring
  • start = 0, the variable that indicates the position from where we will start the search for the longest palindromic substring
  • maxRight = 0, that indicates the highest position of the rightmost character, of every palindrome detected.
  • center = 0, which is nothing but the center of the palindrome detected.
• We would next create a list / array, p that records the width of each palindrome about their center, where the center is the corresponding character in our array sChars.
• Next, we will start a for loop that iterates from 1 to the length of the string, with the loop variable i that increments with every iteration.
• In every iteration, we will check the condition i < maxRight. If it is true, then we will assign the minimum of maxRight – i and p[2 * center – i] to p[i].
• We will next create a nested while loop inside the for loop, to count with width along the center, condition being, sChars[i + p[i] + 1] is equal to sChars[i – p[i] – 1], if yes, increment p[i] by 1.
• To update the center, we need to check if i + p[i] is greater than maxRight, if yes, then we will assign center to be 1, and maxRight to be i + p[i].
• To update the maximum length of the palindromic substring detected, we check if p[i] is greater than maxLen, if yes, then change the value of start to be (i – p[i] – 1) / 2, and maxLen to be p[i].
• Exit the for loop, and return the longest palindromic substring in the given string, starting from start and ending at start + maxLen – 1.

Code Implementation

C++:

#include <bits/stdc++.h>
using namespace std;

string longestPalSubstring(string s){
    /*
        If length of given string is n then its length after
        inserting n+1 "#", one "@", and one "$" will be
        (n) + (n+1) + (1) + (1) = 2n+3
    */
    int strLen = 2 * s.length() + 3;
    char* sChars = new char[strLen];

    /*
        Inserting special characters to ignore special cases
        at the beginning and end of the array
        "abc" -> @ # a # b # c # $
        "" -> @#$
        "a" -> @ # a # $
    */
    sChars[0] = '@';
    sChars[strLen - 1] = '$';
    int t = 1;

    for (char c : s){
        sChars[t++] = '#';
        sChars[t++] = c;
    }
    sChars[t] = '#';

    int maxLen = 0;
    int start = 0;
    int maxRight = 0;
    int center = 0;
    int* p = new int[strLen]; // i's radius, which doesn't include i

    for(int i = 1; i < strLen - 1; i++){
        if (i < maxRight){
            p[i] = min(maxRight - i, p[2 * center - i]);
        }

        // Expanding along the center
        while (sChars[i + p[i] + 1] == sChars[i - p[i] - 1]){
            p[i]++;
        }

        // Updating center and its bound
        if (i + p[i] > maxRight){
            center = i;
            maxRight = i + p[i];
        }

        // Updating ans
        if (p[i] > maxLen){
            start = (i - p[i] - 1) / 2;
            maxLen = p[i];
        }
    }

    // Returning the longest palindromic substring
    return s.substr(start, maxLen);
}

int main(){
	string word = "findnitianhere";
	cout << longestPalSubstring(word) << endl;
	return 0;
}

Java:

class Main {
    public static String longestPalSubstring(String s) {
        /*
         If length of given string is n then its length after
         inserting n+1 "#", one "@", and one "$" will be
         (n) + (n+1) + (1) + (1) = 2n+3
        */
        int strLen = 2 * s.length() + 3;
        char[] sChars = new char[strLen];

        /*
         Inserting special characters to ignore special cases
         at the beginning and end of the array
         "abc" -> @ # a # b # c # $
         "" -> @#$
         "a" -> @ # a # $
        */
        sChars[0] = '@';
        sChars[strLen - 1] = '$';
        int t = 1;
        for (char c : s.toCharArray()) {
            sChars[t++] = '#';
            sChars[t++] = c;
        }
        sChars[t] = '#';

        int maxLen = 0;
        int start = 0;
        int maxRight = 0;
        int center = 0;
        int[] p = new int[strLen]; // i's radius, which doesn't include i
        for (int i = 1; i < strLen - 1; i++) {
            if (i < maxRight) {
                p[i] = Math.min(maxRight - i, p[2 * center - i]);
            }

            // Expanding along the center
            while (sChars[i + p[i] + 1] == sChars[i - p[i] - 1]) {
                p[i]++;
            }

            // Updating center and its bound
            if (i + p[i] > maxRight) {
                center = i;
                maxRight = i + p[i];
            }

            // Updating ans
            if (p[i] > maxLen) {
                start = (i - p[i] - 1) / 2;
                maxLen = p[i];
            }
        }

        // Returning the longest Palindromic substring
        return s.substring(start, start + maxLen);
    }
    
    public static void main(String[] args){
    	String word = "findnitianhere";
    	System.out.println(longestPalSubstring(word));
    }
}

Python:

def longestPalSubstring(s):
    # If length of given string is n then its length after
    # inserting n+1 "#", one "@", and one "$" will be
    # (n) + (n+1) + (1) + (1) = 2n+3
    strLen = 2 * len(s) + 3
    sChars = [0]*strLen

    # Inserting special characters to ignore special cases
    # at the beginning and end of the array
    # "abc" -> @ # a # b # c # $
    # "" -> @#$
    # "a" -> @ # a # $
    sChars[0] = '@'
    sChars[strLen - 1] = '$'
    t = 1
    for i in s:
        sChars[t] = '#'
        t += 1
        sChars[t] = i
        t += 1

    sChars[t] = '#'

    maxLen = int(0)
    start = int(0)
    maxRight = int(0)
    center = int(0)
    p = [0] * strLen  # i's radius, which doesn't include i
    for i in range(1, strLen - 1):
        if i < maxRight:
            p[i] = min(maxRight - i, p[2 * center - i])

        # Expanding along the center
        while sChars[i + p[i] + 1] == sChars[i - p[i] - 1]:
            p[i] += 1

        # Updating center and its bound
        if i + p[i] > maxRight:
            center = i
            maxRight = i + p[i]

        # Updating ans
        if p[i] > maxLen:
            start = int((i - p[i] - 1) / 2)
            maxLen = p[i]

    return s[start:start+maxLen]

if __name__ == "__main__":
	word = "abcbedrardea"
	print(longestPalSubstring(word))

Output:

edrarde

Time Complexity

Time complexity of this approach: O(n) The time complexity of this approach the first time might look like it is O(n²), however, the inner while loop will get executed at most n times, still leaving the time complexity to be linear.

Space Complexity

Space complexity of this approach: O(n) We create an array in this approach of size n and hence, the space complexity is linear as well.

Conclusion

• In this article, we have discussed 4 solutions to the problem statement: Given a string, find the maximum length substring of it that is a palindrome.
• The three approaches discussed are:
  • Brute Force:
    • Time Complexity: O(n³)
    • Space complexity: O(1)
  • Dynamic Programming:
    • Time Complexity: O(n²)
    • Space complexity: O(n²)
  • Optimal approach – Expand Around Centre:
    • Time Complexity: O(n²)
    • Space complexity: O(1)
  • Manachar Algorithm:
    • Time Complexity: O(n)
    • Space complexity: O(n)