Maximum Sum Increasing Subsequence

Problem Statement

An array of positive integers of size n is given. write a program to find the maximum sum increasing subsequence in the given array. The maximum sum increasing subsequence is a subsequence of an integer array where the sum is maximum and all of the elements are sorted in non decreasing order.

Example

Input-1

arr[]: {1, 5, 2, 3, 9, 5}

Output-1

15  

Explanation

Here, we have given an array of integers 1 5 2 3 9 5 and the output should be $$1 + 2 + 3 + 9 = 15$$ because there are two subsequences exists that has a maximum sum of 15 i.e 1 5 9 and 1 2 3 9, they are sorted as well in increasing order.

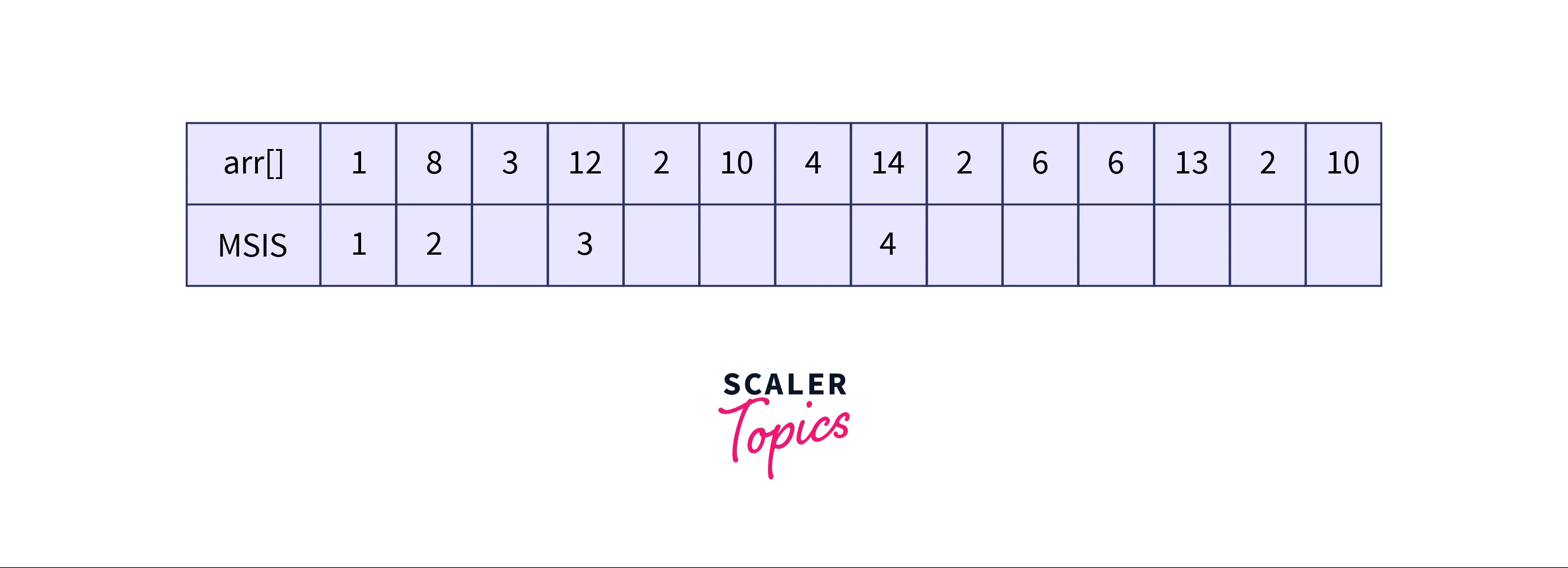
arr[]: {1, 8, 3, 12, 2, 10, 4, 14, 2, 6, 6, 13, 2, 10}

Output-2

35

Explanation

Here, we have given an array of integers 1 8 3 12 2 10 4 14 2 6 6 13 2 10 and the output should be $1 + 8 + 12 + 14 = 35$ because there is one subsequence exists which has a maximum sum of 35 i.e 1 8 12 14, which is also sorted in increasing order.

Constraints

0 <= n <= 20
0 <= n1, n2, .. <= 100

Algorithm 1 – Naive Approach and algo-1: Using Recursion

Intuition

Since this problem is a variation of the standard Longest Increasing Subsequence problem, hence we can use recursion to solve this problem. For each element in the given array, there are two cases:

• If the current element is greater than the previous element, include it.
• Else exclude the current element and use recursion for the remaining elements in the array.

Algorithm

1. Create a function that takes an arr[] array, a variable i for indexing, a prev variable to keep track of previous elements, and a sum variable for calculating the maximum sum.
2. The base case here is when the arr[] is empty.
3. Check for two cases:
   • Call the recursive function without the current element.
   • If the element is greater than the previous element, call the recursive function for the current element.
4. Finally, return the maximum sum of the above two cases.

Code Implementation

Code in C++

// Naive Approach to find maximum sum increasing subsequence Using Recursion
#include <iostream>
#include <vector>
#include <climits>
using namespace std;

// Recursive function
int maximumSubsequence(vector<int> const &arr, int i, int prev, int sum){
    // base case
    if (i == arr.size()) {
        return sum;
    }

    // If the element is greater than the previous element
    int incl = sum;
    if (arr[i] > prev) {
        incl = maximumSubsequence(arr, i + 1, arr[i], sum + arr[i]);
    }

    // Call the recursive function without the current element.
    int excl = maximumSubsequence(arr, i + 1, prev, sum);

    // return the maximum of the above two choices
    return max(incl, excl);
}

int main()
{
    vector<int> arr = { 1, 8, 3, 12, 2, 10, 4, 14, 2, 6, 6, 13, 2, 10 };

    cout << maximumSubsequence(arr, 0, INT_MIN, 0);

    return 0;
}

Code in Java

// Naive Approach to find maximum sum increasing subsequence Using Recursion
class Main
{
    // Recursive function
    public static int maximumSubsequence(int[] arr, int i, int prev, int sum)
    {
        // base case: nothing is remaining
        if (i == arr.length) {
            return sum;
        }

        // If the element is greater than the previous element
        int incl = sum;
        if (arr[i] > prev) {
            incl = maximumSubsequence(arr, i + 1, arr[i], sum + arr[i]);
        }

        // Call the recursive function without the current element.
        int excl = maximumSubsequence(arr, i + 1, prev, sum);

        // return the maximum
        return Integer.max(incl, excl);
    }

    public static void main(String[] args)
    {
        int[] arr = { 1, 8, 3, 12, 2, 10, 4, 14, 2, 6, 6, 13, 2, 10 };

        System.out.println(maximumSubsequence(arr, 0, Integer.MIN_VALUE, 0));
    }
}

Code in Python

# Naive Approach to find maximum sum increasing subsequence Using Recursion
import sys


# Function to find the maximum sum of increasing subsequence
def maximumSubsequence(arr, i=0, prev=-sys.maxsize, total=0):

    # base case: nothing is remaining
    if i == len(arr):
        return total

    # case 1: exclude the current element and process the
    # remaining elements
    excl = maximumSubsequence(arr, i + 1, prev, total)

    # case 2: include the current element if it is greater
    # than the previous element
    incl = total
    if arr[i] > prev:
        incl = maximumSubsequence(arr, i + 1, arr[i], total + arr[i])

    # return the maximum of the above two choices
    return max(incl, excl)


if __name__ == '__main__':

    arr = [1, 8, 3, 12, 2, 10, 4, 14, 2, 6, 6, 13, 2, 10]
    print(maximumSubsequence(arr))

Output

35

Time Complexity

The time complexity is O(nlogn). Since we are going exponentially(not constant) not linearly (constant change) i.e in each iteration there are two cases to find maximum sum increasing subsequence, where n is the size of the given array.

Space Complexity

The space complexity is O(n). Since recursion takes more space in the call stack to find maximum sum increasing subsequence.

Algorithm 2 – Optimal Approach using DP and algo-2

Intuition

The previous approach can be optimized by doing some slight changes in the Dynamic Programming approach to the Longest Increasing Subsequence problem. i.e replace the sum in place of the length of increasing subsequence.

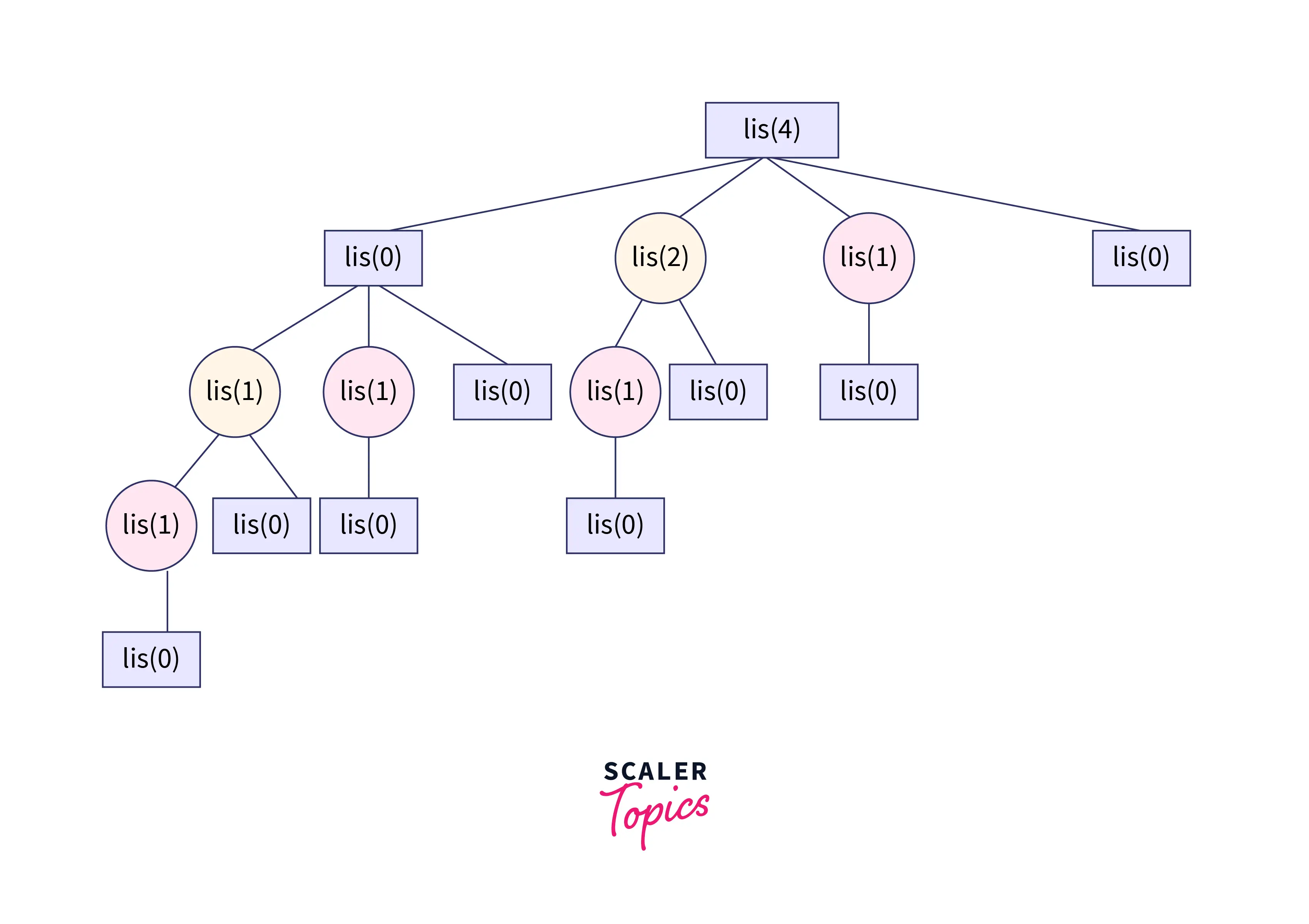
We can also solve the problem in a bottom-up approach. If we draw the recursion tree for the above approach then we can easily see that there are some overlapping subproblems in the picture below, where substructure properties can be used easily.

In the bottom-up manner, we first solve the smaller subproblems and then solve the larger subproblems from them.

Algorithm

1. arr[2] > arr[1] {MSIS[2] = max(MSIS [2], MSIS[1]+1 = 2}
2. arr[3] < arr[1] {No change}
3. arr[3] < arr[2] {No change}
4. arr[4] > arr[1] {MSIS[4] = max(MSIS [4], MSIS[1]+1 = 2}
5. arr[4] > arr[2] {MSIS[4] = max(MSIS [4], MSIS[2]+1 = 3}
6. arr[4] > arr[3] {MSIS[4] = max(MSIS [4], MSIS[3]+1 = 3}

Code Implementation

Code in C++

// Efficient Approach to find maximum sum increasing subsequence Using DP
#include <bits/stdc++.h>
using namespace std;

// function
int maximumSubsequence(int arr[], int n){
    int i, j, max = 0;
    int maximumSubsequence[n];

    // Initialize maximumSubsequence values for all indexes
    for ( i = 0; i < n; i++ )
        maximumSubsequence[i] = arr[i];

    // bottom up manner
    for ( i = 1; i < n; i++ )
            for ( j = 0; j < i; j++ )
                if (arr[i] > arr[j] &&
                    maximumSubsequence[i] < maximumSubsequence[j] + arr[i])
                    maximumSubsequence[i] = maximumSubsequence[j] + arr[i];

    // Find maximum of all 
    for ( i = 0; i < n; i++ )
        if ( max < maximumSubsequence[i] )
            max = maximumSubsequence[i];

    return max;
}

// Main method
int main(){
    int arr[] = { 1, 8, 3, 12, 2, 10, 4, 14, 2, 6, 6, 13, 2, 10 };
    int n = sizeof(arr)/sizeof(arr[0]);
    cout << maximumSubsequence( arr, n ) << endl;
    return 0;
}

Code in Java

// Efficient Approach to find maximum sum increasing subsequence Using DP
class Main{
    // function
    static int maximumSubsequence(int arr[], int n){
        int i, j, max = 0;
        int msis[] = new int[n];

        // Initialize maximumSubsequence values for all indexes
        for (i = 0; i < n; i++)
            msis[i] = arr[i];

        // bottom up manner
        for (i = 1; i < n; i++)
            for (j = 0; j < i; j++)
                if (arr[i] > arr[j] &&
                    msis[i] < msis[j] + arr[i])
                    msis[i] = msis[j] + arr[i];

        // Find maximum of all 
        for (i = 0; i < n; i++)
            if (max < msis[i])
                max = msis[i];

        return max;
    }

    // Main method
    public static void main(String args[]){
        int arr[] = { 1, 8, 3, 12, 2, 10, 4, 14, 2, 6, 6, 13, 2, 10 };
        int n = arr.length;
        System.out.println(maximumSubsequence(arr, n));
    }
}

Code in Python

# Efficient Approach to find maximum sum increasing subsequence Using DP
# function
def maximumSubsequence(arr, n):
    max = 0
    msis = [0 for x in range(n)]

    # Initialize maximumSubsequence values for all indexes
    for i in range(n):
        msis[i] = arr[i]

    # bottom up manner
    for i in range(1, n):
        for j in range(i):
            if (arr[i] > arr[j] and
                msis[i] < msis[j] + arr[i]):
                msis[i] = msis[j] + arr[i]

    # Find maximum of all 
    for i in range(n):
        if max < msis[i]:
            max = msis[i]

    return max

# Driver Code
arr = [1, 8, 3, 12, 2, 10, 4, 14, 2, 6, 6, 13, 2, 10]
n = len(arr)
print(str(maximumSubsequence(arr, n)))

Output

35

Time Complexity

The time complexity is O(n^2^). Since we are using two nested for loops and traversing the array n^2^ times in to find the maximum sum increasing subsequence, where n is the size of the given array.

Space Complexity

The space complexity is O(n). Since we are using an extra array to store MSIS values at each index in the Program to find maximum sum increasing subsequence.

Conclusion

• We have given an array of positive integers of size n is given. write a program to find the maximum sum increasing subsequence in the given array.
• The maximum sum increasing subsequence is a subsequence of an integer array where the sum is maximum and all of the elements are sorted in non-decreasing order.
• For eg, an array {1, 8, 3, 12, 2, 10, 4, 14, 2, 6, 6, 13, 2, 10} is given, here the output should be 1 + 8 + 12 + 14 = 35.
• Since this problem is a variation of the standard Longest Increasing Subsequence problem, hence we can use recursion and DP to solve this problem with a slight change.
• The naive approach takes O(nlogn) time complexity as we are going exponentially not linearly, and O(n) space complexity because of the call stack.
• On the other hand, the efficient approach to Find maximum sum increasing subsequence takes O(n^2^) time complexity and O(n) as a space complexity as we are using an extra array.

FAQ

Q.Why dynaminc programming is the efficient approach?

A. DP is the most efficient approach for maximum sum increasing subsequence because Dynamic programming solves the problem with optimal substructure and overlapping subproblems as DP memorizes subproblem solutions rather than repeatedly computing them.

Q.What is the bottom-up approach?

A. In the bottom-up manner, we first solve the smaller subproblems and then solve the larger subproblems from them.

Q.What are some similar coding questions on Dynamic programming?

A. Refer Longest Increasing Subsequence problem
Refer Coin Change Problem
Refer Climbing Stairs Problem