Merge K Sorted Linked Lists

How to merge K-sorted linked lists

Given K sorted linked lists, merge them in a sorted manner and return the head of the linked list.

• Example 1:

Input: k = 4 
list1 = 1->2->5->null
list2 = 0->7->null
list3 = 4->6->null
list4 = 2->8->11->null

• Output:

0->1->2->2->4->5->6->7->8->11->null

• Example 2:

Input: k = 4
list1 = 1->7->null
list2 = 4->8->null
list3 = 9->14->null
list4 = 1->2->3->17->null

• Output:

1->1->2->3->4->7->8->9->14->17->null

Explanation:

All elements from the sorted lists are merged in a sorted manner and the head of the sorted list is returned.

Constraints :

• k == lists.length
• 0 <= k <= 10^4^
• 0 <= lists[i].length <= 500
• -10^4^ <= lists[i][j] <= 10^4^
• lists[i] is sorted in ascending order.
• The sum of lists[i].length will not exceed 10^4^.

Approach 1(Simple):

• Approach: A straightforward solution is to merge two lists at a time. Merge the 1^st^ list with the 2^nd^ and store the result. While merging we select the smallest of both elements at each step. Next, merge the result with the 3^rd^ list and so on. This can be better explained using the below notation:

KaTeX parse error: $ within math mode

• Implemenation:

Python implementation for merging k sorted linked lists:

# Python3 program to Merge k sorted linked lists
# A linked list Node
class Node:
    #class constructor
    def __init__(self,data):
        self.val = data
        self.next = None
 
# Function to print nodes of the given linked list.
def print_List(Head_1):
    while (Head_1!= None):
        print(Head_1.val, end = " ")
        Head_1= Head_1.next
 
# The function which takes array of lists and returns the sorted merged output
def Merge_K_Lists(Array, Last):
    # Array: array of linkedlists
    # We need to traverse from second  list to last list
    for i in range(1, Last + 1):# To include the last list we have to put last+1
        while (True):
            # merging the first list with second list and storing the result in the first list
            #so every time head_0 is First list which has merged sorted data till i^th list
            Head0 = Array[0]
            Headi = Array[i]
 
            # Base Case
            if (Headi == None):
                break
 
            # Comparing the values of elements present in the nodes 
            if (Head0.val >= Headi.val):
            # if the smaller value is present in the ith list, then we update the first list
                Array[i] = Headi.next
                Headi.next = Head0
                Array[0] = Headi
            else:
                # Traverse the first list till you encounter the greater element in the head_i list
                while (Head0.next != None):
                    # Smaller than next element
                    if (Head0.next.val >=
                        Headi.val):
                        Array[i] = Headi.next
                        Headi.next = Head0.next
                        Head0.next = Headi
                        break
                    # go to next node
                    Head0 = Head0.next
                    # if it is the last node
                    if (Head0.next == None):
                        Array[i] = Headi.next
                        Headi.next = None
                        Head0.next = Headi
                        Head0.next.next = None
                        break
    # returning the head of first list which has the merged data in sorted manner 
    return Array[0]
 
# Driver code
if __name__ == '__main__':
   
    # Number of linked lists taken in the example
    k = 3
    
    # an array of pointers which are storing the head nodes
    # of the linked lists
    
    Array = [0]*k
    # creating k number of linked lists by giving values
    #creating first list with 3 nodes
    Array[0] = Node(1)
    Array[0].next = Node(9)
    Array[0].next.next = Node(15)
    
    #creating second list which has 4 nodes
    Array[1] = Node(12)
    Array[1].next = Node(24)
    Array[1].next.next = Node(66)
    Array[1].next.next.next = Node(78)
     
    #creating the third list which has 4 nodes
    Array[2] = Node(0)
    Array[2].next = Node(9)
    Array[2].next.next = Node(10)
    Array[2].next.next.next = Node(11)
 
    # To merge all k lists call the main function
    result = Merge_K_Lists(Array, k - 1)
    # Print the sorted merged output
    print_List(result)

• Output:

0 1 9 9 10 11 12 15 24 66 78 

Java implementation for merging k-sorted linked lists:

// Java program to merge k sorted linked lists
import java.io.*;
 
// A Linked List node
class Linked_List 
{
  int data;
  Linked_List next;
  // function to create a new node.
  Linked_List(int key)
  {
    data = key;
    next = null;
  }
}
class Solution 
{    
  // linkedlist variables need for traversing and merging
  static Linked_List head;
  static Linked_List temp;
 
  // Function to print nodes of the given linked list
  static void print_Lists(Linked_List Node) 
  {
    while(Node != null)
    {
        // printing each node and updating it with the next node
      System.out.print(Node.data + " ");
      Node = Node.next;
    }
    System.out.println();
  }
 
 //  The function which takes array of lists and returns the sorted merged output
  static Linked_List Merge_K_Lists(Linked_List Array[], int last) 
  {
    // Array: array of linkedlists
    // We need to traverse from second  list to last list
    for (int i = 1; i <= last; i++)
    {
      while(true) 
      {
        // merging the first list with second list and storing the result in the first list
        // so every time head_0 is First list which has merged sorted data till i^th list 
        Linked_List head_0 = Array[0];
        Linked_List head_i = Array[i];
        // Break if list ended
        if (head_i == null)
          break;
 
        //  Comparing the values of elements present in the nodes 
        if(head_0.data >= head_i.data) 
        {
          // if the smaller value is present in the ith list, then we update the first list
          Array[i] = head_i.next;
          head_i.next = head_0;
          Array[0] = head_i;
        }
        else
        {
          // Traverse the first list till you encounter the greater element in the head_i list
          while (head_0.next != null) 
          {
            // Smaller than next element
            if (head_0.next.data >= head_i.data) 
            {
              Array[i] = head_i.next;
              head_i.next = head_0.next;
              head_0.next = head_i;
              break;
            }
            // go to next node
            head_0 = head_0.next;
 
            // if it is the last node
            if (head_0.next == null)
            {
              Array[i] = head_i.next;
              head_i.next = null;
              head_0.next = head_i;
              head_0.next.next = null;
              break;
            }
          }
        }
      }
    }
    // returning the head of first list which has the merged data in sorted manner
    return Array[0];
  }
 
  // Driver program to test
  // above functions 
  public static void main (String[] args) 
  {
    // Number of linked lists for merging
    int k = 3;

    // an array of pointers storing the head of K linked lists
 
    Linked_List[] Array = new Linked_List[k];
    // creating k number of linked lists by giving values
    // creating first list with 3 nodes
    Array[0] = new Linked_List(1);
    Array[0].next = new Linked_List(9);
    Array[0].next.next = new Linked_List(15);
    
    // creating second list which has 4 nodes
    Array[1] = new Linked_List(12);
    Array[1].next = new Linked_List(24);
    Array[1].next.next = new Linked_List(66);
    Array[1].next.next.next = new Linked_List(78);
     
    // creating the third list which has 4 nodes
    Array[2] = new Linked_List(0);
    Array[2].next = new Linked_List(9);
    Array[2].next.next = new Linked_List(10);
    Array[2].next.next.next = new Linked_List(11);
 
    // To merge all k lists call the main function
    head = Merge_K_Lists(Array, k - 1);
    // Print the sorted merged output
    print_Lists(head);
  }
}

• Output:

0 1 9 9 10 11 12 15 24 66 78 

C++ implementation for merging k sorted linked lists:

// C++ program to merge k sorted linked lists
#include <bits/stdc++.h>
using namespace std;
// A Linked List node
struct Node
{
    int data;
    Node* next;
};
 
// Function to print nodes of given linked list
void print_Lists(Node* node) 
{
    while (node != NULL) {
        printf("%d ", node->data);
        node = node->next;
    }
}
// function to create a new node.
Node* new_Node(int data) 
{
    struct Node* temp = new Node;
    temp->data = data;
    temp->next = NULL;
    return temp;
}
 
// Maian function which takes array linked lists and returns sorted output
Node* Merge_K_Lists(Node* arr[], int last) 
{
    // Traverse form second list to last
    for (int i = 1; i <= last; i++) 
    {
        while (true)
        {
            // head of both the lists,
            Node *head_0 = arr[0], *head_i = arr[i];
 
            // Break if list ended
            if (head_i == NULL)
                break;
 
            // Smaller than first element
            if (head_0->data >= head_i->data)
            {
                arr[i] = head_i->next;
                head_i->next = head_0;
                arr[0] = head_i;
            }
            else {
                // Traverse the first list
                while (head_0->next != NULL)
                {
                    // Smaller than next element
                    if (head_0->next->data
                        >= head_i->data) {
                        arr[i] = head_i->next;
                        head_i->next = head_0->next;
                        head_0->next = head_i;
                        break;
                    }
                    // go to next node
                    head_0 = head_0->next;
                }
                    // if last node
                if (head_0->next == NULL) 
                {
                    arr[i] = head_i->next;
                    head_i->next = NULL;
                    head_0->next = head_i;
                    head_0->next->next = NULL;
                    break;
                }
            }
        }
    }
 
    return arr[0];
}
 
// Driver program 
int main() {
    // Number of linked lists
    int k = 3;

    // an array of pointers storing the head of K linked lists
 
    Node* arr[k];
    
    // creating k number of linked lists by giving values
    // creating first list with 3 nodes
    arr[0] = new_Node(1);
    arr[0]->next = new_Node(9);
    arr[0]->next->next = new_Node(15);
    arr[0]->next->next->next = new_Node(68);
    
    // creating second list which has 4 nodes
    arr[1] = new_Node(12);
    arr[1]->next = new_Node(24);
 
    // creating the third list which has 4 nodes
    arr[2] = new_Node(0);
    arr[2]->next = new_Node(9);
    arr[2]->next->next = new_Node(10);
    arr[2]->next->next->next = new_Node(11);
    arr[2]->next->next->next->next = new_Node(78);
 
    // To merge all k lists call the main function
    Node* result = Merge_K_Lists(arr, k - 1);
    // Print the sorted merged output
    print_Lists(result);
 
    return 0;
}

• Output:

0 1 9 9 10 11 12 15 24 68 78

• Explanation :
  Merged lists in a sorted order where every element is greater than the previous element.

Complexity Analysis:

• Time Complexity : O(N*k) where N is the number of elements to be merged. (total number of elements from all k lists given)
  • Traversing every list for merging it with previously merged list and also every node is traversed for atleast once. So to sum up the time complexity would be N times the number of lists given.
• Space Complexity : O(1) No extra space needed (as inplace merging is done)

Approach 2(Using merge sort)

• Approach:

1. Traverse all the linked lists and collect the values of the nodes into an array.
2. Sort and iterate over this array to get the proper value of nodes in a sorted manner.
3. Create a new sorted linked list and extend it with the new nodes.

For example:

Input: k = 3
list1 = 1->4->6->9
list2 = 2->5
list3 = 4->7

Now collect all the values of all nodes into array :

arr=[1,4,6,9,2,5,4,7]

Apply merge sort over the array arr , which takes about O(N logN).

arr=[1,2,4,4,5,6,7,9]

Create a new linked list and extend it with new nodes from the sorted array arr and return the head of the merge sorted linkedlist.

Output:

1->2->4->4->5->6->7->9->null

• Implementation: Below is the implementation of above approach

Python implementation for merging k sorted linked lists using merge sort:

# Python3 program to merge k sorted linked lists.
# A Linked List node
class Node:
    def __init__(self, x=None):
        self.data = x
        self.next = None
 
# Function to print nodes in a given linked list
def printLists(node):
    while(node):
        print(node.data,end = " ")
        node = node.next
 

# The main function that takes an array of lists
# arr[0..last] and generates
# the sorted output 
def MergeKLists(lists):
    if len(lists) == 0:
        return None
        
    curr = lists[0]
        
    for i in range(1, len(lists)):
        curr = mergeTwoList(curr, lists[i])
    return curr


# A sub function used for merging two linkedlists in sorted manner.
def mergeTwoList(head1, head2):
#Creating a dummy node as the head of the linkedlist. 
    dummy = Node()
    curr = dummy
        
    while head1 and head2:
        if head1.data >= head2.data:
            curr.next = head2
            head2 = head2.next
        else:
            curr.next = head1
            head1 = head1.next
        curr = curr.next
            
    if head1:
        curr.next = head1
    else:
        curr.next = head2
    return dummy.next

# Driver code
if __name__ == '__main__':
   
    # Number of linked lists to be merged 
    k = 3
    arr = [None for i in range(k)]
    # Elements of first Linkedlist
    arr[0] = Node(1)
    arr[0].next = Node(3)
    arr[0].next.next = Node(5)
    # Elements of second Linkedlist
    arr[1] = Node(2)
    arr[1].next = Node(4)
    # Elements os third Linkedlist
    arr[2] = Node(0)
    arr[2].next = Node(9)
    arr[2].next.next = Node(11)
 
    # Merge all lists and return head of list to result
    result = MergeKLists(arr)
    # printing the list 
    printLists(result)

• Output

 0 1 2 3 4 5 9 11

Complexity Analysis

• Time complexity : O(N log N) where N is the total number of nodes.
  • Collecting all the values costs O(N) time.
  • A stable sorting algorithm costs O(Nlog N time.
  • Iterating for creating the linked list costs O(N) time.
• Space complexity : O(N)
  • Sorting cost O(N) space (depends on the algorithm you choose).
  • Creating a new linked list costs O(N) space.

Also, this approach does not take advantage of the fact that each list is already in a sorted manner.

Approach 3(Using min-heap):

Min Heap : A Min-Heap is a complete binary tree in which each internal node’s value is less than or equal to the values of the node’s children. Heaps can be represented using arrays. When stored as array they follow the below property:

1. if a node is saved at index k, its left child is stored at index 2k + 1.
2. the right child is stored at index 2k + 2.

• Approach:
  • The idea is to construct a min-heap of size k and insert each list’s first node into it.
  • Then pop the root node (having minimum value) from the heap add it to the output list and insert the next node from the sam list as the popped node.
  • We repeat this process until the min-heap is exhausted.
  • We return the head of sorted merged output.
• Algorithm :

1. Create a min-heap and insert the first element of all the ‘k’ linked lists (Min-heap size is always less than or equal to k).
2. As long as the min-heap is not empty, perform the following steps:
   • Remove the top element of the min-heap (which is the current minimum among all the elements in the min-heap) and add it to the result list.
   • If there exists an element (in the same linked list) next to the element that popped out in the previous step, insert it into the min-heap.
3. Return the head node (result list) of the merged list.

• Implementation: Below is the implementation of above approach:

Python implementation for merging k sorted linked lists using min-heap:

In python implementation we have heap as heapq, where all heap pop, heapify, and heap push all methods are available in the heapq package.

#importing the packages required for heaps
import heapq
from heapq import heappop, heappush

# A Linked List Node
class Node:
    def __init__(self, val, next=None):
        self.val = val
        self.next = next
 
    # min heap condition with nodes(to get min node from the given two nodes)
    def __lt__(self, node):
        return self.val < node.val
 
 
# function to print node data of a linked list
def print_List(Head_1):
    # traverse till the end of linked list
    while Head_1:
        print(Head_1.val,end=" ")
        # moving towards the next node
        Head_1 = Head_1.next
# The function which is used to merge given K sorted linked lists using min-heap.
# this function takes lists which is list of k list and 
#return the head of sorted merged output
def Merge_K_Lists(Lists):
 
    # create a min-heap using the first node of each list
    # therefore the size of min-heap is always k
    Min_Heap = [i for i in Lists]
    # heapify the Min_heap using the heapify method
    heapq.heapify(Min_Heap)
 
    # We need to take two pointers, head & tail in which head
    # points to first node of the sorted merged output and 
    # second pointer points to the last node of the output list
    head = tail = None
 
    # run till min-heap exhausts
    while Min_Heap:
 
        # extract the minimum node from the min-heap 
        # using the heappop function
        minimum = heappop(Min_Heap)
 
        # add the minimum node obtained to the output list
        if head is None:
            #both head and tail are pointing to same list
            head = minimum
            tail = minimum
        else:
            #updating the output list by adding the minimum node
            tail.next = minimum
            tail = minimum
 
        if minimum.next:
            # adding the next node in min-heap which is taken from the same list
            heappush(Min_Heap, minimum.next)
 
    # return head node of the merged list which is sorted
    return head
 
 
if __name__ == '__main__':
 
    # an array of pointers which are storing the head nodes
    # of the linked lists
    k=3
    
    Array = [0]*k
    # creating k number of linked lists by giving values
    #creating first list with 3 nodes
    Array[0] = Node(1)
    Array[0].next = Node(9)
    Array[0].next.next = Node(15)
    
    #creating second list which has 4 nodes
    Array[1] = Node(12)
    Array[1].next = Node(24)
    Array[1].next.next = Node(66)
    Array[1].next.next.next = Node(78)
     
    #creating the third list which has 3 nodes
    Array[2] = Node(0)
    Array[2].next = Node(9)
    Array[2].next.next = Node(10)
    Array[2].next.next.next = Node(11)
 
    
    # Merge all k lists using the main function
    head = Merge_K_Lists(Array)
    # Print the sorted merged output
    print_List(head)

• Output

0 1 9 9 10 11 12 15 24 66 78 

Java implementation for merging k sorted linked lists using min-heap :

// java program for merging K sorted linked lists using min-heap
import java.io.*;
import java.util.*;
// A Linked List Node
class Linked_List
{
    int data;
    Linked_List next;
 
    Linked_List(int key) 
    {
        data = key;
        next = null;
    }
}
// Class implements Comparator to compare Linked_List data
class NodeComparator implements Comparator<Linked_List> 
{
    public int compare(Linked_List k1, Linked_List k2) 
    {
        if (k1.data > k2.data)
            return 1;
        else if (k1.data < k2.data)
            return -1;
        return 0;
    }
}
class Solution 
{
    // Function to merge k sorted linked lists
    static Linked_List merge_K_List(Linked_List[] arr, int K) 
    {
        // Priority queue Queue implemented as min heap using compare function
        PriorityQueue<Linked_List> Queue
            = new PriorityQueue<>(new NodeComparator());
        Linked_List at[] = new Linked_List[K];
        Linked_List head = new Linked_List(0);
        Linked_List last = head;
        
        // Push the head nodes of all linked lists into the queue
        for (int i = 0; i < K; i++)
        {
            if (arr[i] != null)
            {
             Queue.add(arr[i]);
            }
        }

        if (Queue.isEmpty())
            return null;
        // Loop till size of queue is not zero
        while (!Queue.isEmpty()) 
        {
            // Extract the minimum element
            Linked_List curr = Queue.poll();
 
            // Add the top element of 'queue'
            // to the resultant merged list
            last.next = curr;
            last = last.next;
            // Check if there is a node next to in the same list as top node
            if (curr.next != null) {
                // Push the next node of top node in queue
                Queue.add(curr.next);
            }
        }
    
        // head of the merged linked list is returned
        return head.next;
    }
    static void print_Lists(Linked_List Node) 
  {
    while(Node != null)
    {
        // printing each node and updating it with the next node
      System.out.print(Node.data + " ");
      Node = Node.next;
    }
    System.out.println();
  }
 
    public static void main(String[] args)
    {
        // Number of linked lists for merging
    int k = 3;

    // an array of pointers storing the head of K linked lists
 
    Linked_List[] Array = new Linked_List[k];
      
    // creating k number of linked lists by giving values
    // creating first list with 3 nodes
    Array[0] = new Linked_List(1);
    Array[0].next = new Linked_List(9);
    Array[0].next.next = new Linked_List(15);
    
    // creating second list which has 4 nodes
    Array[1] = new Linked_List(12);
    Array[1].next = new Linked_List(24);
    Array[1].next.next = new Linked_List(66);
    Array[1].next.next.next = new Linked_List(78);
     
    // creating the third list which has 4 nodes
    Array[2] = new Linked_List(0);
    Array[2].next = new Linked_List(9);
    Array[2].next.next = new Linked_List(10);
    Array[2].next.next.next = new Linked_List(11);
 
    // To merge all k lists call the main function
    Linked_List head = merge_K_List(Array, k );
    // Print the sorted merged output
    print_Lists(head);
  }
}

• Output

0 1 9 9 10 11 12 15 24 66 78  

C++ implementation for merging k sorted linked lists using min-heap:

// C++ implementation of merging K sorted linked lists
#include <bits/stdc++.h>
using namespace std;
// A linked list Node
struct Linked_List
{
    int data;
    struct Linked_List* next;
};
 
// function to create a new node
struct Linked_List* new_Node(int data) 
{
    // Allocate node from the given data
    struct Linked_List* newnode = new Linked_List();

    newnode->data = data;
    newnode->next = NULL;
    // return the formed new node
    return newnode;
}
 
// compare function used for building the priority queue
struct compare
{
    bool operator()(struct Linked_List* a1, struct Linked_List* b1)
    {
        return a1->data > b1->data;
    }
};
 
// Function to merge k sorted linked lists
struct Linked_List* Merge_K_Lists(struct Linked_List* arr[], int k) 
{
    /// Priority_queue 'queue' implemented as min heap using compare function
    priority_queue<Linked_List*, vector<Linked_List*>, compare> Queue;
 
    // Push the head nodes of all
    // the k lists in 'pq'
    for (int i = 0; i < k; i++)
    {
        if (arr[i] != NULL)
            Queue.push(arr[i]);
     }
      // Push the head nodes of all linked lists into the queue
      if (Queue.empty())
        return NULL;
   
      struct Linked_List *dummy = new_Node(0);
      struct Linked_List *last = dummy;
   
   // Loop till size of queue is not zero
    while (!Queue.empty())
    {
        // Extract the minimum element
        struct Linked_List* curr = Queue.top();
        Queue.pop();
 
        // Add the top element of queue to the resultant merged list
        last->next = curr;
        last = last->next; 
       
        // Check if there is a node next to in the same list as top node
        if (curr->next != NULL)
             
        // Push the next node of top node in queue
        Queue.push(curr->next);
    }
 
    // return the head of resultant list which is starting from dummy->next
    return dummy->next;
}
 
// Function to print the linked list
void print_Lists(struct Linked_List* node)
{
    while (node!= NULL) {
        cout << node->data << " ";
        node = node->next;
    }
}
 
// Driver code
int main()
{
    // Number of linked lists for merging
    int k = 3;
    
    // an array of pointers storing the head of K linked lists
    Linked_List* Array[k];
    // creating k number of linked lists by giving values
    // creating first list with 3 nodes
    Array[0] = new_Node(1);
    Array[0]->next = new_Node(9);
    Array[0]->next->next = new_Node(15);
    
    // creating second list which has 4 nodes
    Array[1] = new_Node(12);
    Array[1]->next = new_Node(24);
    Array[1]->next->next = new_Node(66);
    Array[1]->next->next->next = new_Node(78);
     
    // creating the third list which has 4 nodes
    Array[2] = new_Node(0);
    Array[2]->next = new_Node(9);
    Array[2]->next->next = new_Node(10);
    Array[2]->next->next->next = new_Node(11);
 
    // To merge all k lists call the main function
    Linked_List* result = Merge_K_Lists(Array, k );
    // Print the sorted merged output
    print_Lists(result);
 
    return 0;
}

• Output

0 1 9 9 10 11 12 15 24 66 78 

• Explanation: All elements from the sorted lists are merged in a sorted manner and the head of the sorted list is returned. Merged lists in a sorted order where every element is greater than the previous element.

Complexity Analysis:

• Time Complexity:O(N * log k) , where, ‘N’ is the total number of elements among all the linked lists, ‘k’ is the total number of lists given for merging.
  • Insertion and deletion operation will be performed in min-heap for all N nodes from all lists.
  • Insertion and deletion in a min-heap/priority queue require log ktime(this is the main advantage of why we use min-heap) where k is the length of min-heap
• Space Complexity:O(k)
  • The priority queue/min-heap will have at most ‘k’ number of elements at any point of time, hence the additional space required for our algorithm is O(k).

Approach 5: (Divide and Conquer)

This approach doesn’t require extra space for heap and works in O(n log k).This approach is the modification of the previous approach to reduce the space complexity and make it more efficient for merging the given k sorted linked lists.

• Approach: First step includes the divide step
  • Divide step:
    • Send all k/2 lists to merge function at a time
  Second step includes the merge step
  • Merge step: To consider smaller values and add them to create a new list/ can be done by manipulating the list itself.
    • Create a pointer to return the combined list
    • Add the smaller value by comparing the both lists.
    • Increment pointer of the list from which value has been taken to add it to the result list.
    • Return merged and sorted linked list from taken two lists.
  • For all levels there are N number of nodes present

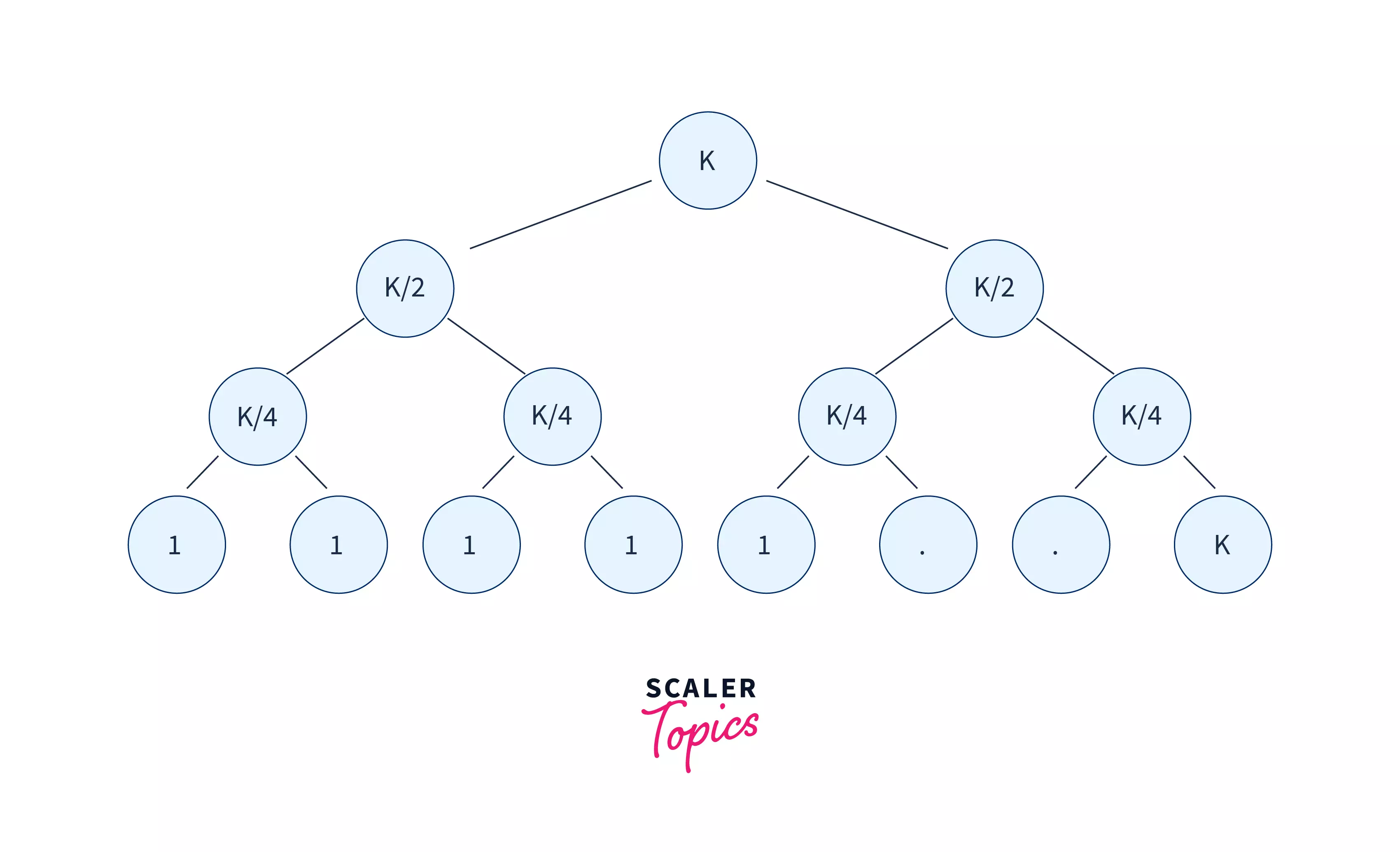
To merge the k linked lists here, we need to know how to merge two sorted linked lists.

• Algorithm:
  1. Pair up k lists and merge each pair.
  2. After the first pairing, k lists are merged into k/2 lists with an average 2N/k length, then k/4, k/8, and so on.
  3. Repeat this procedure until we get the final sorted linked list.
  We don’t need to traverse most nodes many times repeatedly. Thus, we’ll traverse almost N nodes per pairing and merging, and repeat this procedure about log2klog2​k times.
• Implementation: Below is the implementation of this approach.

Python implementation for merging k sorted linked lists using divide and conquer technique:

# Python program to merge k sorted linked lists using divide and conquer technique 
# A linked list node
class Node:
    def __init__(self):
        self.data = 0
        self.next = None
 
# Function to print nodes of given linked list
def print_Lists(head):
 
    while (head != None):
        # printing each node and updating it with the next node
        print(head.data, end = ' ')
        head = head.next
# Take only two lists in sorted manner and merge them in sorted manner

def SortedMerge(a, b):
    result = None
  
    # Base cases
    if (a == None):
        return(b)
    elif (b == None):
        return(a)
  
    # Choose based on the value
    if (a.data <= b.data):
        result = a
        result.next = SortedMerge(a.next, b)
    else:
        result = b
        result.next = SortedMerge(a, b.next)
    # return the result of the head of sorted merged output
    return result

# function to create a new node.
def new_Node(data):
    temp = Node()
    temp.data = data
    temp.next = None
    return temp
 
# Main function which given merged sorted output of all K linked lists
def merge_K_Lists(arr, last):
 
    # Do this until only one list is left
    while (last != 0):
        i = 0
        j = last
  
        # (i, j) forms a pair
        while (i < j):
             
            # merge list i with List j and store result in i
            arr[i] = SortedMerge(arr[i], arr[j])
  
            # Consider next pair
            i += 1
            j -= 1
             
            # If all pairs are merged, update last
            if (i >= j):
                last = j
    # head of the merged linked list is returned
    return arr[0]
 
# Driver code
if __name__=='__main__':
     
    # Number of sorted linked lists
    k = 3
    
    # an array of pointers storing the head of K linked lists
    Arr = [0]*k
    # creating k number of linked lists by giving values
    # creating first list with 3 nodes
    Arr[0] = new_Node(1)
    Arr[0].next = new_Node(10)
    Arr[0].next.next = new_Node(15)
    
    # creating second list which has 4 nodes
    Arr[1] = new_Node(2)
    Arr[1].next = new_Node(4)
    Arr[1].next.next = new_Node(6)
    Arr[1].next.next.next = new_Node(8)
    
    # creating the third list which has 2 nodes
    Arr[2] = new_Node(0)
    Arr[2].next = new_Node(9)
  
    # To merge all k lists call the main function
    head = merge_K_Lists(Arr, k - 1)
    # Print the sorted merged output
    print_Lists(head)

• Output:

0 1 2 4 6 8 9 10 15

Java implementation for merging k sorted linked lists using divide and conquer technique:

// Java program to merge k sorted Linked lists using divide and conquer technique
// A linked list node
class Node
{
    int data;
    Node next;
    Node(int data) 
    {
        this.data = data;
    }
}
public class MergeKSortedLists 
{
    // Take only two lists in sorted manner and merge them in sorted manner
    public static Node SortedMerge(Node a, Node b)
        // Takes O(log n) extra space needed during recursive calls, can be done inplace merging to avoid that
    {
        Node result = null;
        // Base cases 
        if (a == null)
            return b;
        else if (b == null)
            return a;
 
        // choose the data based on the value
        if (a.data <= b.data) 
        {
            result = a;
            result.next = SortedMerge(a.next, b);
        }
        else
        {
            result = b;
            result.next = SortedMerge(a, b.next);
        }
        // return the result of the head of sorted merged output
        return result;
    }
 
   // Main function which given merged sorted output of all K linked lists
    public static Node mergeKLists(Node arr[], int last)
    {
        // Do this until only one list is left
        while (last != 0)
        {
            int i = 0, j = last;
 
            while (i < j) 
            {
                // merge list i with List j and store result in i
                arr[i] = SortedMerge(arr[i], arr[j]);
 
                // consider next pair
                i++;
                j--;
 
                // If all pairs are merged, update last
                if (i >= j)
                    last = j;
            }
        }
        // head of the merged linked list is returned
        return arr[0];
    }
    // Function to print nodes in a given linked list 
    public static void print_Lists(Node node) 
    {
        // printing each node and updating it with the next node
        while (node != null) 
        {   
            System.out.print(node.data + " ");
            node = node.next;
        }
    }
 
    public static void main(String args[]) 
    {
        // Number of linked lists for merging
        int k = 3;
 
         // an array of pointers storing the head of K linked lists
        Node Arr[] = new Node[k];
        // creating k number of linked lists by giving values
        // creating first list with 3 nodes
        Arr[0] = new Node(1);
        Arr[0].next = new Node(10);
        Arr[0].next.next = new Node(15);
        
        // creating second list which has 4 nodes
        Arr[1] = new Node(4);
        Arr[1].next = new Node(7);
        Arr[1].next.next = new Node(16);
        Arr[1].next.next.next = new Node(18);
        
        // creating the third list which has 2 nodes
        Arr[2] = new Node(10);
        Arr[2].next = new Node(29);
 
        // To merge all k lists call the main function
        Node result = mergeKLists(Arr, k - 1);
        // Print the sorted merged output
        print_Lists(result);
    }
}

• Output:

1 4 7 10 10 15 16 18 29 

C++ implementation for merging k sorted linked lists using divide and conquer technique:

// C++ program to merge k sorted linked lists using divide and conquer technique
#include <bits/stdc++.h>
using namespace std;
 
// A Linked List node
struct Node 
{
    int data;
    Node* next;
};
 
// Function to print nodes in a given linked list 
void print_Lists(Node* node)
{
    while (node != NULL) 
    {
        // printing each node and updating it with the next node
        printf("%d ", node->data);
        node = node->next;
    }
}
 // Take only two lists in sorted manner and merge them in sorted manner
Node* SortedMerge(Node* a, Node* b) 
{
    Node* result = NULL;
    // Base case
    if (a == NULL)
        return (b);
    else if (b == NULL)
        return (a);
 
     // choose the data based on the value
    if (a->data <= b->data) 
    {
        result = a;
        result->next = SortedMerge(a->next, b);
    }
    else
    {
        result = b;
        result->next = SortedMerge(a, b->next);
    }
    // return the result of the head of sorted merged output
    return result;
}
 
// Main function which given merged sorted output of all K linked lists
Node* merge_K_Lists(Node* arr[], int last)
{
    // Do this until only one list is left
    while (last != 0) {
        int i = 0, j = last;
 
        // (i, j) forms a pair
        while (i < j) 
        {
            // merge list i with List j and store result in i
            arr[i] = SortedMerge(arr[i], arr[j]);
 
            // consider next pair
            i++, j--;
 
            // If all pairs are merged, update last
            if (i >= j)
                last = j;
        }
    }
    // head of the merged linked list is returned
    return arr[0];
}
 
// function to create a new node.
Node* new_Node(int data) 
{
    struct Node* temp = new Node;
    temp->data = data;
    temp->next = NULL;
    return temp;
}
 
// Driver program to test above functions
int main() 
{
    // Number of sorted linked lists for merging
    int k = 3; 
    // an array of pointers storing the head of K linked lists
    Node* Arr[k];
    // creating k number of linked lists by giving values
    // creating first list with 3 nodes
    Arr[0] = new_Node(1);
    Arr[0]->next = new_Node(10);
    Arr[0]->next->next = new_Node(15);
        
    // creating second list which has 4 nodes
    Arr[1] = new_Node(4);
    Arr[1]->next = new_Node(7);
    Arr[1]->next->next = new_Node(16);
    Arr[1]->next->next->next = new_Node(18);
    
    // creating the third list which has 2 nodes
    Arr[2] = new_Node(10);
    Arr[2]->next = new_Node(29);
 
    // To merge all k lists call the main function
    Node* result = merge_K_Lists(Arr, k - 1);
    // Print the sorted merged output
    print_Lists(result);
 
    return 0;
}

• Output:

1 4 7 10 10 15 16 18 29 

• Explanation: All elements from the sorted lists are merged in a sorted manner and the head of the sorted list is returned. Merged lists in a sorted order where every element is greater than the previous element.

Complexity Analysis:

• Time Complexity: O(Nlogk) where k is the number of linked lists and “N” is the total number of elements among all the linked lists.
  • We can merge two sorted linked list in O(N) time where N is the total number of nodes in two lists.

• Sum up the merge process and we can get: $$ O\big(\sum_{i=1}^{log_{2}{k}}N \big)=O(Nlogk) $$
  (As outer while loop in function mergeKLists() runs log k times and every time it processes n*k elements.)
• Space Complexity: O(1)
  • Auxiliary space is needed to merge the final 2 linked lists of size N/2.
  • We can merge two sorted linked lists in O(1) space by appling in-place merging technique( we can manipulate the pointers itself)

Conclusion:

• We have discussed various approaches to merge K sorted linked lists in a sorted manner.
• The first approach includes merging two lists at a time and the resultant list is merged with the next list and so on, this takes a time complexity of O(N*K) and space complexity of O(1)(in-place merging is done).
• The second approach uses merge sort where all the elements are added in the array and merge sort is applied on it then a new linked list is formed this approach takes a time complexity of O(N logN) and a space complexity of O(N) which is used during merging and for creating new linked list.
• The third approach uses min-heap where the first element from all the k lists is inserted into the min-heap and the root is popped out, now the next element of the list is inserted, and so on till the size of the min-heap becomes zero, the time complexity O(N logK) and the size of min-heap is always K, so space complexity is O(K).
• Final approach uses the divide and conquer technique, in which k-lists are divided into pairs and merged, now the resultant merged list is merged with the another merged list, and so on. This is considered to be more efficient than other approaches with the time complexity O(N logN) and the space complexity O(N), it can also be done in O(1) by manipulating the pointers(in-place).
• Every approach discussed here can be done using in-place merging i.e, by manipulating the existing links, or else a new list can be created which takes an extra space of O(N) where N is the total numbers to be merged from all linked lists.