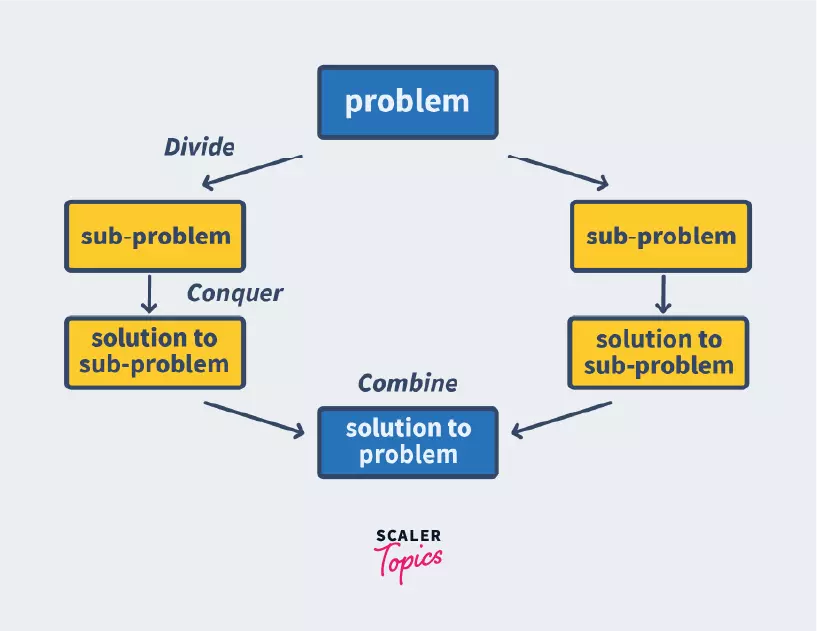
Merge Sort algorithm is a Divide and Conquer algorithm. It divides the input array into two halves, calls itself for the two halves, and then merges the two sorted halves.
Merge Sort algorithm is one of the most respected sorting algorithms, with a worst-case time complexity of O(nlogn).
Merge sort works by dividing the array repeatedly to make several single-element arrays.
The concept of merge sort involves breaking down an array of n elements into n individual elements. Why?
As each element can be considered as a sorted array consisting of one element. Then we start to combine these individual single array elements into one final sorted array.
How Does the Merge Sort Algorithm Work?
Divide and Conquer Strategy
Now that we have a fair understanding of what divide and conquer is, let us try and understand how that is done to sort an array of integers.
Let us consider an array, array that consists of n unsorted integers. Our end goal is to sort the array.
Let us consider an array={38,27,43,3,9,82,10}.

1.Divide In this step, we find the midpoint of the given array by using the formula mid=start+(end-start)/2
2. Conquer In this step, we divide the array into subarrays using the midpoint calculated. We recursively keep dividing the array and keep calculating the midpoint for doing the same. It is important to note that a single array element is always sorted.
So, our aim is to continuously divide until all elements in the array are single array elements. Once that is done, the array elements are combined back to form a sorted array.
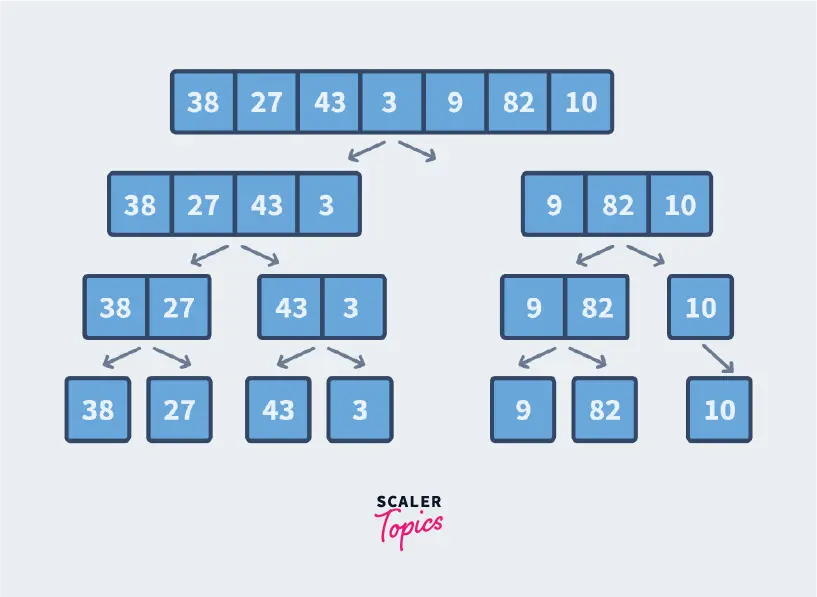
As mentioned above, our goal is to keep dividing till all elements in the array are single array elements hence, this is the base case i.e. when there are n subarrays of the original array that consisted of n integers. It is now the turn is to sort them and combine them.
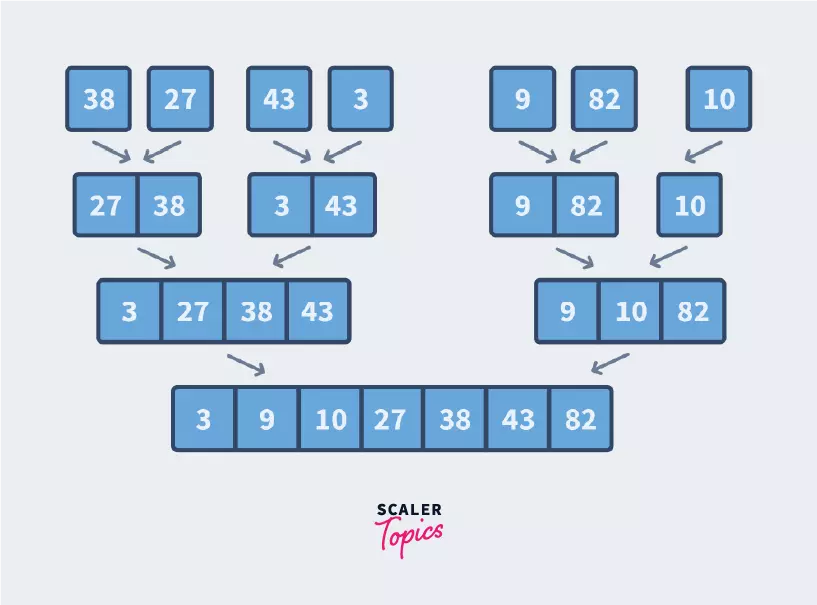
3. Combine
Now that all our subarrays are formed, it is now time to combine them in sorted order.
Implementation of Merge Sort Algorithm
Since we start combining when we have subarrays of length 1, when we get 2 subarrays to combine, they will be sorted amongst each other.
It is our job to sort these and put them together in the final sorted array. We accomplish this by having 3 pointers/references.
- At the beginning of the first subarray
- At the beginning of the second subarray
- At the sorted array
Until we reach the end of either of the subarrays, we keep checking which element is smaller and putting that in the array.
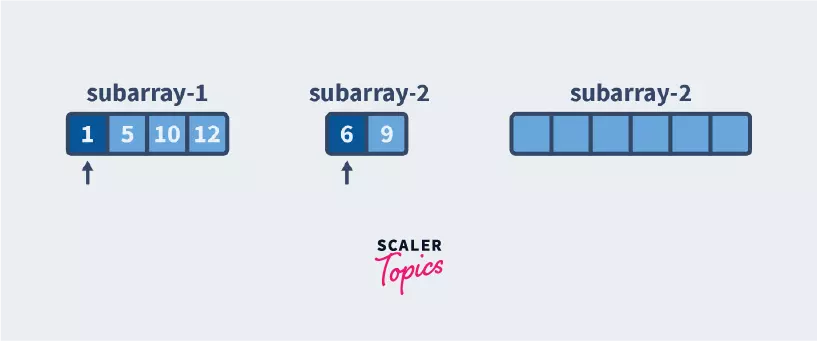
Here 1 is smaller, so we push that to the sorted array and then move the pointer of the subarray that contains 1 as the next number after 1 might be smaller or larger than 6 but the number after 6 is definitely larger than 1. We continue as follows:
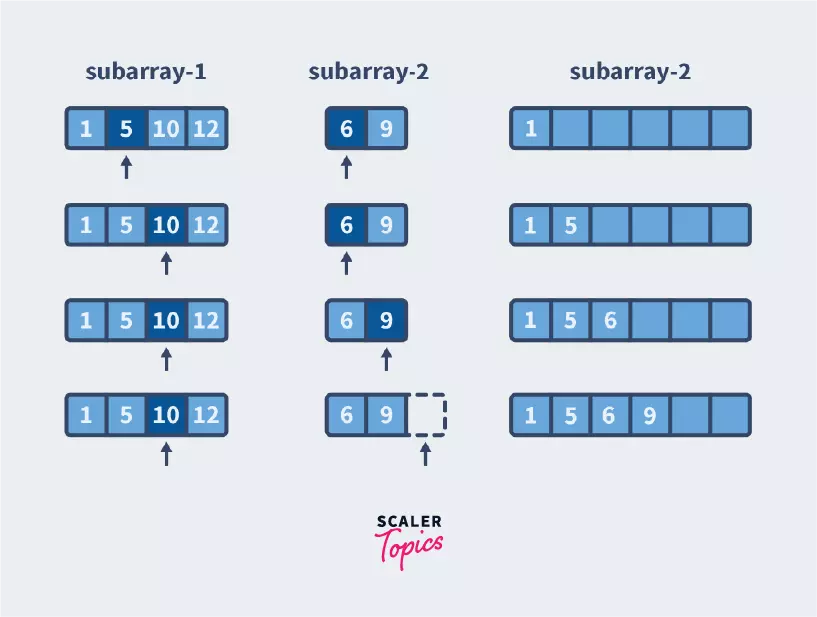
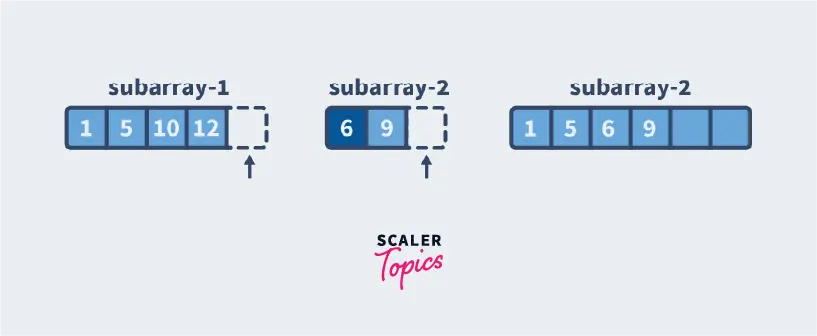
Now we see that we have reached the end of the second subarray. This means that the remaining numbers in the first sub-array are definitely larger and since they are sorted, we insert them in the final sorted array as-is.
1. Merge Sort Code in Java
public class MergeSort {
// Merge two subarrays arr1 and arr2 into sorted
static void merge(int sorted[], int start, toney you have. As in, if you have toney you have. As in, if you have t int mid, int end) {
// Create arr1 ← A[start..mid] and arr2 ← A[mid+1..end]
int m1 = mid - start + 1;
int m2 = end - mid;
int arr1[] = new int[m1];
int arr2[] = new int[m2];
for (int i = 0; i < m1; i++)
arr1[i] = sorted[start + i];
for (int j = 0; j < m2; j++)
arr2[j] = sorted[mid + 1 + j];
// Maintain current index of sub-arrays and main array
int i, j, k;
i = 0;
j = 0;
k = start;
// Until we reach the end of either arr1 or arr2, pick larger among
// elements arr1 and arr2 and place them in the correct position at sorted[start..end]
while (i < m1 && j < m2) {
if (arr1[i] <= arr2[j]) {
sorted[k] = arr1[i];
i++;
} else {
sorted[k] = arr2[j];
j++;
}
k++;
}
// When all elements are traversed in either arr1 or arr2,
// pick up the remaining elements and put in sorted[start..end]
while (i < m1) {
sorted[k] = arr1[i];
i++;
k++;
}
while (j < m2) {
sorted[k] = arr2[j];
j++;
k++;
}
}
// Divide the array into two subarrays, sort them and merge them
static void mergeSort(int sorted[], int start, int end) {
if (start < end) {
// mid is the point where the array is divided into two subarrays
int mid = (start + end) / 2;
mergeSort(sorted, start, mid);
mergeSort(sorted, mid + 1, end);
// Merge the sorted subarrays
merge(sorted, start, mid, end);
}
}
public static void main(String args[]) {
int arr[] = { 6, 5, 12, 10, 9, 1 };
mergeSort(arr, 0, arr.length - 1);
//Print the sorted array
int n = arr.length;
for (int i = 0; i < n; ++i){
System.out.print(arr[i] + " ");
}
System.out.println();
}
}
2. Merge Sort Code in Python
def mergeSort(arr):
if len(arr) > 1:
# Create start ← A[start..mid] and end ← A[mid+1..end]
mid = len(arr)//2
start = arr[:mid]
end = arr[mid:]
# Sort the two halves
mergeSort(start)
mergeSort(end)
i = j = k = 0
# Until we reach the end of either start or end, pick larger among
# elements start and end and place them in the correct position in the sorted array
while i < len(start) and j < len(end):
if start[i] < end[j]:
arr[k] = start[i]
i += 1
else:
arr[k] = end[j]
j += 1
k += 1
# When all elements are traversed in either arr1 or arr2,
# pick up the remaining elements and put in sorted array
while i < len(start):
arr[k] = start[i]
i += 1
k += 1
while j < len(end):
arr[k] = end[j]
j += 1
k += 1
if __name__ == '__main__':
arr = [6, 5, 4, 8, 1, 9]
mergeSort(arr)
for i in range(len(arr)):
print(arr[i], end=" ")
print()
3. Merge Sort Code in C
#include <stdio.h>
// Merge two subarrays arr1 and arr2 into sorted
void merge(int sorted[], int start, int mid, int end) {
// Create arr1 ← A[start..mid] and arr2 ← A[mid+1..end]
int m1 = mid - start + 1;
int m2 = end - mid;
int arr1[m1], arr2[m2];
for (int i = 0; i < m1; i++)
arr1[i] = sorted[start + i];
for (int j = 0; j < m2; j++)
arr2[j] = sorted[mid + 1 + j];
// Maintain current index of sub-arrays and main array
int i, j, k;
i = 0;
j = 0;
k = start;
// Until we reach the end of either arr1 or arr2, pick larger among
// elements arr1 and arr2 and place them in the correct position at sorted[start..end]
while (i < m1 && j < m2) {
if (arr1[i] <= arr2[j]) {
sorted[k] = arr1[i];
i++;
} else {
sorted[k] = arr2[j];
j++;
}
k++;
}
// When all elements are traversed in either arr1 or arr2,
// pick up the remaining elements and put in sorted[start..end]
while (i < m1) {
sorted[k] = arr1[i];
i++;
k++;
}
while (j < m2) {
sorted[k] = arr2[j];
j++;
k++;
}
}
// Divide the array into two subarrays, sort them and merge them
void mergeSort(int arr[], int start, int end) {
if (start < end) {
// mid is the point where the array is divided into two subarrays
int mid = start + (end - start) / 2;
mergeSort(arr, start, mid);
mergeSort(arr, mid + 1, end);
// Merge the sorted subarrays
merge(arr, start, mid, end);
}
}
int main() {
int arr[] = {6, 5, 4, 8, 1, 9};
int size = sizeof(arr) / sizeof(arr[0]);
mergeSort(arr, 0, size - 1);
for (int i = 0; i < size; i++)
printf("%d ", arr[i]);
printf("\n");
}
4. Merge Sort Code in C++
#include <iostream>
using namespace std;
// Merge two subarrays arr1 and arr2 into sorted
void merge(int sorted[], int start, int mid, int end) {
// Create arr1 ← A[start..mid] and arr2 ← A[mid+1..end]
int m1 = mid - start + 1;
int m2 = end - mid;
int arr1[m1], arr2[m2];
for (int i = 0; i < m1; i++)
arr1[i] = sorted[start + i];
for (int j = 0; j < m2; j++)
arr2[j] = sorted[mid + 1 + j];
// Maintain current index of sub-arrays and main array
int i, j, k;
i = 0;
j = 0;
k = start;
// Until we reach the end of either arr1 or arr2, pick larger among
// elements arr1 and arr2 and place them in the correct position at sorted[start..end]
while (i < m1 && j < m2) {
if (arr1[i] <= arr2[j]) {
sorted[k] = arr1[i];
i++;
} else {
sorted[k] = arr2[j];
j++;
}
k++;
}
// When all elements are traversed in either arr1 or arr2,
// pick up the remaining elements and put in sorted[start..end]
while (i < m1) {
sorted[k] = arr1[i];
i++;
k++;
}
while (j < m2) {
sorted[k] = arr2[j];
j++;
k++;
}
}
// Divide the array into two subarrays, sort them and merge them
void mergeSort(int arr[], int start, int end) {
if (start < end) {
// mid is the point where the array is divided into two subarrays
int mid = start + (end - start) / 2;
mergeSort(arr, start, mid);
mergeSort(arr, mid + 1, end);
// Merge the sorted subarrays
merge(arr, start, mid, end);
}
}
int main() {
int arr[] = {6, 5, 4, 8, 1, 9};
int size = sizeof(arr) / sizeof(arr[0]);
mergeSort(arr, 0, size - 1);
//Print the sorted array
for (int i = 0; i < size; i++)
cout << arr[i] << " ";
cout << endl;
return 0;
}
5. Merge Sort Code in JavaScript
<script>
// Merge two subarrays arr1 and arr2 into sorted
function merge(sorted, start, mid, end)
{
var m1 = mid - start + 1;
var m2 = end - mid;
// Create arr1 ← A[start..mid] and arr2 ← A[mid+1..end]
var arr1 = new Array(m1);
var arr2 = new Array(m2);
for (var i = 0; i < m1; i++)
arr1[i] = sorted[start + i];
for (var j = 0; j < m2; j++)
arr2[j] = sorted[mid + 1 + j];
// Maintain current index of sub-arrays and main array
var i = 0;
var j = 0;
var k = start;
// Until we reach the end of either arr1 or arr2, pick larger among
// elements arr1 and arr2 and place them in the correct position at sorted[start..end]
while (i < m1 && j < m2) {
if (arr1[i] <= arr2[j]) {
sorted[k] = arr1[i];
i++;
}
else {
sorted[k] = arr2[j];
j++;
}
k++;
}
// When all elements are traversed in either arr1 or arr2,
// pick up the remaining elements and put them in sorted[start..end]
while (i < m1) {
sorted[k] = arr1[i];
i++;
k++;
}
while (j < m2) {
sorted[k] = arr2[j];
j++;
k++;
}
}
// Divide the array into two subarrays, sort them and merge them
function mergeSort(arr,start, end){
if(start>=end){
return;
}
var mid =start+ parseInt((end-start)/2);
console.log(mergeSort(arr,start,mid));
mergeSort(arr,mid+1,end);
merge(arr,start,mid,end);
}
var arr = [ 12, 11, 13, 5, 6, 7 ];
var n = arr.length;
mergeSort(arr, 0, n - 1);
//Print the sorted array
for (var i = 0; i < n; i++)
document.write(arr[i] + " ");
</script>
Complexity Analysis of Merge Sort Algorithm
Time Complexity of Merge Sort Algorithm
Merge Sort’s time complexity is O(n*Log n) in worst case, average case, and best case, because it always divides the array into two halves and merges the two halves in linear time.
- Worst Case Time Complexity: O(n*log2(n))
- Best Case Time Complexity: O(n*log2(n))
- Average Case Time Complexity: O(n*log2(n))
Space Complexity of Merge Sort Algorithm
The space complexity of the merge sort algorithm is O(n) where ‘n’ is the number of elements in the array being sorted.
Applications of Merge sort Algorithm
- External Merge Sort: Merge sort forms the basis of the external merge sort algorithm, which is commonly used for sorting large datasets that do not fit into main memory. External merge sort divides the data into smaller chunks that can fit into memory, sorts these chunks using merge sort, and then merges the sorted chunks together to produce the final sorted output.
- Network Routing: Merge sort’s divide-and-conquer strategy finds applications in network routing algorithms, where the task involves sorting and merging various routing tables or paths to optimize network traffic flow and minimize congestion.
- File Processing: Merge sort algorithm can be used for sorting large files containing records or data entries. It efficiently handles the sorting process by dividing the file into manageable chunks, sorting them individually, and then merging them back together to produce the sorted output file.
Advantages of Merge Sort
Merge sort offers several advantages:
- Stable Sorting: Merge sort is a stable sorting algorithm, it means that it preserves the relative order of equal elements.
- Predictable Performance: Merge sort has a consistent time complexity of O(n log n) regardless of the input data. This makes it predictable and reliable, especially for large datasets.
- Efficient for Linked Lists: Merge sort performs well with linked lists due to its ability to efficiently merge two sorted lists into one. This makes it a preferred choice for sorting linked lists over other algorithms like quicksort, which relies heavily on random access to elements.
- Parallelizable: Merge sort can be easily parallelized, allowing it to take advantage of multiple processors or cores in a system. This property makes it suitable for implementation in parallel computing environments, where performance can be significantly improved.
- Guaranteed Worst-Case Performance: Unlike quicksort, which can have a worst-case time complexity of O(n^2) for certain input distributions, merge sort always guarantees O(n log n) time complexity, regardless of the input data.
Drawbacks of Merge Sort Algorithm
The drawbacks of Merge Sort are as follows:
- We have seen that we need to store the sorted elements in a separate array of size n, this requires more space thereby increasing the space complexity.
- We have also seen that the pointers traverse through one entire sub-array. Let us consider the case where the subarrays are perfectly sorted.
For example subarray1={1,2,3} and subarray2={4,5,6}. The final sorted array looks like this {1,2,3,4,5,6} which is just subarray2 kept after subarray1 but we still need to traverse the entire array thereby wasting time.
- Merge Sort when considered for smaller arrays can prove to be slower as compared to other algorithms.
Explore Scaler Topics Data Structures Tutorial and enhance your DSA skills with Reading Tracks and Challenges.
Conclusion
- It is a divide and conquers method of sorting.
- Merge sort is a sorting where best, worst and average-case time complexities are the same.
- The algorithm’s worst-case time complexity is O(n*log n), making it suitable for handling large datasets.
- Merge Sort’s space complexity is O(n), as it requires additional space to store temporary arrays during the merge phase.
- Applications of Merge Sort include external sorting, network routing algorithms, and file processing.
- Key advantages of Merge Sort include stable sorting, predictable performance, efficiency with linked lists, parallelizability, and guaranteed worst-case time complexity.
- Despite its advantages, Merge Sort has some drawbacks, such as its space requirements and potentially inefficient traversal of perfectly sorted subarrays.