Merge Two Sorted Arrays without Extra Space

Problem Statement

Given the sorted arrays nums1[]nums1[] and nums2[]nums2[] of sizes n and m in non-decreasing order. Merge without extra space in sorted, non-decreasing order such that nums1 contains the first n elements, and nums2 contains the last m elements.

Example

n = 4, nums1[] = [2 9 11 15]
m = 6, nums2[] = [-18 1 3 7 10 12]

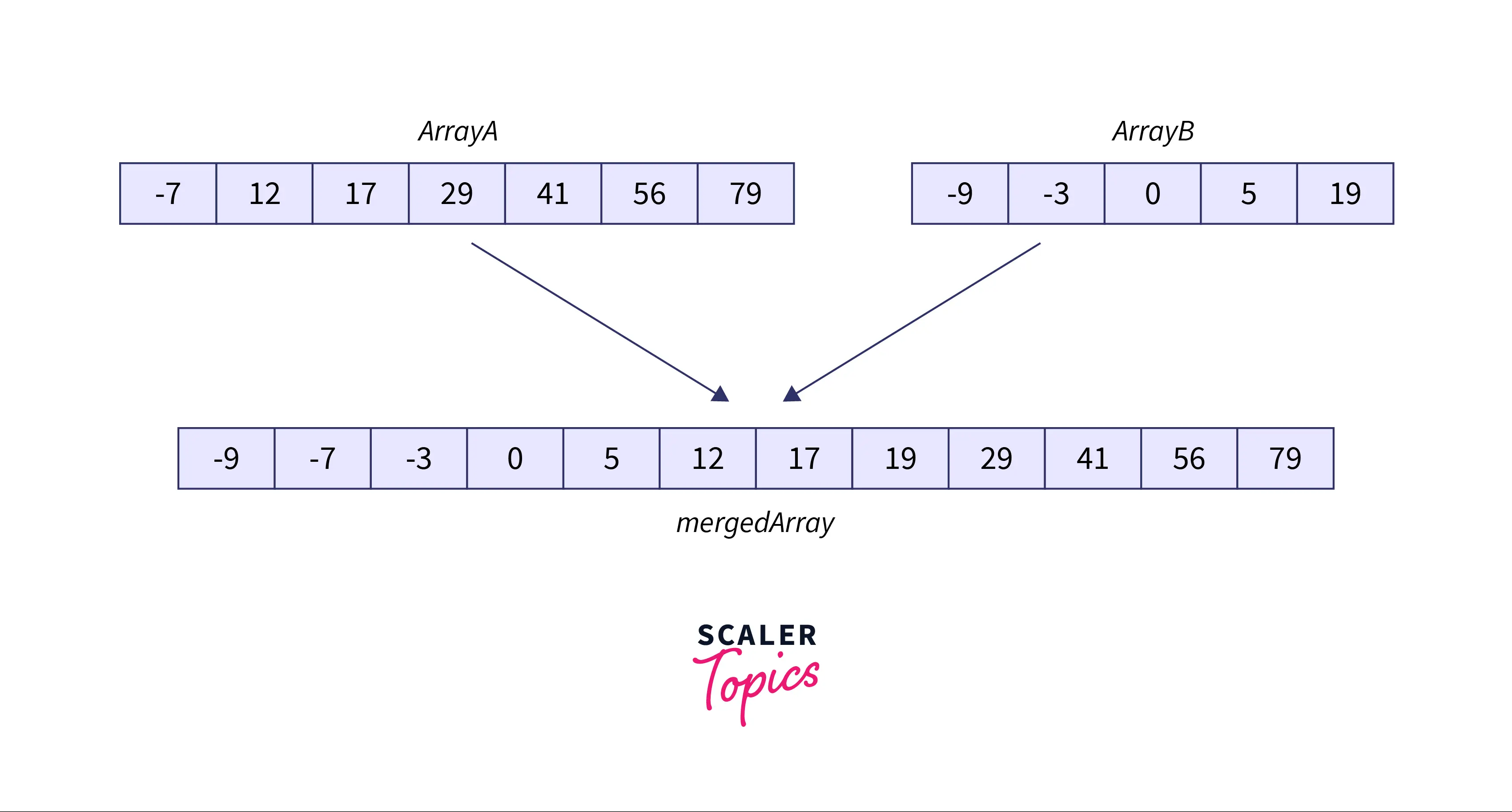
Example Explanation

The following two arrays are given :

n = 4, nums1 = [2 9 11 15]
m = 6, nums2 = [-18 1 3 7 10 12]

Try to merge two sorted arrays without extra space such that the smallest n elements are present in the first array and the remaining m elements in the second array in a non-descending sorted manner.

After merging the two non-decreasing arrays :

-18,1,2,3,7,9,10,11,12,15

The output should be :

nums1 = [-18 1 2 3]
nums2 = [7 9 10 11 12 15]

Input/Output

Input :

There are four lines of input.

• The first line contains the value of ‘n’, which is the length of nums1.
• The second line contains n space-separated integers.
• The third line contains the value of ‘m’, which is the length of nums2.
• The fourth or final line contains m space-separated integers.

Output :

Print values of nums1 and nums2 after modifying them such that nums1 contains the first n elements and nums2 contains the last m elements.

Constraints

$nums1.length = n$
$nums2.length = m$
$1 <= m, n <= 200$
$1 <= m + n <= 200$
$-10^{9} <= nums1[i], nums2[j] <= 10^{9}$

Algorithm – 1 : Brute Force Approach

Algorithm :

• Step 1 :
  In the initial step, build an array ‘merged_array’ of size total_len, where total_len is the sum of the size of nums1 and nums2.
• Step 2 :
  Insert elements from nums1 and nums2 into the merged_array.
• Step 3 :
  Sort merged_array in non-decreasing order.
• Step 4 :
  Fill the first n elements from merged_array into nums1.
• Step 5 :
  Fill the remaining elements (last m elements) of the merged array into nums2.
• Step 6 :
  In the final step print the original arrays and the arrays formed after merging the 2 arrays.

Code Implementation :

C++ :

#include<bits/stdc++.h>
using namespace std;
void merge(int arr1[], int l1, int arr2[], int l2) {
    int total_len=l1+l2;
    int merged_array[total_len];
    int pos = 0;
    /* merging two arrays into one single array */
    for (int i = 0; i < l1; i++) {
      merged_array[pos++] = arr1[i];
    }
    for (int i = 0; i < l2; i++) {
      merged_array[pos++] = arr2[i];
    }
    /*sorting the merged array */
    sort(merged_array,merged_array+total_len);
    pos = 0;
    /* Putting the first l1 (n) elements in the first array. */
    for (int i = 0; i < l1; i++) {
      arr1[i] = merged_array[pos++];
    }
    /* Putting last l2 (m) elements in second array */
    for (int i = 0; i < l2; i++) {
      arr2[i] = merged_array[pos++];
    }
  }
/* Driver code*/
int main() {
    int n = 4;
    int nums1[4] = {2, 9, 11, 15};

    int m = 6;
    int nums2[6] = {-18, 1, 3, 7, 10, 12};

    cout<<"Original arrays:"<<endl;
    cout<<"nums1: "<<"\t";
    for (int i = 0; i < n; i++) {
      cout<<nums1[i]<<" ";
    }
    cout<<endl;
    cout<<"nums2: "<<"\t";
    for (int i = 0; i < m; i++) {
      cout<<nums2[i]<<" ";
    }
    cout<<endl;
    merge(nums1,  n, nums2, m);
    cout<<"Arrays after merging:"<<endl;
    cout<<"nums1: "<<"\t";
    for (int i = 0; i <n; i++) {
      cout<<nums1[i]<<" ";
    }
    cout<<endl;
    cout<<"nums2: "<<"\t";
    for (int i = 0; i < m; i++) {
      cout<<nums2[i]<<" ";
    }
}

Java :

import java.io.*;
import java.util.*;
import java.util.Scanner;

public class Main {

  static void merge(int[] arr1, int l1, int arr2[], int l2) {
    int total_len = l1 + l2;
    int merged_array[] = new int[total_len];
    int pos = 0;
    /* merging two arrays into one single array */
    for (int i = 0; i < l1; i++) {
      merged_array[pos++] = arr1[i];
    }
    for (int i = 0; i < l2; i++) {
      merged_array[pos++] = arr2[i];
    }
    /*sorting the merged array */
    Arrays.sort(merged_array);
    pos = 0;
    /* Putting the first l1 (n) elements in the first array. */
    for (int i = 0; i < l1; i++) {
      arr1[i] = merged_array[pos++];
    }
    /* Putting last l2 (m) elements in second array */
    for (int i = 0; i < l2; i++) {
      arr2[i] = merged_array[pos++];
    }
  }

  /* Driver code*/
  public static void main(String[] args) {
    int n = 4;
    int nums1[] = {2, 9, 11, 15};

    int m = 6;
    int nums2[] = {-18, 1, 3, 7, 10, 12};
    
    System.out.println("Original arrays:");
    System.out.print("nums1: \t");
    for (int i = 0; i < n; i++) {
      System.out.print(nums1[i] + " ");
    }
    System.out.println();
    System.out.print("nums2: \t");
    for (int i = 0; i < m; i++) {
      System.out.print(nums2[i] + " ");
    }
    System.out.println();
    merge(nums1, n, nums2, m);
    System.out.println("Arrays after merging:");
    System.out.print("nums1: \t");
    for (int i = 0; i < n; i++) {
      System.out.print(nums1[i] + " ");
    }
    System.out.println();
    System.out.print("nums2: \t");
    for (int i = 0; i < m; i++) {
      System.out.print(nums2[i] + " ");
    }
  }
}

Python :

def merge( arr1,  l1,  arr2,  l2) :
    total_len = l1 + l2
    merged_array = [0] * (total_len)
    pos = 0
    # merging two arrays into one single array
    for i in range(l1):
        merged_array[pos] = arr1[i]
        pos+=1
    for i in range(l2):
        merged_array[pos] = arr2[i]
        pos+=1
    # sorting the merged array
    merged_array.sort()
    pos = 0
    # Puting the first l1 (n) elements in the first array.
    for i in range(l1):
        arr1[i] = merged_array[pos]
        pos+=1
    # Putting last l2 (m) elements in the second array
    for i in range(l2):
        arr2[i] = merged_array[pos]
        pos+=1

if __name__=="__main__":
    n = 4;
    nums1 = [2, 9, 11, 15];

    m = 6;
    nums2 = [-18, 1, 3, 7, 10, 12];
    
    print("Original arrays:")
    print("nums1: \t", end ="")
    for i in range(n):
        print(str(nums1[i]) + " ", end ="")
    print("\nnums2: \t", end ="")
    for i in range(m):
        print(str(nums2[i]) + " ", end ="")
    merge(nums1, n, nums2, m)
    print("\nArrays after merging:")
    print("nums1: \t", end ="")
    for i in range(n):
        print(str(nums1[i]) + " ", end ="")
    print("\nnums2: \t", end ="")
    for i in range(m):
        print(str(nums2[i]) + " ", end ="")

Input :

N : 4
num1[] : 2 9 11 15
M : 6
nums2[] : -18 1 3 7 10 12

Output :

Original arrays:
nums1: 	2 9 11 15
nums2: 	-18 1 3 7 10 12
Arrays after merging:
nums1: 	-18 1 2 3
nums2: 	7 9 10 11 12 15

Complexity Analysis

Time Complexity :

• To traverse the first array we need $O(n)$ time.
• To traverse the second array we need $O(m)$ time.
• To traverse the merged array time complexity is $O(n+m)$.
• To sort the merged array time complexity will be $O((n+m)log(n+m))$.

So, the overall time complexity for this approach will be O((n+m)log(n+m)).

Space complexity :
Since we use extra space by building a new merged_array of size m+n the space complexity will be O(n+m).

Algorithm – 2 : Without Using Extra Space

Algorithm :

• Step – 1 :
  At the initial step iterate through nums1 using a for loop.
• Step – 2 :
  For every element in nums1 check if it is greater than the first element of nums2.
• Step – 3 :
  If condition satisfies sort nums2 in non-decreasing order.
• Step – 4 :
  Iterate through the loop and repeat the process till the last index of nums1.
• Step – 5 :
  In the final step print the original arrays and the arrays formed after merging the 2 arrays.

Code Implementation :

C++ :

#include <bits/stdc++.h>
using namespace std;
void merge(int arr1[], int l1, int arr2[], int l2) {
    int i;
    for (i = 0; i < l1; i++) {
        /* compare the current element from arr1 with the first element of the second array */
        if (arr1[i] > arr2[0]) {
            /* swap if the element in the first array is greater than the element in the second array */
            swap(arr1[i], arr2[0]);
        }
        /* sort second array in non-decreasing order */
        int first = arr2[0], pos = 1;
        while (pos < l2 && arr2[pos] < first) {
            arr2[pos - 1] = arr2[pos];
            pos += 1;
        }
        arr2[pos - 1] = first;
    }
}
/*driver code*/
int main() {
    int n = 4;
    int nums1[4] = {2, 9, 11, 15};

    int m = 6;
    int nums2[6] = {-18, 1, 3, 7, 10, 12};

    cout << "Original arrays:" << endl;
    cout << "nums1: "
         << "\t";
    for (int i = 0; i < n; i++) {
        cout << nums1[i] << " ";
    }
    cout << endl;
    cout << "nums2: "
         << "\t";
    for (int i = 0; i < m; i++) {
        cout << nums2[i] << " ";
    }
    cout << endl;
    merge(nums1, n, nums2, m);
    cout << "Arrays after merging:" << endl;
    cout << "nums1: "
         << "\t";
    for (int i = 0; i < n; i++) {
        cout << nums1[i] << " ";
    }
    cout << endl;
    cout << "nums2: "
         << "\t";
    for (int i = 0; i < m; i++) {
        cout << nums2[i] << " ";
    }
}

Java :

import java.io.*;
import java.util.*;
import java.util.Scanner;

public class Main {

  static int[] swap(int a, int b) {
    int[] ans = new int[2];
    ans[0] = b;
    ans[1] = a;
    return ans;
  }

  static void merge(int[] arr1, int l1, int arr2[], int l2) {
    int i;
    for (i = 0; i < l1; i++) {
      /* compare the current element from arr1 with the first element of the second array */
      if (arr1[i] > arr2[0]) {
        /* swap if the element in the first array is greater than the element in the second array */
        int[] ans = swap(arr1[i], arr2[0]);
        arr1[i] = ans[0];
        arr2[0] = ans[1];
      }
      /* sort second array in non-decreasing order */
      int first = arr2[0], pos = 1;
      while (pos < l2 && arr2[pos] < first) {
        arr2[pos - 1] = arr2[pos];
        pos += 1;
      }
      arr2[pos - 1] = first;
    }
  }

  /* Driver code*/
  public static void main(String[] args) {
    int n = 4;
    int nums1[] = {2, 9, 11, 15};

    int m = 6;
    int nums2[] = {-18, 1, 3, 7, 10, 12};

    System.out.println("Original arrays:");
    System.out.print("nums1: \t");
    for (int i = 0; i < n; i++) {
      System.out.print(nums1[i] + " ");
    }
    System.out.println();
    System.out.print("nums2: \t");
    for (int i = 0; i < m; i++) {
      System.out.print(nums2[i] + " ");
    }
    System.out.println();
    merge(nums1, n, nums2, m);
    System.out.println("Arrays after merging:");
    System.out.print("nums1: \t");
    for (int i = 0; i < n; i++) {
      System.out.print(nums1[i] + " ");
    }
    System.out.println();
    System.out.print("nums2: \t");
    for (int i = 0; i < m; i++) {
      System.out.print(nums2[i] + " ");
    }
  }
}

Python :

def merge( arr1,  l1,  arr2,  l2) :
    for i in range(l1):
        # compare the current element from arr1 with the first element of the second array
        if (arr1[i] > arr2[0]) :
            # swap if the element in the first array is greater than the element in the second array
            arr1[i], arr2[0] = arr2[0], arr1[i]
        # sort second array in non-decreasing order
        first = arr2[0]
        pos = 1
        while (pos < l2 and arr2[pos] < first) :
            arr2[pos - 1] = arr2[pos]
            pos += 1
        arr2[pos - 1] = first
        i += 1
if __name__=="__main__":
    n = 4;
    nums1 = [2, 9, 11, 15];

    m = 6;
    nums2 = [-18, 1, 3, 7, 10, 12];

    print("Original arrays:")
    print("nums1: \t", end ="")
    for i in range(n):
        print(str(nums1[i]) + " ", end ="")
    print("\nnums2: \t", end ="")
    for i in range(m):
        print(str(nums2[i]) + " ", end ="")
    merge(nums1, n, nums2, m)
    print("\nArrays after merging:")
    print("nums1: \t", end ="")
    for i in range(n):
        print(str(nums1[i]) + " ", end ="")
    print("\nnums2: \t", end ="")
    for i in range(m):
        print(str(nums2[i]) + " ", end ="")

Input :

N : 4
num1[] : 2 9 11 15
M : 6
nums2[] : -18 1 3 7 10 12

Output :

Original arrays:
nums1:     2 9 11 15
nums2:     -18 1 3 7 10 12
Arrays after merging:
nums1:     -18 1 2 3
nums2:     7 9 10 11 12 15

Complexity Analysis

Time Complexity :
While iterating through nums1 of length n, nums2 of length m is also traversed for rearrangement. Hence, the time complexity for this approach is O(m * n).

Space complexity :
The space complexity to merge two sorted arrays without extra space using this approach is O(1).

Algorithm : 3 – Gap Method

Algorithm :

• Step – 1 :
  At the initial step calculate the gap as the ceil value of total_len/2, where total_len = m+n.
• Step – 2 :
  Assign values 0 and gap to pointers ptr1 and ptr2, respectively.
• Step – 3 :
  Iterate through m+n using the pointers.
• Step – 4 :
  Check if the value of location ptr2 is less than the value of location ptr1 points at.
• Step – 5 :
  Swap values, if the condition is satisfied.
• Step – 6 :
  After termination of the loop assign a new value to the gap using the 'nextGap' function.
• Step – 7 :
  Terminate the process when the value of gap becomes less than 0.
• Step – 8 :
  In the final step print the original arrays and the arrays formed after merging the 2 arrays.

Code Implementation :

C++

#include <bits/stdc++.h>
using namespace std;
/* function to take an integer and return the next gap */
int nextGap(int gap){
    if (gap <= 1){
        return 0;
    }
    return (gap / 2) + (gap % 2);
}
/* function to merge arrays in non-ascending order */
void merge(int arr1[], int l1, int arr2[], int total_len) {
    int temp;
    int gap =  ((total_len) / 2) + ((total_len) % 2); /*value of gap */
    while (gap > 0) {
        int ptr1 = 0, ptr2 = gap;
        while (ptr2 < (total_len)) {
            /* comparing elements in first array - if arr1[ptr2]<arr1[ptr1] swap their values */
            if (ptr2 < l1 && arr1[ptr1] > arr1[ptr2]) {
                swap(arr1[ptr1] , arr1[ptr2]);
            }
            /* comparing elements in both arrays */
            else if (ptr2 >= l1 && ptr1 < l1 && arr1[ptr1] > arr2[ptr2 - l1]) {
                swap(arr1[ptr1] , arr2[ptr2 - l1]);
            }
            /* comparing elements in the second array */
            else if (ptr2 >= l1 && ptr1 >= l1 && arr2[ptr1 - l1] > arr2[ptr2 - l1]) {
                swap(arr2[ptr1 - l1] , arr2[ptr2 - l1]);
            }
            ptr2++;
            ptr1++;
        }
        gap = nextGap(gap);
    }
}
/*driver code*/
int main() {
    int n = 4;
    int nums1[4] = {2, 9, 11, 15};

    int m = 6;
    int nums2[6] = {-18, 1, 3, 7, 10, 12};

    cout << "Original arrays:" << endl;
    cout << "nums1: "
         << "\t";
    for (int i = 0; i < n; i++) {
        cout << nums1[i] << " ";
    }
    cout << endl;
    cout << "nums2: "
         << "\t";
    for (int i = 0; i < m; i++) {
        cout << nums2[i] << " ";
    }
    cout << endl;
    merge(nums1, n, nums2, m+n);
    cout << "Arrays after merging:" << endl;
    cout << "nums1: "
         << "\t";
    for (int i = 0; i < n; i++) {
        cout << nums1[i] << " ";
    }
    cout << endl;
    cout << "nums2: "
         << "\t";
    for (int i = 0; i < m; i++) {
        cout << nums2[i] << " ";
    }
}

Java

import java.io.*;
import java.util.*;
import java.util.Scanner;

public class Main {

  /* function to take an integer and return the next gap */
  static int nextGap(int gap) {
    if (gap <= 1) {
      return 0;
    }
    return (gap / 2) + (gap % 2);
  }

  static int[] swap(int a, int b) {
    int[] ans = new int[2];
    ans[0] = b;
    ans[1] = a;
    return ans;
  }

  /* function to merge arrays in non-ascending order */
  static void merge(int[] arr1, int l1, int arr2[], int total_len) {
    int temp;
    int gap = ((total_len) / 2) + ((total_len) % 2);/*value of gap */
    while (gap > 0) {
      int ptr1 = 0, ptr2 = gap;
      while (ptr2 < (total_len)) {
        /* comparing elements in first array - if arr1[ptr2]<arr1[ptr1] swap their values */
        if (ptr2 < l1 && arr1[ptr1] > arr1[ptr2]) {
          int[] ans = swap(arr1[ptr1], arr1[ptr2]);
          arr1[ptr1] = ans[0];
          arr1[ptr2] = ans[1];
        } /* comparing elements in both arrays*/else if (
          ptr2 >= l1 && ptr1 < l1 && arr1[ptr1] > arr2[ptr2 - l1]
        ) {
          int[] ans = swap(arr1[ptr1], arr2[ptr2 - l1]);
          arr1[ptr1] = ans[0];
          arr2[ptr2 - l1] = ans[1];
        } /* comparing elements in the second array*/else if (
          ptr2 >= l1 && ptr1 >= l1 && arr2[ptr1 - l1] > arr2[ptr2 - l1]
        ) {
          int[] ans = swap(arr2[ptr1 - l1], arr2[ptr2 - l1]);
          arr2[ptr1 - l1] = ans[0];
          arr2[ptr2 - l1] = ans[1];
        }
        ptr2++;
        ptr1++;
      }
      gap = nextGap(gap);
    }
  }

  /*driver code*/
  public static void main(String[] args) {
    int n = 4;
    int nums1[] = {2, 9, 11, 15};

    int m = 6;
    int nums2[] = {-18, 1, 3, 7, 10, 12};

    System.out.println("Original arrays:");
    System.out.print("nums1: \t");
    for (int i = 0; i < n; i++) {
      System.out.print(nums1[i] + " ");
    }
    System.out.println();
    System.out.print("nums2: \t");
    for (int i = 0; i < m; i++) {
      System.out.print(nums2[i] + " ");
    }
    System.out.println();
    merge(nums1, n, nums2, m + n);
    System.out.println("Arrays after merging:");
    System.out.print("nums1: \t");
    for (int i = 0; i < n; i++) {
      System.out.print(nums1[i] + " ");
    }
    System.out.println();
    System.out.print("nums2: \t");
    for (int i = 0; i < m; i++) {
      System.out.print(nums2[i] + " ");
    }
  }
}

Python

# function to take an integer and return the next gap
def nextGap(gap):
    if (gap <= 1):
        return 0
    return (gap // 2) + (gap % 2)
# function to merge arrays in non-ascending order
def merge( arr1,  l1,  arr2,  total_len) :
    gap = (int((total_len) // 2)) + ((total_len) % 2)# value of gap
    while (gap > 0) :
        ptr1 = 0
        ptr2 = gap
        while (ptr2 < (total_len)) :
            # comparing elemets in first array - if arr1[ptr2]<arr1[ptr1] swap their values
            if (ptr2 < l1 and arr1[ptr1] > arr1[ptr2]) :
                arr1[ptr1], arr1[ptr2] = arr1[ptr2], arr1[ptr1]
            # comparing elements in both arrays
            elif(ptr2 >= l1 and ptr1 < l1 and arr1[ptr1] > arr2[ptr2 - l1]) :
                arr1[ptr1], arr2[ptr2 - l1] = arr2[ptr2 - l1], arr1[ptr1]
            # comparing elements in the second array
            elif(ptr2 >= l1 and ptr1 >= l1 and arr2[ptr1 - l1] > arr2[ptr2 - l1]) :
                arr2[ptr1 - l1], arr2[ptr2 - l1] = arr2[ptr2 - l1], arr2[ptr1 - l1]
            ptr2 += 1
            ptr1 += 1
        gap = nextGap(gap)

#driver code
if __name__=="__main__":
    n = 4;
    nums1 = [2, 9, 11, 15];

    m = 6;
    nums2 = [-18, 1, 3, 7, 10, 12];

    print("Original arrays:")
    print("nums1: \t", end ="")
    for i in range(n):
        print(str(nums1[i]) + " ", end ="")
    print("\nnums2: \t", end ="")
    for i in range(m):
        print(str(nums2[i]) + " ", end ="")
    merge(nums1, n, nums2, m+n)
    print("\nArrays after merging:")
    print("nums1: \t", end ="")
    for i in range(n):
        print(str(nums1[i]) + " ", end ="")
    print("\nnums2: \t", end ="")
    for i in range(m):
        print(str(nums2[i]) + " ", end ="")

Input :

N : 4
num1[] : 2 9 11 15
M : 6
nums2[] : -18 1 3 7 10 12

Output :

Original arrays:
nums1:     2 9 11 15
nums2:     -18 1 3 7 10 12
Arrays after merging:
nums1:     -18 1 2 3
nums2:     7 9 10 11 12 15

Complexity Analysis

Time Complexity :
Since the pointer iterates through 'total_len' the time complexity for this approach will be O(m+n).

Space complexity :
The space complexity to merge two sorted arrays without extra space using this approach is O(1).

Explore Scaler Topics Data Structures Tutorial and enhance your DSA skills with Reading Tracks and Challenges.

Conclusion

• Approach – 1 :
  Use a new array of size n+m and insert elements from nums1 and nums2, and sort it. Put the first n elements in nums1 and the last m elements in nums2.
• Time Complexity : $O(n * log(n))+O(n)+O(n)$
• Space Complexity : $O(n)$
• Approach – 2 :
  While iterating through nums1, whenever you come across an element greater than the first element of nums2, swap them, and sort the array nums2. Stop iterating after traversing through all the elements.
• Time complexity : $O(n * m)$
• Space Complexity : $O(1)$
• Approach – 3 :
  Implement gap method where gap $= (m+n)/2$ to merge two sorted arrays without extra space. Use two pointers, to iterate through m+n, starting the first pointer from 0 and the second pointer from gap. For every gap value, if second pointer is less than first pointer swap their values. After each iteration, halve the value of the gap and continue the process till $gap>0$.
• Time complexity : $O(n+m)$
• Space Complexity : $O(1)$

Learn More:

• Merge Two Sorted Arrays

FAQ

Q. Why does merge sort require extra space ?

A: While merging two arrays an additional space is needed to create the array for merging.