Mirror Tree Problem – Convert Binary tree to Mirror Tree

Problem Statement

Given a binary tree, our task is to convert this binary tree into its mirror tree. A mirror tree is another form of a binary tree where the left and right children of all non-leaf nodes are interchanged.

Example of Mirror Tree

Let us try to mirror the following binary tree:

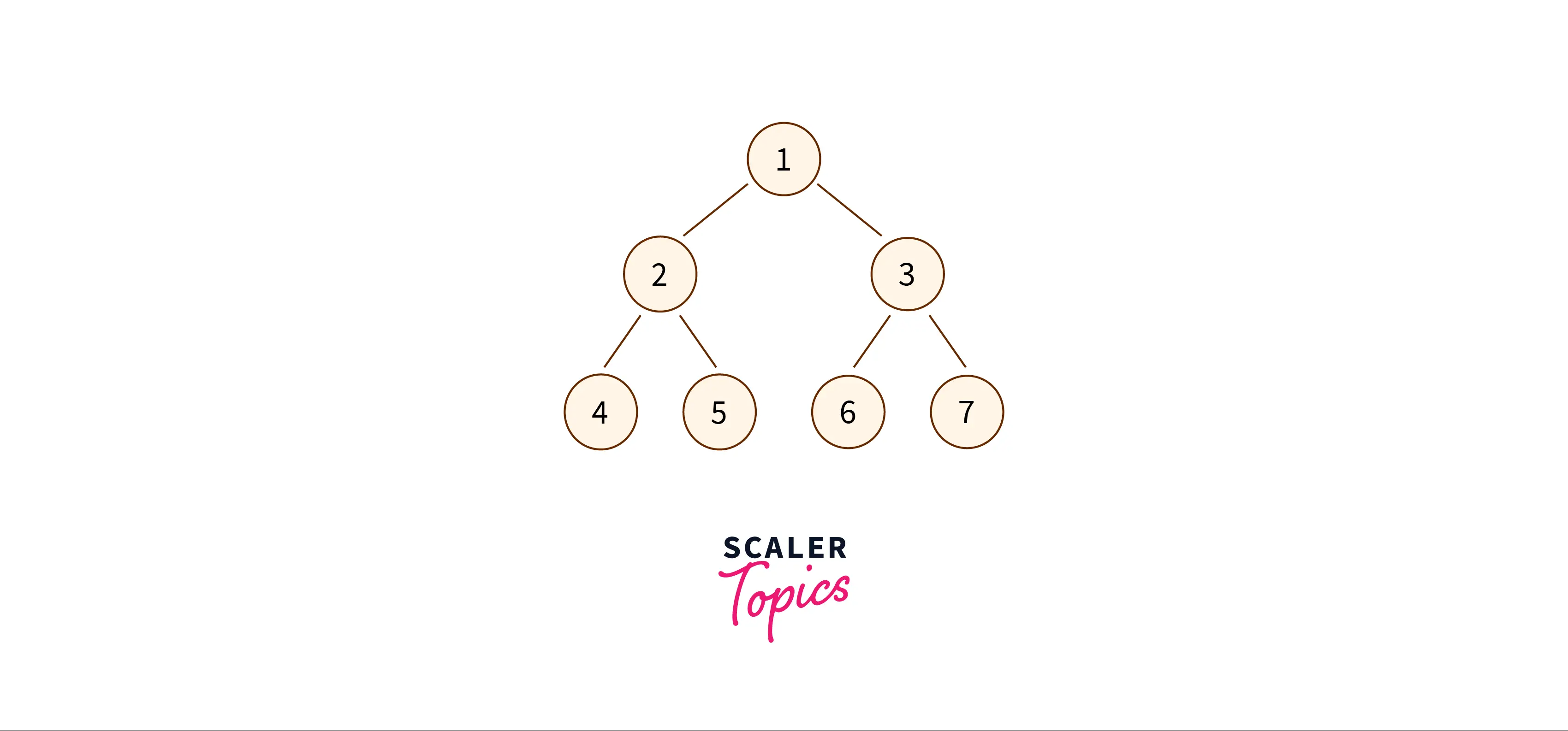
Example Explanation

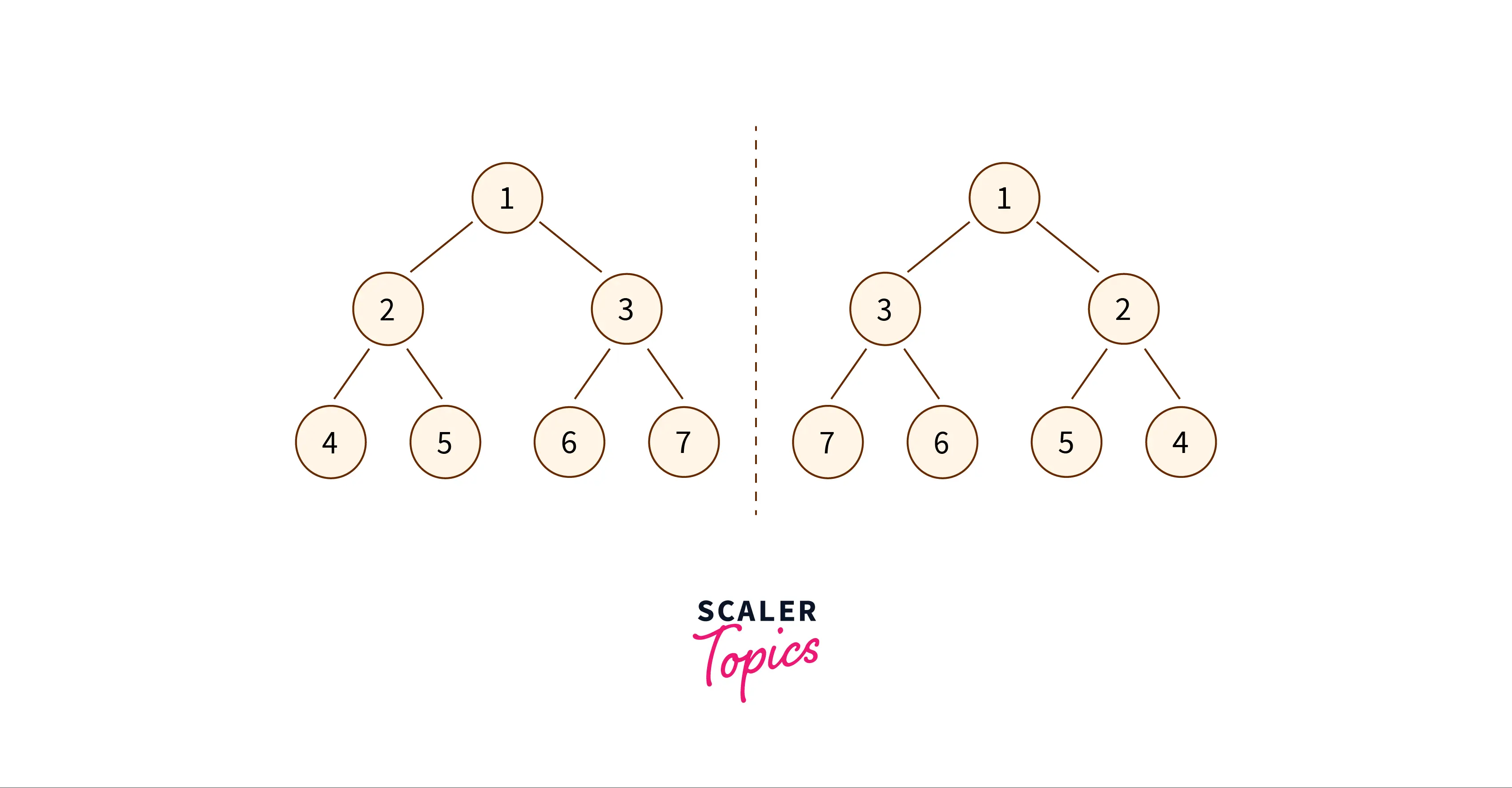
In the above-shown example consider the dotted line as a mirror thus the tree on the left side is the original binary tree while tree on the right is the mirrored binary tree.

Input/ Output of Mirror Tree

The input statement contains each tree node’s data separated by a single space in a single line. If any node in the binary tree is NULL, we will put -1 in its place. Therefore, for the tree depicted in the above example the input will be given as:

1 2 3 4 5 6 7 -1 -1 -1 -1 -1 -1 -1 -1

The output for the above given input will the following:

Inorder traversal of original tree is
4 2 5 1 6 3 7 
Inorder traversal of the mirrored tree is 
7 3 6 1 5 2 4 

Here, output includes the Inorder traversal for both the original and mirrored tree.

Constraints of Mirror tree

$1 <= N <= 3000$
$-10^{9} <= Data <= 10^{9}$

Here N is the number of nodes in the tree, and Data denotes the value contained in the node of the binary tree.

Approach 1- Recursive

The intuition of this approach is to solve the problem using recursion. We will create a mirror() function that will recursively mirror the left and right sub-tree.

• Algorithm The algorithm for this approach is as follows:
  1. Call the mirror function for the left sub-tree, i.e. Mirror(left sub-tree)Call the mirror function for the right sub-tree, i.e. Mirror(right sub-tree)Swap left and right sub-trees using,
     • temp = left sub-treeleft sub-tree = right sub-treeright sub-tree = temp
  After the tree is mirrored, we will traverse it using the Inorder traversal, meaning the left sub-tree is traversed first, followed by the root node and the right sub-tree at the last.

Implementation

Let us now see the implementation of the Mirror for the following binary tree in C++:

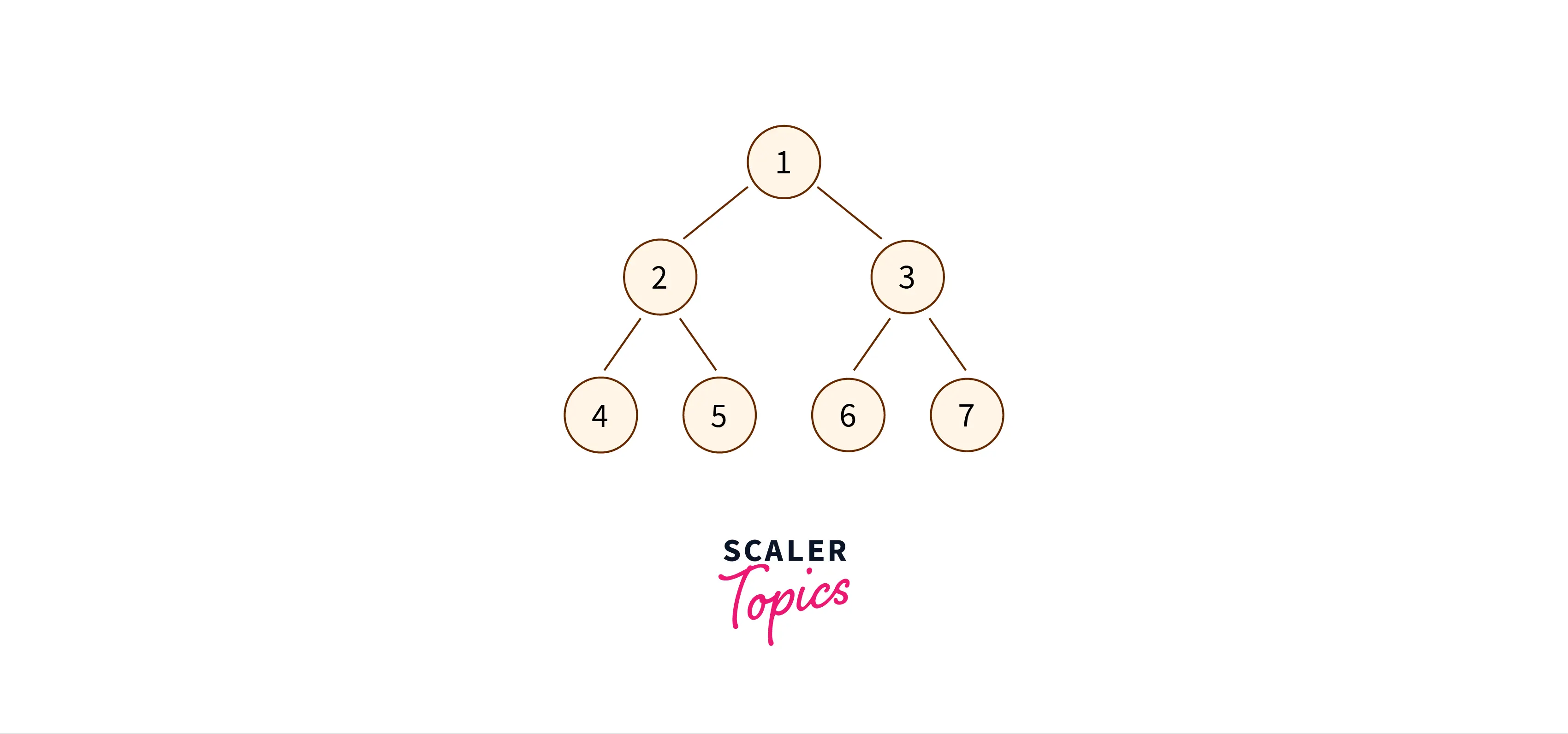
#include<bits/stdc++.h>
using namespace std;

/* a binary tree node has data, pointer
to left child and a pointer to right child */
struct Node {
    int data;
    struct Node* left;
    struct Node* right;
};

/* function that allocates a new node with
the given data and NULL left and right pointers */
struct Node* newNode(int data) {
    struct Node* node = (struct Node*)
                        malloc(sizeof(struct Node));
    node->data = data;
    node->left = NULL;
    node->right = NULL;

    return(node);
}

void mirror(struct Node* node) {
    if (node == NULL)
        return;
    else {
        struct Node* temp;

        // mirror the subtrees
        mirror(node->left);
        mirror(node->right);

        // swapping the pointers for this node
        temp = node->left;
        node->left = node->right;
        node->right = temp;
    }
}

// function to print Inorder traversal
void inorder(struct Node* node) {
    if (node == NULL)
        return;

    inorder(node->left);
    cout << node->data << " ";
    inorder(node->right);
}


int main() {

    struct Node *root = newNode(1); 
    root->left = newNode(2); 
    root->right = newNode(3); 
    root->left->left = newNode(4); 
    root->left->right = newNode(5); 
    root->right->left = newNode(6);
    root->right->right = newNode(7);

    // inorder traversal of the original tree 
    cout << "Inorder traversal of original tree is" << endl;
    inorder(root);

    // mirror the tree
    mirror(root);

    // inorder traversal of the mirrored tree
    cout << "\nInorder traversal of the mirrored tree is \n";
    inorder(root);

    return 0;
}

Output

Inorder traversal of original tree is
4 2 5 1 6 3 7 
Inorder traversal of the mirrored tree is 
7 3 6 1 5 2 4 

Let us now see the implementation of the Mirror binary tree in Java:

import java.util.*;

class Main {

// a binary tree node has data, pointer to
// left child and a pointer to right child
static class Node {
    int data;
    Node left;
    Node right;
}

// function that allocates
// a new node with the given data and null left and right pointers
static Node newNode(int data) {
    Node newNode = new Node();
    newNode.data = data;
    newNode.left = null;
    newNode.right = null;
    return newNode;
}

// function to print Inorder traversal
static void inorder(Node root) {
    if (root == null)
        return;
    inorder(root.left);
    System.out.print(root.data + " ");
    inorder(root.right);
}


static Node mirror(Node root) {
    if (root == null) {
        return null;

    }
    // mirror the subtrees
    Node mirror = newNode(root.data);
    mirror.right = mirror(root.left);
    mirror.left = mirror(root.right);
    return mirror;
}

public static void main(String args[]) {

    Node root = newNode(1); 
    root.left = newNode(2); 
    root.right = newNode(3); 
    root.left.left = newNode(4); 
    root.left.right = newNode(5); 
    root.right.left = newNode(6);
    root.right.right = newNode(7);

    //  inorder traversal of the input tree
    System.out.print("Inorder traversal of original tree is \n");
    inorder(root);

    Node mirror = null;
    mirror = mirror(root);

    // inorder traversal of the mirrored tree
    System.out.print("\nInorder traversal of the mirrored tree is \n");
    inorder(mirror);
    }
}

Output

Inorder traversal of original tree is
4 2 5 1 6 3 7 
Inorder traversal of the mirrored tree is 
7 3 6 1 5 2 4 

Let us now see the implementation of the Mirror binary tree in Python

# function to create a new tree node
class newNode:
    def __init__(self,data):
        self.data = data
        self.left = self.right = None

def mirror(node):

    if (node == None):
        return
    else:
        temp = node

        # mirror the subtrees
        mirror(node.left)
        mirror(node.right)

        # swapping the pointers for this node
        temp = node.left
        node.left = node.right
        node.right = temp

# function to print Inorder traversal
def inorder(node) :

    if (node == None):
        return

    inorder(node.left)
    print(node.data, end = " ")
    inorder(node.right)


root = newNode(1)
root.left = newNode(2)
root.right = newNode(3) 
root.left.left = newNode(4) 
root.left.right = newNode(5) 
root.right.left = newNode(6)
root.right.right = newNode(7)

# inorder traversal of the original tree
print("Inorder traversal of original tree is")
inorder(root)

# mirror the tree
mirror(root)

# inorder traversal of the mirrored tree
print("\nInorder traversal of the mirrored tree is")
inorder(root)

Output

Inorder traversal of original tree is
4 2 5 1 6 3 7 
Inorder traversal of the mirrored tree is 
7 3 6 1 5 2 4 

Time Complexity

• In the above code implementation, we are using the recursive approach along with updating the pointers at every recursive call (that are constant time operations thus having a time complexity of $O(1)$), therefore, the time complexity of this approach will be the same as that of the inorder traversal, which is $O(n)$.

Space Complexity

If we consider the size of the stack for function calls, the space complexity of the above implemented recursive approach is $O(n)$. The recursive approach does not utilise any other auxiliary space other than the space used for the stack calls.

Approach 2- Iterative method using Queues

• The intuition of this approach is to implement level order traversal using the queue data structure. While doing traversal, swap left and right children of every node.
• Algorithm The algorithm for this approach is as follows:
  1. Perform a level order traversal, swapping every left and right child
  2. Create a queue and add the root node to it.
  3. If the queue is not empty,
     • deque node from the queue
     • swap left and right children of the removed node
     • push back the left and right child of the removed node to the queue
     • return to step 3

Implementation

Let us now see the implementation of the Mirror for the following binary tree in C++:

• Let us now see the implementation of the Mirror for the following binary tree in C++:

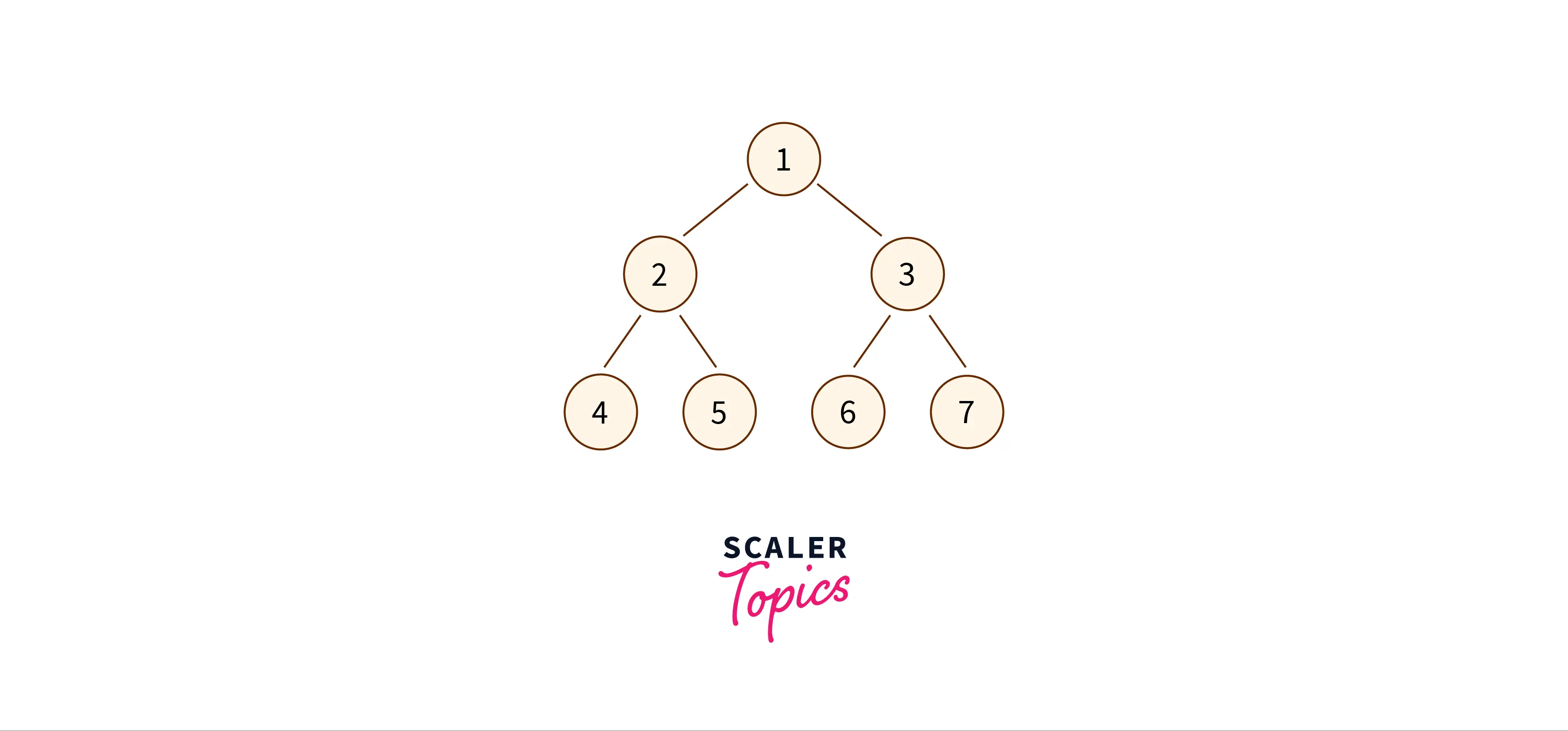
#include<bits/stdc++.h>
using namespace std;

/* a binary tree node has data, pointer to
left child and a pointer to right child */
struct Node {
    int data;
    struct Node* left;
    struct Node* right;
};

/* function that allocates a new node
with the given data and NULL left and right pointers */
struct Node* newNode(int data) {
    struct Node* node = new Node;
    node->data = data;
    node->left = node->right = NULL;
    return(node);
}

void mirror(Node* root) {
    if (root == NULL)
        return;

    queue<Node*> q;
    q.push(root);

    // while implementing level order traversal, keep swapping
    // left and right children
    while (!q.empty()) {
        // pop top node from queue
        Node* curr = q.front();
        q.pop();

        // swap left child with right child
        swap(curr->left, curr->right);

        // push left and right children
        if (curr->left)
            q.push(curr->left);
        if (curr->right)
            q.push(curr->right);
    }
}


// function to print Inorder traversal
void inorder(struct Node* node) {
    if (node == NULL)
        return;
    inorder(node->left);
    cout << node->data << " ";
    inorder(node->right);
}

int main() {

    struct Node *root = newNode(1); 
    root->left = newNode(2); 
    root->right = newNode(3); 
    root->left->left = newNode(4); 
    root->left->right = newNode(5); 
    root->right->left = newNode(6);
    root->right->right = newNode(7);

    // inorder traversal of the original tree 
    cout << "Inorder traversal of original tree is" << endl;
    inorder(root);

    // mirror the tree
    mirror(root);

    // inorder traversal of the mirrored tree
    cout << "\nInorder traversal of the mirrored tree is \n";
    inorder(root);

    return 0;
}

Output

Inorder traversal of original tree is
4 2 5 1 6 3 7 
Inorder traversal of the mirrored tree is 
7 3 6 1 5 2 4 

Let us now see the implementation of the Mirror binary tree in Java:

import java.util.*;
class Main {

/* a binary tree node has data, pointer to
left child and a pointer to right child */
static class Node {
    int data;
    Node left;
    Node right;
};

/* function that allocates a new node
with the given data and null left and right pointers */
static Node newNode(int data) {
    Node node = new Node();
    node.data = data;
    node.left = node.right = null;
    return(node);
}

static void mirror(Node root)
{
    if (root == null)
        return;

    Queue<Node> q = new LinkedList<>();
    q.add(root);

    // while implementing level order traversal, keep swapping
    // left and right children
    while (q.size() > 0) {
        // pop top node from queue
        Node curr = q.peek();
        q.remove();

        // swap left child with right child
        Node temp = curr.left;
        curr.left = curr.right;
        curr.right = temp;

        // push left and right children
        if (curr.left != null)
            q.add(curr.left);
        if (curr.right != null)
            q.add(curr.right);
    }
}

// function to print Inorder traversal
static void inorder( Node node)
{
    if (node == null)
        return;
    inorder(node.left);
    System.out.print( node.data + " ");
    inorder(node.right);
}


public static void main(String args[]) {

    Node root = newNode(1); 
    root.left = newNode(2); 
    root.right = newNode(3); 
    root.left.left = newNode(4); 
    root.left.right = newNode(5); 
    root.right.left = newNode(6);
    root.right.right = newNode(7);

    // inorder traversal of the original tree 
    System.out.print("Inorder traversal of original tree is \n");
    inorder(root);

    // mirror the tree
    mirror(root);

    // inorder traversal of the mirrored tree
    System.out.print("\nInorder traversal of the mirrored tree is \n");
    inorder(root);
    }
}

Output

Inorder traversal of original tree is
4 2 5 1 6 3 7 
Inorder traversal of the mirrored tree is 
7 3 6 1 5 2 4 

Let us now see the implementation of the Mirror binary tree in Python:

# function to create a new tree node
class newNode:
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None

def mirror( root):

    if (root == None):
        return

    q = []
    q.append(root)

    # while implmementing level order traversal, keep swapping
    # left and right children
    while (len(q)):

        # pop top node from queue
        curr = q[0]
        q.pop(0)

        # swap left child with right child
        curr.left, curr.right = curr.right, curr.left

        # append left and right children
        if (curr.left):
            q.append(curr.left)
        if (curr.right):
            q.append(curr.right)

# function to print Inorder traversal 
def inorder( node):
    if (node == None):
        return
    inorder(node.left)
    print(node.data, end = " ")
    inorder(node.right)

root = newNode(1)
root.left = newNode(2)
root.right = newNode(3) 
root.left.left = newNode(4) 
root.left.right = newNode(5) 
root.right.left = newNode(6)
root.right.right = newNode(7)

# inorder traversal of the original tree
print("Inorder traversal of original tree is")
inorder(root)

# mirror the tree
mirror(root)

# inorder traversal of the mirrored tree
print("\nInorder traversal of the mirrored tree is")
inorder(root)

Output

Inorder traversal of original tree is
4 2 5 1 6 3 7 
Inorder traversal of the mirrored tree is 
7 3 6 1 5 2 4 

Time Complexity

We implement level order traversal, which has a time complexity of $O(n)$, as well as the swapping of left and right children, which has a constant time complexity, for a total time complexity of $O(n)$.

Space Complexity

Because this approach employs the queue data structure, the space complexity of this method is $O(n)$.

Conclusion

• A mirror tree is a form of the binary tree where left and right children of all non-leaf nodes are interchanged.
• Complexities for Recursive approach
  • Time Complexity – $O(n)$
  • Space Complexity – $O(n)$
• Complexities for Iterative approach using Queue data structure
  • Time Complexity – $O(n)$
  • Space Complexity – $O(n)$