We come across many query based questions in programming where we are given queries in the form of array and then we answer the queries.
Lets generalise the query based question as finding the sum of given range index l to r in an array. We are given Q queries of the above type. So, for each query we have to traverse the whole array from l to r and output the sum which is very inefficient in terms of time complexity. Time complexity for this naive approach will be $O(Q*N)$ where N is the size of array and Q is the number of queries.
Let us consider a better approach where we divide the array into some blocks of same size and then calculate the sum of the elements of the blocks. By this way we preprocessed the sum beforehand.
This will improve the time complexity of our solution greatly as for each query we arn’t needed to move from l to r by traversing each element of the array. We simply add the ith block(whose sum is precalculated) which is fully inside the range [l,r]. We will discuss this in detail below.
This approach is known as Square root decomposition as the name suggest we divide the array into small blocks of length sqrt(N) and for each block i we’ll precalculate some answers(like sum of subarray or min or max element) in O(sqrt(N)) operations, which is much faster than O(N) for the trivial algorithm.
This algorithm is the pre-requisite to MO’s algorithm which efficiently answer offline queries in less time. Here offline queries are the queries which are known beforehand and no update operations are performed on the given array.
The idea is to answer the queries in a special order based on the indices so that we answer the current query by modifying the result of the previously answered query.
Scope of Article
- In this article we will learn about
square root decompositionand thenMo's algorithm. - We will discuss code implementation, time complexities of each algorithm.
- We will also learn in brief about offline queries in this article.
- This article neither covers any concept related to queries which are not known beforehand nor it covers queries which will update after execution.
Takeaways
- Complexity of
Square Root Decomposition- Time complexity –
O(sqrt(N))
- Time complexity –
- Complexity of
MO's algorithm- Time complexity –
O((N+Q)*sqrt(N))
- Time complexity –
Square Root Decomposition
In this technique, we basically divide the given array into blocks of sqrt(N) elements. We chose sqrt(N) sized blocks so that size of each block as well as total blocks will be sqrt(N).
size of a block= $sqrt(N)$
total blocks = $N/sqrt(N)$ = $sqrt(N)$
We start by taking sum of each element that belongs to a block and putting the sum of ith block into a block array at the index i. This way ith block in block array will have sum of sqrt(N) elements of the given array beforehand. Now, whenever we process a query l to r, we add the block in the answer which is fully inside l to r in O(1) time and add those elements of range [l,r] individually which are partially included in the other blocks. So, in worst case scenerio we include all the sqrt(N) blocks for a given query in O(sqrt(N)) time. Worst case time complexity comes out to be O(sqrt(N)) which is efficient than naive approach.
let us consider an example of range sum query:
$Query: [L,R]=[1,6]$
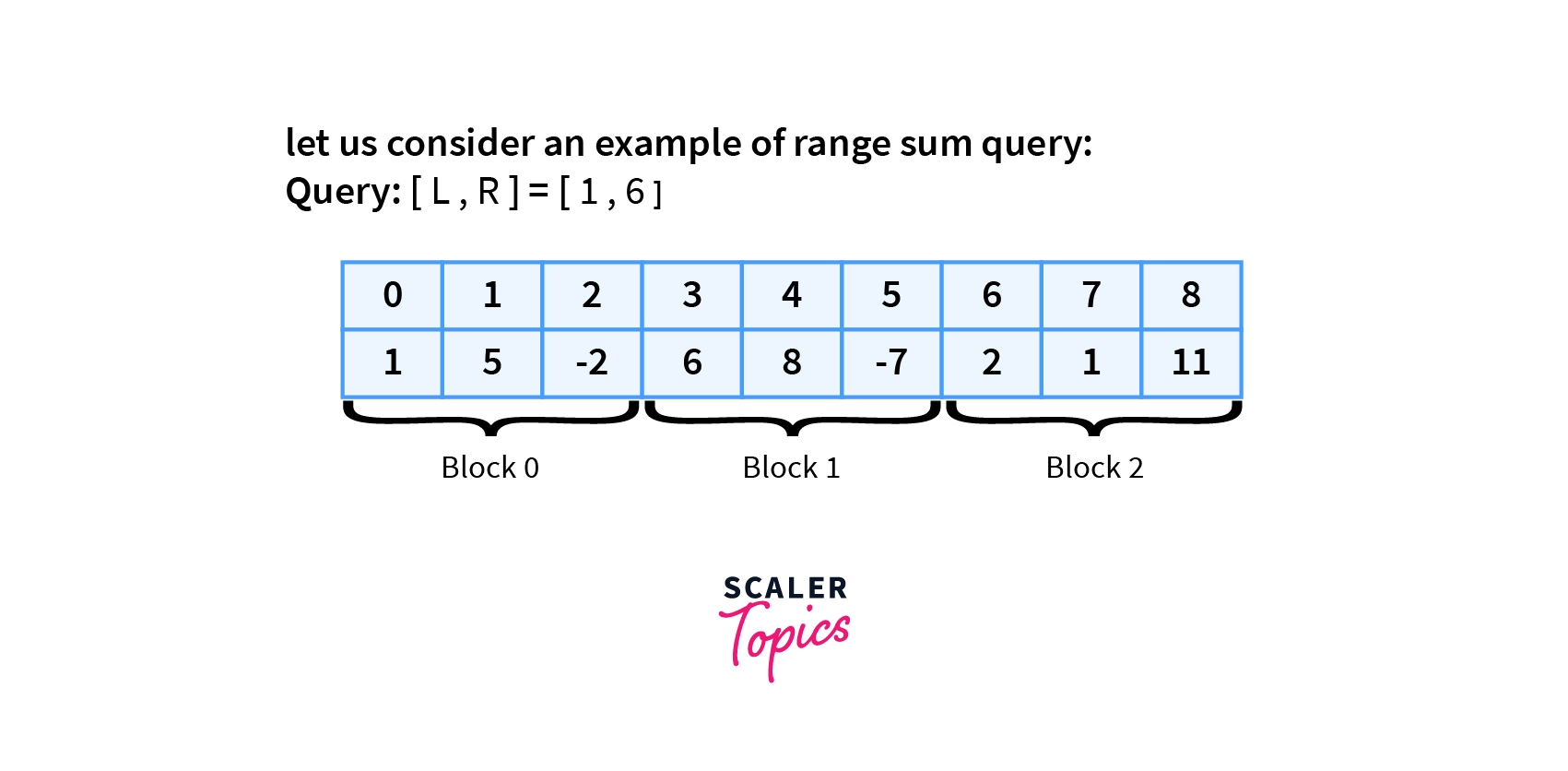
There are 9 elements in the given array.
Block size : sqrt(9)=3.
We put the sum of every block in block array.
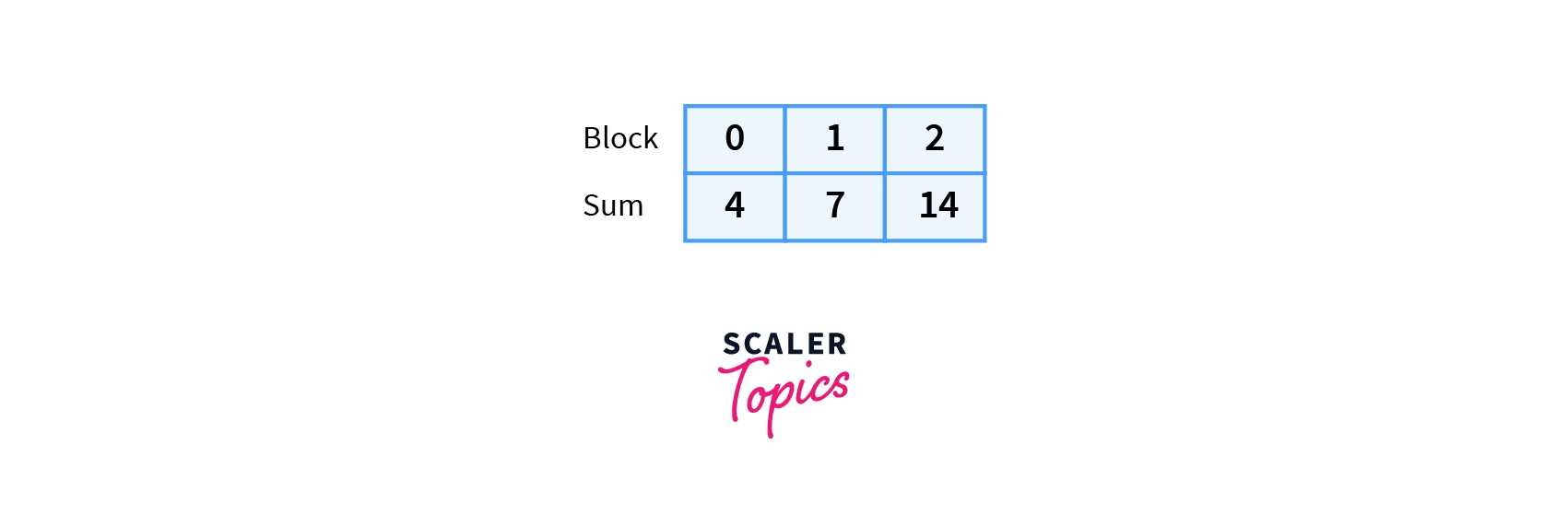
To process the query [1,6], we first find the block index of 1 and 6.
block index= (array_index)/(block_size)
block index of 1 = $1/3 = 0$
block index of 6 = $6/3 = 2$
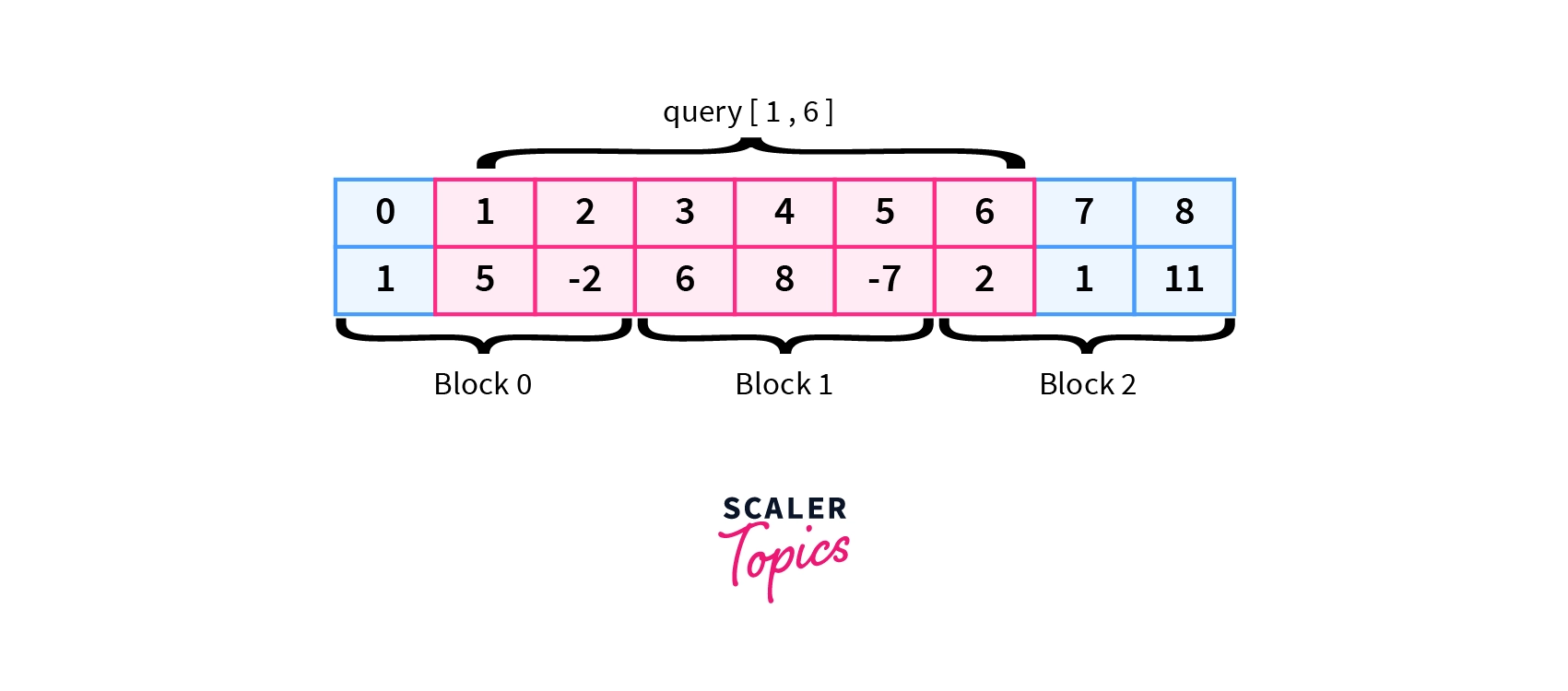
We simply traverse from 1 to 6 and if a block is fully inside the given range i.e. block 1, we directly add its sum from the block array in O(1) time otherwise we add individual elements(arr[1], arr[2], arr[6]) by traversing the range.
initially, $sum=0$
Here 2 elements from block 0 are traversed:
$sum= 5 + (-2)= 3$
Block 1 is fully inside so take sum from block array: $sum= sum + block[1]= 3 + 7= 10$
1 element from block 2 is traversed:
$sum= 10 + 2= 12$
$sum= 12$
This way we efficiently answered the given query in O(sqrt(N)) time.
MO’s Algorithm
After learning sqrt decomposition, we can easily understand MO's algorithm. We are given Q range queries to answer. Suppose we answer the queries in order they are asked. So for every query we have to perform seperate traversal and find the answer. This will take O(N*Q) time where N is size of array and Q queries.
MO's algorithm states that sorting the queries in terms of L values and if same then in terms of R values will basically help the current query to be answered efficiently by taking the result of the previous query.
In other words, MO's algorithm is just an order in which we process the queries. Hence we should have the array of queries beforehand(offline queries).
MO's algorithm is only applicable to problems where:
- All the queries are known beforehand in the form of array so that we can sort them in our desired fashion.
- Queries dont update the given array i.e read only.
- If we know the answer of $[L,R]$ and we can compute the answer of $[L-1,R]$, $[L+1,R]$, $[L,R-1]$, $[L,R+1]$.
The idea of MO’s algorithm is to pre-process all queries so that result of one query can be used in next query.
- By sqrt decomposition we divide the array into blocks of
sqrt(N)size. So, total blocks will beN/sqrt(N) = sqrt(N). There can besqrt(N)+1blocks ifNis not a perfect square. - We store the result(sum or mode) of every block in block array.
- We know that there are approx. $sqrt(N)$ blocks of size $sqrt(N)$.
- we Sort the queries with L values from
0to $sqrt(N)-1$ then $sqrt(N)$ to $2*sqrt(N)$ and so on. - All the queries within a block are sorted with their R values. By this we first sort queries in ascending order of the blocks and then if multiple queries lie in the same block then we sort them according to their R(right) values.
- This scheme of sorting will help us in answering the current query by the use of previous query.
- Process all queries one by one in a way that every query uses the result computed in the previous query.
- Lets say previous query was $[0,6]$ and the current query is $[2,9]$ then we subtract arr[0], arr[1] from the previous result and add arr[7], arr[8], arr[9] to the previous result.
Let’s take the previous example:
Given an array of queries:
Queries$[]$=${$ $[7,8]$, $[1,6]$, $[2,7]$ $}$
We will sort these queries according to the following rule:
- Sort the queries in ascending order of their blocks in terms of their L(left) values and if multiple queries lie in same block then order the queries with respect to their R(right) values:
- block array index of the ith element =
index/total_blocks= i/sqrt(N) - range $[7,8]$ belongs to $7/sqrt(9)$= 2nd block
- range $[1,6]$ belongs to $1/sqrt(9)$= 0th block
- range $[2,7]$ belongs to $2/sqrt(9)$= 0th block
- ranges $[1,6]$ and $[2,7]$ belongs to
0th block so we sort them by their R values. So their sorted order = ${ [1,6], [2,7] }$ - Sorted order: Queries[]= ${$ $[1,6]$, $[2,7]$, $[7,8]$ $}$
- block array index of the ith element =
Queries$[0]$=$[1,6]$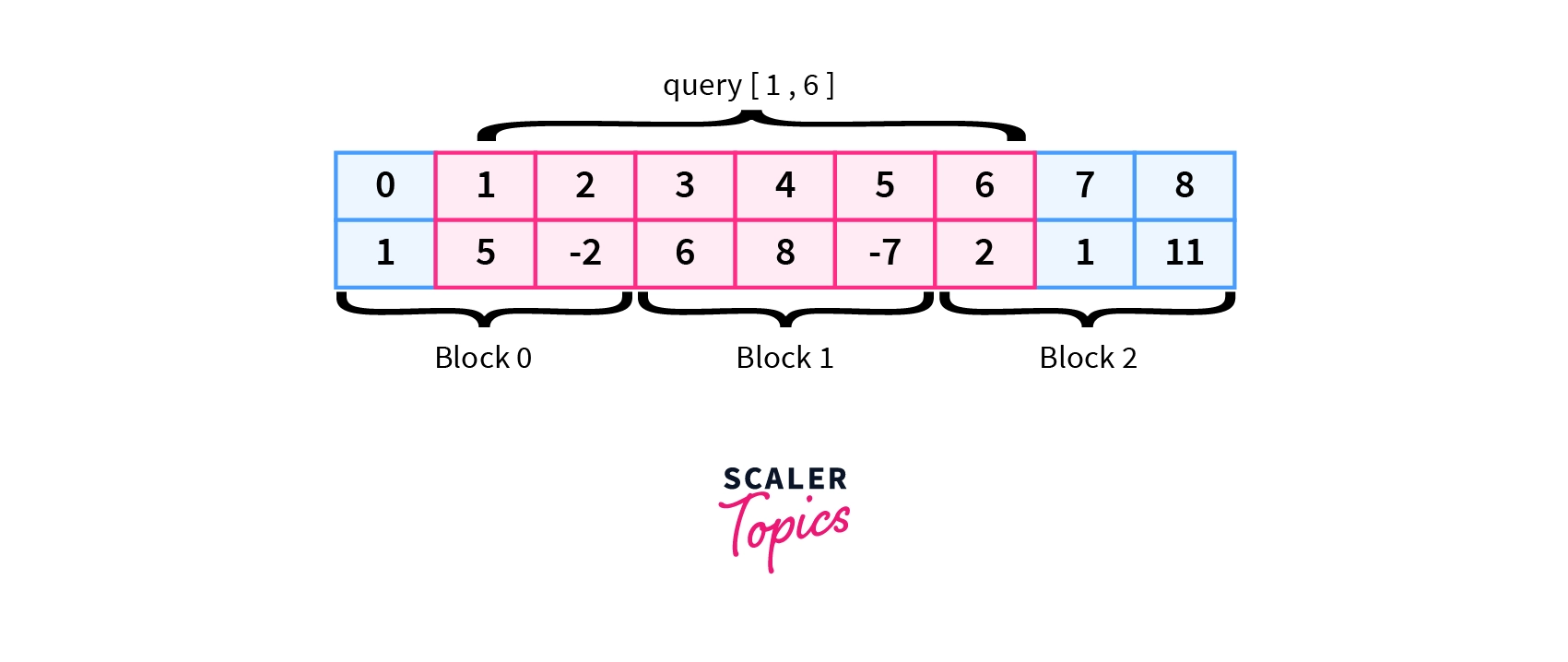
$Sum= arr[1] + arr[2] + block[1] + arr[6]$
$Sum= 3+7+2= 12$
- Queries$[1]$=$[2,7]$
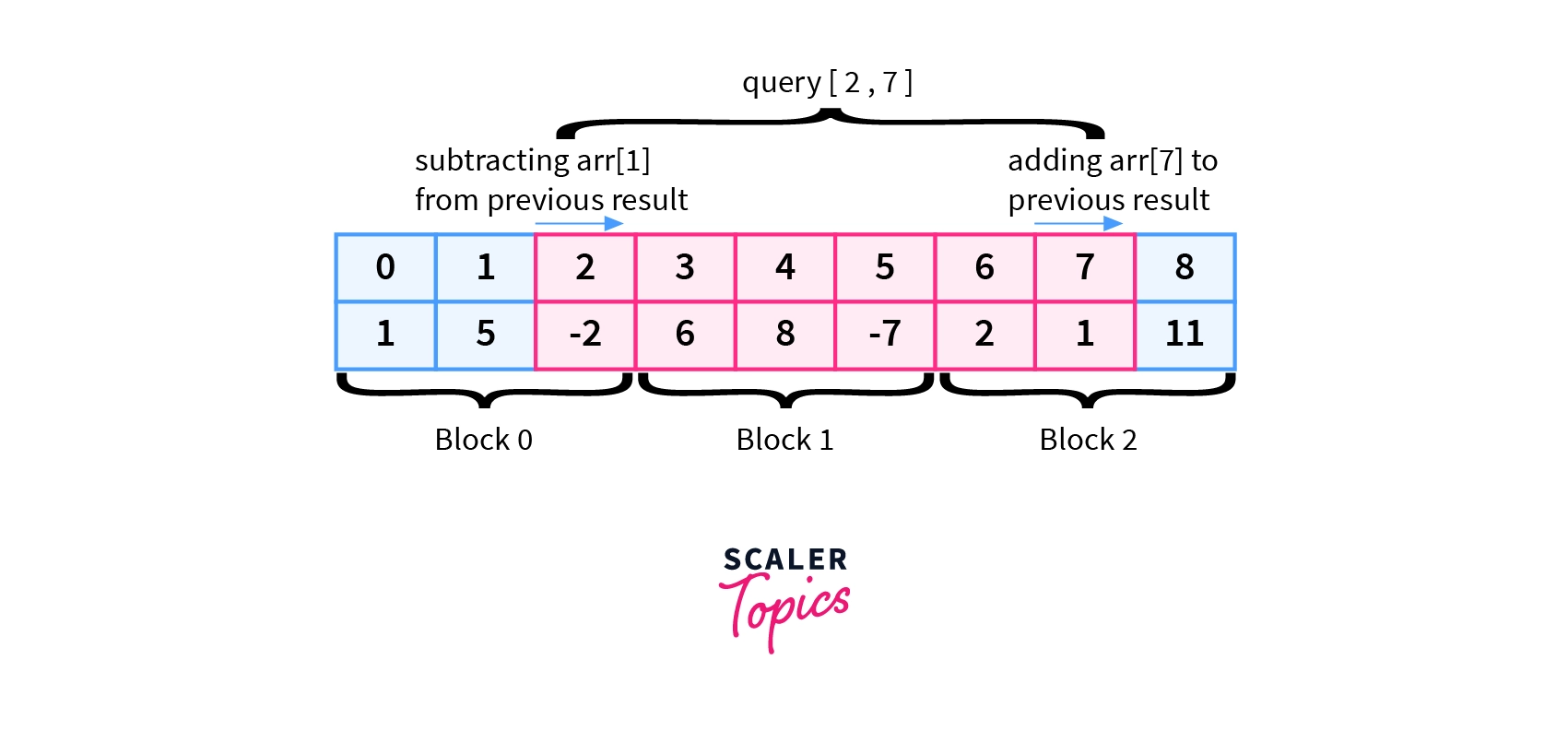
PrevSum= 12 (from query[1,6])
$Sum = PrevSum – arr[1] + arr[7]$
$Sum = 12-5+1= 8$
- Queries$[2]$=$[7,8]$
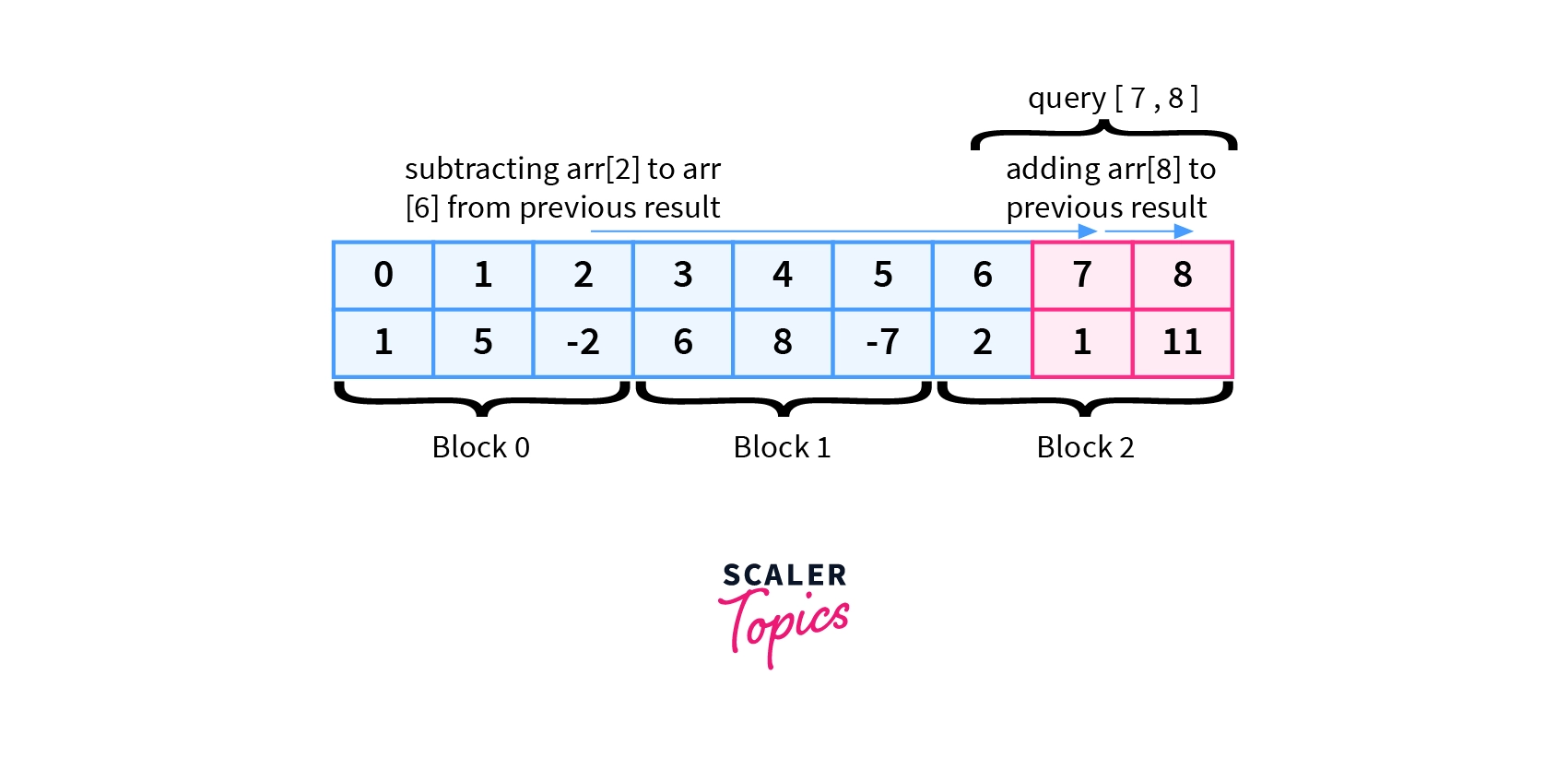
PrevSum= 8 (from query[2,7])
Sum= PrevSum-arr[2]-arr[3]-arr[4]-arr[5]-arr[6]+arr[8]
$Sum= 8-(-2)-6-8-(-7)-2+11$
$Sum= 12$
This way we efficiently used the past result to obtain new query result.
Implementation
Square Root Decompostion
- Firtly, take the array input in
arr[N]with sizeN. - Initialize the block array with size block$[sqrt(N)+1]$.
- Then put sum of subarrays of size
sqrt(N)in block[ ].- block$[i/(sqrt(N)+1)]$ += arr[i]
- Now for each query input $[l,r]$ check if
ithblock is fully inside $[l,r]$.- if it is fully inside then add the sum from the block[ ].
- else add individual elements from arr[ ].
- Ouput the calculated sum.
// C++ implementation of sqrt decomposition algorithm
#include<bits/stdc++.h>
using namespace std;
// put sum of subarrays of size sqrt(n) into block array
void preprocess_blocks(vector<int>&arr, vector<int>& block)
{
int len=block.size();
for(int i=0;i<arr.size();i++)
{
block[i/len]+=arr[i];
}
}
int main()
{
int n;
//input size of array
cin>>n;
vector<int> arr(n);
//input array
for(int i=0;i<n;i++)
cin>>arr[i];
//initialize size of blocks to be sqrt(n)+1
int len= sqrt(n)+1;
vector<int> block( len );
// preprocess blocks with sum
preprocess_blocks(arr, block);
int querySize;
//input total queries
cin>>querySize;
int l,r;
//input all the queries
while(querySize--)
{
//1 indexed
cin>>l>>r;
l--;
r--;
int sum=0;
//traversing l to r efficiently by taking
//already calculated sum from block array
for(int i=l;i<=r;)
{
//if i is the starting index of a block and that block is in
//the range l to r then take precalculated sum
//else take arr[i] to sum
if(i%len==0 && i+len-1<=r)
{
sum+= block[i/len];
i+=len;
}
else
{
sum+=arr[i];
i++;
}
}
//output sum
cout<<sum<<endl;
}
return 0;
}Complexity of sqrt Decomposition
Time Complexity: O(sqrt(N)). For answering a query [L,R] we jump onsqrt(N) blocks instead of every element of array.
Space Complexity: O(sqrt(N)) extra space of block array to store preprocessed result.
MO’s algorithm
- Firtly, take the array input in arr[
N] with sizeN. - Initialize the block size,
block_len = sqrt(N)+1. - Make a structure Query which will hold left value, right value and index of the query.
- Implement a comparator through which sort function will get the sorting technique. For two queries
q1,q2:
if((q1.left)/block_len != (q2.left)/block_len and q1.left/block_len < q2.left/block_len)
return true;
else
return q1.right < q2.right;- Initilize an array of structure of Queries
qand take query input. - Sort the queries with the help the above comparator function.
- Now, for each query maintain two pointers
currLandcurrRwhich will point to range of previously answered query. - Add or subtract the new elements to the currSum by the help
currLandcurrR. - Output the answer of each query in the same order they were asked.
// C++ implementation of MO's algorithm
#include<bits/stdc++.h>
using namespace std;
// block_length
int b_len;
struct Query{
int l,r,idx;
};
// sorting according to blocks and
//if same block then order them according to their r values
bool compare(Query q1, Query q2 )
{
if( (q1.l)/b_len != (q2.l)/b_len )
{
return q1.l/b_len < q2.l/b_len;
}
return q1.r < q2.r;
}
int main()
{
int n;
//input size of array
cin>>n;
vector<int> arr(n);
//input array
for(int i=0;i<n;i++)
cin>>arr[i];
//initialise block size
b_len= sqrt(n)+1;
int querySize;
//input total queries
cin>>querySize;
int l,r,i=0;
Query q[querySize];
//input all the queries
while(i<querySize)
{
//1 indexed
cin>>l>>r;
l--;
r--;
q[i].l=l;
q[i].r=r;
q[i].idx=i;
i++;
}
//sort the queries
sort(q, q+ querySize, compare);
// initialize ans array to store result of the queries asked
vector<int>ans(querySize);
// initialize the curr pointers which will save previous query answer
int currL=0, currR=-1, currAns=0;
for(int i=0;i<querySize;i++)
{
l=q[i].l;
r=q[i].r;
// adding new elements of current range
while(currL>l)
{
currL--;
currAns+=arr[currL];
}
while(currR<r)
{
currR++;
currAns+=arr[currR];
}
//Removing elements of previous range from curr answer
while(currL<l)
{
currAns-=arr[currL];
currL++;
}
while(currR>r)
{
currAns-=arr[currR];
currR--;
}
ans[q[i].idx]=currAns;
}
// output query's answer in the same order they were asked
for(int i=0;i<querySize;i++)
{
cout<<"Sum of "<<q[i].l+1<<" to "<<q[i].r+1<<" -> "<<ans[i]<<"\n";
}
return 0;
}Complexity of MO’s algorithm
Time Complexity: $O((N+Q)*sqrt(N))$.
Sorting all queries will take $O(QlogQ)$.
Block size is $sqrt(N)$, so if we consider queries within the same block then the queries are sorted by right index. Therefore, in worst case we can say that currR is pointing to extreme right in a previous query and the current query wants the currR to shift to extreme left of the given array. This takes O(N) time to shift currR for queries within a single block. So, total time taken for all the blocks will be O(sqrt(N)*N).
And currL (curr left index) can change atmost sqrt(N) times for every new query. So total time taken by all the queries in changing currL is O(sqrt(N)*Q).
Total time complexity : $O((N+Q)*sqrt(N))$.
Space Complexity: O(Q) extra space to store the result of every query in offline mode.
Conclusion
- We learnt
sqaure root decompositionalgorithm to answer a range based query problem efficiently in O(sqrt(N)) time. - Offline queries are the queries which are known beforehand and dont change or update existing array.
- Through
sqrt decompostionwe learntMO's algorithmto answer range based offline queries efficiently by taking previously answered query result into consideration and answering the new query. MO's algorithmtook $O((N+Q)sqrt(N))$ time which is much better than naive approach taking $O(NQ)$ time.- Few of it’s applications are:
- We can use this algorithm to find sum in range query problems in offline mode.
- We can apply this algorithm to find the minimum/maximum element in range query problems.