Problem Statement
We are given an array of integers, and we need to find the next greater element of every array elements. So, we need to find and print the next greater element of every array element.
Note:
- If there is no next greater element present in the array then we need to print -1 as the next greater element of the current element.
- For every last element of the array, the next greater element comes out to be -1.
- If an array is sorted in descending order (non-increasing order) then there is no next greater element, so for every element of such array, -1 is considered as the next greater element.
Refer to the Example and Example Explanation sections for more details and the Approach section to understand how to find the next greater element of each element of an array.
Input & Output
- The first input is the number of elements present in the array i.e. n .
- The second input is the sequential set of elements of the array.
The given input array is: [ 11, 13, 21, 3]
The output is:
The list of the next greater element is:
11 --> 13
13 --> 21
21 --> -1
3 --> -
Since there is no next greater element to 21 and 3, so we printed -1.
Constraints
- 1≤n≤106
- 1≤a[i]≤1018
In some problems, you may find the number of test cases represented by t. So, we only need to call the nextGreaterElement() function t -times.
Example
The given input array is: [ 6, 8, 0, 1, 3 ]
The output is:
The next greater element of the array elements are:
6 --> 8
8 --> -1
0 --> 1
1 --> 3
3 --> -1
Example Explanation
Before getting into the explanation of how to find the next greater element in the array, let us first get a brief introduction about the arrays.
An array is a linear collection of values stored at contiguous memory locations. Array stores homogeneous values(similar data type values).
Example: The array 56, 50, 34, 24, 12 will look like:
In the example above, the input arrays are: [ 6, 8, 0, 1, 3 ].
- The next greater element to 6 is 8.
- There is no next greater element to 8, so we printed -1 (that denotes that the current element has no next greater element).
- 0 has 1 as the next greater element.
- 1 has 3 as the next greater element.
- 3 has no next greater element (also 3 is the last element present in the array), so we printed -1.
Approach 1: Simple Brute-Force Approach
The most basic approach to finding the next greater element of each element of an array can be using nested loops (two loops, one inside the other). The idea is very simple, the outer loop will pick one element at a time. For each selected array element, we will run an inner loop to search for its next greater element. If there is a next greater element to the currently selected element, then we will store the next greater element in the result array for further printing else, we will store -1 at its place in the result array which denotes that there is no next greater element to the currently selected element.
The pseudo-code for the above-discussed algorithm can be:
- Initialize a loop that will iterate over each element of the array.
- Pick one element of the array.
- Initialize an inner loop and find the next greater element for the selected element.
- We can find the next greater element by simply checking all the elements of the array which are present after the current element.
- Store the current answer in the answer array. If there is no next greater element, store -1 as the next greater element of the current element in the answer array.
- Run the above-discussed steps for each element of the array.
Implementation
Let us code the above-discussed algorithm for better understanding.
C++ Code:
#include <bits/stdc++.h>
using namespace std;
/*
A function that will traverse the array and find the next greater element of each element and print the result.
*/
void nextGreaterElement(int a[], int n) {
int nextGreater = -1;
// Selecting each element of the array.
for (int i = 0; i < n; i++) {
nextGreater = -1;
for (int j = i + 1; j < n; j++) {
/*
Simply check all the elements of the array which are present after the current element.
*/
if (a[i] < a[j]) {
nextGreater = a[j];
break;
}
}
// Finally printing the next greater element
cout << a[i] << " --> "
<< nextGreater << endl;
}
}
int main() {
int a[] = {11, 13, 21, 3};
// calling the function that will print the next greater element of array elements.
int n = sizeof(a) / sizeof(a[0]);
cout << "The list of the next greater element is :" << endl;
nextGreaterElement(a, n);
return 0;
}
Java Code:
public class Main{
/*
A function that will traverse the array and find the next greater element of each element and print the result.
*/
static void nextGreaterElement(int a[], int n) {
int nextGreater = -1;
// Selecting each element of the array.
for (int i=0; i<n; i++)
{
nextGreater = -1;
for (int j = i+1; j<n; j++) {
/*
Simply check all the elements of the array which are present after the current element.
*/
if (a[i] < a[j]) {
nextGreater = a[j];
break;
}
}
System.out.println(a[i] + " --> " + nextGreater);
}
}
public static void main(String args[]) {
int a[]= {11, 13, 21, 3};
int n = a.length;
// calling the function that will print the next greater element of array elements.
System.out.println("The list of the next greater element is :");
nextGreaterElement(a, n);
}
}
Python:
"""
A function that will traverse the array and find the next greater element of each element and print the result.
"""
def nextGreaterElement(a):
# Selecting each element of the array.
for i in range(0, len(a), 1):
nextGreater = -1
for j in range(i+1, len(a), 1):
# Simply checking all the elements of the array which are present after the current element.
if a[i] < a[j]:
nextGreater = a[j]
break
# Finally printing the next greater element
print(str(a[i]) + " --> " + str(nextGreater))
if __name__ == "__main__":
a = [11, 13, 21, 3]
# calling the function that will print the next greater element of array elements.
print("The list of the next greater element is :")
nextGreaterElement(a)
Output:
The list of the next greater element is :
11 --> 13
13 --> 21
21 --> -1
3 --> -1
Complexity Analysis
In the brute force or basic approach to find the next greater element of each element of an array, we are using two loops (nested loops).
Time Complexity
Since we are using nested loops, the time complexity comes out to be O(n^2), where n is the number of elements present in the array.
Space Complexity
The space complexity of the above approach is O(1) as we are not using any extra space.
In the above implementation, we are storing the answers in an array but this can be avoided and answers can be printed in the nextGreaterElement() function only. For simplification and easy printing, we have stored the answers in an array.
Approach 2: Efficient Approach Using Stack: Traversing from Left to Right
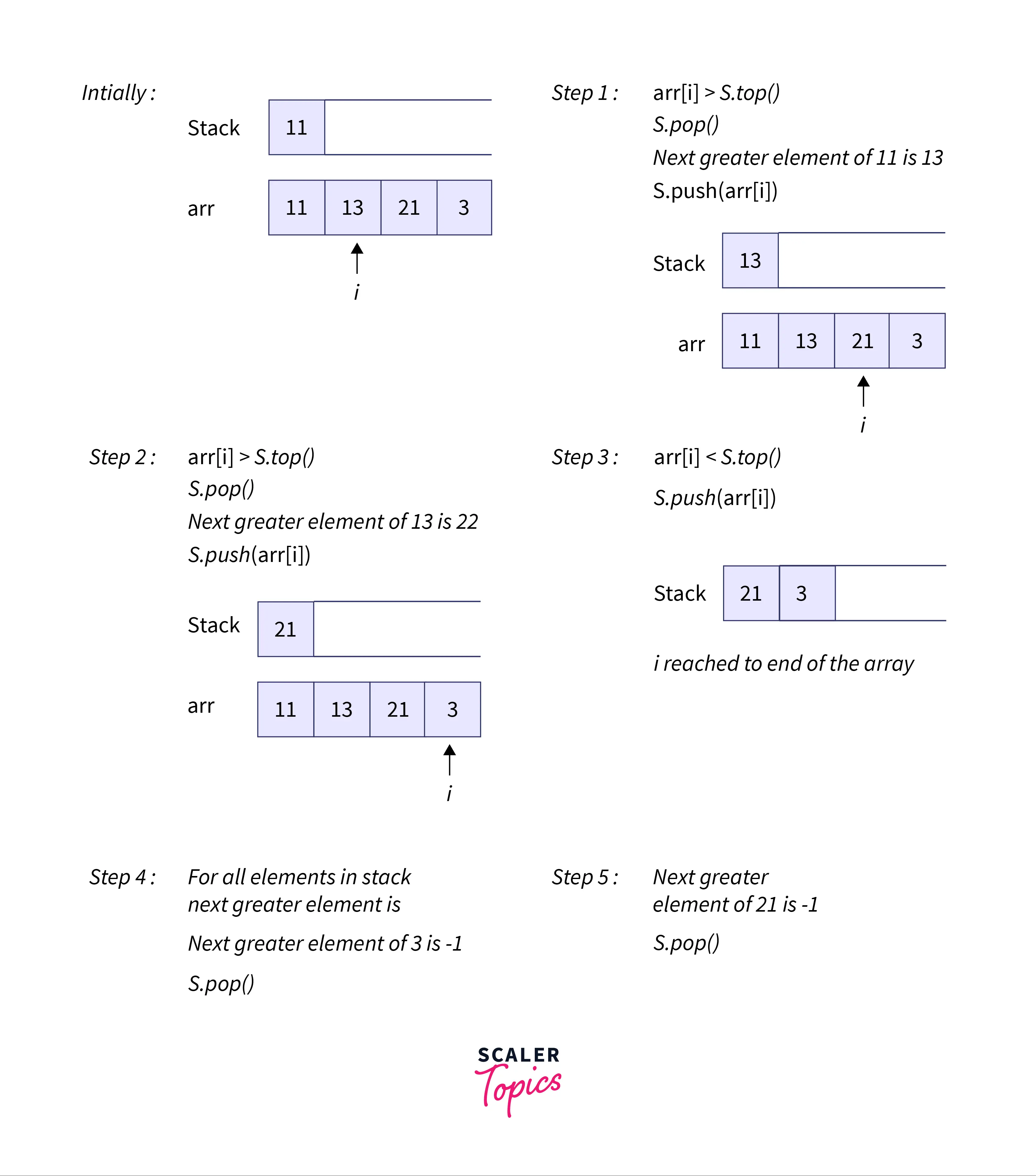
An efficient algorithm for finding the next greater element of each element of an array can be using a stack. The stacks will reduce the O(n^2) complexity to linear time complexity i.e. O(n).
Let us discuss the algorithm using the pseudo-code for better understanding:
- Initialize an empty stack for storing the elements of the array.
- Insert (push) the first element into the stack.
- Run the below-mentioned steps for each element of the array:
- Mark the currently selected element as the next greater element. (i.e. nextGreater variable).
- If the stack is not empty, we need to compare the top element of the stack with the nextGreater element.
- If the nextGreater is greater than the top element of the stack, pop the element from the stack. Now, nextGreater is the next greater element for the popped element.
- We need to keep on popping the elements from the top of the stack until the top element is smaller than the nextGreater. Now, nextGreater becomes the next greater element for all such popped elements.
- At last, push or insert the nextGreater into the stack and after the iteration or traversal is over, pop all the elements from the stack and print -1 as the next greater element for them.
Refer to the dry run shown below for a better understanding.
Implementation
Let us code the above-discussed algorithm for better understanding.
C++ Code:
#include <bits/stdc++.h>
using namespace std;
/*
A function that will traverse the array and find the next greater element of each element using stack. It will also print the result.
*/
void nextGreaterElement(int a[], int n) {
stack<int> s;
// Insert (push) the first element into the stack.
s.push(a[0]);
for (int i = 1; i < n; i++) {
// If the stack is empty, push the current element.
if (s.empty()) {
s.push(a[i]);
continue;
}
/*
We need to keep on popping the elements from the top of the stack until the top element is smaller than the current element.
*/
while (s.empty() == false && s.top() < a[i]) {
cout << s.top()
<< " --> " << a[i] << endl;
s.pop();
}
// push or insert the nextGreater i.e. current element into the stack and after the iteration.
s.push(a[i]);
}
/*
pop all the elements from the stack and print -1 as the next greater element for them.
*/
while (s.empty() == false) {
cout << s.top() << " --> " << -1 << endl;
s.pop();
}
}
int main()
{
int a[] = {11, 13, 21, 3};
// calling the function that will print the next greater element of array elements.
int n = sizeof(a) / sizeof(a[0]);
cout << "The list of the next greater element is :" << endl;
nextGreaterElement(a, n);
return 0;
}
Java Code:
import java.util.*;
public class Main{
/*
A function that will traverse the array and find the next greater element of each element using stack. It will also print the result.
*/
static void nextGreaterElement(int a[], int n) {
Stack<Integer> s = new Stack<>();
for (int i = 0; i < a.length; i++) {
// If the stack is empty, push the current element.
if (s.isEmpty()) {
s.push(a[i]);
continue;
}
/*
We need to keep on popping the elements from the top of the stack until the top element is smaller than the current element.
*/
while (!s.isEmpty() && s.peek() < a[i]) {
System.out.println(s.pop() + " --> "
+ a[i]);
}
// push or insert the nextGreater i.e. current element into the stack and after the iteration.
s.push(a[i]);
}
/*
pop all the elements from the stack and print -1 as the next greater element for them.
*/
while (!s.isEmpty()) {
System.out.println(s.pop() + " --> "
+ "-1");
}
}
public static void main(String args[]) {
int a[] = { 11, 13, 21, 3 };
int n = a.length;
// calling the function that will print the next greater element of array elements
System.out.println("The list of the next greater element is :");
nextGreaterElement(a, n);
}
}
Python:
from collections import deque
"""
A function that will traverse the array and find the next greater element of each element using stack. It will also print the result.
"""
def nextGreaterElement(a):
# initializing an empty stack
s = deque()
for i in range(len(a)):
# If the stack is empty, push the current element.
if len(s) == 0:
s.append(a[i])
continue
while s and s[-1] < a[i]:
print(str(s[-1]), "-->", str(a[i]))
s.pop()
# push or insert the nextGreater i.e. current element into the stack and after the iteration.
s.append(a[i])
"""
pop all the elements from the stack and print -1 as the next greater element for them.
"""
while len(s) > 0:
print(str(s[-1]), "--> -1")
s.pop()
if __name__ == "__main__":
a = [11, 13, 21, 3]
# calling the function that will print the next greater element of array elements.
print("The list of the next greater element is :")
nextGreaterElement(a)
Output:
The list of the next greater element is :
11 --> 13
13 --> 21
3 --> -1
21 --> -1
Complexity Analysis
In the above approach, we have traversed the elements of the array only once from left to right.
Time Complexity
The time complexity of the above approach comes out to be O(n), where n is the number of elements in the array.
Space Complexity
Since we are using a stack for checking the elements, the space complexity of the above approach comes out to be O(n), where n is the size of the array (or the number of the elements present in the array).
How to Get elements in the Same Order as Input?
If we use the above algorithm and implementation, the output may not come in the same order as the input in some cases. So, to the output in the same order as the input, we can run the above-discussed algorithm by traversing the array from right to left i.e. in reverse order.
Approach 3: Efficient Approach Using Stack: Traversing from Right to Left
Another efficient approach for finding the next greater element can be using the stack data structure but traversing the array from the right to left fashion. This simple reversal of traversal helps us to change the array in place.
The idea is the same as the previously discussed algorithm, we will push the element of the array into the stack until we do not find the greatest element in the right of the array.
If all the elements of the array are processed but there are still some elements present in the array then we can surely say that the left-out elements of the stack do not have any next greater element to them. So, we simply pop them out and print -1 at their respective places.
The pseudo-code for the above-discussed algorithm is similar to what we have discussed in the previous section.
Implementation
Let us code the above-discussed algorithm for better understanding.
C++ Code:
#include <bits/stdc++.h>
using namespace std;
/*
A function that will traverse the array and find the next greater element of each element using stack. It will also print the result.
*/
void nextGreaterElement(int a[], int n)
{
// We can use an answer vector or array for storing the results.
vector<int> answer(n, -1);
stack<int> s;
// Iterating the array from right to left for further processing.
for (int i = n - 1; i >= 0; i--) {
/*
Iterate over the array of elements till we find the greater element on the top of the stack or until the stack becomes empty.
*/
while (!s.empty()) {
if (s.top() <= a[i])
s.pop();
/*
Now, the next greater element must be present at the top of the stack, so add it to the answer array at the proper place.
*/
else {
answer[i] = s.top();
break;
}
}
// push current element into the stack
s.push(a[i]);
}
// finally printing the results stored in answer.
for (int i = 0; i < n; i++)
cout << a[i] << " --> " << answer[i] << endl;
}
int main()
{
int a[] = {11, 13, 21, 3};
// calling the function that will print the next greater element of any elements.
int n = sizeof(a) / sizeof(a[0]);
cout << "The list of the next greater element is :" << endl;
nextGreaterElement(a, n);
return 0;
}
Java Code:
import java.util.*;
public class Main{
/*
A function that will traverse the array and find the next greater element of each element using stack. It will also print the result.
*/
static void nextGreaterElement(int a[], int n) {
// We can use an answer array (or vector) for storing the results.
int[] answer = new int[n];
Arrays.fill(answer, -1);
Stack<Integer> s = new Stack<>();
// Iterating the array from right to left for further processing.
for (int i = n - 1; i >= 0; i--)
{
/*
Iterate over the array of elements till we find the greater element on the top of the stack or until the stack becomes empty.
*/
while (!s.empty()) {
if (s.peek() <= a[i])
s.pop();
/*
Now, the next greater element must be present at the top of the stack, so add it to the answer array at the proper place.
*/
else {
answer[i] = s.peek();
break;
}
}
// push current element into the stack.
s.push(a[i]);
}
// finally printing the results stored in answer.
for(int i=0; i<n; i++)
System.out.println(a[i] + " --> " + answer[i]);
}
public static void main(String args[]) {
int a[] = { 11, 13, 21, 3 };
int n = a.length;
// calling the function that will print the next greater element of array elements
System.out.println("The list of the next greater element is :");
nextGreaterElement(a, n);
}
}
Python:
from collections import deque
"""
A function that will traverse the array and find the next greater element of each element using stack. It will also print the result.
"""
def nextGreaterElement(a, n):
# We can use an answer list (or array) for storing the results.
answer = [-1] * n
# initializing an empty stack
s = deque()
# Iterating the array from right to left for further processing.
for i in reversed(range(n)):
"""
Iterate over the array of elements till we find the greater element on the top of the stack or until the stack becomes empty.
"""
while s:
if s[-1] <= a[i]:
s.pop()
# Now, the next greater element must be present at the top of the stack, so add it to the answer array at the proper place.
else:
answer[i] = s[-1]
break
# push the current element into the stack.
s.append(a[i])
# finally printing the results stored in answer.
for i in range(n):
print(a[i], " --> ", answer[i])
if __name__ == "__main__":
a = [11, 13, 21, 3]
# calling the function that will print the next greater element of array elements.
print("The list of the next greater element is :")
nextGreaterElement(a, len(a))
Output:
The list of the next greater element is :
11 --> 13
13 --> 21
21 --> -1
3 --> -1
Complexity Analysis
In the above approach, we have traversed the elements of the array only once from right to left.
Time Complexity
The time complexity of the above approach comes out to be O(n), where n is the number of elements in the array.
Space Complexity
Since we are using a stack for checking the elements, the space complexity of the above approach comes out to be O(n), where n is the size of the array (or the number of elements present in the array).
How to Get Elements in the Same Order as Input?
Since we are traversing the array in reverse order i.e. from the right to left fashion, the order of the elements is the same as the order of input.
Special Case: When the Array is Circular, What will Be the Next Greater Element?
During the search for the next greater element in a circular array, we need to consider the elements of the array that are present on the left of the current array element as well.
For making the above-discussed algorithm work for circular arrays, we need to insert the elements of the array a at the end of a thus making the size double its original size. For searching, we can simply run a loop 2 * n times, where n is the size of the input array a.
Conclusion
- An array is a linear collection of values stored at contiguous memory locations. Array stores homogeneous values(similar data type values).
- The most basic approach to finding the next greater element of each element of an array can be using nested loops. The outer loop will pick one element at a time and we will run an inner loop to search for its next greater element.
- In the brute force or basic approach to find the next greater element, the time complexity comes out to be O(n2), where n is the number of elements present in the array. The space complexity is O(1) as we are not using any extra space.
- An efficient algorithm for finding the next greater element of each element of an array can be using a stack. The stacks will reduce the O(n2) complexity to linear time complexity i.e. O(n).
- So, the time complexity comes out to be O(n), where n is the number of elements in the array. Since we are using a stack for checking the elements, the space complexity comes out to be O(n), where n is the size of the array (or the number of the element present in the array).
- If we use a stack and traverse the stack from left to right, the output may not come in the same order as the input in some cases. So, to the output in the same order as the input, we should traverse the array from right to left i.e. in reverse order.
- During the searching for the next greater element in a circular array, we need to consider the elements of the array that are present on the left of the current array element as well.